Numerical Simulation of Wind Characteristics in Complex Mountains with Focus on Terrain Boundary Transition Curve
Abstract
:1. Introduction
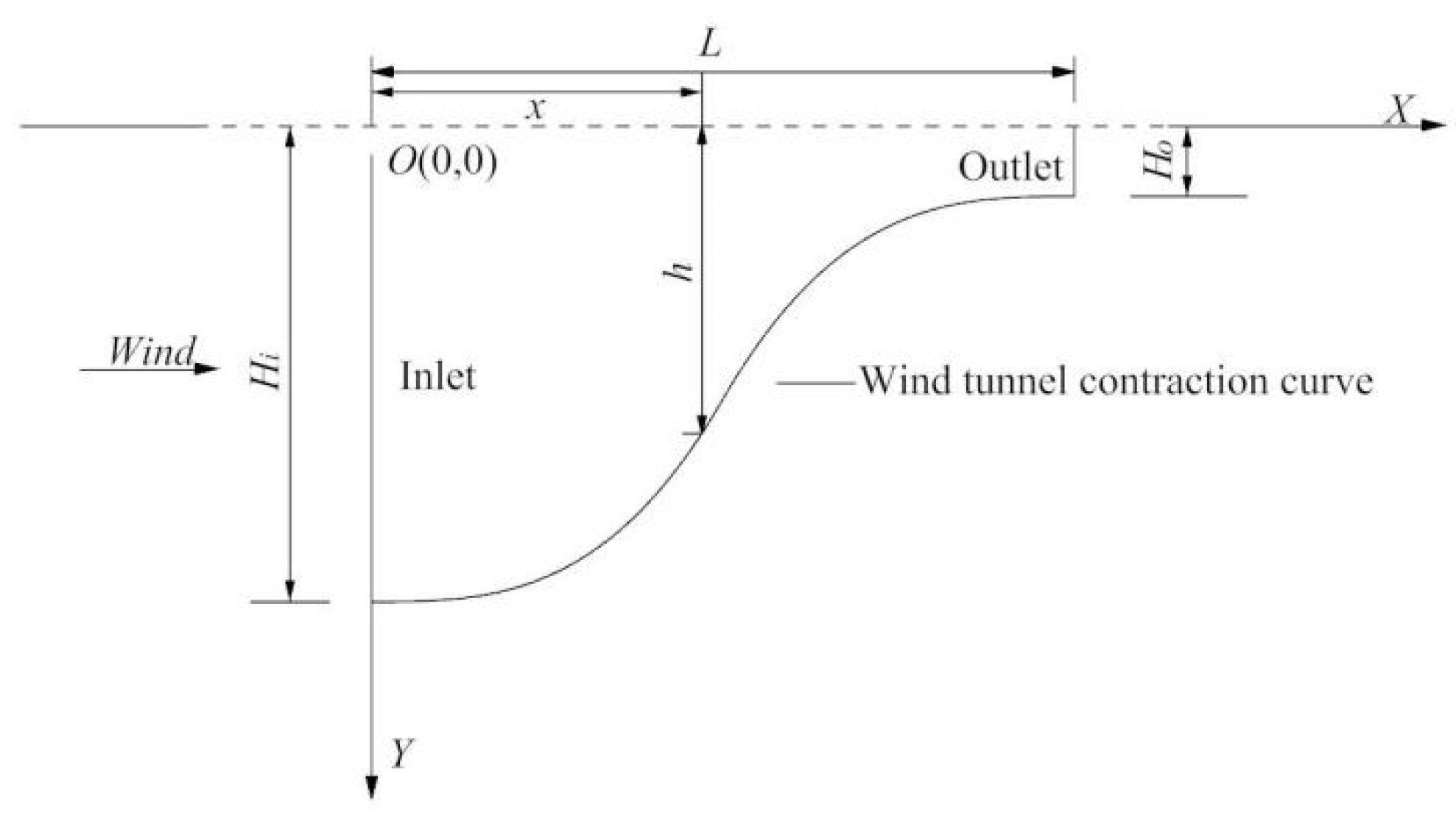
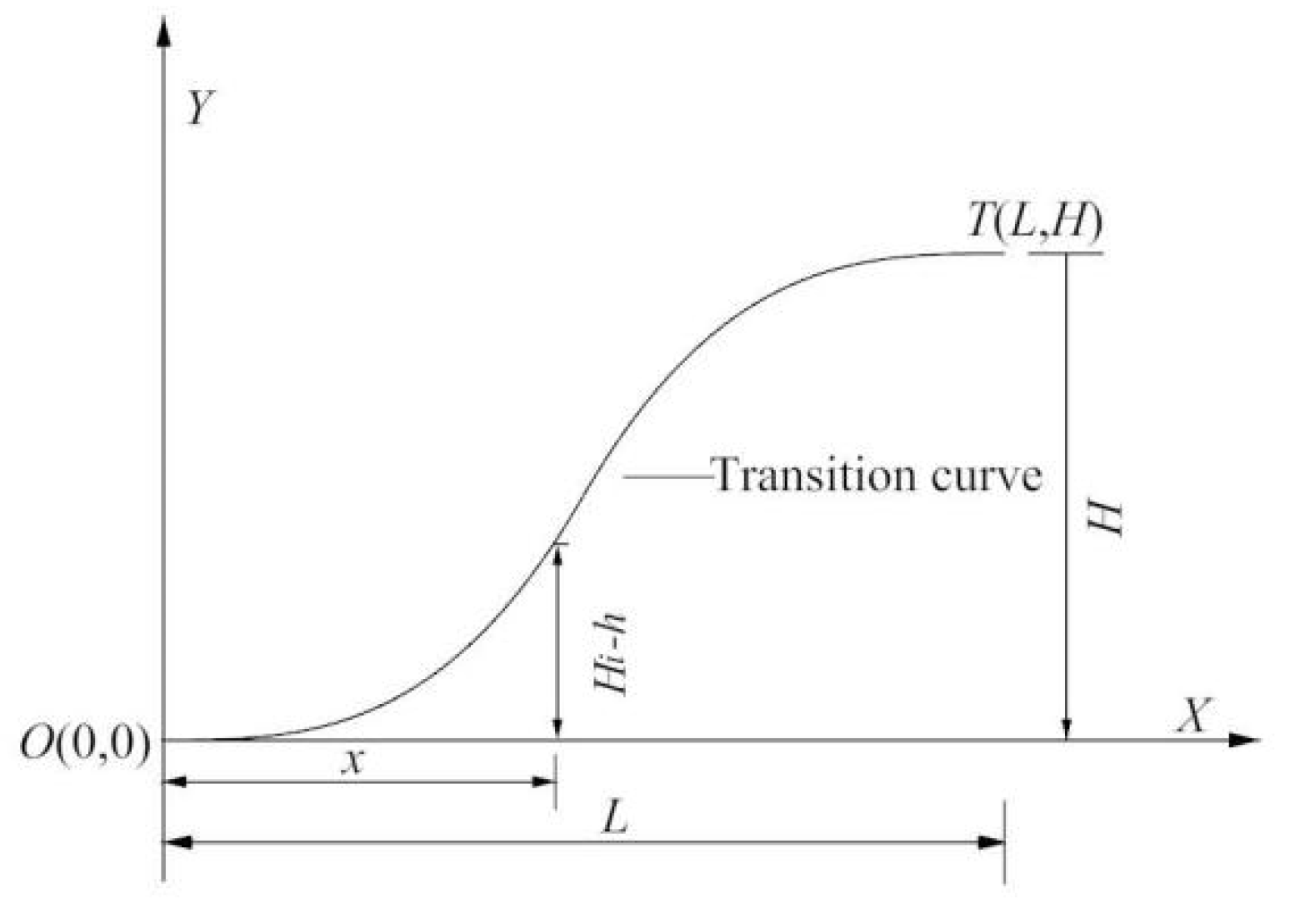
2. Wind Tunnel Contraction Transition Curve
3. Numerical Calculation
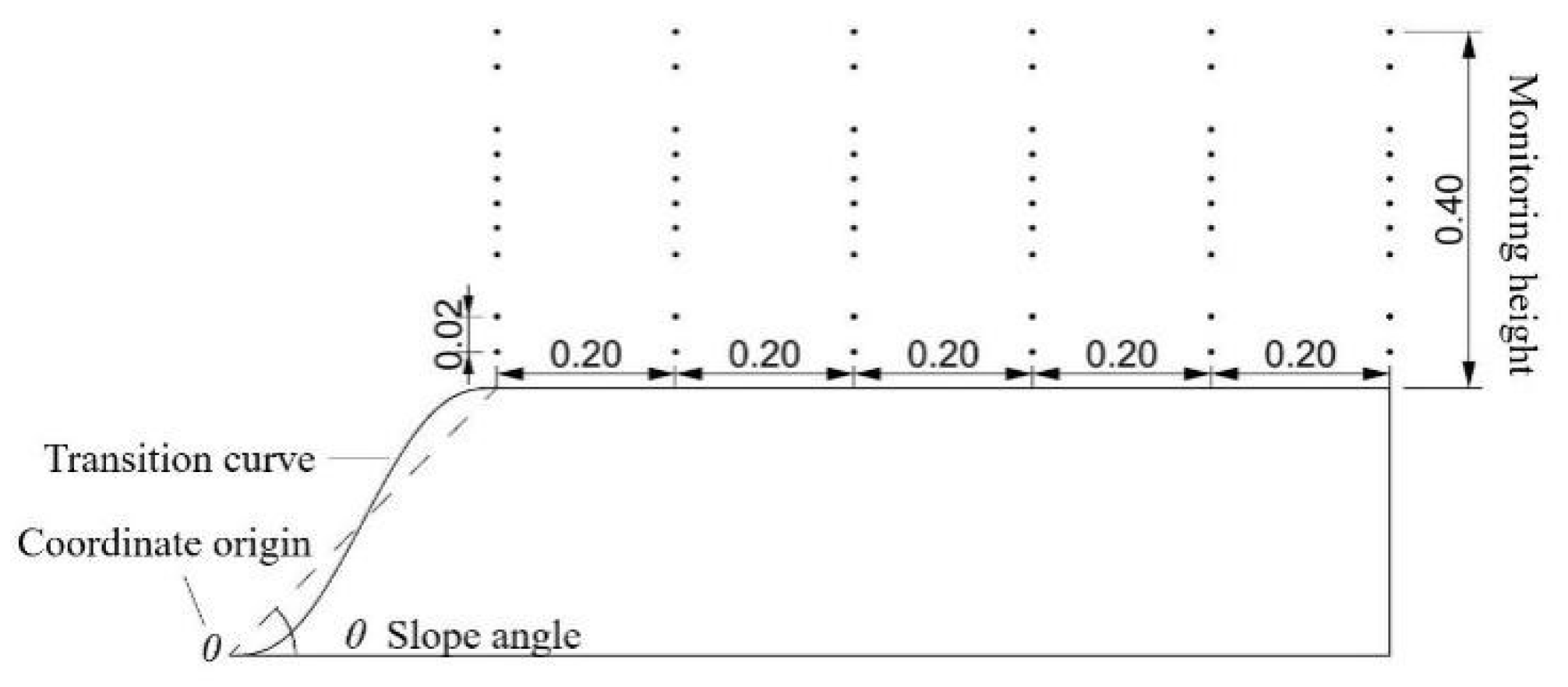
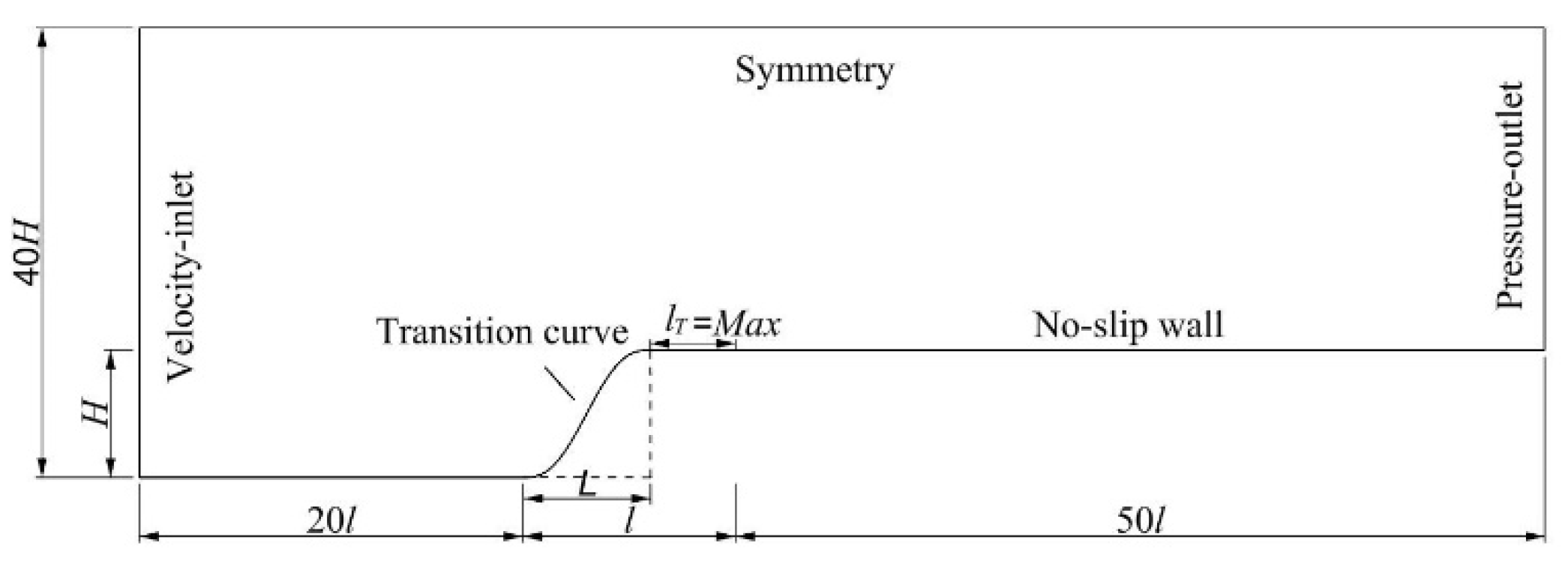
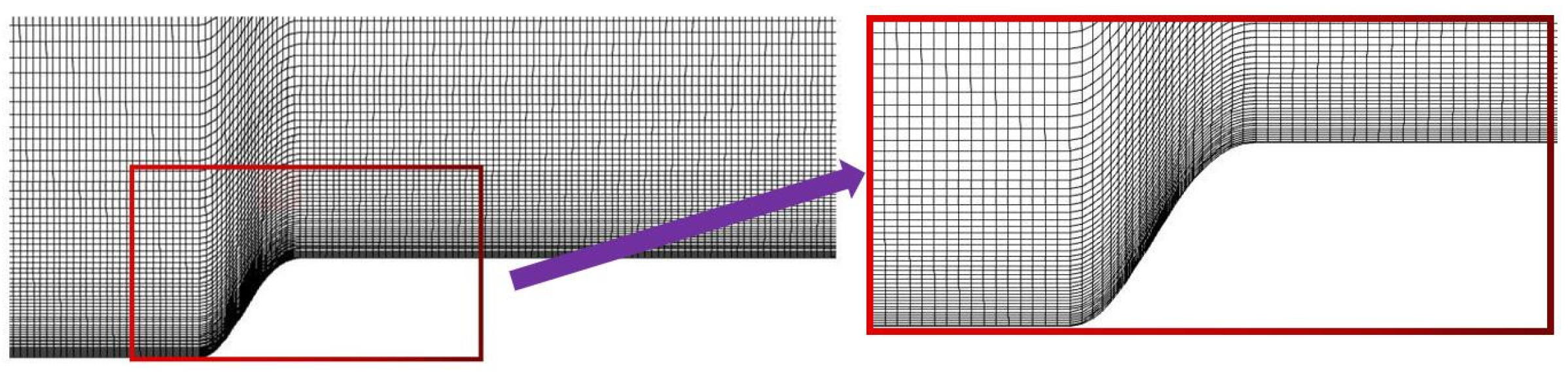
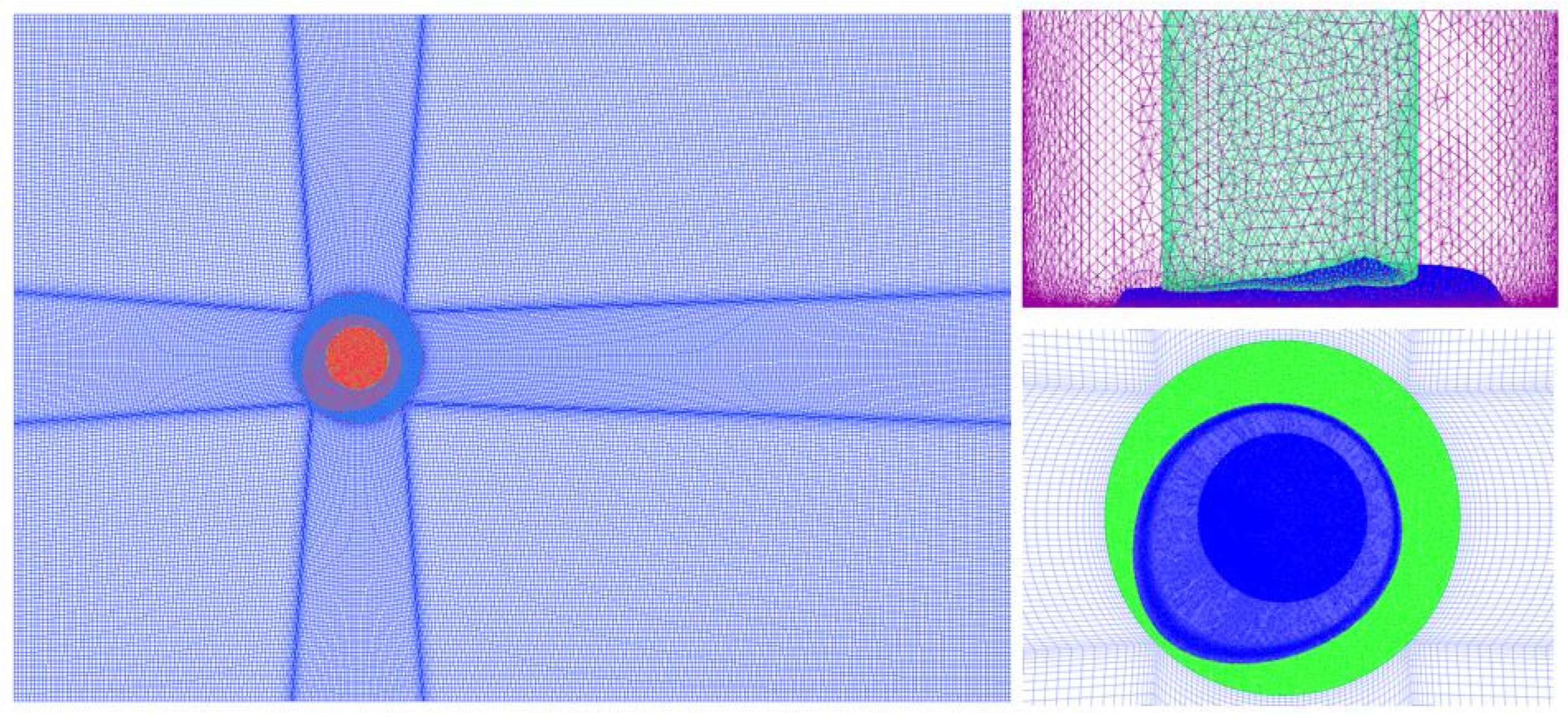
3.1. Parameter Setting and Meshing
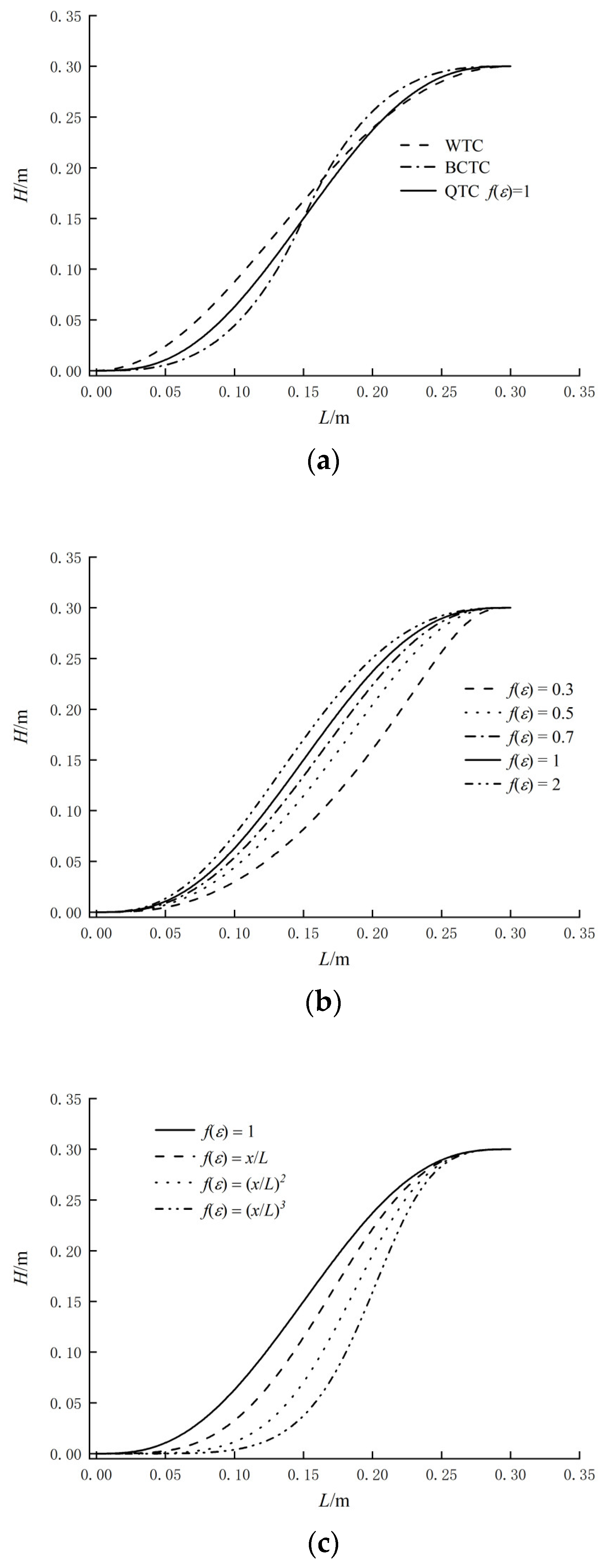
3.2. Transition Performance of Different Transition Curves
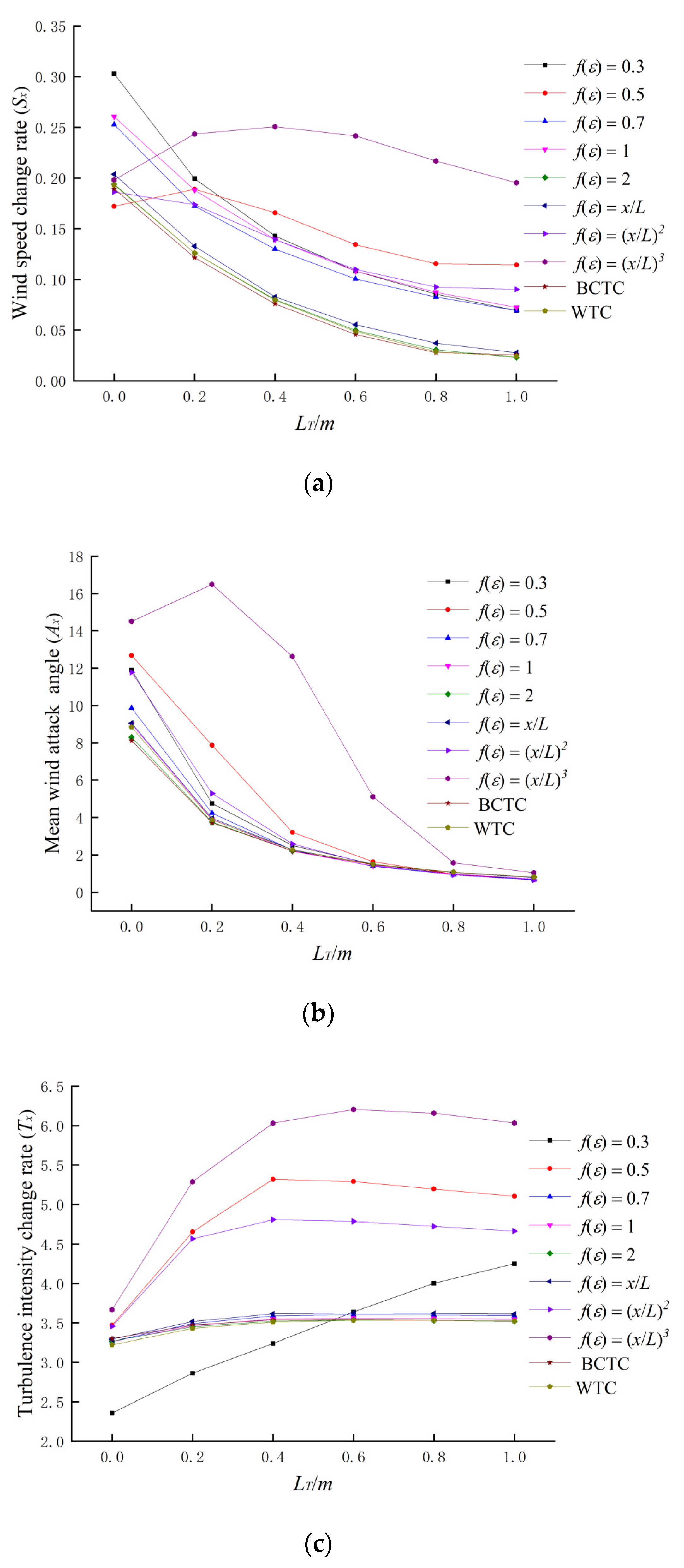
3.3. Evaluation of the Terrain Transition Curve
3.4. Selection of Transition Curve
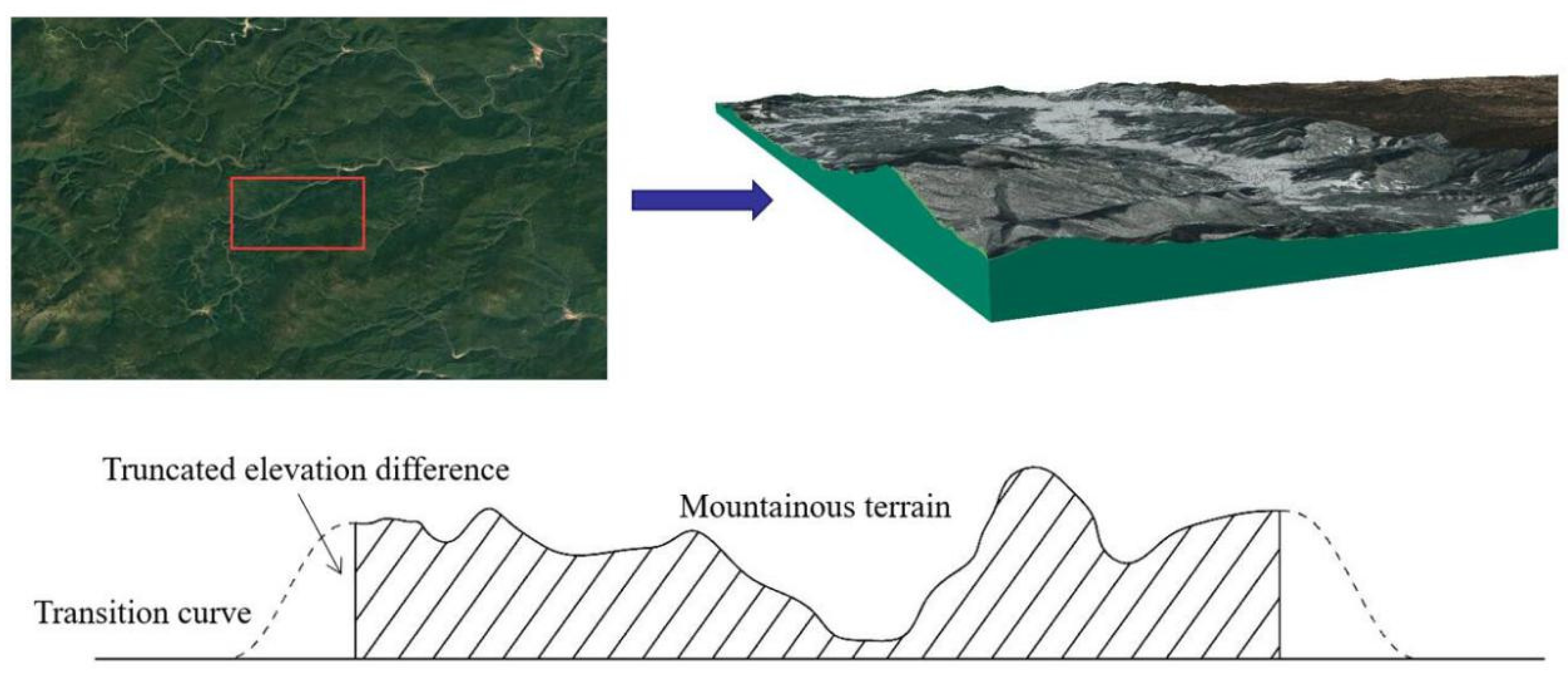
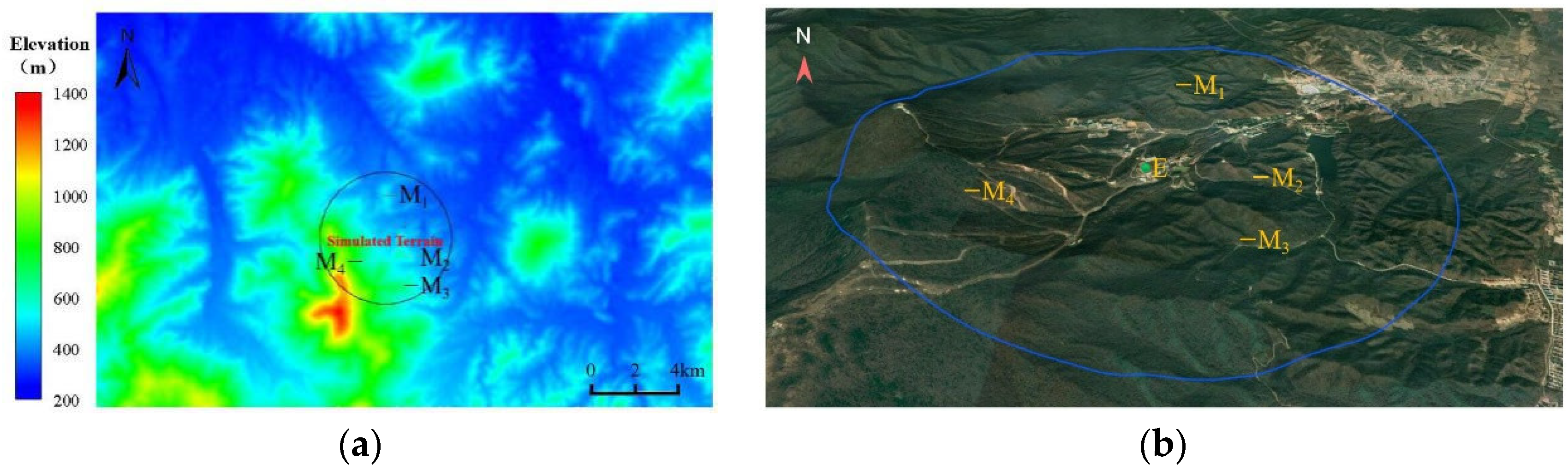
4. Yabuli Ski Resort Wind Field Simulation
4.1. Terrain Model and Mesh
4.2. Parameter Setting and Calculation
4.3. Simulation Results and Analysis
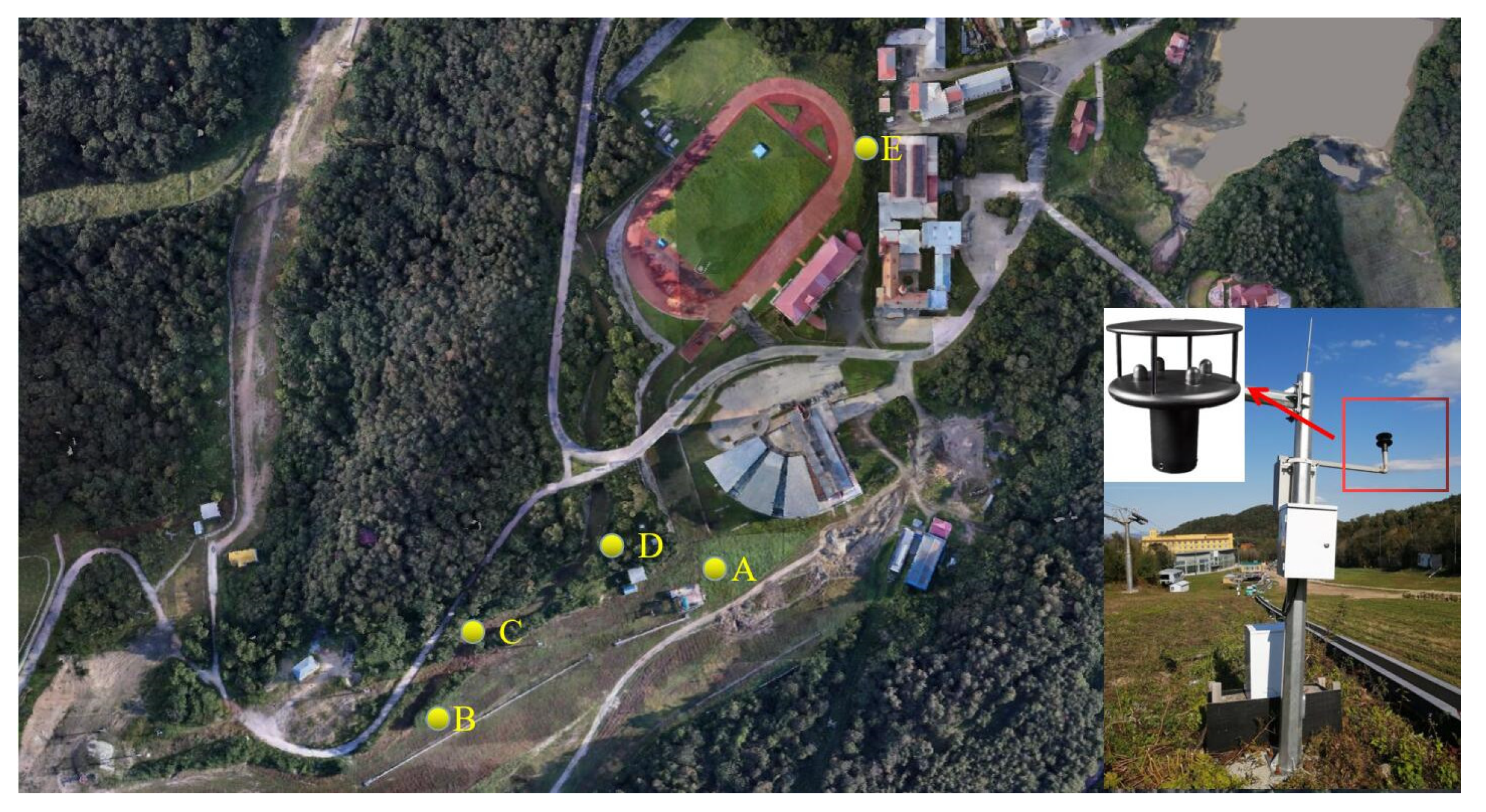
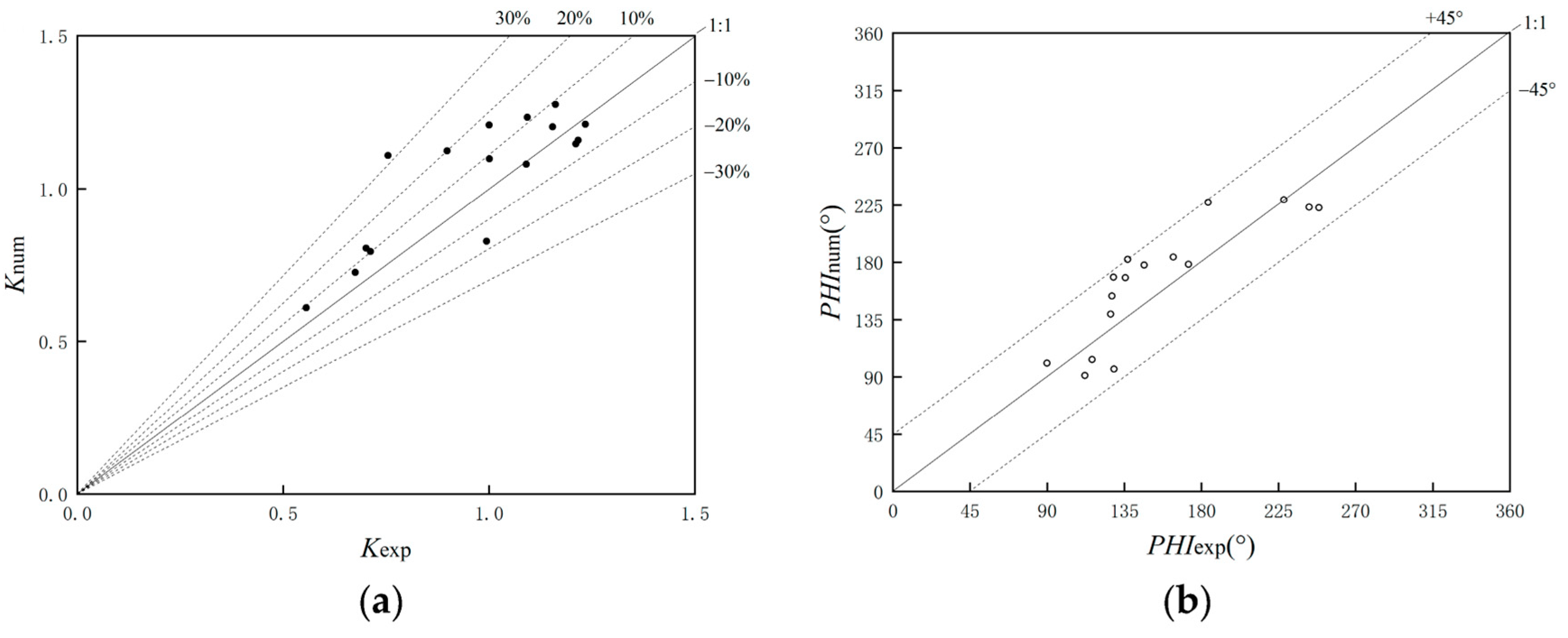
4.3.1. CFD Numerical Simulation Validation
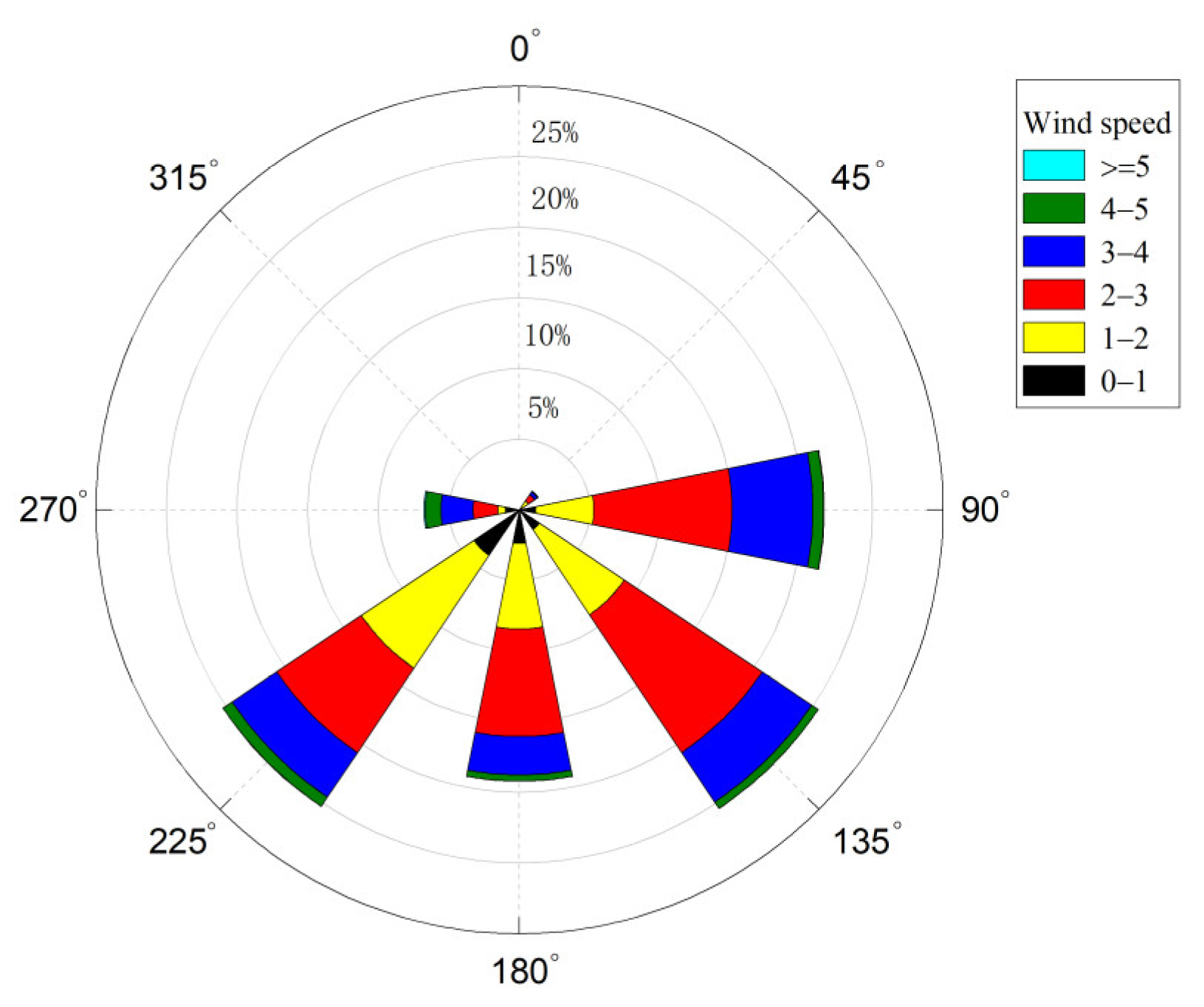
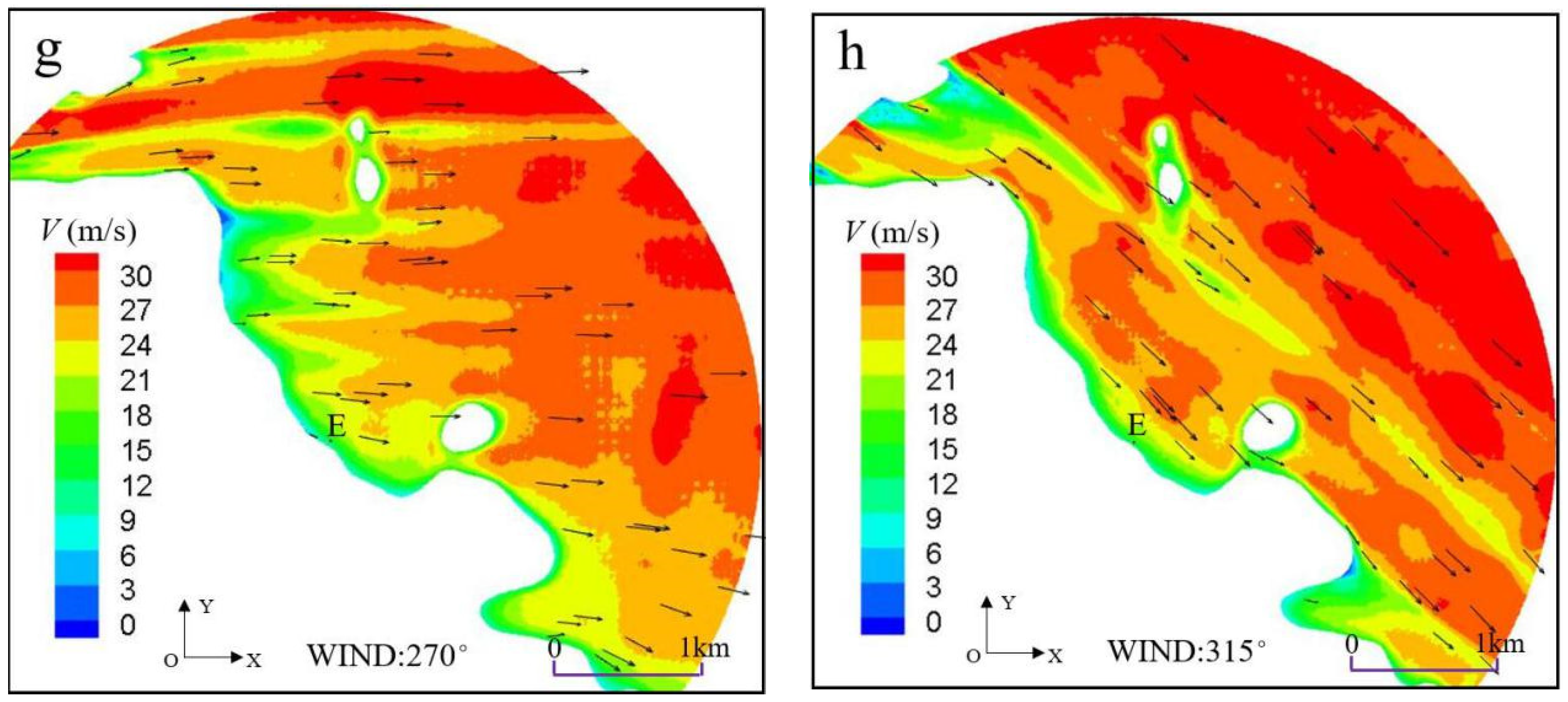
4.3.2. Ski Resort Area Wind Environment
5. Conclusions
- The transition curve proposed in this paper has the best performance compared with the existing transition curves. The mean wind speed variation rate, mean wind attack angle, and turbulence intensity variation rate of the QTC transition curve with f (ε) = 2 are relatively small. The comprehensive evaluation index value (CI) is smaller than that of the other transition curves, which indicates that the impact on the wind characteristics of the incoming wind is the smallest, and the transition performance is the highest.
- The proposed terrain transition curve has good applicability in mountainous terrain modeling. The proposed terrain transition curve is applied to complex mountainous terrain modeling and CFD numerical simulations. Comparison of the wind speed ratio associated with numerical simulations and field measurements, and the error is basically within 20%, indicating a reasonable agreement.
- The terrain transition section is applied to model complex mountainous areas, which can make the incoming wind smoothly transition to the terrain area and reduce the impact of “artificial cliffs” on the numerical simulation results. This method can be applied to CFD numerical simulations to effectively reflect the wind environment characteristics of the ski resort area, which has good applicability to practical engineering and provide a reference for the wind resistance design with complex terrain.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, G.; Jiang, Y.; Peng, L.; Solari, G.; Liao, H.; Li, M. Characteristics of intense winds in mountain area based on field measurement: Focusing on thunderstorm winds. J. Wind Eng. Ind. Aerodyn. 2019, 190, 166–182. [Google Scholar] [CrossRef]
- Jing, H.; Liao, H.; Ma, C.; Tao, Q.; Jiang, J. Field measurement study of wind characteristics at different measuring positions in a mountainous valley. Exp. Therm. Fluid Sci. 2020, 112, 109991. [Google Scholar] [CrossRef]
- Song, J.L.; Li, J.W.; Flay, R.G.J. Field measurements and wind tunnel investigation of wind characteristics at a bridge site in a Y-shaped valley. J. Wind Eng. Ind. Aerodyn. 2020, 202, 104199. [Google Scholar] [CrossRef]
- Ren, W.; Pei, C.; Ma, C.; Li, Z.; Wang, Q.; Chen, F. Field measurement study of wind characteristics at different measuring positions along a bridge in a mountain valley. J. Wind Eng. Ind. Aerodyn. 2021, 216, 104705. [Google Scholar] [CrossRef]
- Jiang, F.; Zhang, M.; Li, Y.; Zhang, J.; Qin, J.; Wu, L. Field measurement study of wind characteristics in mountain terrain: Focusing on sudden intense winds. J. Wind Eng. Ind. Aerodyn. 2021, 218, 104781. [Google Scholar] [CrossRef]
- Hui, M.C.H.; Larsen, A.; Xiang, H.F. Wind turbulence characteristics study at the Stonecutters Bridge site: Part I-Mean wind and turbulence intensities. J. Wind Eng. Ind. Aerodyn. 2009, 97, 22–36. [Google Scholar] [CrossRef]
- Huang, G.; Peng, L.; Liao, H.; Li, M. Field measurement study on wind characteristics at Puli great bridge site in mountainous area. Xinan Jiaotong Daxue Xuebao/J. Southwest Jiaotong Univ. 2016, 51, 349–356. [Google Scholar] [CrossRef]
- Tamura, Y.; Suda, K.; Sasaki, A.; Iwatani, Y.; Fujii, K.; Ishibashi, R.; Hibi, K. Simultaneous measurements of wind speed profiles at two sites using Doppler sodars. J. Wind Eng. Ind. Aerodyn. 2001, 89, 325–335. [Google Scholar] [CrossRef]
- Mattuella, J.M.L.; Loredo-Souza, A.M.; Oliveira, M.G.K.; Petry, A.P. Wind tunnel experimental analysis of a complex terrain micrositing. Renew. Sustain. Energy Rev. 2016, 54, 110–119. [Google Scholar] [CrossRef]
- Hu, P.; Li, Y.; Xu, G.J.; Han, Y.; Cai, C.S.; Xue, F. Investigation of the longitudinal wind power spectra at the gorge terrain. Adv. Struct. Eng. 2017, 20, 1768–1783. [Google Scholar] [CrossRef]
- Lystad, T.M.; Fenerci, A.; Øiseth, O. Evaluation of mast measurements and wind tunnel terrain models to describe spatially variable wind field characteristics for long-span bridge design. J. Wind Eng. Ind. Aerodyn. 2018, 179, 558–573. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J.; Li, Y.; Yu, J.; Zhang, J.; Wu, L. Wind characteristics in the high-altitude difference at bridge site by wind tunnel tests. Wind Struct. An Int. J. 2020, 30, 547–558. [Google Scholar] [CrossRef]
- Chen, F.; Peng, H.; Chan, P.W.; Zeng, X. Wind tunnel testing of the effect of terrain on the wind characteristics of airport glide paths. J. Wind Eng. Ind. Aerodyn. 2020, 203, 104253. [Google Scholar] [CrossRef]
- Hu, P.; Li, Y.; Huang, G.; Kang, R.; Liao, H. The appropriate shape of the boundary transition section for a mountain-gorge terrain model in a wind tunnel test. Wind Struct. An Int. J. 2015, 20, 15–36. [Google Scholar] [CrossRef]
- Li, Y.L.; Xu, X.Y.; Zhang, M.J.; Xu, Y.L. Wind tunnel test and numerical simulation of wind characteristics at a bridge site in mountainous terrain. Adv. Struct. Eng. 2017, 20, 1223–1231. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, J.W.; Zhou, M.; Gao, L. Experimental research on the spatial distribution characteristics of wind field in valley terrain. Zhendong yu Chongji/J. Vib. Shock 2016, 35, 35–40. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Ishihara, T.; Fujino, Y. Experimental study of the wind flow in a coastal region of Japan. J. Wind Eng. Ind. Aerodyn. 2003, 91, 247–264. [Google Scholar] [CrossRef]
- Yan, B.W.; Li, Q.S. Coupled on-site measurement/CFD based approach for high-resolution wind resource assessment over complex terrains. Energy Convers. Manag. 2016, 117, 351–366. [Google Scholar] [CrossRef]
- Tang, X.Y.; Zhao, S.; Fan, B.; Peinke, J.; Stoevesandt, B. Micro-scale wind resource assessment in complex terrain based on CFD coupled measurement from multiple masts. Appl. Energy 2019, 238, 806–815. [Google Scholar] [CrossRef]
- Uchida, T.; Sugitani, K. Numerical and Experimental Study of Topographic Speed-Up Effects in Complex Terrain. ENERGIES 2020, 13, 3896. [Google Scholar] [CrossRef]
- Tang, H.; Li, Y.; Shum, K.M.; Xu, X.; Tao, Q. Non-uniform wind characteristics in mountainous areas and effects on flutter performance of a long-span suspension bridge. J. Wind Eng. Ind. Aerodyn. 2020, 201, 104177. [Google Scholar] [CrossRef]
- Cheynet, E.; Liu, S.; Ong, M.C.; Bogunović Jakobsen, J.; Snæbjörnsson, J.; Gatin, I. The influence of terrain on the mean wind flow characteristics in a fjord. J. Wind Eng. Ind. Aerodyn. 2020, 205, 104331. [Google Scholar] [CrossRef]
- Blocken, B.; van der Hout, A.; Dekker, J.; Weiler, O. CFD simulation of wind flow over natural complex terrain: Case study with validation by field measurements for Ria de Ferrol, Galicia, Spain. J. Wind Eng. Ind. Aerodyn. 2015, 147, 43–57. [Google Scholar] [CrossRef]
- Ren, H.; Laima, S.; Chen, W.-L.; Zhang, B.; Guo, A.; Li, H. Numerical simulation and prediction of spatial wind field under complex terrain. J. Wind Eng. Ind. Aerodyn. 2018, 180, 49–65. [Google Scholar] [CrossRef]
- Ha, T.; Lee, I.; Kwon, K.; Lee, S.-J. Development of a micro-scale CFD model to predict wind environment on mountainous terrain. Comput. Electron. Agric. 2018, 149, 110–120. [Google Scholar] [CrossRef]
- Huang, G.; Cheng, X.; Peng, L.; Li, M. Aerodynamic shape of transition curve for truncated mountainous terrain model in wind field simulation. J. Wind Eng. Ind. Aerodyn. 2018, 178, 80–90. [Google Scholar] [CrossRef]
- Wolf, T. Design of a variable contraction for a full-scale automotive wind tunnel. J. Wind Eng. Ind. Aerodyn. 1995, 56, 1–21. [Google Scholar] [CrossRef]
- Liu, Z.-W.; Chen, X.-Y.; Chen, Z.-Q. Optimization of Transition Sections Around Terrain Model at Mountain Canyon Bridge Site. China J. Highw. Transp. 2019, 32, 266–278. [Google Scholar]
- Brassard, D.; Ferchichi, M. Transformation of a polynomial for a contraction wall profile. J. FLUIDS Eng. ASME 2005, 127, 183–185. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, J.D.; Chen, H.S.; Chen, D.R. Optimized design of the contraction in a minitype high-speed water-tunnel. Chuan Bo Li Xue/J. Sh. Mech. 2009, 13, 513–521. [Google Scholar] [CrossRef]
- Bell, J.H.; Mehta, R.D. Contraction design for small low-speed wind tunnels. Nasa Sti/Recon Tech. Rep. N 1988, Contract NAS2-NCC-2-294. [Google Scholar]
- Bekele, S.A.; Hangan, H. A comparative investigation of the TTU pressure envelope -Numerical versus laboratory and full scale results. Wind Struct. An Int. J. 2002, 5, 337–346. [Google Scholar] [CrossRef]
- Hongmiao, J.; Haili, L.; Cunming, M.; Zhiguo, L. A study on boundary transition of a terrain model for wind field characteristics measurement. J. Vib. Shock 2020, 39, 178–207. [Google Scholar]
- Peng, H.; Yongle, L.; Haili, L. Shape of boundary transition section for mountains-gorge bridge site terrain model. Acta Aerodyn. Sin. 2013, 31, 231–238. [Google Scholar]
- Pattanapol, W.; Wakes, S.J.; Hilton, M.J.; Dickinson, K.J.M. Modeling of surface roughness for flow over a complex vegetated surface. Int. J. Eng. Nat. Sci. 2008, 2, 18–26. [Google Scholar]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Wieringa, J. Updating the Davenport roughness classification. J. Wind Eng. Ind. Aerodyn. 1992, 41, 357–368. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, X. Wind field simulation over complex terrain under different inflow wind directions. Wind Struct. 2019, 28, 239–253. [Google Scholar] [CrossRef]


| f(ε) = 0.3 | f(ε) = 0.5 | f(ε) = 0.7 | f(ε) = 1 | f(ε) = 2 | f(ε) = x/L | f(ε) = x2/L2 | f(ε) = x3/L3 | BCTC | WTC | |
|---|---|---|---|---|---|---|---|---|---|---|
| Sx | 0.07 | 0.11 | 0.07 | 0.07 | 0.02 | 0.03 | 0.09 | 0.20 | 0.03 | 0.02 |
| Ax | 0.68 | 0.66 | 0.68 | 0.72 | 0.80 | 0.79 | 0.65 | 1.04 | 0.81 | 0.82 |
| Tx | 4.25 | 5.10 | 3.59 | 3.55 | 3.52 | 3.61 | 4.67 | 6.03 | 3.52 | 3.53 |
| CI | 1.04 | 1.31 | 0.97 | 1.00 | 0.81 | 0.83 | 1.16 | 1.95 | 0.83 | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Zhang, H.; Zhou, L. Numerical Simulation of Wind Characteristics in Complex Mountains with Focus on Terrain Boundary Transition Curve. Atmosphere 2023, 14, 230. https://doi.org/10.3390/atmos14020230
He J, Zhang H, Zhou L. Numerical Simulation of Wind Characteristics in Complex Mountains with Focus on Terrain Boundary Transition Curve. Atmosphere. 2023; 14(2):230. https://doi.org/10.3390/atmos14020230
Chicago/Turabian StyleHe, Jiawei, Hongfu Zhang, and Lei Zhou. 2023. "Numerical Simulation of Wind Characteristics in Complex Mountains with Focus on Terrain Boundary Transition Curve" Atmosphere 14, no. 2: 230. https://doi.org/10.3390/atmos14020230
APA StyleHe, J., Zhang, H., & Zhou, L. (2023). Numerical Simulation of Wind Characteristics in Complex Mountains with Focus on Terrain Boundary Transition Curve. Atmosphere, 14(2), 230. https://doi.org/10.3390/atmos14020230










