Experimental Study on the Characteristics of the Failure Strain Energy Density of Undisturbed Ice-Rich Frozen Clay
Abstract
1. Introduction
2. Experiment
2.1. Specimen Preparation
2.2. Test Conditions
3. Results and Analyses
3.1. Characterization of Stress-Strain Behavior
3.2. Failure Strain Energy Density Characteristics
3.2.1. Influence of the Confined Pressure on the Failure Strain Energy Density
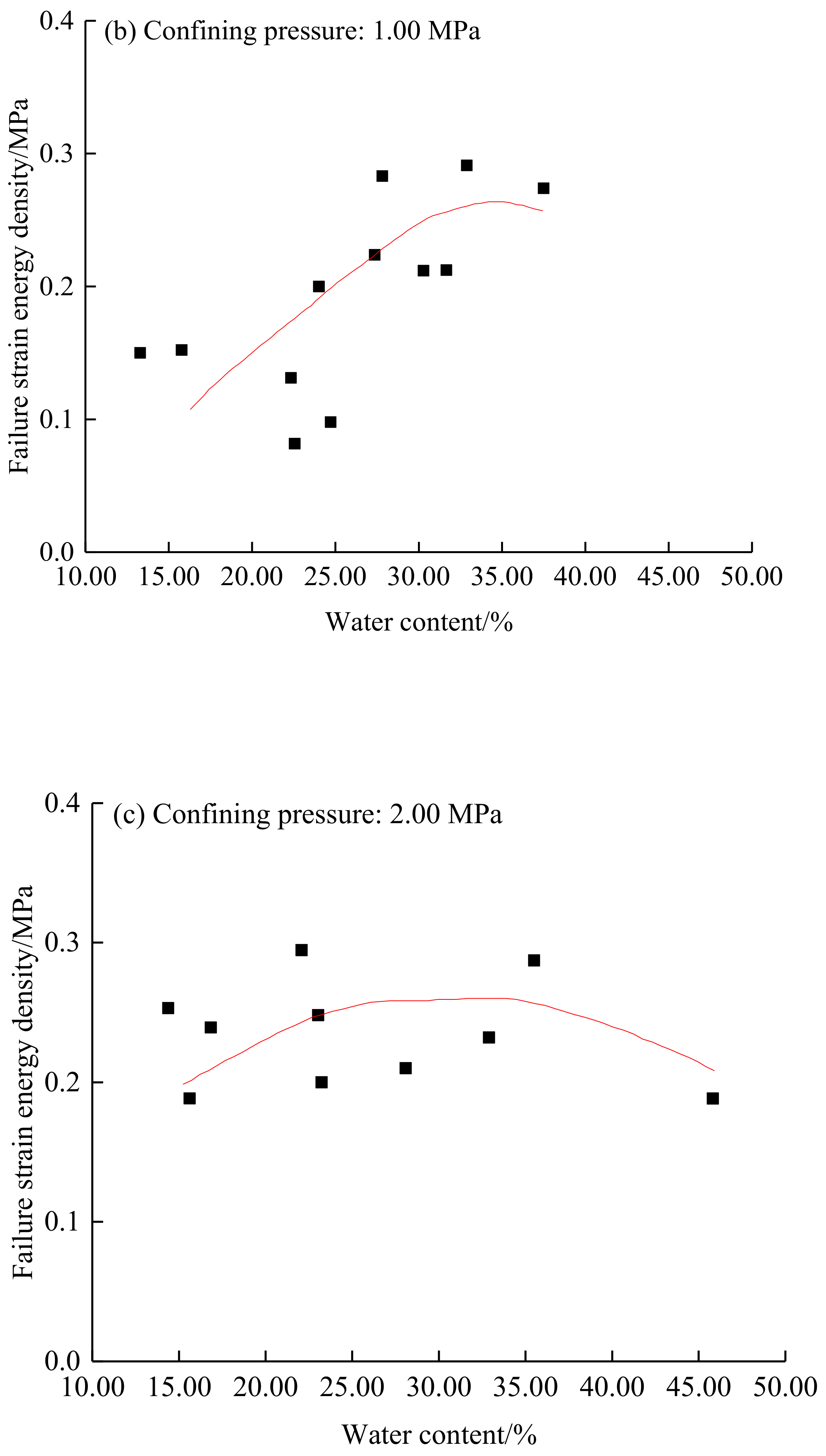
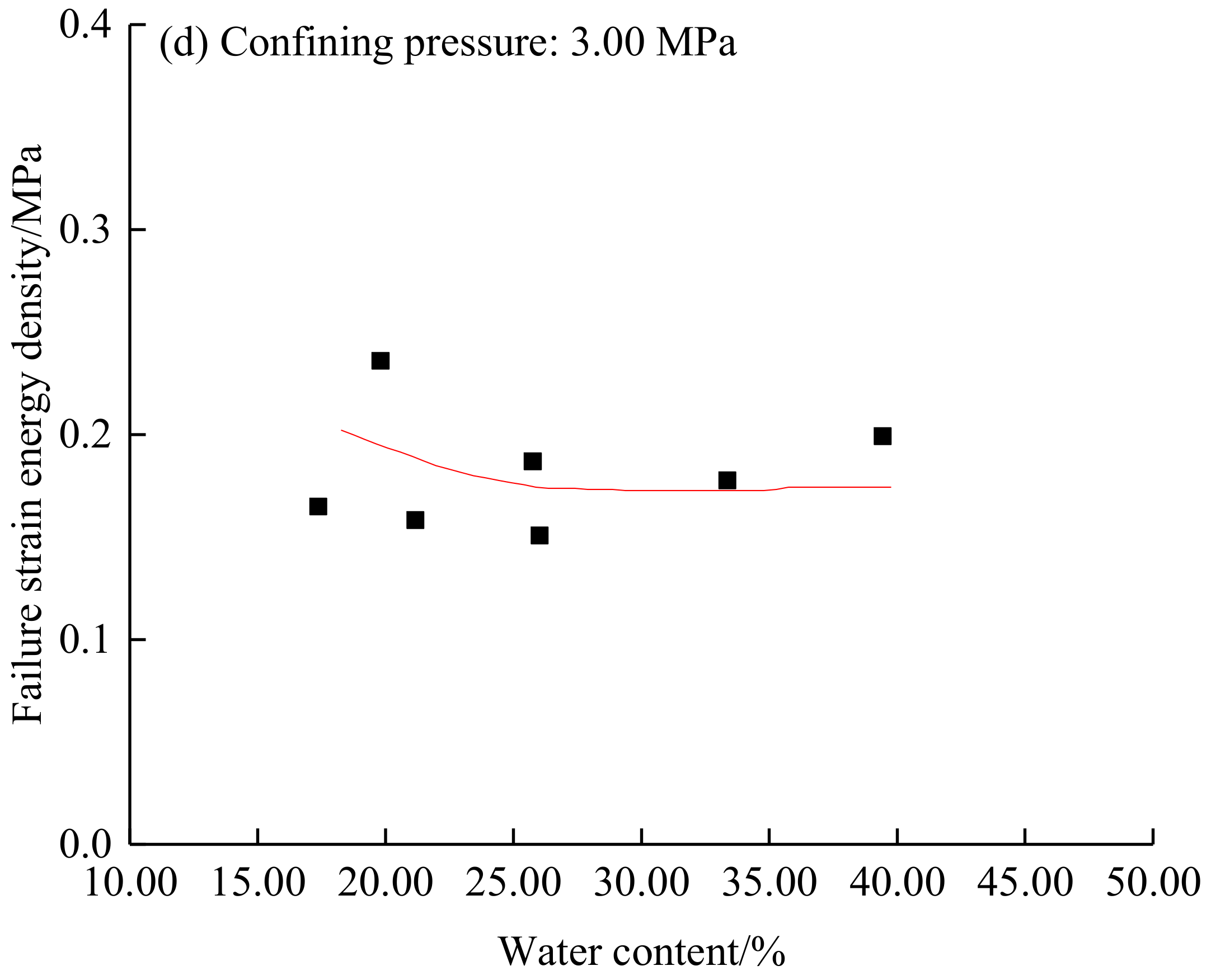
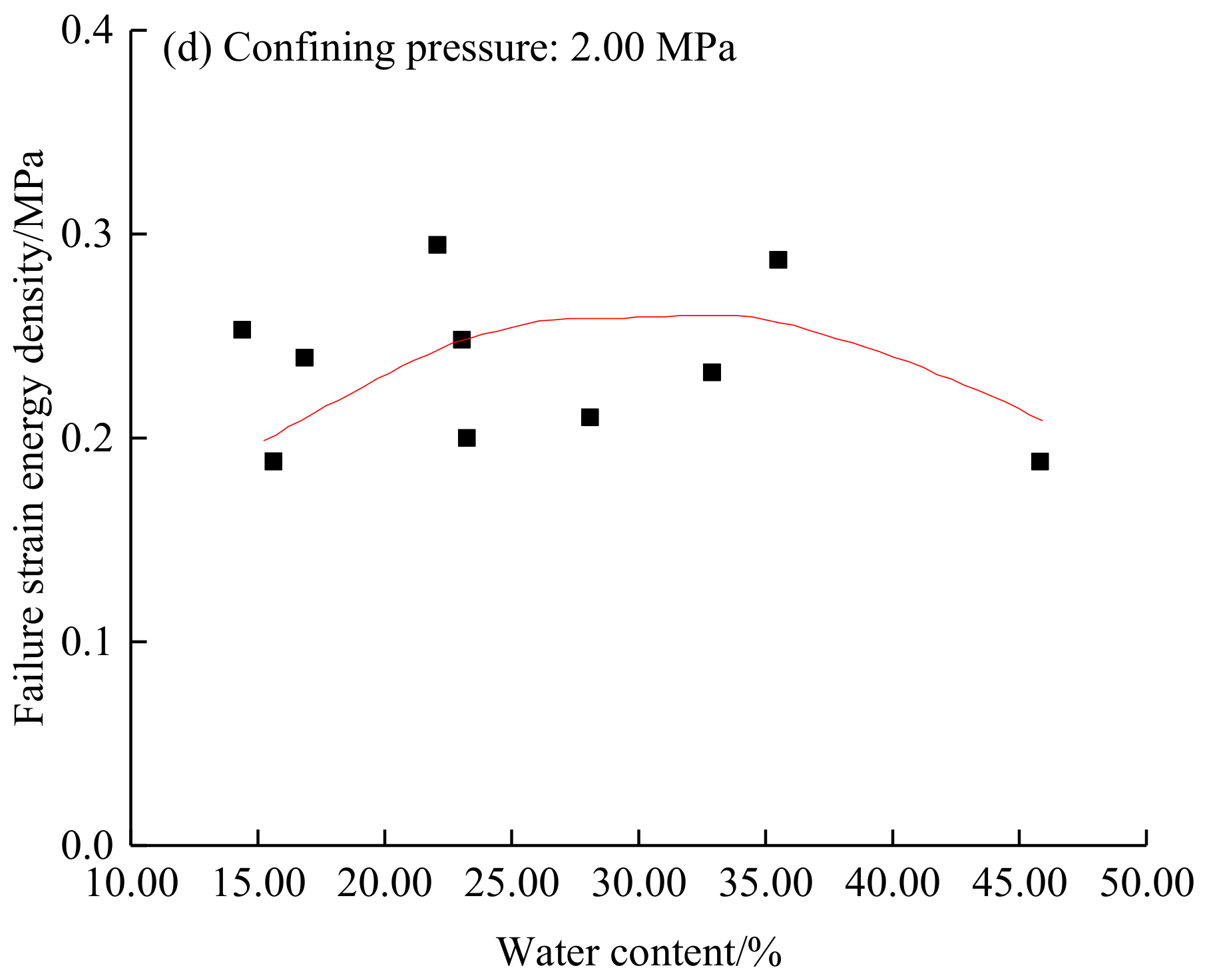
3.2.2. Influence of the Water Content on the Failure Strain Energy Density
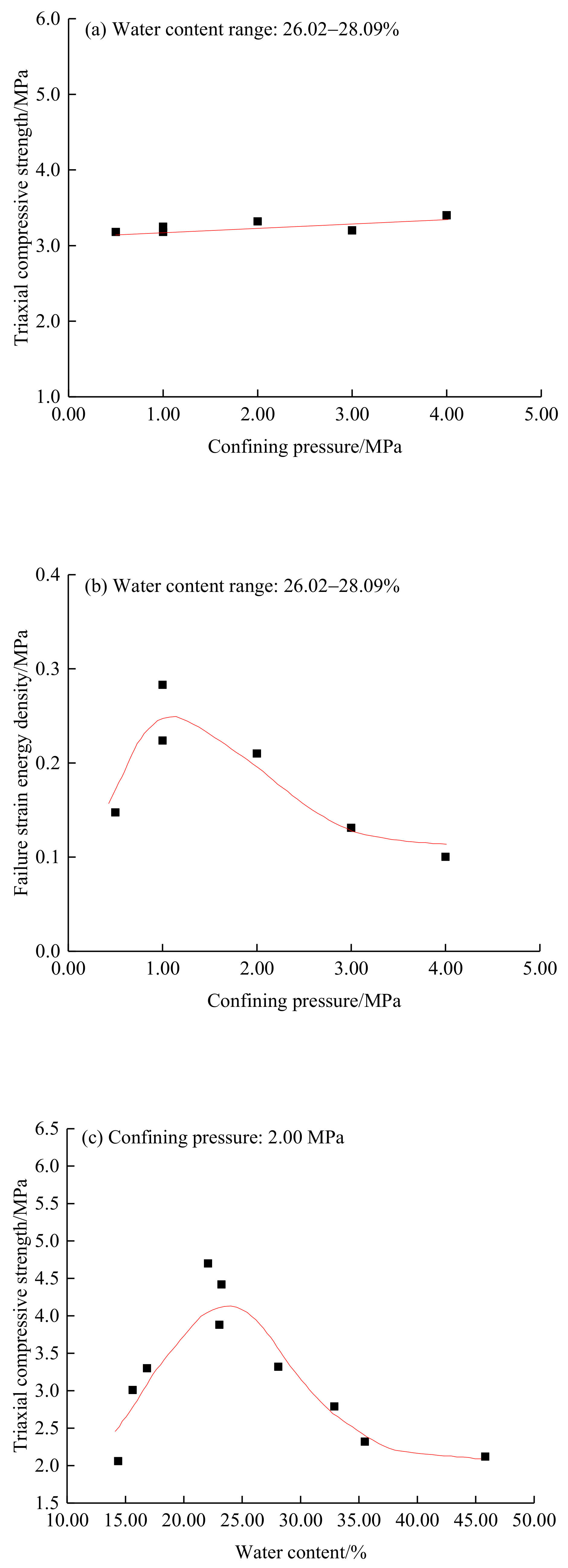
3.2.3. Comparison of the Characteristics of the Triaxial Compressive Strength and the Failure Strain Energy Density
4. Discussion
5. Conclusions
- (1)
- Increasing the confined pressure caused the failure strain energy density to first increase and then decrease. The failure strain energy density reached a maximum at a critical confining pressure of 2.00 MPa for 13.25–25.76% water content and of 1.00 MPa for 26.02–45.82% water content. Increasing the water content caused the critical confined pressure to decline.
- (2)
- At low confined pressures (0.05–0.50 MPa), the failure strain energy density increased when the water content increased, but then declined slightly at intermediate confined pressures (1.00–2.00 MPa). At a high confined pressure of 3.00 MPa, the failure strain energy density declined overall with increasing the water content. With increasing confined pressure, the water content at the maximum failure strain energy density decreased.
- (3)
- Similarities and differences were observed in the change characteristics of the triaxial compressive strength and failure strain energy density. A detailed assessment of the resistance of frozen soil to failure can be performed using the failure strain energy density as a supplementary reference metric.
- (4)
- The variation properties of the failure strain energy density of undisturbed frozen clay and remolded frozen sandy soils were found to be essentially the same. However, some clear differences in the failure strain energy density of these two soil types were also found.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, W.; Mu, Y.H.; Wu, Q.B.; Sun, Z.Z.; Liu, Y.Z. Characteristics and mechanisms of embankment deformation along the Qinghai-Tibet Railway in permafrost regions. Cold Reg. Sci. Technol. 2011, 67, 178–186. [Google Scholar] [CrossRef]
- Wang, F.; Li, G.Y.; Ma, W.; Mu, Y.H.; Zhou, Z.W.; Mao, Y.C. Permafrost thawing along the China-Russia Crude Oil Pipeline and countermeasures: A case study in Jiagedaqi, Northeast China. Cold Reg. Sci. Technol. 2018, 155, 308–313. [Google Scholar] [CrossRef]
- Chen, L.; Lai, Y.M.; Fortier, D.; Harris, S.A. Impacts of snow cover on the pattern and velocity of air flow in air convection embankments of sub-Arctic regions. Renew. Energy 2022, 199, 1033–1046. [Google Scholar] [CrossRef]
- Chen, L.; Voss, C.I.; Fortier, D.; McKenzie, J.M. Surface energy balance of sub-Arctic roads with varying snow regimes and properties in permafrost regions. Permafr. Periglac. Process. 2021, 32, 681–701. [Google Scholar] [CrossRef]
- Chen, L.; Yu, W.B.; Zhang, T.Q.; Yi, X. Asymmetric talik formation beneath the embankment of Qinghai-Tibet Highway triggered by the sunny-shady effect. Energy 2023, 266, 126472. [Google Scholar] [CrossRef]
- Ma, W.; Cheng, G.D.; Wu, Q.B. Construction on permafrost foundations: Lessons learned from the Qinghai-Tibet Railroad. Cold Reg. Sci. Technol. 2009, 59, 3–11. [Google Scholar] [CrossRef]
- Wu, Z.W.; Ma, W. Strength and Creep of Frozen Soils; Lanzhou University Press: Lanzhou, China, 2002. [Google Scholar]
- Chamberlain, E.; Groves, C.; Perham, R. The mechanical behavior of frozen earth materials under high pressure triaxial test conditions. Geotechnique 1972, 22, 469–483. [Google Scholar] [CrossRef]
- Xu, X.T.; Lai, Y.M.; Dong, Y.H.; Qi, J.L. Laboratory investigation on strength and deformation characteristics of ice-saturated frozen sandy soil. Cold Reg. Sci. Technol. 2011, 69, 98–104. [Google Scholar] [CrossRef]
- Baker, T.H.W.; Jones, S.J.; Parameswaran, V.R. Confined and unconfined compression tests on frozen sands. In Proceedings of the 4th Canadian Permafrost Conference, Calgary, AB, Canada, 2–6 March 1981; Nation Research Council of Canada: Ottawa, ON, Canada, 1982; pp. 387–393. Available online: https://www.doc88.com/p-0156903787371.html (accessed on 20 March 2015).
- Ma, W.; Wu, Z.W.; Sheng, Y. Effect of confining pressure on strength behaviour of frozen soil. Chin. J. Geotech. Eng. 1995, 17, 7–11. [Google Scholar]
- Arenson, L.U.; Almasi, N.; Springman, S.M. Shearing response of ice-rich rock glacier material. In Proceedings of the Eighth International Conference on Permafrost, Zurich, Switzerland, 21–25 July 2003; pp. 39–44. Available online: https://www.docin.com/p-1888414281.html (accessed on 15 March 2015).
- Zhang, J.X.; Yang, H.; Shan, R.L.; Sun, S.M.; Xue, D.C. Experimental research on triaxial compressive strength of frozen saturated sandy gravel. Rock Soil Mech 2018, 39, 3993–4001. [Google Scholar] [CrossRef]
- Jessberger, H.L. A state-of-the-art report. Ground freezing: Mechanical properties, processes and design. Eng. Geol. 1981, 18, 5–30. [Google Scholar] [CrossRef]
- Lai, Y.M.; Yang, Y.G.; Chang, X.X.; Li, S.Y. Strength criterion and elastoplastic constitutive model of frozen silt in generalized plastic mechanics. Int. J. Plast. 2010, 26, 1461–1484. [Google Scholar] [CrossRef]
- Zhang, S.J.; Du, H.M.; Harbor, J. The effect of confining pressure and water content on compressive strength and deformation of ice-rich silty sand. Permafr. Periglac. Process. 2017, 28, 298–305. [Google Scholar] [CrossRef]
- Xu, X.T.; Li, Q.L.; Lai, Y.; Pang, W.T.; Zhang, R.P. Effect of moisture content on mechanical and damage behavior of frozen loess under triaxial condition along with different confining pressures. Cold Reg. Sci. Technol. 2019, 157, 110–118. [Google Scholar] [CrossRef]
- Shusherina, E.P.; Bobkov, Y.P. Effect of moisture content on frozen ground strength. In Technical Translation; National Research Council: Ottawa, ON, Canada, 1978; pp. 1–19. [Google Scholar] [CrossRef]
- Xu, X.T.; Zhang, W.D.; Wang, Y.T. Measuring and modeling the dielectric constant of soil during freezing and thawing processes: An application on silty clay. Acta Geotech. 2022, 17, 3867–3886. [Google Scholar] [CrossRef]
- Du, H.M.; Ma, W.; Zhang, S.J.; Zhou, Z.W.; Liu, E.L. Strength properties of ice-rich frozen silty sands under uniaxial compression for a wide range of strain rates and moisture contents. Cold Reg. Sci. Technol. 2016, 123, 107–113. [Google Scholar] [CrossRef]
- Goughnour, R.R.; Andersland, O.B. Mechanical properties of a sand-ice system. J. Soil Mech. Found. Div. ASCE 1968, 94, 923–950. [Google Scholar] [CrossRef]
- Baker, T.H.W. Strain rate effect on the compressive strength of frozen sand. Eng. Geol. 1979, 13, 223–231. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Yang, P.; Jang, W.Y.; Zhang, T.; Chen, L. Effect of water content and strain rate on the strength characteristics of frozen silty clay. J. Zhengzhou Univ. 2020, 41, 79–84. [Google Scholar] [CrossRef]
- Du, H.M.; Zhang, S.J.; Ma, W. Experimental study of uniaxial compressive deformation and strength of frozen silty sand under different initial ice contents. Rock Soil Mech. 2014, 35, 2855–2860. [Google Scholar]
- Ma, X.J.; Zhang, J.M.; Chang, X.X.; Zheng, B.; Zhang, M.Y. Experimental research on strength of warm and ice-rich frozen clays. Rock Soil Mech. 2008, 29, 2498–2502. [Google Scholar] [CrossRef]
- Lai, Y.M.; Zhang, Y.; Zhang, S.J.; Jin, L.; Chang, X.X. Experimental study of strength of frozen sandy soil under different water contents and temperatures. Rock Soil Mech. 2009, 30, 3665–3670. [Google Scholar] [CrossRef]
- Wang, B.X.; Wang, Y.B.; Fan, C.X.; Zhang, W.D. Energy distribution and evolution of frozen silty clay at subzero temperatures under compressive loading. Transp. Geotech. 2021, 31, 100656. [Google Scholar] [CrossRef]
- Chen, S.W.; Lin, B. Contrast test on uniaxial compression of undisturbed and remolded frozen clay. Saf. Coal Mines 2019, 50, 62–66. [Google Scholar]
- Zhang, Y.Q.; Yang, P.; Jang, W.Y.; Zhang, T. Study on triaxial strength and constitutive model of frozen silty clay. Chin. Civil. Eng. J. 2019, 52, 8–15. [Google Scholar]
- Du, H.M.; Ma, W.; Zhang, S.J.; Zhou, Z.W. Effects of strain rate and water content on failure strain energy density of frozen soil. J. Eng. Geol. 2015, 23, 38–43. [Google Scholar] [CrossRef]
- Du, H.M.; Ma, W.; Zhang, S.J.; Zhou, Z.W. Effects of confining pressure and water content on failure strain energy density for frozen silty sands. Rock Soil Mech. 2017, 38, 1943–1950. [Google Scholar] [CrossRef]
- Liu, H.W. Material Mechanics II; Higher Education Press: Beijing, China, 2004; pp. 28–29. [Google Scholar]
- Liu, H.W. Material Mechanics I; Higher Education Press: Beijing, China, 2004; pp. 240–241. [Google Scholar]

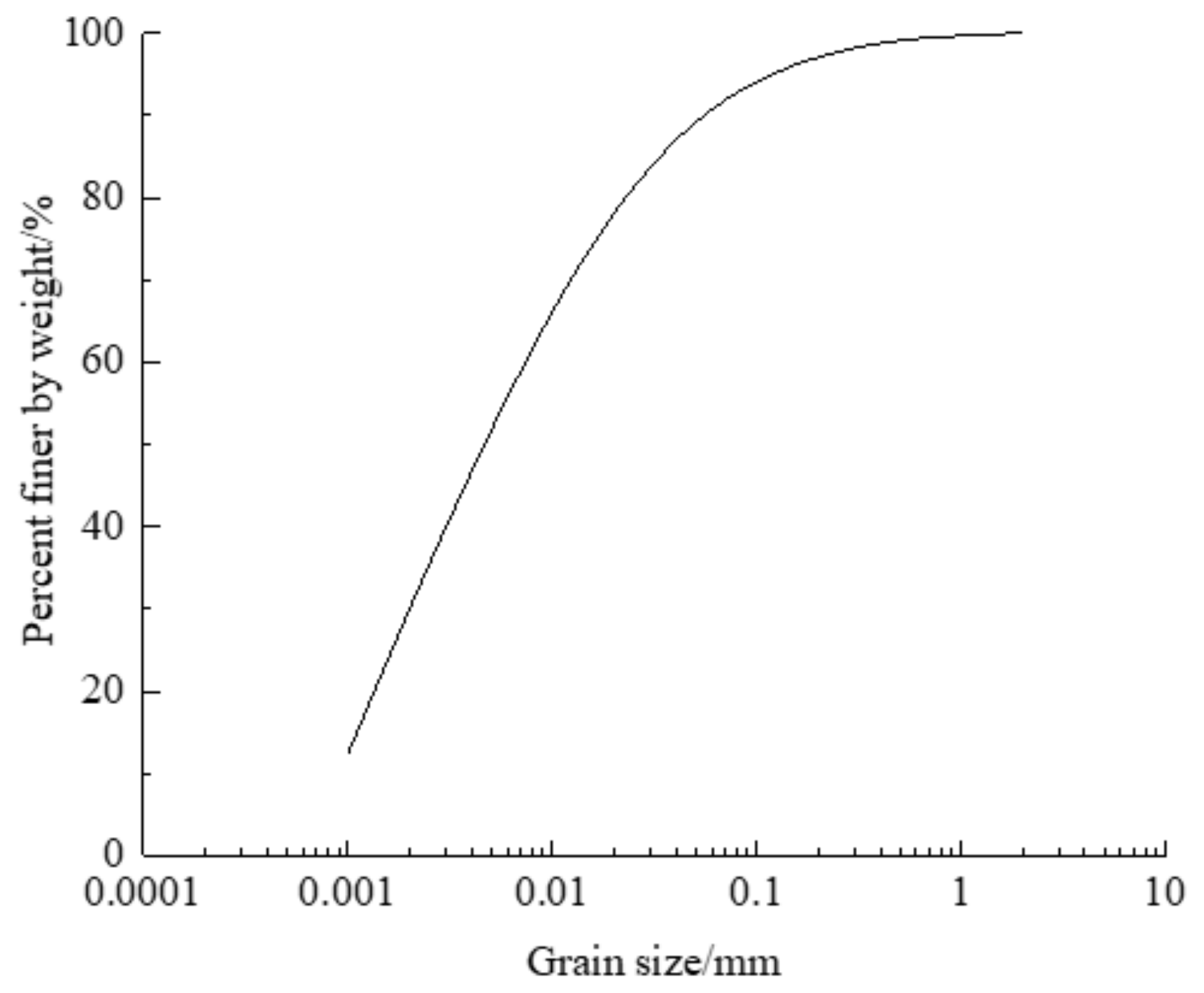

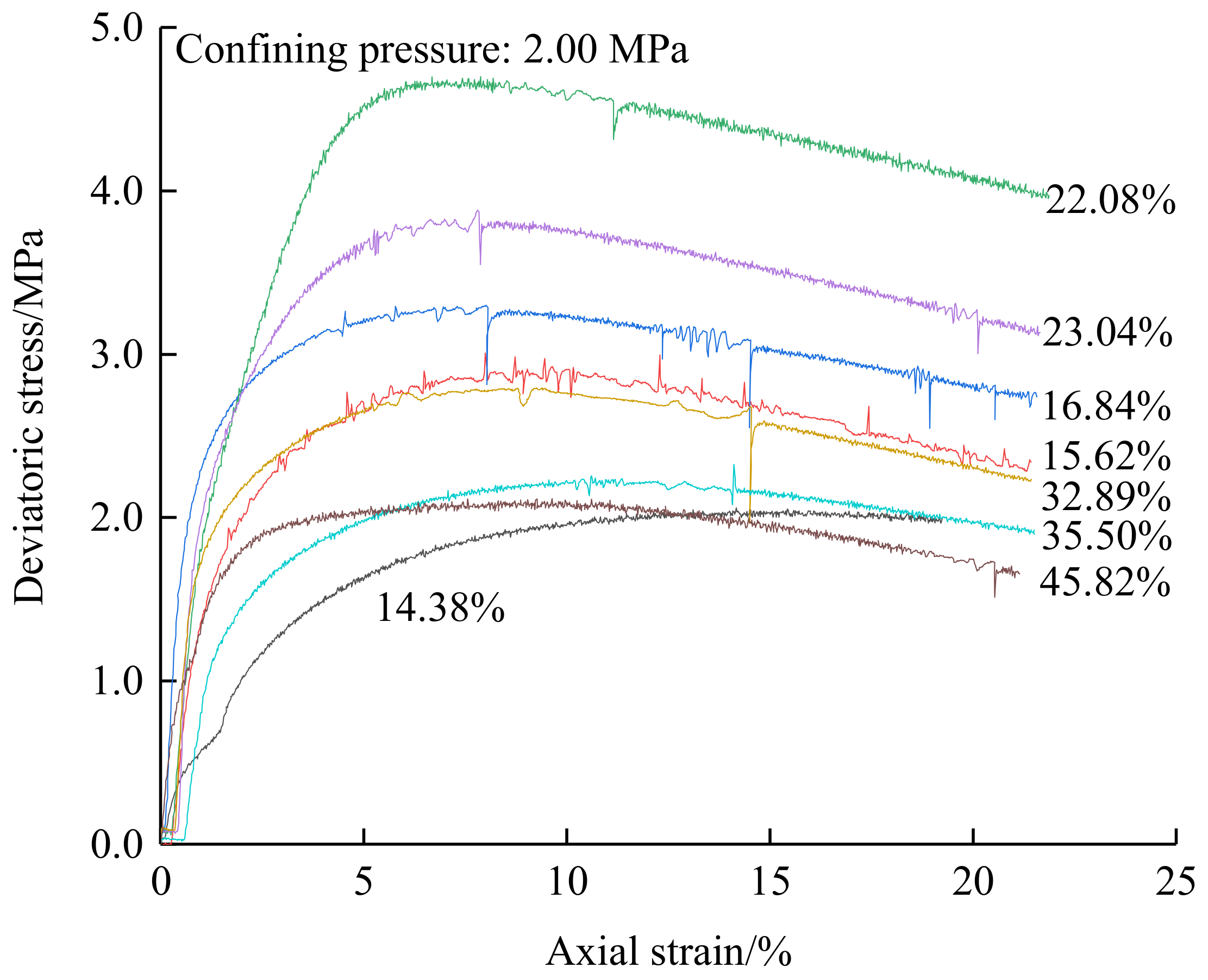

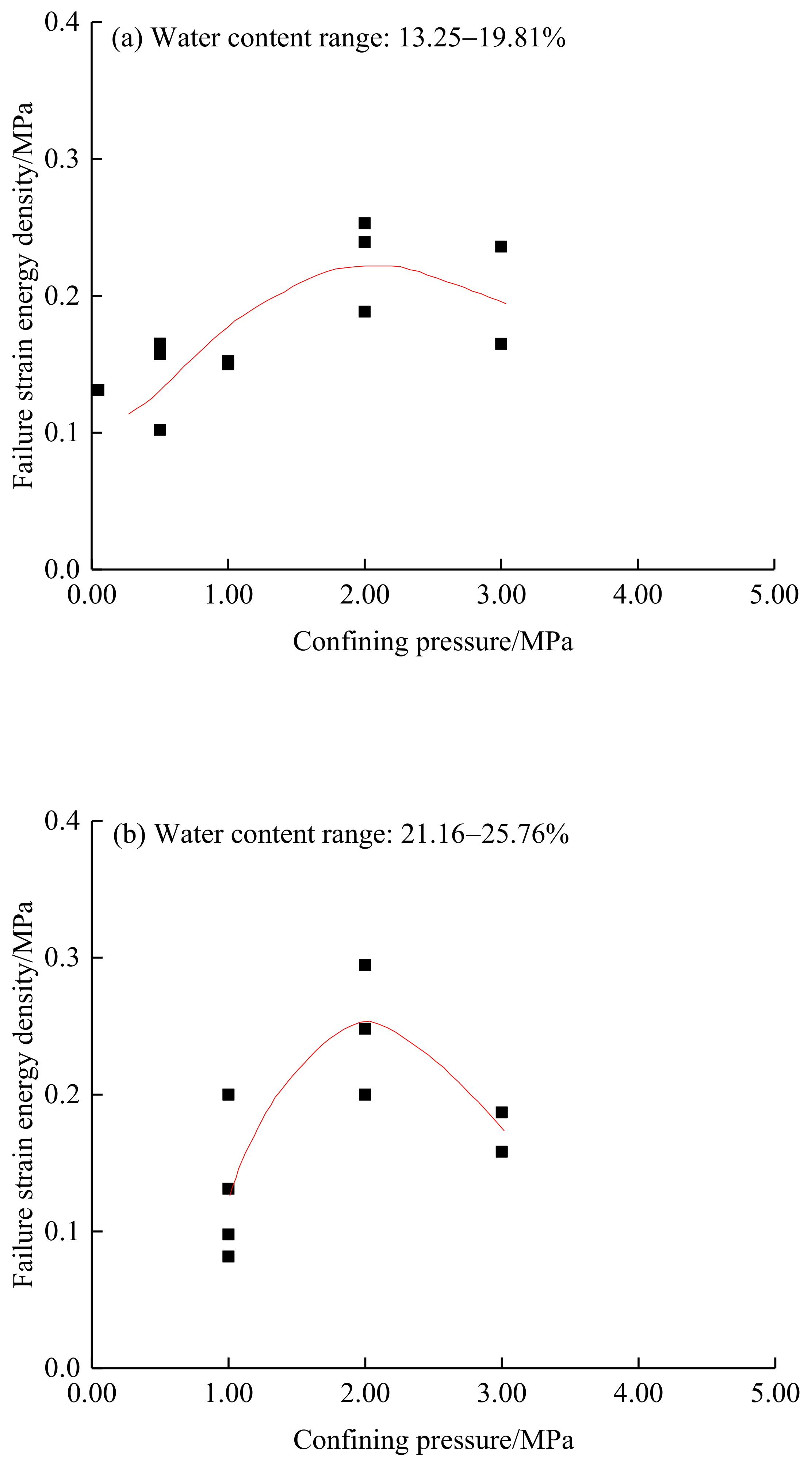

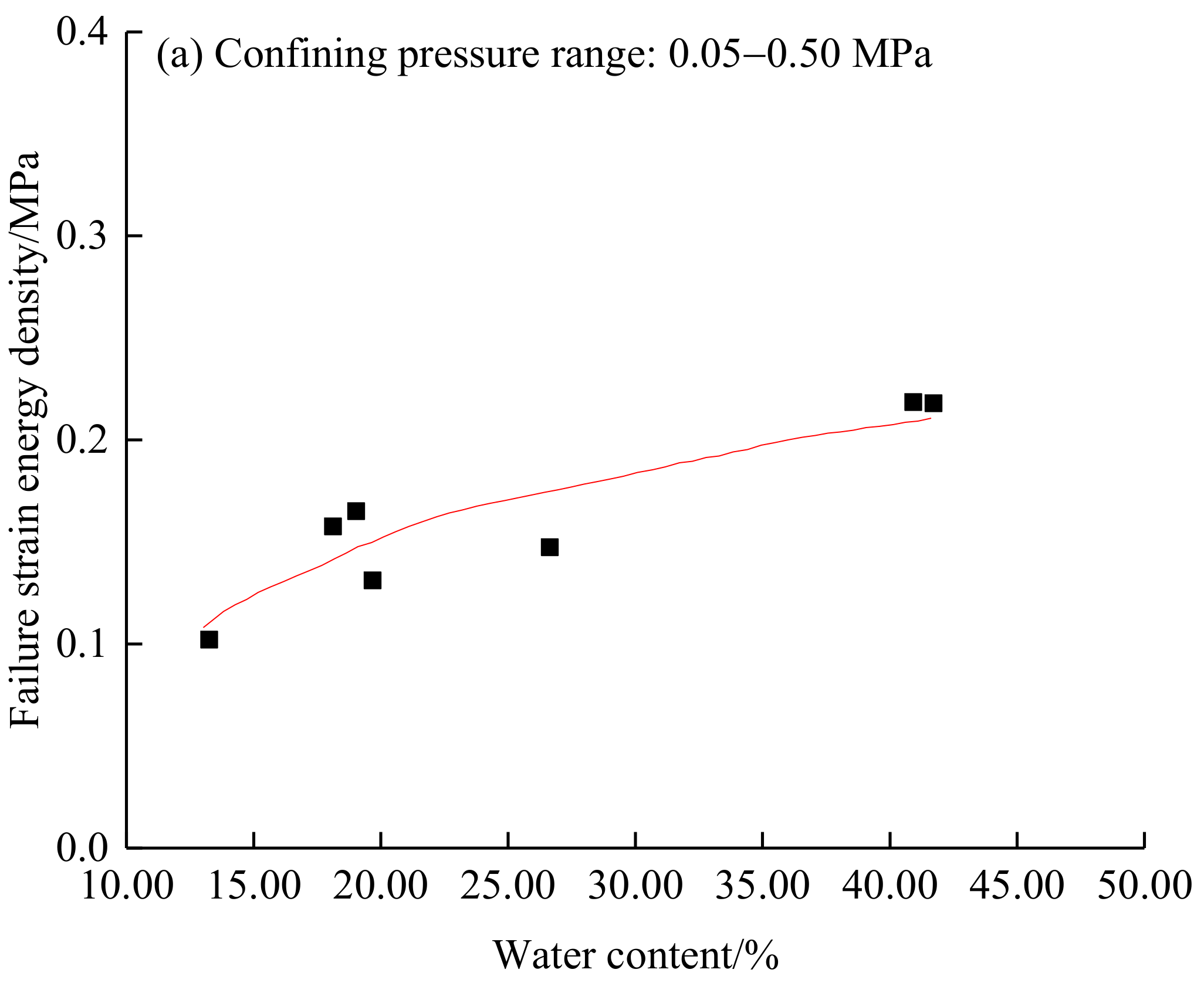
| Sampling Point Number | Sample Depth/m | Water Content/% | Dry Density/(g·cm−3) |
|---|---|---|---|
| 10-1-2# | 2.1 | 32.88 | 1.33 |
| 10-1-2# | 2.3 | 16.84 | 1.84 |
| 10-1-2# | 2.4 | 15.78 | 1.84 |
| 10-1-2# | 2.5 | 18.12 | 1.74 |
| 10-1-2# | 2.7 | 27.36 | 1.49 |
| 10-1-2# | 2.9 | 19.81 | 1.70 |
| 10-1-3# | 2.1 | 39.44 | 1.22 |
| 10-1-3# | 2.3 | 22.34 | 1.62 |
| 10-1-3# | 2.5 | 41.72 | 1.22 |
| 10-1-3# | 3.0 | 23.23 | 1.59 |
| 10-1-3#N 3 m | 2.0 | 35.50 | 1.28 |
| 10-1-3#N 3 m | 2.3 | 31.66 | 1.41 |
| 10-1-3#N 3 m | 2.5 | 25.76 | 1.50 |
| 10-1-3#N 3 m | 3.6 | 40.92 | 1.24 |
| 10-1-3#N 3 m | 3.8 | 37.50 | 1.26 |
| 10-1-3#N 4 m | 2.6 | 33.37 | 1.35 |
| 10-1-3#N 4 m | 2.9 | 32.89 | 1.36 |
| 10-1-3#N 4 m | 3.2 | 27.82 | 1.49 |
| 10- 2-1# | 2.1 | 22.56 | 1.61 |
| 10-2-1# | 2.3 | 26.64 | 1.51 |
| 10-2-1# | 3.6 | 45.82 | 1.07 |
| 10-2-1# | 4.5 | 15.62 | 1.83 |
| 10-2-1# | 4.7 | 17.37 | 1.80 |
| 10-2-2# | 2.8 | 22.08 | 1.60 |
| 10-2-2# | 3.2 | 24.72 | 1.58 |
| 10-2-3# | 2.9 | 26.02 | 1.52 |
| 10-2-3# | 4.3 | 13.29 | 1.94 |
| 10-2-3# | 4.5 | 14.38 | 1.93 |
| 10-2-3# | 4.8 | 13.25 | 1.95 |
| 10-3-1# | 2.8 | 28.09 | 1.44 |
| 10-3-1# | 3.0 | 26.33 | 1.46 |
| 10-3-1# | 3.2 | 21.16 | 1.59 |
| 10-3-1# | 3.8 | 19.03 | 1.76 |
| 10-3-1# | 4.0 | 19.68 | 1.72 |
| 10-3-2# | 3.2 | 24.02 | 1.53 |
| 10-3-2# | 4.4 | 23.04 | 1.59 |
| 10-3-3# | 3.4 | 30.29 | 1.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, H.; Zhang, S.; Ma, W.; Mu, Y.; Cheng, T.; Zhang, Y. Experimental Study on the Characteristics of the Failure Strain Energy Density of Undisturbed Ice-Rich Frozen Clay. Atmosphere 2023, 14, 203. https://doi.org/10.3390/atmos14020203
Du H, Zhang S, Ma W, Mu Y, Cheng T, Zhang Y. Experimental Study on the Characteristics of the Failure Strain Energy Density of Undisturbed Ice-Rich Frozen Clay. Atmosphere. 2023; 14(2):203. https://doi.org/10.3390/atmos14020203
Chicago/Turabian StyleDu, Haimin, Shujuan Zhang, Wei Ma, Yanhu Mu, Tao Cheng, and Yunzhi Zhang. 2023. "Experimental Study on the Characteristics of the Failure Strain Energy Density of Undisturbed Ice-Rich Frozen Clay" Atmosphere 14, no. 2: 203. https://doi.org/10.3390/atmos14020203
APA StyleDu, H., Zhang, S., Ma, W., Mu, Y., Cheng, T., & Zhang, Y. (2023). Experimental Study on the Characteristics of the Failure Strain Energy Density of Undisturbed Ice-Rich Frozen Clay. Atmosphere, 14(2), 203. https://doi.org/10.3390/atmos14020203






