Investigation of Wind Characteristics and Cooling Effects of Crushed-Rock Embankment with Different Pavement Widths in Permafrost Region
Abstract
1. Introduction
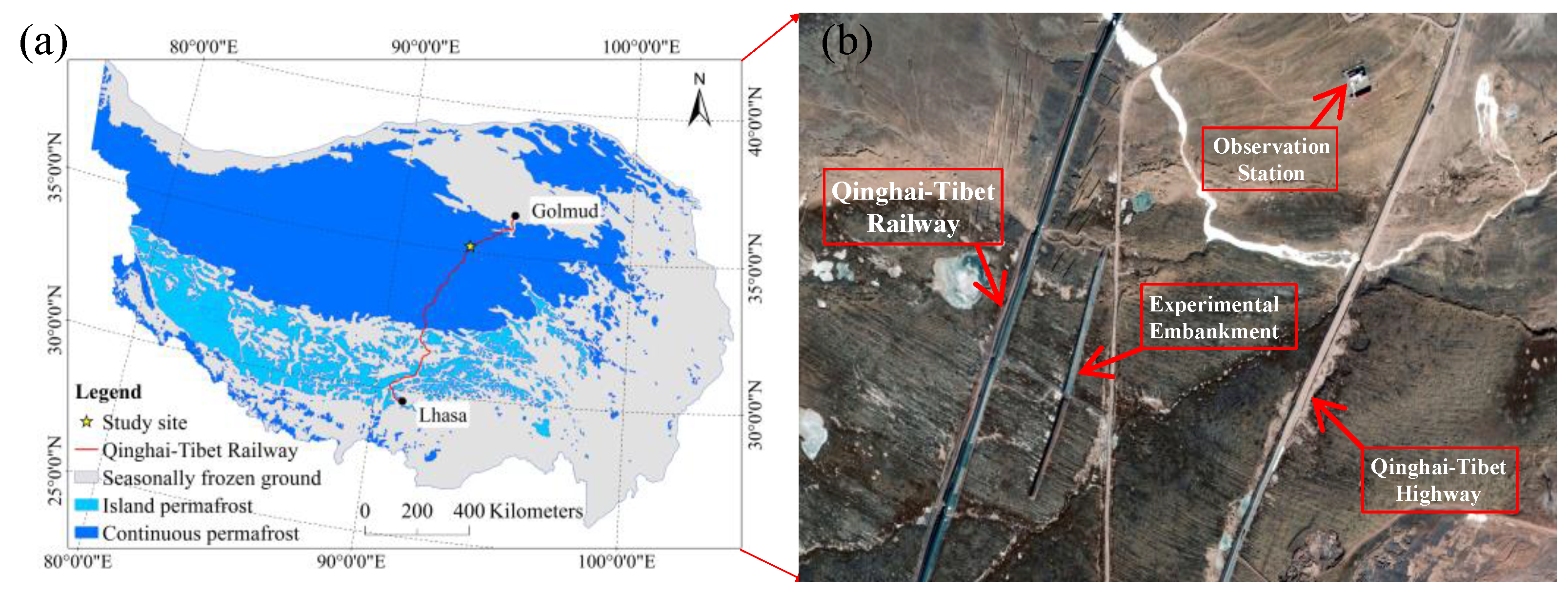
2. Experimental Site and Monitoring System
2.1. Site Description and Monitoring System
2.2. Analysis of the Monitoring Data
3. Numerical Simulation
3.1. Theory Model
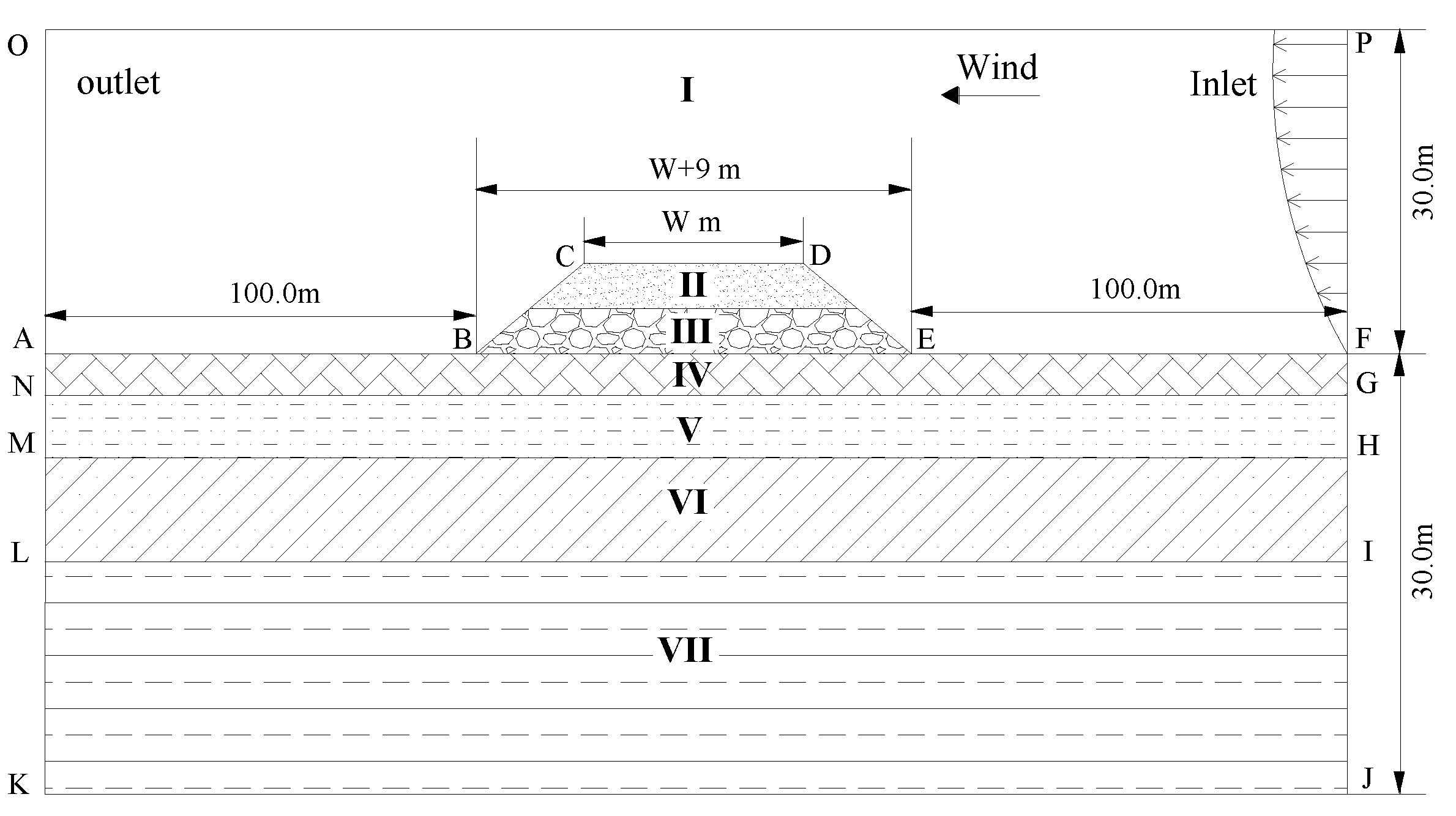
3.2. Physical Model and Parameters
3.3. Boundary and Initial Conditions
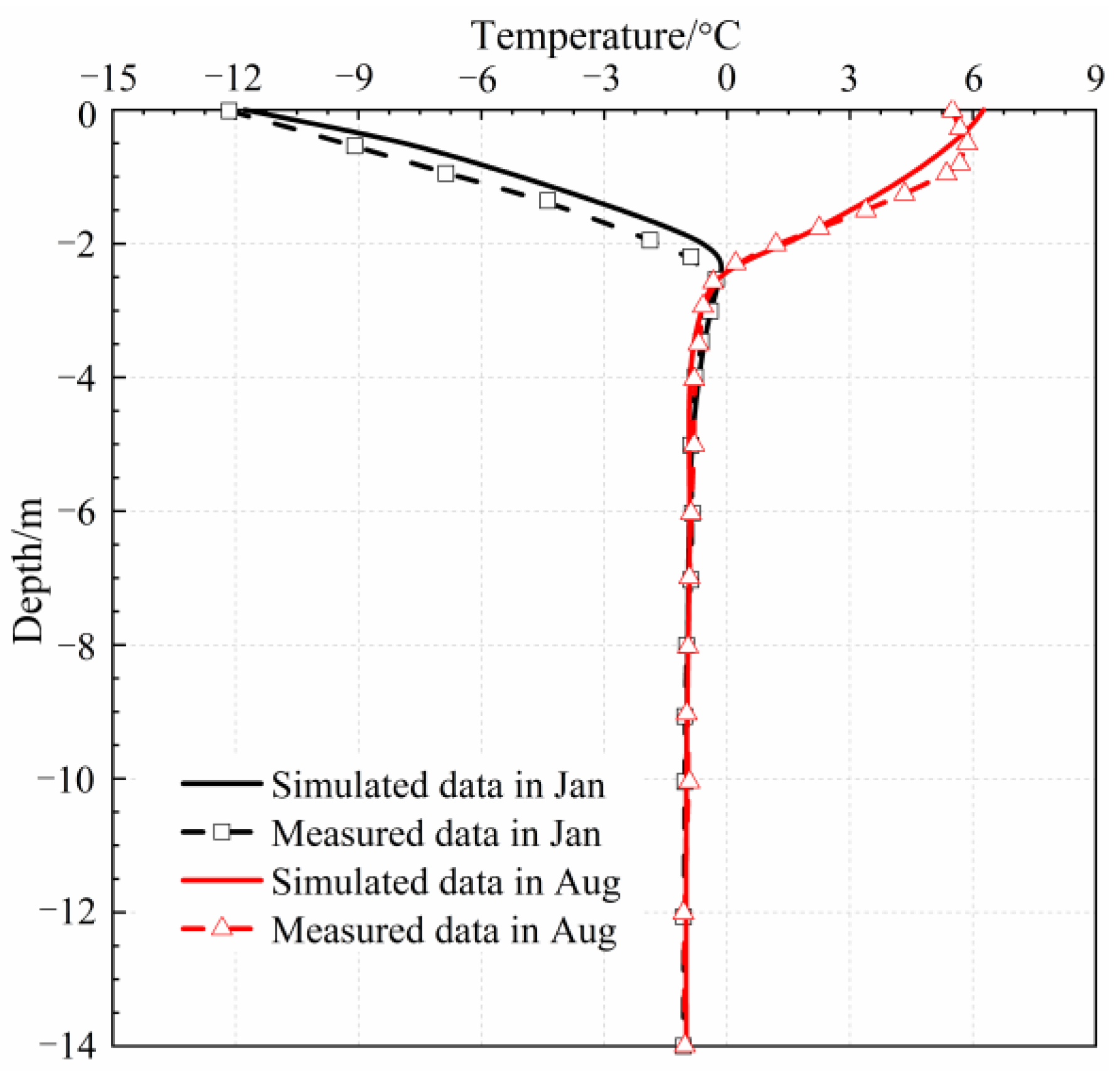
3.4. Model Validation
4. Results and Analysis
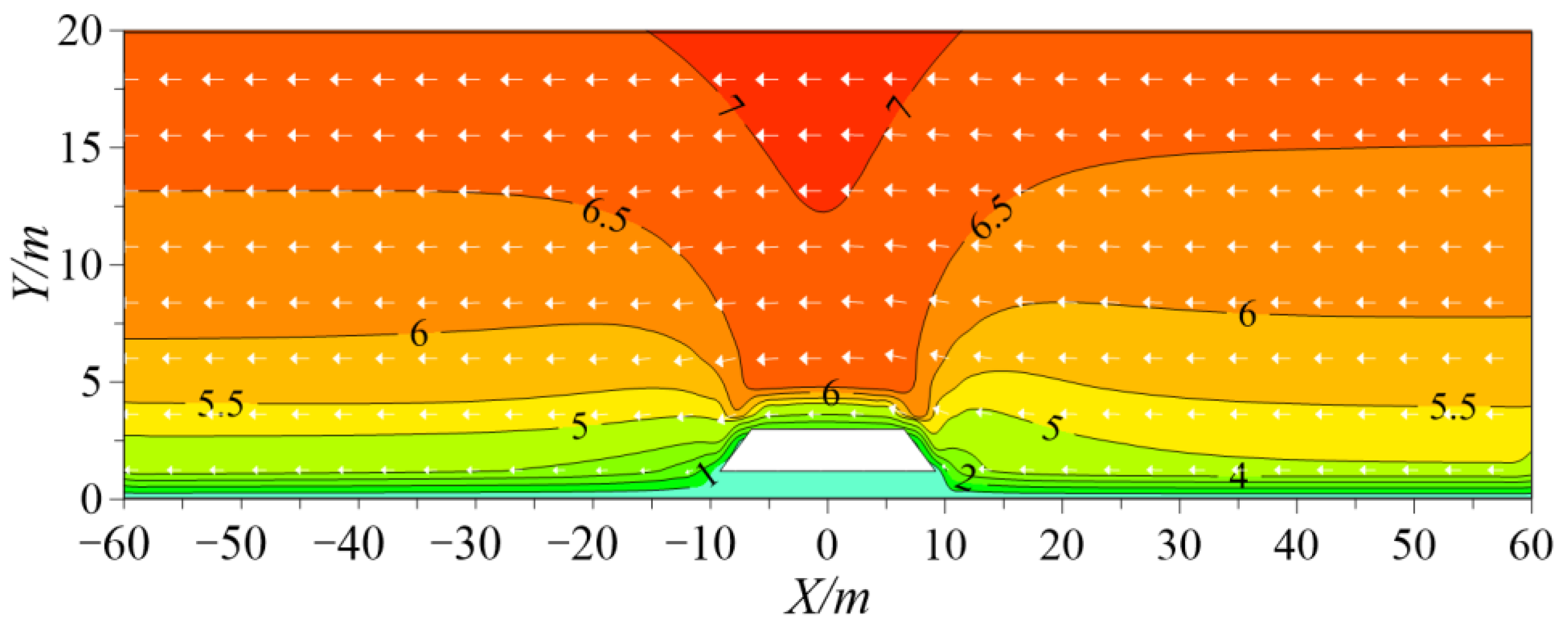
4.1. Characteristics of Wind Flow around the Embankment
4.2. Cooling Effect of the CRE with Different Pavement Widths
5. Discussions and Conclusions
- The existence of the embankment considerably changes the magnitude and direction of wind flow, and the wind speed close to the windward and leeward sides of the embankment decreases significantly. The disturbance range of the embankment on the wind speed was approximately 7 m on the windward side and 54 m on the leeward side horizontally. Additionally, there is an obvious difference in wind speed within the CRL because of the differential pavement width.
- The thermal regimes beneath the embankments are considerably affected by the pavement width. In comparison with the NCRE, the permafrost beneath the WCRE degraded significantly and the soil temperature at the depth of 6 m beneath the center of the embankment warm up 0.34 °C. Because of the abundant heat absorption by the wide pavement and the strong resistance of crushed rock to wind flow within the CRL, the cooling effect of the WCRE cannot effectively protect the underlying permafrost.
- Due to the differential wind flow around the embankment, the soil temperatures beneath the windward and leeward sides of the embankment show an obvious asymmetric distribution. The increase in the pavement width is beneficial to enhance this asymmetry based on the variations in soil temperatures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gruber, S. Derivation and analysis of a high-resolution estimate of global permafrost zonation. Cryosphere 2012, 6, 221–233. [Google Scholar] [CrossRef]
- Wu, Q.B.; Hou, Y.D.; Yun, H.B.; Liu, Y.Z. Changes in active-layer thickness and near-surface permafrost between 2002 and 2012 in alpine ecosystems, Qinghai-Xizang (Tibet) Plateau, China. Glob. Planet. Chang. 2015, 124, 149–155. [Google Scholar] [CrossRef]
- Jin, H.J.; Wu, Q.B.; Vladimir, E.R. Degrading permafrost and its impacts. Adv. Clim. Chang. Res. 2021, 12, 1–5. [Google Scholar] [CrossRef]
- Chen, L.; Voss, C.L.; Fortier, D.; Mckenzie, J.M. Surface energy balance of sub-Arctic roads and highway in permafrost regions. Permafr. Periglac. Process. 2021, 32, 681–701. [Google Scholar] [CrossRef]
- Wu, Q.B.; Niu, F.J. Permafrost changes and engineering stability in Qinghai-Xizang Plateau. Chin. Sci. Bull. 2013, 58, 1079–1094. [Google Scholar] [CrossRef]
- Batenipour, H.; Alfaro, M.; Kurz, D.; Graham, J. Deformations and ground temperatures at a road embankment in northern Canada. Can. Geotech. J. 2014, 51, 260–271. [Google Scholar] [CrossRef]
- Dore, G.; Niu, F.J.; Brooks, H. Adaptation methods for transportation infrastructure built on degrading permafrost. Permafr. Periglac. Process. 2016, 27, 352–364. [Google Scholar] [CrossRef]
- Yuan, C.; Yu, Q.H.; You, Y.H.; Guo, L. Deformation mechanism of an expressway embankment in warm and high ice content permafrost regions. Appl. Therm. Eng. 2017, 121, 1032–1039. [Google Scholar] [CrossRef]
- Wu, Q.B.; Zhao, H.T.; Zhang, Z.Q.; Chen, J.; Liu, Y.Z. Long-term role of cooling the underlying permafrost of the crushed rock structure embankment along the Qinghai-Xizang railway. Permafr. Periglac. Proc. 2020, 31, 172–183. [Google Scholar] [CrossRef]
- Mu, Y.H.; Li, G.Y.; Ma, W.; Song, Z.M.; Zhou, Z.W.; Wang, F. Rapid permafrost thaw induced by heat loss from a buried warm-oil pipeline and a new mitigation measure combining seasonal air-cooled embankment and pipe insulation. Energy 2020, 203, 117919. [Google Scholar]
- Chen, L.; Yu, W.B.; Liu, W.B.; Yi, X. Numerical simulation of pile foundations of Qinghai-Tibet power transmission line: Influence of temperature region. Appl. Mech. Mater. 2014, 501, 218–223. [Google Scholar] [CrossRef]
- Chen, L.; Yu, W.B.; Zhang, T.Q.; Yi, X. Asymmetric talik formation beneath the embankment of Qinghai-Tibet Highway triggered by the sunny-shady effect. Energy 2023, 266, 126472. [Google Scholar] [CrossRef]
- Lai, Y.M.; Zhang, M.Y.; Li, S.Y. Theory and Application of Cold Regions Engineering; Science Press: Beijing, China, 2009; pp. 34–124. [Google Scholar]
- Mu, Y.H.; Ma, W.; Sun, Z.Z.; Liu, Y.Z. Comparative analysis of cooling effect of crushed rock embankment along the Qinghai-Tibet Railway. Rock Soil Mech. 2010, 31, 284–292. [Google Scholar]
- Zhang, M.Y.; Zhang, X.Y.; Li, S.Y.; Wu, D.Y.; Pei, W.S.; Lai, Y.M. Evaluating the cooling performance of crushed-rock interlayer embankments with unperforated and perforated ventilation ducts in permafrost regions. Energy 2015, 93, 874–881. [Google Scholar] [CrossRef]
- Chen, L.; Yu, W.B.; Lu, Y.; Wu, P.; Han, F.L. Characteristics of heat fluxes of an oil pipeline armed with thermosyphons in permafrost regions. Appl. Therm. Eng. 2021, 190, 116694. [Google Scholar] [CrossRef]
- Wu, Q.B.; Liu, G.; Liu, Y.Z.; Zhang, T.J. Thermal performance of embankment within crushed rock layer along Qinghai-Tibet Railway. Int. J. Offshore Polar Eng. 2010, 20, 210–217. [Google Scholar]
- Darrow, M.M.; Jensen, D.D. Modeling the permafrost of an air convection embankment (ACE) with thermal berm over ice-rich permafrost, Lost Chicken Creek, Alaska. Cold Reg. Sci. Technol. 2016, 130, 43–58. [Google Scholar] [CrossRef]
- Mu, Y.H.; Ma, W.; Niu, F.J. Long-term thermal effects of air convection embankments in permafrost zones: Case study of the Qinghai-Tibet Railway, China. J. Cold Reg. Eng. 2018, 32, 05018004. [Google Scholar] [CrossRef]
- Chen, L.; Yu, W.B.; Yi, X.; Hu, D.; Liu, W.B. Numerical simulation of heat transfer of the crushed-rock interlayer embankment of Qinghai-Tibet Railway affected by aeolian sand clogging and climate change. Cold Reg. Sci. Technol. 2018, 155, 1–10. [Google Scholar] [CrossRef]
- Moeseke, G.V.; Gratia, E.; Reiter, S.; Herde, A.D. Wind pressure distribution influence on natural ventilation for different incidences and environment densities. Energy Build. 2005, 37, 878–889. [Google Scholar] [CrossRef]
- Cheng, G.D.; Lai, Y.M.; Sun, Z.Z.; Jiang, F. The ‘thermal semi-conductor’ effect of crushed rocks. Permafr. Periglac. Proc. 2007, 18, 151–160. [Google Scholar]
- Wu, Q.B.; Cheng, H.B.; Jiang, G.L.; Ma, W.; Liu, Y.Z. Cooling mechanism of embankments with block stone interlayer in Qinghai-Tibet railway. Sci. China Ser. E Technol. Sci. 2007, 50, 319–328. [Google Scholar] [CrossRef]
- Chen, L.; Lai, Y.M.; Fortier, D.; Harris, S.A. Impacts of snow cover on the pattern and strength of mobile air flow in air convection embankment in sub-Arctic regions. Renew. Energy 2022, 199, 1033–1046. [Google Scholar] [CrossRef]
- Pei, W.S.; Zhang, M.Y.; Li, S.Y.; Lai, Y.M.; Jin, L. Enhancement of convective cooling of the porous crushed-rock layer in cold regions based on experimental investigations. Int. Commun. Heat Mass Transf. 2017, 87, 14–21. [Google Scholar] [CrossRef]
- Liu, M.H.; Ma, W.; Niu, F.J.; Luo, J.; Yin, G.A. Thermal performance of a novel crushed-rock embankment structure for expressway in permafrost regions. Int. J. Heat Mass Transf. 2018, 127, 1178–1188. [Google Scholar] [CrossRef]
- Zhao, H.T.; Wu, Q.B.; Zhang, Z.Q. Long-term cooling effect of the crushed rock structure embankments of the Qinghai-Tibet Railway. Cold Reg. Sci. Technol. 2019, 160, 21–30. [Google Scholar] [CrossRef]
- Qian, J.; Yu, Q.H.; You, Y.H. Analysis on the convection cooling process of crushed-rock embankment of high-grade highway in permafrost regions. Cold Reg. Sci. Technol. 2012, 78, 115–121. [Google Scholar] [CrossRef]
- Liu, M.H.; Niu, F.J.; Ma, W.; Fang, J.H.; Luo, J. Experimental investigation on the enhanced cooling performance of a new crushed-rock revetment embankment in warm permafrost regions. Appl. Therm. Eng. 2017, 120, 121–129. [Google Scholar] [CrossRef]
- Yu, Q.H.; Fan, K.; Qian, J.; Guo, L.; You, Y.H. Key issues of highway construction in permafrost regions in China. China Sci. Sinica Technol. 2014, 44, 425–432. [Google Scholar]
- Yu, Q.H.; Fan, K.; You, Y.H.; Guo, L.; Yuan, C. Comparative analysis of temperature variation characteristics of permafrost roadbeds with different widths. Cold Reg. Sci. Technol. 2015, 117, 12–18. [Google Scholar] [CrossRef]
- Zhao, M.; Miao, M.Q.; Wang, Y.C. Boundary Layer Meteorology; China Meteorological Press: Beijing, China, 1991. [Google Scholar]
- An, W.D.; Wu, Z.W.; Ma, W. Interaction among Temperature, Moisture and Stress Fields in Frozen Soil; Lanzhou University Press: Lanzhou, China, 1990. [Google Scholar]
- Tao, W.Q. Numerical Heat Transfer; Xi’an Jiaotong University Press: Xi’an, China, 2004. [Google Scholar]
- Li, X.L.; Ma, W.; Mu, Y.H.; Dong, J.H.; Chen, L. Wind field and thermal performances of an expressway constructed with two separated crushed-rock embankments in high-altitude permafrost zones. Transp. Geotech. 2021, 26, 100447. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Lai, Y.M.; Li, D.Q.; Chen, W.; Tong, G.Q. Experimental study on ventilation characteristics of a concrete-sphere layer and a crushed-rock layer. Int. J. Heat Mass Transf. 2013, 59, 407–413. [Google Scholar] [CrossRef]
- Zhang, J.M.; Zhang, J.Z.; Liu, Y.Z. Study on the reasonable embankment height of Qinghai-Tibet railway in permafrost regions. China Railw. Sci. 2006, 27, 28–34. [Google Scholar]
- Zhu, L.N. Study of the adherent layer on different types of ground in permafrost regions on the Qinghai-Xizang Plateau. J. Glaciol. Geocryol. 1988, 10, 8–14. [Google Scholar]
- Qin, D.H. The Comprehensive Evaluating Report on the Environment Evolvement in West China; Science Press: Beijing, China, 2002; pp. 16–44. [Google Scholar]

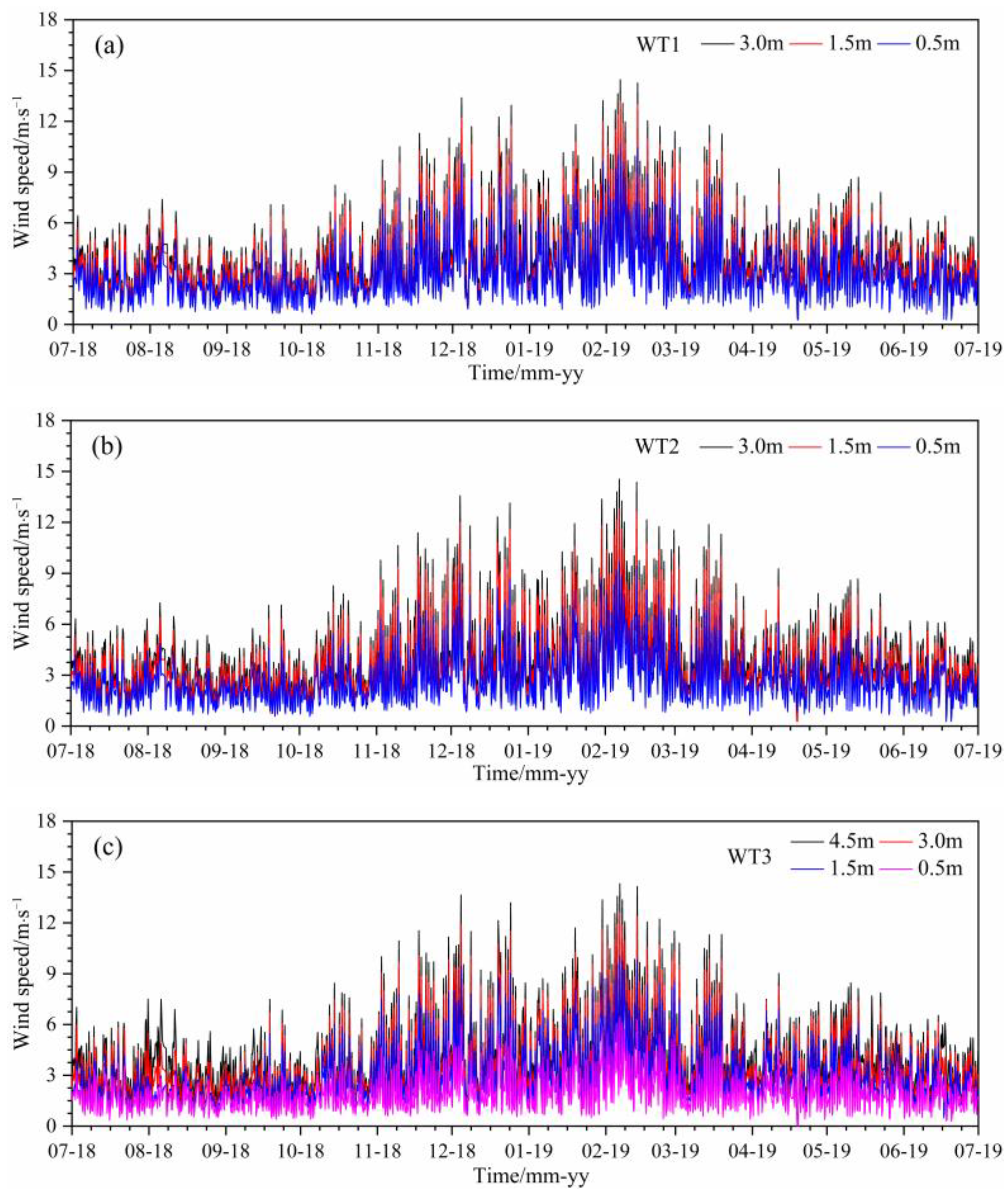
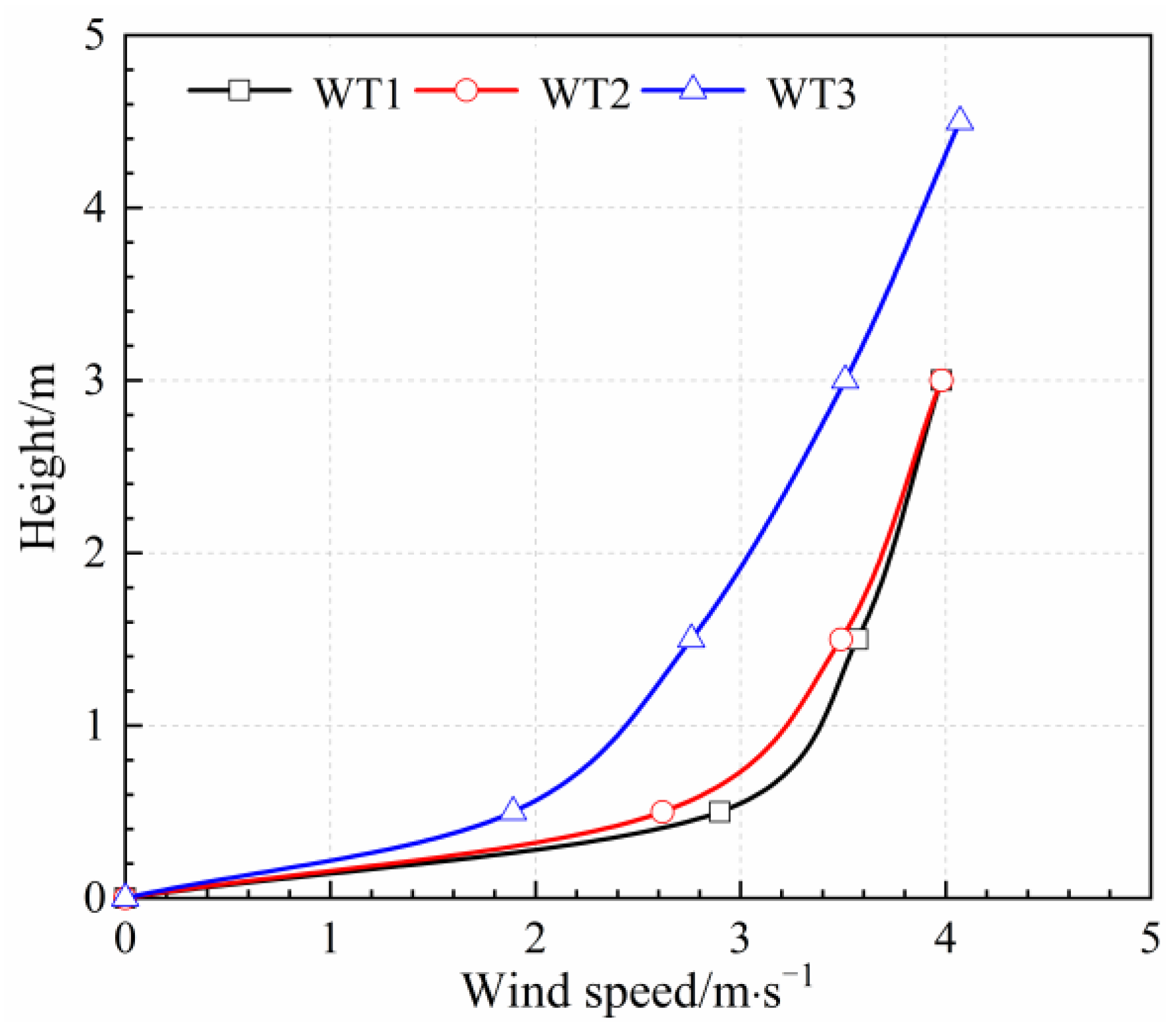

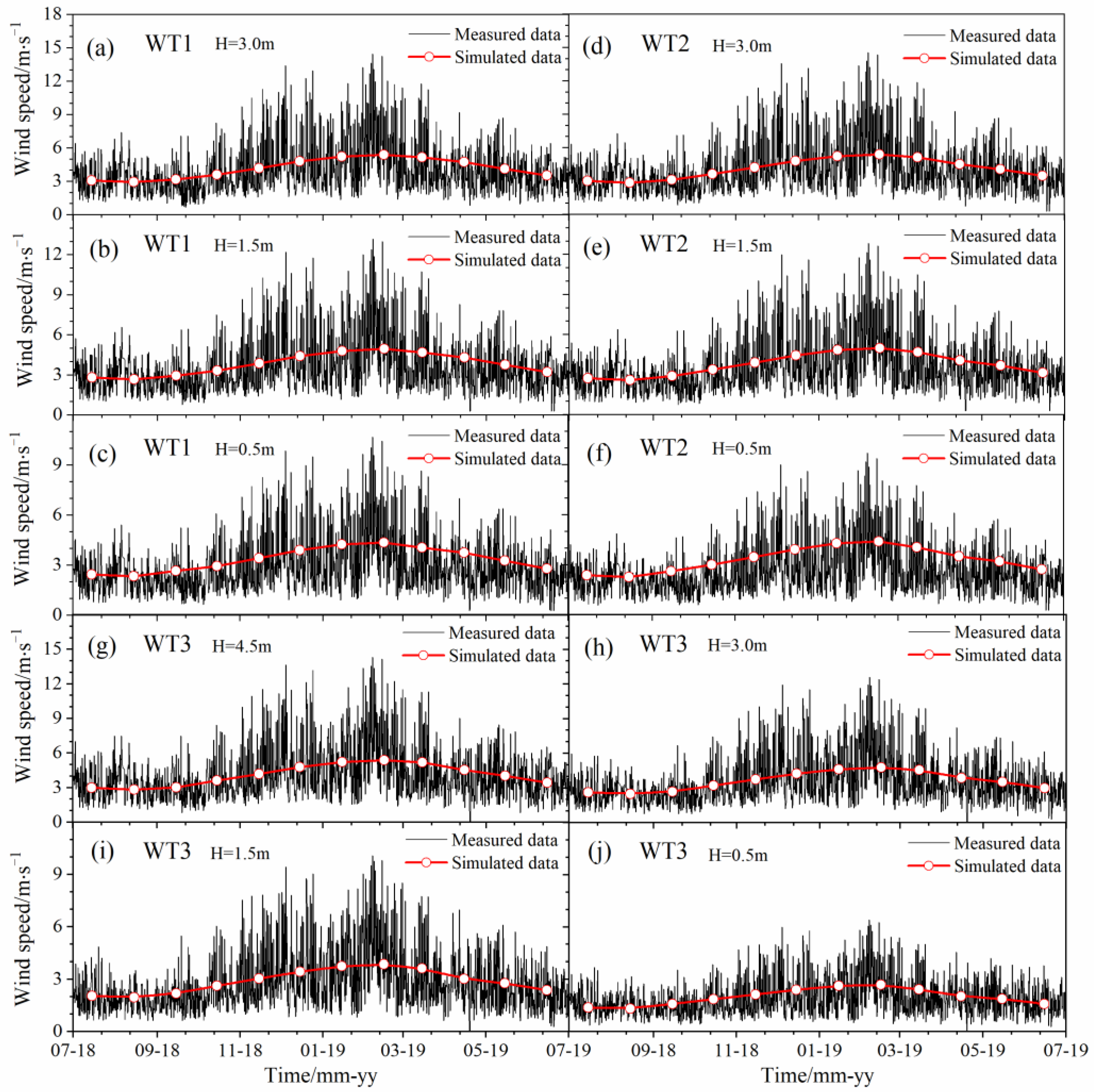


| Wind Speed/m·s−1 | WT1 | WT2 | WT3 |
|---|---|---|---|
| 1–2 | 4.67 | 4.12 | 8.24 |
| 2–3 | 23.35 | 23.63 | 35.16 |
| 3–4 | 28.30 | 28.85 | 26.92 |
| 4–5 | 23.63 | 23.08 | 15.93 |
| 5–6 | 10.44 | 10.44 | 8.79 |
| 6–7 | 5.77 | 5.77 | 2.20 |
| 7–8 | 2.47 | 2.75 | 2.47 |
| 8–9 | 1.10 | 1.10 | 0.27 |
| 9–10 | 0.27 | 0.27 | 0.00 |
| Physical Variable | Ca/(J × m−3 × °C−1) | λa/(W × m−1 × °C−1) | ρa/(kg × m−3) | μ/(kg × m−1 × s−1) |
|---|---|---|---|---|
| Air | 0.644 × 103 | 0.02 | 0.641 | 1.75 × 10−5 |
| Physical Variables | H/m | ρd/(kg × m−3) | ω/% | λ/(W × m−1 × °C−1) | C/(J × m−3 × °C−1) | ||
|---|---|---|---|---|---|---|---|
| λf | λu | Cf | Cu | ||||
| Embankment filling | 3.0~1.2 | 2060 | 6 | 1.40 | 1.15 | 1.543 × 106 | 1.882 × 106 |
| Crushed-rock | 1.2~0.0 | 2500 | 0 | 0.44 | 0.44 | 1.015 × 106 | 1.015 × 106 |
| Gravel and clayey | 0.0~−0.5 | 1800 | 15 | 1.82 | 1.60 | 2.022 × 106 | 2.621 × 106 |
| Gravel soil | −0.5~−2.0 | 1900 | 10 | 2.62 | 1.92 | 1.693 × 106 | 2.182 × 106 |
| Silty clay | −2.0~−8.0 | 1600 | 30 | 2.12 | 1.42 | 2.542 × 106 | 3.345 × 106 |
| Weathered mudstone | −8.0~−30.0 | 1800 | 15 | 1.82 | 1.60 | 2.032 × 106 | 2.633 × 106 |
| Parameters | T0 (°C) | A |
|---|---|---|
| Air (PF) | −3.5 | 11.5 |
| Natural ground surfaces (AB and EF) | −1.0 | 12 |
| Side slope surfaces (BC and DE) | 1.2 | 13 |
| Asphalt pavement surface (CD) | 3.0 | 15 |
| Type | Windward Slope Toe | Center | Leeward Slope Toe | |||
|---|---|---|---|---|---|---|
| WCRE | NCRE | WCRE | NCRE | WCRE | NCRE | |
| Permafrost table/m | −2.62 | −2.61 | −0.52 | −0.35 | −2.99 | −2.69 |
| Soil temperatures/°C | −0.61 | −0.63 | −0.60 | −0.94 | −0.40 | −0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Li, X.; Wu, X. Investigation of Wind Characteristics and Cooling Effects of Crushed-Rock Embankment with Different Pavement Widths in Permafrost Region. Atmosphere 2023, 14, 166. https://doi.org/10.3390/atmos14010166
Zhao H, Li X, Wu X. Investigation of Wind Characteristics and Cooling Effects of Crushed-Rock Embankment with Different Pavement Widths in Permafrost Region. Atmosphere. 2023; 14(1):166. https://doi.org/10.3390/atmos14010166
Chicago/Turabian StyleZhao, Hongting, Xiaolin Li, and Xiaopeng Wu. 2023. "Investigation of Wind Characteristics and Cooling Effects of Crushed-Rock Embankment with Different Pavement Widths in Permafrost Region" Atmosphere 14, no. 1: 166. https://doi.org/10.3390/atmos14010166
APA StyleZhao, H., Li, X., & Wu, X. (2023). Investigation of Wind Characteristics and Cooling Effects of Crushed-Rock Embankment with Different Pavement Widths in Permafrost Region. Atmosphere, 14(1), 166. https://doi.org/10.3390/atmos14010166






