Improved Gravity Wave Drag to Enhance Precipitation Simulation: A Case Study of Typhoon In-Fa
Abstract
:1. Introduction
2. Model and Method
2.1. Description of Typhoon In-Fa (2021)
2.2. The Method of “Scale-Aware” Orography Wave Drag Parameterization
2.3. CMA_GFS Model
2.4. Modification of the Gravity Wave Drag Scheme in CMA_GFS
2.4.1. The Operational Gravity Wave Drag Scheme
2.4.2. The Modification of Flow Blocking Drag
2.5. Numerical Experiment Setup and Evaluated Observations
3. Results
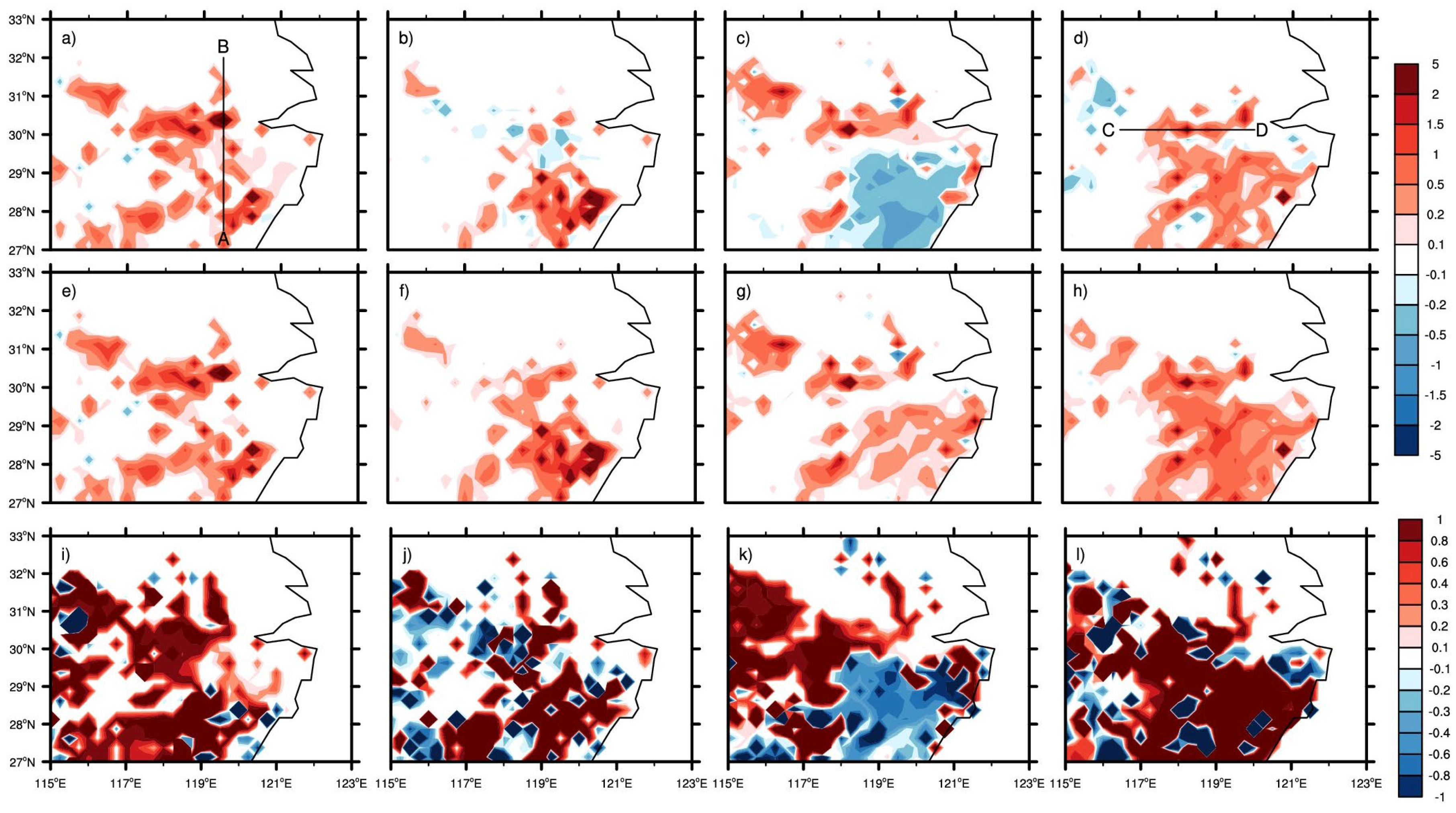
3.1. Spatial Distribution of the SSO
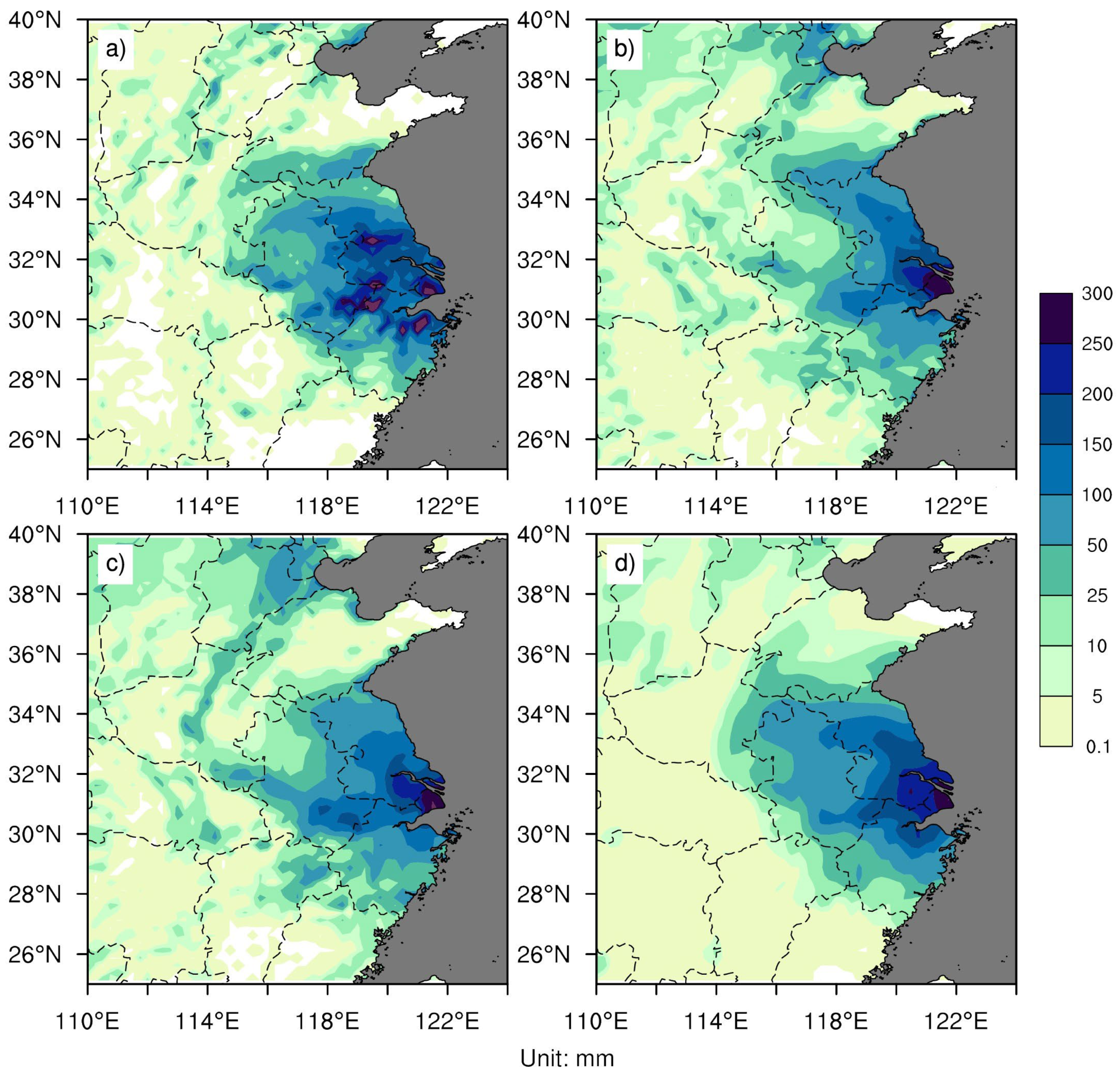
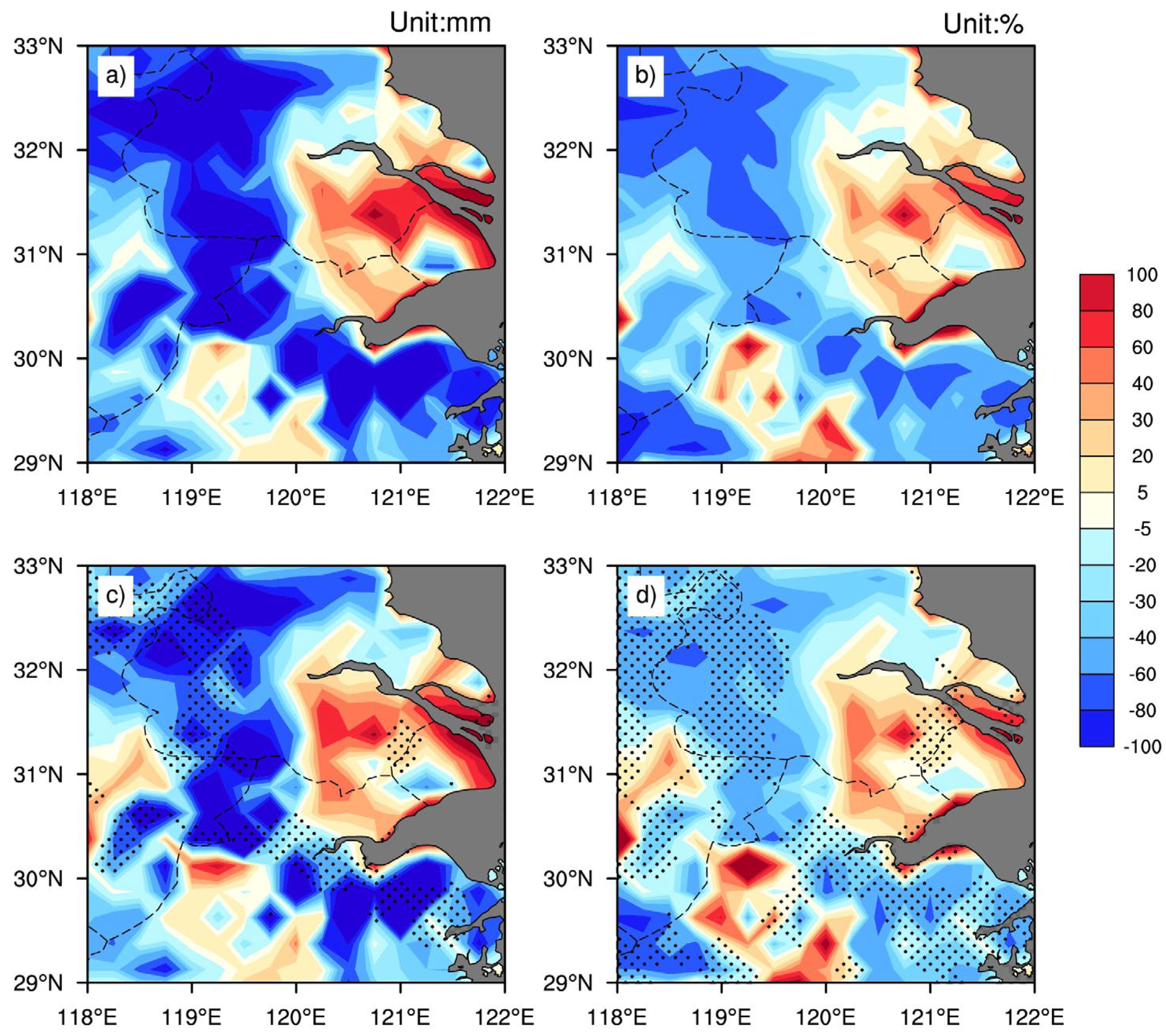
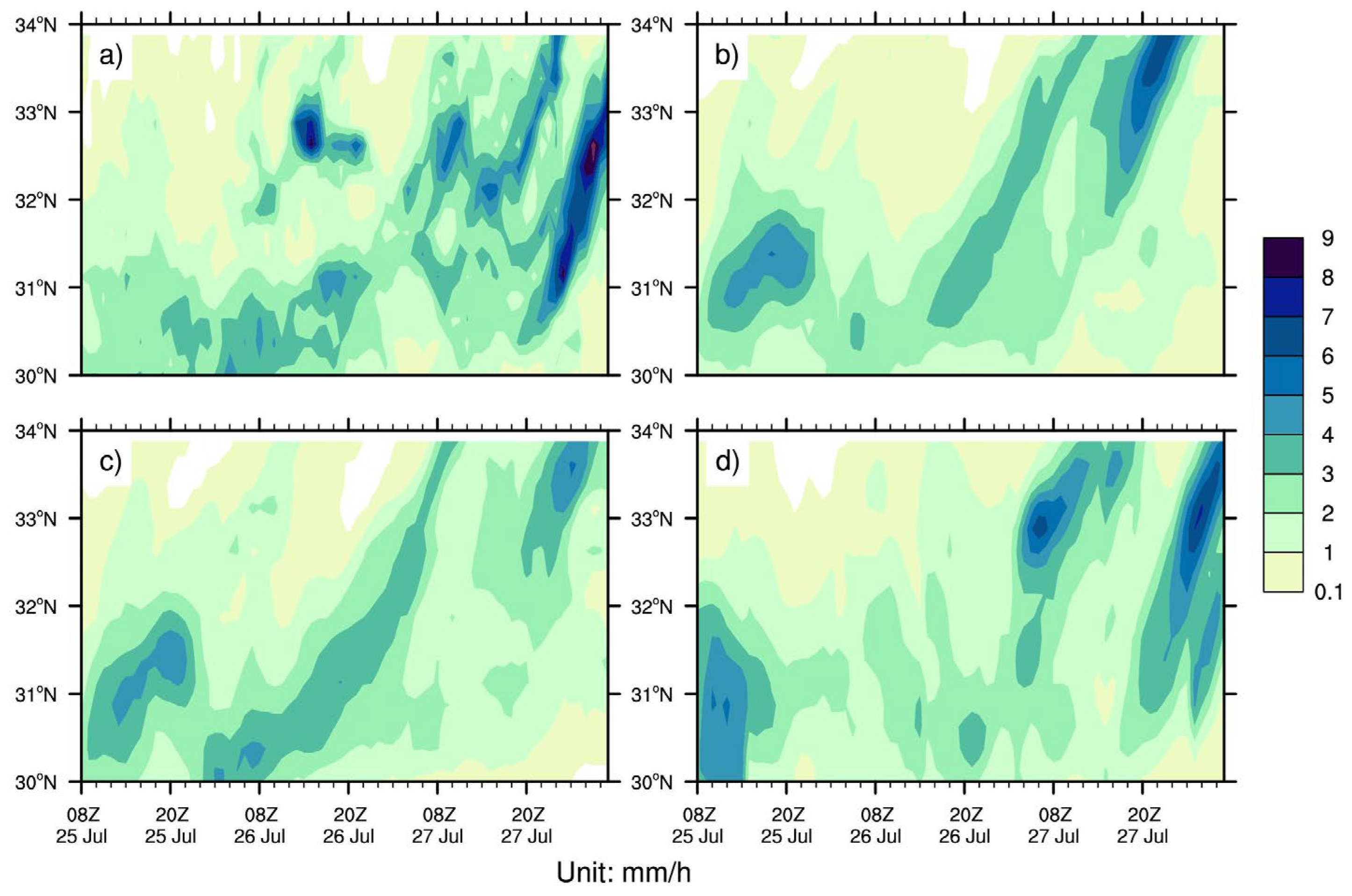
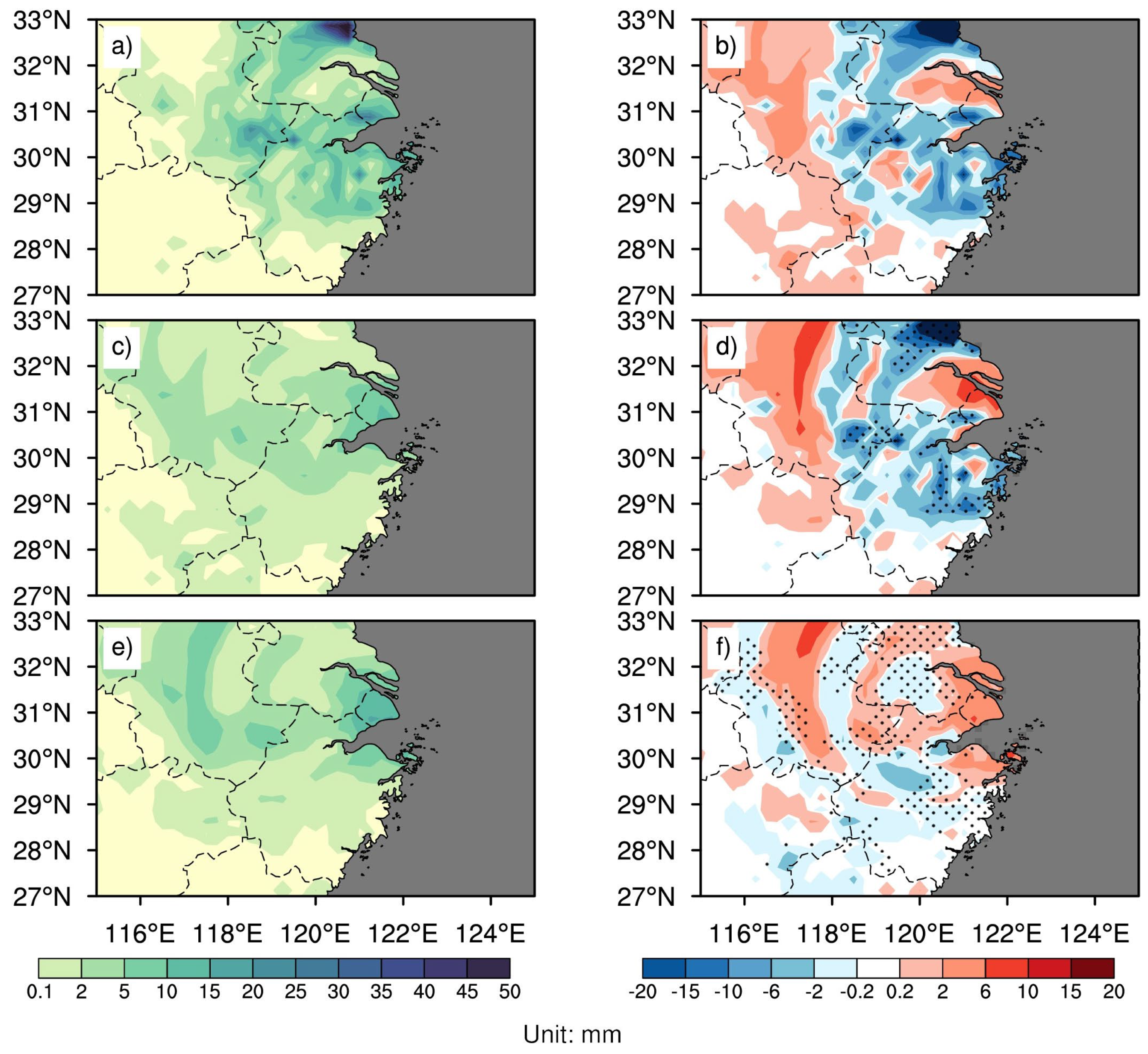
3.2. Influence of the Precipitation
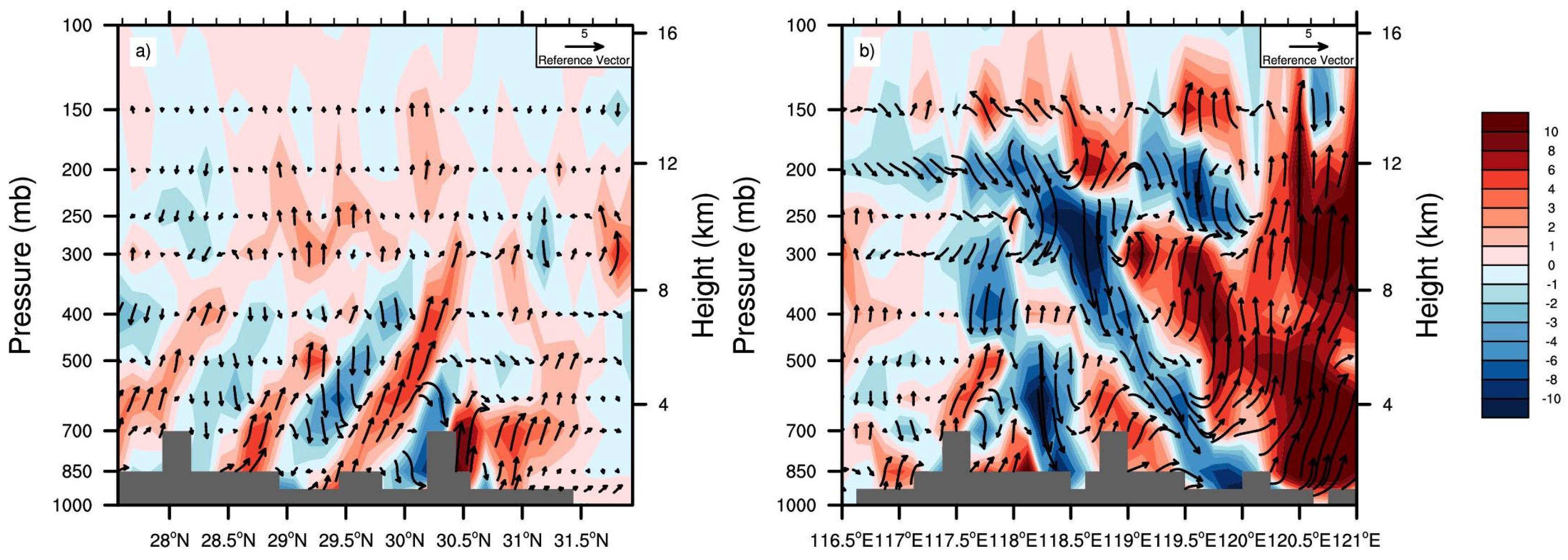
3.3. Influence of the Winds
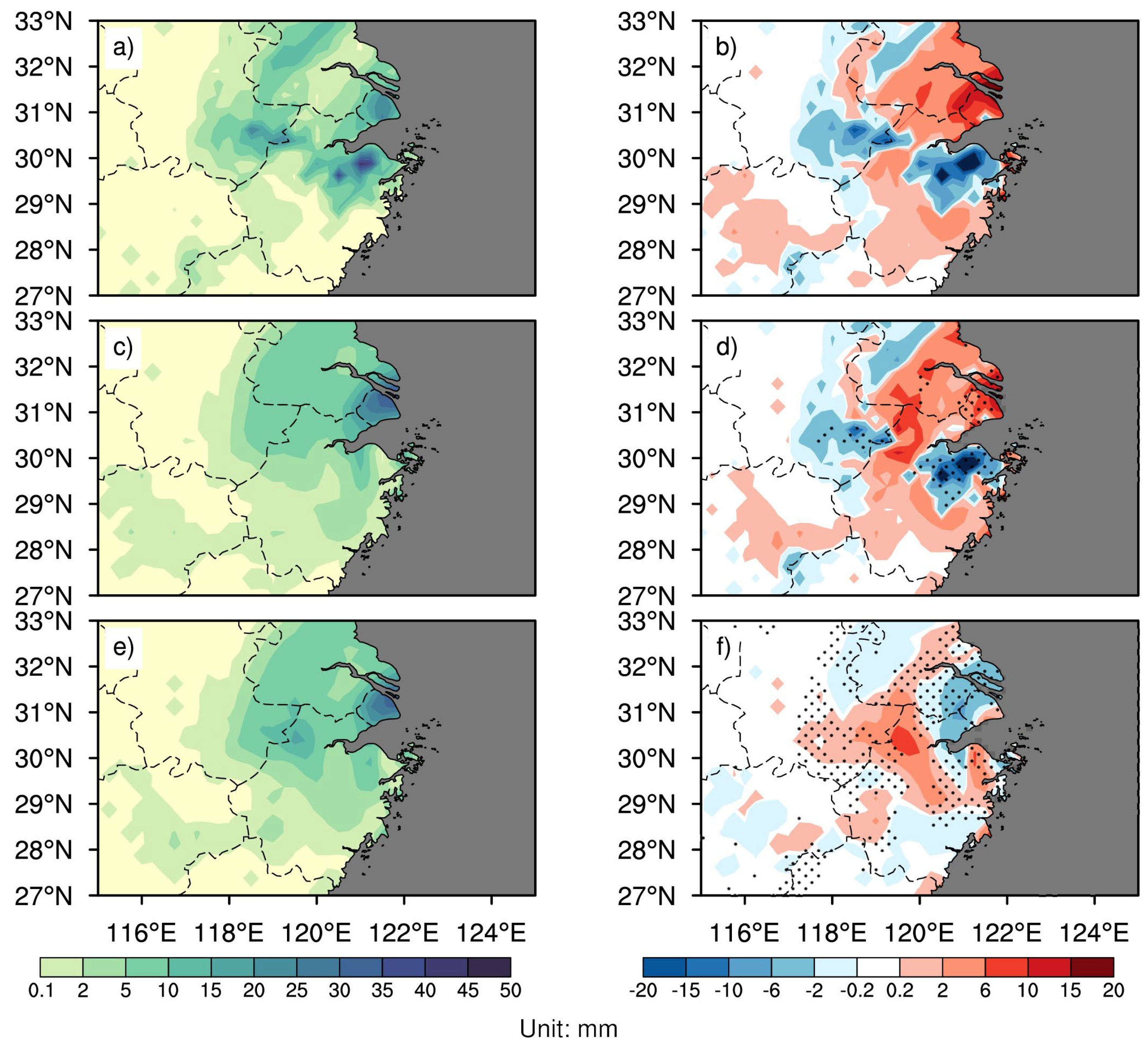
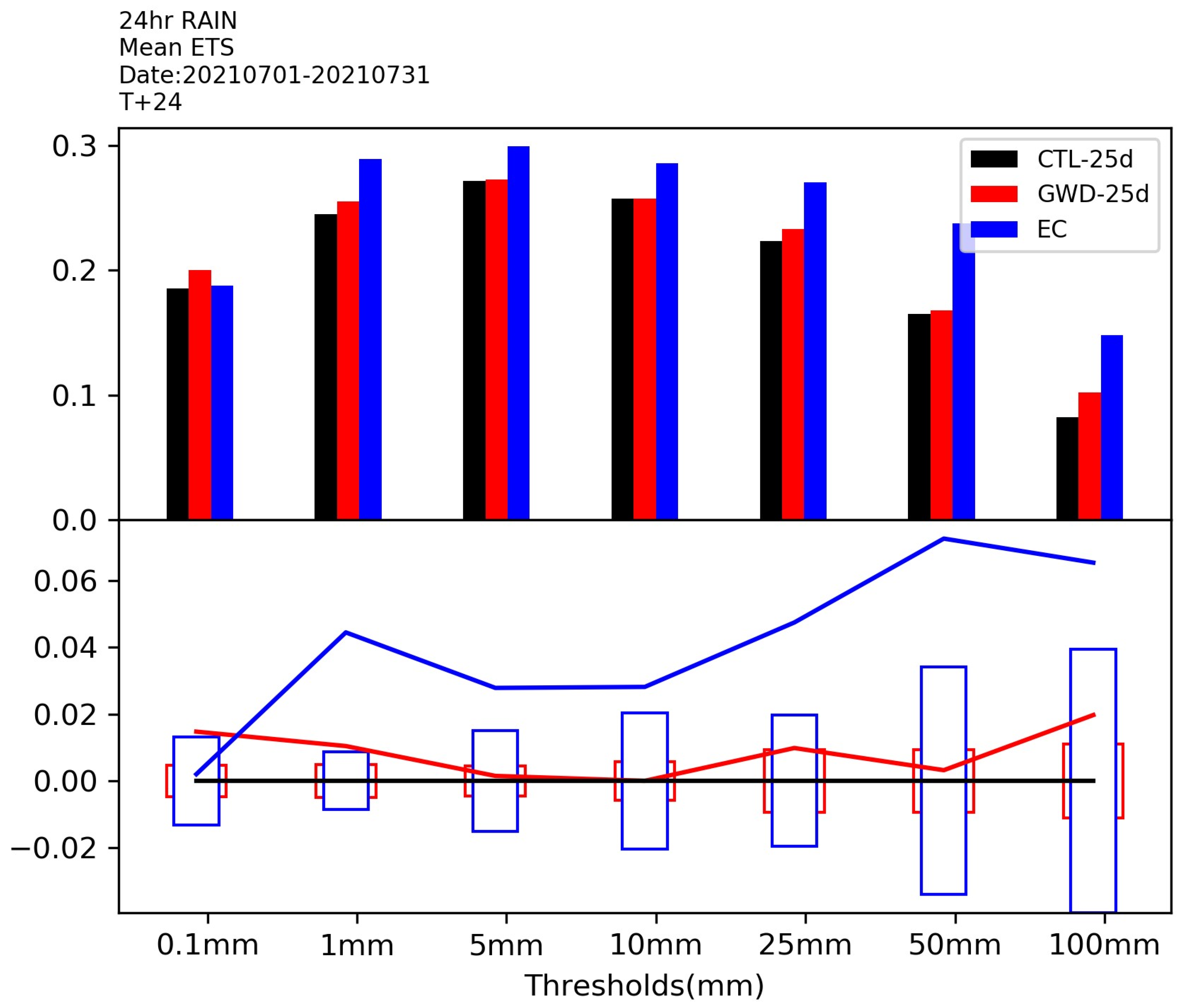
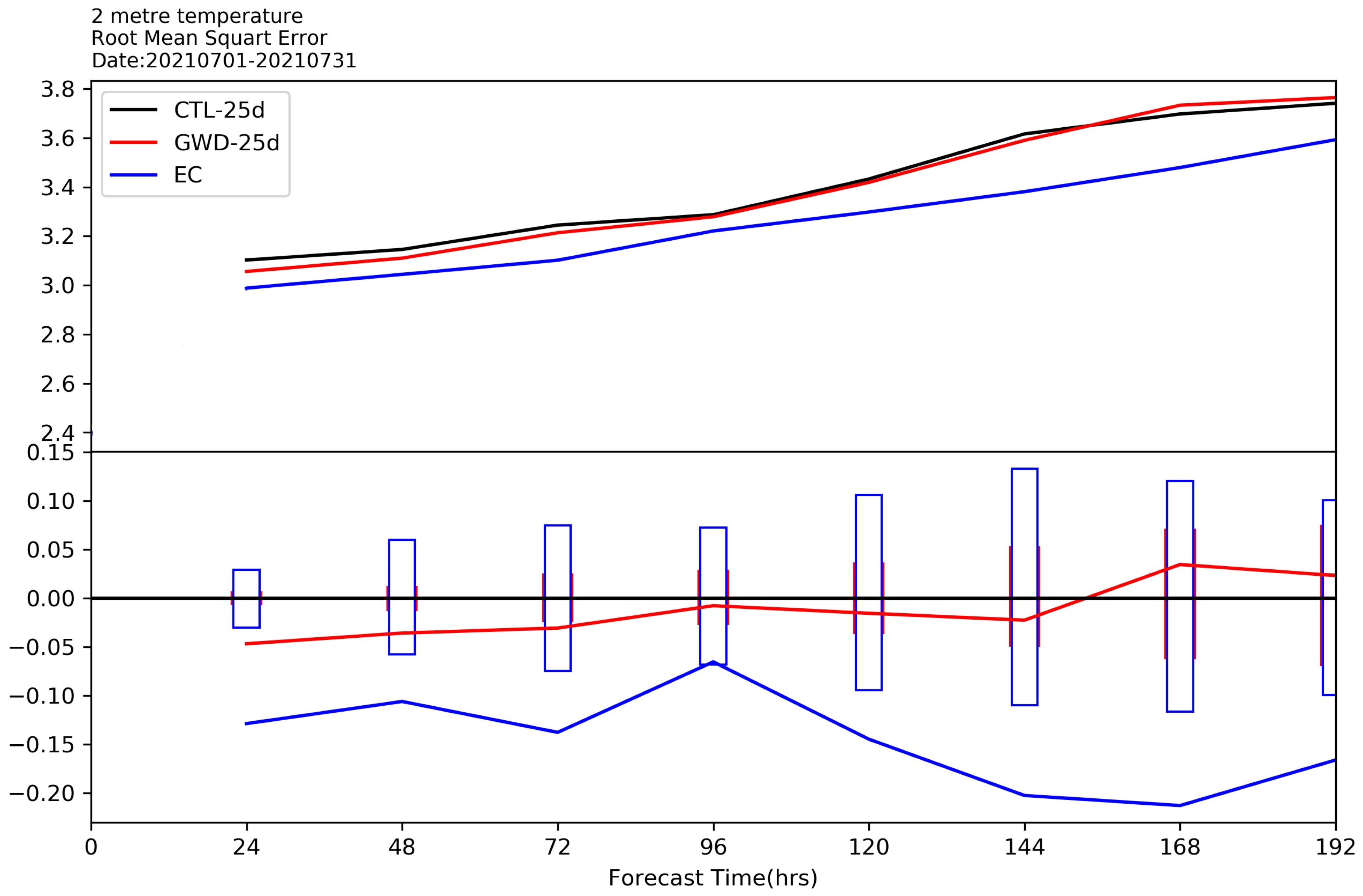
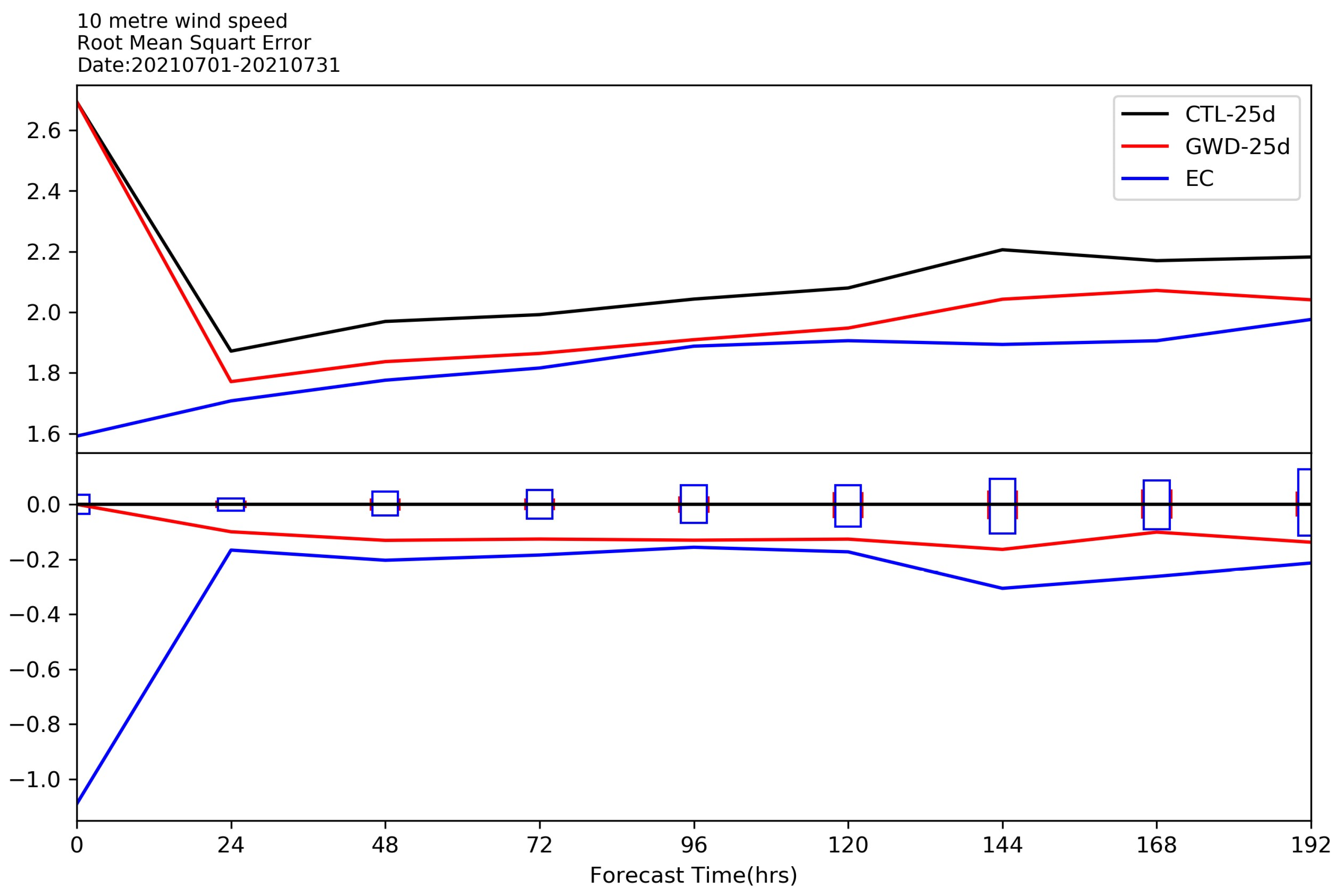
3.4. Medium-Range Forecast Results
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sandu, I.; Van Niekerk, A.; Shepherd, T.G.; Vosper, S.B.; Zadra, A.; Bacmeister, J.; Beljaars, A.; Brown, A.R.; Dörnbrack, A.; McFarlane, N.; et al. Impacts of Orography on Large-Scale Atmospheric Circulation. Npj Clim. Atmos. Sci. 2019, 2, 10. [Google Scholar] [CrossRef]
- Teixeira, M.A.C. The Physics of Orographic Gravity Wave Drag. Front. Phys. 2014, 2, 43. [Google Scholar] [CrossRef]
- Tsiringakis, A.; Steeneveld, G.J.; Holtslag, A.A.M. Small-Scale Orographic Gravity Wave Drag in Stable Boundary Layers and Its Impact on Synoptic Systems and near-Surface Meteorology: Orographic Gravity Wave Drag in Stable Boundary Layers. Q. J. R. Meteorol. Soc. 2017, 143, 1504–1516. [Google Scholar] [CrossRef]
- Van Niekerk, A.; Sandu, I.; Vosper, S.B. The Circulation Response to Resolved Versus Parametrized Orographic Drag Over Complex Mountain Terrains. J. Adv. Model. Earth Syst. 2018, 10, 2527–2547. [Google Scholar] [CrossRef]
- Elvidge, A.D.; Sandu, I.; Wedi, N.; Vosper, S.B.; Zadra, A.; Boussetta, S.; Bouyssel, F.; Niekerk, A.; Tolstykh, M.A.; Ujiie, M. Uncertainty in the Representation of Orography in Weather and Climate Models and Implications for Parameterized Drag. J. Adv. Model. Earth Syst. 2019, 11, 2567–2585. [Google Scholar] [CrossRef]
- Van Niekerk, A.; Sandu, I.; Zadra, A.; Bazile, E.; Kanehama, T.; Köhler, M.; Koo, M.; Choi, H.; Kuroki, Y.; Toy, M.D.; et al. COnstraining ORographic Drag Effects (COORDE): A Model Comparison of Resolved and Parametrized Orographic Drag. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002160. [Google Scholar] [CrossRef]
- Vosper, S.B.; Van Niekerk, A.; Elvidge, A.; Sandu, I.; Beljaars, A. What Can We Learn about Orographic Drag Parametrisation from High-resolution Models? A Case Study over the Rocky Mountains. Q. J. R. Meteorol. Soc. 2020, 146, 979–995. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, K.; Zhou, X.; Chen, D.; Lu, H.; Ouyang, L.; Chen, Y.; Lazhu; Wang, B. Synergy of Orographic Drag Parameterization and High Resolution Greatly Reduces Biases of WRF-Simulated Precipitation in Central Himalaya. Clim. Dyn. 2020, 54, 1729–1740. [Google Scholar] [CrossRef]
- Rodrigues Gonçalves, M.; Rozenman, G.G.; Zimmermann, M.; Efremov, M.A.; Case, W.B.; Arie, A.; Shemer, L.; Schleich, W.P. Bright and Dark Diffractive Focusing. Appl. Phys. B 2022, 128, 51. [Google Scholar] [CrossRef]
- Arbic, B.K. Incorporating Tides and Internal Gravity Waves within Global Ocean General Circulation Models: A Review. Prog. Oceanogr. 2022, 206, 102824. [Google Scholar] [CrossRef]
- Williams, E.F.; Zhan, Z.; Martins, H.F.; Fernández-Ruiz, M.R.; Martín-López, S.; González-Herráez, M.; Callies, J. Surface Gravity Wave Interferometry and Ocean Current Monitoring with Ocean-Bottom DAS. JGR Ocean. 2022, 127, e2021JC018375. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Zimmermann, M.; Efremov, M.A.; Schleich, W.P.; Case, W.B.; Greenberger, D.M.; Shemer, L.; Arie, A. Projectile Motion of Surface Gravity Water Wave Packets: An Analogy to Quantum Mechanics. Eur. Phys. J. Spec. Top. 2021, 230, 931–935. [Google Scholar] [CrossRef]
- Van Niekerk, A.; Vosper, S.B. Towards a More “Scale-aware” Orographic Gravity Wave Drag Parametrization: Description and Initial Testing. Q. J. R. Meteorol. Soc. 2021, 147, 3243–3262. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, Y. Impacts of the Thermal Effects of Sub-Grid Orography on the Heavy Rainfall Events along the Yangtze River Valley in 1991. Adv. Atmos. Sci. 2007, 24, 881–892. [Google Scholar] [CrossRef]
- Choi, H.-J.; Hong, S.-Y. An Updated Subgrid Orographic Parameterization for Global Atmospheric Forecast Models: Subgrid Orographic Parameterization. J. Geophys. Res. Atmos. 2015, 120, 12445–12457. [Google Scholar] [CrossRef]
- Zhong, S.; Chen, Z. Improved Wind and Precipitation Forecasts over South China Using a Modified Orographic Drag Parameterization Scheme. J. Meteorol. Res. 2015, 29, 132–143. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, X.; Wang, Y. Impacts of Subgrid Orographic Drag on the Summer Monsoon Circulation and Precipitation in East Asia. JGR Atmos. 2020, 125, e2019JD032337. [Google Scholar] [CrossRef]
- Deng, L.; Feng, J.; Zhao, Y.; Bao, X.; Huang, W.; Hu, H.; Duan, Y. The Remote Effect of Binary Typhoon Infa and Cempaka on the “21.7” Heavy Rainfall in Henan Province, China. JGR Atmos. 2022, 127, e2021JD036260. [Google Scholar] [CrossRef]
- Wang, L.; Gu, X.; Slater, L.J.; Lai, Y.; Zhang, X.; Kong, D.; Liu, J.; Li, J. Indirect and Direct Impacts of Typhoon In-Fa (2021) on Heavy Precipitation in Inland and Coastal Areas of China: Synoptic-Scale Environments and Return Period Analysis. Mon. Weather. Rev. 2023, 151, 2377–2395. [Google Scholar] [CrossRef]
- Yang, S.; Chen, B.; Zhang, F.; Hu, Y. Characteristics and Causes of Extremely Persistent Heavy Rainfall of Tropical Cyclone In-Fa (2021). Atmosphere 2022, 13, 398. [Google Scholar] [CrossRef]
- Sun, Z. The Extraordinarily Large Vortex Structure of Typhoon In-Fa (2021), Observed by Spaceborne Microwave Radiometer and Synthetic Aperture Radar. Atmos. Res. 2023, 292, 106837. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Zhang, L.; Zheng, H.; Huang, X. A Comparison of Convective and Stratiform Precipitation Microphysics of the Record-Breaking Typhoon In-Fa (2021). Remote Sens. 2022, 14, 344. [Google Scholar] [CrossRef]
- Huang, X.; Chan, J.C.L.; Zhan, R.; Yu, Z.; Wan, R. Record-breaking Rainfall Accumulations in Eastern China Produced by Typhoon In-fa (2021). Atmos. Sci. Lett. 2023, 24, e1153. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, T.; Xie, L.; Zhang, R.-H.; Zhang, W.; Xu, H.; Cao, F.; Chen, B. Tropical Cyclone over the Western Pacific Triggers the Record-Breaking ‘21/7’ Extreme Rainfall in Henan, Central-Eastern China. Environ. Res. Lett. 2022, 17, 124003. [Google Scholar] [CrossRef]
- Rao, C.; Chen, G.; Ran, L. Effects of Typhoon In-Fa (2021) and the Western Pacific Subtropical High on an Extreme Heavy Rainfall Event in Central China. J. Geophys. Research. 2023, 128, e2022JD037924. [Google Scholar] [CrossRef]
- Liu, L.; Ran, L.; Sun, X. Analysis of the Structure and Propagation of a Simulated Squall Line on 14 June 2009. Adv. Atmos. Sci. 2015, 32, 1049–1062. [Google Scholar] [CrossRef]
- Zhuang, Y. Failure and Disaster-Causing Mechanism of a Typhoon-Induced Large Landslide in Yongjia, Zhejiang, China. Landslides 2023, 20, 2257–2269. [Google Scholar] [CrossRef]
- Wu, M.; Dong, M.; Chen, F.; Yu, Z.; Luo, Y. A Comparison of Different Station Data on Revealing the Characteristics of Extreme Hourly Precipitation Over Complex Terrain: The Case of Zhejiang, China. Earth Space Sci. 2023, 10, e2023EA002925. [Google Scholar] [CrossRef]
- Huang, B.; Chen, D.; Li, X.; Li, C. Improvement of the Semi-Lagrangian Advection Scheme in the GRAPES Model: Theoretical Analysis and Idealized Tests. Adv. Atmos. Sci. 2014, 31, 693–704. [Google Scholar] [CrossRef]
- Chen, D.; Xue, J.; Yang, X.; Zhang, H.; Shen, X.; Hu, J.; Wang, Y.; Ji, L.; Chen, J. New Generation of Multi-Scale NWP System (GRAPES): General Scientific Design. Sci. Bull. 2008, 53, 3433–3445. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative Transfer for Inhomogeneous Atmospheres: RRTM, a Validated Correlated-k Model for the Longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Han, J.; Pan, H.-L. Revision of Convection and Vertical Diffusion Schemes in the NCEP Global Forecast System. Weather. Forecast. 2011, 26, 520–533. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Q.; Sun, J. Modification of Cumulus Convection and Planetary Boundary Layer Schemes in the GRAPES Global Model. J. Meteorol. Res. 2015, 29, 806–822. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Pan, H.-L. Nonlocal Boundary Layer Vertical Diffusion in a Medium-Range Forecast Model. Mon. Wea. Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Q.; Zhao, C.; Li, Z.; Wu, X.; Chen, J.; Yu, F.; Sun, J.; Shen, X. Impacts of Transition Approach of Water Vapor-Related Microphysical Processes on Quantitative Precipitation Forecasting. Atmosphere 2022, 13, 1133. [Google Scholar] [CrossRef]
- Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G.; et al. The Common Land Model. Bull. Am. Meteorol. Soc. 2003, 84, 1013–1024. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Arakawa, A. Improvement of Orographic Gravity Wave Parameterization Using a Mesoscale Gravity Wave Model. J. Atmos. Sci. 1995, 52, 1875–1902. [Google Scholar] [CrossRef]
- Lott, F.; Miller, M.J. A New Subgrid-Scale Orographic Drag Parametrization: Its Formulation and Testing. Q. J. R. Meteorol. Soc. 1997, 123, 101–127. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Good, S.; Fiedler, E.; Mao, C.; Martin, M.J.; Maycock, A.; Reid, R.; Roberts-Jones, J.; Searle, T.; Waters, J.; While, J.; et al. The Current Configuration of the OSTIA System for Operational Production of Foundation Sea Surface Temperature and Ice Concentration Analyses. Remote Sens. 2020, 12, 720. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A High Spatiotemporal Gauge-Satellite Merged Precipitation Analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, J.; Wang, D.; Zhang, B.; Chen, F.; Wan, Z.; Sun, S. The GRAPES Evaluation Tools Based on Python (GetPy). CCF Trans. High Perform. Comput. 2022, 1–13. [Google Scholar] [CrossRef]



| Experiments Name | Horizontal Resolution |
|---|---|
| CTL-25d | Global model, 0.25° |
| CTL-125d | Global model, 0.125° |
| GWD-25d | Global model, 0.25° |
| GWD-125d | Global model, 0.125° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Yu, F.; Su, Y.; Zhang, H.; Chen, Q.; Sun, J. Improved Gravity Wave Drag to Enhance Precipitation Simulation: A Case Study of Typhoon In-Fa. Atmosphere 2023, 14, 1801. https://doi.org/10.3390/atmos14121801
Liu K, Yu F, Su Y, Zhang H, Chen Q, Sun J. Improved Gravity Wave Drag to Enhance Precipitation Simulation: A Case Study of Typhoon In-Fa. Atmosphere. 2023; 14(12):1801. https://doi.org/10.3390/atmos14121801
Chicago/Turabian StyleLiu, Kun, Fei Yu, Yong Su, Hongliang Zhang, Qiying Chen, and Jian Sun. 2023. "Improved Gravity Wave Drag to Enhance Precipitation Simulation: A Case Study of Typhoon In-Fa" Atmosphere 14, no. 12: 1801. https://doi.org/10.3390/atmos14121801
APA StyleLiu, K., Yu, F., Su, Y., Zhang, H., Chen, Q., & Sun, J. (2023). Improved Gravity Wave Drag to Enhance Precipitation Simulation: A Case Study of Typhoon In-Fa. Atmosphere, 14(12), 1801. https://doi.org/10.3390/atmos14121801






