Abstract
We investigated the liquid water path and global solar irradiance (Q) at ground level according to the ICON model; CLOUDNET measurements in Lindenberg, Munich, and Jülich; and BSRN observations in Lindenberg. This research is focused on stratiform non-precipitating clouds. The liquid water path (LWP) is underestimated, while Q is overestimated. The lower LWP is due to liquid water content underestimation practically in all atmosphere layers and a lower frequency of liquid cloud occurrence compared to observations. This is partly associated with the structure of the cloud nucleation scheme of the ICON model and with the default cloud condensation nuclei (CCN) number concentration. An increase in CCNs from 250 cm−3 (typical background value for the region of interest) to 1700 cm−3 (characteristic of polluted continental clouds) leads to an increase in the grid-scale liquid water path by 40% and a decrease in Q by 12% in overcast conditions. However, we also showed that the liquid water path is not a key factor of Q overestimation. The main factor is an inaccurate description of the cloud spatial structure, where the correct prediction of the ratio of direct to global irradiance as a spatial characteristic of clouds plays a more important role than the standard cloud fraction.
1. Introduction
Solar irradiance is one of the most important meteorological characteristics; it significantly affects the temperature regime of the atmosphere and the underlying surface [1]. The quality of solar irradiance prediction is determined by a set of atmospheric parameters. Cloudiness is still one of the most difficult issues in the successful numerical forecasting of solar irradiance due to its large scale of spatial and temporal inhomogeneity and uncertainties in optical and microphysical properties [2,3]. For example, the difference in solar irradiance forecasts between “more cloudy” and “less cloudy” atmospheric conditions can reach hundreds of W/m2 [4].
The solar irradiance forecast is directly related to the accuracy of the cloud macro- and microphysical properties [5]. Bulk microphysical schemes are mainly focused on the precipitation forecast rather than on the detailed prediction of cloud macrophysical properties. The effect of an inaccurate forecast of liquid water path (LWP) and size of cloud particles on the cloud–radiation interaction is shown in many studies. Sotiropoulou et al. [6] showed the effect of the cloud parametrization scheme on the summer Arctic clouds and global solar irradiance in the European Centre for Medium-Range Weather Forecasts (ECMWF) model. The study [7] focused on the overestimation of the Weather Research and Forecasting (WRF) model-simulated liquid water path by a factor of 1.1–1.6 in the case of high cloud condensation nuclei content. Dipu et al. [8] found an underestimation of the liquid water path in the COnsortium of Small-Scale MOdelling (COSMO) mesoscale model with the two-moment microphysical scheme in comparison with satellite observations.
At present, cloud–aerosol interaction processes are considered in the development of mesoscale numerical weather prediction (NWP) models [9,10]. Accounting for the impact of cloud condensation nuclei (CCNs) on the liquid water content and the effective radius of cloud droplets in NWP models contributes to the successful evaluation of cloud structure [11]. On the other hand, the operational numerical weather prediction models still work with the bulk microphysical schemes, which use the saturation adjustment approach [12]. The saturation adjustment approach contributes to a lower sensitivity of cloud particle size distribution to CCN content compared to bin microphysical schemes [13]. Wang et al. [14] found a lower simulated liquid water content of maritime warm stratocumulus clouds due to a low condensation rate and high evaporation rate in the bulk scheme compared to the bin scheme in the WRF model.
Global irradiance forecasts also depend on the simulated cloud fraction. The breakthrough of recent decades in the field of weather prediction has not helped to solve many difficulties related to the measurement and forecasting of cloud fractions [15]. Diagnostic and prognostic approaches are used in numerical weather prediction models for cloud fractions. Diagnostic schemes are based on parametrizations of the cloud fraction at each model level using relative humidity or cloud water content [16]. Prognostic schemes suggest an evaluation of cloud fractions through consideration of cloud sources and sinks [17]. Computationally inexpensive but highly efficient diagnostic schemes are widely spread in numerical weather prediction models. However, their physical basis is not able to take into account the variety of cloud processes [18], which results in cloud fraction and solar irradiance errors.
Previous studies of the ICOsahedral Nonhydrostatic (ICON) model have been focused on the evaluation of total cloud cover using satellite data and tuning of the model [19,20,21]. Grundner et al. [22] presented the first parametrization of cloud cover that is based on the ICON model and neural networks. Studies of specific humidity [23] and water vapor path [24] showed a good agreement between ICON-simulated and observed results. De Lucia et al. [25] compared the results of the ICON model with various options for cloud microphysics in Italy and established the single-moment scheme as the best option. The study [26] evaluated ice and snow particles using radar observations and showed a good agreement between the simulated radar reflectivity and surface precipitation rate.
This paper presents a comparative study of the liquid water path according to the ICON model and ground-based and satellite measurements as well as an analysis of the effect of the CCN number concentration on the liquid water path forecast. We also analyze the influence of cloud spatial structure on solar irradiance prediction. This work is structured as follows: Section 2 provides a brief description of the ICON model and the ecRad radiation scheme, as well as measurement data and operating procedures. Section 3 describes the most important results of the analysis of ICON model experiments together with ground-based and satellite observations. Conclusions and a critical evaluation of the results are presented in Section 4 and Section 5.
2. Model and Methods
2.1. ICON Model Configuration
The ICON model is a nonhydrostatic model of weather and climate forecasting and is used operationally in the member countries of the COSMO consortium [27]. Its implementation (ICON-Ru model) operates in the Hydrometeorological Research Center of Russia [28]. Version 2.6.5 of the ICON model was used to perform numerical experiments. ICON separately considers grid-scale clouds, which are prognostic, and subgrid-scale clouds, which are treated diagnostically. In particular, the characteristics of grid-scale (prognostic) clouds in the model are determined by a two-moment microphysical scheme [29]. The nucleation of cloud droplets is represented by the Segal–Khain scheme [30]. The scheme uses the specified number concentration of cloud condensation nuclei, parameters of aerosol size distribution, and grid-scale vertical velocity at the cloud base. The specified CCN value is constant in the lowest 2 km and decreases exponentially above 2 km. As a result, the scheme calculates the profile of particles that are available for condensation in the presence of an appropriate amount of excess water vapor. Warm cloud processes are described according to [30,31]. Ice nucleation processes are presented according to [32,33].
The diagnostic cloud scheme in ICON is used to describe the liquid and ice water content and cloud fraction for subgrid-scale clouds, that is, clouds that cannot be simulated explicitly due to the model’s spatial resolution. The diagnostic clouds are used by the radiation scheme, but not in the microphysical simulations. The diagnostic scheme is based on the division of subgrid clouds into stratiform and convective components. A detailed description of the subgrid cloud scheme is shown in [34]. The specific liquid water content of the subgrid-scale stratiform clouds is assumed to be 0.5% of the saturation specific humidity. The convective subgrid-scale specific liquid and ice water contents are 1% of the saturation specific humidity, but not less than 0.2 g/kg. The cloud fraction at each model level is assumed equal to 1 if there is grid-scale liquid and/or ice water content at the level. If there is no grid-scale cloud fraction, the subgrid-scale convective (Nsgs,con) and/or stratiform (Nsgs,strat) clouds are calculated. Nsgs,con is a function of the geometric thickness of the convective cloud (H, m):
Nsgs,strat is calculated based on the total specific moisture content in gaseous, solid, and liquid form (qtot); saturation specific humidity (qsat); and atmospheric pressure at the model level (p) and at the surface (ps):
The final value of the subgrid-scale cloud fraction is calculated from the stratiform and convective components as follows:
Additionally, the upper troposphere ice cloud fraction is corrected according to [34]. This scheme is also operational in the COnsortium of Small-scale MOdeling, Russian realization (COSMO-Ru) model.
Radiative processes in the ICON model are represented by the ecRad scheme with the Monte Carlo Independent Column Approximation (McICA) solver [35,36]. We used the optical properties of liquid clouds according to the Suite of Community Radiation Codes based on Edwards and Slingo 1996 (SOCRATES) [37] and according to [38,39] for ice clouds. The McICA solver was applied in numerical experiments due to its highest computational efficiency among those presented in the ecRad scheme. Cloud overlap is described by an exponential random scheme [40].
2.2. Experimental Data
Experimental data included both satellite and ground-based measurements. Observations of the CLOUDNET ground-based measurement network [41,42] at the sites in Lindenberg [43], Jülich [44], and Munich were used for characterizing the cloud parameters. The retrievals of liquid water path (LWP) are based on brightness temperature measured by a two-channel microwave radiometer (MWR), with an additional calibration for clear sky cases and validation by lidar data [45]. The liquid water content is retrieved based on the LWP data in the adiabatic approximation. Taking into account the uncertainties, we considered the liquid water path higher than 30 g/m2 [45]. The upper limit of MWR-retrieved LWP was set equal to 800 g/m2 to restrict the analysis to non-precipitating clouds following [46].
Additionally, we used cloud characteristic retrievals from the MODerate resolution Imaging Spectroradiometer (MODIS; Collection 6.1 Level 2, LAADS DAAC system, https://ladsweb.modaps.eosdis.nasa.gov, accessed on 14 October 2023) spectroradiometer [47] for the domain of numerical experiments. The MODIS algorithm of cloud characteristic retrievals above a snowless surface is based on measurements at two wavelengths: 2.1 microns, in the water absorption spectrum, and 650 nm, outside the absorption spectrum, where the surface reflectivity is minimized [48]. The satellite-based LWP is calculated according to cloud optical thickness and cloud droplet effective radius retrievals [48]. We used the pixels with MODIS measurement errors of liquid water path and cloud optical thickness less than 20%. This threshold was taken according to the uncertainty of MODIS retrievals [47].
The study used measurements of the 3-hourly low-level cloud fraction at the Lindenberg site from the database of the Hydrometeorological Research Center of Russia, as well as hourly observations of the total cloud fraction (https://rp5.ru/Weather_archive_in_Lindenberg, accessed on 14 October 2023).
We also used high-precision measurements of global and diffuse solar irradiance at ground level from the Lindenberg Baseline Surface Radiation Network (BSRN) site (https://bsrn.awi.de, accessed on 14 October 2023) and direct irradiance at the horizontal surface, calculated as the difference between them.
Some additional information on measurements, their spatial and temporal resolutions, and statistical characteristics are shown in Table 1. The measurement uncertainties of cloud parameters are presented in the form of average measurement errors given for each moment of observation by data developers [41,48]. Measurement errors of BSRN data are provided in accordance with network standards [49]. We used the BSRN data sample at a solar elevation higher than 15°.

Table 1.
Measurement data and their main characteristics.
The statistical characteristics of clouds in Table 1 show that observations lie in the range of typical values of cloud characteristics in midlatitudes [42,45,50]. The liquid water path in 91% of cases does not exceed 400 g/m2, which corresponds to non-precipitation clouds [51]. The liquid water content in 80% of cases is in the range from 0.01 to 0.5 g/m3. The cloud optical thickness according to the MODIS data does not exceed 20 in 75% of cases, which corresponds to typical values in midlatitudes [52,53]. The observation cases under consideration include both liquid clouds and mixed-phase clouds. In mixed-phase clouds, the ice water content exceeds 0.012 g/m3 in no more than 25% of cases (see Table 1).
2.3. Experiment Design
Numerical experiments were performed over the territory of Europe for domains with a grid spacing of 4.4, 2.2, and 1.1 km and 90 vertical levels. We analyzed the ICON results with a grid spacing of 1.1 km (Figure 1). The model was initialized using the data of the global version of the ICON model with a grid spacing of 13 km. Boundary conditions were provided with a 3 h time step. The experiments were performed for 32 selected days during the warm (snowless) period of 2021 (7 spring days, 19 summer days, 6 autumn days) with a lead time of 36 h. Limiting the study to a warm period avoids large errors associated with the uncertainty of surface albedo evaluation. The choice of the numerical experimental region was determined by the availability of both radar and satellite cloud observations. The forecast started at 12 UTC of the previous day relative to the selected one. Only the last 24 h of the forecast were analyzed to avoid the spin-up period. The selection of days for numerical experiments was carried out according to cloud and radiation measurements at the Lindenberg site with the most complete dataset and under several measuring conditions of stratiform clouds at a solar elevation higher than 15°, without precipitation (less 0.5 mm per day) and a good quality of observations, marked by the corresponding labels. By excluding the situations with precipitation from the analysis, we avoid its influence on cloud droplet distribution, as well as on low-quality measurements in conditions with raindrops on the domes of instruments [46,54]. The BSRN, CLOUDNET, and ICON data were averaged with an hourly resolution. The nearest neighbor method was used for comparisons of model grid data with point observations [55]. We took into account only non-zero simulated and observed values of the liquid water content, the liquid water path, the cloud optical thickness, and the number concentration of cloud droplets in the analysis. The analysis of the profiles was carried out layer by layer.
Figure 1.
The domain (black line) of the ICON simulations with 1.1 km grid spacing and CLOUDNET sites. The figure was created using Google Earth Pro.
Observations and retrievals of cloud droplet number concentrations (Nd) are associated with many methodological assumptions, instrumental limitations and uncertainties [56,57], and the dependence of cloud condensation nuclei (CCNs) on aerosol content. Therefore, the range of Nd values over the European territory is very wide [58,59]. The typical Nd is about 200–300 cm−3 according to [60,61] or ~100–500 cm−3 according to [62]. We used Nd retrievals according to the 1 km resolution MODIS satellite data following the methodology described in [63] and taking into account the restrictions on solar elevation, instrument zenith angle, cloud phase, number of cloud layers, cloud optical thickness, and cloud droplet effective radius. To filter the pixels with precipitation, we additionally applied a restriction on cloud droplet effective radius less than 18 μm [64].
We used the method described in [65] for the droplet concentration (Nd, cm−3) retrievals with the application of the liquid cloud optical thickness (COTliq) and liquid water path (LWP):
where k1 is equal to 157.216 kg5/2 m−8. The average obtained Nd was 245 ± 25 cm−3, with daily Nd varying from 109 to 472 cm−3 for the selected 32 days. Thus, the obtained Nd is close to the typical values in Europe.
The most accurate estimates of the CCN content and its nucleation activity can be obtained using specific experiments [66]. However, such an approach is too detailed for the task of weather forecasting. The application of the background CCN content is more appropriate for weather prediction tasks. Based on the analysis given in [67,68], we can assume that the satellite-derived number concentrations of cloud droplets (Nd) provide information about minimum CCN (CCNmin) content at the cloud base.
Thus, we can apply the obtained Nd values as an estimate of the observed minimum CCN content at the cloud base. The default CCN value in the ICON model, equal to 250 cm−3, is very close to the average satellite-obtained value of 245 cm−3. As a result, the number concentration of cloud condensation nuclei (NCCN) was set to 250 cm−3 in the two-moment microphysical scheme. We should also note that, in the model, not all of the CCNs can be activated as the cloud droplets inside the cloud [30]. This effect is discussed below, in Section 3.
3. Results
3.1. Liquid Water Content
Figure 2 shows the medians of CLOUDNET-observed liquid water content and ICON-simulated grid-scale liquid water content (Figure 2a,c,e) and their frequencies of occurrence (Figure 2b,d,f) in Munich, Lindenberg, and Jülich. The frequency of occurrence of observed and simulated liquid water content was calculated for values greater than 10−6 g/m3.
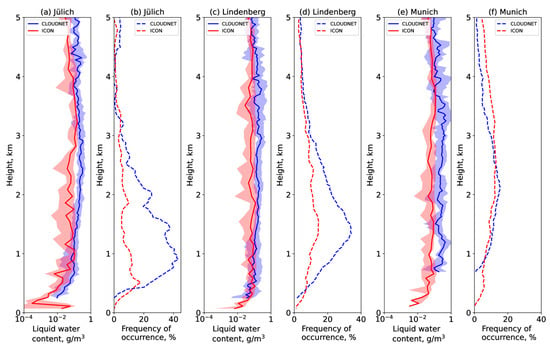
Figure 2.
The median grid-scale liquid water content (a,c,e) and its frequency of occurrence (b,d,f) according to CLOUDNET measurements and ICON simulations in Lindenberg (c,d), Jülich (a,b), and Munich (e,f). The interquartile range is shown by filling. The LWC medians were obtained using hourly average datasets.
Table 2 presents the main statistical parameters of the liquid water path according to hourly average measurements and modeling in Jülich, Lindenberg, and Munich. For ICON simulations, both the grid-scale and the total (grid-scale and subgrid-scale) LWP are shown. Vertical cloud structure is well reproduced by the ICON model, but there is a slight underestimation of liquid water content throughout the profile. As a result, the simulated grid-scale liquid water path is on average underestimated relative to CLOUDNET observations by 68 ± 17 g/m2 (46%). The accounting of subgrid-scale liquid water content leads to an increase in the liquid water path. However, the total liquid water path is still underestimated by 59 ± 16 g/m2 (40%). In addition, model results provide a lower frequency of LWC in Lindenberg and Jülich (Figure 2b,d). A better agreement of model LWC frequency of occurrence over Munich (Figure 2f) could be attributed to a successful forecast of sub-inversion clouds by the ICON model there and, to some extent, much smaller statistics. However, the LWP is underestimated at all CLOUDNET sites, and its interquartile range is lower in Lindenberg and Munich (see Table 2).

Table 2.
Median, interquartile range, and average values of synchronized hourly average liquid water path data according to CLOUDNET observations and ICON simulations. Jülich, Lindenberg, and Munich stations.
All these differences may be associated with the following:
- (1)
- Insufficient concentration of cloud condensation nuclei for droplet nucleation and liquid water content growth in conditions with CCNs = 250 cm−3;
- (2)
- Too-intensive formation of ice crystals, which can lead to a decrease in the excess specific humidity required for the cloud droplet nucleation;
- (3)
- Too-intensive processes of autoconversion and accretion, leading to the transition of cloud water mass into precipitation;
- (4)
- The problems with the saturation adjustment scheme, influencing the deficiency of specific humidity in activating condensation nuclei.
Satellite data provide Nd values that correspond to the cloud base level. ICON provides height-resolved Nd values. To bring ICON results closer to MODIS estimates of Nd (see Section 2.3), we considered hourly average vertically maximum simulated number concentrations of cloud droplets. The maximum cloud droplet number concentration in the model can be higher than that at the cloud base. So, we do not limit the simulated Nd, and we choose the maximum value in each profile. However, even in this case, the Nd concentration exceeds 77 cm−3 in only 25% of the ICON sample. The Nd interquartile range of ICON results is 63 cm−3 with a median of 29 cm−3. The ice water content is also higher than the simulated one, so no intensive nucleation and growth of ice crystals are simulated. To consider the influence of autoconversion and accretion processes on LWP, we compared the measured liquid water path with the simulated liquid and rainwater path (LWP + RWP). Even taking into account raindrops, the simulated LWP is generally underestimated by 17 ± 13 g/m2. This approach does not show enhanced autoconversion and accretion as the principal reason for LWP underestimation. We assume that this mechanism could be important, but there is no experimental data for evaluating the strength of this process. Therefore, we rely on observational data and the conclusions shown above.
The simulated liquid water content may be less than the observed LWC due to an inaccurate prediction of the water vapor path since water vapor is the main source of cloud droplet nucleation and growth. However, according to studies of the ICON model [69,70], this characteristic is predicted quite accurately.
Thus, one of the reasons for the model’s lower liquid water content and liquid water content occurrence may be the saturation adjustment scheme, which is the most important regulator of all microphysical processes. Saturation adjustment leads to lower condensation and higher evaporation rates of droplets in the bulk scheme relative to the spectral microphysical scheme. The work [14] showed that the saturation adjustment contributes to lower LWC for situations of stratocumulus clouds. Khain and Pinsky [3] also showed a negative effect of saturation adjustment on the diffusion growth of cloud particles in different cloud types. Unfortunately, we cannot consider this issue in more detail, since this requires a mixed-phase spectral microphysical scheme, which is closer to the real physics of clouds [13] compared to the saturation adjustment scheme used in the ICON model. The liquid water path underestimation in some cases could be due to the low specified CCN content of 250 cm−3; hence, we conducted a numerical experiment with a higher content of cloud condensation nuclei. Based on satellite measurements and upper-air sounding data, we chose 19 September 2021 as the day with the most uniform clouds over the simulation domain. Figure 3 shows MODIS retrievals of cloud droplet number concentrations at the cloud base according to the method of Equation (4) with an average Nd of 258 cm−3. We carried out a numerical experiment with a high CCN content of 1700 cm−3 since this value is typical for continental or polluted clouds [30,66,71].
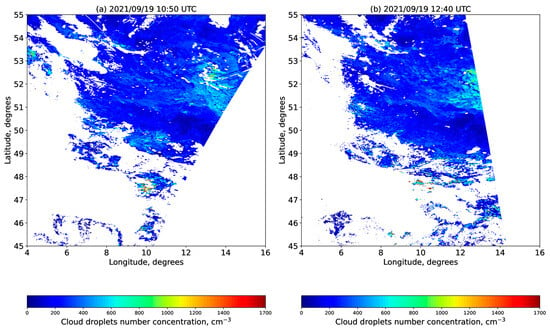
Figure 3.
Cloud droplet number concentrations over the simulation domain at 10:50 h UTC (a) and 12:40 h UTC (b) on 19 September 2021. Calculations from MODIS data with 1 km grid spacing using the method of Equation (4).
Figure 4a shows box plots of simulated cloud droplet number concentration over the CLOUDNET sites with CCN number concentrations of 250 and 1700 cm−3. The whole four-dimension (height–field–time) simulated Nd was taken into account when comparing results for the specified CCNs. The cloud droplet number concentration increases by 94 ± 20 cm−3 (65%) with this increase in CCNs. Median (interquartile range) values of Nd are 22 (62) cm−3 and 84 (127) cm−3 for CCNs = 250 cm−3 and CCNs = 1700 cm−3, respectively.
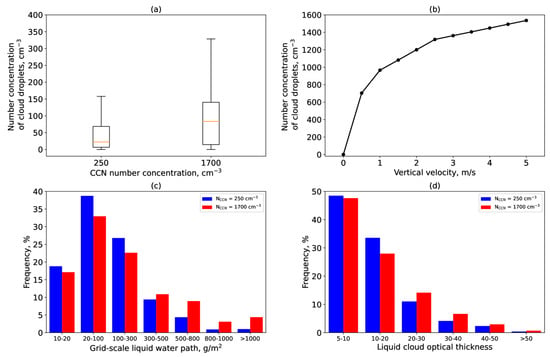
Figure 4.
Effects of CCN increase, case of 19 September 2021: (a) box plots of simulated cloud droplet concentrations at CCN values of 250 and 1700 cm−3 at CLOUDNET sites; (b) the dependence of the concentration of cloud droplets on the vertical velocity at the cloud base in the Segal–Khain scheme at a CCN value of 1700 cm−3 [30]; (c) histograms of grid-scale liquid water path at CCN values of 250 and 1700 cm−3 for the entire modeling area; (d) histograms of cloud optical thickness at CCN values of 250 and 1700 cm−3 for the entire modeling area.
Considering vertically maximum ICON-simulated number concentrations of cloud droplets, median Nd increases from 23 cm−3 with NCCN 250 cm−3 to 89 cm−3 with NCCN 1700 cm−3. Thus, only a small fraction of the CCNs were activated in the model.
Vertical velocity (W) is an important factor in cloud droplet nucleation [64,72]. Kretzschmar et al. [73] showed that one of the reasons for the low Nd and liquid water content in the ICON model may be an insufficient W providing lower CCN activation in the parametrization. Figure 4b illustrates the dependence of cloud droplet concentration on vertical velocity in the Segal–Khain scheme [30] for the CCN value of 1700 cm−3. At low vertical velocities, less than half of the CCNs can be available for nucleation. The maximum value of the simulated grid-scale vertical velocity at levels near the cloud base for 19 September 2021 was 0.9 m/s at CLOUDNET sites. Thus, the CCN concentration was actually in the range of 140 cm−3 to 900 cm−3 at the simulated vertical velocities instead of the specified 1700 cm−3. The CCN content of 140 cm−3 corresponds to the minimum permissible vertical velocity of 0.1 m/s in the cloud droplet nucleation scheme. It should be noted that the CCN content above the 2 km level can be lower than the defined value of 140 cm−3 due to the exponential decrease in CCN content (see Section 2.1) in the Segal–Khain scheme. However, in our experiments, the simulated Nd is significantly less than the satellite-derived Nd. This result can be related to several processes. Firstly, there is a low intensity of cloud droplet nucleation. Secondly, the saturation adjustment scheme may provide errors in cloud evaluation due to the fast realization of the water vapor excess.
In general, an increase in the concentration of cloud condensation nuclei contributed to an increase in the grid-scale liquid water path over the modeling domain (Figure 4c). Following [74], Figure 4c shows only a grid-scale liquid water path of more than 10 g/m2. When the number of cloud condensation nuclei is increased, there is a shift in the distribution of the liquid water path towards higher values. The grid-scale liquid water path increased by an average of 118 ± 2 g/m2 (40%). As a result, the liquid clouds have become more optically thick (in Figure 4d, the cases with liquid cloud optical thickness of more than 5 are shown). However, taking into account the subgrid-scale clouds, the effect of CCNs on the cloud optical thickness is less pronounced. Liquid cloud optical thickness increased by an average of 1 (8%). In order to determine the effect of CCNs on the simulated global irradiance at ground level, we considered cases of overcast conditions with a solar elevation of at least 25° and liquid cloud optical thickness of more than 5. Under these conditions, the increase in CCNs from 250 cm−3 to 1700 cm−3 results in a 9 W/m2 (12%) decrease in the solar irradiance.
3.2. Cloud Optical Thickness and Shortwave Irradiance at Ground Level
Cloud optical thickness and the cloud fraction are the most important factors in the cloudy atmosphere, which determine the global solar irradiance at ground level. Cloud optical thickness is determined by the liquid water content and the effective radius of cloud droplets [75].
In order to exclude the influence of errors in the scheme of cloud optical property evaluation in the ecRad scheme on the cloud–radiation interaction, we compared the liquid cloud optical thickness (COTliq) according to MODIS and ICON data. We considered the cases of LWP prediction successful when the absolute error of the simulated LWP was less than 15% (391,770 pixels) compared to the MODIS LWP. In this case, the median liquid cloud optical thickness and its interquartile range, shown in brackets, are 13.3 (12) and 13.5 (11) according to MODIS and ICON, respectively. The average error of simulated COTliq is +0.04 ± 0.03 (0.02%). When considering all cases, regardless of the quality of the simulated cloud water (8,642,685 pixels), the ICON cloud water path (liquid and ice phases) is on average 52 ± 0.1 g/m2 lower relative to the MODIS retrievals. As a result, the cloud optical thickness is underestimated by 4 ± 0.01 (24%). Hence, the cloud optical thickness is predicted with sufficient accuracy if the liquid water path is successfully estimated.
The cloud fraction is a more difficult parameter for evaluation from both numerical forecasting and observations [76]. Standard verification approaches are not suitable for cloud fraction and total cloud cover analysis; therefore other, more sophisticated methods and measurement data are required [77,78]. Therefore, we not only analyzed total cloud cover but also considered another characteristic—the ratio (R) of direct irradiance at the horizontal surface to global solar irradiance using hourly average data. This value can be considered as an analog of the total cloud cover after the application of the hourly averaging procedure [79]. The hourly R values characterize the proportion of gaps in the clouds.
According to the comparisons with the BSRN observations in cloudy conditions, the simulated global irradiance at ground level is overestimated on average by 46 ± 15 W/m2 (18%). At the same time, the simulated R is overestimated by 0.13 ± 0.02. Figure 5 shows the hourly average values of global irradiance (Q), liquid water path (LWP), and R averaged over the R intervals according to measurements (Figure 5a) and according to measurements and simulations (Figure 5b). The results of the ICON simulations are presented using a CCN number concentration of 250 cm−3. In addition, low-level cloud cover (CLCL, dotted lines) and total cloud cover (CLCT, crosses) are also shown.
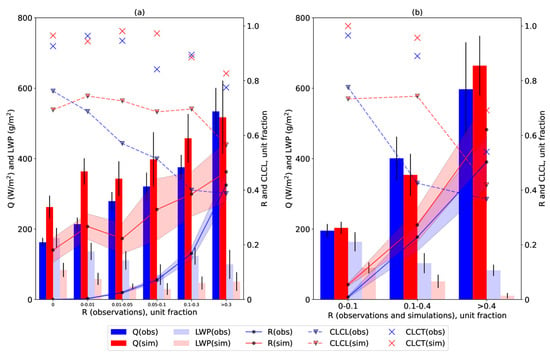
Figure 5.
Global solar irradiance (Q), liquid water path (LWP), low-level cloud fraction (CLCL), total cloud fraction (CLCT), and the R ratio according to simulations (Rsim) and observations (Robs) as a function of R according to measurements ((a) 214 cases) and for consistent R values according to simulations and measurements ((b) 84 cases). Lindenberg site. Simulations with CCN value of 250 cm−3. The solar elevation is above 25°. Confidence intervals are represented by a fill for R and lines for the other variables.
According to the ICON numerical experiments, R values are higher than the observed ones (Figure 5a). For overcast situations (Robs is equal to 0), average Rsim = 0.2 ± 0.04. As a result, the simulated global irradiance is higher than the measured one: 263 ± 33 W/m2 and 162 ± 13 W/m2, respectively. With averaging intervals corresponding to larger R, the Robs grows much faster relative to the simulated R (see Figure 5a). If we rank the cases based on both the measured and simulated R, the differences between simulated and measured global irradiance decrease (Figure 5b). Note that the simulated liquid water path is underestimated compared to the CLOUDNET observations for all considered R intervals (Figure 5a,b). Thus, improving the quality of the forecast of the R contributes to reducing the error of solar irradiance evaluation even with a general underestimation of the liquid water path.
The total cloud cover according to the ICON estimates generally corresponds to the observations (Figure 5a,b), while a more pronounced decrease in CLCL with increasing R is seen in the measurements compared to the simulations. The model CLCLs are overestimated for almost all R intervals. However, even at higher model CLCLs, we observe the overestimation of Q. In addition, the sensitivity of global solar irradiance to cloud fraction is generally less pronounced than its sensitivity to R (see Figure 5). The linear correlation coefficients of global solar irradiance with the ratio of direct radiation at the horizontal surface to global solar irradiance (R), low-level cloud cover (CLCL), and liquid water path (LWP) are presented in Table 3.

Table 3.
The linear correlation coefficients between global solar irradiance (Q) and the ratio of direct radiation at the horizontal surface to global solar irradiance (R), Q and low-level cloud cover (CLCL), and Q and liquid water path (LWP). CLOUDNET, BSRN, and ICON data. Lindenberg site.
The linear correlation coefficients of CLCL and Q are −0.26 and −0.23, while the correlation coefficients between R and Q are 0.78 and 0.86 according to measurement and simulation data, respectively. The correlation coefficients between LWP and Q according to observations and ICON data are closer (–0.39 and –0.38, respectively) than the correlation coefficients between CLCL and Q. It should be noted that the dependence between cloud characteristics and global solar irradiance according to the measurements is slightly more pronounced than that according to the simulations.
Hence, the error in R is the main factor determining the overestimation of simulated global irradiance. This could occur due to an inaccurate overlapping procedure between the layers. For example, Kawai et al. [80] showed the effect of the overlapping scheme on the cloud albedo without changing the total cloud cover in the MRI-ESM2 climate model. Even with the observed liquid water path underestimation, an accurate forecast of R leads to an improvement in the global irradiance prediction. It should be noted that the penetration of direct radiation through the gaps may provide a significant contribution to global solar irradiance and, hence, air temperature. The effect of the liquid water path underestimation on solar radiation is less pronounced since the sensitivity of global irradiance to cloud optical thickness becomes lower with the increase in COT [81], which is also noted as an “accumulation effect” [82]. The quality of the cloud fraction forecast at each model level is directly related to relative humidity (see Section 2.1).
The forecast of broken clouds is known to be the weakest point of cloud cover forecast [83]. Errors in cloud fraction prediction are noted in studies concerning many numerical weather prediction and climate forecasting models [15,18,78,84,85,86]. The main reasons for inaccuracies in the cloud fraction forecast include the errors in the structure of simulated convective clouds, liquid water content of stratiform clouds, and clouds’ frequency of occurrence in general. Errors in solar irradiance prediction, besides cloud cover schemes, depend on the cloud overlap assumption, which is an uncertainty factor both in modeling and observations [87,88]. Many forecasting centers try to reduce the systematic errors in cloud fraction prediction in postprocessing, in particular, using neural networks [89,90]. At the moment, the new ICON diagnostic cloud fraction scheme is being developed [91]. The scheme takes into account a whole complex of physical cloud mechanisms, such as the formation of large-scale clouds, turbulent vertical diffusion, and convective processes [92].
4. Discussion
We found an underestimation in the simulated liquid water path relative to observations at three CLOUDNET sites (Lindenberg, Jülich, and Munich). The main possible reasons for this underestimation are the uncertainties in cloud droplet nucleation and the saturation adjustment scheme. Khain et al. [13] showed that the saturation adjustment scheme leads to a decrease in the sensitivity of microphysical processes to aerosol in bulk schemes. Khain et al. [93] found a good sensitivity in the ICON two-moment bulk scheme to the cloud condensation nuclei content relative to the spectral scheme. However, Khain et al. [93] concluded that the saturation adjustment scheme still should be substituted in the future. With the implementation of a mixed-phase spectral scheme in the ICON model, a more detailed assessment of the effect of the saturation adjustment scheme on the cloud properties will be possible (https://www.cosmo-model.org/content/tasks/priorityProjects/caiir/default.htm, accessed on 14 October 2023).
The model’s cloud condensation nuclei were set to the default value of 250 cm−3. Using MODIS observations and following the method described in [65], we demonstrated that the default CCN content of 250 cm−3 is close to the typical value of Nd over Europe with daily variations in MODIS-derived Nd from 100 to 500 cm−3 on selected days. We chose the CCN number concentration of 1700 cm−3, which corresponds to the polluted continental clouds according to [30], as an upper limit for an additional numerical experiment. As a result, the cloud droplet number concentration and grid-scale liquid water path increased by an average of 65% and 40%, respectively. The changes in cloud structure reduced the solar irradiance at ground level by an average of 12% in overcast conditions with solar elevation above 25° and cloud optical thickness of more than 5. The obtained effects of increasing the cloud condensation nuclei number concentration help to alleviate prediction errors in the liquid water path and solar irradiance at ground level.
Another reason for LWP underestimation may be the significant low nucleation intensity of cloud droplets due to a small vertical velocity specifically for the droplet nucleation process, which has been also obtained in our study. At a vertical velocity of 1 m/s, when the CCN content was set equal to 1700 cm−3, no more than 60% of CCNs were activated. Our results concerning cloud–aerosol interaction are in line with the studies [14,74,94] for other models and geographical regions. In the absence of vertical velocity observations, we cannot state the underestimation of simulated vertical velocity. However, Tonttila et al. [95] found an underestimation of vertical velocity variability at the cloud base in the AROME model with 2.5 km grid spacing. Malavelle et al. [96] showed the positive impact of subgrid-scale vertical velocity on the CCN activation in the Unified Model with 1 km horizontal grid spacing. By taking into account the subgrid-scale vertical velocity, the errors in the cloud droplet nucleation scheme of kilometer-scale models might be significantly reduced [94,97]. This issue is a good point for future research.
We found a sufficient accuracy of cloud optical thickness in cases when liquid water path was predicted successfully in comparison with MODIS data. In broken cloud conditions, the relative humidity prediction uncertainty may be one of the reasons for the cloud fraction prediction error [98]. In the case of the ICON model, this may also happen due to the saturation adjustment scheme, as well as the nucleation scheme of cloud droplets due to its reduced sensitivity to CCN content, as was discussed above for a lower ICON liquid water path. Thus, Van Weverberg and Morcette [98] show that the prognostic and diagnostic cloud fraction schemes have common errors. We plan to conduct a more detailed analysis of this assumption in the future.
To assess the influence of the cloud spatial inhomogeneity, R (the ratio of direct to global solar radiation) was considered. The R parameter is an analog of the cloud fraction regarding cloud spatial heterogeneity, but, in contrast with cloud fraction, R is based on high-precision 10 min observations. We showed that the global solar irradiance correlates more strongly with the forecast of R than with the forecast of liquid water path or total cloud cover. A successful R prediction significantly improves the forecast of solar irradiance compared to the cloud fraction parameter. Cloud fraction prediction errors may be related to the choice of a cloud overlap scheme and the cloud scheme’s approximations in general [40,77]. Since observations and studies of cloud overlap still have some difficulties and uncertainties [87,99], the issue of successful cloud overlap forecasting is still open in numerical weather prediction.
5. Conclusions
This study provides a joint detailed analysis of cloud liquid water content and solar irradiance at ground level according to the ICON numerical weather prediction model, the CLOUDNET ground-based network of cloud characteristics at the three sites (Lindenberg, Jülich, and Munich), the BSRN high-precision ground-based radiation network in Lindenberg, and MODIS observations of cloud characteristics. The main conclusions are as follows:
- -
- A comparison of ICON and CLOUDNET data showed an underestimation of simulated grid-scale liquid water content. Taking into account the subgrid-scale component of clouds, the average liquid water path is still underestimated by 59 ± 16 g/m2.
- -
- An analysis of the case study of 19 September 2021 showed that the CCN growth from 250 cm−3 to 1700 cm−3 led to an increase in cloud droplet number concentration by an average of 94 ± 20 cm−3 (65%), providing an increase in the grid-scale liquid water path and cloud optical thickness by 118 ± 2 g/m2 (40%) and by 1 (8%), respectively. This led to a decrease in solar irradiance at ground level by an average of 9 W/m2 (12%) in overcast conditions. The obtained CCN effects contribute to reducing errors in the liquid water path prediction and solar irradiance at ground level.
- -
- We obtained a sufficient accuracy of cloud optical thickness forecasting using the SOCRATES parametrization of the ecRad scheme [37] in cases when the liquid water path was predicted successfully.
- -
- The solar irradiance at ground level is on average overestimated compared to the BSRN observations. We showed that global irradiance values are more sensitive to the prediction of R (ratio of direct to global solar irradiance) than to the liquid water path and cloud fraction forecast. A successful R prediction significantly improves the forecast of solar irradiance.
Author Contributions
Conceptualization, methodology, formal analysis, investigation, validation, writing—original draft preparation, writing—review and editing, J.S., N.C. and M.S.; software, J.S.; resources, M.S.; data curation, J.S.; visualization, J.S.; supervision, N.C. and M.S.; project administration, N.C.; funding acquisition, N.C. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by a grant from the Ministry of Science and Higher Education of the Russian Federation (project number 075–15–2021–574) and completed at the Lomonosov Moscow State University under the Development Program of the MSU Interdisciplinary Scientific and Educational School “Future Planet and Global Environmental Change”. The configuration of the ecRad radiative scheme in ICON was carried out within Roshydromet Research Work number AAAA-20-120021490079-3.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The results presented in this manuscript were created based on the MODIS dataset available at https://ladsweb.modaps.eosdis.nasa.gov (accessed on 14 October 2023); CLOUDNET observations (available at CLU, 2023); and BSRN observations at Lindenberg Meteorological Observatory, available at https://bsrn.awi.de (accessed on 14 October 2023) on request. We used numerical weather prediction realization of ICON model version 2.6.5 (https://code.mpimet.mpg.de/projects/iconpublic/wiki/How%20to%20obtain%20the%20model%20code, accessed on 14 October 2023). The ecRad radiative transfer scheme is available at https://github.com/ecmwf-ifs/ecrad (accessed on 14 October 2023). A detailed description of the methods is provided in Section 2. Figures were created with Python version 3.10.2, available at https://www.python.org (accessed on 14 October 2023).
Acknowledgments
We are very grateful to the staff of the Lindenberg Meteorological Observatory, the Jülich Observatory, and the Munich supersite for the provision of cloud and radiative data. We are grateful to anonymous reviewers for their valuable notes and comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mauder, M.; Foken, T.; Cuxart, J. Surface-Energy-Balance Closure over Land A Review. Bound.-Layer Meteorol. 2020, 177, 395–426. [Google Scholar] [CrossRef]
- Marshak, A.; Davis, A.B. 3D Radiative Transfer in Cloudy Atmospheres; Springer: Berlin/Heidelberg, Germany, 2005; 686p. [Google Scholar]
- Khain, A.P.; Pinsky, M. Physical Processes in Clouds and Cloud Modeling; Cambridge University Press: Cambridge, UK, 2005; 626p. [Google Scholar] [CrossRef]
- Haiden, T.; Forbes, R.M.; Ahlgrimm, M.; Bozzo, A. The skill of ECMWF cloudiness forecast. ECMWF Newsl. 2015, 143, 14–19. Available online: https://www.researchgate.net/profile/Thomas-Haiden/publication/292989145_The_skill_of_ECMWF_cloudiness_forecasts/links/56b497e608ae922e6c020100/The-skill-of-ECMWF-cloudiness-forecasts.pdf (accessed on 14 October 2023).
- Tuononen, M.; O’Connor, E.J.; Sinclair, V.A. Evaluating solar radiation forecast uncertainty. Atmos. Chem. Phys. 2019, 19, 1985–2000. [Google Scholar] [CrossRef]
- Sotiropoulou, G.; Sedlar, J.; Forbes, R.; Tjernström, M. Summer Arctic clouds in the ECMWF forecast model: An evaluation of cloud parametrization schemes. Q. J. R. Meteorol. Soc. 2016, 142, 387–400. [Google Scholar] [CrossRef]
- Tuccella, P.; Curci, G.; Grell, G.A.; Visconti, G.; Crumeyrolle, S.; Schwarzenboeck, A.; Mensah, A.A. A new chemistry option in WRF-Chem v. 3.4 for the simulation of direct and indirect aerosol effects VBS: Evaluation against IMPACT-EUCAARI data. Geosci. Model Dev. 2015, 8, 2749–2776. [Google Scholar] [CrossRef]
- Dipu, S.; Quaas, J.; Wolke, R.; Stoll, J.; Mühlbauer, A.; Sourdeval, O.; Salzmann, M.; Heinold, B.; Tegen, I. Implementation of aerosol-cloud interactions in the regional atmosphere-aerosol model COSMO-MUSCAT(5.0) and evaluation using satellite data. Geosci. Model Dev. 2017, 10, 2231–2246. [Google Scholar] [CrossRef]
- Baldauf, M.; Seifert, A.; Foerstner, J.; Majewski, D.; Raschendorfer, M.; Reinhardt, T. Operational convective-scale numerical weather prediction with the COSMO model: Description and sensitivities. Mon. Weather Rev. 2011, 139, 3887–3905. [Google Scholar] [CrossRef]
- Xie, X.; Liu, X. Aerosol-cloud-precipitation interactions in WRF model: Sensitivity to autoconversion parameterization. J. Meteorol. Res. 2015, 29, 72–81. [Google Scholar] [CrossRef]
- Muskatel, H.B.; Blahak, U.; Khain, P.; Levi, Y.; Fu, Q. Parametrizations of liquid and ice clouds’ optical properties in operational numerical weather prediction models. Atmosphere 2021, 12, 89. [Google Scholar] [CrossRef]
- Tao, W.-K.; Simpson, J.; McCumber, M. An Ice-Water Saturation Adjustment. Mon. Weather Rev. 1989, 117, 231–235. [Google Scholar] [CrossRef]
- Khain, A.; Beheng, K.D.; Heymsfield, A.; Korolev, A.; Krichak, S.O.; Levin, Z.; Pinsky, M.; Phillips, V.; Prabhakaran, T.; Teller, A.; et al. Representation of microphysical processes in cloud-resolving models: Spectral (bin) microphysics versus bulk parametrization. Rev. Geophys. 2015, 53, 247–322. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, J.; Zhang, R.; Leung, L.R.; Franklin, C. Improving bulk microphysics parametrizations in simulations of aerosol effects. J. Geophys. Res. Atmos. 2013, 118, 5361–5379. [Google Scholar] [CrossRef]
- Haiden, T.; Trentmann, J. Verification of cloudiness and radiation forecasts in the greater Alpine region. Meteorol. Z. 2016, 25, 3–15. [Google Scholar] [CrossRef]
- Sundqvist, H.; Berge, E.; Kristjansson, J.E. Condensation and Cloud Parametrization Studies with a Mesoscale Numerical Weather Prediction Model. Mon. Weather Rev. 1989, 117, 1641–1657. [Google Scholar] [CrossRef]
- Tiedke, M. Representation of Clouds in Large-Scale Models. Mon. Weather Rev. 1993, 121, 3040–3061. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Q.; Zhao, C.; Shen, X.; Wang, Y.; Jiang, J.H.; Li, Z.; Yung, Y. Application and Evaluation of an Explicit Prognostic Cloud-Cover Scheme in GRAPES Global Forecast System. J. Adv. Model. Earth Syst. 2018, 10, 652–667. [Google Scholar] [CrossRef]
- Crueger, T.; Giorgetta, M.A.; Brokopf, R.; Esch, M.; Fiedler, S.; Hohenegger, C.; Kornblueh, L.; Mauritsen, T.; Nam, C.; Naumann, A.K.; et al. ICON-A, the atmosphere component of the ICON Earth system model: II. Model evaluation. J. Adv. Model. Earth Syst. 2018, 10, 1638–1662. [Google Scholar] [CrossRef]
- Giorgetta, M.A.; Brokopf, R.; Crueger, T.; Esch, M.; Fiedler, S.; Helmert, J.; Hohenegger, C.; Kornblueh, L.; Köhler, M.; Manzini, E.; et al. ICON-A, the atmosphere component of the ICON Earth system model: I. Model description. J. Adv. Model. Earth Syst. 2018, 10, 1613–1637. [Google Scholar] [CrossRef]
- Jungclaus, J.H.; Lorenz, S.J.; Schmidt, H.; Brovkin, V.; Brueggemann, N.; Chegini, F.; Crüger, F.; De-Vrese, P.; Gayler, V.; Giorgetta, M.A.; et al. The ICON Earth System Model Version 1.0. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002813. [Google Scholar] [CrossRef]
- Grundner, A.; Beucler, T.; Gentine, P.; Iglesias-Suarez, F.; Giorgetta, M.A.; Eyring, V. Deep learning based cloud cover parameterization for ICON. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002959. [Google Scholar] [CrossRef]
- Bresson, H.; Rinke, A.; Mech, M.; Reinert, D.; Schemann, V.; Ebell, K.; Maturilli, M.; Viceto, C.; Gorodetskaya, I.; Crewell, S. Case study of a moisture intrusion over the Arctic with the ICON model: Resolution dependence of its representation. Atmos. Chem. Phys. 2022, 22, 173–196. [Google Scholar] [CrossRef]
- Heize, R.; Dipankar, A.; Henken, C.C.; Moseley, C.; Sourdeval, O.; Troemel, S.; Xie, X.; Adamidis, P.; Ament, F.; Baars, H.; et al. Large-eddy simulations over Germany using ICON: A comprehensive evaluation. Q. J. R. Meteorol. Soc. 2017, 143, 69–100. [Google Scholar] [CrossRef]
- De Lucia, C.; Bucchignani, E.; Mastellone, A.; Adinolfi, M.; Montesarchio, M.; Cinquegrana, D.; Mercogliano, P.; Schiano, P. A sensitivity study on high resolution NWP ICON-LAM model over Italy. Atmosphere 2022, 13, 540. [Google Scholar] [CrossRef]
- Ori, D.; Schemann, V.; Karrer, M.; Neto, J.D.; Terzi, L.; Seifert, A.; Kneifel, S. Evaluation of ice particle growth in ICON using statistics of multi-frequency Doppler cloud radar observations. Q. J. R. Meteorol. Soc. 2020, 146, 3830–3849. [Google Scholar] [CrossRef]
- Zängl, G.; Reinert, D.; Ripodas, P.; Baldauf, M. The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core. Q. J. R. Meteorol. Soc. 2015, 141, 563–579. [Google Scholar] [CrossRef]
- Rivin, G.S.; Rozinkina, I.A.; Astakhova, E.D.; Blinov, D.V.; Bundel, A.Y.; Kirsanov, A.A.; Shatunova, M.V.; Chubarova, N.Y.; Alferov, D.Y.; Varentsov, M.I.; et al. COSMO-Ru high-resolution short-range numerical weather prediction system: Its development and applications. Hydrometeorol. Res. Forecast. 2019, 374, 37–53. Available online: https://method.meteorf.ru/publ/tr/tr374/03.pdf (accessed on 14 October 2023). (In Russian). [CrossRef]
- Seifert, A.; Beheng, K.D. A two-moment cloud microphysics parameterization for mixed-phase clouds. Part 1: Model description. Meteorol. Atmos. Phys. 2006, 92, 45–66. [Google Scholar] [CrossRef]
- Segal, Y.; Khain, A. Dependence of droplet concentration on aerosol conditions in different cloud types: Application to droplet concentration parameterization of aerosol conditions. J. Geophys. Res. Atmos. 2006, 111, 1–11. [Google Scholar] [CrossRef]
- Seifert, A. On the parametrization of evaporation of raindrops as simulated by a one-dimensional rainshaft model. J. Atmos. Sci. 2008, 65, 3608–3619. [Google Scholar] [CrossRef]
- Kärcher, B.; Hendricks, J.; Lohmann, U. Physically based parameterization of cirrus cloud formation for use in global atmospheric models. J. Geophys. Res. Atmos. 2006, 111, 1–11. [Google Scholar] [CrossRef]
- Phillips, V.T.J.; DeMott, P.J.; Andronache, C. An Empirical Parametrization of Heterogeneous Ice Nucleation for Multiple Chemical Species of Aerosol. J. Atmos. Sci. 2008, 65, 2757–2783. [Google Scholar] [CrossRef]
- Doms, G.; Foerstner, J.; Heise, E.; Herzog, H.-J.; Mironov, D.; Raschendorfer, M.; Reinhardt, T.; Ritter, B.; Schrodin, R.; Schulz, J.-P.; et al. A Description of the Nonhydrostatic Regional COSMO-Model. Part II: Physical Parametrizations (COSMO 6.0); Deutscher Wetterdienst: Offenbach, Germany, 2021; 171p. [Google Scholar] [CrossRef]
- Hogan, R.J.; Bozzo, A. ECRAD: A New Radiation Scheme for the IFS; ECMWF Technical Memoranda; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2016; Volume 787, Available online: https://www.ecmwf.int/sites/default/files/elibrary/2016/16901-ecrad-new-radiation-scheme-ifs.pdf (accessed on 14 October 2023).
- Pincus, R.; Barker, H.W.; Morcrette, J.J. A fast, flexible, approximate technique for computing radiative transfer in inhomogeneous cloud fields. J. Geophys. Res. Atmos. 2003, 108, 1–5. [Google Scholar] [CrossRef]
- Edwards, J.M.; Slingo, A. Studies with a flexible new radiation code. I: Choosing a configuration for a large-scale model. Q. J. Meteorol. Soc. 1996, 122, 689–719. [Google Scholar] [CrossRef]
- Fu, Q. An accurate parametrization of the solar radiative properties of cirrus clouds for climate models. J. Clim. 1996, 9, 2058–2082. [Google Scholar] [CrossRef]
- Fu, Q.; Yang, P.; Sun, W.B. An accurate parameterization of the infrared radiative properties of cirrus clouds for climate models. J. Clim. 1998, 11, 2223–2237. [Google Scholar] [CrossRef]
- Hogan, R.J.; Illingworth, A.J. Deriving cloud overlap statistics from radar. J. Atmos. Sci. 2000, 126, 2903–2909. [Google Scholar] [CrossRef]
- CLU. Cloud Profiling Products: Classification, Liquid Water Content, Categorize; Cloud Profiling Measurements: Microwave radiometer; to 31 October 2021; from Jülich, Lindenberg, Munich. Generated by the Cloud Profiling Unit of the ACTRIS Data Centre. 2023. Available online: https://cloudnet.fmi.fi/collection/4a9e1538-ddb7-4b2d-8fe0-a40b72a19f67 (accessed on 25 November 2023).
- Illingworth, A.J.; Hogan, R.J.; O’Connor, E.J.; Bouniol, D.; Brooks, M.E.; Delanoea, J.; Donovan, D.P.; Eastment, J.D.; Gaussiat, N.; Goddard, J.W.F.; et al. Cloudnet: Continuous evaluation of cloud profiles in seven operational models using ground-based observations. Bull. Am. Meteorol. Soc. 2007, 88, 883–898. [Google Scholar] [CrossRef]
- Görsdorf, U.; Lehmann, V.; Bauer-Pfundstein, M.; Peters, G.; Vavriv, D.; Vinogradov, V.; Volkov, V. A 35-GHz Polarimetric Doppler Radar for Long-Term Observations of Cloud Parameters—Description of System and Data Processing. J. Atmos. Ocean. Technol. 2015, 32, 675–690. [Google Scholar] [CrossRef]
- Löhnert, U.; Scheween, J.H.; Acquistapace, C.; Ebell, K.; Maahn, M.; Barrera-Verdejo, M.; Hirsikko, A.; Bohn, B.; Knaps, A.; O’Connor, E.; et al. JOYCE: Jülich observatory for cloud evolution. Bull. Am. Meteorol. Soc. 2015, 96, 1157–1174. [Google Scholar] [CrossRef]
- Gaussiat, N.; Hogan, R.J.; Illingworth, A.J. Accurate liquid water path retrieval from low-cost microwave radiometers using additional information from a lidar ceilometer and operational forecast models. J. Atmos. Ocean. Technol. 2007, 24, 1562–1575. [Google Scholar] [CrossRef]
- Roebeling, R.A.; Deneke, H.M.; Feijt, A.J. Validation of cloud liquid water path retrievals from SEVIRI using one year of CloudNET observations. J. Appl. Meteorol. Climatol. 2007, 47, 206–222. [Google Scholar] [CrossRef]
- Platnick, S.; Meyer, K.G.; King, M.D.; Wind, G.; Amarasinghe, N.; Marchant, B.; Arnold, G.T.; Zhang, Z.; Hubanks, P.A.; Holz, R.E.; et al. The MODIS cloud optical and microphysical products: Collection 6 updates and examples from Terra and Aqua. IEEE Trans. Geosci. Remote Sens 2016, 55, 502–525. [Google Scholar] [CrossRef] [PubMed]
- Platnick, S.; King, M.D.; Ackerman, S.A.; Menzel, W.P.; Baum, B.A.; Riedi, J.C.; Frey, R.A. The MODIS cloud products: Algorithms and examples from Terra. IEEE Trans. Geosci. Remote Sens. 2003, 41, 459–473. [Google Scholar] [CrossRef]
- McArthur, L.J.B. World Climate Research Programme-Baseline Surface Radiation Network (BSRN)—Operations Manual Version 2.1. WMO/TD-No. 1274. 2005. Available online: https://epic.awi.de/id/eprint/45991/1/McArthur.pdf (accessed on 14 October 2023).
- Gultepe, I.; Isaac, G.A. Liquid water content and temperature relationship from aircraft observations and its applicability to GCMs. J. Clim. 1997, 11, 446–452. [Google Scholar] [CrossRef]
- Löhnert, U.; Crewell, S.; Simmer, C.; Macke, A. Profiling cloud liquid water combining active and passive microwave measurements with cloud model statistics. J. Atmos. Ocean. Technol. 2001, 18, 1354–1366. [Google Scholar] [CrossRef]
- Tselioudis, G.; Rossow, W.B.; Rind, D. Global patterns of cloud optical thickness variation with temperature. J. Clim. 1992, 5, 1484–1495. [Google Scholar] [CrossRef]
- Lau, N.-C.; Crane, M.W. A satellite view of the synoptic-scale organization of cloud properties in Midlatitude and tropical circulation systems. Mon. Weather Rev. 1995, 123, 1984–2006. [Google Scholar] [CrossRef]
- Hogan, R.J.; Illingworth, A.J.; O’Connor, E.J.; Bouniol, D.; Brooks, M.E.; Delanoea, J.; Donovan, D.P.; Eastment, J.D.; Gaussiat, N.; Goddard, J.W.F.; et al. Cloudnet: Evaluation of model clouds using ground-based observations. In Proceedings of the ECMWF Workshop on Parametrization of Clouds in Large-Scale Models, Reading, UK, 13–15 November 2006; Available online: https://www.ecmwf.int/sites/default/files/elibrary/2007/9929-cloudnet-evaluation-model-clouds-using-ground-based-observations.pdf (accessed on 14 October 2023).
- Fix, E.; Hodges, J.L. Discriminatory analysis, nonparametric estimation: Consistency properties. US Air Force Sch. Aviat. Med. 1951, 4, 21–49. [Google Scholar] [CrossRef]
- Merk, D.; Deneke, H.; Pospichal, B.; Seifert, P. Investigation of the adiabatic assumption for estimating cloud micro- and macrophysical properties from satellite and ground observations. Atmos. Chem. Phys. 2016, 16, 933–952. [Google Scholar] [CrossRef]
- Gupta, S.; McFarququhar, G.M.; O’Brien, J.R.; Poellot, M.R.; Delene, D.J.; Chang, I.; Gao, L.; Xu, F.; Redemann, J. In situ and satellite-based estimates of cloud properties and aerosol-cloud interactions over the southeast Atlantic Ocean. Atmos. Chem. Phys. 2022, 22, 12923–12943. [Google Scholar] [CrossRef]
- Hande, L.B.; Engler, C.; Hoose, C.; Tegen, I. Parameterizing cloud condensation nuclei concentrations during HOPE. Atmos. Chem. Phys. 2016, 16, 12059–12079. [Google Scholar] [CrossRef]
- Paramonov, M.; Kerminen, V.-M.; Gysel, M.; Aalto, P.P.; Andreae, M.O.; Asmi, E.; Baltensperger, U.; Bougiatioti, A.; Brus, D.; Frank, G.P.; et al. A synthesis of cloud condensation nuclei counter (CCNC) measurements within the EUCAARI network. Atmos. Chem. Phys. 2015, 15, 12211–12229. [Google Scholar] [CrossRef]
- Li, J.; Jian, B.; Huang, J.; Hu, Y.; Zhao, C.; Kawamoto, K.; Liao, S.; Wu, M. Long-term variation of cloud droplet number concentrations from Space-based Lidar. Remote Sens. Environ. 2018, 213, 144–161. [Google Scholar] [CrossRef]
- Quaas, J.; Boucher, O.; Lohmann, U. Constraining the total aerosol indirect effect in the LMDZ and ECHAM4 GCMs using MODIS satellite data. Atmos. Chem. Phys. 2006, 6, 947–955. [Google Scholar] [CrossRef]
- Fanourgakis, G.S.; Kanakidou, M.; Nenes, A.; Bauer, S.E.; Bergman, T.; Carslaw, K.S.; Grini, A.; Hamilton, D.S.; Johnson, J.S.; Karydis, V.A.; et al. Evaluation of global simulations of aerosol particle and cloud condensation nuclei number, with implications for cloud droplet formation. Atmos. Chem. Phys. 2019, 19, 8591–8617. [Google Scholar] [CrossRef] [PubMed]
- Shuvalova, J.; Chubarova, N.; Shatunova, M. Impact of cloud condensation nuclei reduction on cloud characteristics and solar radiation during COVID-19 lockdown 2020 in Moscow. Atmosphere 2022, 13, 1710. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Zheng, Y.; Hashimshoni, E.; Poehlker, M.L.; Jefferson, A.; Poehlker, C.; Yu, X.; Zhu, Y.; Liu, G.; Yue, Z.; et al. Satellite retrieval of cloud condensation nuclei concentrations by using clouds as CCN chambers. Proc. Natl. Acad. Sci. USA 2016, 113, 5828–5834. [Google Scholar] [CrossRef]
- McComiskey, A.; Feingold, G.; Frisch, A.S.; Turner, D.D.; Miller, M.A.; Chiu, J.C.; Min, Q.; Ogren, J.A. An assessment of aerosol-cloud interactions in marine stratus clouds based on surface remote sensing. J. Geophys. Res. Atmos. 2009, 114, D09203. [Google Scholar] [CrossRef]
- Mikhailov, E.F.; Ivanova, O.A.; Vlasenko, S.S.; Nebos’ko, E.Y.; Ryshkevich, T.I. Cloud Condensation Nuclei Activity of the Aitken Mode Particles near St. Petersburg, Russia. Izv. Atmos. Ocean. Phys. 2017, 53, 326–333. [Google Scholar] [CrossRef]
- Quaas, J.; Arola, A.; Cairns, B.; Christensen, M.; Deneke, H.; Ekman, A.M.L.; Feingold, G.; Fridlind, A.; Gryspeerdt, E.; Hasekamp, O.; et al. Constraining the Twomey effect from satellite observations: Issues and perspectives. Atmos. Chem. Phys. 2020, 20, 15079–15099. [Google Scholar] [CrossRef]
- Painemal, D.; Chang, F.-L.; Ferrare, R.; Burton, S.; Li, Z.; Smith, W.L., Jr.; Minnis, P.; Feng, Y.; Clayton, M. Reducing uncertainties in satellite estimates of aerosol-cloud interactions over the subtropical ocean by integrating vertically resolved aerosol observations. Atmos. Chem. Phys. 2020, 20, 7167–7177. [Google Scholar] [CrossRef]
- Steinke, S.; Eikenberg, S.; Loehnert, U.; Dick, G.; Klocke, D.; Di Girolamo, P.; Crewell, S. Assessment of small-scale integrated water vapour variability during HOPE. Atmos. Chem. Phys. 2015, 15, 2675–2692. [Google Scholar] [CrossRef]
- Kiszler, T.; Ebell, K.; Schemann, V. A Performance Baseline for the Representation of Clouds and Humidity in Cloud-Resolving ICON-LEM Simulations in the Arctic. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003299. [Google Scholar] [CrossRef]
- Schmale, J.; Henning, S.; Henzing, B.; Keskinen, H.; Sellegri, K.; Ovadnevaite, J.; Bougiatioti, A.; Kalivitis, N.; Stavroulas, I.; Jefferson, A.; et al. Collocated observations of cloud condensation nuclei, particle size distributions, and chemical composition. Sci. Data 2017, 4, 170003. [Google Scholar] [CrossRef] [PubMed]
- Twomey, S. The nuclei of natural cloud formation. Part II: The supersaturation in natural clouds and the variation of cloud droplet concentration. Geofis. Pura Appl. 1959, 43, 243–249. [Google Scholar] [CrossRef]
- Kretzschmar, J.; Stapf, J.; Klocke, D.; Wendisch, M.; Quaas, J. Employing airborne radiation and cloud microphysics observations to improve cloud representation in ICON at kilometer-scale resolution in the Arctic. Atmos. Chem. Phys. 2020, 20, 13145–13165. [Google Scholar] [CrossRef]
- Costa-Suros, M.; Sourdeval, O.; Acquistapace, C.; Baars, H.; Henken, C.C.; Genz, C.; Hesemann, J.; Jimenez, C.; König, M.; Kretzschmar, J.; et al. Detection and attribution of aerosol-cloud interactions in large-domain large-eddy simulations with the ICOsahedral Non-hydrostatic model. Atmos. Chem. Phys. 2020, 20, 5657–5678. [Google Scholar] [CrossRef]
- Wood, R. Relationships between Optical Depth, Liquid Water Path, Droplet Concentration, and Effective Radius in Adiabatic Layer Cloud; University of Washington: Seattle, WA, USA, 2006; Available online: https://atmos.uw.edu/~robwood/papers/chilean_plume/optical_depth_relations.pdf (accessed on 14 October 2023).
- Mittermaier, M. A critical assessment of surface cloud observations and their use for verifying cloud forecasts. Q. J. R. Meteorol. Soc. 2012, 138, 1794–1807. [Google Scholar] [CrossRef]
- Hogan, R.J.; O’Connor, E.J.; Illingworth, A.J. Verification of cloud-fraction forecasts. Q. J. R. Meteorol. Soc. 2009, 135, 1494–1511. [Google Scholar] [CrossRef]
- Morcette, C.J.; O’Connor, E.J.; Petch, J.C. Evaluation of two cloud parametrization schemes using ARM and Cloud-Net observations. Q. J. R. Meteorol. Soc. 2012, 138, 964–979. [Google Scholar] [CrossRef]
- Mullammaa, Y.R.; Sulev, M.A.; Pyldmaa, V.K.; Ohvril, H.A.; Niylisk, H.J.; Allenov, M.I.; Tchubakov, L.G.; Kuusk, A.F. Stochastic Structure of Cloud and Radiation fields. NASA TT F-822, Studies in Atmospheric Physics, AN ESR, Institute of Physics and Astronomy. 1975, Volume 18. Available online: https://archive.org/details/nasa_techdoc_19760004517 (accessed on 14 October 2023).
- Kawai, H.; Yukimoto, S.; Koshiro, T.; Oshima, N.; Tanaka, T.; Yoshimura, H.; Nagasawa, R. Significant improvement of cloud representation in the global climate model MRI-ESM2. Geosci. Model Dev. 2019, 12, 2875–2897. [Google Scholar] [CrossRef]
- Tarasova, T.; Chubarova, N. On the calculation of optical thickness of extended low and middle clouds using measurements of solar radiation in three solar spectrum ranges on the Earth’s surface. Izv. Atmos. Ocean. Phys. 1994, 30, 253–257. Available online: https://istina.msu.ru/publications/article/376715/ (accessed on 14 October 2023).
- Crewell, S.; Simmer, C.; Feijt, A.; van Meijgaard, E. CLIWA-NET: BALTEX BRIDGE Cloud Liquid Water Network; International BALTEX Secretariat Publication: Geesthacht, Germany, 2003; Available online: https://baltex-research.eu/publications/SSG_minutes_diverse/BALTEX_NO26.pdf (accessed on 14 October 2023).
- Teixeira, J. Cloud Fraction and Relative Humidity in a Prognostic Cloud Fraction Scheme. Mon. Weather Rev. 2001, 129, 1750–1753. [Google Scholar] [CrossRef]
- Shimpo, A.; Kanamitsu, M.; Iacobellis, S.F. Comparison of Four Cloud Schemes in Simulating the Seasonal Mean Field Forced by the Observed Sea Surface Temperature. Mon. Weather Rev. 2008, 136, 2557–2575. [Google Scholar] [CrossRef]
- Park, R.-S.; Chae, J.-H.; Hong, S.-Y. A revised prognostic cloud fraction scheme in a global forecasting system. Mon. Weather Rev. 2016, 144, 1219–1229. [Google Scholar] [CrossRef]
- Schaefer, S.; Hogan, R.; Rieger, D.; Koehler, M.; Ahlgrimm, M.; Ukkonen, P. Improvements in Radiation, Gas and Cloud Parametrization in ICON with ecRad. ICCARUS 2023. Book of Abstracts 2023. Volume 23. Available online: https://go.dwd-nextcloud.de/index.php/s/cGZw9B35N8W8njF?dir=undefinedpath=%2FTuesdayopenfile=68207 (accessed on 14 October 2023).
- Park, S.; Bretherton, C.S.; Rasch, P.J. Integrating cloud processes in the Community Atmosphere Model, Version 5. J. Clim. 2014, 27, 6821–6856. [Google Scholar] [CrossRef]
- Li, J.; Huang, J.; Wang, T.; Lv, Q.; Jin, H. A global survey of cloud overlap based on CALIPSO and CloudSat measurements. Atmos. Chem. Phys. 2015, 15, 519–536. [Google Scholar] [CrossRef]
- Dupuy, F.; Mestre, O.; Serrurier, M.; Burda, K.V.; Zamo, M.; Citlali, N.; Bakkay, M.C.; Jouhaud, C.G.; Mader, M.A.; Oller, G. ARPEGE Cloud Cover Forecast Postprocessing with Convolutional Neural Network. Weather Forecast. 2021, 36, 567–586. [Google Scholar] [CrossRef]
- Baran, A.; Lerch, S.; El Ayari, M.; Baran, S. Machine learning for total cloud cover prediction. Neural Comput. Appl. 2021, 33, 2605–2620. [Google Scholar] [CrossRef]
- Prill, F.; Reinert, D.; Rieger, D.; Zängl, G. ICON Tutorial. Working with the ICON Model; Deutscher Wetterdienst: Offenbach, Germany, 2023; 272p. [Google Scholar] [CrossRef]
- Muench, S.; Lohmann, U. Developing a Cloud Scheme With Prognostic Cloud Fraction and Two Moment Microphysics for ECHAM-HAM. J. Adv. Model. Earth Syst. 2020, 12, 1–37. [Google Scholar] [CrossRef]
- Khain, P.; Shpund, J.; Levi, Y.; Khain, A. Warm-phase spectral-bin microphysics in ICON: Reasons of sensitivity to aerosols. Atmos. Res. 2022, 279, 106388. [Google Scholar] [CrossRef]
- Rothenberg, D.; Avramov, A.; Wang, C. On the representation of aerosol activation and its influence on model-derived estimated of the aerosol indirect effect. Atmos. Chem. Phys. 2018, 18, 7961–7983. [Google Scholar] [CrossRef]
- Tonttila, J.; O’Connor, E.J.; Niemelae, S.; Raeisaenen, P.; Jaervinen, H. Cloud base vertical velocity statistics: A comparison between an atmospheric mesoscale model and remote sensing observations. Atmos. Chem. Phys. 2011, 11, 9207–9218. [Google Scholar] [CrossRef]
- Malavelle, F.F.; Haywood, J.M.; Field, P.R.; Hill, A.A.; Abel, S.J.; Lock, A.P.; Shipway, B.J.; McBeath, K. A method to represent subgrid-scale updraft velocity in kilometer-scale models: Implication for aerosol activation. J. Geophys. Res. Atmos. 2014, 119, 4149–4173. [Google Scholar] [CrossRef]
- Khain, A.; Pokrovsky, A.; Pinsky, M.; Seifert, A.; Phillips, V. Simulation of effects of atmospheric aerosols on deep turbulent convective clouds using a spectral microphysics mixed-phase cumulus cloud model. Part I: Model description and possible applications. J. Atmos. Sci. 2004, 124, 2963–2982. [Google Scholar] [CrossRef]
- Van Weverberg, K.; Morcette, C.J. Sensitivity of cloud-radiative effects to cloud fraction parametrizations in tropical, midlatitude, and arctic kilometer-scale simulations. Q. J. R. Meteorol. Soc. 2022, 148, 2563–2586. [Google Scholar] [CrossRef]
- Naud, C.M.; Del Genio, A.; Mace, G.G.; Benson, S.; Clothiaux, E.E.; Kollias, P. Impact of dynamics and atmospheric state on cloud vertical overlap. J. Clim. 2008, 21, 1758–1770. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).