Dimensional Transitions in Turbulence: The Effects of Rotation and Stratification
Abstract
1. Introduction
2. Mathematical Models
3. Numerical Results
3.1. Transition in the Absence of Rotation and Stratification
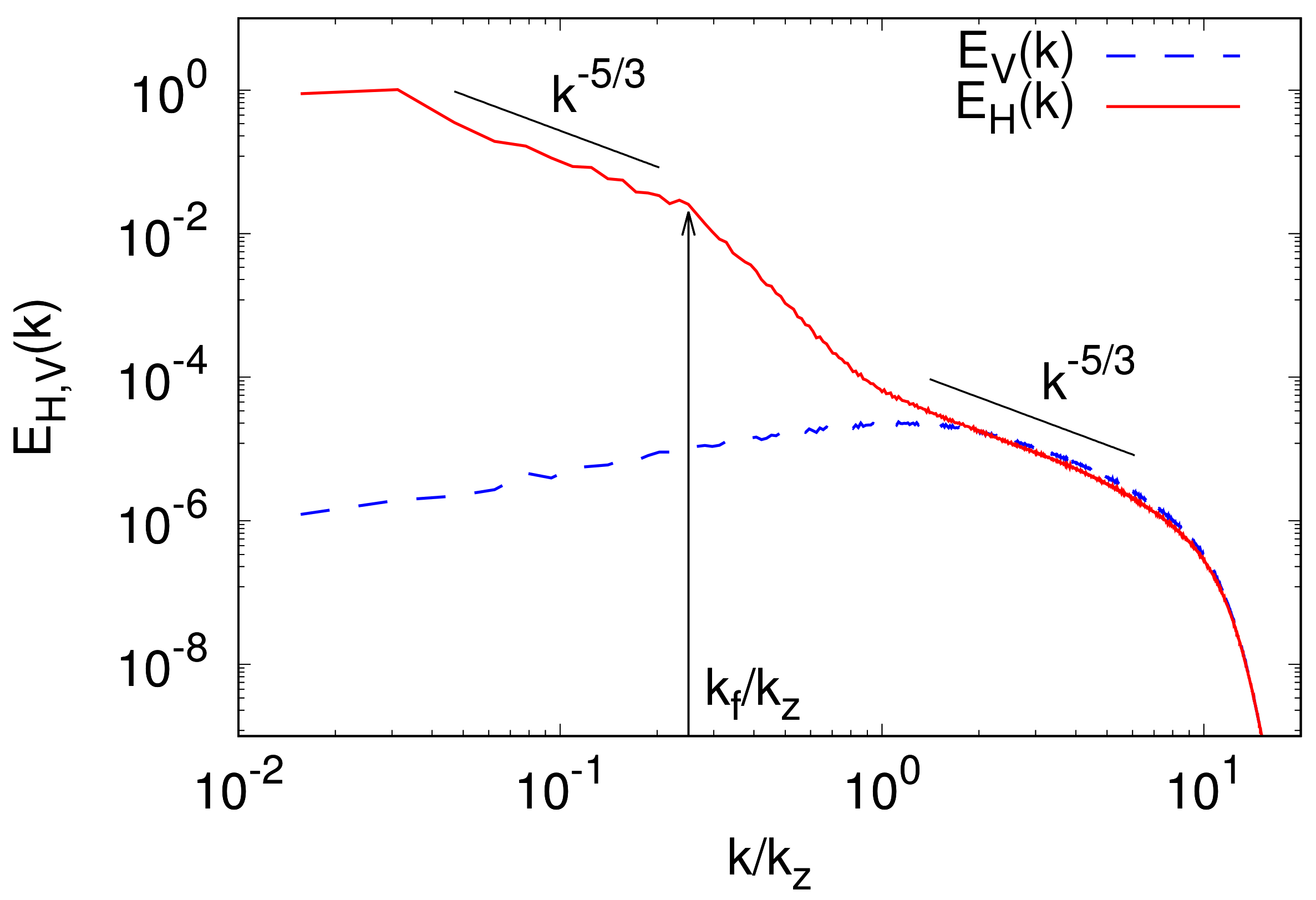
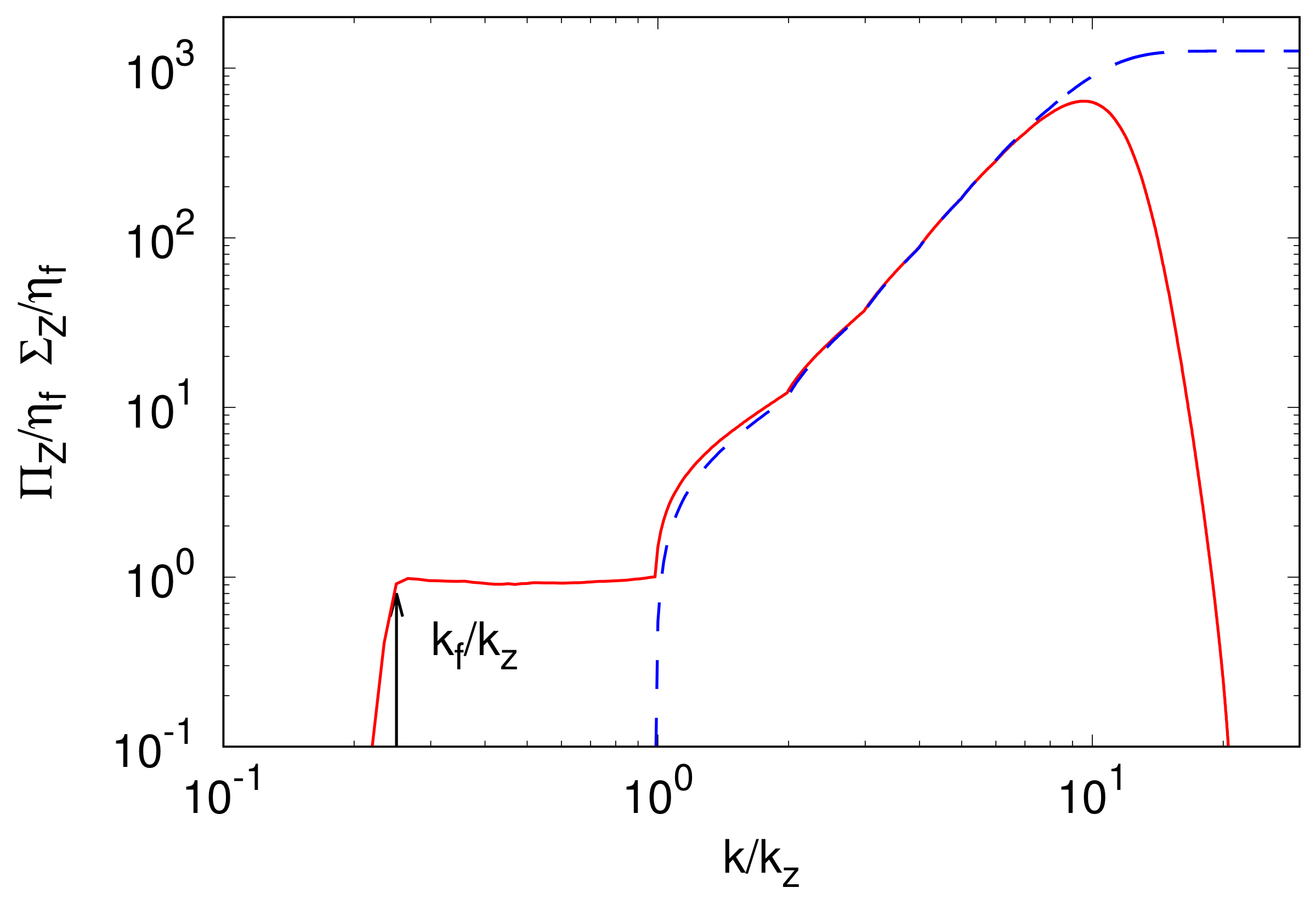
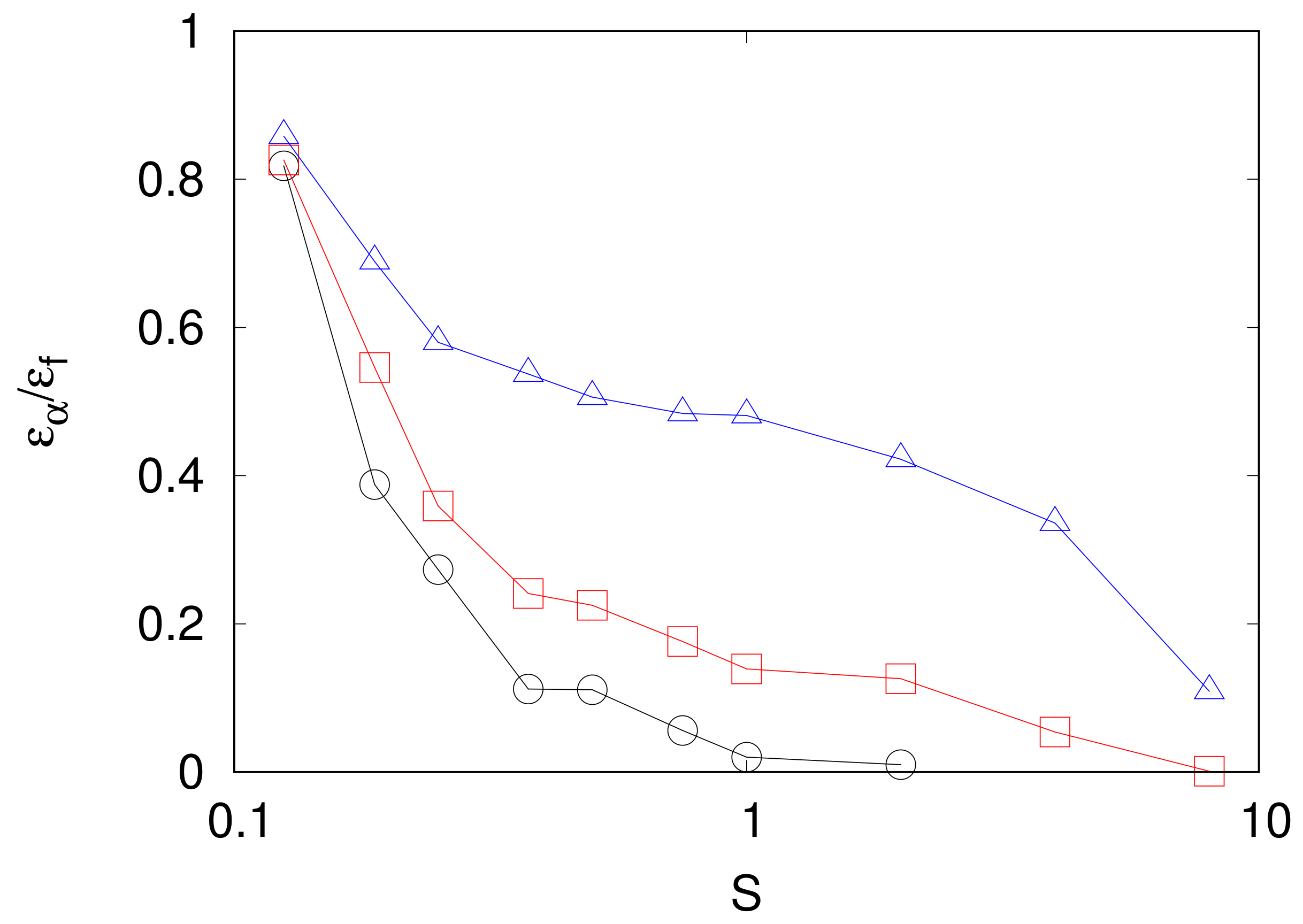
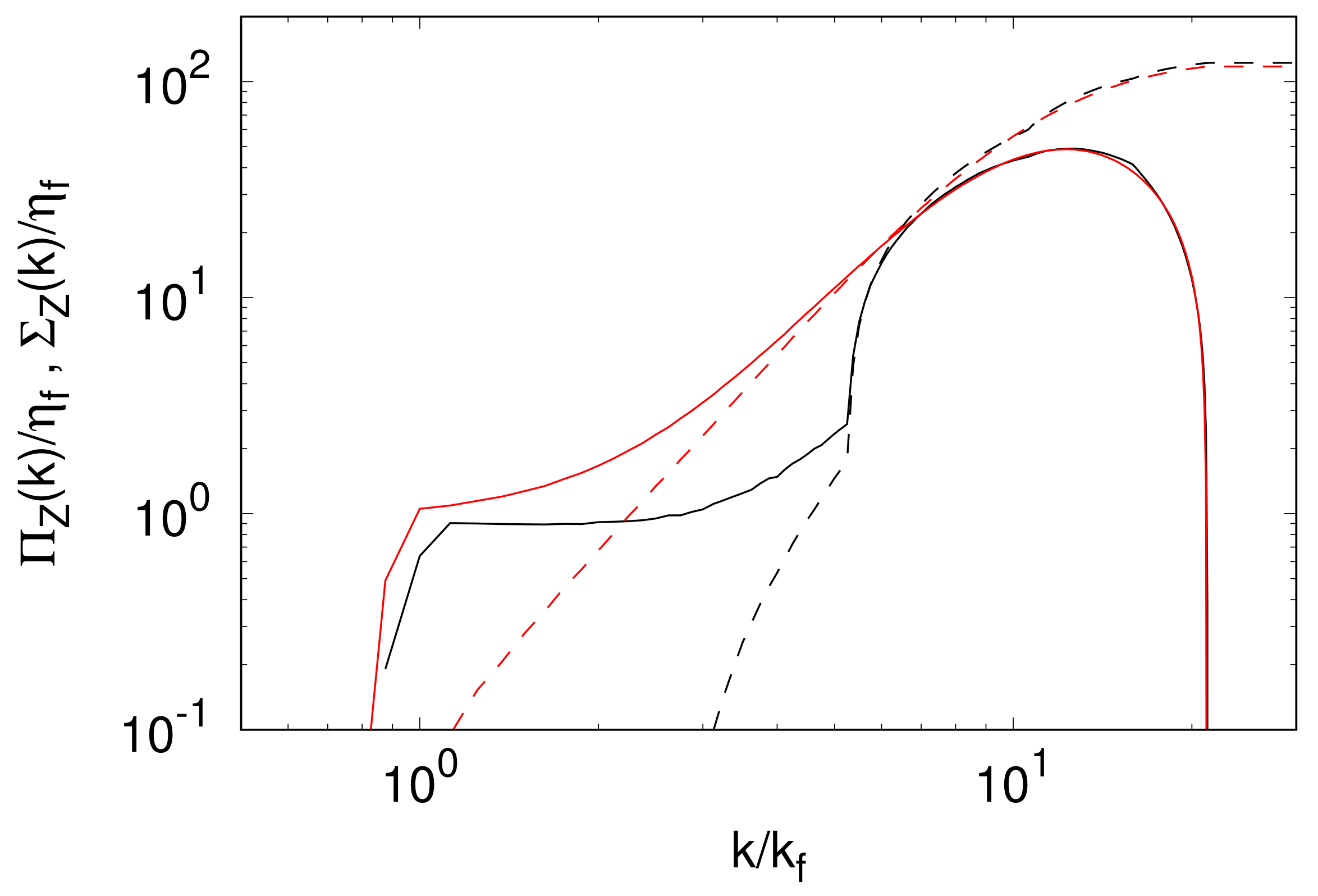
3.2. Dimensional Transition in Rotating Turbulence
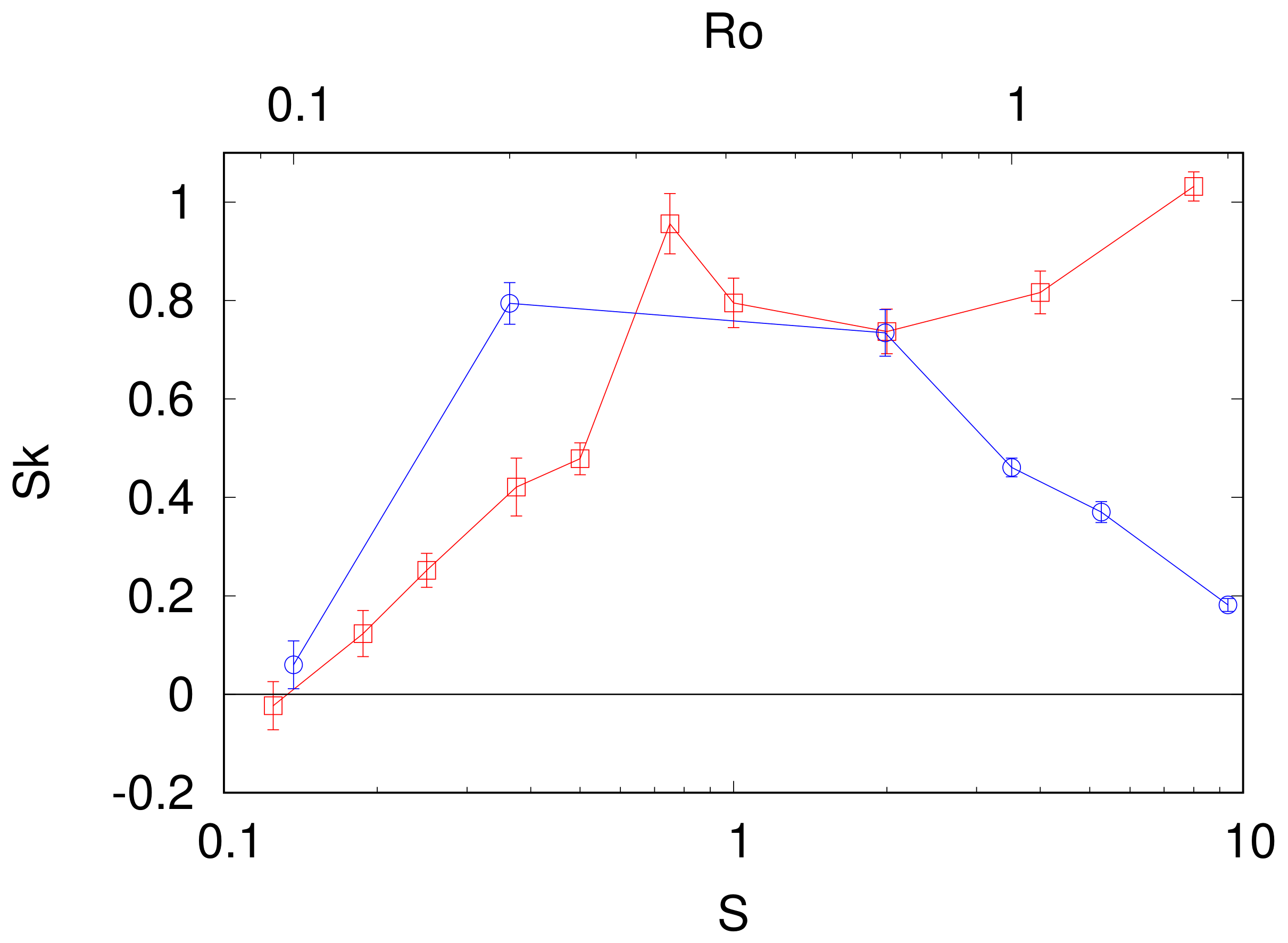
3.3. Cyclonic-Anticyclonic Asymmetry in a Thin Layer
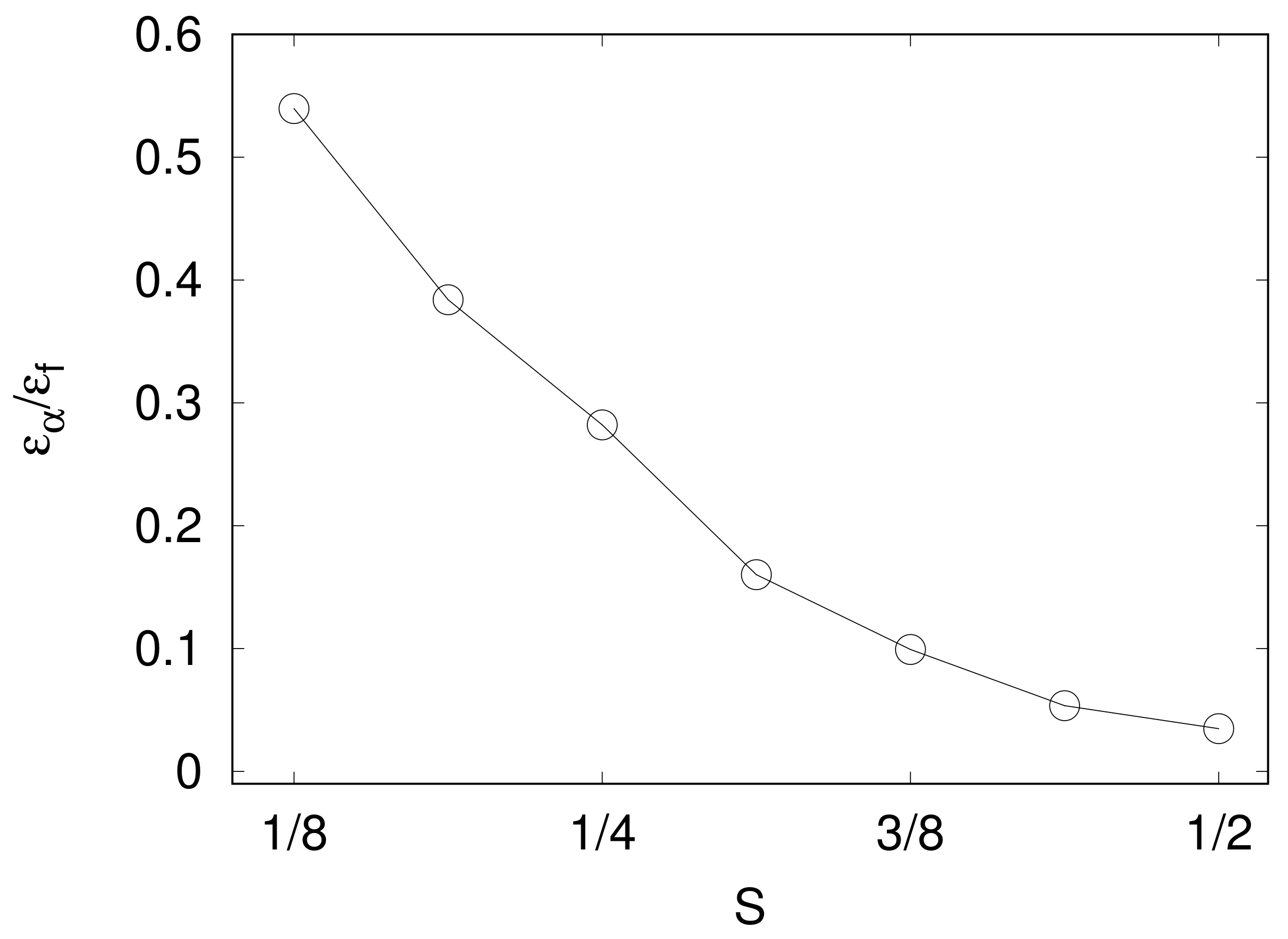
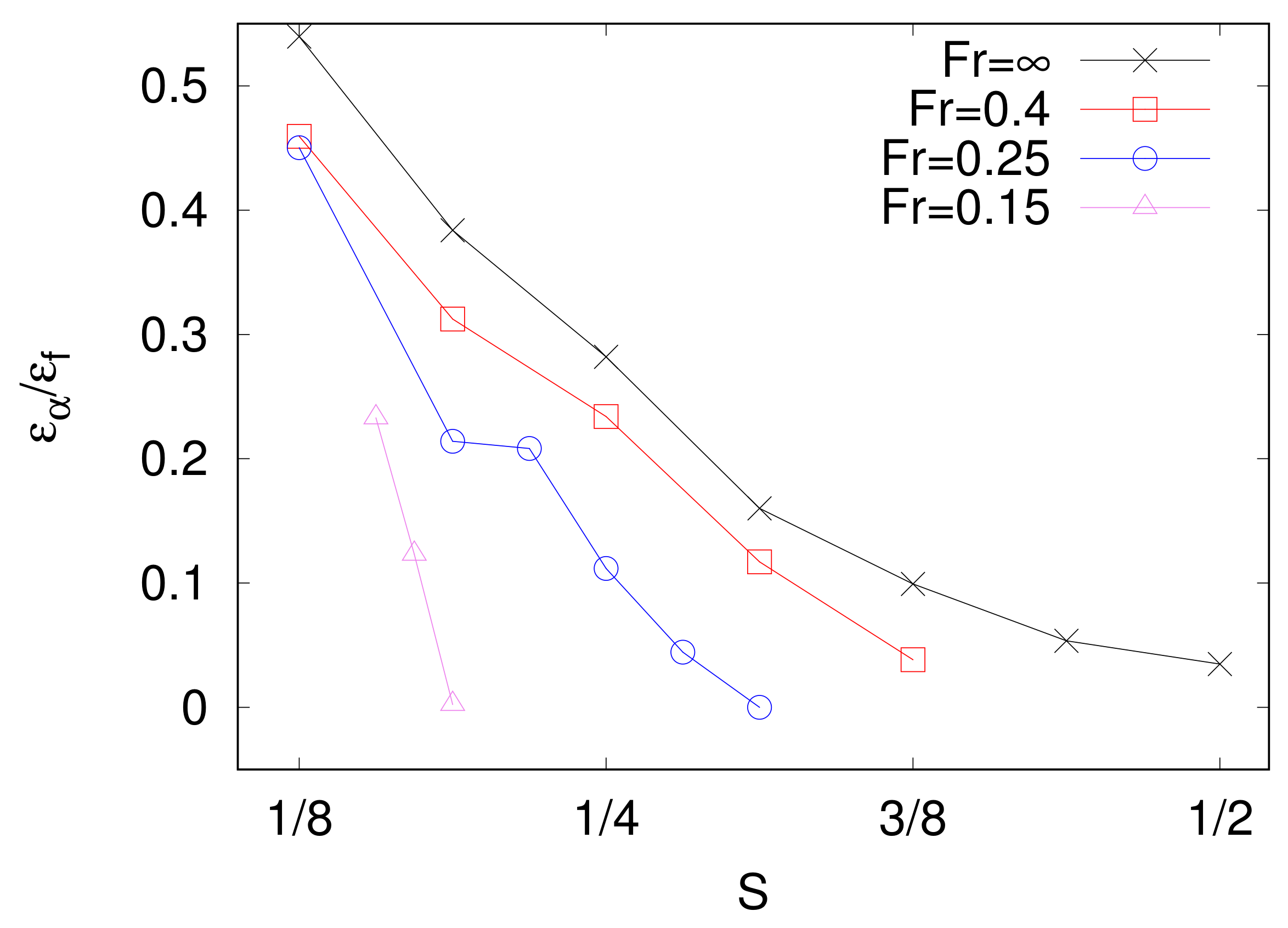
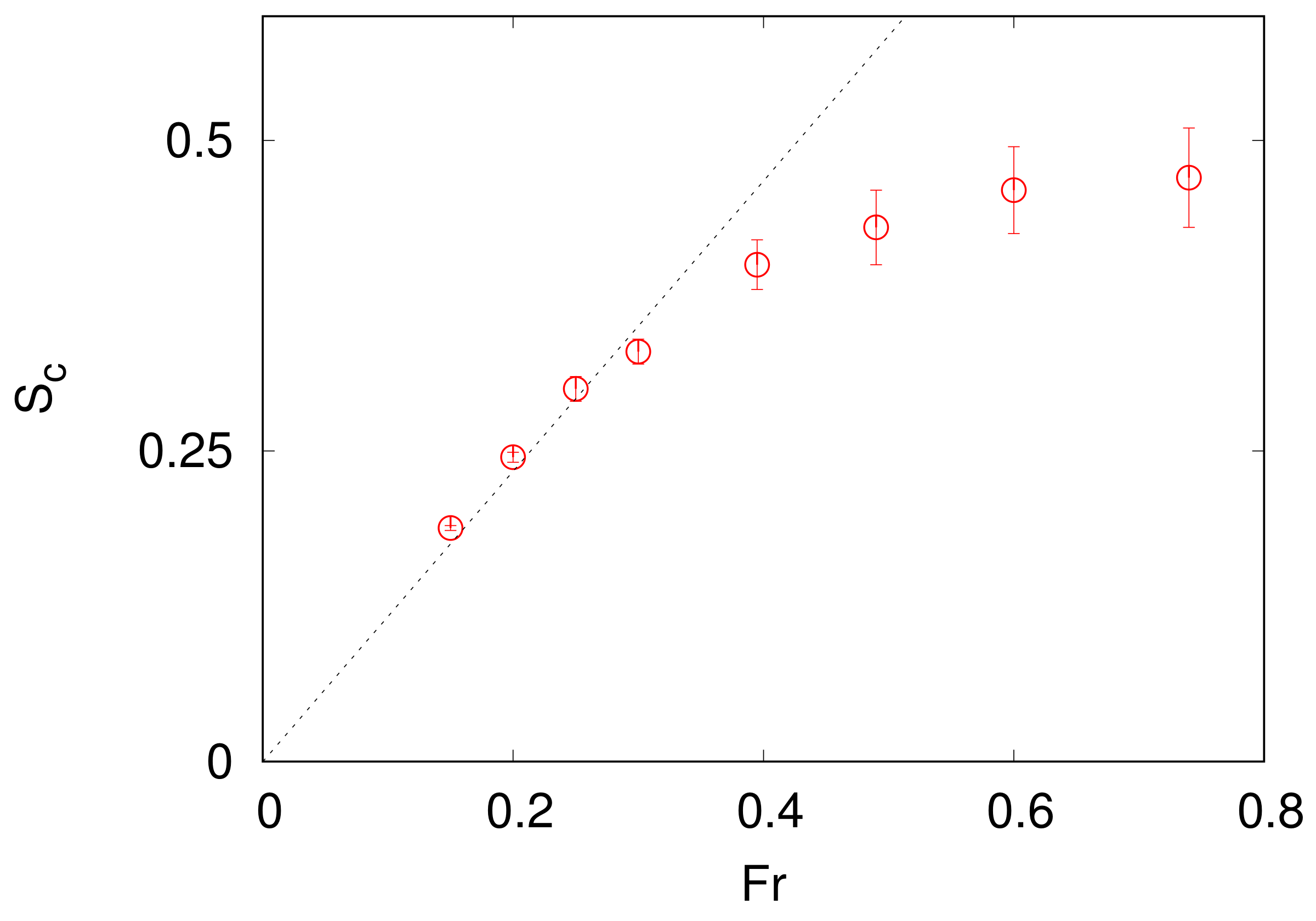
3.4. Dimensional Transition in Stably Stratified Flows
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Frisch, U. Turbulence: The Legacy of AN Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Smith, L.; Chasnov, J.; Waleffe, F. Crossover from Two- to Three-Dimensional Turbulence. Phys. Rev. Lett. 1996, 77, 2467–2470. [Google Scholar] [CrossRef] [PubMed]
- Ngan, K.; Straub, D.; Bartello, P. Aspect ratio effects in quasi-two-dimensional turbulence. Phys. Fluids 2005, 17, 125102. [Google Scholar] [CrossRef]
- Celani, A.; Musacchio, S.; Vincenzi, D. Turbulence in more than two and less than three dimensions. Phys. Rev. Lett. 2010, 104, 184506. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.; Byrne, D.; Falkovich, G.; Shats, M. Upscale energy transfer in thick turbulent fluid layers. Nature Phys. 2011, 7, 321–324. [Google Scholar] [CrossRef]
- Byrne, D.; Xia, H.; Shats, M. Robust inverse energy cascade and turbulence structure in three-dimensional layers of fluid. Phys. Fluids 2011, 23, 95109. [Google Scholar] [CrossRef]
- De Wit, X.M.; Van Kan, A.; Alexakis, A. Bistability of the large-scale dynamics in quasi-two-dimensional turbulence. J. Fluid Mech. 2022, 939, R2. [Google Scholar] [CrossRef]
- van Kan, A.; Nemoto, T.; Alexakis, A. Rare transitions to thin-layer turbulent condensates. J. Fluid Mech. 2019, 878, 356–369. [Google Scholar] [CrossRef]
- Pestana, T.; Hickel, S. Regime transition in the energy cascade of rotating turbulence. Phys. Rev. E 2019, 99, 053103. [Google Scholar] [CrossRef]
- van Kan, A.; Alexakis, A. Critical transition in fast-rotating turbulence within highly elongated domains. J. Fluid Mech. 2020, 899, A33. [Google Scholar] [CrossRef]
- Alexakis, A.; Biferale, L. Cascades and transitions in turbulent flows. Phys. Rep. 2018, 767, 1–101. [Google Scholar]
- Herring, J.; Orszag, S.; Kraichnan, R.; Fox, D. Decay of two-dimensional homogeneous turbulence. J. Fluid Mech. 1974, 66, 417. [Google Scholar] [CrossRef]
- Herring, J.; McWilliams, J. Comparison of direct numerical simulation of two-dimensional turbulence with two-point closure: The effects of intermittency. J. Fluid Mech. 1985, 153, 229–242. [Google Scholar] [CrossRef]
- Herring, J.; Métais, O. Numerical experiments in forced stably stratified turbulence. J. Fluid Mech. 1989, 202, 97–115. [Google Scholar] [CrossRef]
- Lindborg, E.; Brethouwer, G. Stratified turbulence forced in rotational and divergent modes. J. Fluid Mech. 2007, 586, 83–108. [Google Scholar] [CrossRef]
- Boffetta, G.; Musacchio, S.; Mazzino, A.; Rosti, M. Transient inverse energy cascade in free surface turbulence. Phys. Rev. Fluids 2023, 8, 034601. [Google Scholar] [CrossRef]
- Sozza, A.; Boffetta, G.; Muratore-Ginanneschi, P.; Musacchio, S. Dimensional transition of energy cascades in stably stratified forced thin fluid layers. Phys. Fluids 2015, 27, 035112. [Google Scholar] [CrossRef]
- van Kan, A.; Alexakis, A. Condensates in thin-layer turbulence. J. Fluid Mech. 2019, 864, 490–518. [Google Scholar] [CrossRef]
- Musacchio, S.; Boffetta, G. Condensate in quasi-two-dimensional turbulence. Phys. Rev. Fluids 2019, 4, 022602. [Google Scholar] [CrossRef]
- Musacchio, S.; Boffetta, G. Split energy cascade in turbulent thin fluid layers. Phys. Fluids 2017, 29, 111106. [Google Scholar] [CrossRef]
- Deusebio, E.; Boffetta, G.; Lindborg, E.; Musacchio, S. Dimensional transition in rotating turbulence. Phys. Rev. E 2014, 90, 023005. [Google Scholar] [CrossRef] [PubMed]
- Benavides, S.J.; Alexakis, A. Critical transitions in thin layer turbulence. J. Fluid Mech. 2017, 822, 364–385. [Google Scholar] [CrossRef]
- Poujol, B.; van Kan, A.; Alexakis, A. Role of the forcing dimensionality in thin-layer turbulent energy cascades. Phys. Rev. Fluids 2020, 5, 064610. [Google Scholar] [CrossRef]
- Boffetta, G.; Ecke, R. Two-Dimensional Turbulence. Ann. Rev. Fluid Mech. 2012, 44, 427. [Google Scholar] [CrossRef]
- Biferale, L.; Musacchio, S.; Toschi, F. Inverse Energy Cascade in Three-Dimensional Isotropic Turbulence. Phys. Rev. Lett. 2012, 108, 164501. [Google Scholar] [CrossRef]
- Yarom, E.; Vardi, Y.; Sharon, E. Experimental quantification of inverse energy cascade in deep rotating turbulence. Phys. Fluids 2013, 25, 85105. [Google Scholar] [CrossRef]
- Campagne, A.; Gallet, B.; Moisy, F.; Cortet, P.P. Direct and inverse energy cascades in a forced rotating turbulence experiment. Phys. Fluids 2014, 26, 125112. [Google Scholar] [CrossRef]
- Smith, L.; Waleffe, F. Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 1999, 11, 1608–1622. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, S.; Eyink, G.; Holm, D. Resonant interactions in rotating homogeneous three-dimensional turbulence. J. Fluid Mech. 2005, 542, 139–164. [Google Scholar] [CrossRef]
- Cambon, C.; Rubinstein, R.; Godeferd, F.S. Advances in wave turbulence: Rapidly rotating flows. New J. Phys. 2004, 6, 73. [Google Scholar] [CrossRef]
- Scott, J.F. Wave turbulence in a rotating channel. J. Fluid Mech. 2014, 741, 316–349. [Google Scholar] [CrossRef]
- Gallet, B. Exact two-dimensionalization of rapidly rotating large-Reynolds-number flows. J. Fluid Mech. 2015, 783, 412–447. [Google Scholar] [CrossRef]
- Seshasayanan, K.; Gallet, B. Onset of three-dimensionality in rapidly rotating turbulent flows. J. Fluid Mech. 2020, 901, R5. [Google Scholar] [CrossRef]
- Buzzicotti, M.; Aluie, H.; Biferale, L.; Linkmann, M. Energy transfer in turbulence under rotation. Phys. Rev. Fluids 2018, 3, 034802. [Google Scholar] [CrossRef]
- Moisy, F.; Morize, C.; Rabaud, M.; Sommeria, J. Decay laws, anisotropy and cyclone–anticyclone asymmetry in decaying rotating turbulence. J. Fluid Mech. 2011, 666, 5–35. [Google Scholar] [CrossRef]
- Bourouiba, L.; Bartello, P. The intermediate Rossby number range and two-dimensional-three-dimensional transfers in rotating decaying homogeneous turbulence. J. Fluid Mech. 2007, 587, 139. [Google Scholar] [CrossRef]
- Praud, O.; Sommeria, J.; Fincham, A.M. Decaying grid turbulence in a rotating stratified fluid. J. Fluid Mech. 2006, 547, 389–412. [Google Scholar] [CrossRef]
- van Bokhoven, L.J.A.; Cambon, C.; Liechtenstein, L.; Godeferd, F.S.; Clercx, H.J.H. Refined vorticity statistics of decaying rotating three-dimensional turbulence. J. Turbul. 2008, 9, N6. [Google Scholar] [CrossRef][Green Version]
- Gallet, B.; Campagne, A.; Cortet, P.P.; Moisy, F. Scale-dependent cyclone-anticyclone asymmetry in a forced rotating turbulence experiment. Phys. Fluids 2014, 26, 35108. [Google Scholar] [CrossRef]
- Boffetta, G.; Toselli, F.; Manfrin, M.; Musacchio, S. Cyclone–anticyclone asymmetry in rotating thin fluid layers. J. Turb. 2021, 22, 242–253. [Google Scholar] [CrossRef]
- Bartello, P.; Metais, O.; Lesieur, M. Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 1994, 273, 1–30. [Google Scholar] [CrossRef]
- Sreenivasan, B.; Davidson, P.A. On the formation of cyclones and anticyclones in a rotating fluid. Phys. Fluids 2008, 20, 085104. [Google Scholar] [CrossRef]
- Métais, O.; Bartello, P.; Garnier, E.; Riley, J.; Lesieur, M. Inverse cascade in stably stratified rotating turbulence. Dyn. Atmos. Ocean. 1996, 23, 193–203. [Google Scholar] [CrossRef]
- Smith, L.M.; Waleffe, F. Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 2002, 451, 145–168. [Google Scholar] [CrossRef]
- Billant, P.; Chomaz, J.M. Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 2000, 418, 167–188. [Google Scholar] [CrossRef]
- Waite, M.L.; Bartello, P. Stratified turbulence dominated by vortical motion. J. Fluid Mech. 2004, 517, 281–308. [Google Scholar] [CrossRef]
- Marino, R.; Mininni, P.D.; Rosenberg, D.; Pouquet, A. Inverse cascades in rotating stratified turbulence: Fast growth of large scales. Europhys. Lett. 2013, 102, 44006. [Google Scholar] [CrossRef]
- Brethouwer, G.; Billant, P.; Lindborg, E.; Chomaz, J.M. Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 2007, 585, 343–368. [Google Scholar] [CrossRef]
- Lindborg, E. The energy cascade in a strongly stratified fluid. J. Fluid Mech. 2006, 550, 207–242. [Google Scholar] [CrossRef]
- Brunet, M.; Gallet, B.; Cortet, P.P. Shortcut to geostrophy in wave-driven rotating turbulence: The quartetic instability. Phys. Rev. Lett. 2020, 124, 124501. [Google Scholar] [CrossRef]
- Marino, R.; Mininni, P.D.; Rosenberg, D.L.; Pouquet, A. Large-scale anisotropy in stably stratified rotating flows. Phys. Rev. E 2014, 90, 023018. [Google Scholar] [CrossRef]
- Pouquet, A.; Marino, R. Geophysical turbulence and the duality of the energy flow across scales. Phys. Rev. Lett. 2013, 111, 234501. [Google Scholar] [CrossRef] [PubMed]
- Waite, M.L.; Bartello, P. The transition from geostrophic to stratified turbulence. J. Fluid Mech. 2006, 568, 89–108. [Google Scholar] [CrossRef]
- Marino, R.; Pouquet, A.; Rosenberg, D. Resolving the paradox of oceanic large-scale balance and small-scale mixing. Phys. Rev. Lett. 2015, 114, 114504. [Google Scholar] [CrossRef] [PubMed]
- Bartello, P. Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 1995, 52, 4410–4428. [Google Scholar] [CrossRef]
- Herbert, C.; Marino, R.; Rosenberg, D.; Pouquet, A. Waves and vortices in the inverse cascade regime of stratified turbulence with or without rotation. J. Fluid Mech. 2016, 806, 165–204. [Google Scholar] [CrossRef][Green Version]
- Pouquet, A.; Marino, R.; Mininni, P.D.; Rosenberg, D. Dual constant-flux energy cascades to both large scales and small scales. Phys. Fluids 2017, 29, 111108. [Google Scholar] [CrossRef]
- Van Kan, A.; Alexakis, A. Energy cascades in rapidly rotating and stratified turbulence within elongated domains. J. Fluid Mech. 2022, 933, A11. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boffetta, G. Dimensional Transitions in Turbulence: The Effects of Rotation and Stratification. Atmosphere 2023, 14, 1688. https://doi.org/10.3390/atmos14111688
Boffetta G. Dimensional Transitions in Turbulence: The Effects of Rotation and Stratification. Atmosphere. 2023; 14(11):1688. https://doi.org/10.3390/atmos14111688
Chicago/Turabian StyleBoffetta, Guido. 2023. "Dimensional Transitions in Turbulence: The Effects of Rotation and Stratification" Atmosphere 14, no. 11: 1688. https://doi.org/10.3390/atmos14111688
APA StyleBoffetta, G. (2023). Dimensional Transitions in Turbulence: The Effects of Rotation and Stratification. Atmosphere, 14(11), 1688. https://doi.org/10.3390/atmos14111688







