Numerical Simulation on Wind Speed Amplification of High-Rise Buildings with Openings
Abstract
:1. Introduction
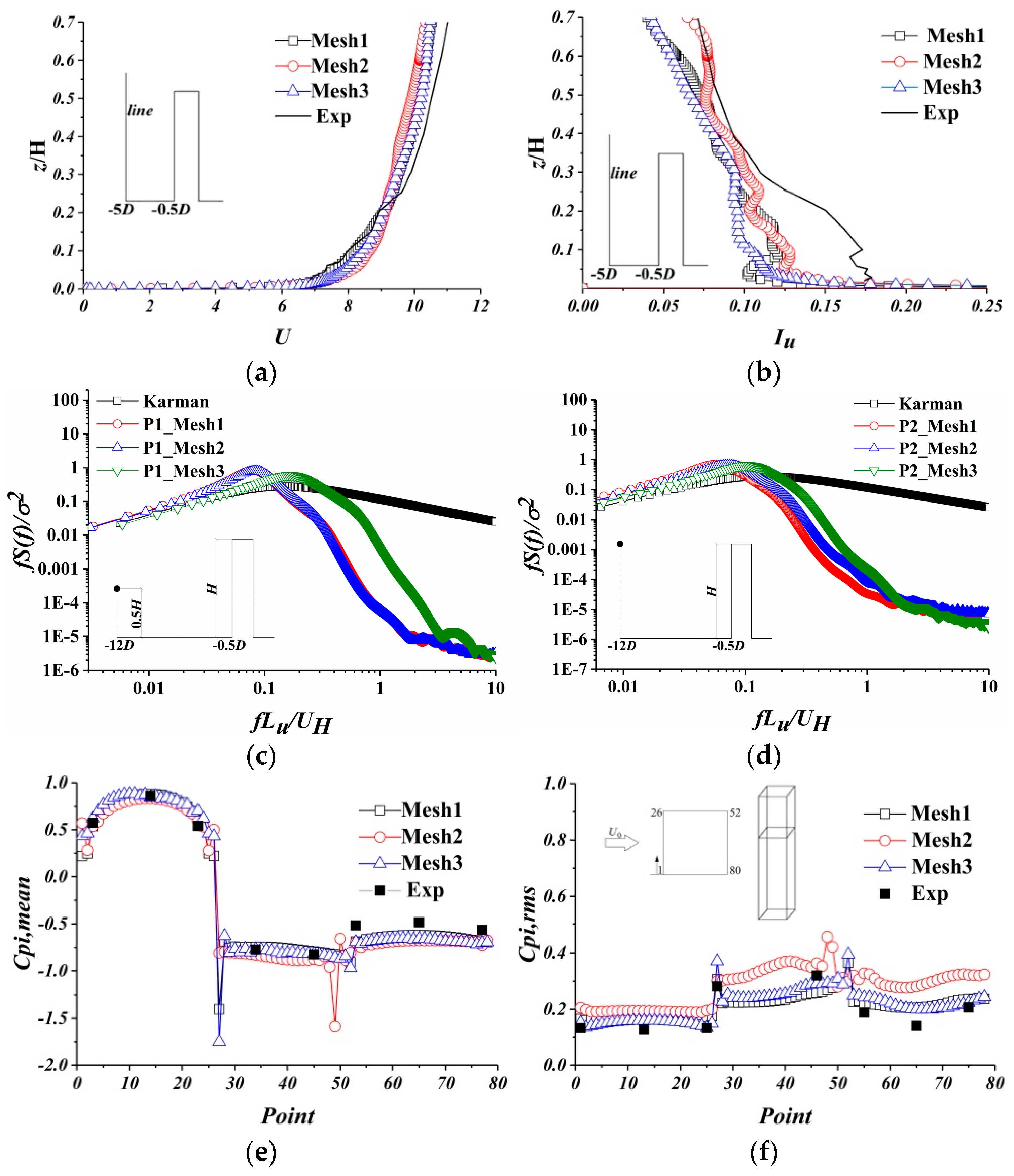
2. CFD Verification and Validation
2.1. Numerical Setups
2.2. Boundary Conditions
3. Results and Discussions
3.1. Effect of Openings on Wind Speed Amplification of High-Rise Buildings
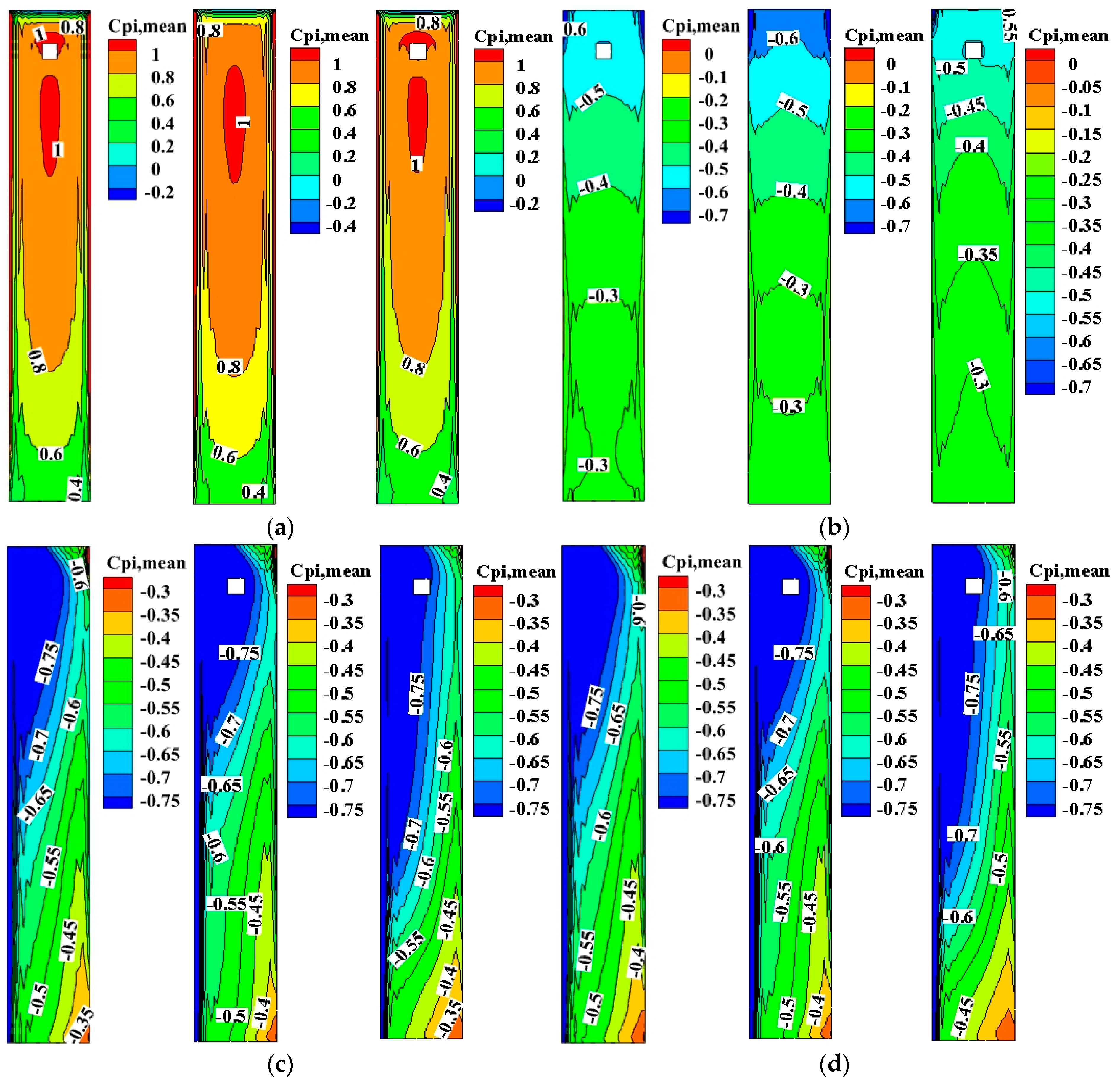
3.2. Distribution of Mean Wind Pressure Coefficients
3.3. Analysis of Time-Averaged Flow Field
- (1)
- In general, one large-size separation vortex and two small-size separation vortices are formed on each side of the standard square cylinder close to the sidewall, and a pair of symmetric vortices of equal size and in opposite direction also exist on the leeward side. The large-size separation vortices and the small-size separation vortices at the upstream corner are connected with the leeward separation vortices. In the longitudinal section, the top of the windward side and the top of the leeward side of the square cylinder are separation points, and flow separation occurs when the air flows through this region. The top of the standard square cylinder and the top of the leeward surface each form a separate vortex, and the two separate vortices exist independently of each other. Due to the shielding effect of the structure, the incoming flow directly acts on the windward side of the structure, and then flow separation occurs at the top and two sides of the windward surface. Therefore, the side face and the top of the structure are in the separation zone. The suction effect is generated by the existence of the separation vortex, resulting in negative pressure on the side face and the top of the structure. The leeward side of the structure is subjected to the mixed effect of the separation vortex on the side face of the structure and the shedding vortex on the top, which produces wind suction, so it is also represented as negative pressure.
- (2)
- When compared with the standard square cylinder, the overall wind pressure distribution on the surface of the three opening models is consistent with the standard square cylinder, showing positive pressure on the windward side and negative pressure on the top, side face and leeward side. However, the wind pressure coefficient at the same position is different. For instance, the flow field around Case 1 changes significantly due to the aerodynamic measures of the X-direction openings. The wind pressure on the windward side is lower and the separation vortices behind the sidewalls of the cylinder are reattached on the flow field of the cross section. Symmetric vortices no longer appear on the leeward side. The incoming flow flows along with the openings, dividing the section into two rectangular sections with a large side ratio. The incoming flow in the openings disperses the large-scale separation vortices on the leeward side, and the generated separation vortices form vortices on the leeward side at the top of the tunnel. The scale of the generated separation vortices is lower than that of the standard square cylinder. The height of the vortex core is equal to the height of the tunnel, which reduces the negative pressure on the leeward side. Therefore, according to the cloud chart of wind pressure coefficient, the wind pressure difference between this area and the entrance of the opening on the windward side forms a narrow tube effect, which leads to a sharp increase in incoming wind speed in the opening due to the opening measure in the X-direction.
- (3)
- Similar to Case 1, the surrounding flow field and wind pressure distribution of Case 2 and Case 3 are clearly different from those of the standard square cylinder due to the opening measures. Under the opening measure in the Y-direction, due to the shielding effect of the windward side, the incoming flow in these openings basically has a lateral effect, and there is no large pressure difference due to the symmetrical distribution of wind pressure at both ends of the openings. As a result, although there is also a large negative pressure in the transverse openings, the X-direction wind speed in this area is significantly lower than that in the X-direction openings at the same height. After the measures for openings in both the X- and Y-directions are taken, the flow field and surface wind pressure distribution around Case 3 are close to those of Case 1. The wind speed under the influence of the measures of openings in both the X- and Y-directions presents an amplification compared to the wind speed of incoming flow at the same height (See Table 4). The wind speed amplification degree is slightly lower than that of Case 1, which also proves that the measure of X-direction openings plays a more important role in the incoming wind speed than that in the Y-direction.
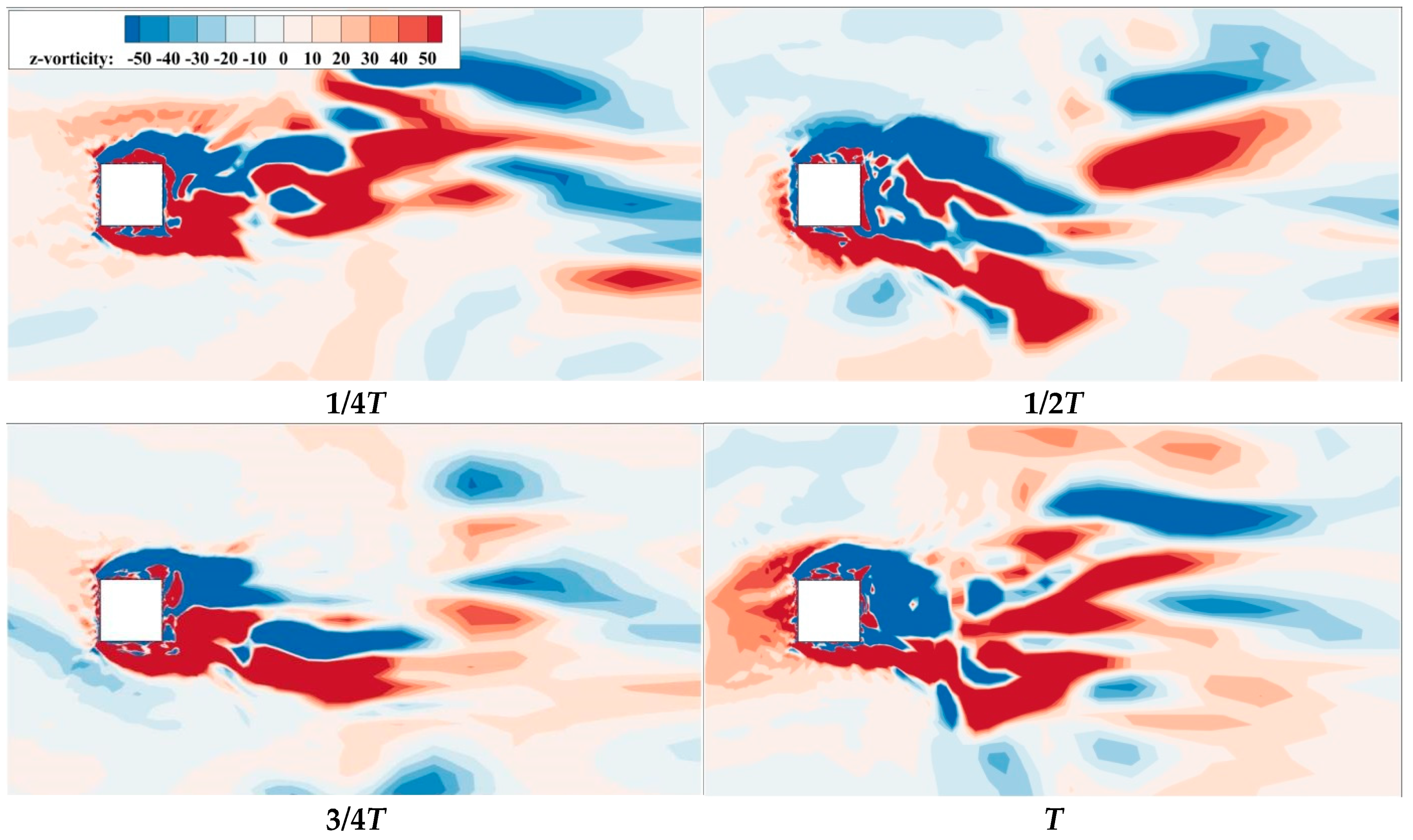
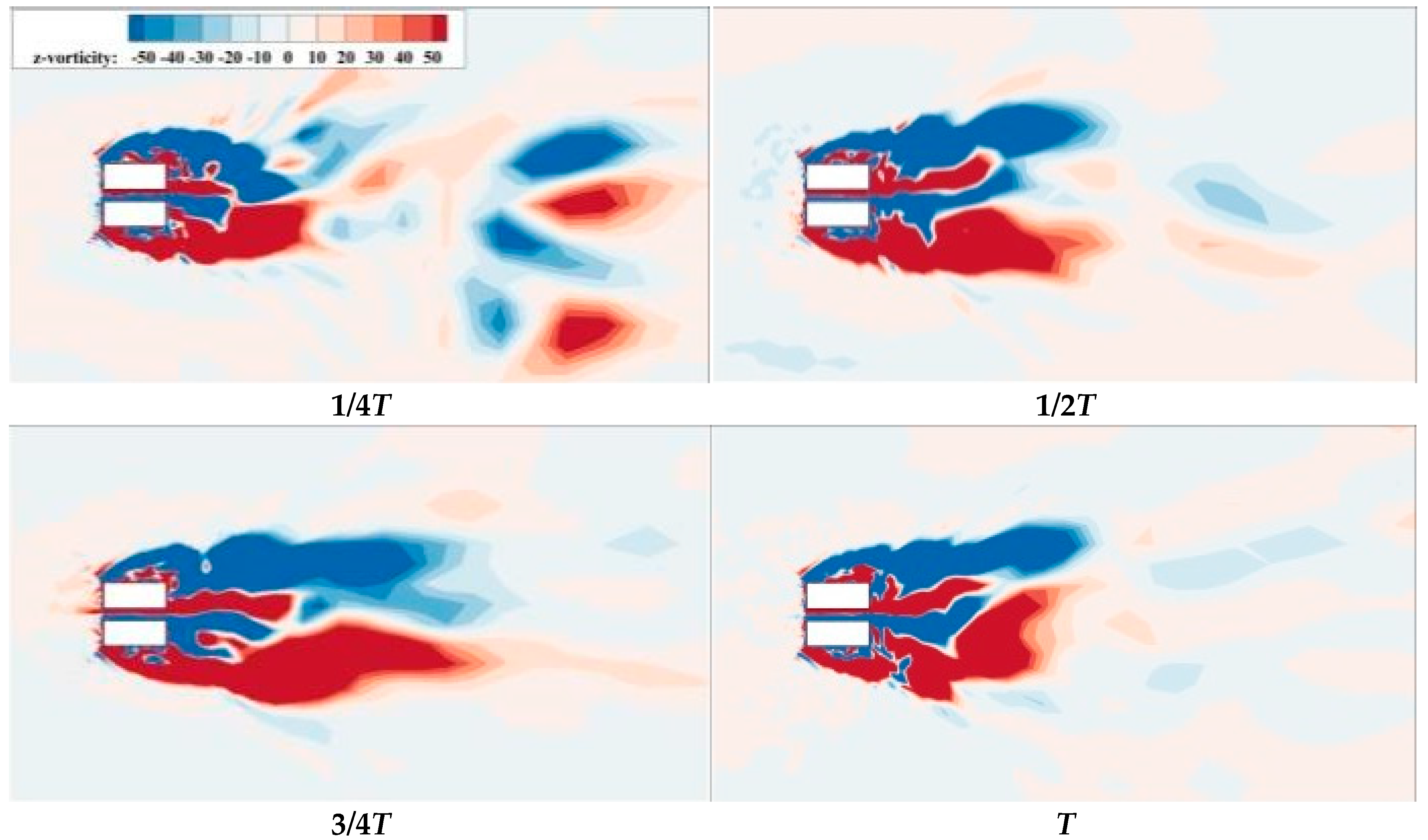
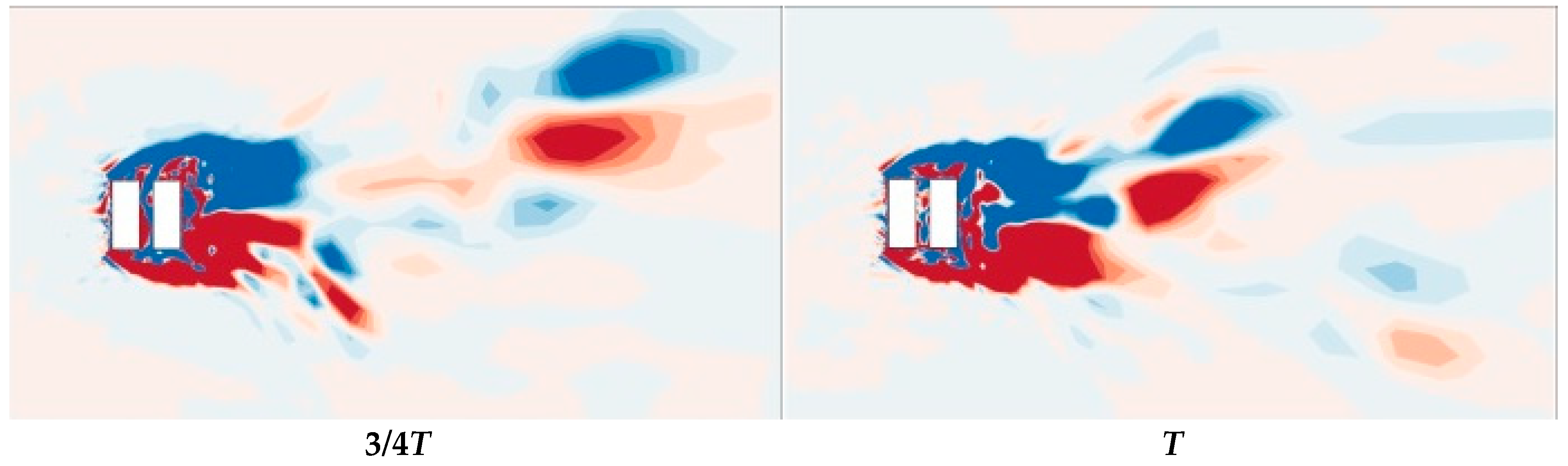
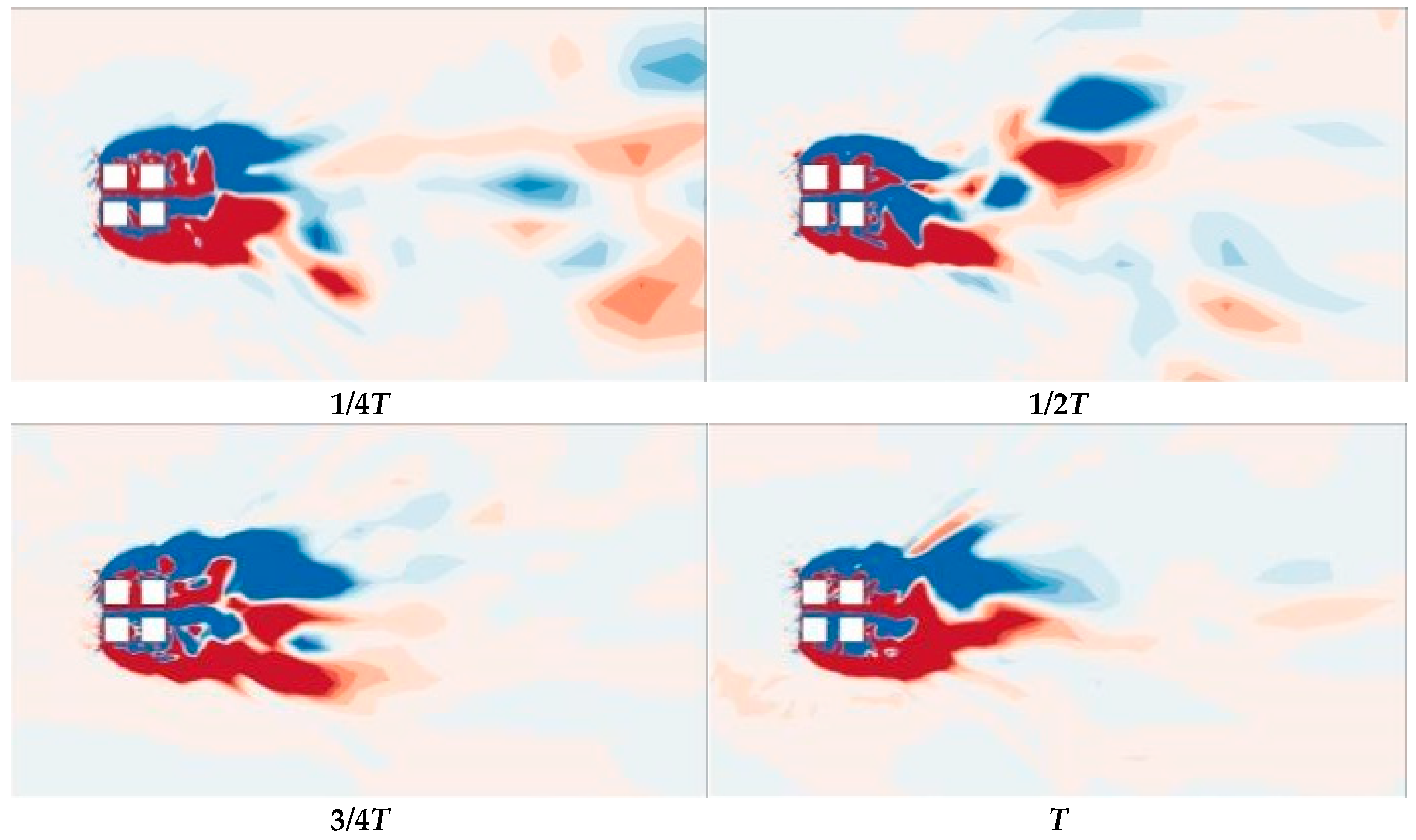
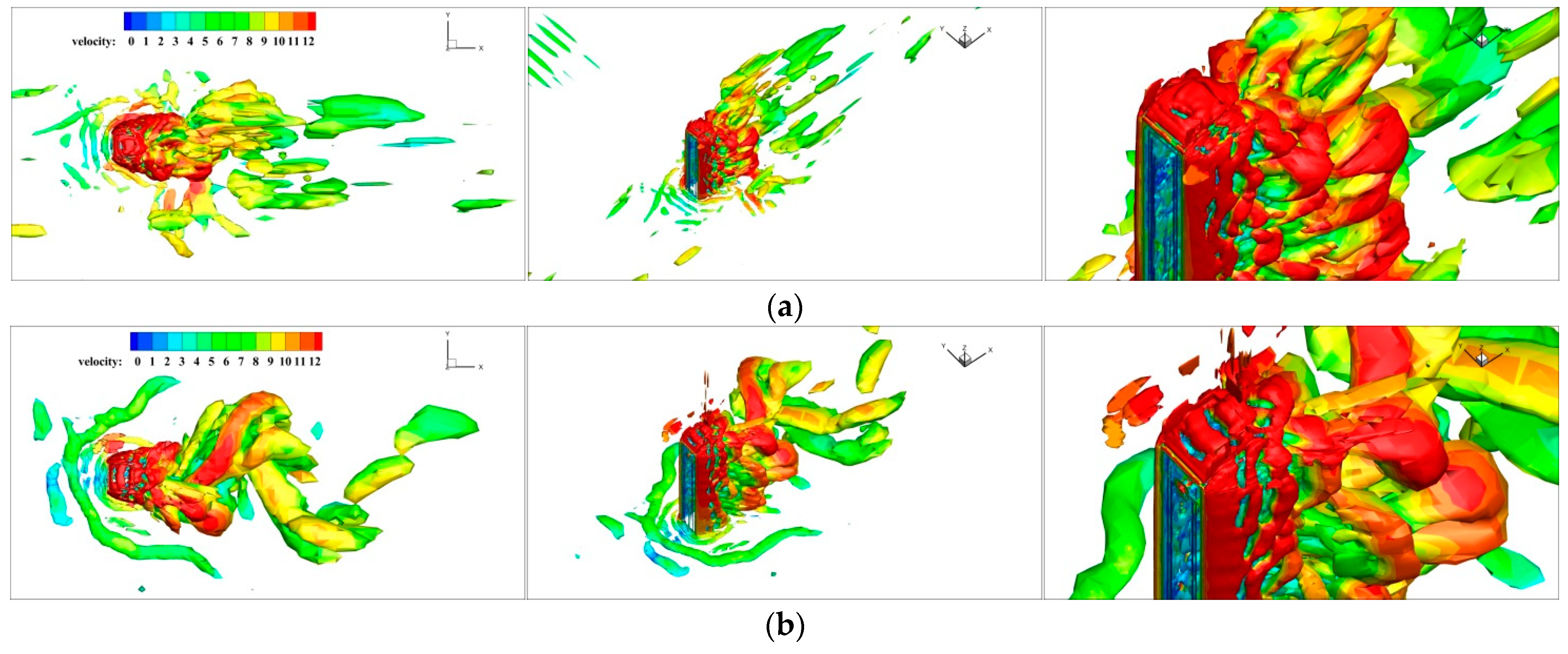
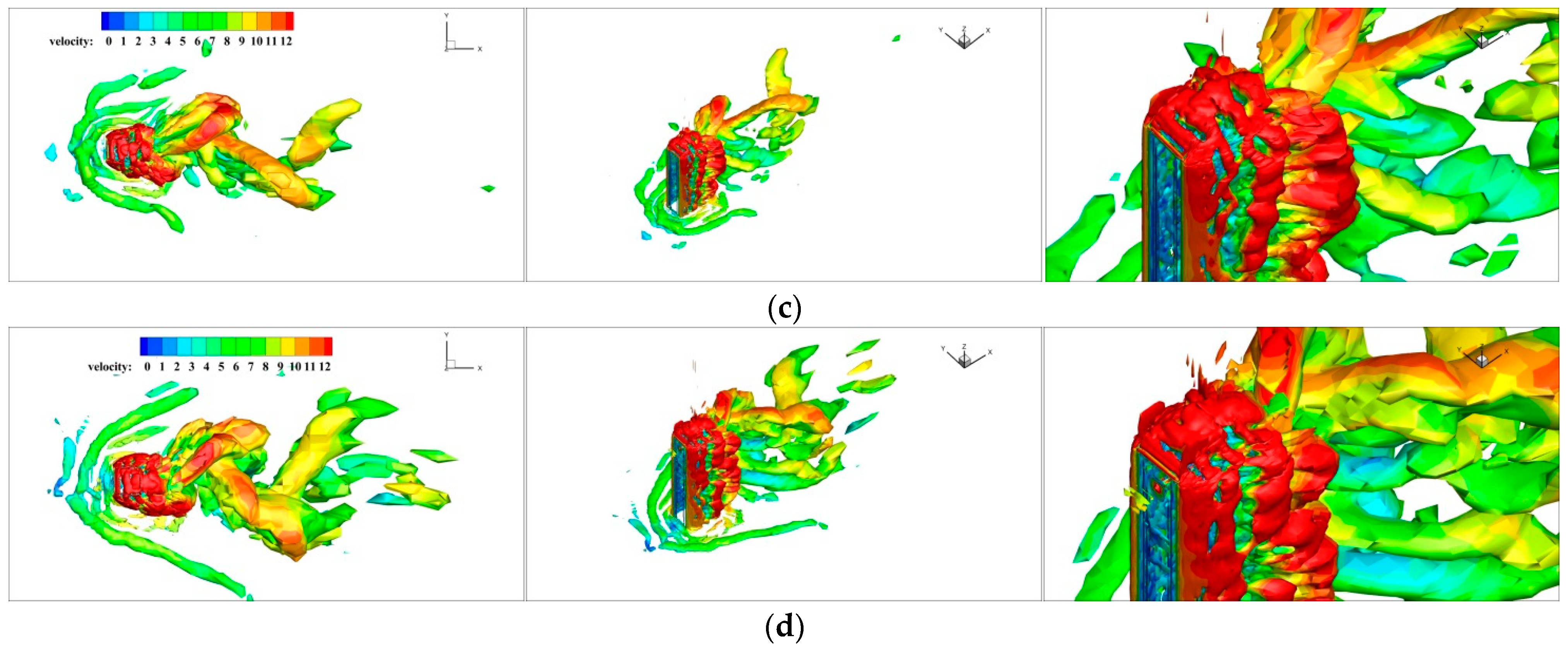
3.4. Analysis of Instantaneous Flow Field
- (1)
- A large number of vortex structures of different sizes and shapes are distributed around the structures. With a change in height, the vortex structures are also distributed differently, showing obvious three-dimensional characteristics. In the top region of the square cylinder, as the strip vortex separates at around the top separation point of the windward side of the upstream square cylinder, it mixes with the separation vortexes on both sides of the top, forming three-dimensional separation shear vortexes on the top of the square cylinder. With the continuous evolution of the vortex structure, the separation vortexes gradually move from the separation region to the downstream region. The measure of openings in the X-direction causes the flow separation point at the edge of the windward side to move down and the vortices at the top of the square cylinder to decrease. After establishing the openings in the X-direction, the narrow tube effect is formed, which not only accelerates the air flow through the entrance but also disorganizes the large-scale vortices on the leeward side. It forms several small-scale vortices near the entrance and on the leeward side, which disperses energy more. However, the measure of openings in the Y-direction leads to the lateral flow of separation vortices on both sides into the openings, which weakens the energy distribution on both sides. As a result, the lateral shear vortices of Case 2 are smaller than those of Case 1 and Case 3 and closer to the wall, which is determined by the variation in the aerodynamic configuration of the building caused by the opening measures.
- (2)
- Due to the friction effect on the ground, curved banded boundary-layer vortexes of different scales are generated in the near-ground region in front of the windward side for the three types of square cylinders with openings. The friction effect of the ground also causes the formation of spiral separation vortices on the side of the square cylinders, which is an embodiment of the turbulence pulsation of the incoming flow. Combined with the horizontal vortex diagrams in Figure 11, Figure 12 and Figure 13, the flow field morphology of Case 1, Case 2 and Case 3 is different after adopting openings in the X-direction, Y-direction and both X- and Y-directions, respectively. The side separation vortices of Case 2 are closer to the wall, and there are abundant small-scale vortices. In addition, three-dimensional strip separation vortices are also formed on the side of the square cylinder. The strip vortices of Case 1 and Case 3 have a larger scale and more concentrated vortex structure, while the strip vortices on the side of the square cylinder of Case 2 have a more dispersed scale. It can also be seen that the wind speed in the X-direction openings of Case 1 and Case 3 is significantly higher than that on the windward side of these square cylinders at the same height, while the windward side of Case 2 presents a lower wind speed as a whole due to the shielding effect. For vortices of various forms around the square cylinder, the larger these vortices are, the more energy they carry, the slower they move, and the smaller the wind pressure pulsation they generate. Conversely, the smaller the scale of the vortices, the more obvious the wind pressure pulsation. It is precisely because the opening measures change the aerodynamic configuration of the square cylinder that Case 1 and Case 3 gather small-scale vortex structures in the X-direction openings, which enhances the wind pressure pulsation and increases the mean and RMS wind speed in the openings, thus affecting the wind load on the surface of the square cylinder.
4. Conclusions
- (1)
- The parameter settings and inflow turbulence based on self-sustaining boundary conditions and generated via LES were adopted. The simulated mean wind profiles and wind velocity spectra are basically consistent with the related wind tunnel test results and can well predict the wind loads of the square cylinders.
- (2)
- Under the effect of the opening measures, the aerodynamic configuration of the square cylinders is changed, and the wind load and incoming wind speed also vary. By adopting the X-direction opening measure, the pressure on the windward side of the square cylinders decreases. Part of the air flow in the square cylinders flows through the tunnel into the wake negative pressure area, which affects the flow separation point location, shear flow diffusion angle and flow reattachment phenomenon. Meanwhile, the wind speed in the openings increases significantly due to the narrow tube effect, which blows away the large-scale vortices on the leeward side, leading to energy dispersion and weakening the wind pressure on the structural surface. In contrast, the wind speed in the openings decreases significantly due to the shielding effect, and the wind load and the wind-induced response on the surface of the square cylinder are not significantly improved.
- (3)
- Under the measure of openings in both the X- and Y-directions, the vortex structures in the openings are more complex, the vortex departure frequency components are more complex, and the energy distribution is more dispersed. The wind speed in the X-direction openings still increases sharply, but the wind speed reduction in the Y-direction openings is weaker than that of Case 2. The wind speed in the central monitoring point still increases significantly under the influence of opening measures in both the X- and Y-directions, which proves that the X-direction openings play a more important role than the openings in the Y-direction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J. Towards a low-carbon future in China’s building sector—A review of energy and climate models forecast. Energy Policy 2008, 36, 1736–1747. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Alrawashdeh, H.; Al-Quraan, A.; Blocken, B.; Dilimulati, A.; Paraschivoiu, M.; Pilay, P. Urban wind energy: Some views on potential and challenges. J. Wind. Eng. Ind. Aerodyn. 2018, 179, 146–157. [Google Scholar] [CrossRef]
- Thellufsen, J.Z.; Lund, H.; Sorknæs, P.; Østergaard, P.A.; Chang, M.; Drysdale, D.; Nielsen, S.; Djørup, S.R.; Sperling, K. Smart energy cities in a 100% renewable energy context. Renew. Sustain. Energy Rev. 2020, 129, 109922. [Google Scholar] [CrossRef]
- Bagheri, M.; Delbari, S.H.; Pakzadmanesh, M.; Kennedy, C.A. City-integrated renewable energy design for low-carbon and climate-resilient communities. Appl. Energy 2019, 239, 1212–1225. [Google Scholar] [CrossRef]
- Stathopoulos, T. Computational wind engineering: Past achievements and future challenges. J. Wind. Eng. Ind. Aerodyn. 1997, 67–68, 509–532. [Google Scholar] [CrossRef]
- Tamura, T.; Itoh, Y.; Wada, A.; Kuwahara, K. Numerical study of pressure fluctuations on a rectangular cylinder in aerodynamic oscillation. J. Wind. Eng. Ind. Aerodyn. 1995, 54–55, 239–250. [Google Scholar] [CrossRef]
- Murakami, S.; Mochida, A.; Sakamoto, S. CFD analysis of wind-structure interaction for oscillating square cylinders. J. Wind. Eng. Ind. Aerodyn. 1997, 72, 33–46. [Google Scholar] [CrossRef]
- Larsen, A. Advances in aeroelastic analyses of suspension and cable-stayed bridges. J. Wind. Eng. Ind. Aerodyn. 1998, 74–76, 73–90. [Google Scholar] [CrossRef]
- Klemm, K.; Marks, W.; Klemm, A.J. Multicriteria optimisation of the building arrangement with application of numerical simulation. Build. Environ. 2000, 35, 537–544. [Google Scholar] [CrossRef]
- Hubbard, H.H.; Shepherd, K.P. Aeroacoustics of large wind turbines. J. Acoust. Soc. Am. 1991, 89, 2495–2508. [Google Scholar] [CrossRef]
- Bouffard, F.; Galiana, F.D. Stochastic Security for Operations Planning With Significant Wind Power Generation. IEEE Trans. Power Syst. 2008, 23, 306–316. [Google Scholar] [CrossRef]
- Hyams, M.A. Wind energy in the built environment. In Metropolitan Sustainability; Woodhead Publishing: Sawston, UK, 2012; pp. 457–499. [Google Scholar]
- Tamura, T.; Miyagi, T.; Kitagishi, T. Numerical prediction of unsteady pressures on a square cylinder with various corner shapes. J. Wind. Eng. Ind. Aerodyn. 1998, 74, 531–542. [Google Scholar] [CrossRef]
- Tamura, T.; Miyagi, T. The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes. J. Wind. Eng. Ind. Aerodyn. 1999, 83, 135–145. [Google Scholar] [CrossRef]
- Wang, X.R.; Gu, M. Experimental study on Re number effects on aerodynamic characteristics of 2D square prisms with corner modifications. Wind. Struct. 2016, 22, 573–594. [Google Scholar] [CrossRef]
- Risø, C. Urban Wind Energy-State of the Art 2009; National Laboratory for Sustainable Energy Technical University of Denmark: Roskilde, Denmark, 2009. [Google Scholar]
- Li, Q.S.; Chen, F.B.; Li, Y.G.; Lee, Y.Y. Implementing wind turbines in a tall building for power generation: A study of wind loads and wind speed amplifications. J. Wind. Eng. Ind. Aerodyn. 2013, 116, 70–82. [Google Scholar] [CrossRef]
- Li, Q.S.; Shu, Z.R.; Chen, F.B. Performance assessment of tall building-integrated wind turbines for power generation. Appl. Energy 2016, 165, 777–788. [Google Scholar] [CrossRef]
- Lu, C.L.; Li, Q.S.; Huang, S.H.; Zhao, S.L.; Zhu, C.N. Wind noise simulation and evaluation of a super high-rise building with wind turbine generators. J. Vib. Shock. 2012, 31, 5–9. (In Chinese) [Google Scholar]
- Chen, F.B.; Wang, X.L.; Zhao, Y.; Li, Y.B.; Li, Q.S.; Xiang, P.; Li, Y.; Mazzotti, C. Study of wind loads and wind speed amplifications on high-rise building with opening by numerical simulation and wind tunnel test. Adv. Civ. Eng. 2020, 2020, 8850688. [Google Scholar] [CrossRef]
- Ruiz, C.A.; Kalkman, I.; Blocken, B. Aerodynamic design optimization of ducted openings through high-rise buildings for wind energy harvesting. Build. Environ. 2021, 202, 108028. [Google Scholar] [CrossRef]
- Aristodemou, E.; Bentham, T.; Pain, C.; Colvile, R.; Robins, A.; ApSimon, H. A comparison of mesh-adaptive LES with wind tunnel data for flow past buildings: Mean flows and velocity fluctuations. Atmos. Environ. 2009, 43, 6238–6253. [Google Scholar] [CrossRef]
- Jiang, Y.; Alexander, D.; Jenkins, H.; Arthur, R.; Chen, Q. Natural ventilation in buildings: Measurement in a wind tunnel and numerical simulation with large-eddy simulation. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 331–353. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.; Stathopoulos, T.; Van Heijst, G.J.F. CFD simulation of near-field pollutant dispersion on a high-resolution grid: A case study by LES and RANS for a building group in downtown Montreal. Atmos. Environ. 2010, 45, 428–438. [Google Scholar] [CrossRef]
- Zheng, D.Q.; Zhang, A.S.; Gu, M. Improvement of inflow boundary condition in large eddy simulation of flow around tall building. Eng. Appl. Comput. Fluid Mech. 2012, 6, 633–647. [Google Scholar] [CrossRef]
- Baetke, F.; Werner, H.; Wengle, H. Numerical simulation of turbulent flow over surface-mounted obstacles with sharp edges and corners. J. Wind. Eng. Ind. Aerodyn. 1990, 35, 129–147. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. I. The basic experiment. Am. Meteorol. Soc. 1963, 91, 99–164. [Google Scholar]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1998, 3, 1760–1765. [Google Scholar] [CrossRef]
- Doormaal, J.V.; Raithby, G.D. Enhancements of the simple method for predicting incompressible fluid flows. Numer. Heat Transf. Appl. 1984, 7, 147–163. [Google Scholar]

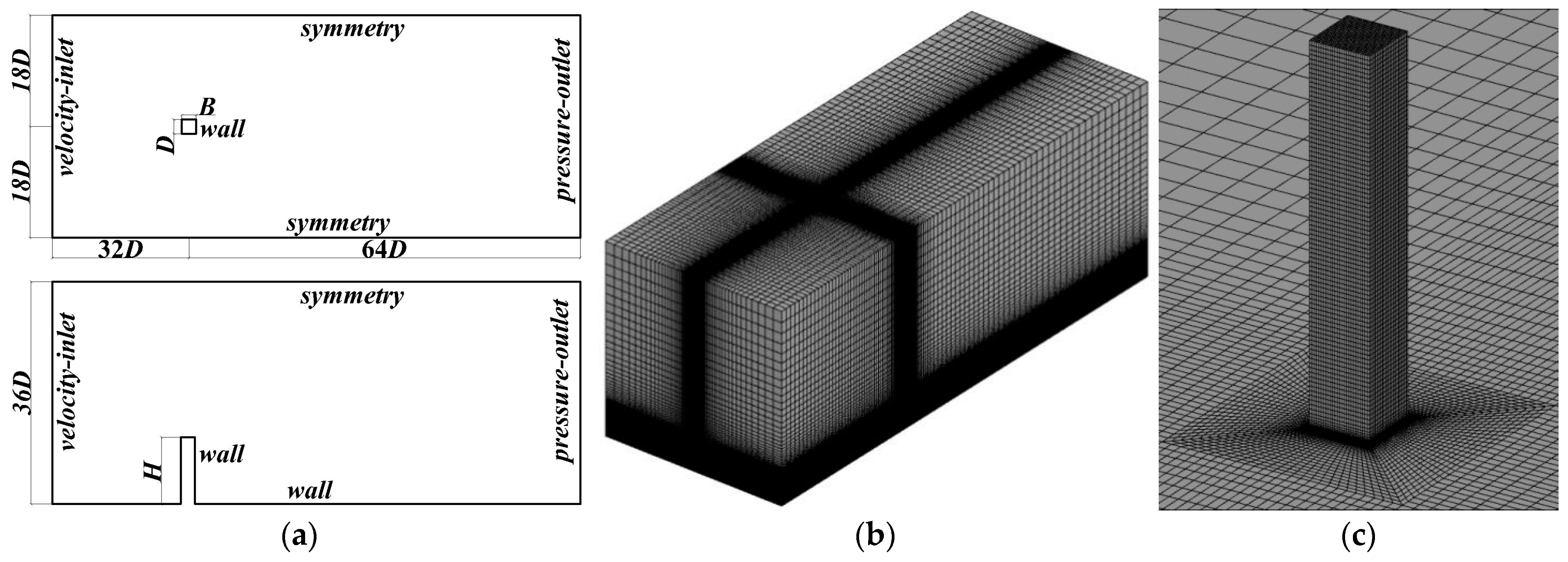
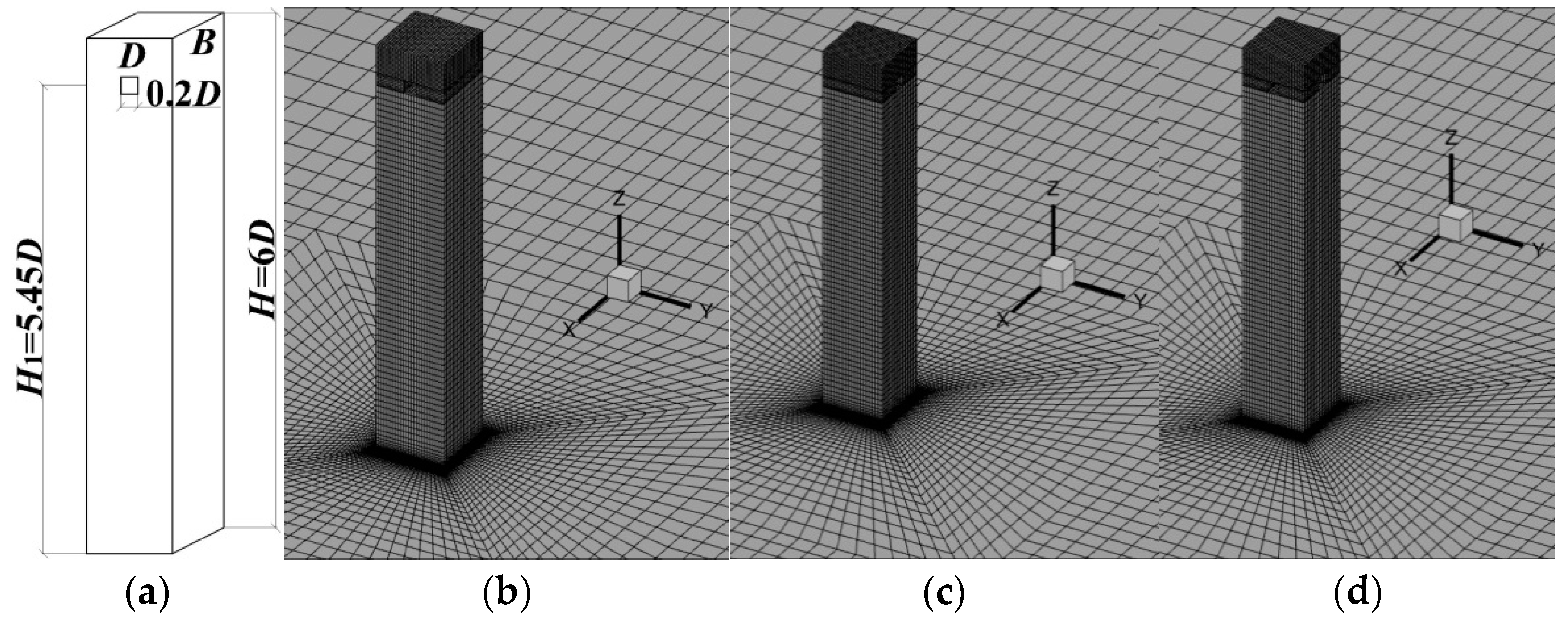


| Case | Minimum Grid Size | Stretch Ratio | Number of Cells | y+ | St |
|---|---|---|---|---|---|
| Standard_Mesh 1 | 0.005D | 1.15 | 896,000 | <30 | 0.098 |
| Standard_Mesh 2 | 0.001D | 1.15 | 896,000 | <15 | 0.096 |
| Standard_Mesh 3 | 0.0005D | 1.10 | 1,508,000 | <5 | 0.098 |
| Case 1 | 0.0005D | 1.10 | 1,540,000 | <5 | 0.092 |
| Case 2 | 0.0005D | 1.10 | 1,540,000 | <5 | 0.09 |
| Case 3 | 0.0005D | 1.10 | 1,400,000 | <5 | 0.092 |
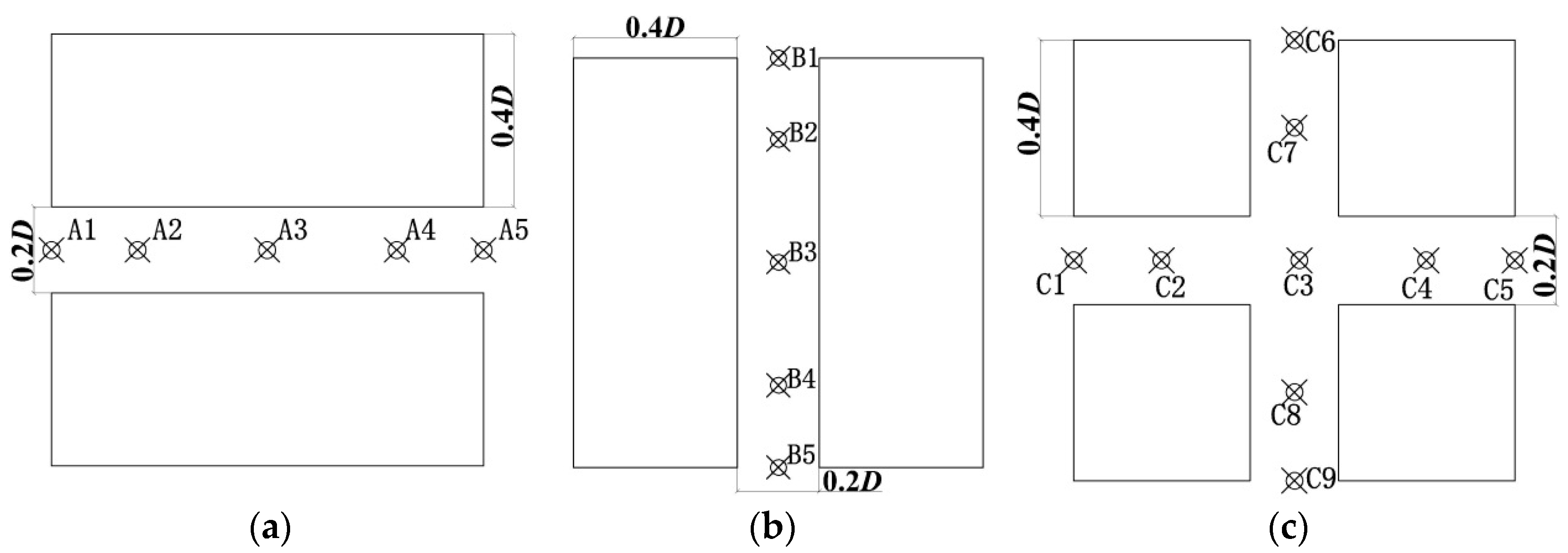
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| Ri | 1.024 | 1.36 | 1.30 | 1.27 | 1.10 |
| Ri,rms | 1.025 | 1.36 | 1.31 | 1.28 | 1.11 |
| B1 | B2 | B3 | B4 | B5 | |
|---|---|---|---|---|---|
| Ri | 0.0055 | −0.001 | 0.00129 | 0.00255 | 0.0001 |
| Ri,rms | 0.077 | 0.049 | 0.049 | 0.052 | 0.093 |
| C1 | C2 | C3 | C4 | C5 | |
| Ri | 1.06 | 1.41 | 1.26 | 1.28 | 1.24 |
| Ri,rms | 1.07 | 1.41 | 1.26 | 1.28 | 1.25 |
| C6 | C7 | C8 | C9 | ||
| Ri | −0.022 | −0.00363 | 0.00248 | 0.028 | |
| Ri,rms | 0.07 | 0.075 | 0.075 | 0.078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Z.; Chen, F.; Zhu, Y.; Mei, Y.; Wang, Z.; Xu, L.; Li, Y. Numerical Simulation on Wind Speed Amplification of High-Rise Buildings with Openings. Atmosphere 2023, 14, 1687. https://doi.org/10.3390/atmos14111687
Gu Z, Chen F, Zhu Y, Mei Y, Wang Z, Xu L, Li Y. Numerical Simulation on Wind Speed Amplification of High-Rise Buildings with Openings. Atmosphere. 2023; 14(11):1687. https://doi.org/10.3390/atmos14111687
Chicago/Turabian StyleGu, Ziqi, Fubin Chen, Yuzhe Zhu, Yu Mei, Zhanli Wang, Linfeng Xu, and Yi Li. 2023. "Numerical Simulation on Wind Speed Amplification of High-Rise Buildings with Openings" Atmosphere 14, no. 11: 1687. https://doi.org/10.3390/atmos14111687
APA StyleGu, Z., Chen, F., Zhu, Y., Mei, Y., Wang, Z., Xu, L., & Li, Y. (2023). Numerical Simulation on Wind Speed Amplification of High-Rise Buildings with Openings. Atmosphere, 14(11), 1687. https://doi.org/10.3390/atmos14111687







