4.1. Sensitivity Tests on Static Stability
The ellipticity condition for the convergent numerical solution of the SE equation requires a standard discriminant that is less than zero ( and ). Generally, < 0 results from static instability (). The static instability of the typhoon vortex was mainly observed in the boundary layer that is less than 1 km in height, and in the upper outflow layer, in the radius of 0.5–1 degrees, at approximately 16 km in height. Therefore, we reset at any grid where to create the vortex in static stability conditions. We investigated the effects of the lower limit value of the static stability on the transverse circulation of Yutu. We chose U1, V0, and W1 for three sensitivity experiments, with the lower limit value of capped at , , and , referred to as N3, N4, and N5, respectively.
The azimuthal-mean radial and vertical wind components of the nonlinear model simulation for CTL, at 48 h, are shown in
Figure 2a,b. There was a strong inflow (with a maximum value of about 28 m s
−1) at a height of less than 2 km, a relatively weak inflow in the mid-troposphere outside the eyewall at 3–9 km height, and a relatively deep outflow in the upper troposphere at 12–18 km height (
Figure 2a). Note that inflow and outflow occurs at heights that are less than and over 19 km, respectively. The vertical velocity field shows an intense updraft at a radius of 0.5 degrees from the typhoon center which extends to the upper troposphere at a height of approximately 17 km, with the strongest upward motion evident at a height of about 9–12 km (
Figure 2b). Moreover, there is a relatively strong updraft in the typhoon center, at a radius of 0.9 degrees, with the strongest updraft occurring at a height of nearly 12 km height and a relatively weak updraft inside the eyewall. Furthermore, there is a weak subsidence in the mid- to upper-troposphere inside the eyewall at a height of 9–18 km, and a relatively larger subsidence in the upper troposphere above heights of 17 km, at a radius of 0.4–0.7 degrees.
The transverse circulations with different lower limit values of
are shown in
Figure 2c–h. Compared with the nonlinear simulation (
Figure 2a,b), the induced transverse circulation is sensitive to the adjustment of the static instability of the typhoon vortex. It is evident that the broad features of the transverse circulation in the nonlinear simulation, such as the three intense updrafts, upper troposphere deep outflow, boundary layer inflow, weak mid-troposphere inflow, and the inflow and outflow at a height of 19 km, are captured in N4 and N5, but they are missing in N3 (
Figure 2c,d). The transverse circulation for N4 aligned well with the nonlinear simulation, although it did not capture the upper-tropospheric subsidence above a height of 17 km, at a radius of 0.4–0.7 degrees, as in the nonlinear simulation; rather, it produced inflow–outflow at a height of 15 km (
Figure 2e,f). In general, the transverse circulation for N5 was most consistent with the nonlinear simulation, and it captured the flow intensity and the height of the upper-level outflow (
Figure 2g,h). The results with the lower limit value of
, reset to
(N6), are similar to the N5 results. For N3, a large portion of the static stability is reset to a larger stability, thus suppressing the transverse circulation. This stability reset is more relieved in N4 and N5. Based on our tests, stability relief, as in N5, is sufficient and will preserve most of the original stability in the nonlinear simulation, without producing divergence in the solution. For N6, we found that the solution may occasionally diverge, and the solution, if converged, is very similar to N5. Thus, we used the lower limit value of
capped at
, in the experiments shown in
Table 1.
4.2. Sensitivity Tests on the Residual Terms
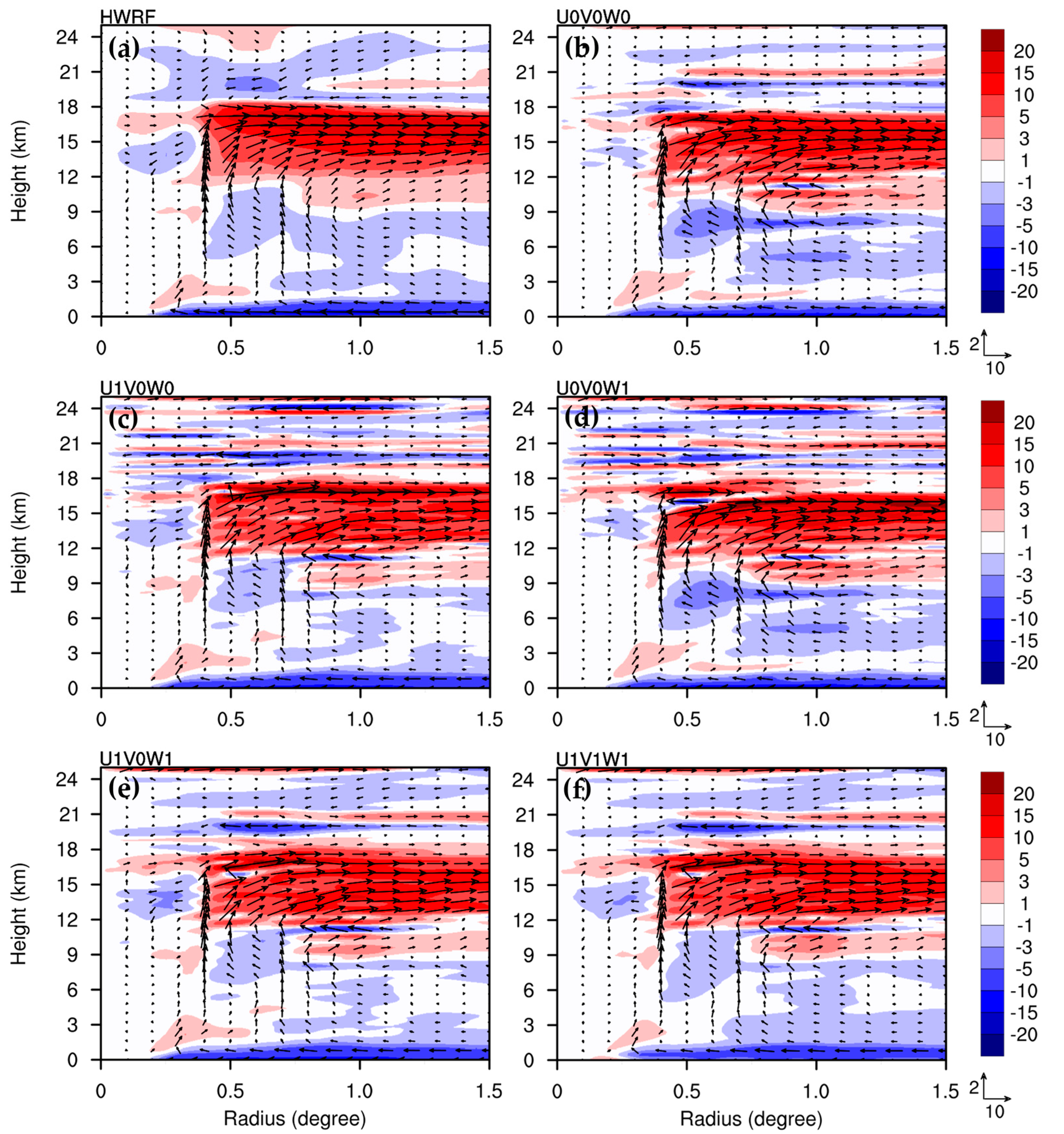
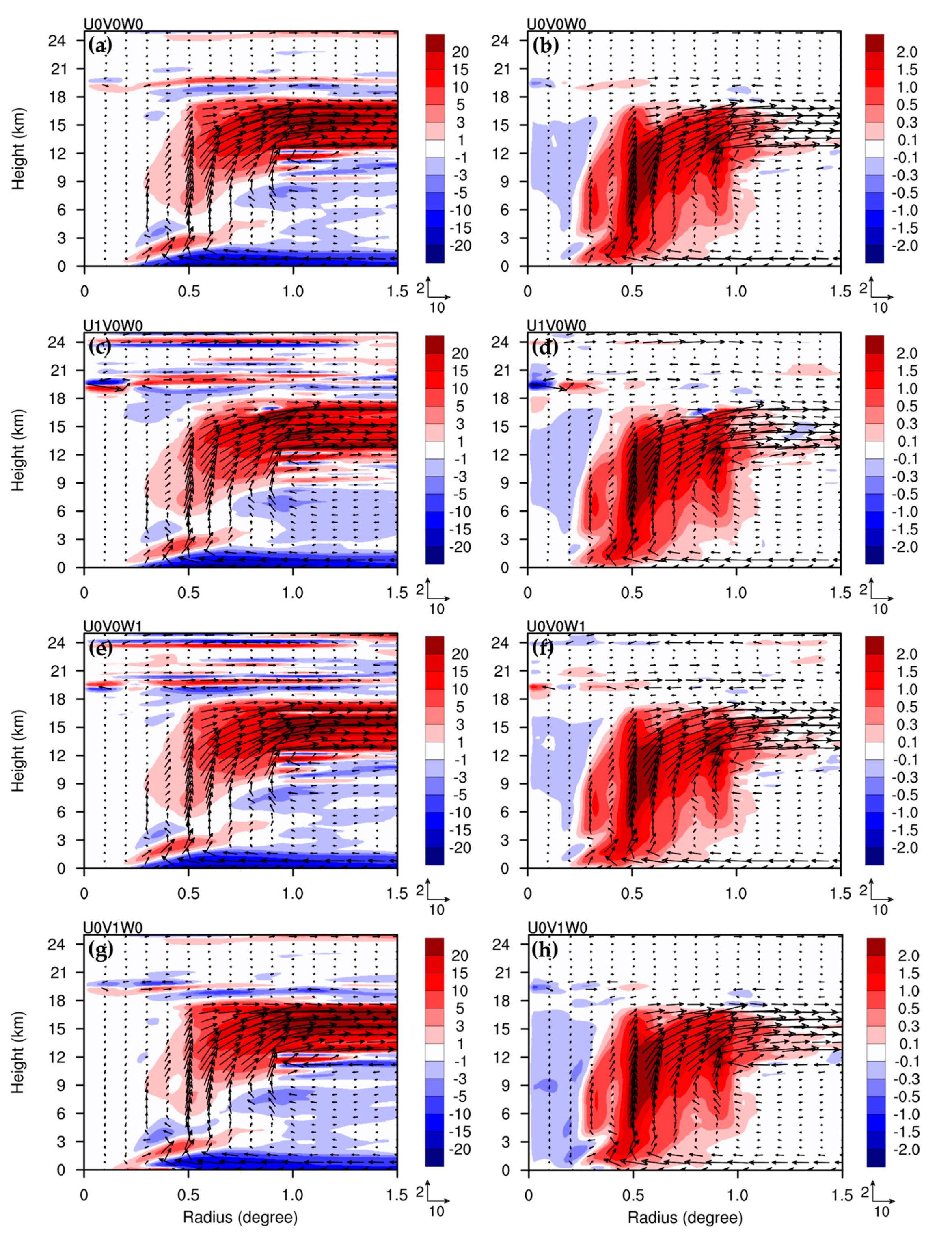
Figure 3 shows the radial wind component for the sensitivity tests, including or ignoring the residual terms in the radial wind, tangential wind, and hydrostatic equations (
, and
, respectively) at 24 h, for the nonlinear simulation, CTL. The induced transverse circulation for U0V0W0 is consistent with the nonlinear simulation (
Figure 3a), except for the somewhat overestimated radial inflow in the mid-troposphere, at a height of 3–9 km, and an overestimated radial flow above a height of 18 km. The features of our U0V0W0 solution in this study align with the unbalanced solutions noted in [
27]. We found that at this time, including
only slightly reduces the radial inflow in the mid-troposphere, and it reduced the radial outflow at a height of 15–18-km (
Figure 3c); however, it produced non-negligible changes in the upper layer, above a height of 18 km. Furthermore, the contribution of
to transverse circulation mainly occurs in the upper layer, above a height of 18 km (
Figure 3d). As the impacts from U1 and W1 cancel each other out above a height of 18 km for U1V0W0 and U0V0W1, the upper-level flow above heights of 18 km in U1V0W1 (
Figure 3e) aligns better with the nonlinear simulation. When all the residual terms are included in U1V1W1 (
Figure 3f), the radial inflow in the boundary layer is somewhat weaker inside the 0.5 degree radius in the typhoon center. In general, the solution of U1V0W1 captures the radial flow better than the solutions of other sensitivity tests (
Table 1). Comparing the results of heights above 20 km, for all tests involving the nonlinear simulation, including any of the three residual terms, resulted in more perturbations in radial flow. We also tested the impacts of U1, V1, and W1 on the SE solution in the absence of the asymmetric eddy heat (the first three terms on the right-hand side (rhs) of Equation (21)) above a height of 20 km. The results indicate that the perturbations exist for U1 and W1, but they disappear for V1. This implies that the effects of the additional source terms (U1 and W1) on the SE solution are treated as part of the known force sources, rather than the implicit solution itself.
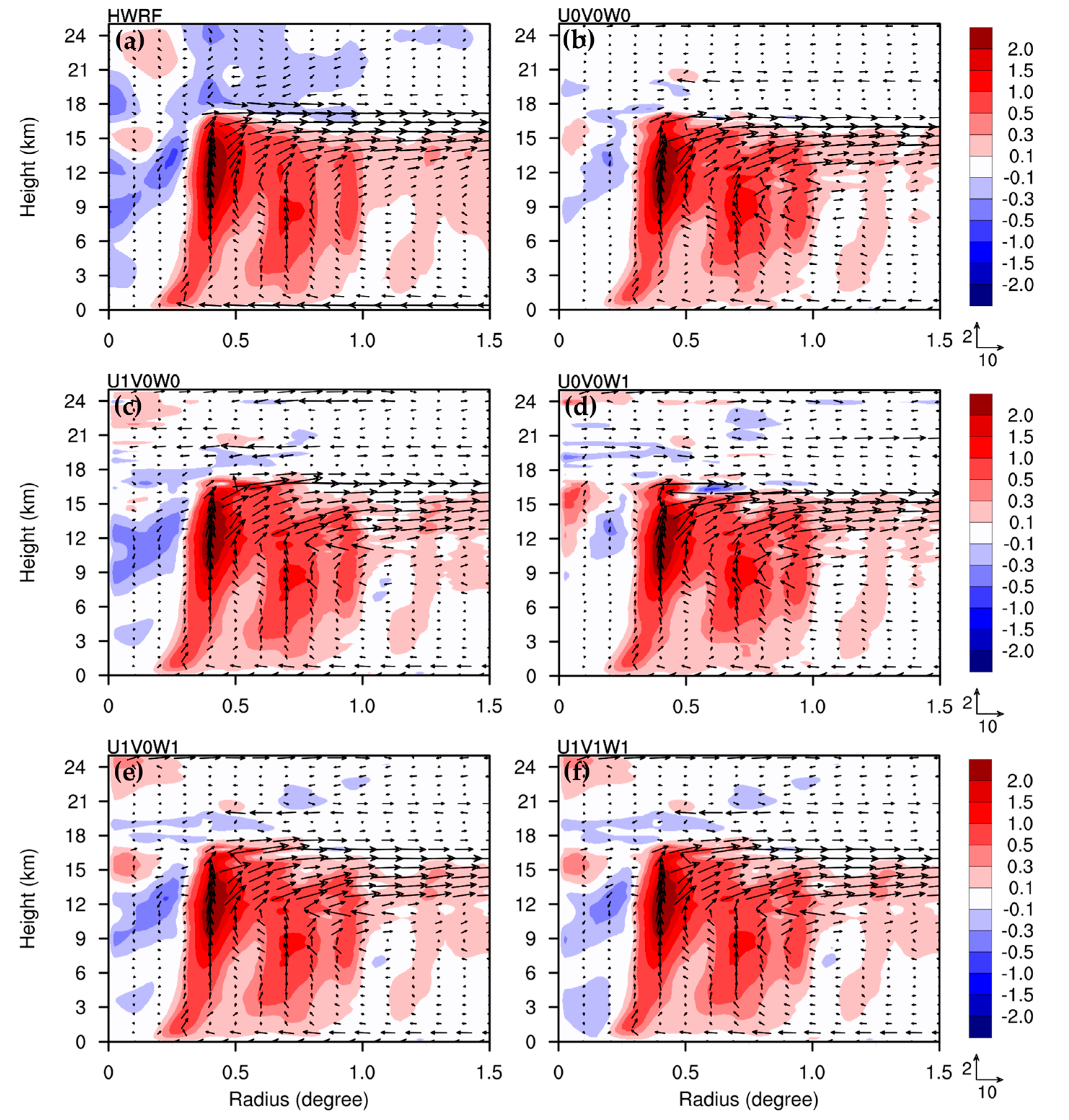
Figure 4 shows the vertical wind components produced by the sensitivity tests, including or ignoring
, and,
, at 24 h, for CTL. At 24 h, U0V0W0 (
Figure 4b) captured the upward motions in the eyewall well, within 0.5 degrees and a region of approximately 0.6–1.0 degrees, as compared with the nonlinear simulation (
Figure 4a). However, it misses the subsidence of the latter above heights of 17 km height, within 0.3–1 degrees, and it causes underestimated downward motions in the mid-troposphere inside of the eyewall. The induced upward motions for the other sensitivity tests (
Figure 4c–f) are similar to U0V0W0, and they are also consistent with the nonlinear simulation. Thus, the contributions of
, and
to the upward motions of Yutu are not significant. All the sensitivity tests cannot capture the upper-tropospheric subsidence well at a radius of 0.3–1.0 degrees in the nonlinear simulation. It appears that the SE solution produces a more perturbed radial flow above the outflow layer, which may be due to the assumption of symmetric vortex dynamics. Only the sensitivity tests, including
(
Figure 4c,e,f), can further capture the subsidence in the mid-troposphere, inside of the eyewall, despite the intensity occasionally being underestimated. The similar vertical motions between U0V0W0 and U1V1W1 (
Figure 4b and
Figure 4f, respectively) indicate that the impacts of including
, and
are not significant as compared with the impacts of the other force terms (momentum source
and heat source
).
Figure 5 shows the radial and vertical wind components for the sensitivity tests including or ignoring
, and
, at 48 h, for CTL. The transverse circulation for Yutu at this time was further intensified compared with its state at 24 h. U0V0W0 (
Figure 5a,b) captures the transverse circulation of the nonlinear simulation well, except for the subsidence above heights of 17 km, at a radius of 0.4–0.7 degrees (
Figure 2a,b). Indeed, for U0V0W0, there was a strong inflow at heights less than 2 km, a relatively weak inflow outside the eyewall at heights of 3–9 km, and a relatively deep outflow in the upper troposphere at heights of 12–18 km (
Figure 5a). Moreover, there was an intense updraft at a radius of 0.5 degrees from the typhoon center that extended to the upper troposphere at heights of approximately 17 km, a relatively strong updraft at a radius of 0.9 degrees, and a relatively weak updraft inside the eyewall (
Figure 5b). The contributions of
and
to the radial wind component mainly occurred above heights of 18 km (
Figure 5c,e). These contributions also largely canceled each other out when both
and
were included (see
Figure 2g). This result is similar to those obtained at 24 h (see
Figure 3e). When
was included, the radial outflow increased in the boundary layer, inside a radius of 0.5 degrees from the typhoon center (
Figure 5g). We note that the weaker boundary-layer inflow was obtained for U0V1W0, rather than U0V0W0, which aligns with the results in [
27], regarding the impact of
. In summary, the contributions of
, and
are more pronounced in the boundary layer of heights less than 1 km, in the mid-troposphere outside the eyewall, and in the upper level above heights of 18 km. For vertical motions, all the sensitivity tests cannot capture the subsidence above heights of 17 km in the eyewall well, nor inside the eyewall at heights less than 18 km in the nonlinear simulation. The sensitivity test with U1, V0, and W1 provides the most consistent solution with the nonlinear simulation than the other tests. Thus, we only included
and
when solving the SE equation in the experiments described in the next section, which investigated the impacts of the total force sources.
As mentioned in the introduction, the SE equation is a linear partial differential equation; thus, to clarify the contributions of
, and
to the induced transverse circulation of the vortex, sensitivity tests, including only
, and
(denoted as U1, V1, and W1, respectively), were conducted. Note that the momentum source
, and heat source
, were not used to solve the solution in these tests. For example, the total force sources of the U1 solution include the forcing terms associated with
only, without the momentum source
, heat source
, or the residual terms,
and
.
Figure 6 shows the radial and vertical wind components for U1, V1, and W1 at 48 h for CTL. The contributions of
to the radial wind component mainly occurred in the upper layer, though it slightly contributed to the radial outflow at heights of approximately 8–13 km (
Figure 6a). However,
does not affect the induced radial inflow in the boundary layer of the SE solution. The contributions of
to the vertical wind component are mainly observed in the mid-troposphere, at heights of approximately 6–17 km (
Figure 6b). Indeed, the induced downward motions for U1 occur in the eyewall and outside the inner eyewall in the mid-troposphere. However, this was not especially evident, as shown in
Figure 5d. The contribution of
to the induced transverse circulation mainly occurred in the layer comprising heights less than 18 km, particularly in the upper-level outflow and in the boundary layer inflow (
Figure 6c,d). Note that a weak radial outflow was observed near the surface in V1, which is the reason for a weaker boundary-layer inflow for U0V1W0, as compared with U0V0W0. The contributions of
to the radial wind component mainly occurred at heights above 15 km (
Figure 6e). We found that including
can reduce the radial outflow in the upper layer comprising heights of nearly 17 km, while increasing the radial outflow below that layer. The contribution of
to the vertical wind component is not significant in the troposphere (
Figure 6f). In general, the contributions of the residual terms are not significant in the troposphere, as compared with the impacts of the heat source
.
comprises uncertain numerical residues in the tangential-wind tendency equation. We simply ignored this uncertain contribution to the SE solution, and it did not affect vortex intensification in the troposphere.
4.3. Sensitivity Tests on the Total Force Sources
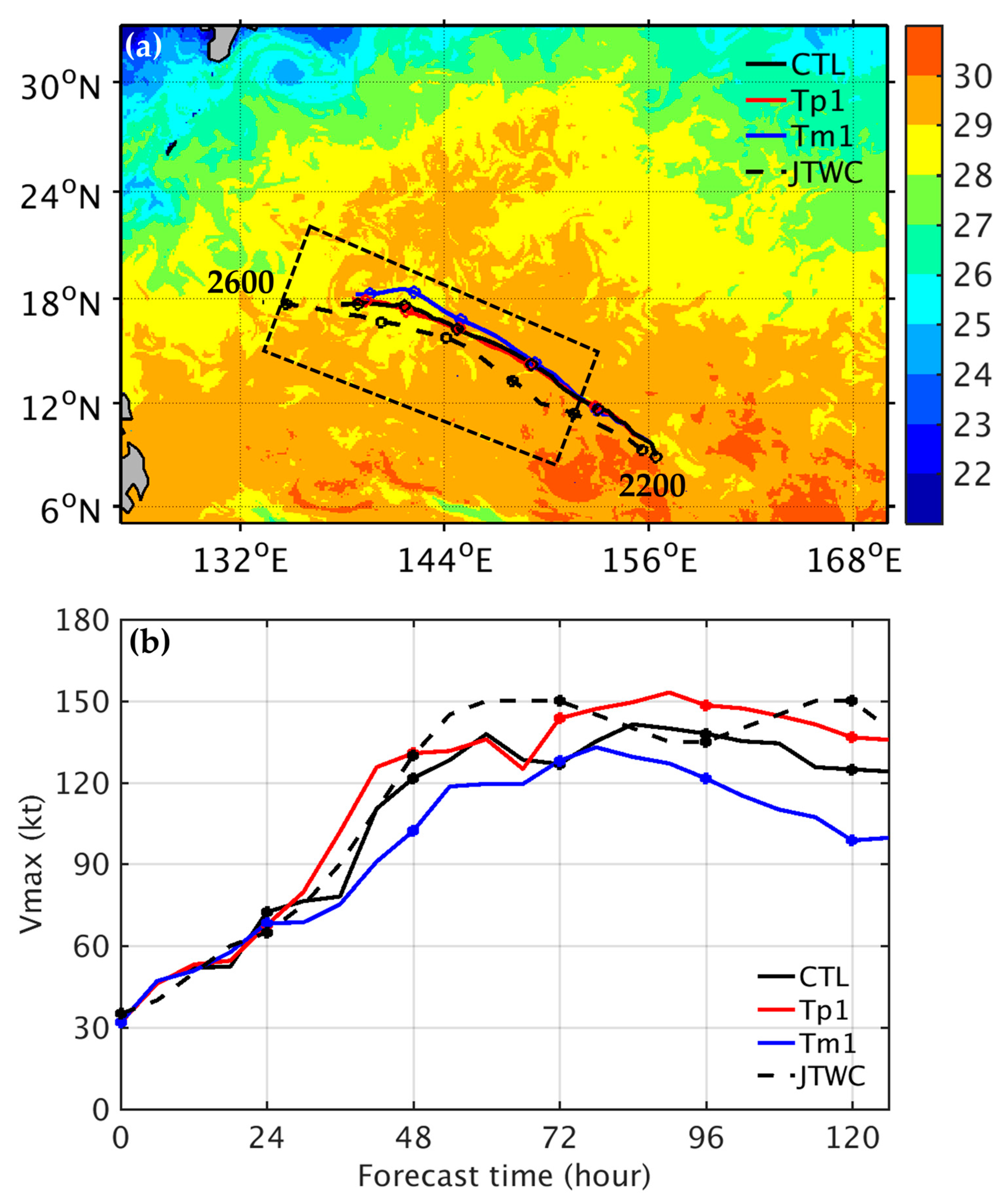
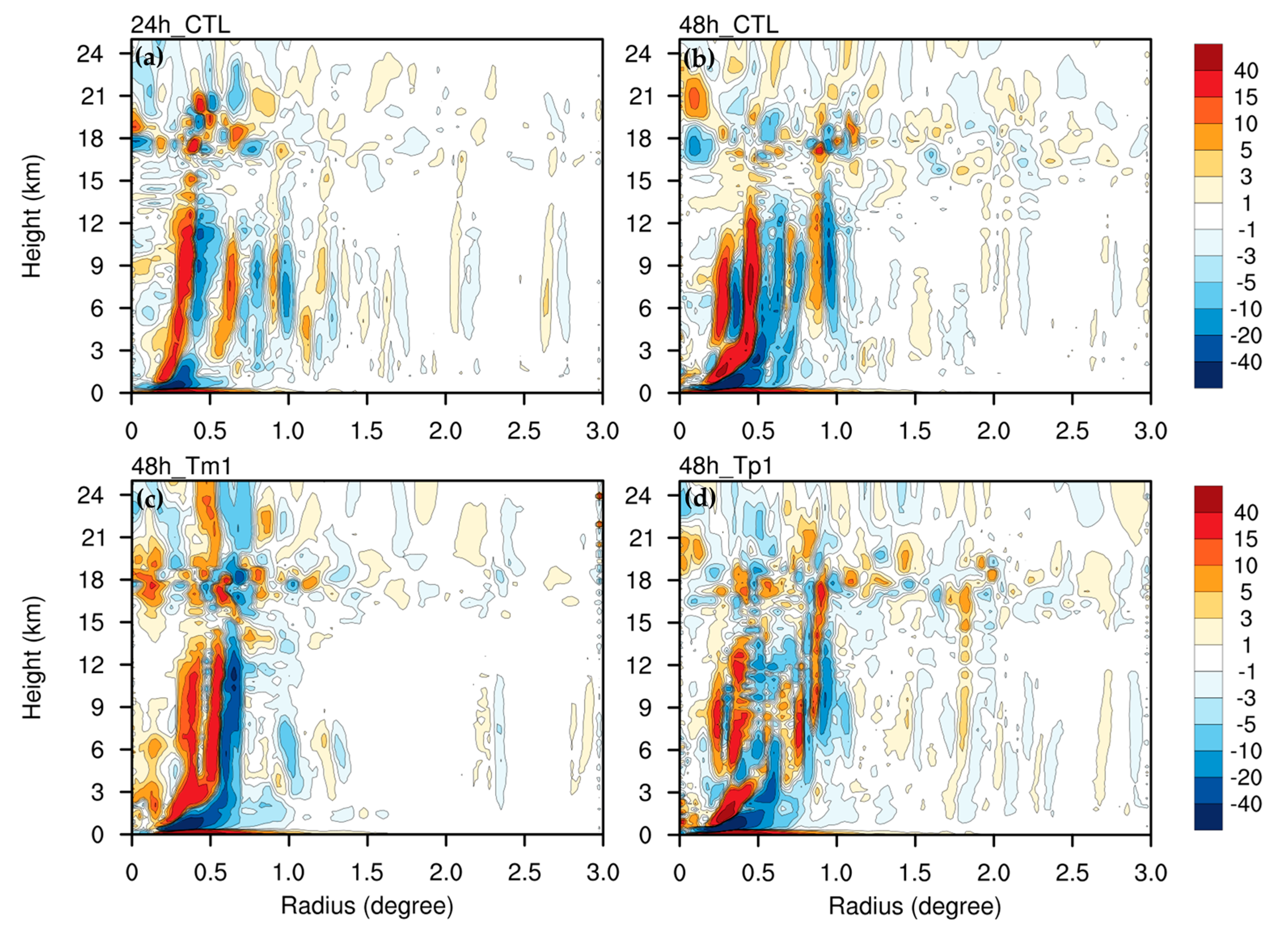
The total force sources (force terms on the rhs of Equation (26), except the fourth term) in the entire domain of the SE solution for CTL, Tp1, and Tm1 are shown in
Figure 7. The total force was mostly concentrated within a radius of 1 degree from the typhoon center for CTL at both 24 h and 48 h, as well as for Tp1 at 48 h (
Figure 7a,b,d); however, it was only concentrated within a radius of 0.6 degrees for Tm1 at 48 h (
Figure 7c). For CTL, the maximum total force source in the inner vortex core at 48 h was approximately double that at 24 h, which is consistent with the stronger intensity of Yutu at 48 h compared with 24 h, as shown in
Figure 1b. Tp1 showed a stronger intensity at 48 h than Tm1 (see
Figure 1b), however, the total force source in the mid-troposphere for Tm1 is stronger than Tp1, in spite of its associated smaller heating force at a height of 2 km in the eyewall (
Figure 7c,d). For Tp1, the structure of the total force source in the mid-troposphere is much different from that of CTL and Tm1. Note that the total force sources in the tropospheric eyewall region, at heights less than 15 km, are mainly caused by the effect of diabatic heating, whereas the total force sources above heights of 15 km contributed to asymmetric eddy heating. Since the total force is insignificant outside a radius of 1.5 degrees from the typhoon center, we focused on the induced transverse circulation within 1.5 degrees.
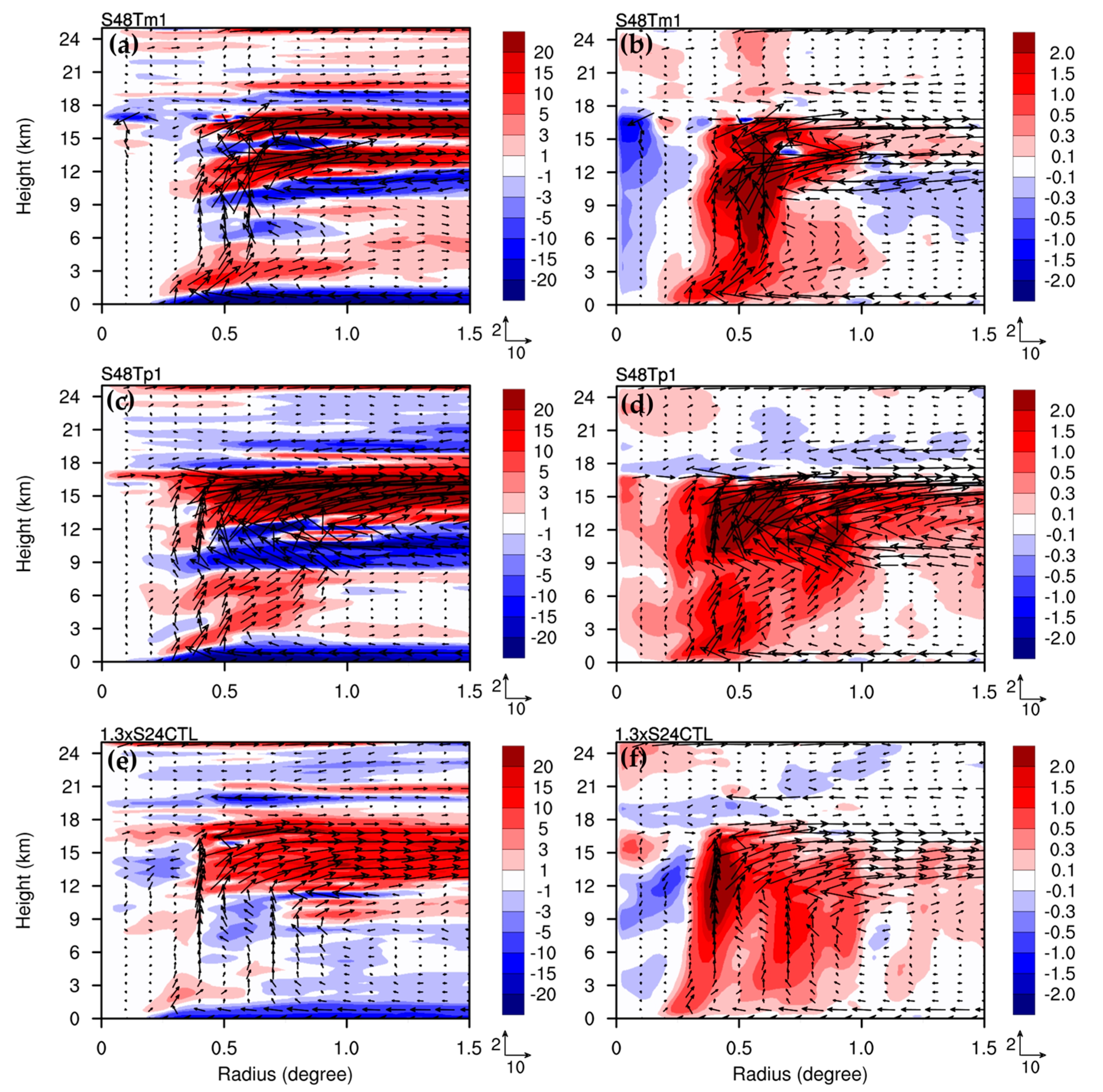
To explore the sensitivity of the induced transverse circulation to the total force sources, the force term (S) of Tm1 and Tp1 at 48 h was used to replace the force in the nonlinear simulation, for CTL, at 24 h, in the experiments S48Tp1 and S48Tm1, respectively. The total force sources for CTL at 24 h, and for S48Tm1 and S48Tp1 at 48 h, are shown in
Figure 7a,
Figure 7c, and
Figure 7d, respectively. At 24 h, the induced transverse circulations for S48Tm1 and S48Tp1 (
Figure 8a–d) were much stronger than those obtained by the original total force of CTL at 24 h (
Figure 3e and
Figure 4e) for the lower-level inflow, upper-level outflow, and upward motion in the eyewall. As shown in
Figure 7, the force sources of S48Tm1 and S48Tp1, inside a radius of 1 degree, were larger than those at 24 h for CTL. Furthermore, the distributions of the force sources of S48Tm1 and S48Tp1 at 48 h were inconsistent with those for CTL at 24 h. Consequently, the induced transverse circulation for S48Tm1 and S48Tp1 at 24 h was overestimated and significantly disorganized. Indeed, the radial inflow at a height of 2–9-km, at 24 h, for U1V0W1, corresponded with the nonlinear CTL, and it was replaced with the radial outflow of the SE solution in S48Tm1 and S48Tp1 (
Figure 8a,c). There was a much stronger radial inflow below the upper-level outflow at a height of 9–12-km that was missing in U1V0W1 and in the nonlinear simulation CTL (see
Figure 3a). The induced transverse circulation for S48Tp1 was stronger than S48Tm1. The subsidence inside the eyewall was observed in S48Tm1, but it was overestimated (
Figure 8b). However, it was not produced in S48Tp1, as an upward motion in the inner TC vortex was produced instead (
Figure 8d). The upward motion at a radius of 0.7 degrees was not clearly induced in S48Tm1 at 24 h, and it was overestimated in S48Tp1 at 24 h. We also conducted one sensitivity experiment with the total force source of CTL at 24 h, but we increased it by 1.3 times (denoted as 1.3xS24CTL). The induced transverse circulation for 1.3xS24CTL (
Figure 8e,f) was similar to U1V0W1 (
Figure 3e and
Figure 4e), which is consistently collocated, but with stronger intensity.
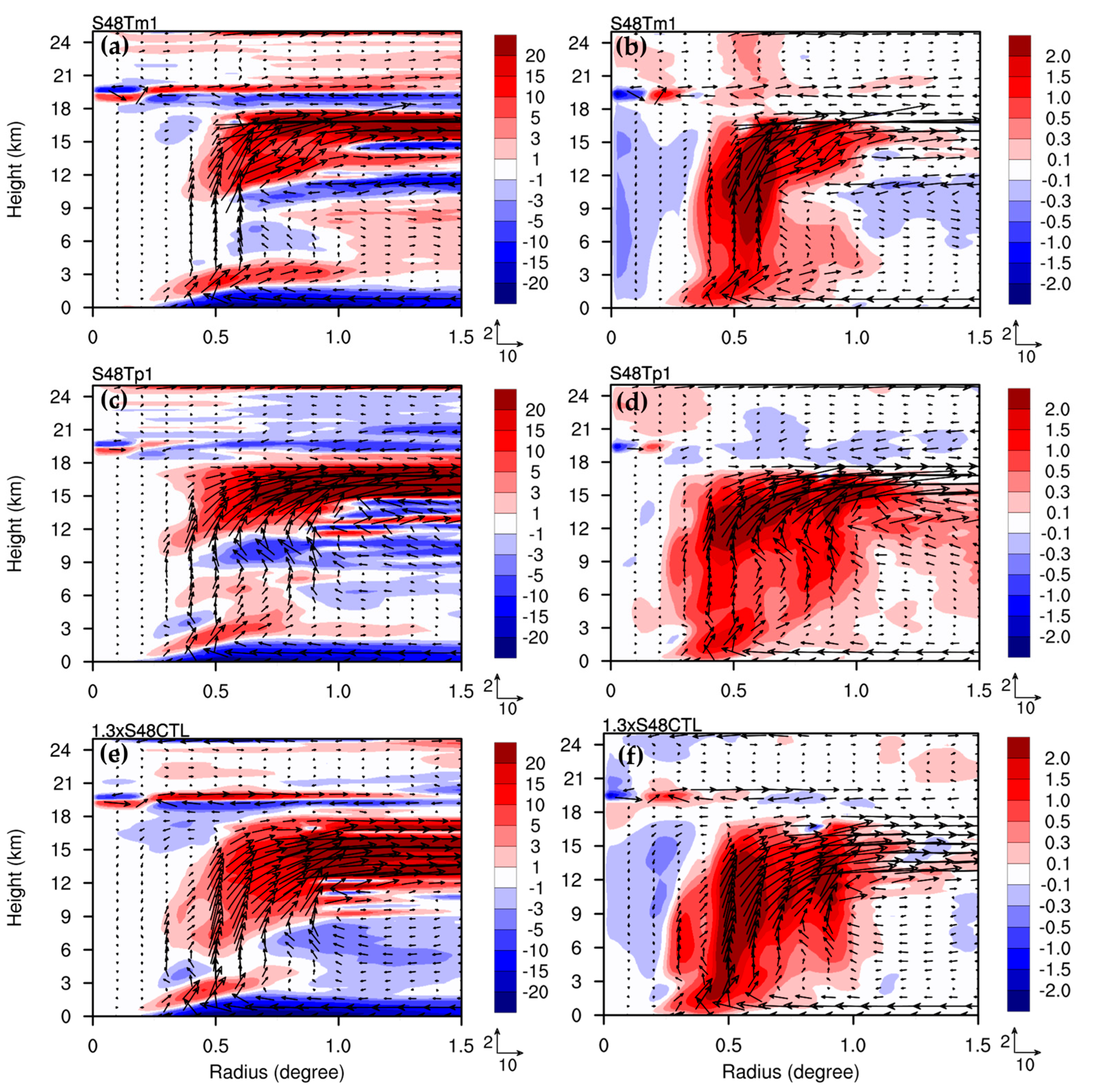
We also used the force terms of S48Tm1 and S48Tp1 at 48 h for U1V0W1 at 48 h to obtain the SE solutions. The induced transverse circulations for S48Tm1 and S48Tp1 at 48 h are shown in
Figure 9a–d. The induced transverse circulations for S48Tm1 and S48Tp1 were more organized at 48 h than 24 h. There was a radial inflow below the upper-level outflow, at a height of 9–12 km, at 48 h, which is similar to the results obtained at 24 h. Note that this radial inflow is missing in U1V0W1 at both 24 h and 48 h. There is a radial outflow and radial inflow above heights of 18 km for S48Tm1 and S48Tp1, respectively (
Figure 9a,c). Upward motions outside the eyewall were not found in S48Tm1 (
Figure 9b), which can be explained by the confined total force of S48Tm1 that was only concentrated in the radius of 0.3 to 0.6 degrees (see
Figure 7c). The experiment, 1.3xS48CTL, conducted with 1.3 times the total force source of CTL at 48 h, provided a similar induced transverse circulation (
Figure 9e,f), but at stronger intensity, compared with U1V0W1 at 48 h. In brief, the sensitivity tests indicate that a structural misplaced change in total force source may cause greater disorganization in the induced transverse circulation, whereas collocated intensity change only results in a proportional enhancement. This also implies that the intensification of the primary vortex in nonlinear processes requires a dynamically consistent force enhancement following the development of transverse circulation. Based on symmetric vortex dynamics, a weaker mean vortex cannot correctly ‘spin up’ with a misplaced stronger force that will produce a largely distorted transverse circulation.
The induced transverse circulation is mainly caused by the effect of diabatic heating (e.g., [
20,
27,
31]). Diabatic heating drives a deep inflow layer in the middle–lower troposphere, and a broad outflow layer in the upper troposphere. Moreover, the upward motion forced by diabatic heating is dominant in the eyewall. The diabatic heating rates derived from the nonlinear simulation for CTL at 24 h, and CTL, Tm1, and Tp1 at 48 h are shown in
Figure 10. At 24 h, there were two maxima of the diabatic heating rate; one occurred near a radius of 0.4 degrees, and the other occurred near a radius of 0.7 degrees, with a maximum magnitude of approximately 10 K h
−1 and 8 K h
−1, respectively (
Figure 10a). The two maxima diabatic heating rates are consistent with the two strong upward motions of CTL at 24 h (see
Figure 4a), and their locations are also consistent with the positions of stronger force sources, as shown in
Figure 7a. At 48 h, diabatic heating developed with three maximum zones (
Figure 10b), which were collocated with the stronger total force, shown in
Figure 7b. The maximum heating rate over 12 K h
−1, at heights of approximately 6–8 km, is stronger than that at 24 h. The diabatic heating rate was largely confined to a vertical column in an annular region, with radii between 0.4–0.6 degrees for Tm1 (
Figure 10c). However, the maximum diabatic heating rate occurred at heights less than 2 km for Tp1 (
Figure 10d). The heating rate was mostly concentrated at heights less than 14 km. The diabatic heating distribution was similar to the vertical motion, as both followed the total force distribution shown in
Figure 7. This implies that the transverse circulation of the intense typhoon was dominated by diabatic heating in the inner vortex.
4.4. Tangential Velocity Tendency
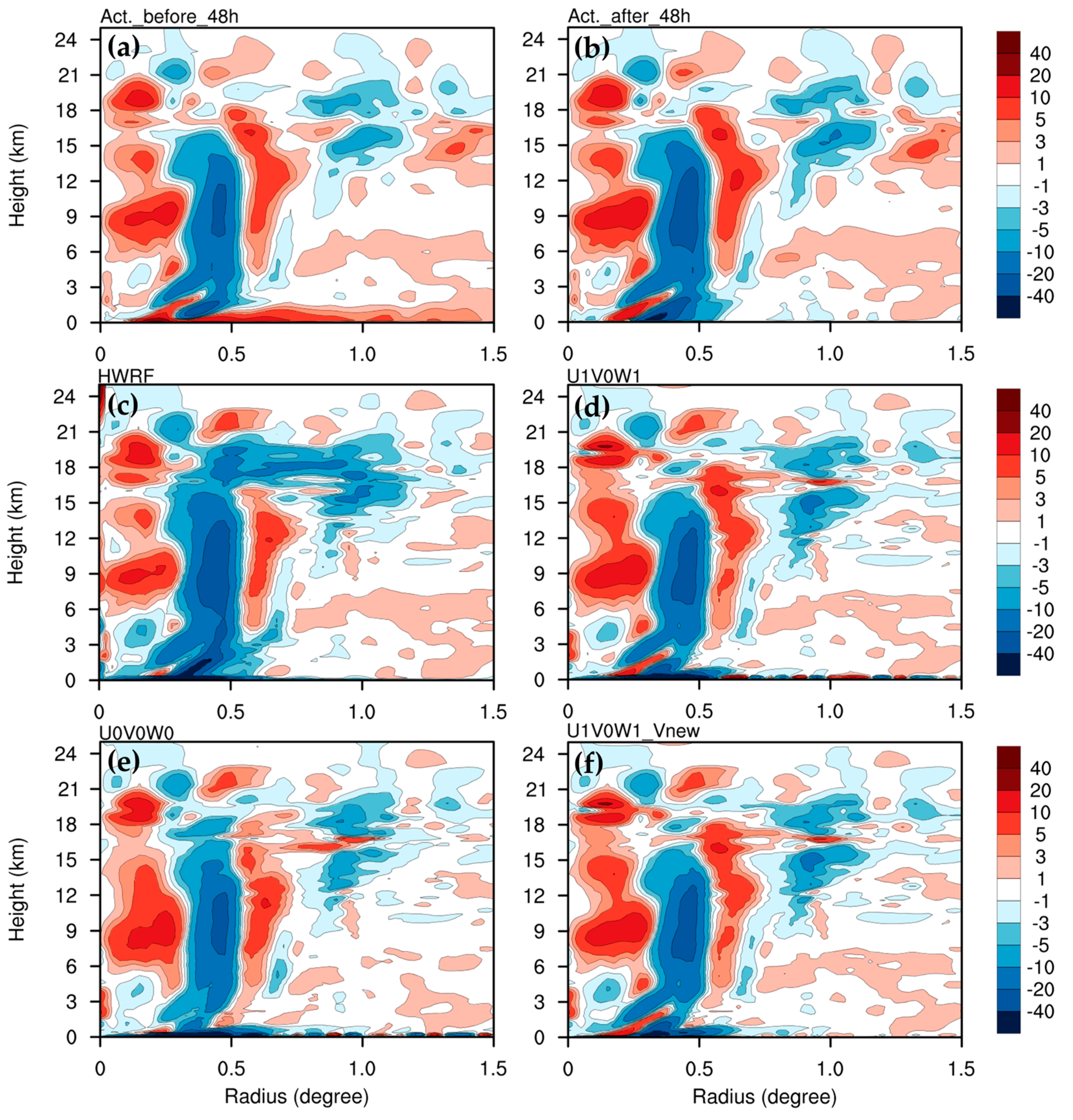
To check the accuracy of the induced tangential wind velocity tendency, we calculated the actual temporal change in tangential velocity, with the model output exhibiting 20 s intervals before (i.e., the result at 48 h minus the result at 20 s before 48 h) and after 48 h (i.e., the result at 20 s after 48 h minus the result at 48 h), as well as the sum of the tangential wind velocity tendency in budgeting terms (the first term on the left-hand side (lhs) of Equation (22)) in the nonlinear simulation and different SE solutions at 48 h. The actual tangential wind velocity tendency and the computed budgets for the tangential wind velocity tendency for the nonlinear simulation, and for the SE solutions, are shown in
Figure 11. The two actual tangential wind velocity tendencies were very similar, with a spinup inside of the inner eyewall, outside of the inner eyewall at heights of 4–18 km in radii of 0.5–0.7 degrees, and in the boundary layer at heights less than 2 km (
Figure 11a,b), except in the lowest boundary layer. In this layer only, the actual velocity change can be swiftly modified from a strong spinup for the former, to a weak spindown for the latter, within a very short period. The nonlinear budget (ignoring all numerical smoothing inherently applied by the non-linear model) captured the actual spinup in the boundary layer well, in addition to the distribution of spinup and spindown in the mid-troposphere (
Figure 11c). However, it did not capture spindowns that occurred at heights of 17–20 km, in radii of 0.4–1.1 degrees, caused by the mean vertical advection of tangential velocity. The nonlinear budget at 48 h was closer to the latter actual nonlinear tendency than the former, particularly in the boundary layer. This may imply that numerical smoothing may introduce some noted differences between the current budget and the two nonlinear tendencies, particularly in the upper-outflow layer and boundary layer. The distributions of spinup and spindown in U1V0W1 are quite similar to the two actual tangential-wind velocity tendencies in the inner vortex, except in the boundary layer comprising heights of less than 2 km with a wavy radial structure of alternating tendency signs near the surface (
Figure 11d). This near-surface, radially alternating tendency was also produced in U0V0W0 (
Figure 11e). This may imply that the irregular spinup and spindown near the surface was not due to the contribution of
and
.
To understand whether the boundary conditions have a significant impact on spinup and spindown in the boundary layer, we set
at
km in the sensitivity test of U1V0W1_Vnew, instead of the no-slip condition,
at
km, which was used in U1V0W1. The tangential-wind velocity tendency for U1V0W1_Vnew is shown in
Figure 11f. The distributions of spinup and spindown in U1V0W1_Vnew were nearly identical to those in U1V0W1, except in the lowest boundary layer. The induced tangential-wind velocity tendency in the boundary layer of U1V0W1_Vnew better aligned with the latter’s actual tendencies, but not the former’s. The vortex intensification within the lowest boundary layer only, was affected by the specified boundary condition for the mean tangential velocity. The constant gradient condition, rather than no-slip condition, was preferred for the SE solution, despite the fact that the nonlinear simulation applied a no-slip condition.
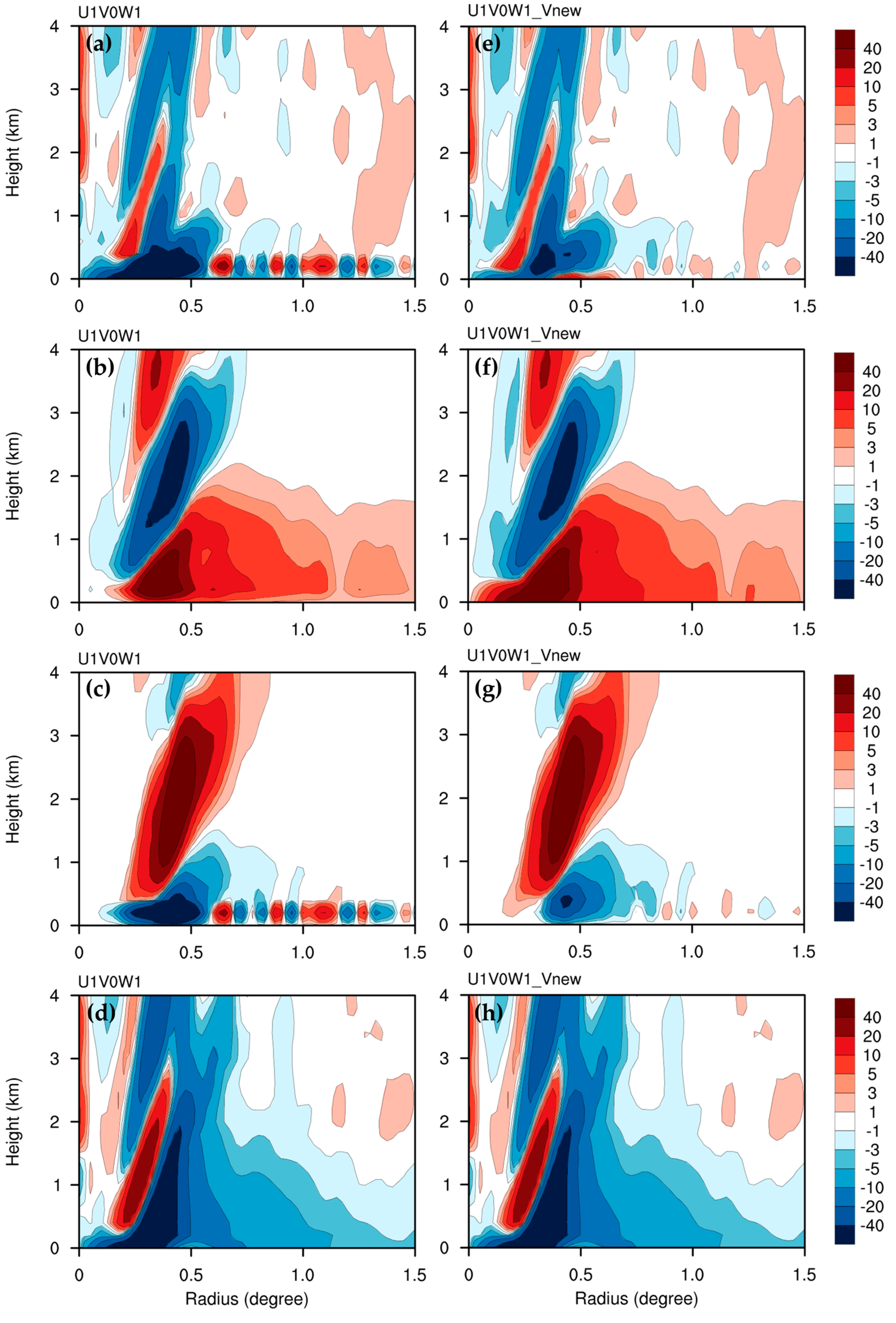
Figure 12 shows the budgeting terms of the tangential-wind velocity tendencym including mean horizontal advection (the first term on the lhs of Equation (22)), mean vertical advection (the second term on the lhs of Equation (22)), as well as the sum of the asymmetric eddy force and mean friction (the first four terms on the rhs of Equation (22)) at heights less than 4 km, at 48 h, for U1V0W1 and U1V0W1_Vnew. Herein, we do not include the mean advection induced by each source term for its contribution. The mean horizontal advection of tangential velocity, contributed by the total source terms, caused a spinup in the inflow layer at heights less than 2 km (
Figure 12b). Most of the tendencies that contributed to the mean horizontal advection in the eyewall were largely counteracted by the mean vertical advection (
Figure 12c). In addition, the radial wavy alternation near the lower surface was clearly induced by the mean vertical advection, with a strong vertical gradient of tangential wind in the presence of a no-slip condition. The asymmetric eddy force and mean friction caused spinup and spindown in the inner part and outer part of the eyewall, respectively. In general, the vortex intensification in the boundary layer, at a height of less than 3 km, near the inner eyewall, was mainly induced by the effects of asymmetric vertical advection and mean friction. The tendency near the surface and outside the eyewall was induced by the mean vertical advection of tangential velocity. The budgeting terms of the tangential wind velocity tendency for U1V0W1_Vnew are similar to those of U1V0W1 (
Figure 12e–h), except that the latter’s are present near the boundary layer at heights of less than 500 m. Similar to U1V0W1, the large tangential wind velocity tendency near the surface was also mainly induced by the mean vertical advection of tangential velocity in U1V0W1_Vnew (
Figure 12g). Comparing the net budget for both tests (
Figure 12a vs.
Figure 12e), major differences existed only within the lowest layer at a height of 500 m. Based on our sensitivity tests, the use of the gradient boundary condition, will ensure that the tangential wind velocity tendency aligns better with the actual tendency.
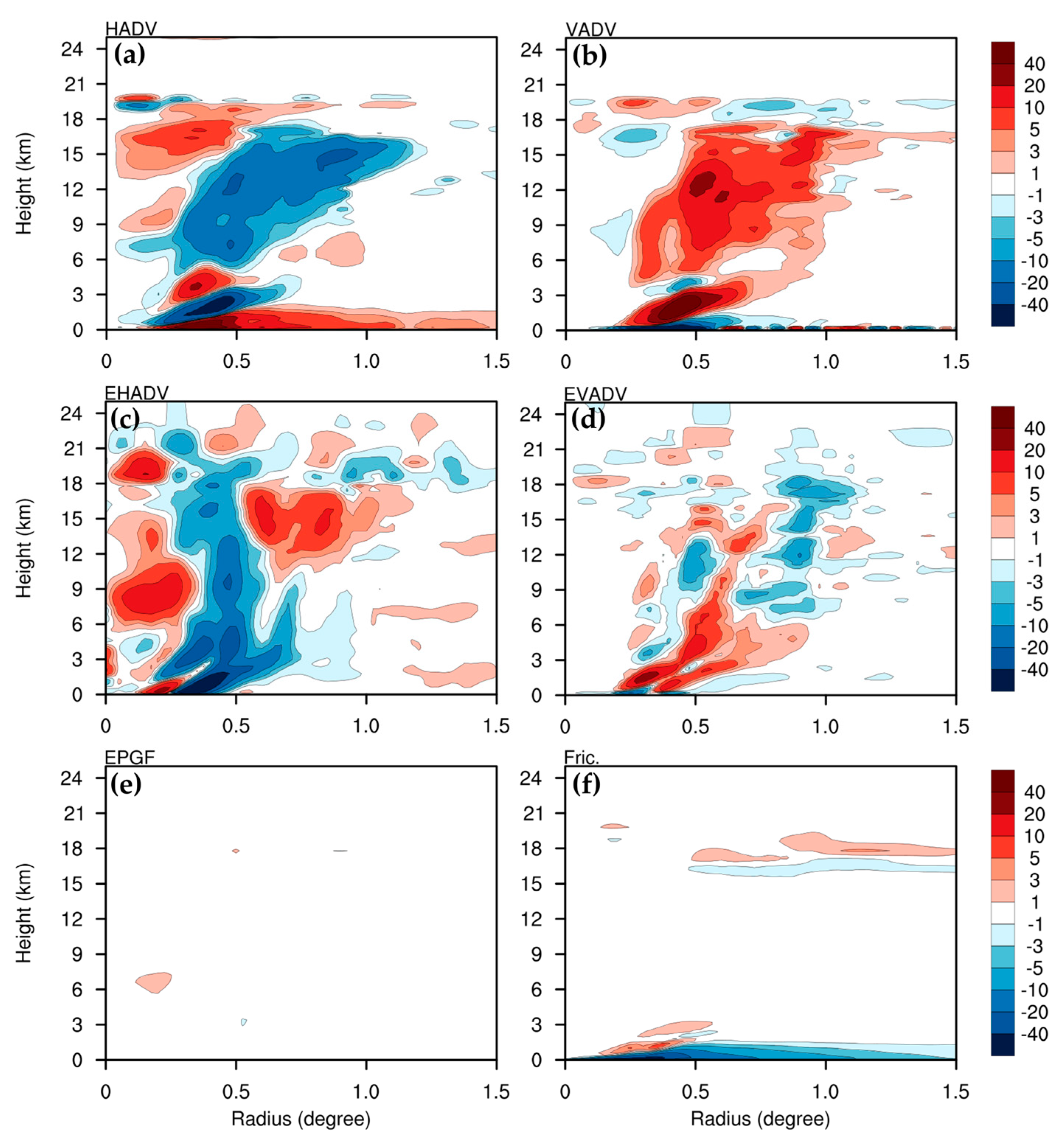
Figure 13 shows all budgeting terms of the tangential wind velocity tendency in Equation (22), at 48 h, for U1V0W1. The mean horizontal advection of the tangential velocity that is caused by all of the induced transverse circulations, as derived from the source terms, caused a spindown in the eyewall at a height of 5–17 km, and less than 3 km. Moreover, it contributed to a spinup inside of the inner eyewall at a height of 13–19-km, in the eyewall at a height of 2–5 km, and in the boundary layer at a height of less than 2 km height (
Figure 13a). Most of the spindown caused by the mean horizontal advection tended to offset the spinup via the mean vertical advection (
Figure 13b). The asymmetric horizontal advection provided a spindown in the eyewall, as well as a spinup inside of the inner eyewall, at a height of 6–20 km. Spinup also occurred outside of the inner eyewall at a height of 11–18 km (
Figure 13c). The tendency caused by the asymmetric vertical advection tends to partially offset the tendency caused by the asymmetric horizontal advection in the eyewall and outside of the inner eyewall (
Figure 13d). The tendency caused by the asymmetric tangential pressure gradient force was much smaller than the other budgeting terms in Equation (22) (
Figure 13e). The turbulent momentum diffusion directly spins down the vortex in the inflow layer at heights less than 2 km (
Figure 13f). In general, the sum of all the budgeting terms (
Figure 11d) shows a spinup inside of the inner eyewall and a spindown in the eyewall; this can be attributed to the mean and asymmetric horizontal advection of tangential velocity, whereas most of the spinup outside of the inner eyewall was caused by the mean vertical advection and asymmetric horizontal advection. Furthermore, as mentioned above, the spinup near the surface in the mean horizontal advection was mainly offset by the spindown caused by the turbulent momentum diffusion; this indicates that the radially alternating tendency in the net budget near the surface (
Figure 11d) is clearly caused by the mean vertical advection of tangential velocity.