ORACLES Campaign, September 2016: Inversion of HSRL-2 Observations with Regularization Algorithm into Particle Microphysical Parameters and Comparison to Airborne In-Situ Data

Abstract

We present microphysical properties of pollution layers observed with NASA Langley Research Center’s airborne high-spectral-Resolution lidar (HSRL-2). The data obtained by HSRL-2 consist of vertical profiles of three backscatter coefficients (β) taken at 355, 532 and 1064 nm and two extinction coefficients (α) measured at 355 and 532 nm. In our study we (1) inverted the 3β + 2α data into particle size distributions with a regularization algorithm, and subsequently computed (2) number concentration and (3) single-scattering albedo for four measurement profiles. We carried out a first comparison to the same particle characteristics measured with airborne in-situ instruments. The in-situ instruments were flown aboard the P-3B aircraft, which followed the flight track of the aircraft ER-2 that carried HSRL-2. We found good agreement of the co-located (space and time) data products, with a degree of reliability reaching 90%. A more detailed study on a larger dataset needs to be carried out in future work to (a) obtain important correction factors, (b) study the influence of different light-scattering models on the inversion results, and (c) identify sources of retrieval and measurement uncertainties.

1. Introduction

Today it is well accepted that atmospheric aerosols play an important role in influencing the radiative flux of solar radiation in the atmosphere. Estimating the radiative forcing of particulate pollution requires knowledge of the height distribution of particle microphysical parameters. Multiwavelength Raman and high spectral resolution lidars (HSRL) have become an established method of providing this kind of information during the past two decades. Aerosol extinction α and backscattering β coefficients measured with these lidars at multiple wavelengths can be inverted into aerosol microphysical properties, using different inversion methods [1,2,3,4,5,6].

Numerous theoretical and experimental studies carried out in the context of development of these inversion methods have demonstrated that a relatively simple configuration of a Nd:YAG laser can be used for estimating vertical profiles of particle properties, such as number, surface-area and volume concentrations, effective radius, complex refractive index (CRI) and single-scattering albedo (SSA). This laser set-up is usually referred to as 3β + 2α configuration. This configuration uses the fundamental as well as the frequency-doubled and frequency-tripled radiation and provides us with vertical profiles of two aerosol extinction coefficients at 355, 532 nm and three backscattering coefficients at 355, 532 and 1064 nm.

Results of particle-properties profiling from previous studies are comparably favorable and confirm that the considered inverse problem can be resolved. Unfortunately, only a few studies on validating the retrieval results of particle microphysical parameter profiles [7,8] and size distributions [9] are available. Here, we aim to extend that list of validation studies and estimate the reliability of the retrieval of both the profiles of the particle parameters and the corresponding particle size distributions (PSDs). Another aim of this study is to develop an approach that allows us to balance the theoretical and measurement (experimental) data. In this regard, we find (1) conditions on which remote (lidar) and in-situ data converge, (2) theoretical estimations that corroborate the high quality of the experimental (lidar and in-situ) results, and (3) a measure and its corresponding magnitude that can be used for assessing the reliability of the particle microphysical parameters retrieved with an inversion method.

The inverse problem that underlies the process of retrieving PSDs from 3β + 2α observations is underdetermined [10]. In fact, the number of input information (5 data points in total) is much smaller than the number of radius grid bins at which the sought size distribution function must be approximated, including sufficient retrieval accuracy [11]. Moreover, the particle-size and spectral dependence of the refractive index, the complexity of the shape of non-spherical particles and their morphology make the underlying ill-posed inverse problem even more complex. Thus, the estimation of particle microphysical properties requires not only numerous assumptions in the retrieval process but also calls for constraints with regard to the range of particle sizes we want to retrieve. Thus, the degree of uncertainty of the retrieved particle parameters and how to compute this uncertainty have always been major concerns [12]. The uncertainty depends for obvious reasons on many factors and includes the type of the investigated aerosols. Estimations of particle microphysical parameters can be performed more accurately when the aerosol size distribution shows a predominant fine mode [7,8].

Another critical factor that influences the quality of the inversion data products is the quality of the input optical data, i.e., their measurement uncertainty, which is defined by bias and noise. In the case of Raman lidar, the extinction coefficient is calculated from relatively weak nitrogen Raman backscatter signals. The corresponding uncertainties depend on temporal and height resolution of the optical profiles. The uncertainties are normally in the range of 10–20% for well-calibrated systems. In observations made with HSRL, the uncertainties of the optical data are generally smaller. The reason for the lower uncertainties compared to uncertainties of Raman lidar observations is the use of signals from comparably strong Rayleigh scattering. Aside from this advantage, the frequency shift between the signal from the molecular channel of HSRL and the laser line is comparably small. Therefore, there is no need to assume the Ångström exponent in the calculation of the backscattering coefficient, which is a fundamental requirement in the analysis of data acquired with Raman lidar. Thus, the best way to validate the results of microphysical retrievals is based on the inversion of HSRL observations and comparison to in-situ data taken with airborne platforms.

The multiwavelength HSRL-2 of NASA Langley Research Center is the world’s most advanced airborne lidar instrument of its kind. The HSRL-2 instrument aboard the ER-2 aircraft has been deployed to a multitude of field campaigns since 2012; for example, the Two-Column Aerosol Project (TCAP) and the DISCOVER-AQ campaigns [7,8]. One of the most recent field campaigns in which HSRL-2 took part was Observations of Aerosols Above Clouds and Their Interactions (ORACLES). ORACLES was carried out in south-western Africa during September 2016. The campaign review, including descriptions of instrumentation, flight tracks, observation methods and measurement data, can be found in Refs. [13,14,15]. Data collected with HSRL-2 and in-situ data are publicly accessible https://espoarchive.nasa.gov/archive/browse/oracles (accessed on 1 September 2023). This campaign provides us with 3β + 2α + 3δ measurements, i.e., particle linear depolarization ratio observations (δ) were carried out at 355, 532 and 1064 nm. Collocated in-situ data that were taken aboard the P-3B aircraft provide us with a unique opportunity for validating the inversion results of the optical data collected with HSRL-2 [9] during ORACLES. The in-situ data are PSDs, number concentrations of cloud condensation nuclei (CCN) and SSA. In our study we retrieved profiles of particle microphysical parameters and SSA from HSRL-2 data using the regularization algorithm described in Ref. [3].

The methodology of our approach is presented in Section 2. In Section 3, we present the results of four measurement cases. We discuss the results in Section 4. Section 5 summarizes our findings.

2. Methodology

2.1. HSRL-2 Optical Data

The detailed description of the goals and objectives of the ORACLES campaign can be found on the web site at https://espoarchive.nasa.gov/archive/browse/oracles (accessed on 1 September 2023). During ORACLES, the airborne HSRL-2 provided profiles of 3β + 2α + 3δ data with 300 m vertical resolution and 1 min horizontal resolution, which corresponds to approximately 6 km distance at nominal aircraft speed (https://espoarchive.nasa.gov/archive/browse/oracles/id8/ER2 (accessed on 1 September 2023)) [7,8]. Figure 1 shows the flight tracks of the aircraft from 12 September 2016 (light green), 20 September 2016 (cyan) and 24 September (orange). Case number, flight date, position of the aircraft (start and end point) and measurement time are shown in

Table 1. HSRL-2 measurement cases considered in this study.

Case	1	2	3	4
Date	12 September 2016	20 September 2016	20 September 2016	24 September 2016
UTC	14:12–14:31	10:14–10:29	11:47–12:24	9:13–9:33
Flight Time, min	852–871	614–629	707–744	553–572
Latitude, deg S	−17.68–−19.19	−17.75–−16.07	−18.30–−16.23	−14.16–−12.03
Longitude, deg W	7.68–9.19	10.50	9.19–9.00	11.00
Height (a.s.l.), m	2848–5051	1589–5681	1274–5681	1589–5681

. Table 1 shows that different averaging times of the optical data were used, increasing from 16 min in the second case to 38 min in the third case. An explanation of the choice of averaging times is given in Section 4. The spatiotemporal distributions of the extinction coefficients α and particle linear depolarization ratios δ at 355 nm for all four measurement cases are shown in Figure 2.

2.2. Regularization Algorithm

The HSRL-2 3β + 2α measurements are inverted to volume PSDs f(r) = dv(r)/dlnr [μm³cm⁻³] with a regularization algorithm [3]. This task is related to solving the Fredholm integral equation of the first kind:

$${\displaystyle \underset{r_{\min }^{}}{\overset{r_{\max }^{}}{\int }}{K}_g(\lambda ,m,r,\epsilon )f(r)dr=g(\lambda )},\hspace{1em}\hspace{1em}\hspace{1em}g=\alpha ,\beta$$

(1)

where the term K_g(λ, m, r, ε) denotes the kernels of the integral equation. The kernel depends on measurement wavelength λ, complex refractive index m = m_R − im_I, particle radius r and shape ε.

Particle linear depolarization ratios δ measured by HSRL-2 at 355, 532 and 1064 nm showed whether non-spherical particles were present along the flight tracks of the aircraft. These depolarization ratios slightly varied with wavelength for the cases mentioned in the previous section. The depolarization ratios δ(355) measured on 12 September 2016 (see Figure 2) were less than 0.05. We defined this number as the threshold value below which we could use the assumption of spherical particles in our regularization algorithm. The δ(355) values taken on 20 and 24 September 2016 were larger and on average varied between 0.05–0.10. Although 0.10 is already outside that range of 0–0.05, we know from a few studies, e.g., [16,17] that the assumption of spherical particle geometry may still work with acceptable accuracy. Thus, in this study, we applied the spherical particle model (Lorenz-Mie’s light-scattering theory) for the computation of the kernels K_g(λ, m, r, ε) [18]. However, we need to keep in mind that δ(355) profiles from 20 September 2016 show linear particle depolarization ratio values as large as 0.15 below 3.5 km height (a.s.l.), which means that there is an additional source of uncertainty in the inversion routine.

Since 2004, the algorithm [3] has been updated with new options that allow for the processing of large volumes of data in an automated, unsupervised fashion [19] for a wide range of particle radii and complex refractive indices. We use the following search range:

r∈[0.03; 10] μm; m_R∈[1.3; 1.8]; m_I∈[0; 0.1]

(2)

In this study we found the solution space in consecutive order from the lowest height bin of the vertical profiles to the topmost height bin (see markers in the first line of Figure 3) without the use of any constraints on domains (2) [19].

Particle microphysical parameters, such as effective/mean radius (r_eff/r_menan), standard deviation (σ), number (n), surface-area (s) and volume (v) concentrations are computed from the retrieved function f(r). SSA at arbitrary wavelength can be estimated from the function f(r), too, if the CRI is known. Our regularization algorithm is capable of estimating the spectrally independent parameter m with a specially developed averaging procedure (see details in [3]). Profiles of particle microphysical parameters, such as effective radius, number, surface-area and volume concentrations (the first and second lines, solid markers), CRI and SSA (the third line, solid markers) are shown in Figure 4, whereas the PSDs retrieved with the regularization algorithm are shown in Figure 5 (solid curves at different heights indicated in the legend).

2.3. In-Situ Data

The particle microphysical and optical properties were measured by in-situ sampling instruments. The particle collection was carried out by an isokinetic, low-turbulence inlet mounted on the port side of the P-3B aircraft [7,8,15]. The samplings with 1 s temporal resolution are available at https://espoarchive.nasa.gov/archive/browse/oracles/P3/mrg1 (accessed on 1 September 2023).

Table 2. In-situ measurement cases considered in this study.

Case	1	2	3	4
Date	12 September 2016	20 September 2016	20 September 2016	24 September 2016
UTC	14:12–14:31	10:15–10:33	11:55–12:24	9:05–9:33
Flight Time, min	852–871	615–633	715–744	548–572
Latitude, deg S	−17.68–−19.19	−17.75–−16.07	−18.30–−16.23	−14.16–−12.03
Longitude, deg W	7.68–9.19	10.50	9.19–9.00	11.00
Height (a.s.l.), m	628–5765	793–4343	1050–5657	1956–4879

shows the case number, flight date, position of the aircraft (start and end point) and measurement time of the in-situ measurements we used in our study. Figure 1 and Figure 2 show the P-3B aircraft trajectories as black dots and black lines in the horizontal and vertical planes, respectively, for these measurements. The trajectories were almost vertical, i.e., the aircraft travelled along the directions of the HSRL-2 sounding tracks. Thus, we can conclude that we had four cases in which HSRL-2 and in-situ measurement profiles were almost collocated in space and in time. There were some temporal delays. We found separations of 4, 8, and 5 min in the first, third, and fourth cases, respectively, between the aircrafts. In view of the duration of data accumulation, we assume that these temporal distances did not significantly influence the results of our comparison study.

We investigated the PSDs (dotted curves with bullets at different heights indicated in the legend of Figure 5) and the profiles of CCN number concentration (the first line, stars) and SSA at 550 nm (the third line, stars) measured in-situ (see Figure 4). Furthermore, the second line of Figure 3 shows profiles of relative humidity measured in situ (stars). We note that in-situ SSA was measured at 450 and 700 nm. We do not show these results because they were close to SSA at 550 nm. The spectral spread was ±0.01.

We applied 300 m vertical-averaging steps for the data collected by the instruments aboard the P-3B aircraft. This smoothing length was the same as that applied to the data taken by HSRL-2. It means the averaging time of the datasets was approximately 2 min. These smoothed data were used for the computation of the in-situ measured CCN number concentration, single-scattering albedo, relative humidity (see star markers) and particle size distribution (dotted curve with bullets are shown at a few height bins only). The standard deviations of these parameters depended on the case number. The mean standard deviations of the profiles in the first case amounted to approximately 10%, 1.5%, 11% and 20% of the respective mean values for CCN number concentration, SSA, relative humidity and particle size distribution at the peak. The respective values in the second case were 18%, 1.5%, 7% and 35%. The mean standard deviations in the third and fourth cases did not exceed the respective values observed in the first and second cases. Moreover, we converted the in-situ values of number PSD n_in-situ(r) [number of particles in units of 1/cm³ per log10 interval] into the unit of a volume PSD dv_in-situ(r)/dlnr [μm³cm⁻³]. As our regularization algorithm produced results in terms of volume particle size distributions, we performed this conversion with the equation:

$$\frac{\mathrm{d}{v}_{in-situ}\left(r_i\right)}{\mathrm{d}\mathrm{l}\mathrm{n}r}=\kappa \frac{4r_i^4}{3\mathrm{l}\mathrm{n}\left(10\right)\mathrm{l}\mathrm{g}\frac{r_{i+1}}{r_i}}{n}_{in-situ}\left(r_i\right); i=1,2,\dots$$

(3)

Here, the correction factor κ was fixed for each of the four cases we considered in our study. We fitted κ so that the best agreement between retrieved and in-situ PSDs was obtained. The parameter r_i denotes the radius bins that were used for the in-situ measurements of the particle size distributions (see dotted curve with bullets in Figure 5). Unfortunately, the in-situ PSD measurements covered only the particle radius range r < 0.5 μm, which usually covers the fine-mode fraction of the PSDs. Thus, we cannot compare the inversion results and the in- situ measurements for particles above 0.5 μm. It also remains unclear whether particle loss effects caused by the aircraft inlet system were significant and how they were corrected for.

3. Case Studies

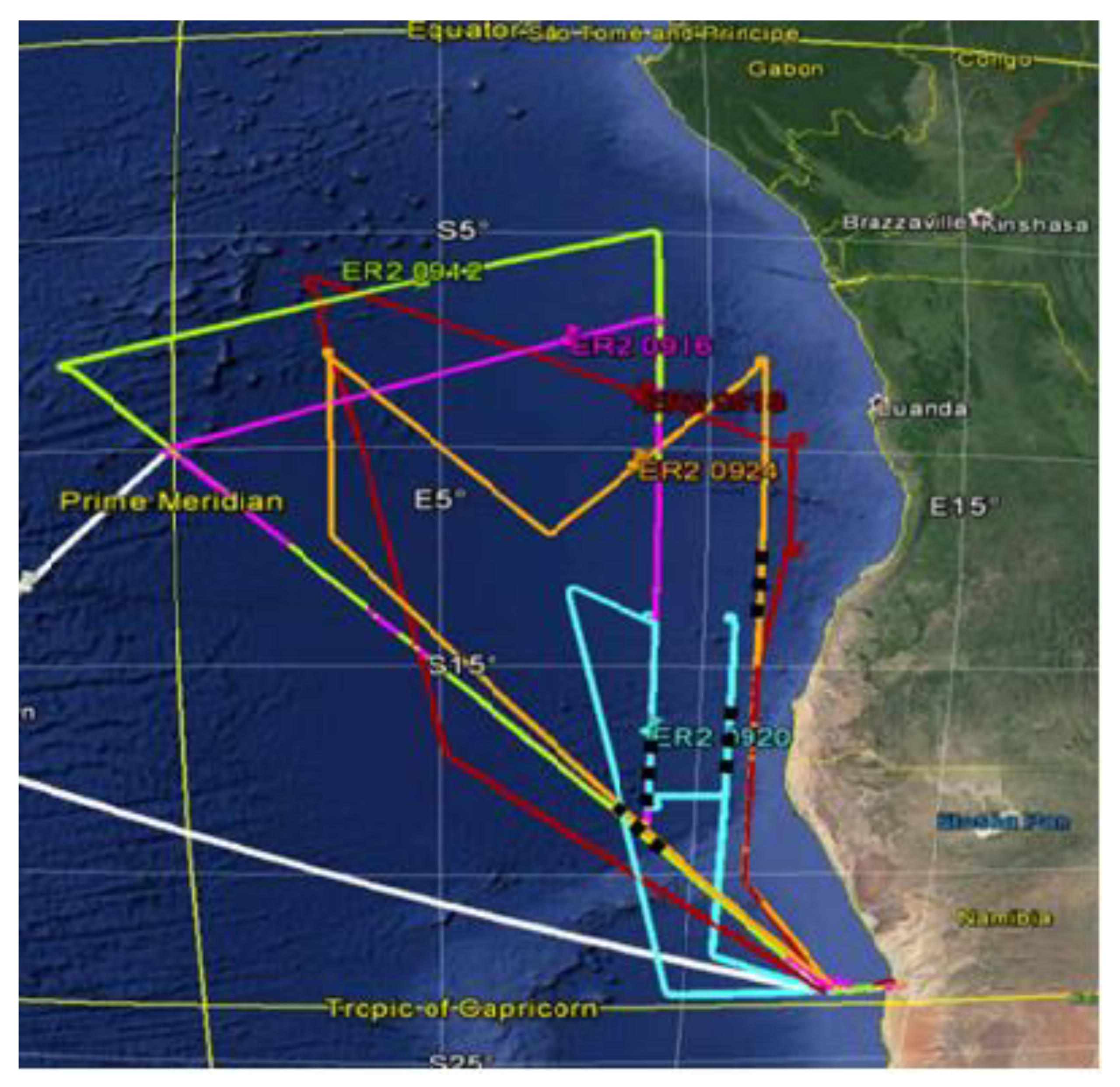
We now describe in detail the results of the four cases of HSRL-2 observations. Optical data were collected along flight tracks marked by the black dots in Figure 1. As noted previously, the time intervals of the lidar observations and the in-situ measurements are summarized in Table 1 and Table 2, respectively.

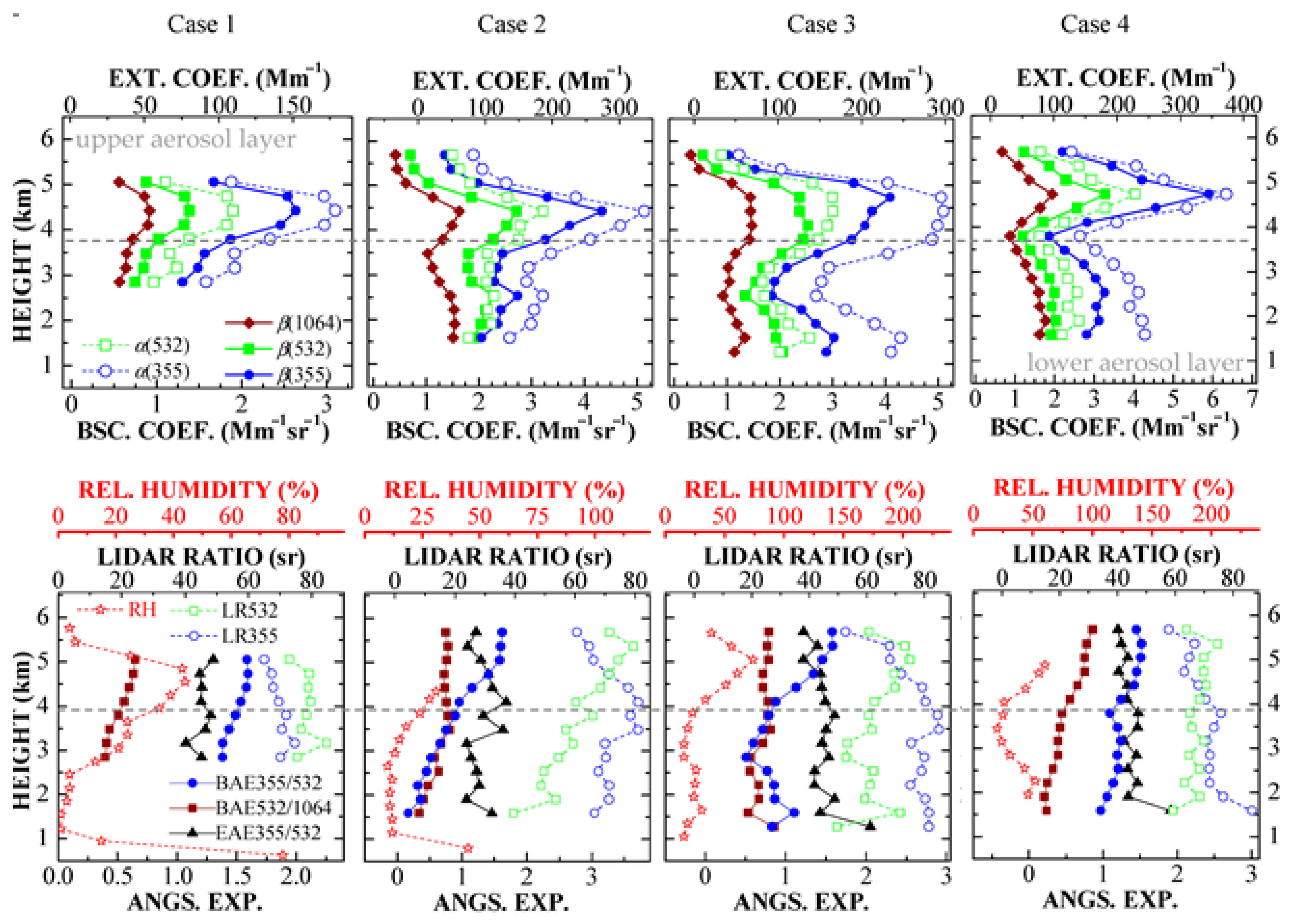
For Case 1, we show optical data of the 3β + 2α-profiles in the height range from 3–5 km (above sea level). For Cases 2–4, we show the optical data in the height range from 1.5–6 km (see the first line in Figure 3). The upper and lower layers in Figure 3 are separated by horizontal lines (dashed lines). The profiles show two pronounced aerosol layers. The upper aerosol layer (above 3.5–3.7 km) shows maximum values of the backscatter and extinction coefficients in the height range from 4.5–4.8 km. The extinction coefficient α(355) peaks at the value of 380 Mm⁻¹ for Case 4 (measurement from 24 September 2016, 9:13–9:33 UTC). The extinction coefficient in the layer below 3.5–3.7 km is lower and considerably more variable.

The particle intensive properties for Cases 1–4, such as lidar ratios Λ(λ) at 355 and 532 nm and extinction-related (EAE)- and backscatter-related (BAE) Ångström exponents are shown in Figure 3 (see second line). Below 3.5 km we see that the lidar ratio Λ(355) > Λ(532) for Cases 2–4. In contrast, we find larger lidar ratios at 532 nm compared to the lidar ratios at 355 nm in the center of the upper aerosol layer, i.e., at around 4.5 km. In that case, Λ(532) increased to a value close to 80 sr (see open symbols).

EAE ($\dot{\alpha }$) at the wavelength pair 355/532 nm varied comparably little between 1.0–1.5 (see triangles in Figure 3) if we exclude from our analysis the lowest height bins in the third and 4fourth cases and some intermediate height bins in the second case (3.5–4.0 km above sea level). The excluded height bins represent outliers, i.e., their values strongly deviate from the mean values of the profiles. The strong deviations were most probably caused by high measurement uncertainty. Values of the EAE in the range from 1.0–1.5 indicate that the PSD was dominated by particles in the fine mode fraction.

The BAE at the wavelength pair 355/532 nm ($\dot{\beta }(355/532)$) was the most variable intensive parameter in our study (blue bullets in the second line of Figure 3). It grew nearly monotonically with height, from 1.4 to 1.6 in the first case, from 0.4 to 1.6 in the second case and from 1.0 to 1.5 in the fourth case. The only exception was the third case. The $\dot{\beta }(355/532)$ decreased from 1.0 to 0.5 with height in the lower aerosol layer and increased to a value of 1.6 in the upper aerosol layer. The BAE for the wavelength pair 532/1064 nm monotonically grew from 0.25 to 0.5 in the lowest height bins (1.5–3.5 km). It varied between 0.6 and 0.8 in the upper height bins in all four cases (brown lines).

Results of the inversion of the optical data, based on the methodology described in Section 2.2, are presented in Figure 4. The extensive microphysical parameters, i.e., number, surface-area, and volume concentrations, are proportional to the magnitude of the optical input data. This variability of these microphysical particle properties can be particularly seen from the variability of the extinction coefficient α(355); see the first and second lines in Figure 4. Surface-area concentration varied from 80 to 600 μm²cm⁻³, number concentration from 350 to 5200 cm⁻³ and volume concentration from 5 to 60 μm³cm⁻³ in all four cases.

We found different values for the CRI in the two aerosol layers (see the third line in Figure 4). The difference in the CRI in the two aerosol layers increased with increasing BAE in cases 2 and 3. The average value of the CRI is approximately 1.62–i0.03 in the lower aerosol layer. In contrast, we found an average value of 1.58–i0.02 in the upper aerosol layer. The difference in the CRIs between the two aerosol layers became smaller in the first case, i.e., we found values of 1.62–i0.03 and 1.62–i0.025. In the fourth case, the profile of the CRI did not change significantly with height in the two aerosol layers. We found on average 1.6–i0.02. The scatter of the real part was ±0.1 in the different height bins. The scatter was ±i0.01 for the imaginary part in the different height bins.

The SSA is one of the key parameters in calculating the impact of aerosol pollution on the sun’s radiation field in the atmosphere. We obtained this parameter by computing it from our retrieval products. Figure 4 (third line) shows these calculated profiles at 355 (blue), 532 (green) and 1064 (brown) nm. The profiles reflect the features (variations of values with height) found for the vertical profiles of the imaginary parts of the CRI in the four cases.

SSA at 532 nm (green square) increased on average from 0.85 in the lower aerosol layer to 0.9 in the upper aerosol layer in the first and third cases and from 0.8 (lower layer) to 0.9 (upper layer) in the second case. In the fourth case, the mean values of the data points of the SSA profile at 532 nm oscillated (i.e., increased and decreased) with height in the same manner as the CRI. The uncertainty bars of SSA at 532 nm are ±0.04. We note that the disagreement we found between the SSA we retrieved at 532 nm and the SSA measured in-situ at 550 nm did not exceed 0.05. We excluded in this comparison the lowest height bins at which the measurement uncertainty was largest.

The available in-situ measurements included CCN number concentration (n). The corresponding profiles are shown in Figure 4 (stars in the first line). We observe that the n-profiles retrieved with the regularization algorithm systematically overestimated the values obtained from the in-situ observations. The bias was minimal in the first case (about 25% difference), increased in the fourth case (values differed by 50%, apart from the lowest height bins) and was maximal in the second and third cases (100% and more). We stress that CCN number concentration derived from the in-situ measurements includes particles larger than 0.05 μm radius. In contrast, the radius domain in which the regularization algorithm was used covered the interval r∈[0.03; 10] μm [see intervals given in Equation (2)]. If we consider in data inversion only particles with radius larger than 0.05 μm, we find that number concentration decreased by approximately 10% in the first case, by 50% in the second and third case, and by 25% in the fourth case.

The maximal and minimal values of n and s are found in the upper aerosol layer, whereas volume concentration reaches its maximal value in the lower aerosol layer (except in the third case). This particularity of the v-profiles can be understood if we analyze the particle sizes and their corresponding PSDs. The upper aerosol layer contained particles of smaller effective radius, i.e., less than 0.3 μm, whereas effective radii of particles in the lower aerosol layer exceeded 0.3 μm (see the first line in Figure 4). 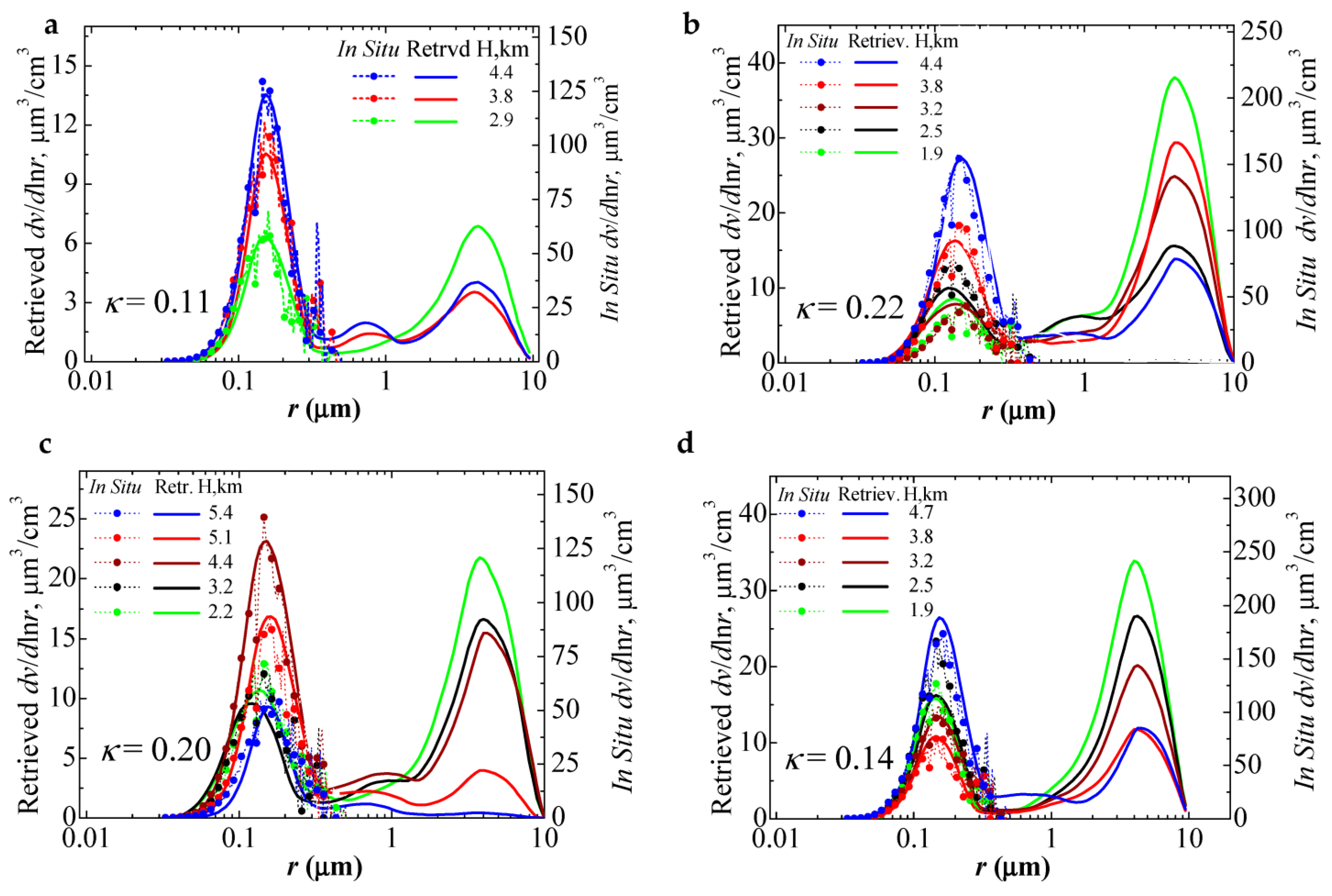Simultaneously, Figure 5 shows the PSDs retrieved for all four cases in height bins that were closest to the height bins used for the in-situ observations. We see that the mean (or effective) radius varied with height within a relatively narrow band around 0.15–0.20 μm, which was indicative of particles in the fine-mode fraction of the PSD. The contribution of coarse-mode particles with r_mean (r_eff) equal to 3–4 μm increased within the lower aerosol layers. Furthermore, the concentration of particles in the coarse mode was maximal in the lowest height bins (see green curves). The larger contribution of coarse-mode particles in the lower layer, compared with the conditions in the upper layer, led to an increase in the total effective radius and volume concentration.

We note that the relative humidity profiles reached 80% in the upper aerosol layer of the third case. We hypothesize that this maximal value of 80% that we found from all four cases might be a threshold (condition) at which particle hygroscopic growth became significant, thus leading to an increase in the particle mean (effective) radius and volume concentration in the upper aerosol layer (see blue and red PSDs for the third case in Figure 5). This observation may explain why the volume concentration of the monomodal PSDs in the upper aerosol layer (blue, red) was higher than the volume concentration of the bimodal PSDs in the lower aerosol layer (black, green) for the third case. The third case also demonstrated that the profile of the mean/effective radius of the fine mode particles was not constant and varied with height. A similar effect was observed for coarse-mode particles during the SAMUM campaign [20].

Figure 5 also shows the PSDs measured in-situ (dotted curves with bullets). We see a strong disagreement between the retrieved and the in-situ measured PSDs. The magnitude of the differences was approximately one order of magnitude for the peak values in the first and fourth case, respectively, and a factor five in the second and third cases, respectively. However, the disagreements are biased. If we properly fit the correction factor in Equation (3) so that κ is equal to 0.11, 0.22, 0.20 and 0.14 for the first, second, third and fourth cases, respectively, this bias vanishes. In the next section, we analyze the magnitude of the correction factors and the sources of the retrieval uncertainties.

4. Discussion

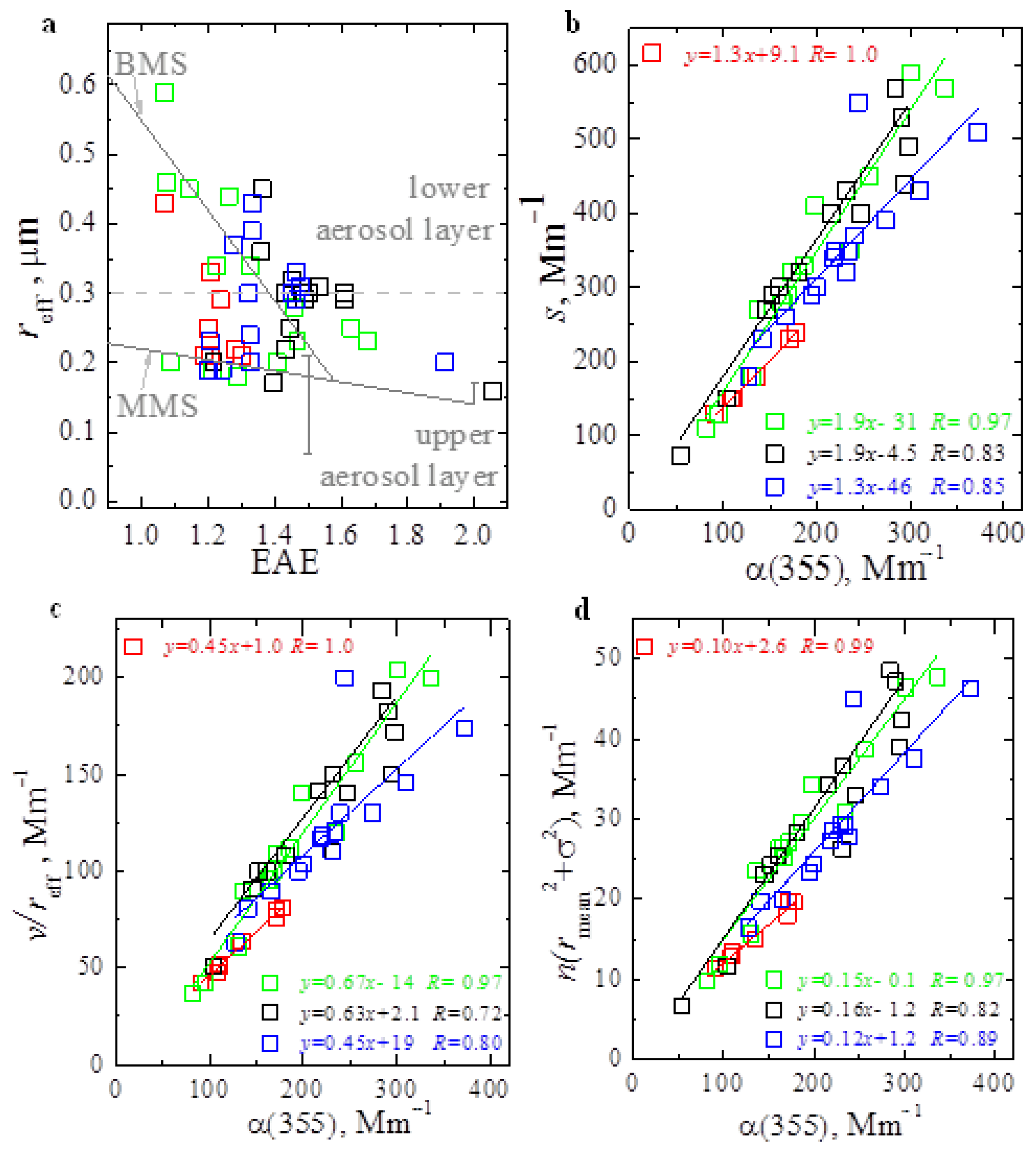
In this section, we describe the quality of the HSRL-2 measurement data and how this data quality affected the accuracy of the retrieved data products. We started our study with the analysis of correlation relationships and regression equations (y = ax + b) that described the interdependencies between particle bulk microphysical parameters and optical data.

The parameters s [b], v/r_eff [c], n (r_mean² + σ²) [d] and α(355) were linearly correlated (see Figure 6). The correlation coefficients were R = 0.83, 0.72, and 0.82, or larger for all four measurement cases. The regression coefficients a and b described the linear correlation relationships (see legends). We conclude that the HSRL-2 3β + 2α data were of high quality for two reasons. (1) The regression coefficients agreed with the values we used in [20], and (2) the values for a_s, a_v and a_n varied inside the intervals [1.3; 1.9], [0.45; 0.67] and [0.10; 0.16], respectively.

We note that the maximal correlation coefficient (R = 0.99–1.0) corresponded to the first measurement case (red symbols), whereas the minimal correlation coefficient (R = 0.72–0.83) was found for the third case (black markers). Simultaneously, the bias between the retrieved and the in-situ number concentration profiles (see previous section) was minimal for the first case (25%) and maximal for the third case (more than 100%). The magnitudes of the correlation coefficients and biases meant that the quality of the retrieval results and hence the quality of the measurement data was best in the first case and worst in the third case. In view of the different data qualities found for the four cases, we used a data averaging time of 38 min for the third case, as the data were the noisiest. We used 16–20 min for the other three cases, as they contained less noisy data (see Table 1). More details on the procedure of estimating averaging times can be found in Ref. [21].

The biases for number concentrations and PSDs in the radius interval r∈[0.03; 10] μm were inversely correlated to each other. We applied compensation factors that lead to a reduction in number concentrations in the retrieved profiles. We used 0.9 in the first case, 0.5 in the second and third case, and 0.75 in the fourth case. This meant that if we applied these factors, we obtained the same solution as if we considered the inversion problem (1) over the radius range [0.05; 10] μm (see previous section). The n-profiles retrieved with these compensation factors then converged with the profiles of CCN number concentration that were measured in-situ. At the same time, the correction factor for the retrieved PSDs became approximately constant, i.e., we obtained

κ ≈ 0.1

(4)

for all four cases. This result means that the data obtained from the lidar observations and the in-situ data converged with each other. We will test in our future studies whether the correction factor κ (≈0.1) needs to be used for a more accurate definition of the volume PSD in Equation (3) in general.

Figure 6a shows effective radius versus EAE for the wavelength pair 355/532 nm for all four cases. The retrieval and measurement results are barely correlated. However, we can remove from our analysis all data for which EAE exceeds 1.5. We are of the opinion that these data are affected by strong errors. In this case, the two patterns that correspond to the monomodal strategy (MMS) and the bimodal strategy (BMS) become more distinguishable. MMS and BMS are explained in detail in Ref. [20]. The MMS represents the upper aerosol layer. Here, we mainly find smaller particles that belong to monomodal PSDs. In contrast, the BMS better matches the conditions in the lower aerosol layer. Here we find bigger particles that may be part of bimodal PSDs. The strategies are described by the regression equations y = −0.08x + 0.26 ± 0.07 = −0.08x + ${0.30}_{-0.11}^{+0.03}$ and y = −0.65x + 1.2, respectively: for details, we refer to Ref. [22].

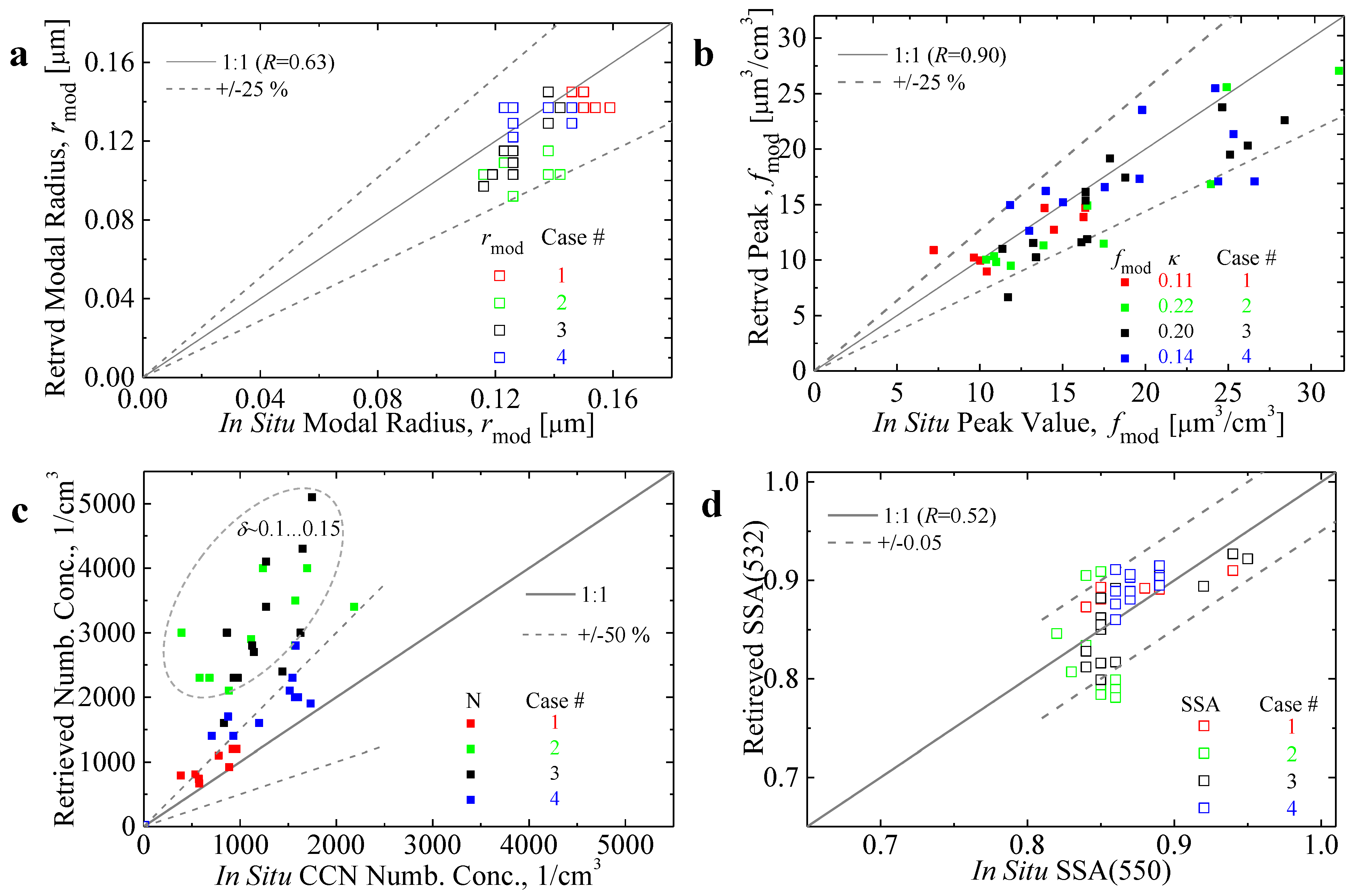
In the next step of our data analysis, we compare the fine-mode radii r_mod and the modal (peak) values f_mod = f(r_mod) = f_max (open and solid squares in Figure 7a,b, respectively), number concentrations and single-scattering albedos (solid and open squares in Figure 7c,d, respectively). We see that all data are distributed along the 1–1-line (grey solid). The deviation of the data points from this 1–1-line does not exceed ±30% for the modal radii and peak values, and ±0.06 for single-scattering albedo (dotted grey lines). However, the scattering of the data around the 1–1 line becomes larger for number concentration. The increased scatter is caused by the two measurement cases from 20 September 2016. Particle linear depolarization ratios were comparably large, i.e., values reached 0.10–0.15 (see Figure 2). The use of the spherical light-scattering model [18] may not work properly for these two cases. Aside from this reason, the measurement uncertainties of the data of the second and third cases are comparably high, which may also lead to the increased scattering of the data points.

With regard to single-scattering albedo at 532 nm, we found in all four cases a strong correlation to the BAE measured at 355/532 nm (see Figure 8b). The linear correlation coefficient was 0.85, and the regression analysis results in y = 0.09x + 0.77 (see legend, dotted line). In the next step, we investigated whether this comparably strong correlation can be explained from the theoretical point of view.

Firstly, we analyzed the statistics of BAE versus SSA from our reference (etalon) look-up table (RLUT). This RLUT consisted of 345,168 synthetic optical sets of 3β + 2α coefficients. The RLUT elements were computed on the basis of logarithmic-normal size distributions for various mean radii, standard deviations and CRIs. For details we refer to [20]. For the analysis of ORACLES optical data, we collected all RLUT elements that fulfill the constraints, i.e.,

m_R = 1.6   r_mod∈[0.1; 0.17] μm    σ∈[1.45; 1.95]    BAE(355/532) < 1.7

(5)

and simultaneously also represent the fine-mode particles we found in our study (see Figure 3, Figure 5 and Figure 7a).

Figure 8a shows the statistics of the entries denoted by solid circles and a solid grey line. Each of these elements can be described by a mean radius r_mean (in terms of number size distribution) in the interval [0.055; 0.115] μm (see legend) and an imaginary part of the complex refractive index in the interval [0.0; 0.05]. Both BAE and SSA depend on particle size. Hence, we found a layer structure (Figure 8a) in which each layer corresponded to a different standard deviation σ. However, the major factor that decided on the values of these parameters was the imaginary part. Variations in m_I between 0 and 0.05 resulted in an interdependency between BAE and SSA. This interdependency can be described by the linear regression equation y = 0.19x + 0.61. The correlation coefficient in this case was R = 0.75.

We also analyzed the statistics of BAE versus SSA using the RLUT elements that fulfilled the constraints (5) at m_R = 1.4 (see open circles and dotted grey line in Figure 8a). The behavior of BAE versus SSA was similar to the one we found for m_R = 1.6. The main difference was the bias along the ordinate axis. As a result, the intercept of the regression equation (y = 0.21x + 0.72) at m_R = 1.4 increased.

Secondly, we investigated the influence of coarse-mode particles on BAE $\dot{\beta }(355/532)$ and SSA ω(532). In the case of bimodal PSDs the following equations hold true:

$${\dot{\beta }}_{}(355/532)=\ln [(1-{\varphi }_{\beta (532)}){(\frac{532}{355})}^{{\dot{\beta }}_{\mathrm{fine}}(355/532)}+{\varphi }_{\beta (532)}{(\frac{532}{355})}^{{\dot{\beta }}_{\mathrm{coarse}}(355/532)}]{\ln }^{-1}(\frac{532}{355})$$

(6)

$$\omega (532)=[(1-{\varphi }_{\beta (532)}){\Lambda }_{\mathrm{fine}}(532){\omega }_{\mathrm{fine}}(532)+{\varphi }_{\beta (532)}{\Lambda }_{\mathrm{coarse}}(532){\omega }_{\mathrm{coarse}}(532)]{\Lambda }^{-1}(532)$$

(7)

The parameter ϕ_β(532) denotes the coarse-mode portion of the total (fine + coarse) backscatter coefficient β(532). BAE and SSA are monotonically decreasing functions if plotted versus ϕ_β(532) because coarse-mode parameters ${\dot{\beta }}_{\mathrm{coarse}}(355/532)$ and ω_coarse(532) are typically lower than the respective parameters for the fine-mode particles ${\dot{\beta }}_{\mathrm{fine}}(355/532)$ and ω_fine(532).

To illustrate this interdependency of BAE and SSA for different portions of ϕ_β(532), we selected two RLUT elements that can be described by such parameters of fine- and coarse-mode particles, i.e.,

r_mean,fine = 0.095 μm   σ_fine = 1.45   m_fine = 1.6–i0.02

r_mean,coarse = 0.295 μm σ_coarse = 2.55    m_coarse = 1.6–i0.02

Figure 8a shows the curve (grey asterisks) computed at values ϕ_β(532) = 0.30, 0.39, 0.50, 0.63, 0.79, and 1.00. The regression equation for these data was y = 0.09x + 0.78. The correlation coefficient R was close to 1. The main property of this interdependency of BAE and SSA for a bimodal PSD was the slope, which was a = 0.09. This number was lower than the one we found for fine-mode particles, i.e., a = 0.19 and 0.21. We note that the regression equations for the bimodal PSDs (theoretical values) and the retrieved PSDs (experimental values) were close to each other (see grey dotted and asterisk lines in Figure 8b). We believe that the use of a priori information that takes account of this strong correlation between BAE and SSA may be useful for future studies.

We found another pattern for the retrieval and measurement results. It was the magnitude of ratios between the parameters from the upper (up) and lower (low) aerosol layers in all four cases. The magnitude was equal to ρ = 1.5–2 for the extinction coefficient (for example, at 532 nm) and number concentration. In the case of effective radius, we can use the inverse value 1/ρ, i.e.,

$$\rho =\frac{\alpha {(532)}^{\mathrm{up}}}{\alpha {(532)}^{\mathrm{low}}}\approx \frac{n^{\mathrm{up}}}{n^{\mathrm{low}}}\approx \frac{r_{\mathrm{eff}}^{\mathrm{low}}}{r_{\mathrm{eff}}^{\mathrm{up}}}=1.5\dots 2.0$$

(8)

We show in the Appendix A the equations that can be used when particles of the fine-mode coalesce. This process simultaneously increases the portion of coarse-mode particles in accordance with the law of mass conservation if no scavenging effects (particle loss) happen. Particle transformation from fine to coarse mode and vice versa may explain why the extinction coefficient is inversely proportional to particle size, in spite of the fact that for theoretical reasons extinction coefficients at the shortest measurement wavelength were proportional to the cross section or even the volume of particles of one and the same mode.

Finally, we assessed the level of reliability of the results retrieved with the regularization algorithm. We used the correlation coefficient R that described the degree of interdependency of the data. We considered R as a measure of the reliability of the retrieval results. In our study, the correlation coefficients of the retrieved and in-situ results were 0.52, 0.63 and 0.9 for SSA, modal radius and modal (peak) values of volume PSD, respectively (see Figure 7a,b,d). This result implies that the data points from both methods were comparatively well-correlated to each other, especially in the case of the parameter f_mod. Based on this observation, we conclude that the degree of reliability of the retrieval results reached 90%. Moreover, in view of the data spread, the uncertainties of the retrieval results for the parameters SSA, r_mod and f_mod were ±0.06, ±25% and ±30%, respectively (see dotted lines in Figure 7). However, we stress that this magnitude of 90% was achievable mainly because the correction factor κ could be optimally fitted in this study, which eventually allowed for reaching the best agreement between lidar and in-situ data. More generally, the regularization algorithm tends to overestimate number concentration [1]. Therefore, in practice, an overestimation mainly of number concentration needs to be suppressed in the inversion routine. This suppression can be achieved if we choose a value for the parameter r_min (it describes the lower limit of the inversion window) that is not too small. For example, we selected r_min ≥ 0.05 μm. We can achieve a similar effect if we narrow down the CRI intervals used by the inversion algorithm in the search routines. Another, more sophisticated manner of suppression includes the use of the proper correlation relationships between microphysical parameters and optical data (see Figure 6). We recently published these results; see [20,21].

5. Conclusions

We present the first results of a comparison of particle microphysical characteristics retrieved with a regularization algorithm [3] and measured with airborne in-situ instruments during the ORACLES campaign. The campaign took place off the southwest coast of Africa in September 2016. NASA Langley Research Center’s airborne HSRL-2 instrument provides optical profiles of 3β + 2α data which can be used as input for our retrieval algorithm. These data are publicly accessible and can be downloaded from https://espoarchive.nasa.gov/archive/browse/oracles/id8/ER2 (accessed on 1 September 2023). We found in total four measurement cases for which HSRL-2 and in-situ measurements were co-located in space and in time close enough so that we could carry out a detailed comparison of the data products provided by the two particle characterization methodologies.

We identified two distinct aerosol layers in all four measurement cases. The lower aerosol layers reached up to 3.5 km height above sea level in all four cases. This layer was characterized by a bimodal particle size distribution and effective radii (r_eff) exceeding 0.3 μm. In the upper aerosol layer above 3.5 km height the coarse mode disappeared. Particle effective radius dropped to values less than 0.3 μm. Simultaneously, the imaginary part of the complex refractive index (single-scattering albedo at 532 nm) tended to decrease (increase) to 0.02 (0.90) in the upper aerosol layer compared to values of 0.025–0.03 (0.80–0.85) in the lower layer. Particle extensive microphysical parameters, i.e., number (n), surface-area (s) and volume (v) concentrations, are proportional to the magnitude of optical data taken with HSRL-2. These three parameters varied between 350 and 5200 cm⁻³, 80 and 600 μm²cm⁻³ and 5 and 60 μm³cm⁻³, respectively.

Our analysis of interdependencies between bulk microphysical parameters and optical data showed a high linear correlation of the parameters s, v/r_eff and n (r_mean² + σ²) with the extinction coefficient α(355). We found comparably high correlation coefficients for the interdependency of v/r_eff versus α(355). Correlations vary between R = 0.72 and R = 1.0. We also found high correlations between effective radius and the extinction-related Ångström exponent (wavelength pair 355 and 532 nm) considering separately the interdependencies in the upper aerosol layer (characterized by monomodal particle size distributions) and the lower aerosol layer (characterized by bimodal particle size distributions).

The data products obtained with our regularization algorithm agree within reasonable limits to the same data products measured with the in-situ instruments. We obtained the following results:

• particle size distributions agreed within ±25% uncertainty if we used the correction factor in the interval κ∈[0.11; 0.22];
• single-scattering albedo at 532 nm agreed with an uncertainty of ±0.05;
• number concentrations (obtained with our regularization algorithm) versus CCN number concentrations (measured with in-situ instrumentation) agreed within an uncertainty of ±50%. The uncertainty increased to 100% and above with increasing particle linear depolarization ratio δ and measurement noise.

We found a comparably high correlation coefficient of R = 0.85 between single-scattering albedo retrieved with our regularization algorithm at 532 nm and the backscatter-related Ångström exponent measured with HSRL-2 at the wavelength pair 355 and 532 nm. We found comparably good agreement between the results retrieved with the regularization algorithm and measured in-situ. The degree of reliability was as large as 90% if HSRL-2 data were averaged for at least 16–20-min.

We shall carry out a more detailed study in future research work (1) to test the correction factors κ that describe the bias between retrieved and in-situ particle size distributions, (2) to investigate the influence of different light-scattering models, including the light-scattering model that uses spheroidal particle shape [23], on our results, as well as (3) to analyze the uncertainties of the optical input data and uncertainties of the data products we inferred from the regularization algorithm and measured with the in-situ instruments.