Abstract
The Western Balkans (WB) region is highly prone to water erosion processes, and therefore, the estimation of rainfall erosivity (R-factor) is essential for understanding the complex relationships between hydro-meteorological factors and soil erosion processes. The main objectives of this study are to (1) estimate the spatial-temporal distribution R-factor across the WB region by applying the RUSLE and RUSLE2 methodology with data for the period between 1991 and 2020 and (2) apply cluster analysis to identify places of high erosion risk, and thereby offer a means of targeting suitable mitigation measures. To assess R-factor variability, the ERA5 reanalysis hourly data (0.25° × 0.25° spatial resolution) comprised 390 grid points were used. The calculations were made on a decadal resolution (i.e., for the 1990s, the 2000s, and the 2010s), as well as for the whole study period (1991–2020). In order to reveal spatial patterns of rainfall erosivity, a k-means clustering algorithm was applied. Visualization and mapping were performed in python using the Matplotlib, Seaborn, and Cartopy libraries. Hourly precipitation intensity and monthly precipitation totals exhibited pronounced variability over the study area. High precipitation values were observed in the SW with a >0.3 mm h−1 average, while the least precipitation was seen in the Pannonian Basin and far south (Albanian coast), where the mean intensity was less than an average of 0.1 mm h−1. R-factor variability was very high for both the RUSLE and RUSLE2 methods. The mean R-factor calculated by RUSLE2 was 790 MJ mm ha−1·h−1·yr−1, which is 58% higher than the mean R-factor obtained from RUSLE (330 MJ mm ha−1·h−1·yr−1). The analysis of the R-factor at decadal timescales suggested a rise of 14% in the 2010s. The k-means algorithm for both the RUSLE and RUSLE2 methods implies better spatial distribution in the case of five clusters (K = 5) regarding the R-factor values. The rainfall erosivity maps presented in this research can be seen as useful tools for the assessment of soil erosion intensity and erosion control works, especially for agriculture and land use planning. Since the R-factor is an important part of soil erosion models (RUSLE and RUSLE2), the results of this study can be used as a guide for soil control works, landscape modeling, and suitable mitigation measures on a regional scale.
1. Introduction
The Western Balkans (WB) region includes the territories of Albania and the former Socialist Federal Republic of Yugoslavia (excluding Slovenia and Croatia, respectively), with an area of approximately 208,000 km2 and a population of 18 million citizens [1]. The region spans the low-altitude Pannonian Basin in the north, the mountain regions in the central-south and west, and the coastal area of the Adriatic Sea. Livelihoods are heavily dependent on weather-sensitive sectors (such as agriculture, forestry, tourism, and supporting services) [2]. The WB is highly prone to water erosion processes [3], and, in some areas, erosion has reached a critical stage of irreversibility due to the limited soil cover. For locations with a very slow rate of soil formation, any soil loss exceeding 1.0 t ha−1 yr−1 may be regarded as irreversible over a time span of 50–100 years [4], and for the southern part of Europe, the tolerable soil erosion rate is ca. 0.3 t ha−1 yr−1 [5].
The earliest reports of water-related soil erosion at global and European levels include the WB, but the information is sparse [4]. All erosion maps of former Yugoslav countries were prepared in the 1980s based on the expert judgment of field data and maps generated via the erosion potential method (EPM) [6] as one of the most widely accepted and applied empirical models in the Balkan region, East, and Central Europe, also known as the Gavrilović method (e.g., Refs. [7,8,9,10,11]). The Gavrilović method is an empirical, semi-quantitative model established on erosion field research in the Morava River catchment area (Serbia) and encompasses erosion mapping, sediment quantity estimation, and torrent classification [6]. EPM is convenient for areas where minimal data are available or where there is a lack of previous erosion research, but it does not explore in depth the physics of erosion processes [11].
Numerous studies across Europe and the world have confirmed the scientific verification of the EPM model and its modifications. The erosion map of Albania was prepared following the one-dimensional hydrology, vegetation, and erosion model (RDI/CSEP) by Grazhdani et al. [12], whereas the erosion map for Bosnia and Herzegovina (BiH) was prepared using the universal soil loss equation (USLE) for agricultural land and EPM for the whole area [4,13,14].
The EU (European Union) Joint Research Centre (JRC) provided a rainfall erosivity (R-factor) map with a horizontal resolution of 500 m and an extensive database of 30 min (minute) rainfall records in Europe [15,16,17,18,19,20,21,22]. Another study applied the revised universal soil loss equation (RUSLE) methodology, with rainfall erosivity estimation based on a long time series comprised 30 min resolution rainfall observations [23]. However, data about water erosion rates in the WB countries were not included. Instead, contemporary research regarding the WB region was conducted only in sub-regional studies based on the precipitation data for smaller territories covering [12,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41] or partial regional studies based on gridded rainfall datasets [42].
Traditionally, precipitation data for rainfall erosivity studies was obtained from ground-based meteorological instruments and rain-gauge observations at fixed points. Consequently, their spatial resolution is relatively poor, susceptible to various regional climatic influences, and has insufficient accuracy for high-resolution soil erosion modeling. Without such information, it is hard to benchmark the impact of future climate variability and change on the rainfall erosivity of a region [43]. However, problems with uneven distributions of meteorological sites and radar signal interference can be avoided by using precipitation estimates from remote sensing [44]. Gridded datasets are particularly relevant to soil erosion because they quantify both the temporal and spatial variability of precipitation [45].
The evaluation of the vulnerability of soils to rainfall erosivity is vital in the context of sustainable agricultural practices [37], especially as the role of agriculture in the WB countries is greater than the average for EU countries (covering approximately 42% of the area compared with 41% of the total land area of the EU and the United Kingdom) [46,47]. A good understanding of climate variability and precipitation features is of great importance, especially when dealing with rainfall erosivity in agricultural and mixed agricultural areas. The Climate Change 2022: Impacts, Adaptation and Vulnerability report [48] presents evidence of how these changes are already affecting food security through various land degradation processes. Climate change also has significant impacts on soil health indicators such as soil organic matter. Moreover, precipitation extremes can reduce soil biological functions, and increase surface flooding, waterlogging, soil erosion, and susceptibility to salinization [48].
Four countries in the WB region have EU candidate status (Albania, the Republic of North Macedonia, Montenegro, and Serbia), and one has potential candidate status (BiH) for EU accession. Further EU integration will have implications for their climate and environmental policies, laws, and action measures. All these countries are motivated to respect the main principles of the Paris Agreement and to achieve EU2020 and EU2030 goals in greenhouse gas emission reduction, increased energy efficiency, and energy production from renewable sources through the European Green Deal agenda [49]. This program places a healthy environment at the core of policy-making initiatives. Due to its nature, the soil is a central consideration when developing and implementing actions in many areas, from biodiversity to agriculture and climate. Therefore, soils and their management play a key role in future environmental, agricultural, and climate actions [47], and large-scale monitoring and modeling tools are needed to ensure the proper development, implementation, and tracking of soil-related policies in the WB [50].
The two main objectives of this study are to (1) estimate the spatial-temporal rainfall erosivity (R-factor) across the WB region by applying the RUSLE and RUSLE2 methodology with data for the period 1991–2020 and then; (2) apply cluster analysis to identify the places of greatest erosion risk, and thereby offer a means of targeting mitigation measures. To achieve these objectives, the ERA5 reanalysis of hourly precipitation data was used (given a lack of high-resolution observed precipitation data for the region). Our overall motivation was to put a spotlight on the WB, which stands out as a hotspot for climate change and hydro-meteorological hazards [3,51]. This study also provides useful information for more detailed and dynamic soil erosion assessments, as well as for the analysis of extreme erosive events on a regional scale.
2. Materials and Methods
2.1. Study Area
Balkan, by etymology, is a Turkish word for forested mountain. This reflects the fact that 70% of the region has high relief, comprised mountain chains rising from the narrow coasts of the Adriatic, Ionian, and Aegean Seas of the northern Mediterranean Basin (Figure 1). Apart from BiH (2386 m.a.s.l.), all WB countries have mountain peaks above 2500 m.a.s.l. The highest peak in the WB region is the Korab (2752 m.a.s.l.), which is situated on the national borders of Albania and North Macedonia. A topographic gradient exists between the eastern and western Balkan Peninsula. In the east, the slopes of the Balkan Mountains are very gentle, although there are some high ranges to the south. In the west, the Dinaric Alps and Pindus Mts. rise very steeply from the coastal zone, with a clear boundary between the northern Dinarides and the Pannonian Plain. The north of the study area contains most of the Pannonian Basin, with the river valleys of the Danube and its tributaries [52].
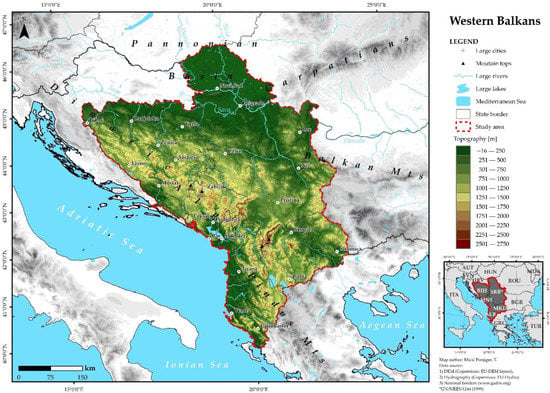
Figure 1.
The WB study area and the surrounding region.
Various climate types and regimes are observed in the WB. The Mediterranean climate with humid, mild winters and dry, warm summers are characteristic of Albania, the southern part of Montenegro, and the coastal and lowland areas of BiH [53,54,55]. The rest of BiH ranges from moderately continental to alpine conditions (in mountainous parts). The central and northern parts of Montenegro have mountain climates, except for the far north, as it has a continental climate that is under the influence of the Adriatic Sea. The climate in the Republic of North Macedonia [56] varies from sub-Mediterranean to moderately continental/sub-Mediterranean to continental and from cold-continental to an alpine sub-climate. The Republic of Serbia’s climate varies from moderately continental in the north (the Pannonian Basin) [57,58,59,60] to continental in the mountains (central Serbia) [61], and Mediterranean subtropical and continental in the southwest (Kosovo and Metohija (KiM)) [49,62].
Patterns of annual precipitation over the WB are highly variable and influenced mainly by the orography, with major variations between western and eastern coasts and between lowland and mountainous areas [52]. The peaks of the southern Dinarides have the highest mean annual precipitation values in Europe. Here, a mean annual precipitation of >4600 mm was recorded in Crkvice, Montenegro (1050 m.a.s.l.) due to the combined influence of the orientation of relief, the steepness of the topography away from the coastal zone, and the influence of humid southwesterly airflows. Precipitation decreases from Crkvice in all directions: mean annual totals are typically <1000 mm for the Adriatic coast, 600–700 mm for the Pannonian Plain, and just 350–400 mm along the Albanian coastline [52].
Seasonal precipitation variations tend to exhibit winter maxima in the central and Eastern Mediterranean and autumn and/or spring maxima in the northern Balkans, which are in the transitional zone between the Mediterranean summer-dry climate and the continental interior. Much of the ‘true’ continental interior is under the influence of dry anticyclones during winter, so spring or summer maxima are pronounced [63]. Hence, there are pronounced regional contrasts between the summer and winter seasons. The main areas of maxima summer precipitation are located in the north and northeast, on the northern slopes of the Carpathian and Balkan Mountains. This is typical of central European patterns of airflow with an intermittent polar influence. The rest of the WB region has a very dry summer season, decreasing southwards to ca. 30 mm in Shköder (Albania). The northern Adriatic Sea area, in the lee of the Alps, and the sea surfaces west of Crete, are two of the four main Mediterranean regions of cyclogenesis that generate most of the depressions during the winter and spring seasons [52].
2.2. Methodology
All the steps, procedures, and quantitative approaches used in this study are summarized in the following workflow (Figure 2). Each key element is described in turn.
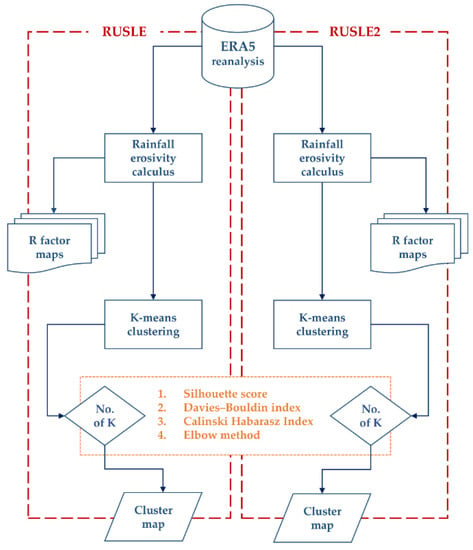
Figure 2.
Research workflow.
2.2.1. Database
Climate reanalysis data have been widely used in various fields and applications (e.g., for precipitation forecasting, trend analysis, and soil moisture monitoring), and ERA5 has been favored by many studies [23,44,64,65,66]. Here, we used the ERA5 reanalysis [67] as reference data to calculate the R-factor (see Section 2.2.2) across the WB region at a horizontal resolution of 0.25° × 0.25°. The WB study area and statistical analysis cover 390 reanalysis grid cells; however, a larger domain comprising 1081 cells was extracted to facilitate a comparison with other research (Figure A1). Note that when calculating the R-factor, only liquid precipitation was used; snowfall amounts were not included. The calculations were made on a decadal resolution (i.e., for the 1990s, the 2000s, and 2010s), as well as for the whole study period (1991–2020). This is consistent with the World Meteorological Organization (WMO) recommendation that 30-year standard reference periods should be updated every decade in order to better reflect the changing climate [37].
2.2.2. Rainfall Erosivity: R-Factor Calculation
Rainfall erosivity is determined by various characteristics of rainfall events, such as rainfall intensity and duration, the kinetic energy of raindrops, drop size (diameter), and terminal velocity [68]. The R-factor in this paper was computed using the RUSLE [69] and RUSLE2 [70] equations.
According to Wischmeier [71], rainfall erosivity is composed of rainfall energy and the maximum continuous 30-min intensity during the individual storm. All events with cumulative values >12.7 mm were considered erosive events and were divided into two parts when their cumulative depth for a duration of 6 h at a certain location was <1.27 mm (e.g., Refs. [72,73,74]). The authors of this study opted to use the well-established threshold of 12.7 mm, which is defined as a precipitation event that has erosive power [15]. The rainfall kinetic energy for each rainfall event (e) was calculated from an empirical equation in the form introduced by Kinnell [75]:
where a and b are empirical coefficients, i stands for rainfall intensity [mm h−1], and emax is the maximum unit energy as intensity approaches infinity. For the RUSLE model, Renard et al. [69] adopted an empirical equation (Equation (2)) from Brown and Foster [72]:
e = emax [1 − a exp(−b·i)],
e = 0.29·[1 − 0.72 exp(−0.05·i)] [MJ·mm−1·ha−1],
The value of emax was taken as 0.29 based on the work of Rosewell [76]. The value of coefficient a was taken to be 0.72 based on work by McGregor and Mutchler [77], and the value of coefficient b was taken to be 0.05. A new b coefficient was adopted in the development of RUSLE2, following the work of McGregor [78]:
e = 0.29·[1 − 0.72 exp(−0.082·i)] [MJ·mm−1·ha−1],
The change in the b coefficient regarding RUSLE2 methodology was also accepted as a better choice by the developers of RUSLE methodology, Brown and Foster, as the previous one (Equation (2)) was not designed and tested to be used directly in a soil loss equation [79]. However, as many scientists have continued to use RUSLE methodology (e.g., Refs. [80,81]), it was taken into account together with RUSLE2. In the next step, the energy of the storm (E) was estimated by multiplying the kinetic energy per event (e) with rainfall intensity (i) in the time interval (Δt) using Equation (4):
E = e*i*Δt [MJ·ha−1],
The rainfall erosivity factor (Rk) per erosive rainfall event was calculated by multiplying E with the corresponding I60 value [mm·h−1]. The R-factor was set equal to the average of the summation of the erosivity values for every year of rainfall and defined by the product of an erosive rainfall event’s kinetic energy and the maximum intensity of a 30-min duration rainfall during the rainfall event, known as EI30 [79]. In this study, EI60 was used instead of EI30 due to the inaccessibility of sub-hourly data at the regional scale (Equation (5)):
Rk = EI = E × I60 [MJ·mm·ha−1·h−1],
Here, a well-known and proven limitation of I60 should be emphasized: it underestimates the values of the R-factor for 10–25% in comparison to the I30 parameter (e.g., Refs. [74,82]). Annual rainfall erosivity (R) was determined using Equation (6), where n is the number of years for the given dataset (here, 30 years for EI60), and m is the number of erosive events during year j.
2.2.3. k-Means Clustering
A k-means clustering algorithm was used to reveal spatial patterns of rainfall erosivity [18,20]. It is a centroid-based clustering technique, whereby clusters are represented by a central vector. The number of clusters is fixed to K and the algorithm finds the K cluster centers and assigns objects (O) to the nearest cluster center, so that the squared distances from the cluster are minimized [83] In computer science and pattern recognition communities, the k-means algorithm is often termed Lloyd’s Algorithm I [84]. Here, the augmented k-means++ was applied, as the augmentation O(log k) provided by Arthur and Vassilvitskii [85] improved both the speed and the accuracy of the k-means algorithm. To avoid the algorithm becoming trapped in a local minimum, the following metrics were applied: the Calinski–Harabasz index (CHI) [86]; the Davies–Bouldin index (DBI) [87]; the silhouette score [88]; and the elbow method [89]. Cluster computation and metric evaluations were obtained via the Scikit-Learn module [90] in python. Visualization was also performed in python using the Matplotlib [91], Seaborn [92], and Cartopy [93] modules. The study area map was created via ArcGIS®.
3. Results and Discussion
3.1. Precipitation Variation
South-East Europe is a complex region climatically, with marked variations in its precipitation regime [94]. Patterns of annual precipitation over the WB are highly variable and influenced largely by the orography, with major differences between the western and eastern coasts or between the lowlands and mountainous areas [52]. The SW-NE precipitation gradient across the study area ranges from a maximum of 0.25 mm h−1 to a minimum of 0.05 mm h−1 (Figure 3a), as the WB region is exposed to the inflow of moist air masses coming from the Adriatic Sea and topographically-induced precipitation by the Dinaric Alps which also present a barrier to moist air reaching the NE area of WB [95]. The number of erosive rainfall events (the number of storms) and spatial distribution are in good accordance with the mean precipitation distribution (Figure 3b).
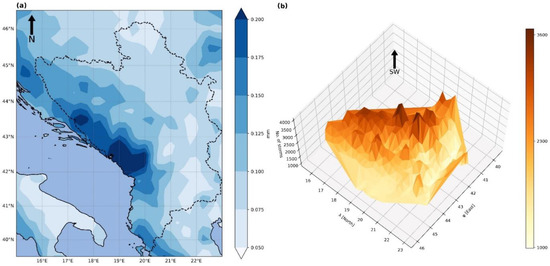
Figure 3.
(a) Distribution of hourly mean precipitation across the study area (b) 3D model of the cumulative number of erosive rainfall events for the total study period 1991–2020.
In terms of seasonal precipitation variations, the central and Eastern Mediterranean tends to exhibit winter maxima, whereas the northern Balkans have an autumn and/or spring maximum due to their location in the transitional zone between the Mediterranean summer-dry climate and continental interior [63]. This is evident from the “U” shape (Figure 4) of the intra-annual variation in monthly precipitation with the winter maxima for Livno, Mostar, Crkvice, Podgorica, Bar, Shköder, Tirana, Bitola, Vlorë, and Gjirokastër and autumn/spring maxima for Bihać, Žabljak, Skopje, and Strumica. On the other hand, much of the ‘true’ continental interior is under the influence of anticyclones during winter, so spring or summer maxima are pronounced in Novi Sad, Belgrade, Banjaluka, Zenica, Sarajevo, Užice, Priština, and Niš (Figure 4). Therefore, regional contrasts between the summer and winter seasons are strongly defined. The main areas of maximum summer precipitation are located in the north and northeast, on the northern slopes of the Carpathian and Balkan Mountains (Bor), reflecting central European patterns of airflow with an intermittent polar influence (Tuzla). The northern Adriatic sea area, in the lee of the Alps, and the sea surfaces west of Crete are two of the four main Mediterranean regions of cyclogenesis, which generates internally most of the depressions during winter and spring seasons, where further storms shift toward the mountains of Central Europe [52].
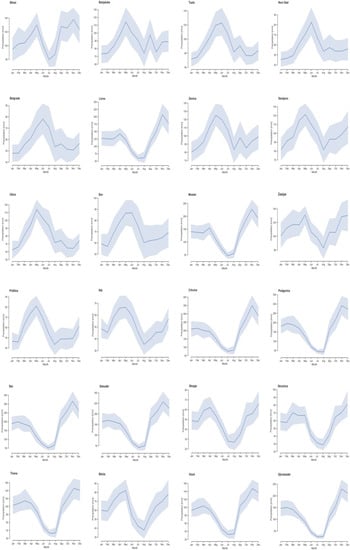
Figure 4.
Intra-annual variations in monthly precipitation [mm] for the period 1991–2020 were obtained from the nearest ERA5 grid cell to the city (for more details see Figure A1). The shaded area represents the 95% confidence interval.
To better understand precipitation variations across the WB region, precipitation anomalies are shown in Figure 5. Two contrasting years emerge from the annual totals for the region as a whole (Figure 5a), which are then shown as maps of rainfall in (Figure 5b–d). The first anomaly minimum was recorded for the year 2000 and is already annotated as one with severe droughts in the WB region [96,97]. Patterns of mean hourly anomalies show negative values across the WB region, with >−0.04 mm h−1 in the central and eastern BiH, western Serbia, and southern parts of North Macedonia (Figure 5c). Even more pronounced negative anomalies were evident in 2011, ranging from −0.03 mm h−1 in northern and central Serbia, KiM, and southern parts of North Macedonia to −0.08 mm h−1 /h in the Adriatic coast (Montenegro, NW Albania) [16,18]. Conversely, maximum anomalies were recorded between the years 2010 and 2014, which is consistent with widespread reports of wetter conditions and floods [36,42,98,99] (Figure 5c,e). During May 2014, the WB region was under the influence of the Tamara cyclone [100]. This slowly moving depression tracked from the Adriatic Sea to the Balkan Peninsula caused extreme precipitation totals (250–400 mm during 72 h) [101]. In Figure 5e, it can be seen that the highest anomalies (>+0.08 mm h−1) can be observed in the areas where the cyclone had the most severe impact (the central part of the WB region, eastern BiH, and western, central, and eastern Serbia).
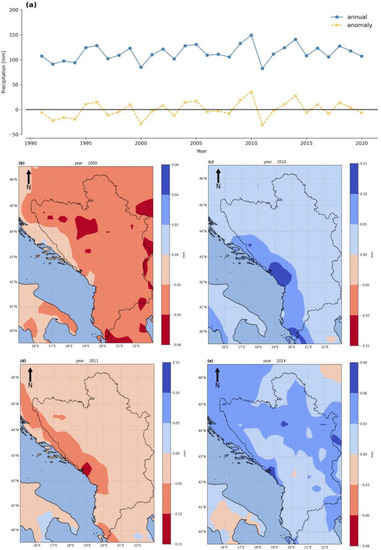
Figure 5.
Anomaly variation based on average total annual distribution of hourly precipitation for the total study area (a) and years with maximum (2010, 2014) and minimum (2000, 2011) anomalies pronounced (b–e).
3.2. R-Factor Variability
Nearing et al. [79] assert that “it is of great importance to understand, when considering the calculations of rainfall erosivity, that even though the researcher intends to represent rainfall energy the entire calculation of energy, is based on rainfall intensity”. However, by comparing RUSLE and RUSLE2 methodologies—which both use a threshold of 12.7 mm for a storm event [72]—our focus is on the rainfall kinetic energy parameter b. By recalibrating b from 0.05 to 0.082, the RUSLE2 methodology gives R-factor values that are 58% higher than the RUSLE method (when both use the ERA5 reanalysis dataset for WB) (Figure 6). Since the R-factor erosivity classes have different scales (due to the different b parameter), the authors preserved their unique scales (for both eight classes of the R-factor distributions), as a strong spatial correlation between the results could be observed.
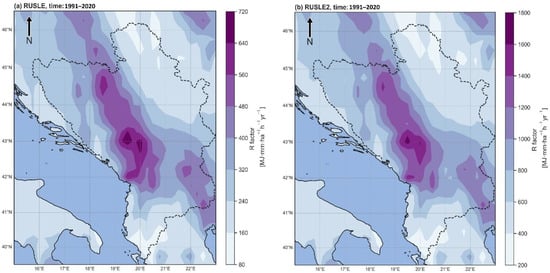
Figure 6.
R-factor obtained for a total 30-year period by (a) RUSLE and (b) RUSLE2 methodology.
Across the WB, the mean value of the R-factor calculated by the RUSLE methodology for the period 1991–2020 (Figure 6a) is 330 MJ mm ha−1 h−1 yr−1 with a standard deviation of 130 MJ mm ha−1 h−1 yr−1. The median (50th percentile) is 300 MJ mm ha−1 h−1 yr−1, whilst 25% of the erosivity values (25th percentile) are lower than 220 MJ mm ha−1 h−1 yr−1 and the highest 25% (75th percentile) are above 400 MJ mm ha−1 h−1 yr−1. According to the erosivity map, the highest values occur in eastern BiH, western Serbia, over Montenegro, N Albania, and SE North Macedonia. The lowest erosivity values mainly occur in NE Serbia and the far south of Albania.
RUSLE model calculations are consistent with the results from local studies, e.g., the territory of the Bačka region [35] in NW Serbia, which ranges from 180 MJ mm ha−1 h−1 yr−1 to 270 MJ mm ha−1 h−1 yr−1. However, the study of Panagos et al. [102] produced a map of long-term erosivity patterns where the R-factor values vary between 400 MJ mm ha−1 h−1 yr−1 and 3100 MJ mm ha−1 h−1 yr−1. Unfortunately, the results of this study cannot be compared with our findings due to the interpolation of the observed rainfall data. As the authors used the “Rainfall Erosivity database at European Scale (REDES), which includes 1675 rainfall stations in the European Union and Switzerland”, there are no data regarding the WB region countries, and all values regarding this region are obtained by the spatial interpolation of the R-factor point values [102].
As it is noted by Bezak [19,20], R-factors based on the REDES database depends on the interpolation procedure and so should be interpreted with care. As the results for the study covered area have been scarce so far, this paper provided the foundation for R-factor distribution analysis over the WB by using the RUSLE methodology.
Despite using the same input data, higher erosion rates are evident in Figure 6b for the RUSLE2 methodology. The mean R-factor for the WB is 790 MJ mm ha−1 h−1 yr−1 with high variability as expressed by the standard deviation of 310 MJ mm ha−1 h−1 yr−1. The median (50th percentile) is 730 MJ mm ha−1 h−1 yr−1, whilst 25% of the erosivity values are below 530 MJ mm ha−1 h−1 yr−1 or above 990 MJ mm ha−1 h−1 yr−1.
Our RUSLE2 results can be compared with Bezak et al. [66], as both use the ERA5 reanalysis dataset with a horizontal resolution of 0.25° × 0.25° and a similar study period (1998–2019) but with monthly precipitation resolution to compute the rainfall erosivity for erosivity density estimations. This research [66] shows significant spatial patterns and ranges as the lowest values were 200 MJ mm ha−1 h−1 yr−1 to 400 MJ mm ha−1 h−1 yr−1, and the largest span was 1700 MJ mm ha−1 h−1 yr−1 to 3100 MJ mm ha−1 h−1 yr−1, following the calculated maximum for the WB region from this study (1793.7 MJ mm ha−1 h−1 yr−1).
The use of a time series covering several decades enables the evaluation of long-term rainfall erosivity variability, which is of interest in the context of climate change [103]. The first insight from the decadal analysis (the 1990s, the 2000s, and the 2010s) of the R-factor is the stationarity of the patterns, with minor spatial variations over time (Figure 7).
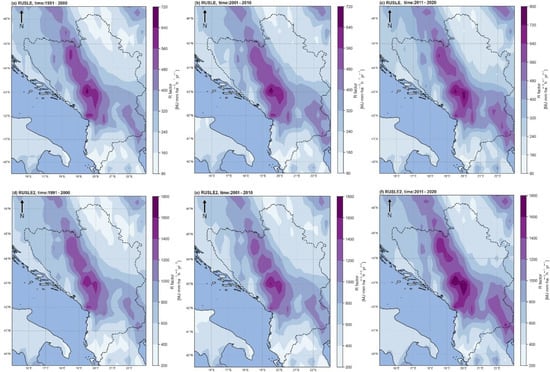
Figure 7.
R-factor calculated using the RUSLE (a–c) and RUSLE2 (d–f) methodologies.
The RUSLE methodology shows that the mean R-factor is unchanged between the 1990s and the 2000s (respectively 310 MJ mm ha−1 h−1 yr−1 to 320 MJ mm ha−1 h−1 yr−1) but increases in the 2010s to 360 mm ha−1 h−1 yr−1. The same trend is seen in the median (50th percentile): from around 290 MJ mm ha−1 h−1 yr−1 in the 1990s and the 2000s to 330 MJ mm ha−1 h−1 yr−1 in the 2010 s. Maximum values >680 MJ mm ha−1 h−1 yr−1 occur in the 1990s and the 2000s (Figure 7a,b), but >750 MJ mm ha−1 h−1 yr−1 in the 2010s (Figure 7c) covers the whole of Montenegro, eastern BiH, western Serbia, N Albania, and SE of North Macedonia. The lowest erosivity values (90–125 MJ mm ha−1 h−1 yr−1) mainly occurred in NE Serbia and far south of Albania. This rise in the R-factor over the last decade is consistent with positive anomalies in the mean total annual 60 min precipitation, as well as with the results reported by Lukić et al. [36] and Micić Ponjiger et al. [42] for change in the rainfall erosivity factor over the Pannonian Basin. The rise is also detected in neighboring Greece; on the south of the Balkan Peninsula (the 1990s R-factor was 249.5 mm ha−1 h−1 yr−1, the 2000s R-factor was 297 mm ha−1 h−1 yr−1, the 2010s R-factor was 516.28 mm ha−1 h−1 yr−1) and this is in good agreement with a study from the broader area that used ground (rain gauge) data [104].
The results from the RUSLE2 methodology show that the R-factor mean increased slightly from 740 MJ mm ha−1 h−1 yr−1 in the 1990s to 755 MJ mm ha−1 h−1 yr−1 in the 2000s and 865 MJ mm ha−1 h−1 yr−1 in the 2010 s. The same trend is evident in the median through the decades: 690 MJ mm ha−1 h−1 yr−1 in the 1990s, 700 MJ mm ha−1 h−1 yr−1 in the 2000s, and 790 MJ mm ha−1 h−1 yr−1 in the 2010s. Maximum values of >1600 MJ mm ha−1 h−1 yr−1 occur in the 1990s and the 2000s (Figure 7d,e) then >1700 MJ mm ha−1 h−1 yr−1 in the 2010s (Figure 7f).
Due to the very limited number of research regarding the WB study area, the obtained results can also be compared with the work of Rousseva and Stefanova and Rousseva and Marinov [105,106] on the borderline with Serbia and N. Macedonia, as they used the USLE methodology for neighboring Bulgaria. The results for the USLE methodology are similar to the RUSLE2 methodology [79] and so can only be compared with RUSLE2. The values differ from 600 to 800 MJ mm ha−1 h−1 yr−1 in the north of Bulgaria (east Serbia borderline) to 400–600 MJ mm mm ha−1 h−1 yr−1 in (N. Macedonia). On the other hand, the work of the above-mentioned authors [105,106] differs from this study due to the precipitation data resolution (30 min, I30) and data source (ground, gauge data). Hence, it can be noticed that R-factor values are somewhat more appropriate when derived by the RUSLE2 approach.
As noted by Nearing et al. [79], the RUSLE yields reasonable results in terms of quantifying relative spatial or temporal differences in erosivity but significantly underestimates erosivity when compared to RUSLE2. The results obtained in this study (for the whole study period as well as on the decade level) support this view.
3.3. Clustering
The k-means algorithm was applied to both the RUSLE and RUSLE2 outputs to generate maps of homogeneous areas for the R-factor values. This is the most widely used algorithm across the study domains, according to Ezugwu et al. [107]. For the optimization of the number of clusters (K), four metrics were used: CHI, DBI, the silhouette score, and the elbow method. For the computation of the k-means cluster, only R-factor values for the full study period (1991–2020) were used.
According to the CHI, DBI, silhouette score, and elbow methods, the optimal number of K were four and five (Figure A2)—so maps were produced for each K-value (Figure 8a,b). When using four cluster centers, it is evident that all maximum R-factor values (>600 mm ha−1 h−1 yr−1) fall into cluster 4, whereas the maximum R-factors for cluster 5 have a less homogeneous distribution. The 75th percentile values were mainly captured in cluster 2, with a small overlapping with cluster 3 when K = 4 and again the mixture of clusters is presented regarding clustering with K = 5.
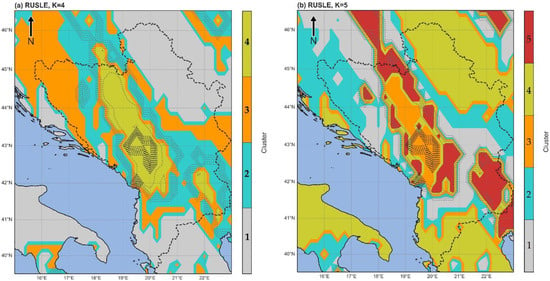
Figure 8.
k-means clustering of R-factors calculated by the RUSLE methodology when (a) K = 4 and (b) K = 5. Light grey dotted lines present R-factor values >400 mm ha−1 h−1 yr−1, and dark grey dotted lines are R-factor values >600 mm ha−1 h−1 yr−1.
A more detailed examination of the R-factor distribution captured by the clustering can be observed in the box and whisker graphs (Figure 9). The ranges between the R-factor values are clean-cut by the algorithm, without any overlapping in whiskers. Observing the clusters with the highest R-factor, it can be seen that the median for K = 4 (cluster no. 4) is lower than in the case of K = 5 (cluster no. 3). Therefore, K = 5 provides better a delimitation of the zones with the max values. On the other hand, for min values (K = 4 cluster no. 1 and K = 5 cluster no. 4), the R-factor distributions are almost the same.
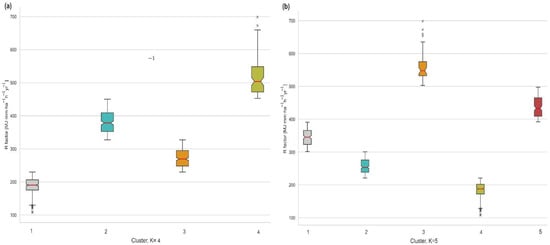
Figure 9.
The difference in the R-factor distribution (RUSLE methodology) between the clusters for the total 30-year period if (a) K = 4 and (b) K = 5.
When calibrating the ideal number of clusters (K) regarding the R-factor from the RUSLE2 methodology, the observed metrics showed very similar results as for the RUSLE distributions (Figure A3). Once again, 4 and 5 were the best candidates for the ideal number of K’s. In Figure 10, the spatial presentation of both clustering and scenarios is presented. The spatial distribution with 4 clusters shows the total overlapping with areas of R-factor values >1200 mm ha−1 h−1 yr−1 (cluster no. 4), as well as the spatial distribution with 5 clusters (cluster no. 4). Once again, complementing the maps with additional box and whisker plots (Figure 11), the advantage when K = 5 is a better separation for extremely high values of the R-factor (>1200 mm ha−1 h−1 yr−1). The lowest values (25th percentile of distribution) are in both scenarios included in cluster no. 1, as it is for the RUSLE methodology distribution. These similarities in clustering results regarding the RUSLE and RUSLE2 methodology are expected, bearing in mind that only values are changed (increased for RUSLE2 due to the change in the b parameter in Equations (2) and (3)), but the spatial distribution has not been disturbed.
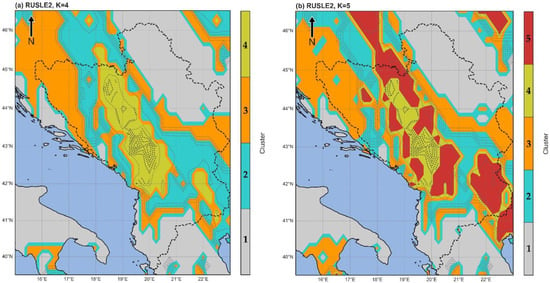
Figure 10.
As in Figure 9, except for the RUSLE2 methodology with light grey, dotted lines represent R-factor values >800 mm ha−1 h−1 yr−1, and dark grey dotted lines are R-factor values >1200 mm ha−1 h−1 yr−1.
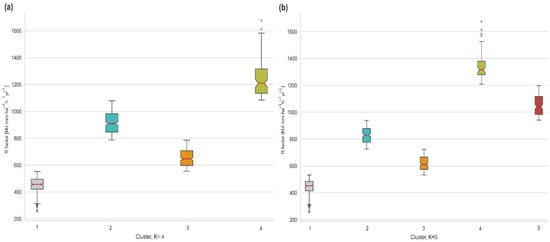
Figure 11.
The difference in the R-factor distribution (RUSLE2 methodology) between the clusters for the total 30-year period if (a) K = 4 and (b) K = 5.
3.4. Policy, Practical Implications and Study Limitations
Detailed information on erosion by water processes, acquired through both modeling and measurements, is lacking in large parts of the world. Through this research, we have begun to address a knowledge gap for the WB region, which was hitherto literally a blank on the map of European soil erosion. Since the results obtained for the R-factor show an increase in values during the last decades, it is necessary to draw more attention to studies regarding this type of hydro-meteorological hazard.
To protect areas that are potentially endangered by rainfall erosion, it is necessary to assess the intensity of these processes and then evaluate the negative impact they pose to social structures. This information makes it possible to formulate the appropriate model for preventive and remedial measures, which is of paramount importance for vulnerable areas affected by erosion due to water processes, as the R-factor is one driver for the soil erosion process. These measures are primarily determined through the prism of physical and socioeconomic frameworks and form the basis for the further development of technical-engineering measures [83].
The main policy instrument dedicated to soil protection in the EU is the Soil Thematic Strategy, where soil erosion is classified as one of the eight threats. Soil erosion indicators have been included in monitoring the performance of the Common Agricultural Policy (CAP) since 2009 when EU Member States had the compulsory requirement to keep their land in good agricultural and environmental conditions [108]. In 2013 the CAP 2014–2020 reform proposed the sustainable management of natural resources as one of its main objectives. Under CAP 2023–2027, EU members continue developing an efficient stratified monitoring network and informing targeted mitigation strategies [109]. As an example, during the discussion in the European Parliament regarding the post2020 CAP reform, one of the early proposed indicators stated that the Member States of the EU would reduce the percentage of agricultural land under severe erosion (>11 t ha−1 yr−1) [108]. As stated in the introduction of this study, all states from the WB region are EU candidates (except BiH as a potential candidate). Therefore, the transposition and implementation of this policy in the states of the WB region are particularly important.
But, before adopting a policy on the level of the EU, the WB region states must also adapt their state frameworks regarding soil erosion assessment and mitigation measures.
The conceptual Soil Erosion Assessment and Mitigation Measures Framework (SEAMMF) offered by this study (Figure 12) comprises a series of steps that must be taken to ensure early detection, as well as the sustainable preventive actions needed in potentially vulnerable areas in the WB region.
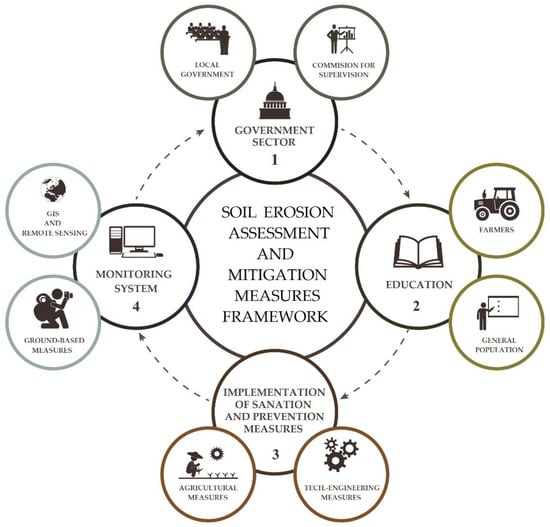
Figure 12.
Soil erosion assessment and mitigation measures framework (SEAMMF).
The first step in the SEAMMF formulated as the government sector (Figure 12, step 1) defines the initial outlines of every system responsible for managing any kind of activity performed at the national level. In addition to the main state institutions, local government institutions are also included in the system for the management of hydro-meteorological hazards. Once logistics support is established in the organizational units, it is necessary to define the committees that will monitor the process, collect and analyze the data, and finally transfer information to different levels of governmental institutions. The role of public institutions and non-governmental organizations is equally important for the adapting, administering, and monitoring of agricultural policy directives at the national, regional, and local levels [110]. Risk communication is thus an important tool since it represents an exchange of knowledge and information between risk managers, decision-makers, public authorities, and the general public [111]. Besides the established organizational units, economic status plays a key role in the successful prevention and remediation of erosion by water processes in potentially endangered areas. Higher economic income has a dual impact on vulnerability: the potential losses are higher (especially material), but overcoming the crisis and disaster recovery is faster [112].
As observed by Borrelli et al. [63], unsustainable soil erosion rates occur not only because of a lack of sound policies but also due to a lack of knowledge. Education is directly related to the socioeconomic status of the region. Better education ensures quality living conditions, which has an impact on the reduction in vulnerability during natural hazard events (Figure 12, step 2). A less educated population narrows the opportunities for learning about hydro-meteorological hazards and their impact, as well as access to the information relevant to a faster recovery. This causes an increase in vulnerability to given natural hazards [113,114]. The greatest attention regarding the education of the population should be focused on agricultural land users/farmers. This will directly reduce the human impact on erosion processes if appropriate erosion control works are used during agricultural activities.
After a thorough study of the nature and intensity of erosion by water processes, it is possible to determine the best solutions for the protection and re-cultivation of degraded areas or to implement preventive measures in potentially endangered areas (Figure 12, step 3). Depending on the intensity of the R-factor, the physical properties of the endangered area, and the possibilities to implement a variety of erosion control works can be divided into two major groups: agricultural (e.g., Ref. [115]) and technical engineering (e.g., Refs. [116,117]).
The systematic monitoring of soil loss induced by erosion and water processes in larger areas (such as the WB region) is often very challenging. Study findings indicate that RUSLE-type models have been extensively used as the most employed erosion-by-water modeling tool during the past decades [79,118]. Therefore, parameters such as the R-factor are key features for the estimation of soil-erosion rates in the WB region.
Various parameters derived from different data sources, such as DEM (digital elevation model), soil properties, and climate characteristics (ground stations and remotely-sensed data repositories), may have different data formats, projections, data quality, and spatial resolutions (Figure 12, step 4). A greater density of precipitation values within the gridded datasets of higher spatial resolution (ERA5 reanalysis, 0.25 deg.) and an R-factor model based on RUSLE and RUSLE2 guidelines tend to ensure a quality regional model framework. By applying cluster analysis, a more dynamic erosion by water rates assessment and the identification of places of high erosion risks (on a regional scale) can be derived. Due to the addressed data scarcity related to the WB region, methodological approaches in this research could help to fill in the gaps in the contemporary rainfall erosivity map of Europe [15,18,42]. Despite the shortcomings and underestimation of the R-factor, by using the satellite-based precipitation products during ERA5 reanalysis (as previously addressed by respective studies [44,66]) in regions with limited observation precipitation data—such as the WB region—these results can be useful for periods and/or locations as transitory where rainfall erosion measurements and high-resolution ground-monitoring data are not publicly available at the moment. By applying the ERA5 reanalysis dataset with hourly data resolution, future research activities should encompass the cross-validation of the results of this study against other existing data sets, respectively (e.g., REDES, CMORPH, and GloREDa databases).
4. Conclusions
This study is the first to derive R-factors for the WB region using both the RUSLE and RUSLE2 methodology and then to identify the coherent areas of high erosivity via cluster analysis. As rainfall erosivity estimation requires long-term precipitation data at the highest possible temporal frequency (ideally ≤1 h), the ERA5 reanalysis was used for a standard climate period (1991–2020). Hourly precipitation intensity and monthly precipitation totals (summed from hourly data) exhibit a marked variability over the region. High total precipitation values are observed in the SW with >0.3 mm h−1 average totals, while the least total precipitation is seen in the Pannonian Basin and far south (Albanian coast), where the mean intensity is less than 0.1 mm/h.
R-factor variability is very high for both the RUSLE and RUSLE2 methods. The mean R-factor calculated by RUSLE2 is 787 MJ mm ha−1 h−1 yr−1 which is 58% higher than the mean R-factor obtained from RUSLE (328 MJ mm ha−1 h−1 yr−1). The analysis of the R-factor at decadal timescales suggests a rise of 14% in the 2010s. The results obtained with the RUSLE methodology were comparable with small-scale studies conducted for some parts of the WB region as this methodology is more accepted by European researchers, and the results are in a vast majority compatible with this study. On the other hand, it has already been well addressed in public that RUSLE provides reasonable results in terms of quantifying relative spatial or temporal differences in erosivity but significantly underestimates the erosivity compared with the RUSLE2. Therefore, it is a recommendation to use the RUSLE2 method, but with critical caution concerning the results due to the data source resolution of 1 h, which also tends to underestimate the R-factor value (in comparison with 30 min data resolution). Regarding clusterization, for both the RUSLE and RUSLE2 methodology, a 5 cluster (K = 5) division should be used, as it shows the best spatial and statistical distribution with the highest metrics obtained in relation to the R-factor.
The rainfall erosivity maps presented in this research may be regarded as useful tools for soil erosion evaluation and control, especially for agriculture and land use planning. Also, as the R-factor is an important part of erosion models, such as RUSLE and RUSLE2, it can be used as a guide for soil conservation practices and landscape modeling.
Author Contributions
Conceptualization, T.M.P., T.L. and R.L.W.; methodology, T.M.P., T.L. and R.L.W.; software, A.V., I.P., U.D. and M.M.M.; validation, S.D., D.M. and N.M.; formal analysis, T.M.P., T.L. and R.L.W.; investigation, S.B.M., S.D. and M.B.G.; resources, B.B.; data curation, M.M.M., V.G. and C.M.; writing—original draft preparation, T.M.P. and T.L.; writing—review and editing, T.L., R.L.W. and M.B.G.; visualization, T.M.P.; supervision, T.L.; project administration, T.L., V.G. and C.M.; funding acquisition, B.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the H2020 WIDESPREAD-05-2020—Twinning: EXtremeClimTwin project, which has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 952384.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The ERA5 reanalysis dataset was downloaded through Copernicus CDS [67].
Acknowledgments
This research was supported by the H2020 WIDESPREAD-05-2020—Twinning: EXtremeClimTwin which has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 952384. The authors from the Department of Geography, Tourism and Hotel Management, Faculty of Sciences, University of Novi Sad are grateful to The Ministry of Education, Science and Technological Development of the Republic of Serbia (Grant No. 451-03-68/2022-14/200125) for their support. The authors from the Faculty of Geography, University of Belgrade are grateful to The Ministry of Education, Science and Technological Development of the Republic of Serbia (Grant No. 451-03-68/2022-14/200091) for their support. Tin Lukić and Biljana Basarin acknowledge partial support of the H2020-LC-GD-2020-3 GreenScent – Smart Citizen Education for a Green Future (grant agreement No 101036480) that have received funding from the European Union’s Horizon 2020 research and innovation programme. We confirm that all the authors made an equal contribution to the study’s development. The authors are grateful to the anonymous reviewers whose comments and suggestions greatly improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
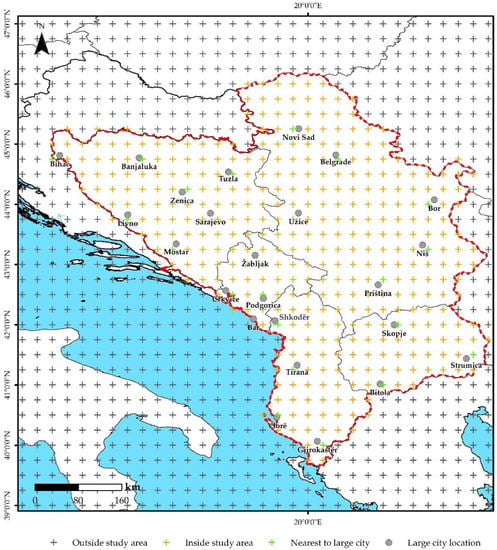
Figure A1.
Position of gridded data outside (grey colour) and inside study area (orange colour), and position of the grid nearest to the large city (lawn green colour).
Appendix B
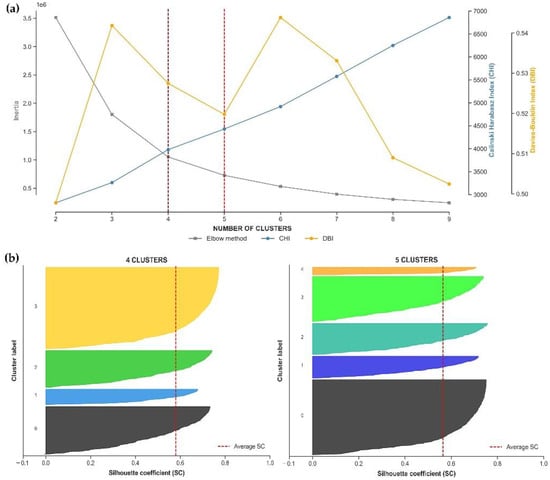
Figure A2.
Cluster metrics for R-factor calculated by the RUSLE methodology including (a) CHI, DBI, the elbow method and (b) the silhouette score coefficient.

Figure A3.
Cluster metrics for R-factor calculated by the RUSLE2 methodology including (a) CHI, DBI, the elbow method and (b) the silhouette score coefficient.
References
- Daskalov, R.D.; Mishkova, D.; Marinov, T.; Vezenkov, A. Entangled Histories of the Balkans—Volume Four; BRILL: Leiden, The Netherlands, 2017; ISBN 9789004337824. [Google Scholar]
- Vuković, A.; Mandić, M.V. Study on Climate Change in the Western Balkans Region; Regional Cooperation Council Secretariat: Sarajevo, Bosnia and Herzegovina, 2018. [Google Scholar]
- Füssel, H.-M.; Jol, A.; Marx, A.; Hildén, M. (Eds.) Climate Change, Impacts and Vulnerability in Europe 2016: An Indicator-Based Report; European Environment Agency: Copenhagen, Denmark, 2017; ISBN 1977-8449. [Google Scholar]
- Blinkov, I. Review and Comparison of Water Erosion Intensity in the Western Balkan and Eu Countries. Contrib. Sect. Nat. Math. Biotech. Sci. 2017, 36, 27–42. [Google Scholar] [CrossRef][Green Version]
- Verheijen, F.G.A.; Jones, R.J.A.; Rickson, R.J.; Smith, C.J. Tolerable versus actual soil erosion rates in Europe. Earth-Sci. Rev. 2009, 94, 23–38. [Google Scholar] [CrossRef]
- Gavrilović, S. Inženjering o Bujičnim Tokovima i Erozij (on Serbian); Izgradnja: Beograd, Serbian, 1972; pp. 1–292. [Google Scholar]
- Milanesi, L.; Pilotti, M.; Clerici, A.; Gavrilovic, Z. Application of an improved version of the erosion potential method in alpine areas. Ital. J. Eng. Geol. Environ. 2015, 1, 17–30. [Google Scholar]
- Kostadinov, S.; Zlatic, M.; Nada, D.; Gavrilovic, Z. Serbia and Montenegro. In Soil Erosion in Europe; Boardman, J., Poesen, J., Eds.; Wiley: Chichester, UK, 2006; pp. 271–277. [Google Scholar]
- Efthimiou, N.; Lykoudi, E.; Panagoulia, D.; Karavitis, C. Assessment of soil susceptibility to erosion using the EPM and RUSLE Models: The case of Venetikos River Catchment. Glob. NEST J. 2016, 18, 164–179. [Google Scholar]
- Globevnik, L.; Holjevic, D.; Petkovsek, G.; Rubinic, J. Applicability of the Gavrilovic method in erosion calculation using spatial data manipulation techniques. Int. Assoc. Hydrol. Sci. 2003, 297, 224–233. [Google Scholar]
- Dragičević, N.; Karleuša, B.; Ožanić, N. Erosion Potential Method (Gavrilović method) sensitivity analysis. Soil Water Res. 2017, 12, 51–59. [Google Scholar] [CrossRef]
- Boardman, J.; Poesen, J. Grazhdani Albania. In Soil Erosion in Europe; Boardman, J., Poesen, J., Eds.; Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Tošić, R.; Dragićevic, S.; Kostadinov, S.; Dragović, N. Assessment of soil erosion potential by the USLE method: Case study, Republic of Srpska—BiH. Fresenius Environ. Bull. 2011, 20, 1910–1917. [Google Scholar]
- Tošić, R.; Dragićević, S.; Lovrić, N. Assessment of soil erosion and sediment yield changes using erosion potential model—Case study: Republic of Srpska (BiH). Carpathian J. Earth Environ. Sci. 2012, 7, 147–154. [Google Scholar]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef]
- Panagos, P.; Meusburger, K.; Ballabio, C.; Borrelli, P.; Beguería, S.; Klik, A.; Rymszewicz, A.; Michaelides, S.; Olsen, P.; Tadić, M.P.; et al. Reply to the comment on “Rainfall erosivity in Europe” by Auerswald et al. Sci. Total Environ. 2015, 532, 853–857. [Google Scholar] [CrossRef] [PubMed]
- Panagos, P.; Borrelli, P.; Spinoni, J.; Ballabio, C.; Meusburger, K.; Beguería, S.; Klik, A.; Michaelides, S.; Petan, S.; Hrabalíková, M.; et al. Monthly Rainfall Erosivity: Conversion Factors for Different Time Resolutions and Regional Assessments. Water 2016, 8, 119. [Google Scholar] [CrossRef]
- Ballabio, C.; Borrelli, P.; Spinoni, J.; Meusburger, K.; Michaelides, S.; Beguería, S.; Klik, A.; Petan, S.; Janeček, M.; Olsen, P.; et al. Mapping monthly rainfall erosivity in Europe. Sci. Total Environ. 2017, 579, 1298–1315. [Google Scholar] [CrossRef] [PubMed]
- Bezak, N.; Ballabio, C.; Mikoš, M.; Petan, S.; Borrelli, P.; Panagos, P. Reconstruction of past rainfall erosivity and trend detection based on the REDES database and reanalysis rainfall. J. Hydrol. 2020, 590, 125372. [Google Scholar] [CrossRef]
- Bezak, N.; Borrelli, P.; Panagos, P. A first assessment of rainfall erosivity synchrony scale at pan-European scale. Catena 2021, 198, 105060. [Google Scholar] [CrossRef]
- Diodato, N.; Borrelli, P.; Panagos, P.; Bellocchi, G. Global assessment of storm disaster-prone areas. PLoS ONE 2022, 17, e0272161. [Google Scholar] [CrossRef]
- Borrelli, P.; Alewell, C.; Alvarez, P.; Anache, J.A.A.; Baartman, J.; Ballabio, C.; Bezak, N.; Biddoccu, M.; Cerdà, A.; Chalise, D.; et al. Soil erosion modelling: A global review and statistical analysis. Sci. Total Environ. 2021, 780, 146494. [Google Scholar] [CrossRef]
- Padulano, R.; Rianna, G.; Santini, M. Datasets and approaches for the estimation of rainfall erosivity over Italy: A comprehensive comparison study and a new method. J. Hydrol. Reg. Stud. 2021, 34, 100788. [Google Scholar] [CrossRef]
- Tošić, R.; Kapović Solomun, M.; Lovrić, N.; Dragicević, S. Assessment of soil erosion potential using RUSLE and GIS: A case study of Bosnia and Herzegovina. Fresenius Environ. Bull. 2013, 22, 3415–3423. [Google Scholar]
- Milanović, M.M.; Perović, V.S.; Tomić, M.D.; Lukić, T.; Nenadović, S.S.; Radovanović, M.M.; Ninković, M.M.; Samardžić, I.; Miljković, Đ. Analysis of the state of vegetation in the municipality of Jagodina (Serbia) through remote sensing and suggestions for protection. Geogr. Pannonica 2016, 20, 70–78. [Google Scholar] [CrossRef]
- Perović, V.; Životić, L.; Kadović, R.; Đorđević, A.; Jaramaz, D.; Mrvic, V.; Todorović, M. Spatial modelling of soil erosion potential in a mountainous watershed of South-eastern Serbia. Environ. Earth Sci. 2013, 68, 115–128. [Google Scholar] [CrossRef]
- Perović, V.; Jakšić, D.; Jaramaz, D.; Koković, N.; Čakmak, D.; Mitrović, M.; Pavlović, P. Spatio-temporal analysis of land use/land cover change and its effects on soil erosion (Case study in the Oplenac wine-producing area, Serbia). Environ. Monit. Assess. 2018, 190, 675. [Google Scholar] [CrossRef] [PubMed]
- Perović, V.; Čakmak, D.; Mitrović, M.; Pavlović, P. The Potential Impact of Climate Change and Land Use on Future Soil Erosion, Based on the Example of Southeast Serbia. In Advances in Understanding Soil Degradation; Springer: Cham, Switzerland, 2022; pp. 207–228. [Google Scholar]
- Agaj, T.; Bytyqi, V. Analysis of Soil Erosion Risk in a River Basin—A Case Study from Hogoshti River Basin (Kosovo). Ecol. Eng. Environ. Technol. 2022, 23, 162–171. [Google Scholar] [CrossRef]
- Miftari, L.; Gjoka, F.; Toromani, E. Assessment of soil loss in watershed of location in Ulza Basin, Albania. J. Balk. Ecol. 2018, 21, 400–413. [Google Scholar]
- Zdruli, P.; Karydas, C.G.; Dedaj, K.; Salillari, I.; Cela, F.; Lushaj, S.; Panagos, P. High resolution spatiotemporal analysis of erosion risk per land cover category in Korçe region, Albania. Earth Sci. Inform. 2016, 9, 481–495. [Google Scholar] [CrossRef]
- Nikolova, E. Soil Erosion Modeling Using RUSLE and GIS in the Republic of Macedonia; Polytechnic University of Milan: Milan, Italy, 2016. [Google Scholar]
- Blinkov, I.; Kostadinov, S.; Marinov, I.T. Comparison of erosion and erosion control works in Macedonia, Serbia and Bulgaria. Int. Soil Water Conserv. Res. 2013, 1, 15–28. [Google Scholar] [CrossRef]
- Golijanin, J.; Nikolić, G.; Valjarević, A.; Ivanović, R.; Tunguz, V.; Bojić, S.; Grmuša, M.; Lukić Tanović, M.; Perić, M.; Hrelja, E.; et al. Estimation of potential soil erosion reduction using GIS-based RUSLE under different land cover management models: A case study of Pale Municipality, B&H. Front. Environ. Sci. 2022, 10, 1257. [Google Scholar] [CrossRef]
- Milentijević, N.; Ostojić, M.; Fekete, R.; Kalkan, K.; Ristić, D.; Bačević, N.; Stevanović, V.; Pantelić, M. Assessment of Soil Erosion Rates Using Revised Universal Soil Loss Equation (RUSLE) and GIS in Bačka (Serbia). Pol. J. Environ. Stud. 2021, 30, 5175–5184. [Google Scholar] [CrossRef]
- Lukić, T.; Lukić, A.; Basarin, B.; Ponjiger, T.M.; Blagojević, D.; Mesaroš, M.; Milanović, M.; Gavrilov, M.; Pavić, D.; Zorn, M.; et al. Rainfall erosivity and extreme precipitation in the Pannonian basin. Open Geosci. 2019, 11, 664–681. [Google Scholar] [CrossRef]
- Lukić, T.; Micić Ponjiger, T.; Basarin, B.; Sakulski, D.; Gavrilov, M.; Marković, S.; Zorn, M.; Komac, B.; Milanović, M.; Pavić, D.; et al. Application of Angot precipitation index in the assessment of rainfall erosivity: Vojvodina Region case study (North Serbia). Acta Geogr. Slov. 2021, 61, 123–153. [Google Scholar] [CrossRef]
- Perović, V.; Đorđević, A.; Životić, L.; Nikolić, N.; Kadović, R.; Belanović, S. Soil Erosion Modelling in the Complex Terrain of Pirot Municipality. Carpathian J. Earth Environ. Sci. 2012, 7, 93–100. [Google Scholar]
- Belanović, S.; Perović, V.; Vidojević, D.; Kostadinov, S.; Knežević, M.; Kadović, R.; Košanin, O. Assessment of soil erosion intensity in Kolubara District, Serbia. Fresenius Environ. Bull. 2013, 22, 1556–1563. [Google Scholar]
- Životić, L.; Perović, V.; Jaramaz, D.; Đorđević, A.; Petrović, R.; Todorović, M. Application of USLE, GIS, and Remote Sensing in the Assessment of Soil Erosion Rates in Southeastern Serbia. Pol. J. Environ. Stud. 2012, 21, 1929–1935. [Google Scholar]
- Perović, V.; Kostadinov, S.; Jaramaz, D.; Kadović, R. Overview of the most important models for the soil loss assessment due to water erosion. Geonauka 2013, 1, 6–11. [Google Scholar] [CrossRef][Green Version]
- Micić Ponjiger, T.; Lukić, T.; Basarin, B.; Jokić, M.; Wilby, R.L.; Pavić, D.; Mesaroš, M.; Valjarević, A.; Milanović, M.M.; Morar, C. Detailed Analysis of Spatial–Temporal Variability of Rainfall Erosivity and Erosivity Density in the Central and Southern Pannonian Basin. Sustainability 2021, 13, 13355. [Google Scholar] [CrossRef]
- Wilby, R.L.; Yu, D. Rainfall and temperature estimation for a data sparse region. Hydrol. Earth Syst. Sci. 2013, 17, 3937–3955. [Google Scholar] [CrossRef]
- Jiao, D.; Xu, N.; Yang, F.; Xu, K. Evaluation of spatial-temporal variation performance of ERA5 precipitation data in China. Sci. Rep. 2021, 11, 17956. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, M. Inter-comparison of ERA-5, ERA-interim and GPCP rainfall over the last 40 years: Process-based analysis of systematic and random differences. J. Hydrol. 2020, 583, 124632. [Google Scholar] [CrossRef]
- Matkovski, B.; Zekić, S.; Đokić, D.; Jurjević, Ž.; Đurić, I. Export Competitiveness of Agri-Food Sector during the EU Integration Process: Evidence from the Western Balkans. Foods 2021, 11, 10. [Google Scholar] [CrossRef]
- Panagos, P.; Montanarella, L.; Barbero, M.; Schneegans, A.; Aguglia, L.; Jones, A. Soil priorities in the European Union. Geoderma Reg. 2022, 29, e00510. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2022: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Pörtner, H.O., Roberts, D.C., Tignor, M., Poloczanska, E.S., Mintenbeck, K., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022. [Google Scholar]
- Knez, S.; Štrbac, S.; Podbregar, I. Climate change in the Western Balkans and EU Green Deal: Status, mitigation and challenges. Energy Sustain. Soc. 2022, 12, 1. [Google Scholar] [CrossRef]
- Orgiazzi, A.; Panagos, P.; Fernández-Ugalde, O.; Wojda, P.; Labouyrie, M.; Ballabio, C.; Franco, A.; Pistocchi, A.; Montanarella, L.; Jones, A. LUCAS Soil Biodiversity and LUCAS Soil Pesticides, new tools for research and policy development. Eur. J. Soil Sci. 2022, 73, e13299. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Matthews, F.; Liakos, L.; Bezak, N.; Diodato, N.; Ballabio, C. Global rainfall erosivity projections for 2050 and 2070. J. Hydrol. 2022, 610, 127865. [Google Scholar] [CrossRef]
- Reed, J.M.; Kryštufek, B.; Eastwood, W.J. The Physical Geography of The Balkans and Nomenclature of Place Names. In Balkan Biodiversity; Springer Netherlands: Dordrecht, The Netherlands, 2004; pp. 9–22. [Google Scholar]
- Tošić, I. Spatial and temporal variability of winter and summer precipitation over Serbia and Montenegro. Theor. Appl. Climatol. 2004, 77, 47–56. [Google Scholar] [CrossRef]
- Papić, D.; Bačević, N.R.; Valjarević, A.; Milentijević, N.; Gavrilov, M.B.; Živković, M.; Marković, S.B. Assessment of air temperature trend in South and Southeast Bosnia and Herzegovina from 1961 to 2017. Időjárás 2020, 124, 381–399. [Google Scholar] [CrossRef]
- Porja, T. Heat Waves Affecting Weather and Climate over Albania. J. Earth Sci. Clim. Chang. 2013, 4, 4. [Google Scholar] [CrossRef]
- Monevska, S.A. Climate Changes in Republic of Macedonia. In Climate Change and Its Effects on Water Resources; Baba, A., Tayfur, G., Gündüz, O., Howard, K., Friedel, M., Chambel, A., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 203–213. [Google Scholar]
- Tošić, I.; Hrnjak, I.; Gavrilov, M.B.; Unkašević, M.; Marković, S.B.; Lukić, T. Annual and seasonal variability of precipitation in Vojvodina, Serbia. Theor. Appl. Climatol. 2014, 117, 331–341. [Google Scholar] [CrossRef]
- Hrnjak, I.; Lukić, T.; Gavrilov, M.B.; Marković, S.B.; Unkašević, M.; Tošić, I. Aridity in Vojvodina, Serbia. Theor. Appl. Climatol. 2014, 115, 323–332. [Google Scholar] [CrossRef]
- Gavrilov, M.; Markovic, S.; Jarad, A.; Korac, V. The analysis of temperature trends in Vojvodina (Serbia) from 1949 to 2006. Therm. Sci. 2015, 19, 339–350. [Google Scholar] [CrossRef]
- Gavrilov, M.B.M.B.; Radaković, M.G.M.G.; Sipos, G.; Mezősi, G.; Gavrilov, G.; Lukić, T.; Basarin, B.; Benyhe, B.; Fiala, K.; Kozák, P.; et al. Aridity in the Central and Southern Pannonian Basin. Atmosphere 2020, 11, 1269. [Google Scholar] [CrossRef]
- Radaković, M.G.; Tošić, I.; Bačević, N.; Mladjan, D.; Gavrilov, M.B.; Marković, S.B. The analysis of aridity in Central Serbia from 1949 to 2015. Theor. Appl. Climatol. 2018, 133, 887–898. [Google Scholar] [CrossRef]
- Gavrilov, M.B.; Marković, S.B.; Janc, N.; Nikolić, M.; Valjarević, A.; Komac, B.; Zorn, M.; Punišić, M.; Bačević, N. Assessing average annual air temperature trends using the Mann–Kendall test in Kosovo. Acta Geogr. Slov. 2018, 58, 7–25. [Google Scholar] [CrossRef]
- Barry, R.G.; Chorley, R.J. Atmosphere, Weather and Climate, 7’11 ed.; Routledge: London, UK, 1998. [Google Scholar]
- Varlas, G.; Stefanidis, K.; Papaioannou, G.; Panagopoulos, Y.; Pytharoulis, I.; Katsafados, P.; Papadopoulos, A.; Dimitriou, E. Unravelling Precipitation Trends in Greece since 1950s Using ERA5 Climate Reanalysis Data. Climate 2022, 10, 12. [Google Scholar] [CrossRef]
- Bandhauer, M.; Isotta, F.; Lakatos, M.; Lussana, C.; Båserud, L.; Izsák, B.; Szentes, O.; Tveito, O.E.; Frei, C. Evaluation of daily precipitation analyses in E-OBS (v19.0e) and ERA5 by comparison to regional high-resolution datasets in European regions. Int. J. Climatol. 2022, 42, 727–747. [Google Scholar] [CrossRef]
- Bezak, N.; Borrelli, P.; Panagos, P. Exploring the possible role of satellite-based rainfall data in estimating inter- and intra-annual global rainfall erosivity. Hydrol. Earth Syst. Sci. 2022, 26, 1907–1924. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Petan, S.; Rusjan, S.; Vidmar, A.; Mikoš, M. The rainfall kinetic energy–intensity relationship for rainfall erosivity estimation in the mediterranean part of Slovenia. J. Hydrol. 2010, 391, 314–321. [Google Scholar] [CrossRef]
- Renard, K.G.K.; Foster, G.R.G.; Weesies, G.A.G.; McCool, D.K.; Yoder, D.C.D. Predicting soil erosion by water: A guide to conservation planning with the revised universal soil loss equation (RUSLE). In U.S. Department of Agriculture, Agriculture Handbook; ARS: Washington, DC, USA, 1997; Volume 703, p. 404. ISBN 0160489385. [Google Scholar]
- USDA. Draft Science Documentation: Revised Universal Soil Loss Equation Version 2 (RUSLE2); USDA-Agricultural Research Service: Washington, DC, USA, 2008.
- Wischmeier, W.H. A rainfall erosion index for a universal soil-loss equation. Soil Sci. Soc. Am. J. 1959, 23, 246–249. [Google Scholar] [CrossRef]
- Brown, L.C.; Foster, G.R. Storm erosivity using idealized intensity distributions. Am. Soc. Agric. Biol. Eng. 1987, 30, 379–386. [Google Scholar] [CrossRef]
- Vantas, K.; Sidiropoulos, E.; Evangelides, C. Rainfall Erosivity and Its Estimation: Conventional and Machine Learning Methods. In Soil Erosion—Rainfall Erosivity and Risk Assessment; IntechOpen: London, UK, 2019. [Google Scholar]
- Raj, R.; Saharia, M.; Chakma, S.; Rafieinasab, A. Mapping rainfall erosivity over India using multiple precipitation datasets. Catena 2022, 214, 106256. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Rainfall Intensity-Kinetic Energy Relationships for Soil Loss Prediction1. Soil Sci. Soc. Am. J. 1981, 45, 153–155. [Google Scholar] [CrossRef]
- Rosewell, C.J. Rainfall kinetic energy in eastern Australia. J. Clim. Appl. Meteorol. 1986, 25, 1695–1701. [Google Scholar] [CrossRef]
- McGregor, K.C.; Mutchler, C.K. Status of the R factor in northern Mississippi. In Soil Erosion: Prediction and Control; Soil and Water Conservation Society: Ankeny, IA, USA, 1976; pp. 135–142. [Google Scholar]
- McGregor, K.C.; Bingner, R.L.; Bowie, A.J.; Foster, G.R. Erosivity index values for northern Mississippi. Trans. ASAE 1995, 38, 1039–1047. [Google Scholar] [CrossRef]
- Nearing, M.A.; Yin, S.; Borrelli, P.; Polyakov, V.O. Rainfall erosivity: An historical review. Catena 2017, 157, 357–362. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Borrelli, P.; Diodato, N.; Panagos, P. Rainfall erosivity in Italy: A national scale spatio-temporal assessment. Int. J. Digit. Earth 2016, 9, 835–850. [Google Scholar] [CrossRef]
- Dash, C.J.; Das, N.K.; Adhikary, P.P. Rainfall erosivity and erosivity density in Eastern Ghats Highland of east India. Nat. Hazards 2019, 97, 727–746. [Google Scholar] [CrossRef]
- Bock, H.-H. Clustering Methods: A History of k-Means Algorithms. In Selected Contributions in Data Analysis and Classification; Springer: New York, NY, USA, 2007; pp. 161–172. [Google Scholar] [CrossRef]
- Lloyd, S.P. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-Means++: The Advantages of Careful Seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 1027–1035. [Google Scholar]
- Calinski, T.; Harabasz, J. Communications in Statistics A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Thorndike, R.L. Who belongs in the family? Psychometrika 1953, 18, 267–276. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.; Botvinnik, O.; O’Kane, D.; Hobson, P.; Lukauskas, S.; Gemperline, D.C.; Augspurger, T.; Halchenko, Y.; Cole, J.B.; Warmenhoven, J.; et al. Mwaskom/Seaborn: v0.8.1 (September 2017); Zenodo: Genève, Switzerland, 2017. [Google Scholar] [CrossRef]
- Met Office. Cartopy: A Cartographic Python Library with a Matplotlib Interface; Exeter: Devon, UK, 2010.
- Nistor, M.-M.; Mîndrescu, M. Climate change effect on groundwater resources in Emilia-Romagna region: An improved assessment through NISTOR-CEGW method. Quat. Int. 2019, 504, 214–228. [Google Scholar] [CrossRef]
- Milošević, D.; Stojsavljević, R.; Szabó, S.; Stankov, U.; Savić, S.; Mitrović, L. Spatio-temporal variability of precipitation over the western balkan countries and its links with the atmospheric circulation patterns. J. Geogr. Inst. Jovan Cvijic SASA 2021, 71, 29–42. [Google Scholar] [CrossRef]
- Županić, F.Ž.; Radić, D.; Podbregar, I. Climate change and agriculture management: Western Balkan region analysis. Energy. Sustain. Soc. 2021, 11, 51. [Google Scholar] [CrossRef]
- WMO; UNCCD; FAO; UNW-DPC. Country Report. Drought Conditions and Management Strategies in Serbia. Initiative on Capacity Development to Support National Drought Management Policy; WMO: Belgrade, Serbia, 2013. [Google Scholar]
- Gocic, M.; Trajkovic, S. Spatiotemporal characteristics of drought in Serbia. J. Hydrol. 2014, 510, 110–123. [Google Scholar] [CrossRef]
- Glock, K.; Tritthart, M.; Mlađan, D.; Galjak, M.; Stanojević, P.; Gocić, M.; Trajković, S.; Milanović, M.; Talijan, M.; Slavković, R.; et al. Report on Natural Disasters in the Western Balkans. Analysis of Natural Disasters Needed to Be Managed in Western Balkan Regions. NatRisk project (reference number 573806-EPP-1-2016-1-RS-EPPKA2-CBHE-JP), Niš, Serbia. 2017. Available online: http://www.natrisk.ni.ac.rs/files/activities/1-1/Report_on_natural_disasters_in_WB.pdf (accessed on 16 October 2022).
- Anđelković, G.; Jovanović, S.; Manojlović, S.; Samardžić, I.; Živković, L.; Šabić, D.; Gatarić, D.; Džinović, M. Extreme precipitation events in Serbia: Defining the threshold criteria for emergency preparedness. Atmosphere 2018, 9, 188. [Google Scholar] [CrossRef]
- Abolmasov, B.; Marjanović, M.; Đurić, U.; Krušić, J.; Katarina, A. Massive Landsliding in Serbia Following Cyclone Tamara in May 2014 (IPL-210). In Advancing Culture of Living with Landslides; Sassa, K., Mikoš, M., Yin, Y., Eds.; Springer: Cham, Switzerland, 2017; pp. 473–487. ISBN 978-3-319-53500-5. [Google Scholar]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Jae Lim, K.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef]
- Beguería, S.; Serrano-Notivoli, R.; Tomas-Burguera, M. Computation of rainfall erosivity from daily precipitation amounts. Sci. Total Environ. 2018, 637–638, 359–373. [Google Scholar] [CrossRef] [PubMed]
- Margiorou, S.; Kastridis, A.; Sapountzis, M. Pre/Post-Fire Soil Erosion and Evaluation of Check-Dams Effectiveness in Mediterranean Suburban Catchments Based on Field Measurements and Modeling. Land 2022, 11, 1705. [Google Scholar] [CrossRef]
- Rousseva, S.; Stefanova, V. Assessment and mapping of soil erodibility and rainfall erosivity in Bulgaria. In Proceedings of the Conference on Water Observation and Information System for Decision Support “BALWOIS”, Ohrid, Republic of Macedonia, 23–26 May 2006 ; pp. 23–36. [Google Scholar]
- Rousseva, S.S.; Marinov, I.T. Soil Erosion and Flooding in Bulgaria-Risk Assessment and Prevention Measures. In Global Degradation of Soil and Water Resources; Springer Nature Singapore: Singapore, 2022; pp. 383–397. [Google Scholar]
- Ezugwu, A.E.; Ikotun, A.M.; Oyelade, O.O.; Abualigah, L.; Agushaka, J.O.; Eke, C.I.; Akinyelu, A.A. A comprehensive survey of clustering algorithms: State-of-the-art machine learning applications, taxonomy, challenges, and future research prospects. Eng. Appl. Artif. Intell. 2022, 110, 104743. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Poesen, J.; Lugato, E.; Scarpa, S.; Montanarella, L.; Borrelli, P. A Soil Erosion Indicator for Supporting Agricultural, Environmental and Climate Policies in the European Union. Remote Sens. 2020, 12, 1365. [Google Scholar] [CrossRef]
- Borrelli, P.; Panagos, P.; Alewell, C.; Ballabio, C.; de Oliveira Fagundes, H.; Haregeweyn, N.; Lugato, E.; Maerker, M.; Poesen, J.; Vanmaercke, M.; et al. Policy implications of multiple concurrent soil erosion processes in European farmland. Nat. Sustain. 2022. [Google Scholar] [CrossRef]
- Efthimiou, N.; Psomiadis, E.; Papanikolaou, I.; Soulis, K.X.; Borrelli, P.; Panagos, P. Developing a high-resolution land use/land cover map by upgrading CORINE’s agricultural components using detailed national and pan-European datasets. Geocarto Int. 2022, 1–36. [Google Scholar] [CrossRef]
- Kuhlicke, C.; Steinführer, A.; Begg, C.; Bianchizza, C.; Bründl, M.; Buchecker, M.; De Marchi, B.; Di Masso Tarditti, M.; Höppner, C.; Komac, B.; et al. Perspectives on social capacity building for natural hazards: Outlining an emerging field of research and practice in Europe. Environ. Sci. Policy 2011, 14, 804–814. [Google Scholar] [CrossRef]
- Adger, W.N. Vulnerability. Glob. Environ. Chang. 2006, 16, 268–281. [Google Scholar] [CrossRef]
- Kovačević-Majkić, J.; Milošević, M.V.; Panić, M.; Miljanović, D.; Ćalić, J. Risk education in Serbia. Acta Geogr. Slov. 2014, 54, 163–178. [Google Scholar] [CrossRef]
- Sun, X.; Li, C.; Kuiper, K.F.; Zhang, Z.; Gao, J.; Wijbrans, J.R. Human impact on erosion patterns and sediment transport in the Yangtze River. Glob. Planet. Chang. 2016, 143, 88–99. [Google Scholar] [CrossRef]
- Panagos, P.; Standardi, G.; Borrelli, P.; Lugato, E.; Montanarella, L.; Bosello, F. Cost of agricultural productivity loss due to soil erosion in the European Union: From direct cost evaluation approaches to the use of macroeconomic models. Land Degrad. Dev. 2018, 29, 471–484. [Google Scholar] [CrossRef]
- Rosas, M.A.; Gutierrez, R.R. Assessing soil erosion risk at national scale in developing countries: The technical challenges, a proposed methodology, and a case history. Sci. Total Environ. 2020, 703, 135474. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Zhen, L. Soil erosion control practices in the Chinese Loess Plateau: A systematic review. Environ. Dev. 2020, 34, 100493. [Google Scholar] [CrossRef]
- Bezak, N.; Borrelli, P.; Mikoš, M.; Panagos, P. Outreach and Post-Publication Impact of Soil Erosion Modelling Literature. Sustainability 2022, 14, 1342. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).