Abstract
The urban thermal environment is affected by multiple urban form and natural environment factors; research on the accurate prediction of the urban thermal environment, considering the interaction among different urban environmental factors, is still lacking. The development of a machine learning model provides a good means of solving complex problems. This study aims to clarify the relationship between urban environmental variables and the urban thermal environment through high-precision machine learning models as well as provide scenarios of future urban thermal environment developments. We defined an urban thermal environment index (UTEI), considering twelve urban form and natural indicators sourced from the remote sensing data of 150 cities in the Jing-Jin-Ji region from 2000 to 2015. We achieved accurate predictions of UTEI through training a gradient-boosted regression trees model. By unpacking the model, we found that the contribution rate of elevation (ELEV) was the highest. Among all the urban form indicators, the elongation index (ELONG), urban population (POP), nighttime light intensity (NLI), urban area size (AREA), and urban shape index (SHAPE) also had high contributions. We set up five scenarios to simulate the possible impact of different urban form factors on the overall urban thermal environment quality in the region. Under extremely deteriorated patterns that do not control urban expansion and vegetation reduction, the average UTEI could be as high as 0.55–0.76 °C in summer and 0.24–0.29 °C in winter, yet in the extremely optimized situation, UTEI decreased by 0.69 °C in summer and 0.56 °C in winter. Results showed that better urban form improves the quality of urban environments and can provide important insights for urban planners to mitigate urban heat island problems.
1. Introduction
Cities are growing at an alarming rate. As the United Nations predicts, nearly 66% of the world’s population will live in cities by 2050 [1]. Therefore, the improvement of urban thermal environment quality, which has an important impact on human health and energy consumption, is more and more significant in order to promote sustainable development and improve human health and well-being [2,3]. The changes in surface heat flux, moisture flux, and air circulation caused by thermal environment change have a negative impact on water resources, air quality, and human health [2,4,5]. How to effectively evaluate the negative impact of urban development on the thermal environment in the current century has become a key issue on the recent global agenda, according to The 2030 Agenda for Sustainable Development [6] and The New Urban Agenda [7].
The deterioration of the urban thermal environment, which is often measured by the magnitude of the urban heat island effect and the rise of land surface temperature, is affected by complicated urbanization processes and natural environment factors [8,9,10,11,12,13]. In recent years, more and more studies have shown that urban form and natural factors have multi-path effects on urban thermal environment quality, and their relationship has been proved to be nonlinear in previous studies [14]. For example, some studies have shown that the effect of city size on the intensity of the urban heat island effect shows a marginal decreasing effect [15,16]. Urban layout and population density have a strong interaction with urban air pollution or other environmental problems [17], and their contributions to the urban thermal environment might demonstrate unique change patterns along the urban development gradient [14].
Although some scholars have done research in the related field, some have only focused on a few indicators that influence the urban thermal environment, and they lack consideration of other dimensions of urban environmental factors [18,19]. Otherwise, many studies have adopted the ordinary least squares (OLS) model and other traditional regression models that cannot accurately detect the nonlinear influence of urban form on the thermal environment and the complex relationship between urban form and natural factors [20,21,22].
Recently, machine learning models have been successfully applied for scenario prediction and pattern recognition in various real-world situations [23,24,25,26] since they are useful in identifying the underlying relationship between different sources of data [27,28]. Antonio et al. [29] found that the modeling of environmental noise in urban environments was a nonlinear problem and proved that machine learning regression methods widely outperformed multiple linear regression models. There are also other cases of using machine learning models to solve urban environmental problems. Alavipanah et al. [30] used a boosted regression tree (BRT) to explore the influence of 2D and 3D building indicators and vegetation coverage on the thermal environment. Zhang et al. [31] predicted future changes in land use/land cover and land surface temperature based on an artificial neural network (ANN) model. Sun et al. [32] found that urban density exhibited significant positive effects on LST in Ningbo city based on random forest regression (RF). Machine learning models can better deal with identifying the complex relationship between urban natural and social environmental elements and can help to accurately predict the changes in the urban thermal environment under different urban development scenarios. Nonetheless, using a machine learning model to explore the influencing factors of the urban thermal environment is still in the early stages and comparatively lacking.
To fill the gaps, the objective of this study is to analyze the multivariate correlation between urban indicators and the urban thermal environment through a high-precision prediction model and simulate the possible development changes under typical urbanization scenarios. We used urban form indicators (UFIs), including urban area size (AREA), nighttime light intensity (NLI), urban population (POP), the urban shape index (SHAPE), the elongation index (ELONG), the urban aggregation index (AI), and urban vegetation cover (UVC), combining natural factors such as urban altitude (ELEV), wind speed (WIN), air relative humidity (RHU), precipitation (PREC), and solar radiation intensity (RADI) in the Jing-Jin-Ji region from 2000 to 2015. Six linear regression and nonlinear machine learning models were constructed for model comparison. We finally verified the optimal prediction performance of a gradient-boosted regression trees model and calculated the relative importance of each factor. According to historical trends, we built five scenarios and simulated the possible impact of different urban form indicators on the overall urban thermal environment in the region by calculating the PDF value. The innovation of this study is to provide deeper insights on how to alleviate the UHI effect and improve the urban thermal environment by optimizing the local urban form.
2. Materials
2.1. Study Area
The study area is located in north China and is commonly known as the Jing-Jin-Ji region (Figure 1). It covers an area of 218,000 km2 and is one of the fastest developing urban agglomerations in China. During the study period of 2000 to 2015, the Jing-Jin-Ji region experienced rapid population growth and urbanization processes, causing severe environmental deterioration and urban thermal environment problems [33]. The region mainly belongs to the temperate monsoon climate zone [34]; most areas have four distinct seasons, which are characterized by hot and rainy summers, dry and rainy springs, sunny autumns with sand storms, and cold winters. The region is comprised of a large number of cities, and we extracted 150 urban patches based on land use products in 2015.
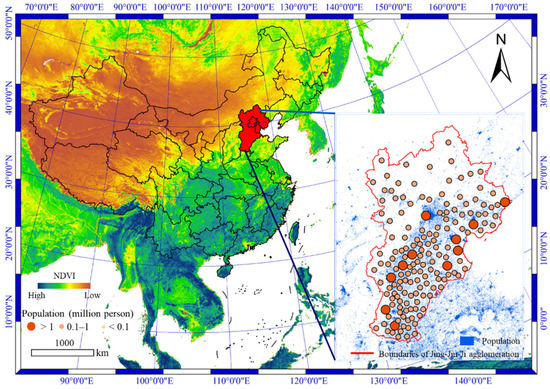
Figure 1.
Geographical location of the research area and the scale of the cities.
2.2. Data Source
2.2.1. Urban Thermal Environment Index
We defined the urban thermal environment index (UTEI) to characterize the thermal environment of the study area. It was calculated by the average of the land surface temperature (LST). LST has the advantage of being spatially explicit, while the commonly used meteorological station data cannot accurately reflect the temperature difference between each city region [35]. Therefore, we used remotely sensed land surface temperature data from the MOD11A2 dataset (http://www.gscloud.cn, accessed on 15 March 2019) with 1 km resolution as the source of land surface temperature. The MOD11A2 Version 6 product provides an average 8-day per-pixel LST, so we calculated monthly and yearly UTEI using Equation (1) for the years 2000, 2005, 2010, and 2015:
where xm,n stands for a single pixel value in the LST grid, and m × n calculates the number of pixels in the region. The mean LSTs for both summer and winter were summarized by overlaying the regulatory observation grid unit layers and are specified as the dependent variables for further analysis.
2.2.2. Natural Indicators
We selected five commonly used natural indicators [14], including elevation (ELEV), the precipitation rate (PRE), solar radiation (RADI), air relative humidity (RHU), and wind speed (WIN). Illustration of the indicators’ major impact pathways on UTEI is represented in Figure 2, and the physical definitions of these natural indicators are listed in Table 1. In order to achieve better spatiotemporal resolution and accuracy to reflect the urban natural environment, we also used remotely sensed land surface data as data sources. The elevation (ELEV) data were retrieved from the Shuttle Radar Topography Mission (SRTM; 30 m resolution) (https://earthdata.nasa.gov/, accessed on 30 March 2019). Wind speed (WIN), the precipitation rate (PRE), air relative humidity (RHU), and solar radiation (RADI) were sourced from the China Meteorological Forcing Dataset (CMFD) [36]. The CMFD is a high spatial–temporal resolution gridded near-surface meteorological dataset developed specifically for studies of land surface processes in China, with a temporal resolution of three hours and a spatial resolution of 0.1°.
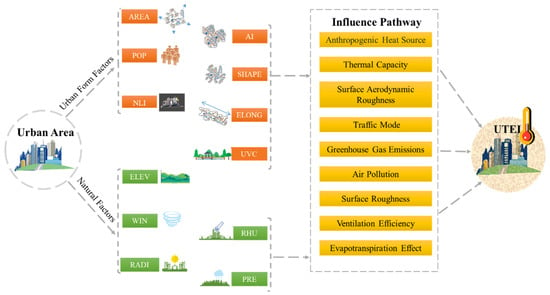
Figure 2.
Schematic diagram of the mechanism of urban form and natural factors affecting the heat island effect.

Table 1.
Natural indicators used.
2.2.3. Urban Form Indicators
Urban form is a multi-dimensional concept containing urban structures and geometric forms as well as urban development factors. We used three widely applied landscape indexes to represent the urban geometric form, including the urban shape index (SHAPE), the urban aggregation index (AI), and the elongation index (ELONG). These indicators were calculated in fragstats 4.2, and the calculation methods are shown in Table 2.

Table 2.
Computational method and description of geometric urban form indicators.
We used night light data to represent the level of urban development. The nighttime light intensity (NLI) was from the Defense Meteorological Satellite Program Operational Linescan System (DMSP-OLS), with an approximately 1 km resolution. We used the ridge line method to correct the nighttime light data time series to obtain consistent time series data and then obtained the final urban nighttime night index (NLI) [37]. Due to the lack of night light data in 2015, we used the data from 2013 instead. Urban area (AREA) indicates urban size and was obtained from the remote sensing monitoring data of land use status in China. It was downloaded from the Resource and Environment Data Cloud Platform (http://www.resdc.cn/DataList.aspx, accessed on 1 May 2020), with 30 m resolution. Urban population density was used to measure urban density, which was obtained from the Center for International Earth Science Information Network at Columbia University (http://sedac.ciesin.columbia.edu/data/set/gpw-v4-population-density-rev10, accessed on 12 March 2020), with a resolution of 1 km. The population density data and area data were log-transformed to make their distributions more normal and to increase the predictive ability of some linear models for comparison [38]. We also achieved the monthly normalized differential vegetation index (NDVI) from MODIS datasets (MOD13Q1) of July and December, with 250 m spatial resolution to represent urban vegetation cover (UVC).
3. Methods
Based on the natural and urban form indicators obtained in Part 2.2, our research methods are mainly divided into three steps. The first step is to screen and establish the optimal prediction model. In this process, we divided the sample dataset set into a training set, a validation set, and a test set for supervised training and improved the generalization performance of the model by regularization methods. Then, we obtained the best model by comparing the results of cross-validation. The second step is to analyze the relative importance of urban form and natural indicators based on our interpretable machine learning model. The third step is to simulate the possible impacts of urban form changes in the next fifteen years by setting up different scenarios through the statistical data of historical changes. An overview of all processes is shown in Figure 3.
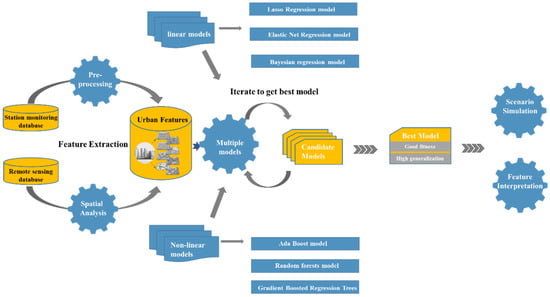
Figure 3.
Flow chart of data processing, prediction modeling, model interpretation, and scenario simulation.
3.1. Linear Regression Models
Linear regression is the simplest and most widely used statistical technique for predictive modeling. We implemented three widely used linear regression models: the lasso regression model, the Bayesian ridge regression model, and the elastic net regression model. The lasso regression model is a regression analysis method that performs both variable selection and regularization in order to enhance the prediction accuracy and interpretability of the statistical model it produces [39]. The Bayesian regression model is an approach to linear regression in which statistical analysis is undertaken within the context of Bayesian inference [40]. When the regression model has errors that have a normal distribution, and if a particular form of the prior distribution is assumed, explicit results are available for the posterior probability distributions of the model’s parameters. The elastic net regression model is a regularized regression method that linearly combines both penalties L1 and L2 of the lasso and ridge regression methods [41]. It is useful when there are multiple correlated features.
3.2. Nonlinear Regression Models
We also used three nonlinear models for supervised training: the random forests (RF) model, the Adaboost model, and gradient-boosted regression trees (GBRT) model.
The random forest regression model is an ensemble learning method for classification, regression, and other tasks that operate by constructing a multitude of decision trees at training time and outputting the class that is the mode of the classes (classification) or the mean prediction (regression) of the individual trees [42,43,44]. In prediction tasks, each decision tree is constructed using the best split for each node among a subset of predictors randomly chosen at that node. In the end, a simple majority vote is taken for the prediction.
Adaboost (short for adaptive boosting) is a popular boosting algorithm introduced to fit a sequence of weak learners on repeatedly modified versions of the data [45]. It is sensitive to noisy data and outliers. In some problems, it can be less susceptible to the overfitting problem than other learning algorithms.
The gradient-boosted regression trees (GBRT) model is a generalization of boosting to arbitrary differentiable loss functions and is an accurate and effective off-the-shelf procedure that can be used for regression problems. This model has been used in a variety of areas, with advantages that include the ability to find nonlinear transformations, the ability to handle skewed variables without requiring transformations, computational robustness, and high scalability [23,46,47]. This method progressively fits the base learner to the current pseudo-residual by the least squares method in every iteration. Initially, the average Y value is used as an assumption for predicting all of the observations, which is similar to fitting a linear regression model.
We first adopted a grid search for two parameters (number of estimators and max-leaf nodes) to make the GBRT model have the least mean square error. Then, in order to effectively overcome the overfitting problem of the model, we adopted two regularization methods, shrinkage and subsampling. The shrinkage strategy was proposed by Friedman to introduce the learning rate to scale the step length of the gradient descent procedure [48]. Empirical evidence suggests that small values of the learning rate favor better test errors [49]. The subsampling strategy allowed us to combine gradient boosting with bootstrap averaging (bagging). For each iteration, the base classifier was trained on the basis of a fraction subsample of the available training data. Root mean squared error (RMSE), mean absolute error (MAE), coefficient of determination (R2), and explained variance (EV) were used to evaluate and compare the nonlinear regression models.
3.3. Calculation Method of Feature Importance
We further calculated the contribution of each feature to the prediction results based on the trained GBTR model. In the model, since the decrease in impurity from splitting them to create a normalized estimate of the predictive power of that feature was combined with the fraction of samples a feature contributes to, we calculated the contribution of each variable to the reduction of impurity, and the common contribution of several variables could be obtained in the scikit-learn framework. The equation is given as:
where p(t) is the proportion of samples reaching t and where jt denotes the identifier of the variable used for splitting node t. Here, we used the Gini index as the impurity function, which is known as the Gini importance [50].
3.4. Set-Up of Simulation Scenarios
We adopted a method to determine scenario settings by statistical analysis of historical changes, which is widely used in spatial–temporal predictive simulation [51]. We built five scenarios of UFI projection to 2030 based on the UFI in 2015 and the historical urban UFI change from 2000 to 2015. We first calculated the UTEI change every five years using the dataset of the 150 cities and fit the probability density function (PDF) of the five-year changes. Then, we counted the data distribution of five-year changes in all urban morphological indicators, including AREA, NLI, POP, NDVI, SHAPE, AI, and ELONG. These UFIs can reflect the changes in urban characteristics brought about by urbanization, and they are also aspects of urban planning that need to be focused on. We defined the indicators that increase the intensity of the heat island effect as positive indicators and defined other indicators as negative indicators.
From the PDF of each UFI change, we drew the extremely low (10%), low (25%), medium (50%), high (75%), and extremely high (90%) annual UFI change. We defined 90% of the change in positive indicators and 10% of the change in negative indicators as extreme deterioration scenarios (EDs). In this changing situation, this means that the urban form in the next five years will advance in a direction that is not conducive to the improvement of thermal environment quality. Similarly, we took the first 75% of the change of positive indicators and the first 25% of the change of negative indicators as sub-deterioration scenarios (SDs), 50% of the change of positive indicators and 50% of the change of negative indicators as keeping the existing trend scenarios (KTs), 25% of the change of positive indicators and 75% of the change of negative indicators as slight optimization scenarios (SOs), and 10% of the change of positive indicators and 90% of the change of negative indicators as an extreme optimization scenario (EO). Note that the optimization and deterioration we mentioned here are only for the urban thermal environment.
4. Results and Discussions
4.1. Model Comparison and Evaluation Results
Optimization of the GBRT model parameters was obtained by grid searching; the number of estimators was best set to 944, while max depth was best set to 40 (the result is shown in Figure 4a). The effect of regularization strategies to prevent overfitting in the test dataset is shown in Figure 4b. As depicted, when shrinkage was not used, the yellow curve decreased the fastest, which indicated that better deviation can be achieved in fewer iterations, but with the increase of iterations, the deviation will increase to an extent. By contrast, the best result was that only shrinkage was used, of which the deviation of the test set was significantly lower than that of other methods. Therefore, in the final prediction model, we set the learning rate of the model to 0.1.
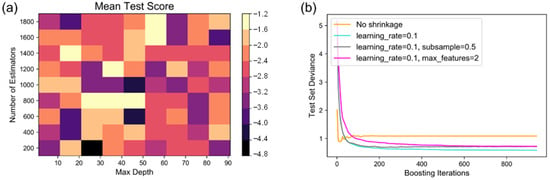
Figure 4.
(a) GBRT parametric grid search result. Note that the mean test score is the negative mean squared error. (b) Effect of shrinkage and subsampling on the goodness-of-fit of the GBRT model. The abscissa is the number of boosting iterations, and the ordinate is the deviation of the test set.
All six models were firstly trained with default parameter data, and the results of the five-fold cross-validation are shown in Table 3, including the resultant R2, EV, MAE, and RMSE for the validating and testing processes. All the urban form indicators and natural indicators were considered in the model estimation process.

Table 3.
Predictive performance of the models on summer and winter datasets.
All the nonlinear regression models had higher R2 and lower RMSE values than the three linear regression models in both summer and winter. Regarding the values of RMSE, all the models had slightly higher performances in winter than in summer, which seemed to relate to the much larger dynamic range of summer UTEI than winter UTEI [32].
The GBRT model explained 89% (RMSE = 0.77 °C, MAE = 0.61) of the UTEI in summer and captured 89% (RMSE = 1.11 °C, MAE = 0.83) of the UTEI in winter. Among all the six models, the prediction performance of GBRT was the most stable in both summer and winter. However, the results of other methods in cross-validation results were not so good, with the R2 being low or fluctuating sharply.
4.2. Relative Importance of Urban Form and Natural Factors
The contribution of all factors to predictive ability was obtained by factor importance analysis, as shown in Figure 5. The results showed that the order of contribution of all factors was similar in summer and winter, only slightly different. The contribution rate of ELEV was the highest in both seasons (about 21% in both summer and winter). Relative humidity and solar radiation also had high contribution rates (about 10%). In addition to natural factors, urban form factors also played an important role. Among them, POP and ELONG had the highest contribution rates; their contribution rates reached 7–10%. The contribution ratio of other UFIs was about one order of magnitude with climate factors, mostly within 10%. Among them, AI, SHAPE, and AREA contributed less but also reached 3–6%, which was close to that of UVC. Furthermore, by comparing the contribution rates of each season in a year, we found that natural factors contributed more in summer while urban form factors contributed more in winter.
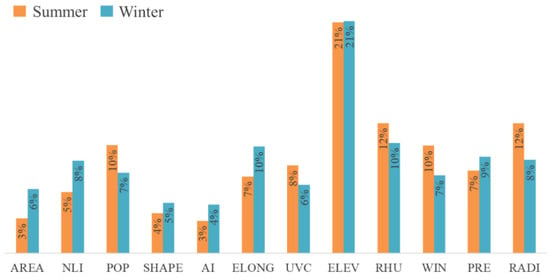
Figure 5.
Contribution of all factors to the UTEI in summer and winter.
4.3. Scenario Simulation Results
Based on previous studies [15,19,52,53], we took AREA, NLI, POP, SHAPE, and AI as positive indicators because their increases played enhanced roles in the UTEI. We used UVC and ELONG as negative indicators. According to our scenario setting method, we noted the change of each indicator over the course of fifteen years in the future under each scenario (Table 4). Taking 2015 as the baseline, we further calculated the presumptive value of each urban form index in 2030. In all scenarios, we set the value of urban form factors beyond the reasonable range of the urban form index as the critical value. Based on the estimation results of urban form changes under five scenarios, we forecasted the changes of UTEI in 2030 under five scenarios, as shown in Figure 6 (specific data in Table 4 is available in Table A1 in Appendix A).

Table 4.
Setting of urban form indicators’ change from 2015 to 2030 under five scenarios.
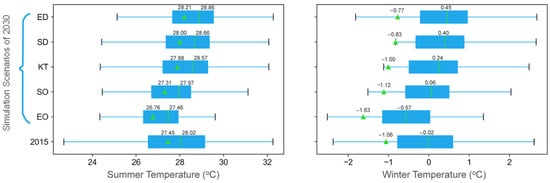
Figure 6.
Box plots of simulation results of five scenarios. Black lines stand for the maximum and minimum values, green line represents the median value and the green triangle is on behalf of the mean value.
The results show that under the KT scenario, the average UTEI of Jing-Jin-Ji cities will continue to increase. The average summer and winter UTEIs increase to 0.43 and 0.06 °C, respectively, by 2030. This means that if the government does not take measures to restrain the development of the UTEI, the problem of the urban thermal environment will become more and more serious in the future, especially in summer, when the heat pressure is higher. Under the two scenarios of optimizing the urban form, the average level of UTEI will decrease. In the SO scenario, the UTEI declined slightly, ranging from 0.05 to 0.13 °C, while in the EO scenario, the heat island effect was significantly alleviated, with decreases in the UTEI reaching 0.69 °C in summer and 0.56 °C in winter, respectively. In deteriorating situations, the UTEI enhancements were very significant, especially in summer. The average UTEI enhancements were as high as 0.55–0.76 °C in summer. In winter, the average level of the UTEI rose relatively little, but it also reached 0.24–0.29 °C. Our findings indicate that the UTEI will not be aggravated only under the SO and EO scenarios. Nevertheless, in order to improve the thermal environment of the city, it is better to develop the EO scenario.
Specifically, in the context of rapid urban development, compared with natural factors, it is more operable and meaningful to optimize urban form factors to alleviate urban thermal environment problems. At present, many studies have proved that urban form is an effective tool to alleviate the negative impact of urbanization on the thermal environment [54,55,56,57]. In spite of this, as the changes in urban structures are varied in cities and regions, the effectiveness of urban forms in mitigating heat-related risks also varies. Therefore, city managers need to combine regional characteristics, establish links between the thermal environment and various social and natural factors, clarify the direction and intensity of each factor’s effect on the thermal environment, and exercise targeted macro-control on urban building expansion directions and surface vegetation coverage in the process of urban planning. Attention should be paid to changes in urban expansion trends, urban vegetation cover, and other natural–human factors that would influence the UTEI in the process of urban development. Changes that are conducive to alleviating the UTEI problem should be encouraged, and trends that promote the UTEI problem should be adjusted and improved.
5. Conclusions and Limitations
This study explores the influences of urban form and natural indicators on the urban thermal environment in the Jing-Jin-Ji urban agglomeration. Through the comparison of six linear and nonlinear models, we selected the best prediction model and calculated relative feature importance. We also simulated the possible urban variables and urban thermal environment changes under typical urbanization scenarios.
Results showed that nonlinear models (Adaboost, RF, and GBRT) performed better in predicting the UTEI than linear models (Lasso, BN, and BR models), among which the GBRT model had the highest prediction accuracy (the value of its ten-fold cross-validation reached 0.89). Feature relative importance results showed that natural factors and urban form factors had certain influence on the UTEI. Relative humidity and solar radiation have high contribution rates (about 10%). ELONG, POP, NLI, AREA, and SHAPE have high contributions to the generation of the UTEI among all the urban form indicators. We also confirmed the seasonal differences in the contribution of the urban environmental factors to the UTEI. Natural factors contribute more in summer, while urban form factors contribute more in winter.
The five scenarios’ analyses showed that under the extremely deteriorated patterns, the average UTEI could be as high as 0.55–0.76 °C in summer and 0.24–0.29 °C in winter. On the other hand, in an extremely optimized situation, UTEI decreased by 0.69 °C in summer and 0.56 °C in winter. Overall, it indicated that cities need to develop under the two optimization scenarios in order to improve the urban thermal environment. City managers should pay more attention to changes in urban expansion trends, urban vegetation cover, and other natural–human factors that would influence the UTEI in the process of urban development. Changes that are conducive to alleviating the UTEI problem should be encouraged, and trends that promote the UTEI problem should be adjusted and improved. The research results also have important reference significance for future macro planning at the urban scale. Our research has successfully built high-precision machine learning models to clarify the influencing factors of the UTEI and set scenarios for future urban environment development. As there is a growing need for practical solutions to decreasing the urban thermal environment in the process of urbanization, it is a good attempt to apply machine learning models to solve the problem.
Several limitations of this paper can be summarized as follows: Firstly, this paper mainly studied the cities of the Jing-Jin-Ji region in China, most of which are small- and medium-sized cities. For bigger cities, the forecasting effect needs further confirmation. Secondly, the factors of the urban form we used are still limited. It is difficult to obtain more information on urban forms on an urban scale for a large number of cities. However, the multi-center structure of a city, the three-dimensional characteristics of a city, and so on, can provide more information about the city’s social and economic activities and physical characteristics, which can be used as the direction of future research. Thirdly, this study considered the interaction between urban form factors and selected natural factors but did not elaborate on the mediating or moderating effects of the urban form and how much the mediating or moderating effects account for the change of the UTEI. We will further explore it in the future. Another limitation of this study was that some of our scenario settings may be difficult to achieve for all cities. In the future, the scenario setting method based on historical change statistics and expert experience could be combined with our model to explore the potential impact of urban form change on urban thermal environments.
Author Contributions
Conceptualization, Y.W. and Z.L.; methodology, Y.W.; validation, J.D.; formal analysis, Y.W.; investigation, F.W. and J.S.; resources, F.W. and Y.W.; data curation, Y.W.; writing—original draft preparation, Z.L. and J.D.; writing—review and editing, Y.W.; visualization, Y.W.; supervision, S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Major Projects of the National Natural Science Foundation of China, grant number 41590843.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We are grateful to the editor and the reviewers for their helpful comments. In addition, we appreciate Xuliang Zhang for helping us with language editing.
Conflicts of Interest
No conflict of interest exists in the submission of this manuscript, and it has been approved by all authors for publication. The work described is original research that has not been published previously and is not under consideration for publication elsewhere, in whole or in part. All of the authors listed have approved the manuscript that is enclosed.
Appendix A

Table A1.
UTEI data distribution statistics of all cities in 2030 under five simulated scenarios.
Table A1.
UTEI data distribution statistics of all cities in 2030 under five simulated scenarios.
| EO_2030 | SO_2030 | KT_2030 | SD_2030 | ED_2030 | ||
|---|---|---|---|---|---|---|
| Summer | mean | −0.69 | −0.13 | 0.43 | 0.55 | 0.76 |
| 25% | −0.22 | 0.16 | 0.67 | 0.82 | 1.11 | |
| 50% | −0.56 | −0.05 | 0.55 | 0.64 | 0.84 | |
| 75% | −1.22 | −0.64 | 0.13 | 0.21 | 0.4 | |
| Winter | mean | −0.56 | −0.05 | 0.06 | 0.24 | 0.29 |
| 25% | −0.37 | 0.2 | 0.28 | 0.46 | 0.56 | |
| 50% | −0.55 | 0.07 | 0.26 | 0.42 | 0.47 | |
| 75% | −0.57 | −0.1 | 0.12 | 0.28 | 0.36 |
EO, extremely optimized situation; SO, slightly optimized; KT, keeping the trend; SD, slightly deteriorated; ED, extremely deteriorated.
References
- Desa, U. World Urbanization Prospects: The 2018 Revision, Key Facts; The United Nations Department of Economic and Social Affairs: New York, NY, USA; Available online: https://population.un.org/wup/Publications (accessed on 20 December 2018).
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global Change and the Ecology of Cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed]
- Patz, J.A.; Campbell-Lendrum, D.; Holloway, T.; Foley, J.A. Impact of regional climate change on human health. Nature 2005, 438, 310–317. [Google Scholar] [CrossRef] [PubMed]
- Hallegatte, S.; Corfee-Morlot, J. Understanding climate change impacts, vulnerability and adaptation at city scale: An introduction. Clim. Chang. 2011, 104, 1–12. [Google Scholar] [CrossRef]
- Hondula, D.M.; Georgescu, M.; Balling, R.C. Challenges associated with projecting urbanization-induced heat-related mortality. Sci. Total Environ. 2014, 490, 538–544. [Google Scholar] [CrossRef] [PubMed]
- The United Nations. The 2030 Agenda for Sustainable Development; The United Nations Department of Economic and Social Affairs: New York, NY, USA, 2015; Available online: https://sdgs.un.org/2030agenda (accessed on 1 January 2020).
- UNEP. The New Urban Agenda. 2016. Available online: https://www.un.org/sustainabledevelopment/blog/2016/10/newurbanagenda (accessed on 1 January 2020).
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef] [PubMed]
- Perini, K.; Magliocco, A. Effects of vegetation, urban density, building height, and atmospheric conditions on local temperatures and thermal comfort. Urban For. Urban Green. 2014, 13, 495–506. [Google Scholar] [CrossRef]
- Xiao, X.D.; Dong, L.; Yan, H.; Yang, N.; Xiong, Y. The influence of the spatial characteristics of urban green space on the urban heat island effect in Suzhou Industrial Park. Sustain. Cities Soc. 2018, 40, 428–439. [Google Scholar] [CrossRef]
- Li, D.; Sun, T.; Liu, M.; Wang, L.; Gao, Z. Changes in wind speed under heat waves enhance urban heat islands in the Beijing metropolitan area. J. Appl. Meteorol. Climatol. 2016, 55, 2369–2375. [Google Scholar] [CrossRef]
- Yan, L.; Jia, W.; Zhao, S. The cooling effect of urban green spaces in metacities: A case study of Beijing, China’s capital. Remote Sens. 2021, 13, 4601. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, H. Experimental analysis of the influence of urban morphological indices on the urban thermal environment of Zhengzhou, China. Atmosphere 2021, 12, 1058. [Google Scholar] [CrossRef]
- Liang, Z.; Wu, S.; Wang, Y.; Wei, F.; Huang, J.; Shen, J.; Li, S. The relationship between urban form and heat island intensity along the urban development gradients. Sci. Total Environ. 2020, 708, 135011. [Google Scholar] [CrossRef] [PubMed]
- Oke, T.R. City size and the urban heat island. Atmos. Environ. 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Takebayashi, H.; Senoo, M. Analysis of the relationship between urban size and heat island intensity using WRF model. Urban Clim. 2018, 24, 287–298. [Google Scholar] [CrossRef]
- Liang, Z.; Wei, F.; Wang, Y.; Huang, J.; Jiang, H.; Sun, F.; Li, S. The context-dependent effect of urban form on air pollution: A panel data analysis. Remote Sens. 2020, 12, 1793. [Google Scholar] [CrossRef]
- Laugesen, M.J.; Vargas-Bustamante, A. A patient mobility framework that travels: European and United States-Mexican comparisons. Heal. Policy 2010, 97, 225–231. [Google Scholar] [CrossRef]
- Zhou, B.; Rybski, D.; Kropp, J.P. The role of city size and urban form in the surface urban heat island. Sci. Rep. 2017, 7, 4791. [Google Scholar] [CrossRef]
- Peng, J.; Jia, J.; Liu, Y.; Li, H.; Wu, J. Seasonal contrast of the dominant factors for spatial distribution of land surface temperature in urban areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Logan, T.M.; Zaitchik, B.; Guikema, S.; Nisbet, A. Night and day: The influence and relative importance of urban characteristics on remotely sensed land surface temperature. Remote Sens. Environ. 2020, 247, 111861. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, B.; Glockmann, M.; Kropp, J.P.; Rybski, D. Context sensitivity of surface urban heat island at the local and regional scales. Sustain. Cities Soc. 2021, 74, 103146. [Google Scholar]
- Nieto, P.J.G.; García-Gonzalo, E.; Lasheras, F.S.; Fernández, J.R.A.; Muñiz, C.D.; Juez, F.J.D.C. Cyanotoxin level prediction in a reservoir using gradient boosted regression trees: A case study. Environ. Sci. Pollut. Res. Int. 2018, 25, 22658–22671. [Google Scholar] [CrossRef]
- Yazdi, M.D.; Kuang, Z.; Dimakopoulou, K.; Barratt, B.; Suel, E.; Amini, H.; Lyapustin, A.; Katsouyanni, K.; Schwartz, J. Predicting fine particulate matter (PM2.5) in the greater london area: An ensemble approach using machine learning methods. Remote Sens. 2020, 12, 914. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Zhao, J.; Gao, Y.; Gu, Z. Prediction and evaluation of spatial distributions of ozone and urban heat island using a machine learning modified land use regression method. Sustain. Cities Soc. 2022, 78, 103643. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, P.; Zhang, H.; Cheng, P. Study on urban heat island intensity level identification based on an improved restricted boltzmann machine. Int. J. Environ. Res. Public Health 2018, 15, 186. [Google Scholar] [CrossRef] [PubMed]
- Chun, B.; Guldmann, J.-M. Impact of greening on the urban heat island: Seasonal variations and mitigation strategies. Comput. Environ. Urban Syst. 2018, 71, 165–176. [Google Scholar] [CrossRef]
- Sévellec, F.; Drijfhout, S.S. A novel probabilistic forecast system predicting anomalously warm 2018–2022 reinforcing the long-term global warming trend. Nat. Commun. 2018, 9, 3024. [Google Scholar] [CrossRef] [PubMed]
- Torija, A.J.; Ruiz, D.P. A general procedure to generate models for urban environmental-noise pollution using feature selection and machine learning methods. Sci. Total Environ. 2015, 505, 680–693. [Google Scholar] [CrossRef]
- Alavipanah, S.; Schreyer, J.; Haase, D.; Lakes, T.; Qureshi, S. The effect of multi-dimensional indicators on urban thermal conditions. J. Clean. Prod. 2017, 177, 115–123. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, C.; Kafy, A.-A.; Tan, S. Simulating the relationship between land use/cover change and urban thermal environment using machine learning algorithms in Wuhan city, China. Land 2021, 11, 14. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, C.; Li, J.; Wang, R.; Liu, J. Quantifying the effects of urban form on land surface temperature in subtropical high-density urban areas using machine learning. Remote Sens. 2019, 11, 959. [Google Scholar] [CrossRef]
- Kang, S.; Eltahir, E.A.B. North China Plain threatened by deadly heatwaves due to climate change and irrigation. Nat. Commun. 2018, 9, 2894. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Weng, Q. Remote sensing of impervious surfaces in the urban areas: Requirements, methods, and trends. Remote Sens. Environ. 2012, 117, 34–49. [Google Scholar]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef]
- Zhang, Q.; Pandey, B.; Seto, K.C. A robust method to generate a consistent time series from DMSP/OLS nighttime light data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5821–5831. [Google Scholar] [CrossRef]
- Fang, C.; Wang, S.; Li, G. Changing urban forms and carbon dioxide emissions in China: A case study of 30 provincial capital cities. Appl. Energy 2015, 158, 519–531. [Google Scholar] [CrossRef]
- Dalalyan, A.S.; Hebiri, M.; Lederer, J. On the prediction performance of the Lasso. Bernoulli 2017, 23, 552–581. [Google Scholar]
- Chen, T.; Martin, E. Bayesian linear regression and variable selection for spectroscopic calibration. Anal. Chim. Acta 2009, 631, 13–21. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using Random Forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Timm, B.C.; McGarigal, K. Fine-scale remotely-sensed cover mapping of coastal dune and salt marsh ecosystems at Cape Cod National Seashore using Random Forests. Remote Sens. Environ. 2012, 127, 106–117. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Shen, Y.; Jiang, Y.; Liu, W.; Liu, Y. Multi-class AdaBoost ELM. In Proceedings of ELM-2014 Volume 2; Springer International Publishing: Berlin, Germany, 2015. [Google Scholar]
- Pilière, A.; Schipper, A.M.; Breure, T.M.; Posthuma, L.; de Zwart, D.; Dyer, S.D.; Huijbregts, M.A.J. Unraveling the relationships between freshwater invertebrate assemblages and interacting environmental factors. Freshw. Sci. 2014, 33, 1148–1158. [Google Scholar] [CrossRef]
- Torres-Barrán, A.; Alonso, Á.; Dorronsoro, J.R. Regression tree ensembles for wind energy and solar radiation prediction. Neurocomputing 2019, 326, 151–160. [Google Scholar] [CrossRef]
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Rosa, G.J.M. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Hastie, T., Tibshirani, R., Friedman, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 66, p. 1315. [Google Scholar]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar]
- Güneralp, B.; Zhou, Y.; Ürge-Vorsatz, D.; Gupta, M.; Yu, S.; Patel, P.L.; Fragkias, M.; Li, X.; Seto, K.C. Global scenarios of urban density and its impacts on building energy use through 2050. Proc. Natl. Acad. Sci. USA 2017, 114, 8945–8950. [Google Scholar] [CrossRef]
- Debbage, N.; Shepherd, J.M. The urban heat island effect and city contiguity. Comput. Environ. Urban Syst. 2015, 54, 181–194. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.-M.; Nan, H.; Zhou, L.; Myneni, R.B. Surface urban heat island across 419 global big cities. Environ. Sci. Technol. 2012, 46, 696–703. [Google Scholar] [CrossRef]
- Frolking, S.; Milliman, T.; Seto, K.C.; Friedl, M.A. A global fingerprint of macro-scale changes in urban structure from 1999 to 2009. Environ. Res. Lett. 2013, 8, 024004. [Google Scholar] [CrossRef]
- Dhar, T.K.; Khirfan, L. A multi-scale and multi-dimensional framework for enhancing the resilience of urban form to climate change. Urban Clim. 2017, 19, 72–91. [Google Scholar] [CrossRef]
- Zhang, N.; Ye, H.; Wang, M.; Li, Z.; Li, S.; Li, Y. Response relationship between the regional thermal environment and urban forms during rapid urbanization (2000–2010–2020): A case study of three urban agglomerations in China. Remote Sens. 2022, 14, 3749. [Google Scholar] [CrossRef]
- Lu, Y.; Yue, W.; He, T.; Shan, Z. Urban form centrality and thermal environment: An empirical study of Chinese megacities. Sustain. Cities Soc. 2022, 83, 103955. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).