Reduced-Precision Chemical Kinetics in Atmospheric Models
Abstract
1. Introduction
1.1. Floating Point Representation
1.2. Related Developments and Advancements
2. Reduced Precision in Earth System Models
3. Model Configuration
3.1. The Kinetic PreProcessor (KPP)
3.2. Benchmark Chemical Mechanisms
- CBM
- Chap.
- The Chapman mechanism describes the photolytic ozone cycle in the stratosphere. The version included in KPP also implements catalytical loss reactions.
- SAPR
- Saprc-99 is a detailed mechanism for the gas-phase atmospheric reactions of VOCs and oxides of nitrogen (NOx). This mechanism is utilized for urban atmospheres in regional models [35].
- Small
- The “Small” stratospheric mechanism includes Chapman’s cycle with catalytical loss reactions plus oxygen in atomic excited state reactions.
- Strato
- is a more sophisticated stratosphere model that includes major stratospheric trace gases, including acids and oxides.
- Smog
- is a generalized reaction mechanism for photochemical smog [26].
- Tropo
- describes reactions in the troposphere, relevant for air quality modelling [27].
3.3. Error Considerations
3.4. Accuracy Metrics
- Species concentration over time. The concentration of all species for every integration step was compared to reference values to ensure that there are no species with concentrations diverging from currently accepted results.
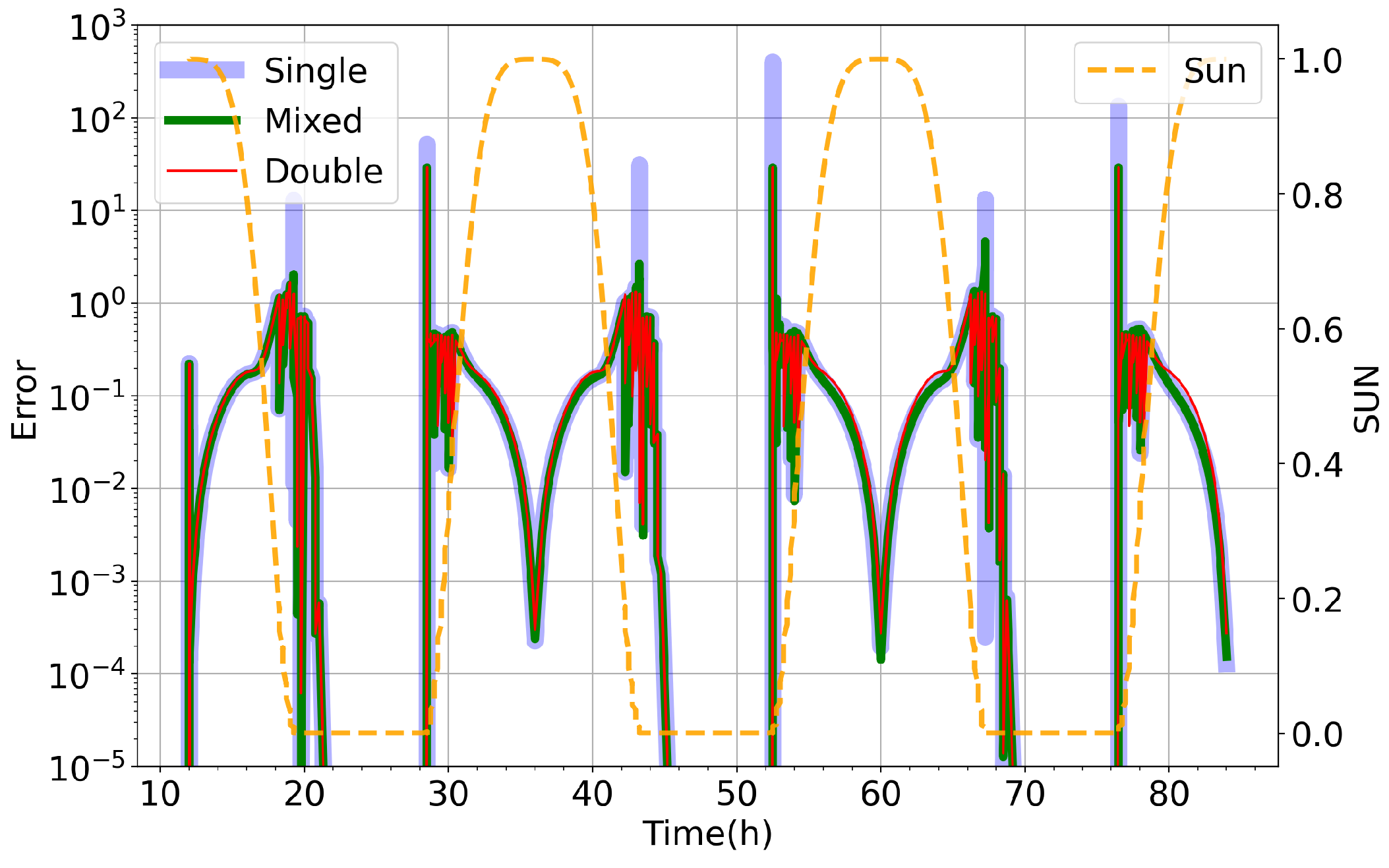
- Species error as calculated by KPP. The KPP Rosenbrock integrator calculates the species error vector (Section 3.3). We modified KPP to monitor the history of all species on both accepted and rejected sub-steps. The resulting error vectors are compared against reference values to check consistency at the sub-step level.
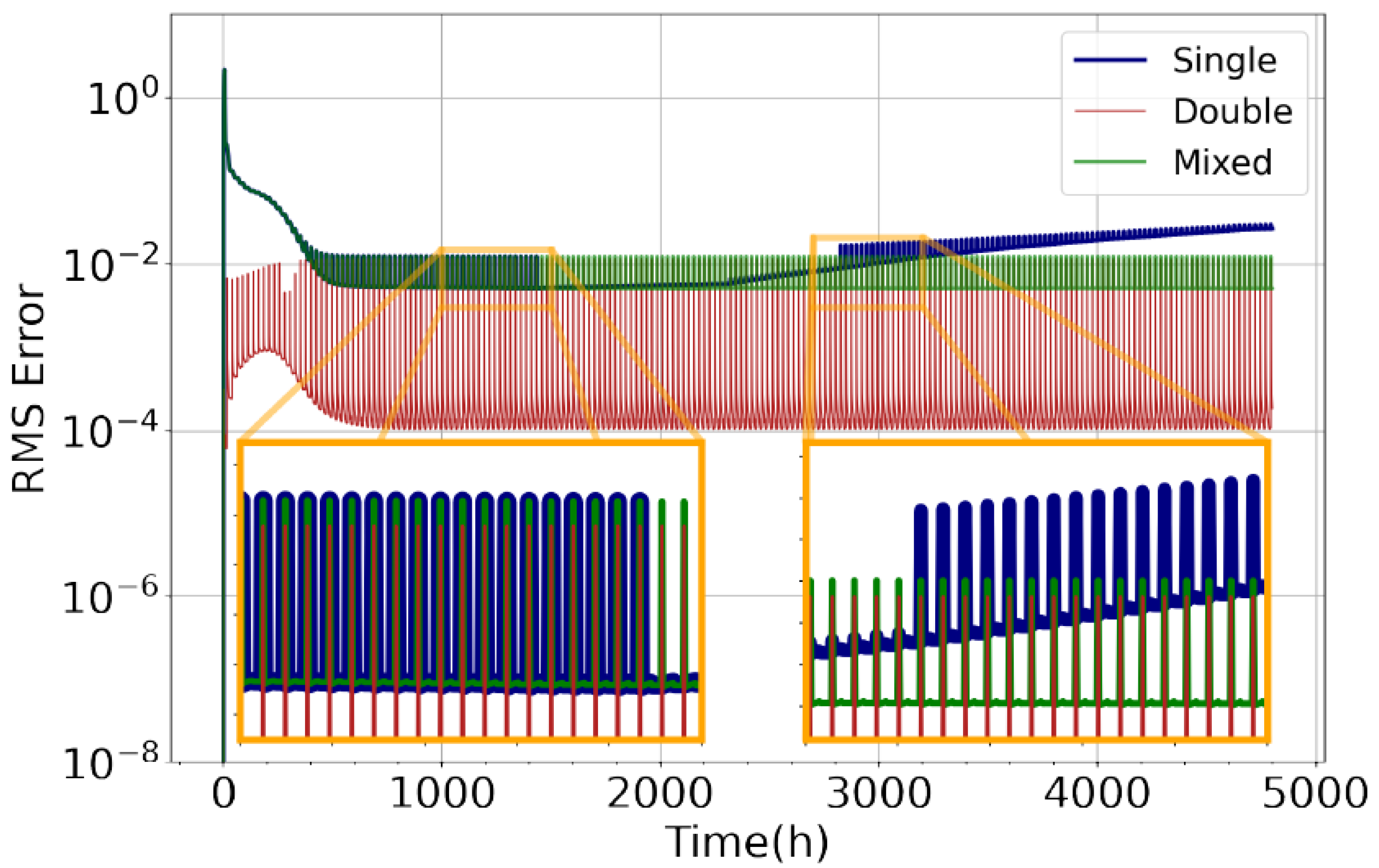
- Total error over time. This represents the cumulative error for all species as is calculated by KPP.
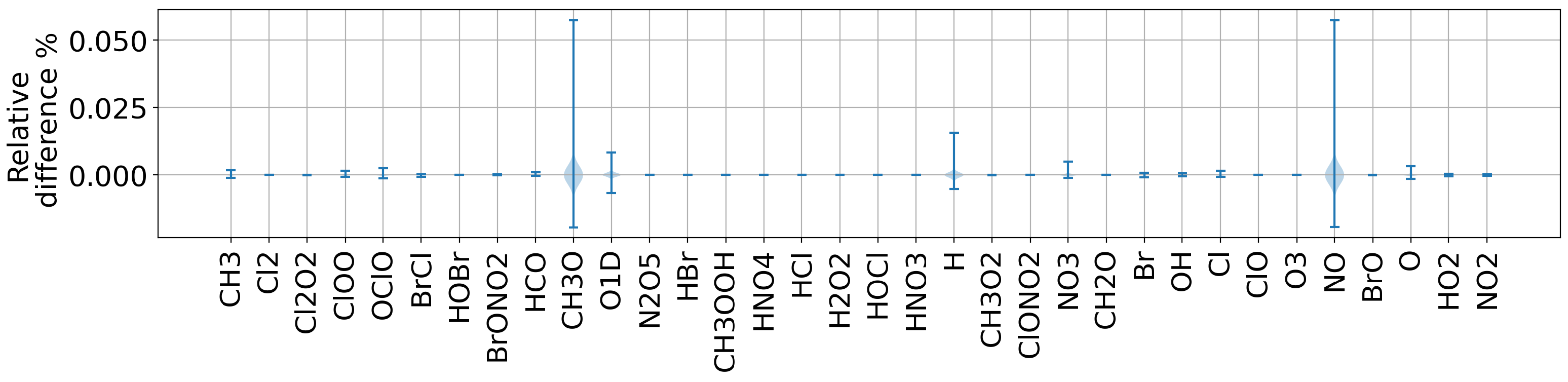
- Species concentration relative difference on every accepted integration step (corresponding to output in production simulations).
3.5. Control Experiments
4. Kinetic Pre-Processor Refactoring
4.1. Data Structures
4.2. Vectorisation
4.3. Time Step Length Control
5. Performance Results
5.1. Accuracy and Precision
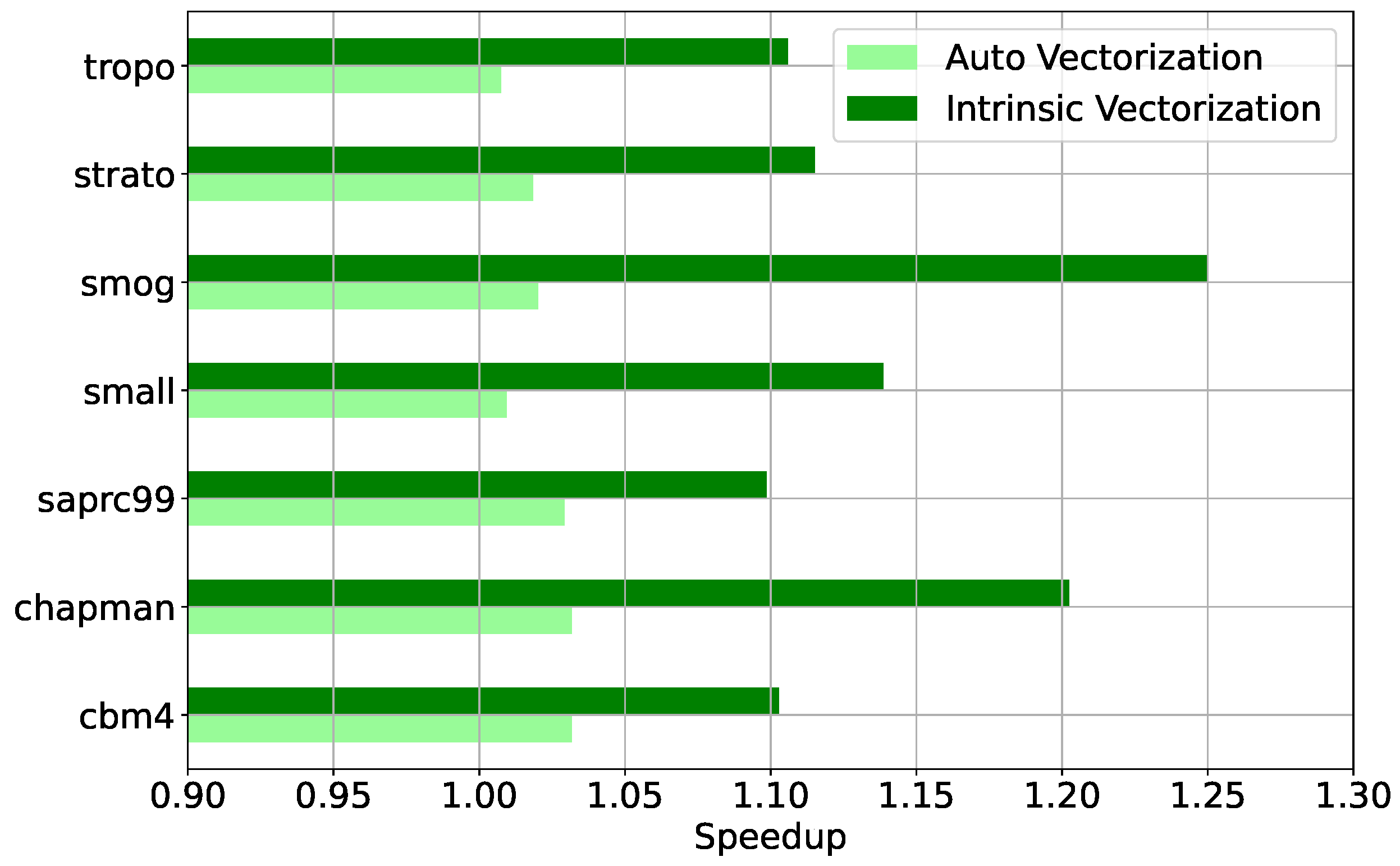
5.2. Vectorisation and Compiler Optimisations
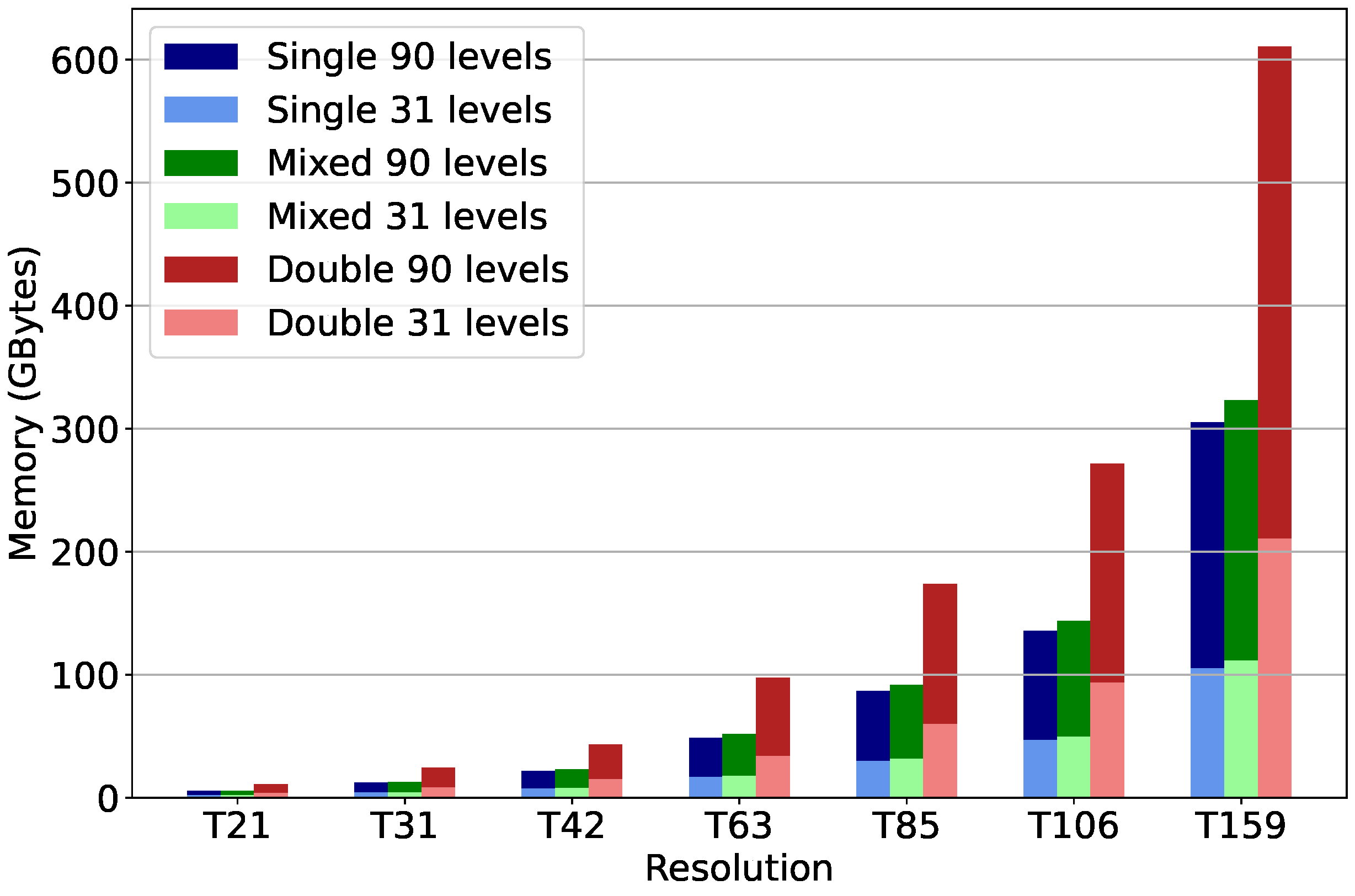
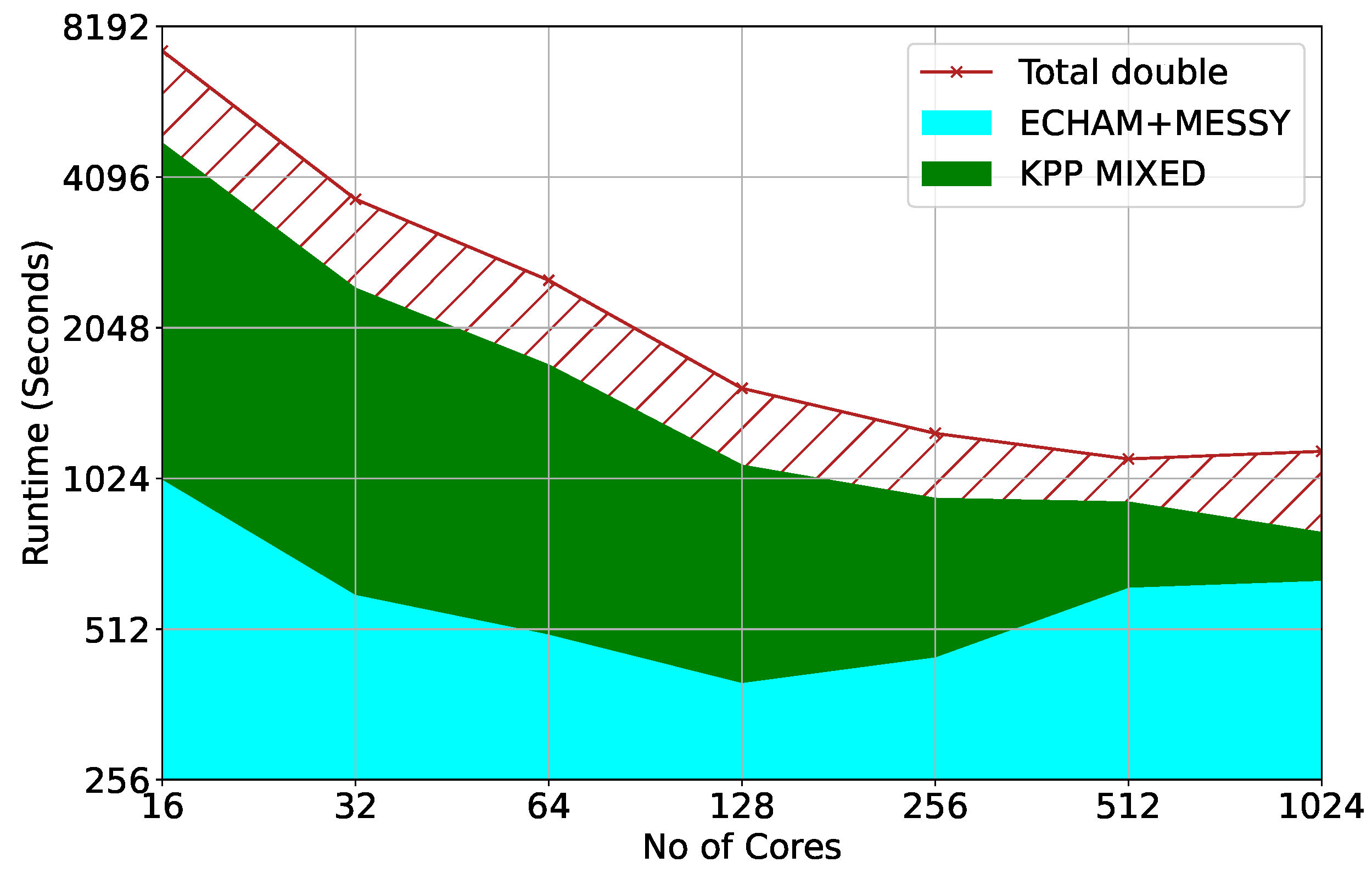
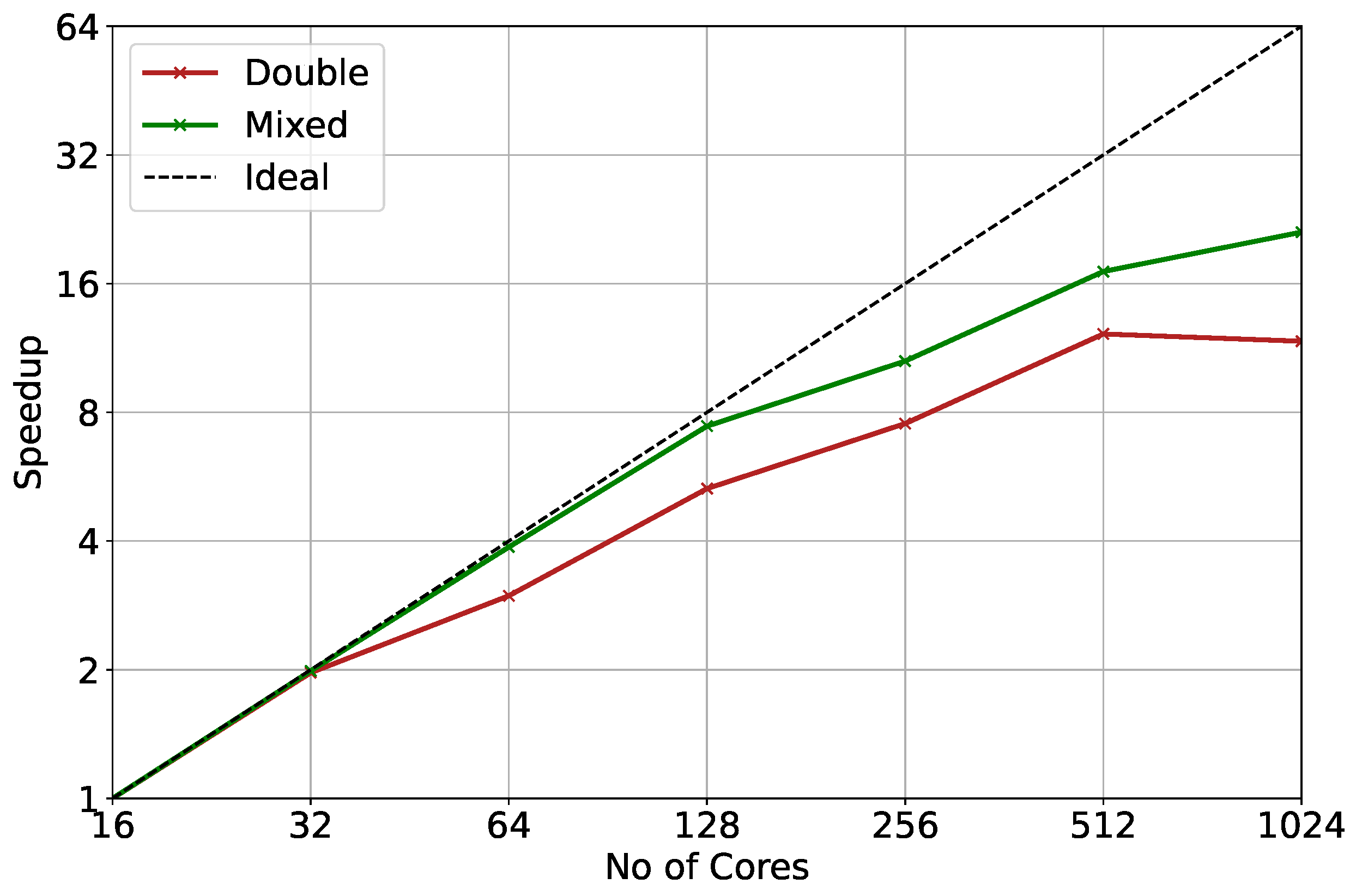
5.3. Performance at Scale
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. (Eds.) Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021; in press. [Google Scholar]
- Düben, D.P.; Palmer, T.N. Benchmark tests for numerical weather forecasts on inexact hardware. Mon. Weather. Rev. 2014, 142, 3809–3829. [Google Scholar] [CrossRef]
- Nakano, M.; Yashiro, H.; Kodama, C.; Tomita, H. Single precision in the dynamical core of a nonhydrostatic global atmospheric model: Evaluation using a baroclinic wave test case. Mon. Weather. Rev. 2018, 146, 409–416. [Google Scholar] [CrossRef]
- Wedi, N.P. Increasing horizontal resolution in numerical weather prediction and climate simulations: Illusion or panacea? Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2014, 372, 20130289. [Google Scholar] [CrossRef] [PubMed]
- Masters, J. IBM Introducing the World’s Highest-Resolution Global Weather Forecasting Model. Weather Underground. Available online: https://www.wunderground.com/cat6/IBM-Introducing-Worlds-Highest-Resolution-Global-Weather-Forecasting-Model (accessed on 8 January 2019).
- Shapiro, M.; Shukla, J.; Brunet, G.; Nobre, C.; Béland, M.; Dole, R.; Wallace, J.M. An earth-system prediction initiative for the twenty-first century. Bull. Am. Meteorol. Soc. 2010, 91, 1377–1388. [Google Scholar] [CrossRef][Green Version]
- Shukla, J.; Palmer, T.; Hagedorn, R.; Hoskins, B.; Kinter, J.; Marotzke, J.; Miller, M.; Slingo, J. Toward a new generation of world climate research and computing facilities. Bull. Am. Meteorol. Soc. 2010, 91, 1407–1412. [Google Scholar] [CrossRef]
- Yashiro, H.; Terasaki, K.; Kawai, Y.; Kudo, S.; Miyoshi, T.; Imamura, T.; Tomita, H. A 1024-member ensemble data assimilation with 3.5-km mesh global weather simulations. In Proceedings of the SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, Atlanta, GA, USA, 9–19 November 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Zhang, H.; Linford, J.C.; Sandu, A.; Sander, R. Chemical mechanism solvers in air quality models. Atmosphere 2011, 2, 510–532. [Google Scholar] [CrossRef]
- Christou, M.; Christoudias, T.; Morillo, J.; Alvarez, D.; Merx, H. Earth system modelling on system-level heterogeneous architectures: EMAC (version 2.42) on the Dynamical Exascale Entry Platform (DEEP). Geosci. Model Dev. 2016, 9, 3483–3491. [Google Scholar] [CrossRef]
- Alvanos, M.; Christoudias, T. Accelerating Atmospheric Chemical Kinetics for Climate Simulations. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 2396–2407. [Google Scholar] [CrossRef]
- IEEE Std 754–2008; IEEE Standard for Floating-Point Arithmetic. IEEE: Piscataway, NJ, USA, 2008; pp. 1–70. [CrossRef]
- Düben, P.D.; McNamara, H.; Palmer, T.N. The use of imprecise processing to improve accuracy in weather & climate pre-diction. J. Comput. Phys. 2014, 271, 2–18. [Google Scholar] [CrossRef]
- Düben, P.D.; Russell, F.P.; Niu, X.; Luk, W.; Palmer, T.N. On the use of programmable hardware and reduced numerical precision in earth-system modeling. J. Adv. Model. Earth Syst. 2015, 7, 1393–1408. [Google Scholar] [CrossRef]
- Düben, P.; Diamantakis, M.; Lang, S.; Saarinen, S.; Sandu, I.; Wedi, N. Tomas WilhelmssonProgress in using single precision in the IFS. ECMWF Newsl. 2018, 157, 26–31. Available online: https://www.ecmwf.int/en/elibrary/18705-newsletter-no-157-autumn-2018 (accessed on 5 April 2022).
- Palem, K.V. Energy aware algorithm design via probabilistic computing: From algorithms and models to Moore’s law and novel (semiconductor) devices. In Proceedings of the 2003 International Conference on Compilers, Architecture, and Synthesis for Embedded Systems, San Jose, CA, USA, 30 October–1 November 2003; IEEE: Piscataway, NJ, USA; pp. 113–116. [Google Scholar] [CrossRef]
- Palem, K.V. Energy aware computing through probabilistic switching: A study of limits. IEEE Trans. Comput. 2005, 54, 1123–1137. [Google Scholar] [CrossRef]
- Palem, K.V.; Lingamneni, A. Ten years of building broken chips: The physics and engineering of inexact computing. ACM Trans. Embedded Comput. Syst. 2013, 12, 87. [Google Scholar] [CrossRef]
- Sartori, J.; Sloan, J.; Kumar, R. Stochastic computing: Embracing errors in architecture and design of processors and applications. In Proceedings of the 2011 International Conference on Compilers, Architecture, and Synthesis for Embedded Systems, Taipei, Taiwan, 9–14 October 2011; IEEE: Piscataway, NJ, USA; pp. 135–144. [Google Scholar]
- Palem, K.V. Inexactness and a future of computing. Philos. Trans. R. Soc. 2014, 372A, 2018. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Madec, G. NEMO Ocean Engine, Note du Pole de Modelisatio. 2008, pp. 1288–1619. Available online: https://www.nemo-ocean.eu/wp-content/uploads/Doc_OPA8.1.pdf (accessed on 1 July 2019).
- Dawson, A.; Düben, P.D. Rpe v5: An emulator for reduced floating-point precision in large numerical simulations. Geosci. Model Dev. 2017, 10, 2221–2230. [Google Scholar] [CrossRef]
- Tintó Prims, O.; Acosta, M.C.; Moore, A.M.; Castrillo, M.; Serradell, K.; Cortés, A.; Doblas-Reyes, F.J. How to use mixed precision in ocean models: Exploring a potential reduction of numerical precision in NEMO 4.0 and ROMS 3.6. Geosci. Model Dev. 2019, 12, 3135–3148. [Google Scholar] [CrossRef]
- Moore, A.; Arango, H.; Broquet, G.; SPowell, B.; Weaver, A.; Zavala-Garay, J. The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems Part I—System overview and formulation. Prog. Oceanogr. 2011, 91, 34–49. [Google Scholar] [CrossRef]
- Colin, A.J. CHEMSODE: A stiff ODE solver for the equations of chemical kinetics. Comput. Phys. Commun. 1996, 97, 304–314. [Google Scholar]
- Damian, V.; Sandu, A.; Damian, M.; Potra, F.; Carmichael, G.R. The kinetic preprocessor KPP-a software environment for solving chemical kinetics. Comput. Chem. Eng. 2002, 26, 1567–1579. [Google Scholar] [CrossRef]
- Adrian, S.; Sander, R. Simulating chemical systems in Fortran90 and Matlab with the Kinetic PreProcessor KPP-2.1. Atmos. Chem. Phys. 2006, 6, 187–195. [Google Scholar]
- Sander, R.; Baumgaertner, A.; Gromov, S.; Harder, H.; Jöckel, P.; Kerkweg, A.; Kubistin, D.; Regelin, E.; Riede, H.; Sandu, A.; et al. The atmospheric chemistry box model CAABA/MECCA-3.0. Geosci. Model Dev. 2011, 4, 373–380. [Google Scholar] [CrossRef]
- Peckham, S.E. WRF/Chem Version 3.3 User’s Guide; National Center for Atmospheric Research (NCAR): Boulder, CO, USA, 2012. [Google Scholar]
- Lu, S.; Jacob, D.J.; Santillana, M.; Wang, X. An adaptive method for speeding up the numerical integration of chemical mechanisms in atmospheric chemistry models: Application to GEOS-Chem version 12.0.0. Geosci. Model Dev. 2020, 13, 2475–2486. [Google Scholar]
- Martin, R.V.; Eastham, S.D.; Bindle, L.; Lundgren, E.W.; Clune, T.L.; Keller, C.A.; Downs, W.; Zhang, D.; Lucchesi, R.A.; Sulprizio, M.P.; et al. Improved Advection, Resolution, Performance, and Community Access in the New Generation (Version 13) of the High Performance GEOS-Chem Global Atmospheric Chemistry Model (GCHP). Geosci. Model Dev. Discuss. 2022, 1–30, in press. [Google Scholar]
- Jöckel, P.; Kerkweg, A.; Pozzer, A.; Sander, R.E.; Tost, H.; Riede, H.; Baumgaertner, A.; Gromov, S.; Kern, B. Development cycle2 of the Modular Earth Submodel System (MESSy2). Geosci. Model Dev. 2010, 3, 717–752. [Google Scholar] [CrossRef]
- Gery, M.W.; Whitten, G.Z.; Killus, J.P.; Dodge, M.C. A photochemical kinetics mechanism for urban and regional scale computer modeling. J. Geophys. Res. Atmos. 1989, 94, 12925–12956. [Google Scholar] [CrossRef]
- Cao, L.; Li, S.; Yi, Z.; Gao, M. Simplification of Carbon Bond Mechanism IV (CBM-IV) under Different Initial Conditions by Using Concentration Sensitivity Analysis. Molecules 2019, 24, 2463. [Google Scholar] [CrossRef] [PubMed]
- Carter, W.P.L. Documentation of the SAPRC-99 chemical mechanism for VOC reactivity assessment. Contract 2000, 92, 95–308. [Google Scholar]
- Ernst, H.; Wanner, G. Stiff differential equations solved by Radau methods. J. Comput. Appl. Math. 1999, 111, 93–111. [Google Scholar]
- Pozzer, A.; Reifenberg, S.F.; Kumar, V.; Franco, B.; Kohl, M.; Taraborrelli, D.; Gromov, S.; Ehrhart, S.; Jöckel, P.; Sander, R.; et al. Simulation of organics in the atmosphere: Evaluation of EMACv2. 54 with the Mainz Organic Mechanism (MOM) coupled to the ORACLE (v1. 0) submodel. Geosci. Model Dev. 2022, 15, 2673–2710. Available online: https://gmd.copernicus.org/articles/15/2673/2022/ (accessed on 1 April 2022). [CrossRef]
- Roeckner, E.; Bäuml, G.; Bonaventura, L.; Brokopf, R.; Esch, M.; Giorgetta, M.; Hagemann, S.; Kirchner, I.; Kornblueh, L.; Manzini, E.; et al. The Atmospheric General Circulation Model ECHAM 5. PART I: Model Description; Max Planck Society: Munich, Germany, 2003. [Google Scholar]
- Christoudias, T.; Kirfel, T.; Kerkweg, A.; Taraborrelli, D.; Moulard, G.; Raffin, E.; Azizi, V.; Oord, G.; Werkhoven, B. GPU Optimizations for Atmospheric Chemical Kinetics. In Proceedings of the HPC Asia 2021: The International Conference on High Performance Computing in Asia-Pacific Region, Virtual, 20–21 January 2021; pp. 136–138. [Google Scholar]
- Alvanos, M.; Christoudias, T. GPU-accelerated atmospheric chemical kinetics in the ECHAM/MESSy (EMAC) Earth system model (version 2.52). Geosci. Model Dev. 2017, 10, 3679–3693. [Google Scholar] [CrossRef]
| Chemistry Mechanism | Total Species | Active | Fixed | Reactions | Simulation Time |
|---|---|---|---|---|---|
| CBM-IV | 33 | 32 | 1 | 81 | 5 days |
| Chapman | 7 | 5 | 2 | 6 | 3 days |
| SAPRC-99 | 79 | 74 | 5 | 211 | 5 days |
| Small Stratospheric | 7 | 5 | 2 | 10 | 3 days |
| Photochemical Smog | 16 | 12 | 4 | 12 | 1 min |
| Stratosphere (strato) | 40 | 34 | 6 | 109 | 3 days |
| Troposphere (tropo) | 88 | 84 | 4 | 178 | 5 days |
| Solver | Precision | Total | Accepted | Rejected | AWRT |
|---|---|---|---|---|---|
| Ros2 | Double | 1182 | 1022 | 160 | 87 |
| Single | 1860 | 1768 | 92 | 245 | |
| Mixed | 1097 | 977 | 120 | 105 | |
| Ros3 | Double | 676 | 574 | 102 | 96 |
| Single | 1226 | 1176 | 50 | 191 | |
| Mixed | 647 | 554 | 93 | 79 | |
| Ros4 | Double | 638 | 567 | 71 | 22 |
| Single | 1673 | 1606 | 67 | 729 | |
| Mixed | 637 | 566 | 71 | 17 | |
| Rodas3 | Double | 417 | 395 | 22 | 10 |
| Single | 590 | 563 | 27 | 7 | |
| Mixed | 423 | 400 | 23 | 6 | |
| Rodas4 | Double | 318 | 313 | 5 | 12 |
| Single | 733 | 716 | 17 | 10 | |
| Mixed | 318 | 313 | 5 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sophocleous, K.; Christoudias, T. Reduced-Precision Chemical Kinetics in Atmospheric Models. Atmosphere 2022, 13, 1418. https://doi.org/10.3390/atmos13091418
Sophocleous K, Christoudias T. Reduced-Precision Chemical Kinetics in Atmospheric Models. Atmosphere. 2022; 13(9):1418. https://doi.org/10.3390/atmos13091418
Chicago/Turabian StyleSophocleous, Kyriacos, and Theodoros Christoudias. 2022. "Reduced-Precision Chemical Kinetics in Atmospheric Models" Atmosphere 13, no. 9: 1418. https://doi.org/10.3390/atmos13091418
APA StyleSophocleous, K., & Christoudias, T. (2022). Reduced-Precision Chemical Kinetics in Atmospheric Models. Atmosphere, 13(9), 1418. https://doi.org/10.3390/atmos13091418







