Abstract
There are significant challenges to model the ionosphere due to different anomalies, especially under the increasing requirements for precision level. We used network theory to construct an ionospheric network analysis based on the data of global ionospheric maps for the period from 1998 to 2015. The network approach revealed different domains in the ionosphere. Besides the well-known equatorial anomaly, we revealed two more essential areas with “anomalous” behavior in the total electron content (TEC). Both anomalies are located at mid-latitudes: the first over most of North America, and the second one over the southeast part of Australia and the adjacent part of the Indian Ocean. The revealed areas partly coincide with the winter anomaly regions. Our results demonstrate that complex ionosphere/magnetic field/neutral atmosphere interaction can result in atypical ionosphere dynamics in huge areas.
1. Introduction
The ionosphere is the region of the Earth’s upper atmosphere, from about 60 km to 1000 km, that contains electrons and electrically charged atoms and molecules. Its importance, in practical terms, is that it enables the propagation, reflection or refraction of radio wave signals that can be transmitted to distant places on Earth. The radio propagation depends uniquely on electron density. Hence, temporal and spatial variability in ionospheric electron density considerably affects the functionality of radio communication [1] and global navigation satellite systems (GNSS) such as GPS or GLONASS [2].
The ionosphere coexists with the upper portion of the neutral atmosphere called the thermosphere [3,4]. In simplified terms, the solar radiation spectrum determines the ionosphere‘s vertical structure, while the geomagnetic field determines its latitudinal structure [4]. Moreover, the global circulation of the thermosphere significantly impacts the global ionization distribution [5,6].
Scientists use the satellite and ground-based facilities to study the ionosphere around the globe. The total electron content (TEC) is an important measured quantity for the ionosphere of the Earth. TEC is the total number of electrons in a column of the unit area defined as TECU = 1016 el/m2, where TEC varies between 2 and 200 TEC units. The seasonal anomalies within the context of seasonal changes in the TEC (e.g., [5]) are an area of intensive research, e.g., the Weddell Sea anomaly [7], the Midlatitude summer evening anomaly [8].
The location and geographical boundaries of the anomaly areas are crucial for the development of ionosphere semiempirical models such as the international reference ionosphere (IRI) [9]. The models are used operationally for predicting radar range errors [10], for microwave remote sensing [11], for validation of TEC profiles obtained by radio occultation technique with the satellites to forecast the environment state (e.g., NASA’s International Solar-Terrestrial Physics Program (http://istp.gsfc.nasa.gov [accessed on 13 July 2022]) or VarSITI (http://www.varsiti.org, etc.)).
The ionospheric model is a mathematical description of the ionosphere as a function of location, altitude, day of a year, phase of the sunspot cycle and geomagnetic activity. GPS satellites broadcast the parameters of the Klobuchar ionospheric empirical model for single-frequency users [12]. The model assumes that the electron density is concentrated in a thin layer. The model reduces up to the 50% RMS ionospheric range error worldwide.
However, the difference between the real ionosphere and a model used in single-frequency GNSS (NeQuick-G [13] model in Galileo, Klobuchar model [12] in GPS, BDGIM model in BeiDou [14]) could cause significant errors in user-position estimation [15], e.g., GNSS of smartphones, drones, airborne GNSS receivers, etc. To improve navigation, engineers and scientists need to improve the global ionospheric models. Different spatial and temporal anomalies still challenge ionosphere modelling, especially under the increasing requirements for precision level. In this paper, we step forward to improve the accuracy of the current description of the global ionosphere via new ways to catch spatial anomalies.
Recently, McGranaghan et al. [16] involved network theory for the high-latitude ionosphere based on Madrigal TEC data to study multiscale connectivity in the geospacer. They showed that network analysis can identify significant patterns in observational data and revealed that distinct regions emerge within the dayside and night-side systems that react to geophysical processes together. Lu et al. [17] developed an ionospheric network based on global ionosphere maps for 2012. They showed that ionospheric network is not scale-free so there is no unique spatial position acting as the source or sink.
On the basis of observational results (for the period from 1998 to 2015), below we show that there are two essential areas with “anomalous” behavior in the total electron content (TEC). A method of an ionospheric network construction is developed, showing that anomalies can be effectively detected in the total electronic content. We further discuss the origins of these patterns, suggesting possible relations between anomalies and other effects.
2. Materials and Methods
2.1. Data
Global ionospheric maps (GIM) of total electron content in the ionosphere were used in the study. Several scientific groups produce GIM [18]. They cover the whole globe: from –87.5° to 87.5° in latitude and 360° in longitude (but note that 0° and 360° are the same longitudes). Each cell has the size of 2.5° in latitude and 5° in longitude and contains the value of the vertical total electron content (TEC). Depending on technique/analytic center, maps are generated every 15 min, 1 h or 2 h and are available since 1998. Data on a separate map are arranged on the grid with the size of 71 × 72 cells, so we have 5112 different cells in total.
The initial data for the maps are “slant” TEC series obtained from several hundred GNSS stations [2]. Each analytic center uses its own approach to reconstruct “vertical” TEC and spatial interpolation [19,20,21,22]. Therefore, following the general tendency, the maps of different centers differ from each other [18].
In the paper, we used the GIM final product (CODG) made by the Center for Orbit Determination in Europe (CODE), which applies the single-layer spherical harmonic model to reconstruct the TEC value [21,22]. Figure 1 shows an example of the map on 1 January 2008, at 16:00, UT. The TEC value is in TECU units (1016 electron/m2). Global ionosphere maps in the IONEX format [23] are freely available via the Internet (https://cddis.nasa.gov, accessed on 12 July 2022).
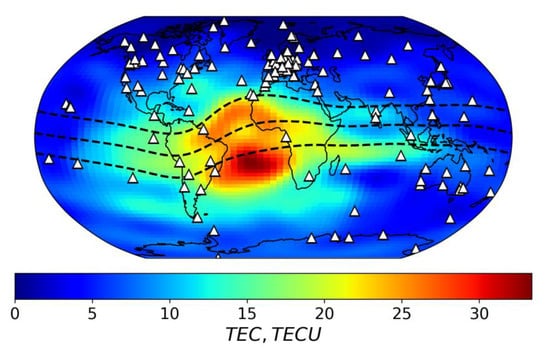
Figure 1.
Global ionospheric map of TEC based on CODE data for 1 January 2008, at 16:00 UT. Dashed line indicates geomagnetic equator and geomagnetic parallels, triangles are GPS/GLONASS stations used to create the map.
2.2. Method
We used the GIMs for the period from 1 June 1998 to 31 December 2015. The total number of treated files was 8495.
For each GIM cell over that period, we calculated the deviation series of TEC mean diurnal value from the mean annual value in a moving window of ±182 days :
where is the current day, and are latitude and longitude of a current GIM cell, is the mean diurnal TEC value in the cell, and is the mean TEC value calculated with the moving average in the sample window of ±182 days relative to .
A network approach was applied to these data. This approach is well developed and is applied to investigate different complicated systems [24], including neutral atmosphere [25]. The application of the network approach allows us to detect the relation between different regions and to find the regions with special dynamics of TEC.
The network theory deals with a set of nodes (or vertices) and the links (or edges) between them. A node is an object with some properties. One can consider any object as a node if we have a set of objects and some links between them. Examples of nodes/links include people/know each other; web servers/connected; cities/roads between; and many others. A node and a link can be described by different parameters. Below we use the term “degree”, i.e., how many links the node has.
We consider the ionosphere as a spatial network, where a GIM cell is a node. Thus, each node is associated with geographical coordinates and TEC deviation series calculated by equation (1) for this cell. Any two GIM cells form a node pair. In total, we have million pairs.
To find links between a node pairs we need a rule. Investigations often use correlation analysis to reveal interconnection [26]. If the cross-correlation function exceeds some limit, we consider the nodes to be linked. As the criterion of the link between two nodes, we used the maximum value rmax of cross-correlation function r(Δt) in the window of Δt = ±1 day.
where N is a number of days (8495), dI1,1 and dI2,2 corresponds TEC deviations at first and second nodes, Δt is the time lag of −1, 0, or +1 day.
We need to calculate rmax (rather than just the Pearson correlation coefficient r(0)) to remove diurnal variation effects. UT time is used in the initial time series of TEC, so variation maxima may turn out to be in different days according to LT.
We consider two nodes to be linked when the value rmax between two series exceeds the threshold A ≈ 0.86. It corresponds to the value of the third quartile Q3 (75%) on the distribution of values rmax calculated between all the possible series of node pairs (Figure 2).
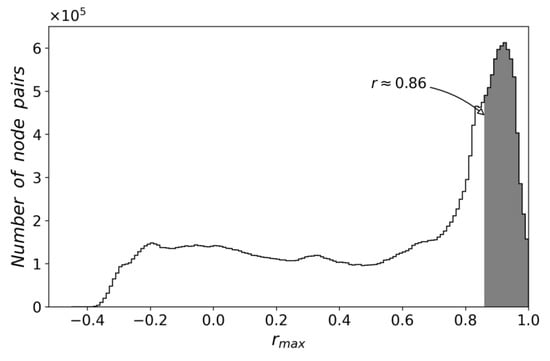
Figure 2.
Distribution of maxima rmax of cross-correlation functions calculated for the series of deviations of mean daily TEC values from the mean annual TEC dI for the period from 1998 to 2015; the shaded area indicates the values where rmax is higher than the threshold A = 0.86.
3. Ionospheric Network
The analysis of the distribution of rmax values made it possible to choose the threshold. The distribution is bimodal and the values are distributed more or less evenly to some inflexion point ~0.7, after which sudden growth begins (Figure 2). We think that the processes responsible for correlation coefficient value change qualitatively in the vicinity of this point, so it is reasonable to choose the threshold here or higher. At this stage, we chose Q3 because this value is deliberately higher than the inflexion point and is easily estimated for any set of initial data.
Having determined the nodes and the link criterion, we constructed an ionospheric network. To make it visual, we referred to the fact that each node is associated with the geographical coordinates of a GIM cell. That is why we put the degree, i.e., how many links the node has, of each node on the geographical map (Figure 3).
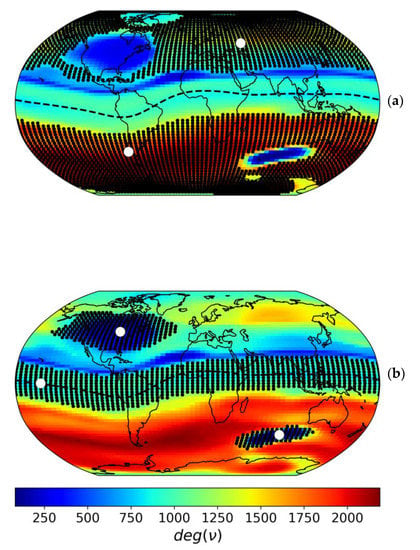
Figure 3.
Ionospheric network. Color indicates the degree—how many links each node υ of the network has. Dashed lines on both panels indicate the geomagnetic equator. A large white circle is an example of a node in the chosen region, and small black circles are the nodes directly linked with it (so-called neighbors). Panel (a) shows nodes (−75° E, −42.5° N) and (50° E, 52° N) with their neighbors in the regions of the North American and Australian anomalies. Panel (b) shows node (−155° E, 0° N) in the equatorial region, node (−85° E, 45° N) in the northern hemisphere and node (90° E, −45°N) in the southern hemisphere with their neighbors.
The maximal value of a node’s degree can be 5111, i.e., the number of GIM cells minus the current. However, the nodes in different hemispheres are almost not connected. Therefore, the actual maximal value of the degree is 2188, the minimal value is 81 and the median value is about 1200.
Figure 3 shows the main domains with separate dynamics. A large white circle is an example of a node and small black circles are the nodes directly linked with it (so-called neighbors). Panel (a) shows nodes (−75° E, −42.5° N) and (50° E, 52° N) with their neighbors in the regions of the North American and Australian anomalies. Panel (b) shows node (−155° E, 0° N) in the equatorial region, node (−85°E, 45° N) in the northern hemisphere and node (90° E, −45° N) in the southern hemisphere with their neighbors.
The topology of the obtained network features typical spatial distribution and dynamics of the ionospheric plasma. It is generally assumed to divide the ionosphere into several latitudinal regions: high-, mid-, and low-latitude regions with the equatorial anomaly [27]. They appear as domains, large, isolated parts, in the network. Nodes inside the domain are linked, and the domains almost do not have links outside (Figure 3). Panel (b) shows two nodes in the middle of these regions and the corresponding neighbors. Thus, TEC dynamics inside the domains have the same character. The domains of the hemispheres (northern and southern), equator and equatorial anomaly regions are clearly seen in the figure, whereas the polar regions are weakly marked.
Moreover, the network contains two “anomalies”, clear patterns over North America and in the region of Australia, located symmetrically relative to the geomagnetic axis. They are characterized by a fewer number of links in comparison to the rest of the part of corresponding hemispheres (Figure 3). The North American anomaly has a minimum number of “outside” links and, thus, is virtually closed upon itself. The Australian anomaly has a greater (in comparison to the North American one) number of links and is more extended in the longitudinal direction. The patterns standing out against the domains indicate that TEC dynamics inside these regions differ from those in the larger part of the corresponding hemispheres.
4. Discussion
Can the obtained results be just some artifacts? We supposed that the patterns have a natural character and are not artifacts which appeared in the process of the reconstruction of global ionospheric maps. To verify that, we constructed an ionospheric network based on the data of another scientific group. The group of Astronomy and Geomatics of the Polytechnic University of Catalonia (gAGE/UPC) applies an approach different from the Center for Orbit Determination in Europe to recover TEC: they apply the two-layer tomographic model to reconstruct the TEC value [28]. In spite of that, the network obtained on the basis of UQRG data differs in detail but has a similar typology with clearly defined domains of the hemispheres and “anomaly” patterns (not shown here).
We suppose that patterns are associated with the seasonal anomaly of the ionosphere F-region. The seasonal (or winter) anomaly is the situation in which the highest value of electron density maximum NmF2 (or critical frequency foF2 values) is observed in winter [5]. It occurs due to the transfer of the atmosphere neutral component by vertical and horizontal winds associated with the global thermospheric circulation [5,6]. Winter anomaly also affects the total electron content [29].
TEC seasonal variations significantly influence the value of the correlation coefficient between the used TEC deviation series dI. TEC initial values are daily averaged and the most evident harmonics in the series obtained by equation (1) are seasonal changes. The differences in the TEC seasonal variations cause the decrease in the correlation coefficient between nodes inside and outside an “anomalous” region, which decreases the degree of a node in the “anomalous” regions.
The geographical location of patterns in our network is similar to the location of seasonal (winter) anomaly regions [30]. Torr and Torr [30] drew maps which reflect the regions where noon value of the critical frequency foF2 reaches its maximum in winter. The most outstanding feature of these maps is the presence of regions with strong seasonal anomaly at middle latitudes in the North American and European sectors. There is also such a region near Australia, though its area is significantly lesser. Winter anomaly intensity and regions depend on solar cycle and geomagnetic activity [31]. During the solar minima, the winter anomaly disappears in Australia and changes over North America and Europe (but is still well defined here).
At the same time, the spatial patterns of the ionospheric network differ from the patterns of the winter anomaly [30]. The network shows no peculiarities over Europe, but the winter anomaly does. The differences may be the result of the fact that different time periods and various ionospheric parameters were used. The data on which the network is based cover the period from 1998 to 2015. It includes two cycles of solar activity with F10.7 [32] varying within 65–325 s.f.u. (“solar flux units”). Whereas foF2 maps [30] correspond to 1958, 1969 and 1964 for very high (mean annual value F10.7 ≈ 241 s.f.u), moderate (≈151 s.f.u.) and low solar activity (≈72 s.f.u.), respectively. In addition, noon NmF2 (or TEC) values are usually considered in the investigation of the seasonal anomaly, but we used mean daily values.
Yasyukevich et al. [31] showed that the winter anomaly in TEC resembles the winter anomaly in foF2, especially at the solar maximum. Figure 4 compares the ionospheric network and the winter anomaly. We still see a clear difference for these “anomalies”, but the close position implies that the ionospheric network catches manifestation of the winter anomaly.
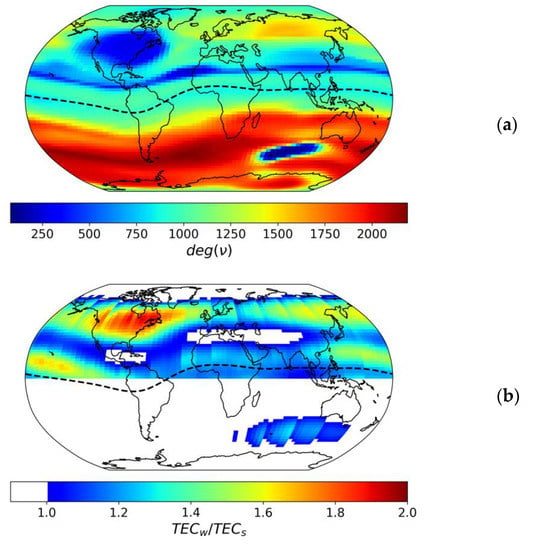
Figure 4.
Comparison of ionospheric network based on CODE data (a) and the winter anomaly intensity in TEC (b). In panel (a), color shows the degree (deg, how many links the node has) for each node v of the network. In panel (b), the color shows the winter anomaly intensity (winter-to-summer TEC) at high solar activity (F10.7 = 200 s.f.u.) and moderate geomagnetic activity. Panel (b) was re-drawn from Figure 4f in [31]. Dashed lines show the geomagnetic equator.
Current research used only one metric (cross-correlation between nodes, only one parameter), the deviation between diurnal mean TEC and semi-annual mean TEC and only one chosen period. Other parameters/metrics/input data could provide a deeper insight into the ionospheric dynamics.
5. Conclusions
The ionospheric network has been constructed. Experimental data of GIM CODG for the period from 1998 to 2015 were used. We showed that network topology corresponds to general conception on the dynamics and spatial distribution of ionospheric plasma. The main finding is that the network contains two clear patterns over North America and Australia. We attribute their occurrence to the winter anomaly. The obtained results open the possibility to better understand the interaction of geographically different regions of the ionosphere. We hope that researchers will use the suggested technique to validate and improve the ionospheric models.
Author Contributions
Conceptualization, I.V.Z. and Y.V.Y.; methodology, I.V.Z.; software, I.V.Z.; validation, I.V.Z. and Y.V.Y.; formal analysis, I.V.Z.; investigation, I.V.Z. and Y.V.Y.; resources, I.V.Z.; data curation, I.V.Z.; writing—original draft preparation, I.V.Z. and Y.V.Y.; writing—review and editing, I.V.Z. and Y.V.Y.; visualization, I.V.Z.; supervision, I.V.Z.; project administration, Y.V.Y.; funding acquisition, Y.V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education of the Russian Federation.
Data Availability Statement
Global ionosphere maps are available via the Internet (https://cddis.nasa.gov/Data_and_Derived_Products/GNSS/atmospheric_products.html (accessed on 12 July 2022)).
Acknowledgments
The authors are grateful to Elena Surovyatkina for her discussion and her help in the abstract and introduction preparation, to Tamara Gulyaeva for her interest in the paper and valuable comments, to Konstantin Ratovsky and Maxim Klimenko for their meaningful discussions and to NASA’s Archive of Space Geodesy Data, CODE, and gAGE/UPC for the GIM data. Figures in the paper were made by the packages of Python matplotlib [33] and cartopy [34].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cannon, P.S. Mitigation and exploitation of the ionosphere: A military perspective. Radio Sci. 2009, 44, RS0A20. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems. GPS, GLONASS, Galileo, and more; Springer: Wien, Austria, 2008; p. 518. ISBN 978-3-211-73012-6. [Google Scholar] [CrossRef]
- Rishbeth, H. Some problems of the F region. Radio Sci. 1974, 9, 183–187. [Google Scholar] [CrossRef]
- Giraud, A.; Petit, M. Ionospheric Techniques and Phenomena; Springer: Dordrecht, The Netherlands, 1987; p. 265. [Google Scholar] [CrossRef]
- Rishbeth, H. How the thermospheric circulation affects the ionospheric F2-layer. J. Atmos. Sol. Terr. Phys. 1998, 60, 1385–1402. [Google Scholar] [CrossRef]
- Rishbeth, H.; Mendillo, M. Patterns of F2-Layer Variability. J. Atmos. Sol-Terr. Phys. 2001, 63, 1661–1680. [Google Scholar] [CrossRef]
- Karpachev, A.; Gasilov, N.; Karpachev, O. Morphology and causes of the Weddell Sea anomaly. Geomagn. Aeron. 2011, 51, 812–824. [Google Scholar] [CrossRef]
- Klimenko, M.; Klimenko, V.; Ratovsky, K.; Zakharenkova, I.; Yasyukevich, Y.V.; Korenkova, N.; Cherniak, I.; Mylnikova, A. Mid-latitude Summer Evening Anomaly (MSEA) in F2 layer electron density and Total Electron Content at solar minimum. Adv. Space Res. 2015, 56, 1951–1960. [Google Scholar] [CrossRef]
- Bilitza, D.; McKinnell, L.-A.; Reinisch, B.; Fuller-Rowell, T. The International Reference Ionosphere (IRI) today and in the future. J. Geod. 2011, 85, 909–920. [Google Scholar] [CrossRef]
- Ovodenko, V.B.; Trekin, V.V.; Korenkova, N.A.; Klimenko, M.V. Investigating range error compensation in UHF radar through IRI-2007 real-time. Adv. Space Res. 2015, 56, 900–906. [Google Scholar] [CrossRef]
- Abraham, S.; Le Vine, D.M. Use of IRI to model the effect of ionosphere emission on earth remote sensing at L-band. Adv. Space Res. 2004, 34, 2059–2066. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric time-delay algorithm for single-frequency GPS users. IEEE Trans. Aerosp. Electron. Syst. 1987, 23, 325–331. [Google Scholar] [CrossRef]
- European Union. European GNSS (Galileo) Open Service-Ionospheric Correction Algorithm for Galileo Single Frequency Users. 1.2. 2016. Available online: http://www.gsc-europa.eu/system/files/galileo_documents/Galileo_Ionospheric_Model.pdf (accessed on 13 July 2022).
- Wang, N.; Li, Z.; Yuan, Y.; Huo, X. BeiDou Global Ionospheric delay correction Model (BDGIM): Performance analysis during different levels of solar conditions. GPS Solut. 2021, 25, 97. [Google Scholar] [CrossRef]
- Angrisano, A.; Gioia, C.; Gaglione, S.; del Core, G. GNSS Reliability Testing in Signal-Degraded Scenario. Int. J. Navig. Obs. 2013, 2013, 870365. [Google Scholar] [CrossRef][Green Version]
- McGranaghan, R.M.; Mannucci, A.J.; Verkhoglyadova, O.; Malik, N. Finding multiscale connectivity in our geospace observational system: Network analysis of total electron content. J. Geophys. Res. Space Phys. 2017, 122, 7683–7697. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, H.; Li, X.; Li, Y.; Niu, C.; Yang, X.; Liu, D. Complex network description of the ionosphere. Nonlin. Processes Geophys. 2018, 25, 233–240. [Google Scholar] [CrossRef]
- Roma-Dollase, D.; Hernández-Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Li, Z.; Zhang, H.; Shi, C.; Wang, C.; et al. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geod. 2018, 92, 691–706. [Google Scholar] [CrossRef]
- Schaer, S.; Beutler, G.; Rothacher, M. Mapping and predicting the ionosphere. In Proceedings of the 1998 IGS Analysis Center Workshop, Darmstadt, Germany, 9–11 February 1998; pp. 307–320. [Google Scholar]
- Mannucci, A.J.; Wilson, B.D.; Yuan, D.N.; Ho, C.M.; Lindqwister, U.J.; Runge, T.F. A global mapping technique for GPS-derived ionospheric TEC measurements. Radio Sci. 1998, 33, 565–582. [Google Scholar] [CrossRef]
- Schaer, S.; Beutler, G.; Mervart, L.; Rothacher, M.; Wild, U. Global and regional ionosphere models using the GPS double difference phase observable. In Proceedings of the IGS Workshop on Special Topics and new Directions, Potsdam, Germany, 15–17 May 1995; pp. 77–92. [Google Scholar]
- Hernandez-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Schaer, S.; Gurtner, W.; Feltens, J. IONEX: The IONosphere Map Exchange Format; Version 1. In Proceedings of the 1998 IGS Analysis Center Workshop, Darmstadt, Germany, 9–11 February 1998; pp. 233–247. Available online: http://ftp.aiub.unibe.ch/ionex/draft/ionex11.pdf (accessed on 13 July 2022).
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Stolbova, V.; Martin, P.; Bookhagen, B.; Marwan, N.; Kurths, J. Topology and seasonal evolution of the network of extreme precipitation over the Indian subcontinent and Sri Lanka. Nonlin. Processes Geophys. 2014, 21, 901–917. [Google Scholar] [CrossRef]
- Timchenko, A.V.; Bessarab, F.S.; Klimenko, M.V.; Radievsky, A.V.; Klimenko, V.V. Correlation Analysis of Global Ionospheric Total Electron Content Maps in March 2015. Geomagn. Aeron. 2022, 62, 217–226. [Google Scholar] [CrossRef]
- Schunk, R.W.; Nagy, A.F. Ionospheres: Physics, Plasma Physics, and Chemistry; Cambridge University Press: Cambridge, UK, 2009; p. 628. [Google Scholar] [CrossRef]
- Hernandez-Pajares, M.; Juan, J.; Sanz, J. New approaches in global ionospheric determination using ground GPS data. J. Atmos. Sol. Terr. Phys. 1999, 61, 1237–1247. [Google Scholar] [CrossRef]
- Zhao, B.; Wan, W.; Liu, L.; Mao, T.; Ren, Z.; Wang, M.; Christensen, A.B. Features of annual and semiannual variations derived from the global ionospheric maps of total electron content. Ann. Geophys. 2007, 25, 2513–2527. [Google Scholar] [CrossRef]
- Torr, M.R.; Torr, D. The seasonal behaviour of the f2-layer of the ionosphere. J. Atmos. Terr. Phys. 1973, 35, 2237–2251. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Yasyukevich, A.S.; Ratovsky, K.G.; Klimenko, M.V.; Klimenko, V.V.; Chirik, N.V. Winter anomaly in NmF2 and TEC: When and where it can occur. J. Space Weather Space Clim. 2018, 8, A45. [Google Scholar] [CrossRef]
- Tapping, K.F. The 10.7 cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Met Office. Cartopy: A Cartographic Python Library with a Matplotlib Interface. Exeter, Devon, 2010–2015. Available online: http://scitools.org.uk/cartopy (accessed on 13 July 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).