Abstract
Potential prediction is an important research content of thunderstorm gale weather forecast, and it is still a challenge because the environmental field of thunderstorm gale presents different characteristics under different weather conditions. Using the 12-year thunderstorm gale data of Hubei province in central China and the reanalysis data of National Center for Environmental Prediction (NCEP), this study analyzed the percentile distribution of environmental physical quantities of thunderstorm gale, and the continuous probability method was adopted to establish the probability forecast models of thunderstorm gale in four different types of weather situation, which are in the rear of trough type, in front of trough type, in the periphery of the western Pacific subtropical high type and easterly airflow type. Finally, probability prediction was realized by objective classification criterion in operation. The results show that the method based on objective classification and continuous probability can significantly improve the probability of thunderstorm gale detection, and also reduce the missing alarm rate of thunderstorm gale. Moreover, the quantitative test of 16 weather processes under four types of weather situations also shows that the continuous probability method has a higher probability of detection than the bisection method, and significantly reduces the missing alarm of extreme wind by the bisection method.
1. Introduction
Surface gales driven by convection occurs suddenly and are destructive, with short defense time and great forecast difficulty [1,2]. Early forecasting of thunderstorm is essential in order to safeguard and prevent the damages resulting from these violent thunderstorms.
Thunderstorm gales forecast includes nowcasting forecast and potential forecast. Nowcasting forecast of thunderstorm gales are mainly based on the morphology of radar echo. For example, organized linear storms, the type of storm that has a wide influence range and the longest duration in thunderstorm gales [3,4,5,6]. However, Schoen and Ashley [7] classified 191 non-tornadic convective gale events and found that 45% of non-tornadic gales were unorganized or quasi-organized cell storms. Organized multi-cell storms accounted for 19%. Organized linear storms: squall line events accounted for 19%, bow echoes accounted for 24%. Guo and Sun [8] classified the organizational morphology of severe convective winds in Hubei Province from 2012 to 2017, and found that nonlinear mesoscale convective systems and isolated convective storms were the primary systems causing strong convective gales in Hubei Province. These studies showed that most thunderstorm gales occur in nonlinear and isolated storms. Therefore, in addition to the morphology of the organization, the identification of radar echo features, based on individual storms, such as mesocyclones, hook echo storms, gust front, bow echo and radial velocity convergence in middle and low levels, has become an essential means for the early warning of thunderstorm gales [9,10,11,12,13,14]. However, the nowcasting forecast based on radar echo cannot meet the forecast demand of more than 6 h. Therefore, thunderstorm gales potential forecast is still very important.
There are two main types of potential forecasts for thunderstorm gales: the identification method based on weather situations [15] and the prediction method based on environmental parameters [16]. For the identification of thunderstorm gales based on weather situations, Fang et al. [10] divided the weather situations of regional thunderstorm gales into three types, namely in the rear of trough type (REA_T), in front of trough type (FRO_T) and in the periphery of the western Pacific subtropical high (WPSH) type (PER_W). The weather situations of thunderstorm gales in Shandong from 1971 to 2008 was classified into four types by Yang et al. [17], including transverse trough type and the above three types. Moreover, they pointed out that there were differences in characteristics of physical quantities among different types. Wei et al. [18] categorized the weather situations of thunderstorm gales in Hubei Province from 2007 to 2015 into four types: high-level cold advection forced type, low-level warm advection forced type, baroclinic frontogenesis and quasi-barotropic type, and they also proposed that there were obvious differences among the different types in seasons, regions and environmental conditions. All above studies have pointed out the importance of weather situations, but only subjective classification is applied, the application of objective identification and forecast of thunderstorm gales has not been reported. At present, the forecast model of thunderstorm gales mainly depends on the research and application of environmental parameters, for example, Lei et al. [19] used radiosonde data to identify the severe convection weather in Beijing, and then calculated the occurrence probability of severe convection at the grid according to the basic radiosonde elements in the BJ-RUC model. This analysis showed that the probability forecast of severe convective weather is achievable, and the probability forecast of thunderstorm gales also has a certain success rate. Zeng et al. [20] obtained the piecewise function of the frequency distribution according to the spectral distribution of the featured convection parameters. Then, they established the probability forecast of classified severe convective weather in Jiangsu Province based on the mesoscale numerical model predictions, historical frequency distribution and weight allocation of the featured convection parameters. Therefore, the advantage probability was regarded as a classification criterion to carry out the forecast of the classified severe convection. Ma et al. [21] compared the critical environmental parameters of extreme thunderstorm gales and ordinary thunderstorms in various regions of China from 2002 to 2017. They revealed that there were apparent differences in atmospheric precipitable water, convective available potential energy (CAPE), vertical temperature lapse rate in the middle and lower troposphere, downdraft convective available potential energy, average wind velocity in the entrainment zone and vertical wind shear. Cohen et al. [22] examined 186 soundings taken in the environment of three quasi-linear MCS categories. Differences in the variables among weak, severe, and derecho-producing MCS categories were identified and discussed. Wang et al. [23] showed that there were obvious differences in storm types, surface gale distribution and disaster degree between the thunderstorm gales occurring successively in the two adjacent regions affected by the sub-synoptic-scale transverse trough behind the cold vortex on 3 June 2009. These differences were mainly due to the different environmental characteristics in these two regions. These studies indicate that there are certain differences in the corresponding environmental parameters of thunderstorm gales in different environments or in different stages of a process. Therefore, great uncertainty may exist in the forecast of thunderstorm wind solely relying on environmental parameters. Although machine learning can theoretically compensate for this uncertainty, its practical effects are still being tested. For example, Zhou et al. [24] used the GFS (Global Forecasting System) forecast data to construct the forecast model of thunderstorms, short-term heavy precipitation, hail and thunderstorm gales based on a deep convolution neural network method. The forecast product from this forecast model are being applied and tested in the operational forecast of severe convective weather at the National Meteorological Center.
The above studies have demonstrated that thunderstorm gales can occur in a various weather situations, and there are obvious differences in environmental field characteristics. The accuracy of the subjective forecast of thunderstorm gales is still low [25]. As shown in Yu and Zheng [26], combining the identification method based on weather situations with the prediction method based on environmental parameters can achieve the best forecast results. However, it is not common to use this fusion method to objectively forecast thunderstorm gales. Furthermore, all large-scale and mesoscale numerical models do not have direct forecast products of thunderstorm gales at present. Although there are still many uncertainties in numerical weather prediction (NWP) products, the NWP products from high-resolution regional numerical models and their application are still the main technical support for the short-term forecast of severe convective weather [16,27,28]. In this study, we focus on the differences of physical quantities in environmental fields under different weather situations and develop a probability forecast product of thunderstorm gales based on objective classification. This probability forecast product can resolve the problems that the existing severe convection weather forecast products cannot be classified, identified and automated grid forecast, and provide a useful reference for thunderstorm gale forecasts.
2. Data and Methods
2.1. Data
The data used in this study include: (1) The actual surface weather data provided by the National Meteorological Science Data Center (http://data.cma.cn, accessed on 10 January 2017), including special weather observations and hourly surface gale observations. In this study, the definition of thunderstorm gale given by Tang et al. [29] (instantaneous wind speed of ≥17.2 m∙s−1) is used as the standard. According to this standard, there are 235 thunderstorm gale samples from 60 severe convective weather processes was selected based on surface observation data of Hubei Province from 2005 to 2016. (2) The data used for statistical analysis and construction of probabilistic forecast models are from Historical Unidata Internet Data Distribution (IDD) Gridded Model Data (ds335.0) of National Centers for Environmental Prediction (NCEP, https://rda.ucar.edu/datasets, accessed on 10 October 2016). These data include multi-layer pressure field data of global temperature, pressure, wet wind and other elements since November 2006, with spatial resolution of 0.5° × 0.5° and temporal resolution of 6 h, which can accurately represent the characteristics of the environmental field [30]. The data from 2005 to 2006 are supplemented by FNL Operational Model Global Tropospheric Analysis Data (ds083.2) from NCEP, with spatial resolution of 1° × 1° and temporal resolution of 6 h, which could also accurately reproduce the environmental field features [30]. (3) The data used to generate real-time probabilistic forecast products are delivered from the China Meteorological Administration (CMA) through the operational Intranet. Delivered data are the real-time Numerical Weather Forecasts (NWP) products from European Centre for Medium-Range Weather Forecasts (ECMWF), have the same elements as NCEP data. The spatial resolution was 0.25° × 0.25°, and the temporal resolution was 3 h.
2.2. Weather Classification
Hubei Province is located in Central China, with mountainous areas in the west and plain areas in the middle and east (Figure 1). Under the influence of the Qingha–Tibet Plateau, North China Plain and the oceans of eastern and southern China, Central China is often affected by the westerly trough and WPSH, resulting in complex and diverse weather conditions that cause thunderstorms gales. Based on the method of Fang et al. [10] and Yang et al. [17], this study classifies the weather situations of 235 thunderstorm gale samples by similarity, and divided them into four types according to the weather situations of thunderstorm gale in Hubei Province, namely in the rear of trough type (REA_T, 24 samples), in front of trough type (FRO_T, 124 samples), in the periphery of the WPSH type (PER_W, 60 samples) and easterly airflow type (EAS_A, 27 samples). According to the weather situation, the physical quantities [19,31] associated with dynamic conditions, water vapor, atmospheric instability and temperature stratification are calculated by the NCEP reanalysis data. The specific physical quantities are shown in Table 1. The values of physical quantities under different weather types are selected according to the proximity principle and the closest time before the occurrence of thunderstorm gales.
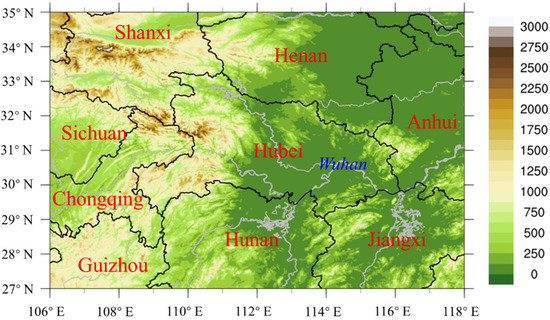
Figure 1.
Topography and area name of the study. The filled color indicates terrain. The red characters are the province name and the blue character is the city name.

Table 1.
Physical quantities and values of different weather situations used for prediction.
The criteria for the objective identification of weather situations is the 500 hPa zonal wind characteristics. If the 500 hPa zonal wind is dominated by an easterly component, the weather situations are identified as EAS_A. In the case of the 500 hPa zonal wind dominated by a westerly component, if the meridional wind is dominated by a northerly component, the weather situations is identified as REA_T. Otherwise, in the case of meridional wind dominated by a southerly component, the weather situation is classified as FRO_T (vertical wind shear ≥ 10 m∙s−1) and WPSH edge types (vertical wind shear < 10 m∙s−1) according to the 0–6 km vertical wind shear intensity respectively. Different weather situations identified objectively correspond to different probability forecast schemes.
2.3. Method of the Continuous Probability Modeling
Given inherent uncertainties in storm development, it is intuitive to predict severe storms in a probabilistic manner [32,33]. The probability forecast method developed in this study is based on an objective identification of weather situations and the continuous probability method [19]. A membership function is adopted in the continuous probability calculation method. In classical sets, the characteristic function can only take two values of 0 and 1, which is the concept of the bisection method. In fuzzy sets, the value range of the characteristic function is extended from two elements to the continuous interval of (0, 1) [34]. In order to distinguish the two sets, the characteristic function of fuzzy sets is called the membership function.
The methods for selecting membership function include the fuzzy statistics method, expert experience method and “Proving by Examples” method [35,36]. In this study, the fuzzy statistics method is used to select the membership function through the probability distribution characteristics of physical quantities. The probability density distribution of physical quantities related to four types of thunderstorm gale samples is calculated, as shown in Figure 2. For instance, the Covective available potential energy (CAPE) and Temperature-dew point spread (T−Td) at 700 hPa in front of trough display the characteristics of dense distribution with a fast variation of values in the middle and sparse distribution with a slow variation of values at both ends. According to these probability distribution characteristics, the ascending and descending half ridge functions are selected as the membership functions [37,38], as shown in Equations (1) and (2).
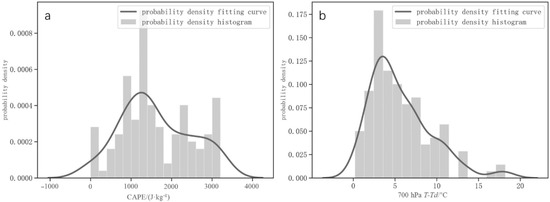
Figure 2.
Probability density distribution and fitting curve of physical quantities (a). CAPE, (b). 700 hPa T−Td) in weather situation of FRO_T.
For the physical quantities with a positive correlation with the probability of thunderstorm gales, the membership function adopts the ascending half ridge function, and vice versa, it selects the descending half ridge function. In terms of small probability events such as thunderstorm gales, since the harmfulness of the missing report is greater than that of the false forecast, the values of a and b are determined according to the percentile values of physical quantities, and they are taken based on the following two principles. First, for most physical quantities whose probabilities are calculated by using the ascending half ridge function, the values of a and b are taken as the 25% and 50% percentile values, respectively. For dew point (Td) representing the absolute water vapor content and T850−500 representing the atmospheric vertical temperature difference, a is taken as the minimum value (excluding outliers), and b is taken as the 50% percentile value. This way of taking values is mainly because Td and T850 hPa − T500 hPa (T850−500) are the basic atmospheric physical quantities, and the errors between the outputs of models and observations are small. Thus, the minimum values (excluding outliers) of physical quantities also need to be fully considered in probability calculation. Second, in terms of the descending half ridge function, the values of a and b are taken as the 50% and 75% percentile values, respectively, which fully consider the possibility of severe weather. That is, the missing report rate is reduced, and the excessive false reports caused by the low values of a and b can be avoided.
2.4. Quantitative Test Algorithm
In order to quantitatively test the effect of thunderstorm gale prediction products based on objective classification and continuous probability, the 12–36 thunderstorm gales probability forecast products from ECMWF was tested hourly by using the spatial neighborhood method (the radius of 40 km, referring to the test scheme of the national intelligent forecast technology method competition). The probability of ≥60% is regarded as the critical threshold for judging the occurrence of thunderstorm gales. The threat score (TS) [39] has been used in many operational forecast verification tests. The other three skill scores (the probability of detection (POD), missing alarm rate (MAR) and the false alarm rate (FAR)) [40] were also calculated as follows:
where h, m, and f are defined as hits, misses, and false alarms, respectively.
3. Construction of the Probability Forecast Method for Thunderstorm Gales
3.1. Forecast Scheme
In this paper, the probability forecast method of thunderstorm gale is divided into three steps:
First, the ECMWF NWP data are read in real time, and all physical quantities required in the probability forecast of thunderstorm gales are calculated. Although the parameter values of the continuous probability method based on objective classification are derived from NCEP reanalysis data, the operational forecast product based on ECMWF numerical forecast data has achieved good forecast effect since it was put into real-time operation since 2017. See Section 4 for detailed product test.
Second, one of the key technologies of this forecast scheme is to objectively identify weather situations based on the distribution characteristics of wind fields on grid points. This step aims to develop different forecast schemes for different weather situations in order to improve the accuracy of probability forecast products.
Third, this step is to calculate the occurrence probability of thunderstorm gales at grids. This scheme is based on a continuous probability method rather than bisection method to perform the probability calculation. This is because, in the bisection method, a discriminant condition, i.e., a threshold value, needs to be pre-set for physical quantity parameters. All cases where parameters meet the discriminant condition are recorded as 1. Otherwise, they are recorded as 0. Through experiments, we found that the calculation results of the bisection method highly rely on the discriminant condition. For example, in terms of the instability index T850−500, we assume that the discriminant condition is T850−500 ≥ 25 °C. Suppose the T850−500 values at two adjacent grid points i and j are 24.9 °C and 25.0 °C (a slight T850−500 difference). In that case, the judgment results at the two adjacent grid points are obviously different, which is overly extreme compared with the actual situation. Therefore, a continuous probability calculation method is adopted in this scheme to avoid the shortcoming of the bisection method. In this method, quantitative relationship between each physical quantity value and its corresponding probability is established according to statistics and membership function [41]. Based on this, the total probability can be obtained by calculating the probabilities of multiple physical quantities, as shown in Equation (3).
where Q denotes the probability value, f (x) the membership function of a physical quantity, W the weight coefficient and n the number of physical quantities. Previous studies [42] have shown that different physical quantities have different skill scores in predicting thunderstorm events. Therefore, the weight coefficients of physical quantities on thunderstorm gale prediction still needs further study. In this scheme, the weight coefficients of each physical quantity remain the same for the time being. According to the modeling principle, the forecast parameters and values based on the continuous probability method under different weather situations are shown in Table 1. The flow chart of the forecast scheme is shown in Figure 3.
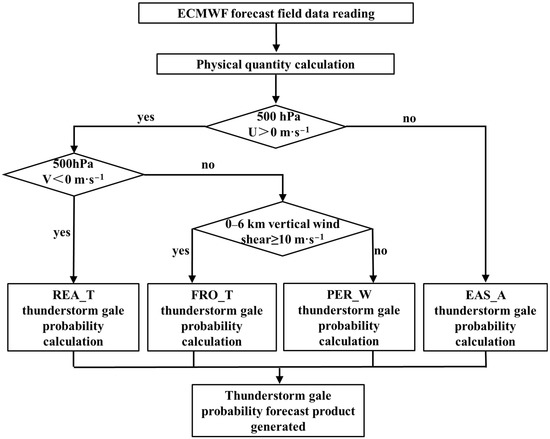
Figure 3.
Flow chart of thunderstorm gale probability forecast based on objective classification.
3.2. Parameter Settings of Different Weather Types
The statistical results of various physical quantities under different weather situations show that there are differences in the distribution of most physical quantities, and some physical quantities have large differences. Table 2 shows the statistical values of the 25%, 50% and 75% quantiles of most physical quantities. It can be found that the low-level humidity corresponding to REA_T is obviously lower than the other three types, but the value span from 25% to 75% is larger than that of the other three types. FRO_T has the highest K index, but it is not for the other unstable energy index. The vertical wind shear and boundary layer convergence of FRO_T and EAS_A are obviously weaker than those of the other two types. Figure 4 shows the boxplot of physical quantities with great differences in the four types of weather situations and the corresponding membership function. The results indicate that, under the influence of the probability distributions of physical quantities for different weather situations, both the variation rates of membership functions and the variation intervals of the corresponding physical quantities are different. For example, in the variation interval (0, 1) of the T850−500 membership function, the corresponding T850−500 values for EAS_A are between 23.0 °C and 26.5 °C, with an interval length of 3.5 °C. This interval length is 2 °C longer than that for PER_W. However, the T850−500 values for EAS_A are lower than those in REA_T (26.5 °C–29.5 °C). Thus, it is necessary to identify the weather situation objectively.

Table 2.
Statistical values of 25%, 50% and 75% of physical quantities.
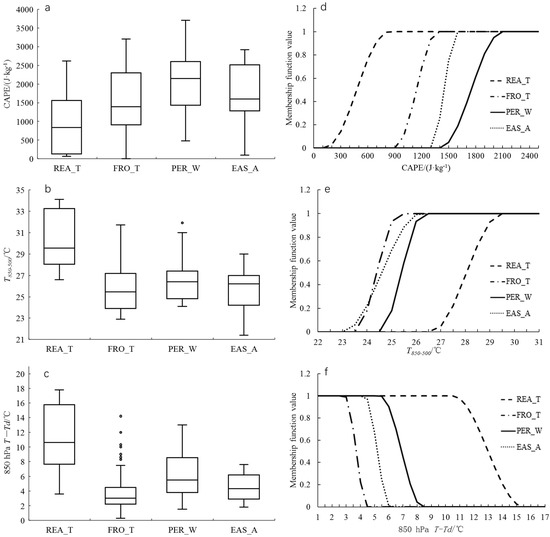
Figure 4.
Boxplots (a–c) and the corresponding membership function (d–f) of physical quantities in the four types of weather situations. (a,d) are the boxplots and the corresponding membership function of CAPE in the four types of weather situations. (b,e) are the boxplots and the corresponding membership function of T850-500 in the four types of weather situations. (c,f) are the boxplots and the corresponding membership function of 850 hPa T−Td in the four types of weather situations. In boxplots, the ○ at the top or bottom represents the outliers, and the short line at the top and bottom represents the maximum and minimum value (excluding outliers). The three lines from top to bottom of the box are the 75% percentile, the median and the 25% percentile respectively.
4. Results and Discussion
4.1. Compared with the Prediction Results of Reflectivity Factor
The radar reflectivity factor of China Meteorological Administration Mesoscale model (CMA-MESO) is used for comparison, because radar reflectivity monitoring is still the main monitoring technology for nowcasting and warning of thunderstorm gale at present. Just as Lin [35] used the radar reflectivity ≥40 dBZ as the thunderstorm live in objective prediction of warm season afternoon thunderstorms in northern Taiwan using a fuzzy logic approach, we also used the CMA-MESO hourly radar reflectivity factor of ≥40 dBZ as a comparison tests. The probability of ≥60% is regarded as the critical threshold for judging the occurrence of thunderstorm gales. Based on the 12–36 h probability forecast products of thunderstorm gales at 0800 BJT and 2000 BJT from April to September in 2020 and the corresponding CMA-MESO radar reflectivity factor prediction product, the hourly thunderstorm gale quantitative tests was conducted by using the spatial neighborhood method. The specific tests are shown in Table 3. The POD of probability prediction is 68.72%, the MAR is 31.28%, and the TS is 0.49%. Compared with the hourly CMA-MESO prediction product based on radar reflectivity factor, the POD of the forecast product generated in this study increases dramatically, and the MAR decreases obviously. Tang et al. [29] studied the scores of the subjectively identified national prediction products of severe convective weather. The results revealed that for the 6-h and 12-h forecasts of thunderstorm gales and hail, the minimum and maximum values of the MAR are 84% and 95%. Therefore, the method developed in this study obviously reduces the MAR and prolongs the forecasting time.

Table 3.
POD, MAR, FAR and TS of the thunderstorm gale probability forecast products and the CMA-MESO reflectivity factor.
4.2. The Advantage of Continuous Probability Method
The continuous probability method based on objective classification has been tested and operated in Central China Regional Meteorological Center since 2017. The characteristic function of probability prediction in the early stage was calculated on the bisection method (PPB). Statistics showed that there was too high MAR, and the FAR increased even if the parameter threshold was adjusted. Starting from 2019, the PPB characteristic function has been replaced by the membership function, namely continuous probability prediction method based on half-ridge function (PPCP) introduced in Section 2.3. Under the same objective classification, it can be found that the PPCP has obvious advantages by comparing with the PPB in the process of thunderstorm gale under four weather types. The quantitative test also shows that the PPCP can obviously reduce the MAR of thunderstorm gale.
Table 4 shows the quantitative test of two methods for predicting thunderstorm gale under four weather situations. It can be found that POD based on PPCP is higher than PPB for most cases, only two cases of FRO_T are low. However, FRO_T is the easiest type to forecast among the four types, and its average FAR is 33.05%, which is significantly lower than the other three types. This is also related to the fact that it is easier to forecast convective winds in the FRO_T weather with warm upper and cold lower layers and dry lower layers. The PPCP can significantly reduce the MAR of most cases, especially the MAR of the cases of REA_T and EAS_A. These two types of thunderstorms gales are less frequent occur, difficult to forecast, and have high MAR. The average MAR of these two types of thunderstorms gales based on PPB is 99.14%, of which 5/7 have MAR of 100%. The PPCP reduces the average MAR of them to 57.68%, but it is still lower than the average MAR (37.83%) of PER_W and FRO_T. In the following, the advantages of PPCB versus PPB in thunderstorm gales prediction will be analyzed by classifying typical cases.

Table 4.
Quantitative test of thunderstorm gale process corresponding to two methods under different type of weather situations.
4.2.1. A Case Study for REA_T Type
The REA_T thunderstorm gale is similar to the Type II in Maddox [43], which is caused by the influence of the cold air behind the trough. Based on the statistics of historical cases of thunderstorm gale in Hubei province, the proportion of the REA_T thunderstorm gale is very small, which is different from Maddox [43] and result in a certain deviation in the accuracy of the model. Therefore, it is the most missed in the probability forecast of the four types of thunderstorm gale. For example, the thunderstorm gale process on 11 August 2019 is a typical weather situations of REA_T. The weather situation (Figure 5a) shows that Hubei Province is controlled by the northerly airflow in the rear of the upper-level trough at 500 hPa. The ground observation (Figure 5b) illustrates that a large number of stations in western Hubei, northern Chongqing and southern Henan observed thunderstorm gales with wind speed above 17.2 m∙s−1 from 1400 BJT to 2100 BJT on 11 August. Specifically, the extreme wind speed in northern Chongqing (near 110° E, 31° N) occurred in 1500–1600 BJT, with wind speed of 35.1 m∙s−1 (Grade 12). From 1600 BJT to 1700 BJT, the extreme wind in northwest of Hubei (near 112° E, 32.5° N) reached 31.5 m∙s−1 (Grade 11), and the extreme wind in southwest of Hubei (near 111° E, 30° N) reached 28.5 m∙s−1 (Grade 11). After 1700 BJT, the extreme wind speed in all regions gradually decreased. Figure 5c exhibits the forecast results based on the PPCP. The model is run from 2000 BJT on 10 August 2019, and the forecast time of the thunderstorm gale process is 1400 BJT on 11 August. The results of the PPCP indicate that the thunderstorm gales with the probability ≥ 60% are mainly distributed in western Hubei and Chongqing, which is basically consistent with the observations. The probability in northern Chongqing is ≥70%, and the maximum reaches 84%, which is favorable to the early warning of the gale processes with an intensity of Grade 12 in northern Chongqing. However, the thunderstorm gales in the northern Henan and Anhui were missed. The forecast results based on the PPB are presented in Figure 5d, with the same starting time and forecast time as those of the PPCP. The probability obtained by the PPB is low in all regions, and the probability in western Hubei is below 60%. According to the quantitative test rules, when the probability reaches more than 60%, the thunderstorm gales are correctly predicted, and the PPB missed alarm the thunderstorm gales in western Hubei. Therefore, compared with the PPB, the PPCP can obviously reduce the MAR, and the areas with high probability value have a good indication of strong gales above Grade 11, even the PPCP still has a certain range of MAR.
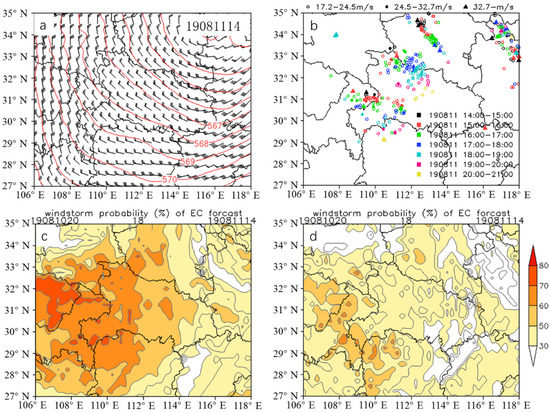
Figure 5.
A case study of REA_T thunderstorm gale on 11 August 2019: (a) Geopotential height (contours; dagpm) and wind field (vectors; m∙s−1). The number 19081114 in the upper right corner represents 14:00 on 11 August 2019 (b) The evolution of the surface wind speed ≥ 17.2 m∙s−1 in the case of 11 August 2019 (data from the surface weather observation provided by the National Meteorological Science Data Center). Different colors indicate different times, circles indicate wind speed between 17.2 and 24.5, dots indicate wind speed between 24.5 and 32.7, triangles indicate wind speed above 32.7. (c) Forecast results based on the PPCP. The number 19081020 in the upper left corner indicates that the running time is 20:00 on 10 August 2019, and the number 19081114 in the upper right corner indicates that the forecast time is 14:00 11 August 2019 (d) Forecast results based on the PPB.
4.2.2. A Case Study for FRO_T Type
In statistical analysis, FRO_T thunderstorm gale is the most common Type in Hubei Province, which is similar to Type III in Maddox [43]. For such thunderstorm gale, southwest airflow in front of trough superimposed low-level monsoon airflow, and this is consistent with the study of Fuelberg and Biggar [44], which pointed out that the strong convection was coupled with southwesterly winds [35]. It is found that for this type, the FAR is more and the MAR is less; moreover, the wind speed extreme value of thunderstorm gale is very high, which caused by the combination of southwest airflow in front of the trough and low-level southwest jet. For example, the case on 10 May 2021 is a thunderstorm gale process of FRO_T. The weather situation (Figure 6a) presents that central and eastern Hubei are controlled by the southwesterly airflow, and the 0–6 km vertical wind shear in southern Hubei generally exceeds 10 m∙s−1 (figure not shown). This thunderstorm gale process affected the central and eastern Hubei at 1200–1700 BJT on 10 May (Figure 6b). From 1400 BJT to 1500 BJT, the extreme wind speed at Erqi Yangtze River Bridge station in Wuhan was 44.9 m∙s−1, reaching the intensity of Grade 14. The forecast results of this thunderstorm gale process based on the PPCP at 1400 BJT on 10 May are shown in Figure 6c, with simulation starting time of 2000 BJT on 9 May 2021. Apparently, there are large areas in central and eastern Hubei with a probability ≥ 70%, and this is consistent with the observed thunderstorm gale regions. Moreover, two areas with a probability of ≥80% are found in central and eastern Hubei, with a northwest–southeast distribution, similar to the distribution in Figure 6b at 1400–1500. The PPB results are presented in Figure 6d, with the same starting time and forecast time as those in Figure 6c. The comparison suggests that there is a wide range with FAR of this thunderstorm gale process in Guizhou and Hunan Provinces for both the PPCP and PPB results. However, the large range of this thunderstorm gale process in central and eastern Hubei is predicted by the PPCP (Figure 6c), with an obviously high probability. The PPCP results provide a good indication for this extreme gale process in the Erqi Yangtze River Bridge in Wuhan. Similarly, with the probability threshold of ≥60%, the PPB results show a missing alarm in Wuhan. Thus, the forecast performance of the PPCP is better than that of the PPB. The shortcoming of the PPCP is that it fails to alarm thunderstorm gale process in Guizhou and Hunan Provinces.
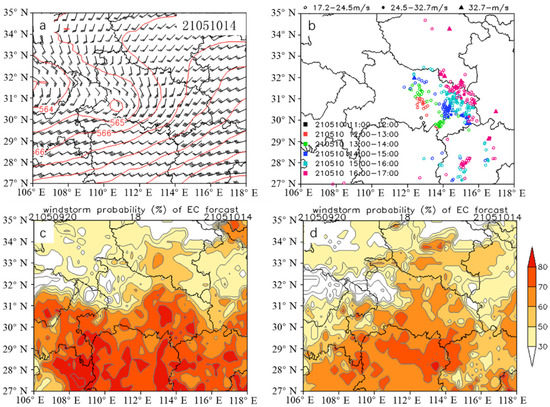
Figure 6.
Same to Figure 5 but for a FRO_T thunderstorm gale on 10 May 2021: (a) Geopotential height (contours; dagpm) and wind field (vectors; m∙s−1). The number 21051014 in the upper right corner represents 14:00 on 10 May 2021. (b) The evolution of the surface wind speed ≥ 17.2 m∙s−1 in the case. Different colors indicate different times, circles indicate wind speed between 17.2 and 24.5, dots indicate wind speed between 24.5 and 32.7, triangles indicate wind speed above 32.7. (c) Forecast results based on the PPCP. The number in the upper left corner indicates the running time, and the number in the upper right corner indicates the forecast time. (d) Forecast results based on the PPB.
4.2.3. A Case Study for PER_W Type
PER_W thunderstorm gale is the second most common weather type in Hubei province. During the WPSH extension to the west and jump to the north, there are high temperature and humidity in the middle and lower layers, and thermal instability. As Type I in Maddox [43], the severe thunderstorm are the result of northward and westward movement of the ridge position in southwest subtropical region. Due to the great uncertainty of cold advection in such type [17], the FAR is still high. The case on 20 August 2020 is a thunderstorm gale process of PER_W type. The weather situation in Figure 7a illustrates that eastern Hubei is controlled by the southerly airflow from the periphery of the WPSH. The extreme gales occurred in many places around Wuhan and in southern Anhui during this thunderstorm gale process (Figure 7b). During 1200–1300 BJT, the 31 m∙s−1 wind speed (Grade 11) was observed in the central urban area of Wuhan. Thereafter, the gale region expanded obviously at 1300–1700 BJT. In addition, five stations in eastern Hubei and southern Anhui observed the extreme wind speed exceeding Grade 10. Figure 7c shows the PPCP results at 1400 BJT on 20 August with starting time of 2000 BJT on 19 August 2020. Obviously, there are two regions with the probability ≥ 70% in eastern Hubei and Anhui, which is consistent with observations in Figure 7b. Compared with the PPB results at the same forecast time (Figure 7d), the probability of thunderstorm gales from the PPCP is 80% near Wuhan, higher than that of the PPB (<60%) in Wuhan. Clearly, the PPB misses the extreme gales near Wuhan. Moreover, the probability from the PPB is less than 70% in other areas. Hence, the PPCP performs better than the PPB in forecasting this thunderstorm gale process. However, both methods fail to forecast the thunderstorm gales in western Hubei.
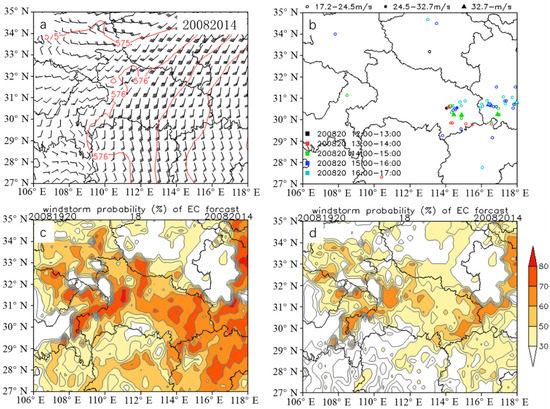
Figure 7.
Same to Figure 5 but for a PER_W thunderstorm gale on 20 August 2020: (a) Geopotential height (contours; dagpm) and wind field (vectors; m∙s−1). The number 20082014 in the upper right corner represents 14:00 on 20 August 2020. (b) The evolution of the surface wind speed ≥ 17.2 m∙s−1 in the case. Different colors indicate different times, circles indicate wind speed between 17.2 and 24.5, dots indicate wind speed between 24.5 and 32.7, triangles indicate wind speed above 32.7. (c) Forecast results based on the PPCP. The number in the upper left corner indicates the running time, and the number in the upper right corner indicates the forecast time. (d) Forecast results based on the PPB.
4.2.4. A Case Study for EAS_A Type
EAS_A thunderstorm gale is rare and less reported [10,17,39,45], and also it is difficult to predict. The case on 16 August 2020 is a local thunderstorm gale process of EAS_A. In this process, almost all current operational forecasting products failed to forecast. The weather situation in Figure 8a indicates that central and eastern China are controlled by the WPSH, and the Hubei province is in the easterly airflow on the south side of the WPSH. As shown in Figure 8b, the thunderstorm gale appeared from the south to the north in southeastern Hubei during 1500–1800 BJT on 16 August, and the extreme wind speed was observed at 1600–1700 BJT, with the value of 30.4 m∙s−1 (Grade 11). The forecast results from the PPCP at 1700 BJT on 16 August are presented in Figure 8c, with starting time of 2000 BJT on 15 August. It is found that the PPCP probability in southeastern Hubei is 82%, which is consistent with the observed thunderstorm gale center. However, the PPCP fails to forecast the thunderstorm gales in Henan and northwestern Hubei Provinces. Similarly, the PPB also fails to forecast the thunderstorm gales in Henan, especially the PPB completely misses the thunderstorm gales in southeastern Hubei (Figure 8d).
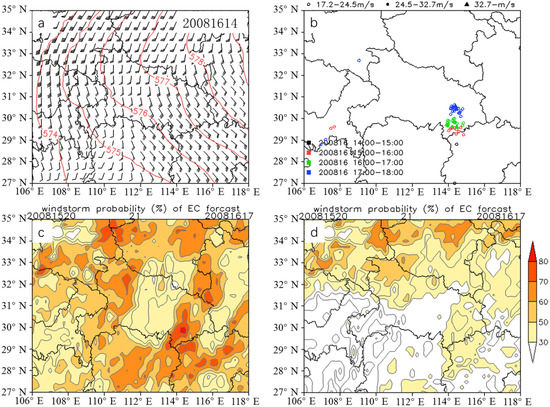
Figure 8.
Same to Figure 5 but for an EAS_A thunderstorm gale on 16 August 2020 (a) Geopotential height (contours; dagpm) and wind field (vectors; m∙s−1). The number 20081614 in the upper right corner represents 14:00 on 16 August 2020. (b) The evolution of the surface wind speed ≥ 17.2 m∙s−1 in the case. Different colors indicate different times, circles indicate wind speed between 17.2 and 24.5, dots indicate wind speed between 24.5 and 32.7, triangles indicate wind speed above 32.7. (c) Forecast results based on the PPCP. The number in the upper left corner indicates the running time, and the number in the upper right corner indicates the forecast time. (d) Forecast results based on the PPB.
5. Conclusions
In this study, the weather situations of thunderstorm gales are divided into four types of REA_T, FRO_T, PER_W and EAS_A according to objective identification. Then, based on the ECMWF NWP products, the probability forecast products of thunderstorm gales are calculated at grid points by using a continuous probability method. The main conclusions are as follows.
The objective identification scheme of weather situations introduced in this study can well identify the difference of environmental fields under different weather situations during thunderstorm gale processes, which is favorable for exploring the physical mechanism of thunderstorm gales and accurately forecasting the occurrence probability of thunderstorm gales.
The continuous probability method can solve the problem of “either 0 or 1” caused by the bisection method. The statistical results indicate that under the four types of weather situations, there are differences in the environmental physical quantity distribution during thunderstorm gale processes, such as the CAPE, T850–500 and 850 hPa T−Td. The half-ridge membership function can better reflect the relationship between the physical quantity and the probability of occurrence.
The quantitative test results of the 12–36 h probability products of thunderstorm gales from reveal that with the probability threshold of ≥60%, the POD is 68.7%, while the MAR is 31.28%, and the forecast leading time is 12–24 h. Compared with the hourly CMA-MESO prediction product based on radar reflectivity factor, the POD of the forecast product generated in this study increases dramatically, and the MAR decreases obviously. These probability forecast products provide a good reference for short-term potential forecasts and early warning of thunderstorm gale processes.
The case studies of the four typical thunderstorm gale processes suggest that the PPCP can give better predict on the period, location and range of thunderstorm gale occurrence than PPB. The PPCP obviously reduces the MAR of extreme gales compared with the PPB. However, both these two methods still show certain false reports.
In the follow-up study, the forecast method will be improved further based on more case samples through the reasonable adjustment of the weight coefficient of each physical quantity, and the effective elimination of false reports is also required. In addition, study based on mesoscale numerical models with high spatio-temporal resolutions may also be conducted to improve the present forecast performance.
Author Contributions
Writing, Y.G.; methodology, Y.G.; conceptualization, M.Z.; formal analysis, M.Z.; data curation, X.C.; visualization, Y.G.; funding acquisition, Z.Z.; specific tests, G.X. (Guanyu Xu); data download, L.D.; form inspection, G.X. (Guirong Xu). All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 41905071), Meteorological Forecast Operation Key Technology Development Project (No. YBGJXM (2020) 3A-08) and Key Project of Science and Technology Development Fund of Hubei Meteorological Bureau (No. 2020Z02).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Surface observation data are available from http://data.cma.cn, accessed on 10 January 2017. NCEP reanalysis data are available from https://rda.ucar.edu/datasets, accessed on 10 October 2016. ECMWF products are available from the CMA through the opera-tional Intranet.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kelly, D.L.; Schaefer, J.T.; Doswell, C.A. Climatology of Nontornadic Severe Thunderstorm Events in the United States. Mon. Weather Rev. 1985, 113, 1997–2014. [Google Scholar] [CrossRef]
- Doswell, C.A. Severe Convective Storms; American Meteorological Society: Boston, MA, USA, 2001; pp. 1–26. [Google Scholar]
- Wu, D.; Meng, Z.; Yan, D. The Predictability of a Squall line in South China on 23 April 2007. Adv. Atmos. Sci. 2013, 30, 485–502. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Gong, D. Raindrop Size Distribution in a Midlatitude Continental Squall Line Measured by Thies Optical Disdrometers over East China. J. Appl. Meteorol. Climatol. 2016, 55, 621–634. [Google Scholar] [CrossRef]
- Campbell, M.A.; Cohen, A.E.; Coniglio, M.C.; Dean, A.R.; Corfidi, S.F.; Corfidi, S.J.; Mead, C.M. Structure and Motion of Severe-Wind-Producing Mesoscale Convective Systems and Derechos in Relation to the Mean Wind. Weather Forecast. 2017, 32, 423–439. [Google Scholar] [CrossRef]
- Surowiecki, A.; Taszarek, M. A 10-Year Radar-Based Climatology of Mesoscale Convective System Archetypes and Derechos in Poland. Mon. Weather Rev. 2020, 148, 3471–3488. [Google Scholar] [CrossRef]
- Schoen, J.M.; Ashley, W.S. A Climatology of Fatal Convective Wind Events by Storm Type. Weather Forecast. 2011, 26, 109–121. [Google Scholar] [CrossRef]
- Guo, Y.; Sun, J. Characteristics of Strong Convective Wind Events Caused by Three Types of Convective Systems in Hubei Province. Chin. J. Atmos. Sci. 2019, 43, 483–497. [Google Scholar] [CrossRef]
- Albers, S.C.; McGinley, J.A.; Birkenheuer, D.L.; Smart, J.R. The Local Analysis and Prediction System (LAPS): Analyses of Clouds, Precipitation, and Temperature. Weather Forecast. 1996, 11, 273–287. [Google Scholar] [CrossRef]
- Fang, C.; Zheng, Y.; Lin, Y.; Zhu, W. Classification and Characteristics of Cloud Patterns Triggering Regional Thunderstorm High Winds. Meteor. Mon. 2014, 40, 905–915. [Google Scholar] [CrossRef]
- Xu, X.; Xue, M.; Wang, Y. Mesovortices within the 8 May 2009 Bow Echo over the Central United States: Analyses of the Characteristics and Evolution Based on Doppler Radar Observations and a High-Resolution Model Simulation. Mon. Weather Rev. 2015, 143, 2266–2290. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, A.; Xu, B.; Chen, J.; Li, J. Analysis on mesoscale characteristics and causes of an extreme thunderstorm gale event in Jiangxi. Torrential Rain Disasters 2019, 38, 126–134. [Google Scholar] [CrossRef]
- Luchetti, N.T.; Friedrich, K.; Rodell, C.E.; Lundquist, J.K. Characterizing Thunderstorm Gust Fronts near Complex Terrain. Mon. Weather Rev. 2020, 148, 3267–3286. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, Y.; Leng, L.; Fu, Z.; Guan, Z. Doppler radar observation and analysis of two convective gale weather events in Wuhan in May 2021. Torrential Rain Disasters 2022, 41, 119–129. [Google Scholar] [CrossRef]
- Mcnulty, R.P. Severe and Convective Weather: A Central Region Forecasting Challenge. Weather Forecast. 1995, 10, 187–202. [Google Scholar] [CrossRef]
- Doswell, C.A., III; Brooks, H.E.; Maddox, R.A. Flash Flood Forecasting: An Ingredients-Based Methodology. Weather. Forecast. 1996, 11, 560–581. [Google Scholar] [CrossRef]
- Yang, X.; Hu, S.; Jiang, P.; Wan, M.; Wang, W.; Liu, G.; Gao, H.; Zhangxu, P.U.; Hua, W. Research of Synoptic Model and Physical Quantity Parameter of Thunder-Gust Winds Impact Area. Plateau Meteorol. 2014, 33, 1057–1068. [Google Scholar] [CrossRef]
- Wei, H.; Guanyu, X.U.; Liu, X.; Zhang, J.; Shuangjun, L.I.; Jiang, J. Spatial-temporal distribution and environmental parameter characteristics for different types of thunderstorm gales in Hubei Province. Torrential Rain Disasters 2022, 41, 66–75. [Google Scholar] [CrossRef]
- Lei, L.; Sun, J.; Wang, G.; Guo, R. An experimental study of the summer convective weather categorical probability forecast based on the rapid updated cycle system for the Beijing area (BJ-RUC). Acta Meteorol. Sin. 2012, 70, 752–765. [Google Scholar] [CrossRef]
- Zeng, M.; Wang, G.; Wu, H.; Shen, Y.; Li, X. Study of the forecasting method for the classified severe convection weather based on a meso-scale numerical model. Acta Meteorol. Sin. 2015, 73, 868–882. [Google Scholar] [CrossRef]
- Ma, S.; Wang, X.; Yu, X. Environmental parameter characteristics of severe wind with extreme thunderstorm. J. Appl. Meteor. Sci. 2019, 30, 292–301. [Google Scholar] [CrossRef]
- Cohen, A.E.; Coniglio, M.C.; Corfidi, S.F.; Corfidi, S.J. Discrimination of mesoscale convective system environments using sounding observations. Weather Forecast. 2007, 22, 1045–1062. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, X.; Yu, X. Comparative study of environmental characteristics of a windstorm and their impacts on storm structures. Acta Meteorol. Sin. 2013, 5, 839–852. [Google Scholar] [CrossRef]
- Zhou, K.; Zheng, Y.; Li, B.; Dong, W.; Zhang, X. Forecasting Different Types of Convective Weather: A Deep Learning Approach. J. Meteorol. Res. 2019, 33, 797–809. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, Q.; Liu, X.; Zhu, W.; Mao, X. Anlyisis on Verification of National Severe Convective Weather Categorical Forecasts. Meteor. Mon. 2017, 43, 67–76. [Google Scholar] [CrossRef]
- Yu, X.; Zheng., Y. Advances in severe convective weather research and operational service in China. Acta Meteorol. Sin. 2020, 78, 391–418. [Google Scholar] [CrossRef]
- Tian, F.; Zheng, Y.; Zhang, T.; Zhang, X.; Mao, D.; Sun, J.; Zhao, S. Statistical characteristics of environmental parameters for warm season short-duration heavy rainfall over central and eastern China. J. Meteorol. Res. 2015, 29, 370–384. [Google Scholar] [CrossRef]
- Lakshmanan, V.; Crockett, J.; Sperow, K.; Ba, M.; Xin, L. Tuning AutoNowcaster Automatically. Weather Forecast. 2012, 27, 1568–1579. [Google Scholar] [CrossRef]
- Tang, J.; Guo, X.; Chang, Y.; Lu, G.; Qi, P. Temporospatial Distribution and Trends of Thunderstorm, Hail, Gale, and Heavy Precipitation Events over the Tibetan Plateau and Associated Mechanisms. J. Clim. 2021, 34, 9623–9646. [Google Scholar] [CrossRef]
- Kanwal, A.; Tahir, Z.R.; Asim, M.; Hayat, N.; Farooq, M.; Abdullah, M.; Azhar, M. Evaluation of Reanalysis and Analysis Datasets against Measured Wind Data for Wind Resource Assessment. Energy Environ. 2022, 0958305X2210840. [Google Scholar] [CrossRef]
- Kuchera, E.L.; Parker, M.D. Severe Convective Wind Environments. Weather Forecast. 2006, 21, 595–612. [Google Scholar] [CrossRef]
- Cintineo, J.L.; Pavolonis, M.J.; Sieglaff, J.M.; Lindsey, D.T. An Empirical Model for Assessing the Severe Weather Potential of Developing Convection. Weather Forecast. 2014, 29, 639–653. [Google Scholar] [CrossRef]
- Skinner, P.S.; Wheatley, D.M.; Knopfmeier, K.H.; Reinhart, A.E.; Choate, J.J.; Jones, T.A.; Creager, G.J.; Dowell, D.C.; Alexander, C.R.; Ladwig, T.T.; et al. Object-Based Verification of a Prototype Warn-on-Forecast System. Weather Forecast. 2018, 33, 1225–1250. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Lin, P.; Chang, P.; Jou, B.J.; Wilson, J.W.; Roberts, R.D. Objective Prediction of Warm Season Afternoon Thunderstorms in Northern Taiwan Using a Fuzzy Logic Approach. Weather Forecast. 2012, 27, 1178–1197. [Google Scholar] [CrossRef]
- Park, S.; Kim, J.; Ko, J.; Lee, G. Identification of Range Overlaid Echoes Using Polarimetric Radar Measurements Based on a Fuzzy Logic Approach. J. Atmos. Ocean. Technol. 2016, 33, 61–80. [Google Scholar] [CrossRef]
- Zhu, Y.; Niu, X.; Gu, C.; Dai, B.; Huang, L. A Fuzzy Clustering Logic Life Loss Risk Evaluation Model for Dam-Break Floods. Complexity 2021, 2021, 14. [Google Scholar] [CrossRef]
- Liu, S.; Wang, R.; Huang, J.; Liu, K. Intelligent Diagnosis Method of Metering Cabinet Health State Based on Multi-source Information and Fuzzy Comprehensive Evaluation. In Proceedings of the 2021 International Conference on Advanced Electrical Equipment and Reliable Operation (AEERO), Beijing, China, 15–17 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Bermowitz, R.J.; Zurndorfer, E.A. Automated Guidance for Predicting Quantitative Precipitation. Mon. Weather Rev. 1979, 107, 122–128. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Brier, G.W. Some Applications of Statistics to Meteorology; Earth and Mineral Sciences Continuing Education, College of Earth and Mineral Sciences: State College, PA, USA, 1968; p. 224. [Google Scholar]
- Medasani, S.; Kim, J.; Krishnapuram, R. An Overview of Membership Function Generation Techniques for Pattern Recognition. Int. J. Approx. Reason. 1998, 19, 391–417. [Google Scholar] [CrossRef]
- Tyagi, B.; Naresh Krishna, V.; Satyanarayana, A.N.V. Study of Thermodynamic Indices in Forecasting Pre-Monsoon Thunderstorms over Kolkata during STORM Pilot Phase 2006–2008. Nat. Hazards 2011, 56, 681–698. [Google Scholar] [CrossRef]
- Maddox, R.A.; McCollum, D.M.; Howard, K.W. Large-Scale Patterns Associated with Severe Summertime Thunderstorms over Central Arizona. Weather Forecast. 1995, 10, 763–778. [Google Scholar] [CrossRef]
- Fuelberg, H.E.; Biggar, D.G. The preconvective environment of summer thunderstorms over the Florida panhandle. Weather Forecast. 1999, 9, 316–326. [Google Scholar] [CrossRef]
- Mazon, J.J.; Castro, C.L.; Adams, D.K.; Chang, H.; Carrillo, C.M.; Brost, J.J. Objective Climatological Analysis of Extreme Weather Events in Arizona during the North American Monsoon. J. Appl. Meteorol. Climatol. 2016, 55, 2431–2450. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).