Modelling Cloud Cover Climatology over Tropical Climates in Ghana
Abstract
:1. Introduction
2. Methodology
2.1. Study Area
2.2. Data
2.3. Theoretical Background
2.4. Statistical Tools Analysis
3. Results and Discussions
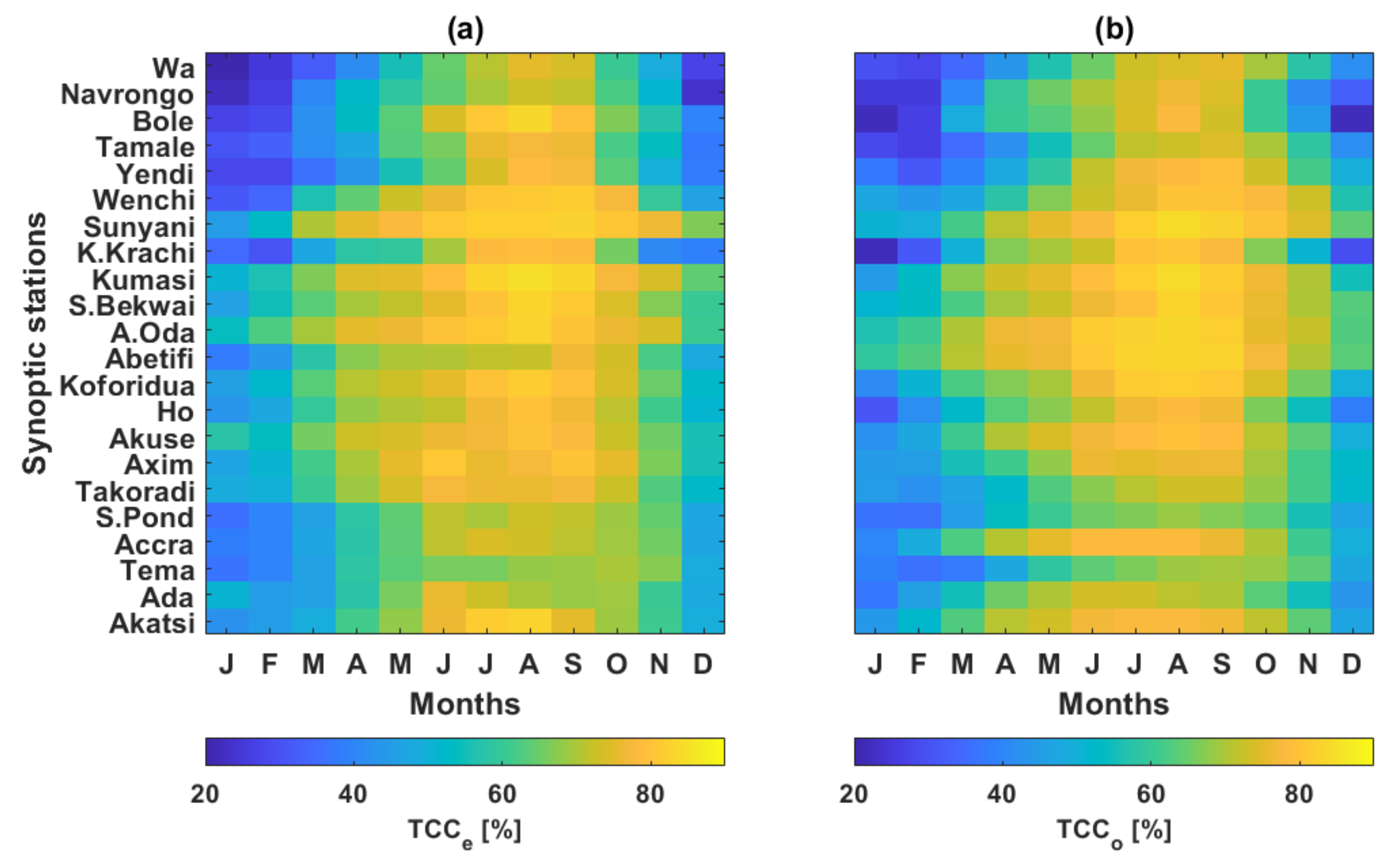
3.1. Performance of Empirical Cloud Cover Estimation and Bias Correction
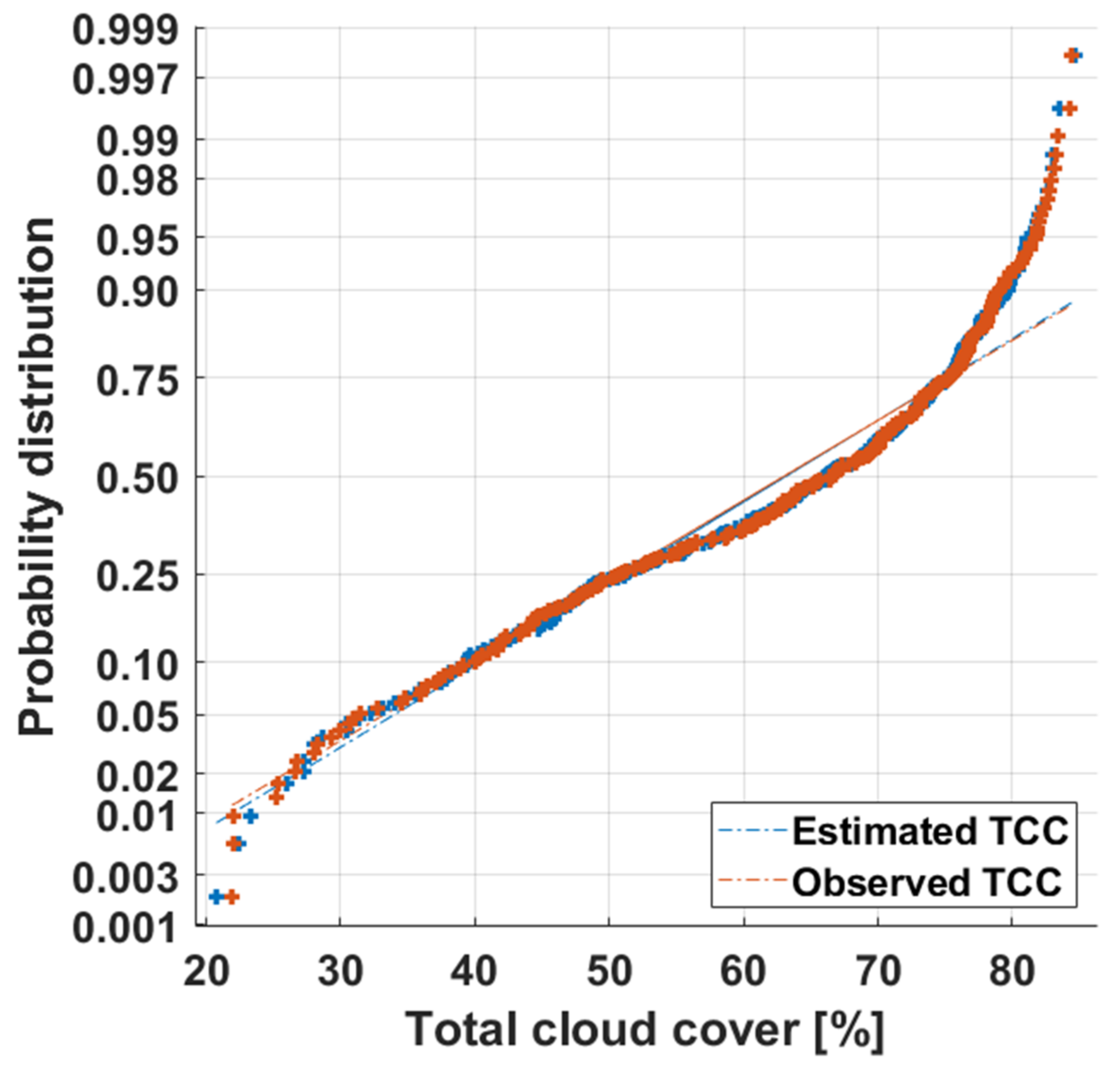
3.2. Total Cloud Cover Distribution: Comparison of Estimated and Observed
3.3. Statistical Evaluation of Cloud Cover Estimation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mulkey, S.S.; Kitajima, K.; Wright, S.J. Plant physiological ecology of tropical forest canopies. Trends Ecol. Evol. 1996, 11, 408–412. [Google Scholar] [CrossRef]
- Shen, L.; Zhao, C. Dominance of shortwave radiative heating in the sea-land breeze amplitude and its impacts on atmospheric visibility in Tokyo, Japan. J. Geophys. Res. Atmos. 2020, 125, e2019JD031541. [Google Scholar] [CrossRef]
- Silva, A.A.; Souza-Echer, M.P. Ground-based observations of clouds through both an automatic imager and human observation. Meteorol. Appl. 2016, 23, 150–157. [Google Scholar] [CrossRef] [Green Version]
- Hill, P.G.; Allan, R.P.; Chiu, J.C.; Bodas-Salcedo, A.; Knippertz, P. Quantifying the contribution of different cloud types to the radiation budget in southern West Africa. J. Clim. 2018, 31, 5273–5291. [Google Scholar] [CrossRef]
- van der Linden, R.; Fink, A.H.; Redl, R. Satellite-based climatology of low-level continental clouds in southern West Africa during the summer monsoon season. J. Geophys. Res. Atmos. 2015, 120, 1186–1201. [Google Scholar] [CrossRef]
- Fink, A.H.; Paeth, H.; Ermert, V.; Pohle, S.; Diederich, M. I-5.1 Meteorological processes influencing the weather and climate of Benin. Int. J. Climatol. 2010, 5, 135–149. [Google Scholar]
- Jeppesen, J.H.; Jacobsen, R.H.; Inceoglu, F.; Toftegaard, T.S. A cloud detection algorithm for satellite imagery based on deep learning. Remote Sens. Environ. 2019, 229, 247–259. [Google Scholar] [CrossRef]
- Rossow, W.B.; Schiffer, R.A. ISCCP cloud data products. Bull. Am. Meteorol. Soc. 1991, 72, 2–20. [Google Scholar] [CrossRef]
- Asilevi, P.J.; Quansah, E.; Amekudzi, L.K.; Annor, T.; Klutse, N.A.B. Modeling the spatial distribution of Global Solar Radiation (GSR) over Ghana using the Ångström-Prescott sunshine duration model. Sci. Afr. 2019, 4, e00094. [Google Scholar] [CrossRef]
- Amekudzi, L.K.; Yamba, E.I.; Preko, K.; Asare, E.O.; Aryee, J.; Baidu, M.; Codjoe, S.N. Variabilities in rainfall onset, cessation and length of rainy season for the various agro-ecological zones of Ghana. Climate 2015, 3, 416–434. [Google Scholar] [CrossRef]
- Asante, F.A.; Amuakwa-Mensah, F. Climate change and variability in Ghana: Stocktaking. Climate 2015, 3, 78–99. [Google Scholar] [CrossRef] [Green Version]
- Chaboureau, J.-P.; Söhne, N.; Guichard, F. Verification of Cloud Cover Forecast with Satellite Observation over West Africa. Mon. Weather Rev. 2008, 136, 4421–4434. [Google Scholar]
- Knippertz, P.; Fink, A.H.; Schuster, R.; Trentmann, J.; Schrage, J.M.; Yorke, C. Ultra-low clouds over the southern West African monsoon region. Geophys. Res. Lett. 2011, 38, 1–7. [Google Scholar] [CrossRef] [Green Version]
- World Meteorological Organization. WMO-NO.544—Manual on the Global Observing System; WMO: Geneva, Switzerland, 2003. [Google Scholar]
- Baumgartner, D.J.; Pötzi, W.; Freislich, H.; Strutzmann, H.; Veronig, A.M.; Foelsche, U.; Rieder, H.E. A comparison of long-term parallel measurements of sunshine duration obtained with a Campbell-Stokes sunshine recorder and two automated sunshine sensors. Theor. Appl. Climatol. 2018, 133, 263–275. [Google Scholar] [CrossRef] [Green Version]
- Badescu, V.; Paulescu, M. Statistical properties of the sunshine number illustrated with measurements from Timisoara (Romania). Atmos. Res. 2011, 101, 194–204. [Google Scholar] [CrossRef]
- Neske, S. About the Relation between Sunshine Duration and Cloudiness on the Basis of Data from Hamburg. J. Sol. Energy 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Ahamed, M.S.; Guo, H.; Tanino, K. Evaluation of a cloud cover based model for estimation of hourly global solar radiation in Western Canada. Int. J. Sustain. Energy 2019, 38, 64–73. [Google Scholar] [CrossRef]
- Sarkar, M.N.I. Estimation of solar radiation from cloud cover data of Bangladesh. Renew. Wind Water Sol. 2016, 3, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Wu, B.; Yan, N.; Ma, Z.; Wang, L.; Liu, W.; Xing, Q.; Xu, J. Estimating sunshine duration using hourly total cloud amount data from a geostationary meteorological satellite. Atmosphere 2020, 11, 26. [Google Scholar] [CrossRef] [Green Version]
- Michelangeli, P.A.; Vrac, M.; Loukos, H. Probabilistic downscaling approaches: Application to wind cumulative distribution functions. Geophys. Res. Lett. 2009, 36, 1–6. [Google Scholar] [CrossRef]
- Polo, J.; Fernández-Peruchena, C.; Salamalikis, V.; Mazorra-Aguiar, L.; Turpin, M.; Martín-Pomares, L.; Kazantzidis, A.; Blanc, P.; Remund, J. Benchmarking on improvement and site-adaptation techniques for modeled solar radiation datasets. Sol. Energy 2020, 201, 469–479. [Google Scholar] [CrossRef]
- Tahir, Z.u.R.; Asim, M.; Azhar, M.; Moeenuddin, G.; Farooq, M. Correcting solar radiation from reanalysis and analysis datasets with systematic and seasonal variations. Case Stud. Therm. Eng. 2021, 25, 100933. [Google Scholar] [CrossRef]
- Schumann, K.; Beyer, H.G.; Chhatbar, K.; Meyer, R. Improving satellite-derived solar resource analysis with parallel ground-based measurements. In Proceedings of the ISES Solar World Congress, Kassel, Germany, 28 August–2 September 2011. [Google Scholar]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Mahmoud, M.A.; Henderson, G.R.; Epprecht, E.K.; Woodall, W.H. Estimating the Standard Deviation in Quality-Control Applications. J. Qual. Technol. 2017, 42, 348–357. [Google Scholar] [CrossRef]
- Kim, S.T.; Jeong, H.I.; Jin, F.F. Mean Bias in Seasonal Forecast Model and ENSO Prediction Error. Sci. Rep. 2017, 7, 6029. [Google Scholar] [CrossRef] [Green Version]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Pereira, H.R.; Meschiatti, M.C.; Pires, R.C.D.M.; Blain, G.C. On the performance of three indices of agreement: An easy-to-use r-code for calculating the Willmott indices. Bragantia 2018, 77, 394–403. [Google Scholar] [CrossRef] [Green Version]
- Kavassalis, S.C.; Murphy, J.G. Understanding ozone-meteorology correlations: A role for dry deposition. Geophys. Res. Lett. 2017, 44, 2922–2931. [Google Scholar] [CrossRef]
- Danso, D.K.; Anquetin, S.; Diedhiou, A.; Lavaysse, C.; Kobea, A.; Touré, N.D.E. Spatio-temporal variability of cloud cover types in West Africa with satellite-based and reanalysis data. Q. J. R. Meteorol. Soc. 2019, 145, 3715–3731. [Google Scholar] [CrossRef] [Green Version]
- Asilevi Junior, P.; Opoku, N.K.; Martey, F.; Setsoafia, E.; Ahafianyo, F.; Quansah, E.; Dogbey, F.; Amankwah, S.; Padi, M. Development of High Resolution Cloud Cover Climatology Databank Using Merged Manual and Satellite Datasets over Ghana, West Africa. Atmos. Ocean 2022, 1–14. [Google Scholar] [CrossRef]
- File, D.J.M.; Derbile, E.K. Sunshine, temperature and wind. Int. J. Clim. Change Strateg. Manag. 2020, 12, 22–38. [Google Scholar] [CrossRef]
- Junior, P.A.; Quansah, E.; Dogbey, F. Satellite-based estimates of photosynthetically active radiation for tropical ecosystems in Ghana—West Africa. Trop. Ecol. 2022, 1–11. [Google Scholar] [CrossRef]
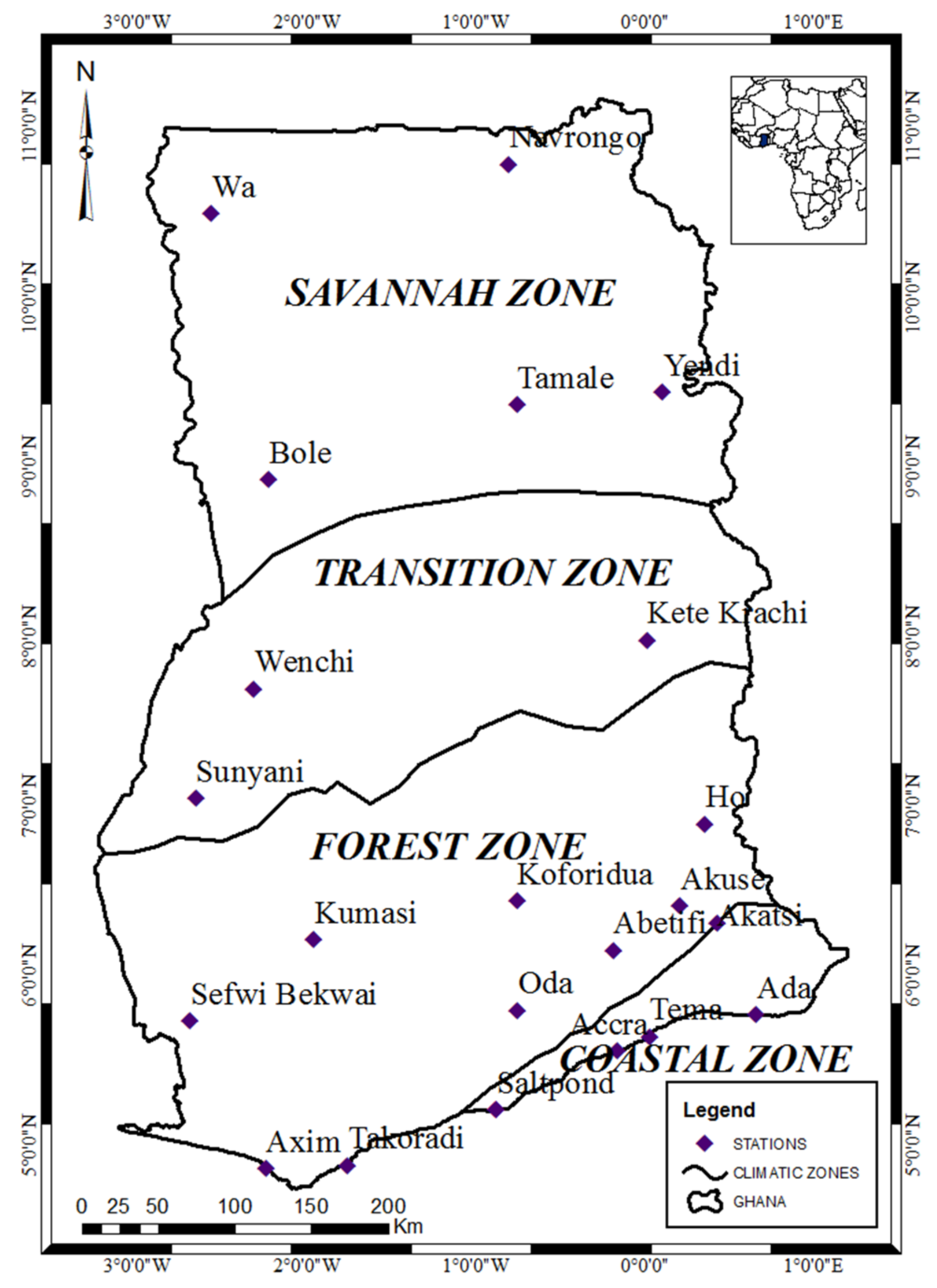



| Station | Station Code | Latitude (°) | Longitude (°) | Elevation (m) |
|---|---|---|---|---|
| Savannah | ||||
| Wa | 65,404 | 10.05 | −2.50 | 305 |
| Navrongo | 65,401 | 10.90 | −1.10 | 197 |
| Bole | 65,416 | 9.33 | −2.48 | 247 |
| Tamale | 65,418 | 9.42 | −0.85 | 152 |
| Yendi | 65,420 | 9.45 | −0.17 | 157 |
| Transition | ||||
| Wenchi | 65,432 | 7.75 | −2.10 | 299 |
| Sunyani | 65,439 | 7.33 | −2.33 | 305 |
| Kete Krachi | 65,437 | 7.82 | −0.33 | 92 |
| Forest | ||||
| Kumasi | 65,442 | 6.72 | −1.60 | 256 |
| Sefwi Bekwai | 65,445 | 6.20 | −2.33 | 187 |
| Oda | 65,457 | 5.93 | −0.98 | 151 |
| Abetifi | 65,450 | 6.67 | −0.75 | 601 |
| Koforidua | 65,459 | 6.83 | −0.25 | 199 |
| Ho | 65,453 | 6.60 | 0.47 | 154 |
| Akuse | 65,460 | 6.10 | 0.12 | 108 |
| Axim | 65,465 | 4.90 | −2.25 | 71 |
| Takoradi | 65,467 | 4.88 | −1.77 | 74 |
| Coastal | ||||
| Saltpond | 65,469 | 5.20 | −1.67 | 77 |
| Accra | 65,472 | 5.60 | −0.17 | 91 |
| Tema | 65,473 | 5.62 | 0.00 | 79 |
| Ada | 65,475 | 5.78 | 0.63 | 15 |
| Akatsi | 65,462 | 6.12 | 0.80 | 66 |
| Stations | RMSE | MBE | r |
|---|---|---|---|
| Wa | 4.66 | 2.39 | 0.97 |
| Navrongo | 4.19 | 1.30 | 0.96 |
| Bole | 5.93 | −2.49 | 0.94 |
| Tamale | 3.89 | −1.07 | 0.96 |
| Yendi | 5.07 | 3.06 | 0.98 |
| Wenchi | 6.11 | 0.81 | 0.90 |
| Sunyani | 2.76 | −0.84 | 0.96 |
| Kete Krachi | 5.07 | 0.78 | 0.95 |
| Kumasi | 2.60 | −1.20 | 0.98 |
| Sefwi Bekwai | 1.62 | 0.51 | 0.98 |
| Oda | 1.08 | 0.42 | 0.99 |
| Abetifi | 9.14 | 6.15 | 0.96 |
| Koforidua | 1.76 | −0.51 | 0.99 |
| Ho | 4.83 | −2.69 | 0.99 |
| Akuse | 4.01 | −1.59 | 0.97 |
| Axim | 3.77 | −2.45 | 0.98 |
| Takoradi | 6.17 | −3.69 | 0.90 |
| Salt Pond | 3.24 | −2.02 | 0.99 |
| Accra | 5.90 | 3.24 | 0.91 |
| Tema | 3.32 | −1.37 | 0.96 |
| Ada | 4.49 | −0.32 | 0.87 |
| Akatsi | 4.38 | 1.60 | 0.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dogbey, F.; Asilevi, P.J.; Dzrobi, J.F.; Koffi, H.A.; Klutse, N.A.B. Modelling Cloud Cover Climatology over Tropical Climates in Ghana. Atmosphere 2022, 13, 1265. https://doi.org/10.3390/atmos13081265
Dogbey F, Asilevi PJ, Dzrobi JF, Koffi HA, Klutse NAB. Modelling Cloud Cover Climatology over Tropical Climates in Ghana. Atmosphere. 2022; 13(8):1265. https://doi.org/10.3390/atmos13081265
Chicago/Turabian StyleDogbey, Felicia, Prince Junior Asilevi, Joshua Fafanyo Dzrobi, Hubert Azoda Koffi, and Nana Ama Browne Klutse. 2022. "Modelling Cloud Cover Climatology over Tropical Climates in Ghana" Atmosphere 13, no. 8: 1265. https://doi.org/10.3390/atmos13081265
APA StyleDogbey, F., Asilevi, P. J., Dzrobi, J. F., Koffi, H. A., & Klutse, N. A. B. (2022). Modelling Cloud Cover Climatology over Tropical Climates in Ghana. Atmosphere, 13(8), 1265. https://doi.org/10.3390/atmos13081265






