Abstract
Land and forest fires in Southeast Asia often coincide with severe dry seasons in the specific region caused by the warm phase of an El Niño Southern Oscillation (ENSO) and Indian Ocean Dipole (IOD). This research aims to identify and quantify the ENSO–IOD effect on a joint pattern between the dry season and land and forest fires in Southeast Asia. This research provides a quantitative result which represents the ENSO–IOD’s impact in Southeast Asia for hotspots, dry spells, and precipitation anomalies. The methods used in this research are singular value decomposition, probability density skill score, and coherence analysis. Cambodia, Myanmar, and Thailand gave a similar result with less than a 25% increasing severity in the hotspots from normal to either El Niño, positive IOD, or El Niño–positive IOD years. The maximum increase in hotspot severity in North Sumatra was 13.06% and happened during a weak El Niño and positive IOD. Meanwhile, South Sumatra had a maximum accumulation of more than 89% and Kalimantan had more than a 72% increase during the strong El Niño in 2015. Even though the relationship between the ENSO and IOD was inconsistent, the occurrence of both phenomena in the same year can lead to fires and need to be considered.
1. Introduction
Southeast Asia’s forests play essential roles in biodiversity conservation and global carbon (C) balance, covering 15% of the world’s tropical forests [1]. However, Southeast Asia (SEA) has one of the highest deforestation rates in the tropics [2]. Deforestation in SEA occurs fast due to the increased land used for agriculture and urban development [3]. Therefore, understanding the types of deforestation and forest degradation as well as the cause of the problem is essential to suppress deforestation rates in the future [4]. Many of these deforestations are correlated with land and forest fires and have already become common issues in the last decade in SEA [5,6,7,8]. Land and forest fire management in SEA countries is a complex and challenging problem. The solution to this problem requires detailed information about the occurrence, geographic variation, trends, anomalies, and main causes of land and forest fire within the region [9] as well as cooperation from all relevant stakeholders. Land and forest fire severity often coincides with the dry season of the respective area. The worst land and forest fires with vast smoldering combustion areas for several months coincide with severe drought conditions related to El Niño [10].
In the last few decades, the El Niño Southern Oscillation (ENSO) has contributed to the increasing number of extreme climate changes (drought/flood) in the region around the Pacific Ocean [11,12,13]. The ENSO is a phenomenon formed by the impact of a sea surface temperature anomaly around the Pacific Ocean (5° N–5° S, 170° W–120° W). The strong El Niño (the warm phase of the ENSO) could significantly affect the dry season severity by reducing precipitation and extending the duration of the dry season itself [14,15,16]. However, the magnitude of the impact differs among regions, especially in Southeast Asia (SEA), which is an archipelago region. The ENSO impacts in SEA are very diverse due to the contribution of the local Sea Surface Temperature (SST) affecting the dry season [17,18,19,20]. Furthermore, there is a phenomenon called the Indian Ocean Dipole (IOD) which is also associated with drought conditions in SEA [21], especially during a positive IOD. A positive IOD is a phenomenon formed by warm anomalies in the equatorial Western Indian Ocean (10° S–0°, 110° E–70° E) and cold anomalies in the east (10° S–10° N, 50° E–70° E) [22,23].
The ENSO and IOD are the dominant modes of climate variability at inter-annual time scales in SEA [24] that can cause severe drought during its warm phase (an El Niño and positive IOD) [25]. Besides their standalone impact [26], the ENSO and IOD also have a joint impact since both of their warm phases (the El Niño and positive IOD) can potentially occur during the same period. The ENSO and IOD are positively correlated from September until November; hence, it is difficult to separate their effects [27]. The drought conditions of the affected regions become much more severe when an El Niño and positive IOD occur simultaneously [21,27,28,29,30]. The severity increases are caused by more deficits in precipitation and longer durations of the dry season than that of the droughts affected by the standalone impact of an El Niño or positive IOD. Therefore, identifying and quantifying the ENSO–IOD impact on the problem that occurred during drought conditions is urgently needed. Much research has shown the impact of the ENSO–IOD in various regions, such as in India [29], Korea [30], Australia [27], and Southeast Asia [31]. The precipitation anomalies in the southern part of SEA, such as in Sumatra, Java Island, and southern Borneo, are affected significantly during June to August, while the other areas, such as northern Borneo and the southern Philippines, are more pronounced during December to February [21]. However, there is still no research which explains the ENSO–IOD impact on land and forest fire events in SEA.
This research aims to identify and quantify the ENSO–IOD effect on the joint pattern between the dry season and land and forest fires in SEA. Both the ENSO and IOD are non-stationary phenomena. Their variability evolves on multi-time scales [31], so quantifying its variability and impact remains a significant challenge to the scientific community [32]. This research uses Empirical Orthogonal Function (EOF) analysis based on covariance singular value decomposition (SVD) to find the joint pattern between the dry season and land and forest fires. EOF analysis is often used to study possible spatial patterns in climate variability and its evolution on multi-time scales [33,34]. This method effectively finds the joint pattern among two variables in high-dimensional data that are difficult to analyze directly.
The land and forest fire indicator used in this research is the monthly number of hotspots. Meanwhile, the dry season indicators used are the dry spells (the number of days without rain) and precipitation anomalies. To quantify the ENSO and IOD’s impact, the results of the EOF analysis will be categorized based on the strength of the El Niño in each year. Then, this research will provide a comparison between the distribution of the variables among each category. This research gives a quantitative result that can represent the impact of the ENSO on the dry season and forest fires better than that of a qualitative one. The results can be used as additional information to develop a quantitative prediction model of land and forest fires based on the strength of the ENSO and IOD.
2. Materials and Methods
This research uses hotspot data as the land and forest fire indicator. Meanwhile, dry spells and precipitation anomalies are used for the dry season indicators. The data are monthly data carried out from November 2001 to May 2021 with a grid resolution of 0.25° × 0.25°. The area observed in this research is Southeast Asia (25° N–11° S, 93° E–141° E). A hotspot is an indicator of forest and land fires that detects a location with a relatively high temperature compared to its surroundings. The hotspot data were produced by the National Aeronautics and Space Administration (NASA). The data were derived from the Moderate Resolution Imaging Spectroradiometer (MODIS) sensors of the Terra and Aqua Satellites and were processed in order to become grid data with a spatial resolution of 0.25° × 0.25°, which contain hotspot observation with more than an 80% confidence level [35]. The precipitation anomaly and dry spell data used in this research are the Climate Prediction Center Morphing Technique (CMORPH) data [36] produced by the National Oceanic and Atmospheric Administration (NOAA), specifically the satellite–gauge merged product (CMORPH BLD) [37]. Both data were processed so that the information for a month showed the average precipitation anomaly and the accumulation of dry spells for the last three months. The dry spell data used was a conversion of the daily precipitation data from the same data source with a threshold for non-rainy days of 1 mm. The used ENSO and IOD data were also produced by NOAA using Hadley Centre Sea Surface Temperature (HadISST) data [38].
In order to find a joint pattern between the dry season and the land and forest fire indicator, this research used an Empirical Orthogonal Function based on covariance singular value decomposition. We used the covariance-based SVD to maximize the contribution on the joint patterns that lie in the data [33,39,40]. To compare the character of the pattern, this research used the Probability Density Function (PDF) skill score from a distribution of the data [41]. The distribution was obtained by estimating each data distribution using negative log likelihood (NlogL) [42] and Bayesian Information Criterion (BIC) [43]. From the estimation process, the best result for each variable was the Rayleigh distribution [44] for the hotspots, Generalized extreme value [45] for the dry spells, and the T location scale [46] for the precipitation anomalies.
2.1. Empirical Orthogonal Function Based on Covariance Singular Value Decomposition
Singular value decomposition (SVD) is a decomposition method using a singular value as the main factor. Suppose a matrix with rank r; there is an orthogonal matrix and a diagonal matrix , which is shown in Equation (1):
The , is a singular value from matrix A and r is the number of singular values obtained from the decomposition. When , A has in addition to the singular zero value. The factorization in Equation (1) is the SVD of matrix A. The columns in U and V represent the left singular vector and the right singular vector of A, respectively [47].
For this research, the hotspot data will be represented as matrix A, and the dry spell data will be represented as matrix B. Then, both matrices will be multiplied to obtain the matrix . Then, SVD will be used to decompose matrix C following Equation (1) to obtain the U, L, and V matrices. In this case, L represents the singular value of C, U represents the singular vector of A, and V represents the singular vector of B. Each pair of singular vectors is a mode of co-variability between the A and B data. Therefore, each column in the U and V matrix is the spatial pattern of each data. The expansion coefficient for the data is introduced to describe how each mode variability oscillates spatially and temporally, calculated by multiplying the original data with its singular vector matrix. Therefore, will be the expansion coefficient of A and will be the expansion coefficient of B. The contribution of each mode to the data will be calculated using a Squared Covariance Fraction (SCF) following the equation below
where is the square of the singular value and is the total square of the singular value. The mode with the highest SCF value will be used spatially and temporally for subsequent analysis [48].
2.2. Distribution Analysis
In this research, we evaluate characteristics of the observed data distribution for each variable. The evaluation is conducted to understand the important aspects of the whole data, such as the average value, mode, extreme value, differences in character among the classifications, and other essential properties that are hard to identify while working with raw data. The fitting distribution process is carried out by using the allfitdist function in Matlab, using either NLogL or BIC as the parameter to represent how accurate the fitted distribution is to all the classifications. The chosen parameter is dependent on which one gives a better distribution type to represent the data.
NlogL is simply the negative value of the log likelihood (LogL). Instead of using LogL to determine the maximum probability, NLogL is used to optimize the fitted distribution to represent the estimate’s error. So, the model with the lowest NLogL is preferred to obtain a better representation [42]. The likelihood function is defined as
In [49], the solution for the normal maximum log likelihood estimation is obtained by following the equation:
When using minimize negative log likelihood estimation, the solution will be obtained by
BIC is a statistical measure developed by [50]. BIC is used as a criterion for fitted distribution selection among a finite set of distributions in this research. Similar to NLogL, the distribution with the lowest BIC is preferred to obtain a better result. It is based, in part, on the likelihood function by introducing a penalty term for the number of parameters in the distribution [50]. The BIC formula is
where:
- = the maximized value of the likelihood function,
- n = the number of data points (the sample size),
- k = the number of parameters estimated by the model (the fitted distribution) [43].
This research uses a difference value calculated using the PDF skill score to compare each category’s distribution. Commonly, the PDF skill score is calculated to measure the similarity of the distribution by the following equation
where n is the number of x used to calculate the PDF, is the probability of in distribution A, and is the probability of in distribution B [51]. Then, we calculate the difference value and represent it as a percentage with the following equation
where a 0% DV means that both the distributions are the same and a 100% DV means that both the distributions are entirely different from each other.
2.3. Wavelet Coherence Analysis
Wavelet Coherence is a bi-variate framework used to study the interaction between different time series and their evolution over a continuous time and frequency space [52]. Wavelet coherence analysis is commonly used to identify the interaction between two climate phenomena, which is hard to analyze directly [26,53,54]. The denote is a time series of the Niño3.4 index and is a time series of DMI. The cross-wavelet transform is calculated by multiplying the wavelet transformation of and , defined as . The wavelet coherence is defined as
where S is a smoothing operator [55]. Equation (9) resembles a traditional correlation coefficient, so the wavelet coherence can be considered a localized correlation coefficient in the time–frequency space. The smoothing operator S is defined as
where denotes smoothing along the wavelet scale axis and denotes smoothing in the time axis [56].
3. Results
In this research, satellite-derived grid data is cut on a SEA domain, specifically 25° N–11° S and 93° E–141° E. Hotspot and dry spell (the number of days without rain) data are used to obtain the joint pattern between land and forest fires and drought conditions. Dry spell data represent the accumulation of the number of days without rain for the last three months. The accumulation is conducted to obtain a relationship where forest fires are caused by the accumulated drought conditions from the last three months. Before processing, a filtering process is carried out by only taking the spatial locations where there were at least ten hotspots in a month from 2001 to 2020 and where this occurred more than once. First of all, the SVD analysis is carried out to the entire SEA region. The SVD process resulted in a total of 240 modes in the decomposition. Of all these modes, there were two dominant modes with a total SCF of 95.5%. Both modes were taken based on having the largest singular value and there were significant differences in both the spatial and temporal patterns. The main focus of this research was hotspot characteristics, so only the hotspot temporal patterns are shown. However, it was extracted from its joint pattern with the dry spells.
Mode 1 of the hotspot and dry spell joint pattern, which had an SCF value of 83.8%, was dominated by hotspots that occurred around Myanmar, Thailand, and Cambodia (the green-to-red color in the hotspot’s spatial Figure 1). Additionally, there were hotspots in the northern part of Sumatra and the southern part of Kalimantan (also called Borneo) that were relatively very minor and had a smaller coverage area than the previous three regions. Based on the temporal pattern, the first mode was dominated by hotspots occurring at the beginning of the year (January–June). However, several anomalies appeared in the first mode pattern, indicating a relatively high number of hotspots in the mid-to-end of the year (June–November) in 2002, 2004, 2006, 2009, 2015, and 2019. Looking at the global climate phenomenon in these years from [57,58], 2004 was a weak El Niño year, 2002 and 2009 were moderate El Niño years, 2015 was a very strong El Niño year, and 2006 and 2019 were weak El Niño combined with positive IOD years. This result indicates that the hotspot anomalies were influenced by the ENSO and IOD. The peak impact of both the El Niño and positive IOD occurred at the mid-to-end of the year [27]. This fact resulted in a minor effect of the ENSO and IOD on the whole mode 1 joint pattern.
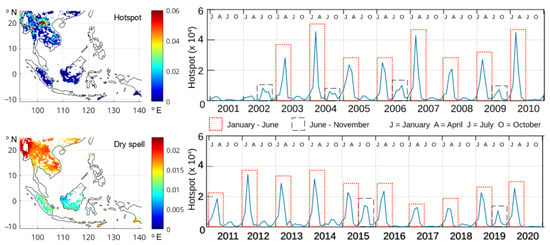
Figure 1.
Southeast Asia analysis—first spatial pattern of the hotspot (top) and dry spell (bottom), as well as temporal pattern of a hotspot, 83.8% of SCF value.
Mode 2 obtained from the SVD analysis had an SCF of 11.7%. Based on the temporal pattern, mode 2 showed different behavior from mode 1, dominated by hotspots in June–November (Figure 2). The positive high dry season was focused on the area below the equator. There were a few hotspot occurrences with a negative value in the temporal pattern. These hotspots were related to the region with a negative value of dry spell patterns, which was around Cambodia and Thailand, which was already described in the first mode. Therefore, the negative value in the temporal pattern can be ignored. The second mode pattern resulted in many hotspots appearing in the southern parts of Kalimantan and Sumatra during June–November. This mid-year dry season happened in the same period with the El Niño or/and positive IOD’s impact in Indonesia. Therefore, the years that were influenced by the El Niño or/and positive IOD, such as 2002, 2006, 2009, 2015, and 2019, produced a significantly higher number of hotspots than the other years. This result shows that the El Niño and positive IOD impacted land and forest fires in Kalimantan and the southern part of Sumatra.
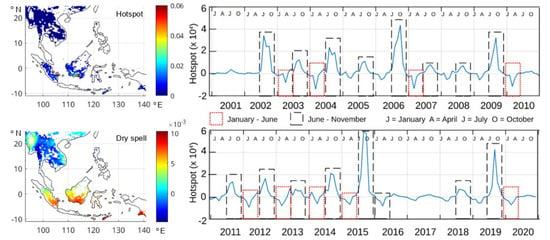
Figure 2.
Southeast Asia analysis—second spatial pattern of the hotspot (top) and dry spell (bottom), as well as temporal pattern of a hotspot, 11.7% of SCF value.
Based on those two modes, the land and forest fire phenomena in Southeast Asia can be divided into two groups, namely: land and forest fires at the beginning of the year (Myanmar, Thailand, Cambodia, and northern part of Sumatra) and land and forest fires in the middle of the year (Kalimantan and southern Part of Sumatra). Because there is a far distance between some region, separated by sea, mountain, and some are in different countries, a further analysis will be carried out specifically for each land and forest fires region. The analysis will be divided into several categories based on the strength of the ENSO and IOD described by [57] and BOM [58] to analyze the effects of both phenomena. Therefore, the categorization will follow the period of the El Niño, which starts from June to May. For example, a strong El Niño occurred in the mid-to-end of 2015, so 2015/2016 is categorized as a strong El Niño year, which is from June 2015 to May 2016. The impact of the weak El Niño is not very significant compared to a normal year [34], so weak El Niño years are combined with the normal years. However, if a weak El Niño occurred simultaneously with a positive IOD, the impact can be multiplied [59]. Therefore, it needs to be separated from the other weak El Niño years. The categorization of the years in this research is
- La Niña: 2005/2006, 2007/2008, 2008/2009, 2010/2011, 2011/2012, 2016/2017, 2017/2018
- Normal and weak El Niño: 2001/2002, 2003/2004, 2004/2005, 2012/2013, 2013/2014, 2014/2015, 2018/2019, 2020/2021,
- Moderate El Niño: 2002/2003, 2009/2010,
- Strong El Niño: 2015/2016,
- Weak El Niño during a positive IOD: 2006/2007, 2019/2020.
This research only analyzed hotspots that were related to drought conditions. Normally, hotspots during drought conditions have a negative correlation with precipitation anomalies. Having hotspot occurrences during the wet season will disturb the results because they have a positive correlation with precipitation anomalies. Therefore, the analysis is only carried out in the period of the dry season from each region in order to obtain better results.
3.1. Myanmar
Based on the previous analysis, forest fires in the Myanmar region occurred early to mid year. Meanwhile, in the central dry zone of Myanmar, the dry season occurred from December to May [60]. In the analysis of the Myanmar region, one dominant mode was obtained with a 98% SCF. This result shows that Myanmar had very homogeneous characteristics of land and forest fires. The spatial attributes in Figure 3 show the location of the hotspot occurrences in Myanmar over the 20 years of observation. The temporal pattern of mode one is presented using a bubble plot by grouping the years according to the year categories. Figure 3 shows that the El Niño did not have a consistent impact on the number of hotspots in Myanmar. This was indicated by the multiple dry seasons having more than 80 dry spells and precipitation anomalies, with a high number of hotspots occurring during the normal and La Niña years. However, the bubble plot shows that the dry spells had more of an effect on the number of hotspots than the precipitation anomalies. This was indicated by several high numbers of hotspot occurrences during more than 80 dry spells while the precipitation anomaly value was positive. The positive values of the precipitation anomaly indicated that the monthly rainfall was above the long-term mean of rainfall on the respective regions. To obtain different insights into each category’s distribution, Table 1 shows the difference in each Probability Density Function (PDF), which was calculated using a PDF skill score.
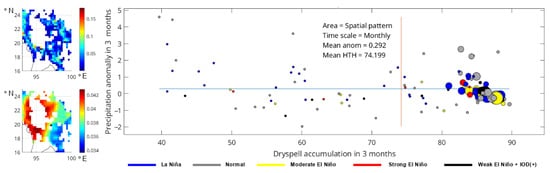
Figure 3.
Myanmar—spatial graph of hotspots (top) and dry spells (bottom) as well as bubble plot of the monthly fire events for all categories. Blue and orange lines represent average value of respective variables. Size of the bubble represents the number of hotspots for each particular month. Extracted from first mode of SVD with 98% of SCF value.

Table 1.
Myanmar—difference value of the PDF from years categories.
Table 1 shows that both the El Niño and IOD did not have a consistent impact on both the dry season and hotspots in Myanmar. Even though a moderate El Niño increased the probability of the dry season from normal, a strong El Niño had the opposite impact. However, this result could be due to the impact of the strong El Niño, which only happened once during the last 20 years. The difference between the normal and positive IOD was 19.93%, with more severe conditions during the positive IOD. However, the positive IOD had the opposite impact on the dry spells and precipitation anomalies. Even though it was only around 3%, this result shows the inconsistent and small impact of the positive IOD in Myanmar. Overall, the difference between the normal years to the other categories varied, with less than 23% for all the variables. The precipitation anomaly had the bigger difference compared to the dry spell. Nonetheless, the difference in the dry spell had a more consistent direction to the hotspot than that of the precipitation anomaly. The dry spell’s difference only failed to give the same direction with the hotspot on the La Niña. Still, the hotspot difference was very small, with an impact of only less than 3%. This result coincides with the previous statement taken from Figure 3, where the high number of hotspots in Myanmar was more related to the dry spells rather than the precipitation anomalies.
3.2. Thailand
April is the hottest month for all regions of Thailand [61]. The analysis on Thailand’s regions produced one dominant mode with an SCF value of 98%. The spatial and temporal characteristics of mode one are shown in Figure 4. Similar to Myanmar, the El Niño did not consistently impact Thailand’s hotspots. This was demonstrated by the bubble plot, where the high number of hotspots happened in all categories. The bubble plot in Figure 4 shows that the worst dry season happened during a weak El Niño and positive IOD. Looking at the raw data, this event happened during the 2006/2007 dry season. However, we can see that the trigger for a large number of hotspots was the severity of its dry season, which is indicated by dry spells and precipitation anomalies.
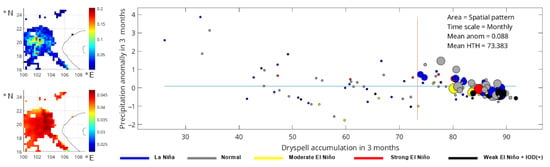
Figure 4.
Thailand—spatial graph of hotspots (top) and dry spells (bottom) as well as bubble plot of the monthly fire events for all categories. Blue and orange lines represent average value of respective variables. Size of the bubble represents the number of hotspots for each particular month. Extracted from first mode of SVD with 98% of SCF value.
Table 2 shows interesting results, where the ENSO and IOD had a consistent impact on all the variables, except for the strong El Niño category. The largest difference in hotspot probability was obtained from the normal–moderate El Niño, with 22.91% increments alongside a 17.49% difference in the dry spells and an 11.19% difference in the precipitation anomaly. However, this behavior was not followed by other increments in the strong El Niño. The hotspots during the strong El Niño were only 6.42% more severe than normal, while decrements appeared in both the dry season variables by around 23%. Meanwhile, the positive IOD and moderate El Niño resulted in a quite comparable hotspot severity, with only a 1.98% difference. However, the impact on the dry season’s variables were different, where the moderate El Niño had a higher increment of dry spells (17.46%) and the positive IOD has higher increments of precipitation anomalies (15.03%). Nonetheless, both the dry seasons behaved similarly compared to the Myanmar one. The strong El Niño result was clearly irrelevant since the dry season condition had an opposite behavior with the hotspot. This result indicates that the hotspot event in Myanmar during the strong El Niño was not produced and spread naturally.

Table 2.
Thailand—difference value of the PDF from years categories.
3.3. Cambodia
Cambodia’s climate is influenced by monsoons and is characterized by two major seasons: a rainy season from May to early October and a dry season from November to April [62]. Land and forest fires in Cambodia usually occur from the beginning to the middle of the year. In the Cambodia region, one dominant mode was obtained with an SCF value of 95.7%, representing a high homogeneity level in Cambodia’s land and forest fires.
Like the two previous regions, the El Niño had inconsistent impacts on the hotspots in Cambodia. Many high numbers of hotspots occurred during the normal and even the La Niña years. The lack of separation between each category in the bubble plot indicates that both the dry season and the hotspots in Cambodia were not affected by the strength of the El Niño and positive IOD. Figure 5 shows that the dry spells also had more influence than the precipitation anomalies on the hotspots. The high number of hotspots occurred when the dry spell value was more than 78, regardless of the precipitation anomaly’s value. The increase in the dry spells had a more consistent impact on the number of hotspots indicated by the magnitude of the circles on Figure 5’s bubble plot. Meanwhile, most of the high numbers of hotspot events happened around the average line of the precipitation anomaly. This result indicates that the precipitation anomaly’s value remained similar during peak dry season, regardless of the El Niño/IOD strength or the dry spell value.
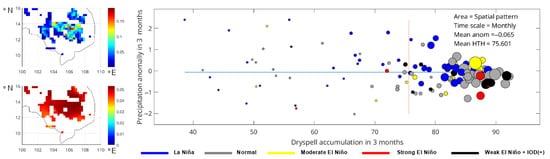
Figure 5.
Cambodia—spatial graph of hotspots (top) and dry spells (bottom) as well as bubble plot of the monthly fire events for all categories. Blue and orange lines represent average value of respective variables. Size of the bubble represents the number of hotspots for each particular month. Extracted from first mode of SVD with 96% of SCF value.
Table 3 shows that the hotspot severity only increased during the strong El Niño, which is an opposite behavior compared to the previous two regions. However, the increments were only around 5% for the hotspot and were less than 11% for the dry season indicators. Considering that the strong El Niño only occurred in 2015/2016, this result cannot be used to describe the El Niño’s impact in Cambodia. Moreover, there were many severe conditions during the normal year, as shown by Figure 5. Overall, the El Niño and positive IOD strength seemed to have less impact on Cambodia’s dry season relative to Myanmar and Thailand’s dry seasons. However, the La Niña had more of an impact on reducing the dry season and hotspot conditions in Cambodia than that of the two previous regions.

Table 3.
Cambodia—difference value of the PDF from years categories.
3.4. Northern Part of Sumatra
Next is an analysis of land and forest fires in the northern part of Sumatra, especially around Riau, the hub of hotspot occurrences. The northern part of the Sumatra regions had a six-month land and forest fire period, which was related to two dry seasons in 1 year, namely at the beginning of the year (December–February) and in the middle of the year (June–August) [8]. Therefore, the northern part of Sumatra will be analyzed separately for these two dry seasons.
3.4.1. Early Year Dry Season
Figure 6 shows the first joint pattern between the dry spells and hotspots with an SCF value of 95.5%. The first dry season in this region happened in a similar period with the three previous regions. Therefore, the obtained result was expected to be close to those three regions, which were less affected by El Niño and positive IOD.
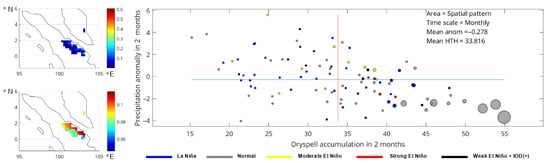
Figure 6.
Early year dry season of northern Sumatra—spatial graph of hotspots (top) and dry spells (bottom) as well as bubble plot of the monthly fire events for all categories. Blue and orange lines represent average value of respective variables. Size of the bubble represents the number of hotspots for each particular month. Extracted from first mode of SVD with 95.5% of SCF value.
Figure 6 shows that both the El Niño and positive IOD had no impact on the number of hotspots. Most of the higher number of hotspots occurred in a normal year. Not only that, the most severe condition of the dry season (represented by the dry spell and precipitation anomaly) also happened during a normal year. This result supports previous research [34], which states the unclear impact of ENSO and IOD on the early year dry season of Riau. This statement is reinforced by the distribution analysis shown in Table 4. Table 4 shows that both strengths of the ENSO and IOD did not impact the severity of the dry season or hotspot occurrence. All the analyzed variables had a lower probability of hotspot occurrence compared to the normal year. This result shows that there are other phenomena which influence hotspot occurrences and cannot be described by this analysis. On the good side, all the variables had the same direction of behavior for all the categories. Therefore, from Figure 4 we can obtain a threshold for both dry spells and precipitation anomalies, which can be used to predict hotspot occurrences. The dry spell threshold was 41 days. For the precipitation anomalies, the threshold was −2 mm days−1.

Table 4.
Early year dry season—difference value of the PDF from years categories.
3.4.2. Mid-Year Dry Season
The mid-year dry season analysis of the northern part of Sumatra gave one dominant pattern with a contribution of 90.2%, shown in Figure 7. The story was quite different from the first dry season. Figure 7 shows that the El Niño and IOD phenomena’s strength consistently impacted the dry season conditions. The stronger El Niño phenomenon made the drought conditions in that year worse.
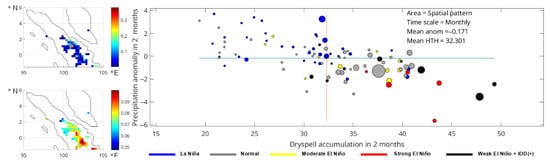
Figure 7.
Mid-year dry season of northern Sumatra—spatial graph of hotspots (top) and dry spells (bottom) as well as bubble plot of the monthly fire events for all categories. Blue and orange lines represent average value of respective variables. Size of the bubble represents the number of hotspots for each particular month. Extracted from first mode of SVD with 90.2% of SCF value.
A very strong El Niño in 2015 and 2019’s positive IOD significantly impacted the dry season’s characteristics. Especially in 2019, the positive IOD caused the dry spell values to reach 49 days, which was more than 50% longer than the average condition. Moreover, the precipitation anomaly almost reached −2 mm days−1 (Table 5). However, these severe dry seasons did not produce a high number of hotspots compared to the normal years, especially during 2015’s El Niño. The significant increment of the hotspots during the 2015 El Niño was absent while the dry season conditions increased significantly.

Table 5.
Mid-year dry season—difference value of the PDF from years categories.
The results from the skill score analysis reinforced the previous statement regarding the ENSO and IOD’s impact on the second dry season of North Sumatra, especially for the dry spell indicator. Compared to the normal year, the value of the dry spell had a positive reaction to the strength of the ENSO in all the ENSO categories. Even though the precipitation anomaly decreased in the moderate El Niño, the decrement was only less than 4%. Other than that, the precipitation anomaly showed similar behavior with the dry spell. Meanwhile, the positive IOD had quite a significant impact by doubling the increment of the moderate El Niño. Similar to the bubble plot analysis, both the strong ENSO and positive IOD did not have a high impact on the number of hotspots distribution, shown by the fewer increments of hotspot severity compared to a normal year (3–14%). This result indicates that there were other factors that influenced hotspot occurrence in the northern part of Sumatra during the second dry season, both in the natural and unnatural factors. The natural factors were indicated by the same direction of changes between the hotspot and dry season’s indicators, while the unnatural ones were indicated by the mixed direction of changes in the moderate El Niño.
3.5. Southern Part of Sumatra
The southern part of the Sumatra region analysis resulted in a high-level homogeneity of one dominant mode with an SCF of 94.8%. Figure 8 shows that there was some separation between each category’s events, especially during the high number of hotspots. The moderate El Niño did not give a clear separation in the bubble plot, which indicates that it did not have a significant impact on the dry season and hotspots in the southern part of Sumatra. The impact was only significant when the strong El Niño happened. However, if a weak El Niño occurred simultaneously with a positive IOD, the impact was quite significant, resulting in up to more than 90 days of dry spells as well as less than a −4 mm precipitation anomaly. These dry season conditions were comparable with 2015’s El Niño. This result indicates that the positive IOD highly impacted the dry season in the southern part of Sumatra. This statement is strengthened with the result of the distribution analysis shown in Table 6.
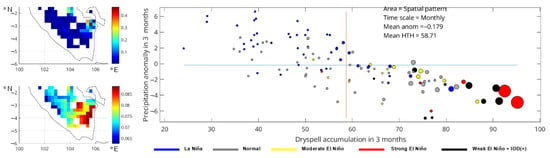
Figure 8.
Southern part of Sumatra—spatial graph of hotspots (top) and dry spells (bottom) as well as bubble plot of the monthly fire events for all categories. Blue and orange lines represent average value of respective variables. Size of the bubble represents the number of hotspots for each particular month. Extracted from first mode of SVD with 94.8% of SCF value.

Table 6.
South Sumatra—difference value of the PDF from years categories.
Table 6 shows that the increase in the El Niño’s strength was positively related to the rise of the dry season and hotspot distribution. The moderate El Niño had an immense impact on the dry season’s severity, with 30.84% for a dry spell and 33.69% for a precipitation anomaly. However, the hotspot distribution was slightly different from the normal one, only 18.78%. This result confirmed the previous statement regarding the small impact of the moderate El Niño in the southern part of Sumatra. The strong El Niño had a massive impact on the hotspot distribution, with an 89.37% difference compared to normal. The dry season condition also increased significantly, with 52.45% for the dry spell and 56.1% for the precipitation anomaly. Table 6 shows that we need to highly consider the El Niño and positive IOD conditions when anticipating hotspot occurrences in the southern part of Sumatra. Even though it occurred during a weak El Niño, it can lead to much more severe conditions that are close to a strong El Niño’s conditions if accompanied by a positive IOD.
3.6. Kalimantan
Kalimantan was one of the regions with a high correlation between their dry season and El Niño [63,64]. In the Kalimantan analysis, there was one dominant mode with an SCF value of 94.8%. Figure 8 shows that the El Niño and positive IOD clearly affected the dry season and hotspot conditions in Kalimantan. The impact of the El Niño was even higher than that of the southern Sumatra analysis. The moderate El Niño impacted the hotspot and dry season conditions until it was close to a strong El Niño. Meanwhile, the positive IOD could raise the impact of the weak El Niño until it was comparable with the moderate and strong El Niño. This result represents the multiplication impact of the ENSO–IOD teleconnections.
Table 7 shows that the ENSO had a positive correlation with all the analyzed variables. A La Niña significantly decreased the hotspot distribution as well as the dry season indicator distributions. The occurrence of the moderate El Niño was relatively high, with a 64.28% difference from the normal condition. This result is close to a normal-to-strong El Niño, with a 72.87% difference. Comparing the moderate-to-strong El Niño, the difference was only 14.96%. Table 7 shows that the hotspot in Kalimantan was highly sensitive to the El Niño’s strength and positive IOD occurrence, where the moderate El Niño had a close impact to the strong El Niño. Even during the weak El Niño, the condition was very close to a moderate El Niño if accompanied by a positive IOD. Even though the hotspot was more sensitive compared to the southern part of Sumatra, the dry season indicators were less sensitive compared to the southern part of Sumatra indicators.

Table 7.
Kalimantan—difference value of the PDF from years categories.
The difference in the dry season indicators in Kalimantan was only less than 30% for the dry spells and less than 39% for the precipitation anomaly. This result indicates that many hotspots could have occurred in Kalimantan even during a normal year, which is also shown in Figure 9, on an area with more than 70 days of dry spells. Both the El Niño and positive IOD elongated the duration of the dry season, so it caused much drier land conditions. Eventually, the land became easier to burn and increased the spreading rate of the hotspot.
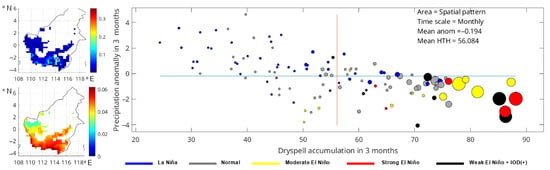
Figure 9.
Kalimantan—spatial graph of hotspots (top) and dry spells (bottom) as well as bubble plot of the monthly fire events for all categories. Blue and orange lines represent average value of respective variables. Size of the bubble represents the number of hotspots for each particular month. Extracted from first mode of SVD with 94.8% of SCF value.
3.7. Probability Analysis
From all of the previous analyses, the variables in each region had a unique behavior in response to both the ENSO and IOD, representing the diverse characteristics of each region. Even though we can divide the land and forest fires into two groups (early to mid year events, mid to end year events), the specific impact of the ENSO and IOD cannot be generalized. This section analyzed the probability of a dry season and hotspots that are more severe than the average condition for the last 20 years. The probability was calculated from the distribution of each variable obtained from the joint pattern of the SVD analysis. Figure 10 shows the changes in probability in each Niño category and region with the criteria for each distribution as follows:
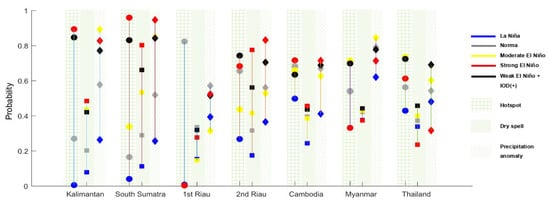
Figure 10.
Probabilities graph where each variable is more than the average value in each category for the year and region being analyzed.
- Hotspots: probability of hotspots in 1 month on each observation grid more than the regional hotspot mode in the last 20 years,
- Dry spell: probability of three months of a dry spell accumulation on each observation grid is more than the regional average in the last 20 years,
- Precipitation anomaly: probability of the average precipitation decline in each observation grid is less than the regional average in the last 20 years.
Figure 10 shows that the El Niño and IOD consistently impacted all the variables in Kalimantan and the southern Sumatra regions, except for the precipitation anomaly of Kalimantan. Consistency in this case means that the probability value increased, following the strength of the ENSO and IOD. In Kalimantan, the precipitation anomaly failed to represent the hotspot by having the highest probability during the moderate El Niño. In South Sumatra, the precipitation anomaly also failed to describe the hotspot probability by having a similar probability during the moderate El Niño and positive IOD. Meanwhile, the dry spell had a better ability to represent the difference in the hotspot probability in the positive IOD and moderate El Niño in South Sumatra. This result shows that the dry spells had a better performance and consistency when used to analyze the number of hotspots in both Kalimantan and the southern part of Sumatra.
A different story was obtained in the northern part of Sumatra (called Riau in Figure 10), where the ENSO and IOD phenomena only affected the second dry season. Both the ENSO and IOD affected the severity of the second dry season in North Sumatra, especially the dry spell. However, only the positive IOD and strong El Niño had a higher probability value of hotspots than a normal year, which coincides with the previous section’s analysis. Meanwhile, all the categories in the first dry season had a lower probability value than a normal year. This result reinforces the previous section’s result, which states that both the ENSO and IOD did not affect both the dry season and hotspots in the northern part of Sumatra during the early year dry season.
The Cambodia, Myanmar, and Thailand analysis gave similar interpretations to each region’s analysis in the previous sections. Only the strong El Niño potentially increased the probability of both hotspots and the dry season in Cambodia. Even so, the increase was only 0.033 for the hotspots, 0.083 for the dry spells, and 0.018 for the precipitation anomalies. In Thailand, only the positive IOD had a consistent impact, while the moderate and strong El Niño gave the opposite result. The positive IOD potentially increased the probability of the hotspot and dry season by around 0.08–0.15, which is very small. Meanwhile, both the ENSO and IOD did not consistently impact the probability of hotspots and the dry season in Myanmar. Despite the probability value on the moderate El Niño being consistently higher than a normal year, the probability value on the strong El Niño was much lower than a normal year, which was the opposite of the impact of the moderate El Niño.
3.8. ENSO and IOD Relation Analysis
The ENSO and IOD are phenomena that could impact drought and forest fires in SEA, especially in regions which have dry season periods similar to the warm phase of both phenomena. Some of the previous analyses showed that the impact of the ENSO and IOD were multiplied when both phenomena occurred simultaneously. Therefore, understanding the relationship between both phenomena is essential to anticipate future drought as well as land and forest fires. The relation was analyzed using wavelet coherence analysis utilizing monthly Niño3.4 and DMI indexes from June 1970 until May 2020.
The wavelet coherence analysis showed no consistency in the high coherency between the ENSO and IOD phenomena from the last 50 years with the same period (Figure 11). The high coherency of both phenomena occurred during 1970–1980 with a period of 4 years. From 1990 until 2000, the period was in the range of 1–3 years, which was smaller than the previous decade. In general, the periods of significant relation between the ENSO and IOD decreased. One of the reasons for the decrease is global warming [65], which is related to previous research showing that climate change contributes to more frequent El Niño [66] and positive IOD [67] events from time to time.

Figure 11.
Wavelet coherence plot of Niño3.4 and DMI index from 1971–2021 with a different time lag (from left to right: same month, one month earlier of Niño3.4, two months earlier of Niño3.4, one month earlier of DMI, and two months earlier of DMI).
In the last 50 years, most El Niño events did not generate concurrent IOD events [68,69]. The complex evolution of the ENSO–IOD relationship was mainly controlled by their variability at the three dominant timescales, which were 1.5, 3, and 24 years. The different decadal time scales of the ENSO and IOD indicate their different modes of climate variability [32]. Moreover, the correlation between the time series of the IOD and ENSO peaked at lag +1 year, so that the IOD tended to occur in the following year after an El Niño’s peak [27].
4. Discussion
The analyses in Section 3.1, Section 3.2 and Section 3.3 show that both the ENSO and IOD had inconsistent or/and small impacts on the hotspots and dry seasons of Myanmar, Thailand, and Cambodia. The impacts of the ENSO and IOD usually occurred from June to November, while the hotspots in these three areas occurred from early to mid year. Therefore, when the dry season occurred, the impact of the ENSO and IOD were already over or had decreased significantly, resulting in a small impact on the three regions. Even for Cambodia, which had its dry season period starting from November, the impact of the ENSO was only noticeable during the very strong El Niño that occurred in 2015/2016, with only less than a 15% difference. This result is in line with previous research showing that the ENSO weakly influenced the negative extreme rainfall and had a negative covariation during the dry season period of the three regions [64]. However, Figure 3, Figure 4 and Figure 5 show that the hotspot in those three regions were highly affected by the dry season condition of each year, which is in line with previous research.
In Cambodia, the annual mean temperature was the most influential predictor for forest loss [70]. From November to April, Cambodia had the highest temperature of 40 °C with the lowest humidity, when fires most likely occurred [71]. During the highest forest fire in Myanmar in 2007, the causative factors of the fires were not documented [72]. Natural factors like climate, fuel characteristics, and increased anthropogenic pressure were expected to contribute to the high number of fires in Myanmar. Meanwhile, the average rainfall in Thailand during fire season is lower than in normal years [73]. The story is quite different for the southern part of SEA, which is Indonesia. Indonesian dry season is distinctively influenced by the ENSO and IOD because of its location between the Pacific and Indian Oceans and the dry season period that coincides with the peak of both phenomena’s warm phase [28,63]. In addition to the northern part of Sumatra, Indonesian land and forest fires are affected by the El Niño’s occurrence and positive IOD [28,34,64]. Obviously, the impact varies, corresponding to the dry season and fire characteristics in each region.
Land and forest fire events in northern Sumatra are mainly related to deforestation [74,75]. Due to the short duration of the dry season, the scale of the event is much smaller compared to other regions. However, the scale of the fire event can increase significantly when a climate anomaly happens, such as in mid 2013 and early 2014. Other than the policy not being implemented optimally [76], there was a climate anomaly in 2013 which produced the highest number of hotspots during the mid-year dry season for the last 20 years [77]. Not only that, a high number of hotspots also occurred in early 2014, caused by the cold phenomenon and the contraction of the Intertropical Convergence Zone (ICTZ) [78] and Madden–Julian Oscillation [79], resulting in a severe dry season in the northern part of Sumatra.
Not only the severity of the dry season, but the number of hotspots that occur in the southern part of Sumatra and Kalimantan are also affected by the strength of El Niño and positive IOD [80,81]. However, the impact of positive IOD in Kalimantan is not as high as in southern Sumatra. This result is in line with previous research [28] and relates to the location of the IOD, which is closer to southern Sumatra than Kalimantan. The proportion of quantitative representation between the ENSO and IOD impact is more balanced in South Sumatra [81]. Meanwhile, it is dominated by the ENSO in Kalimantan. Even though the relationship between the ENSO and IOD is not constant in time [82], the occurrence of both phenomena in the same year can lead to a much more severe dry season and fire events and needs to be considered.
5. Conclusions
El Niño and positive IOD are well known as phenomena that affect the dry season as well as land and forest fires in SEA. The impacts vary from region to region. From the analysis, we can conclude that El Niño do not impact land and forest fire events in the northern part of SEA, which are Myanmar, Thailand, and Cambodia. The difference in hotspot severity in those three regions was less than 25% for all categories compared to a normal year. However, the direction of the impact was not always positively corelated with El Niño and positive IOD. All three regions have dry season periods different from the peak impact of ENSO and IOD. Therefore, the impact of both phenomena was low and inconsistent. The inconsistency also occurred in the northern part of Sumatra’s early year dry season, while an insignificant impact occurred during the mid-year dry season.
Kalimantan is an area with a high sensitivity to the strength of the El Niño phenomenon. The moderate El Niño’s impact on Kalimantan was almost as strong as a strong El Niño, with more than a 64% increase in the moderate El Niño, and more than a 72% increase in the strong El Niño. The impact of the weak El Niño was multiplied when the positive IOD occurred (also called the ENSO–IOD teleconnection), resulting in a similar impact to the moderate El Niño, with only less than a 1% difference. The impact of the ENSO–IOD teleconnection was even higher in the southern Sumatra analysis. A weak El Niño and positive IOD could increase the severity of the hotspots by almost 70% from a normal year, which is more than a 3 × increase than the moderate El Niño. The severity of the dry season and the number of hotspots also increased dramatically when the strong El Niño occurred, with more than an 89% increment in the hotspots as well as more than a 50% increment in the dry season.
The results in Section 3.7 show the potential usage of a dry spell and precipitation anomaly to predict the number of hotspots in the future, which is different for each region. Even though the dry spell value was more consistent with the increased number of hotspots, the precipitation anomaly can make a different impact, especially in extreme conditions. Overall, a dry spell can represent the increase in hotspot probability better than precipitation anomalies (Figure 10).
The Kalimantan, South Sumatra, and mid-year dry season of North Sumatra analysis shows how important a teleconnection between the ENSO and IOD is in terms of increasing hotspot and dry season severities. Even though both phenomena have a low and inconsistent coherency, this research shows that the combined impact of both phenomena can multiply each standalone impact significantly. The impact of a weak El Niño and positive IOD may become higher than a moderate El Niño, especially in regions which have their dry season period from June–November.
Author Contributions
Conceptualization, S.N. and A.S.; methodology, A.S. and P.S.; software, P.S.; validation, S.N., A.S. and P.S.; formal analysis, S.N.; investigation, A.S.; resources, S.N. and A.S.; data curation, P.S.; writing—original draft preparation, P.S.; writing—review and editing, S.N.; visualization, P.S.; supervision, S.N. and A.S.; project administration, S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Department of Mathematics, IPB University, and the Meteorological, Climatological, and Geophysical Agency (BMKG) for their invaluable support and assistance throughout this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stibig, H.-J.; Achard, F.; Carboni, S.; Raši, R.; Miettinen, J. Change in tropical forest cover of Southeast Asia from 1990 to 2010. Biogeosciences 2013, 11, 247–258. [Google Scholar] [CrossRef] [Green Version]
- Estoque, R.C.; Ooba, M.; Avitabile, V.; Hijioka, Y.; DasGupta, R.; Togawa, T.; Murayama, Y. The future of Southeast Asia’s forests. Nat. Commun. 2019, 10, 1829. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tölle, M. Impact of Deforestation on Land–Atmosphere Coupling Strength and Climate in Southeast Asia. Sustainability 2020, 12, 6140. [Google Scholar] [CrossRef]
- Ken, S.; Sasaki, N.; Entani, T.; Ma, H.O.; Thuch, P.; Tsusaka, T.W. Assessment of the Local Perceptions on the Drivers of Deforestation and Forest Degradation, Agents of Drivers, and Appropriate Activities in Cambodia. Sustainability 2020, 12, 9987. [Google Scholar] [CrossRef]
- Syaufina, L.; Ainuddin, A. Impacts of Fire on SouthEast Asia Tropical Forests Biodiversity: A Review. Asian J. Plant Sci. 2011, 10, 238–244. [Google Scholar] [CrossRef]
- Page, S.E.; Hooijer, A. In the line of fire: The peatlands of Southeast Asia. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371, 20150176. [Google Scholar] [CrossRef] [Green Version]
- Nurdiati, S.; Sopaheluwakan, A.; Agustina, A.; Septiawan, P. Multivariate analysis on Indonesian forest fire using combined empirical orthogonal function and covariance matrices. IOP Conf. Ser. Earth Environ. Sci. 2019, 299, 012048. [Google Scholar] [CrossRef]
- Septiawan, P.; Nurdiati, S.; Sopaheluwakan, A. Numerical Analysis using Empirical Orthogonal Function Based on Multivariate Singular Value Decomposition on Indonesian Forest Fire Signal. IOP Conf. Ser. Earth Environ. Sci. 2019, 303, 012053. [Google Scholar] [CrossRef]
- Vadrevu, K.P.; Lasko, K.; Giglio, L.; Schroeder, W.; Biswas, S.; Justice, C. Trends in Vegetation fires in South and Southeast Asian Countries. Sci. Rep. 2019, 9, 7422. [Google Scholar] [CrossRef]
- Fisher, D.; Wooster, M.J.; Xu, W.; Thomas, G.; Lestari, P. Top-Down Estimation of Particulate Matter Emissions from Extreme Tropical Peatland Fires Using Geostationary Satellite Fire Radiative Power Observations. Sensors 2020, 20, 7075. [Google Scholar] [CrossRef]
- Ismail, N.W.; Chan, S.M. Impacts of the El Niño-Southern Oscillation (ENSO) on Paddy Production in Southeast Asia. Clim. Dev. 2019, 12, 636–648. [Google Scholar] [CrossRef]
- Saunders, K.; Stephenson, A.G.; Taylor, P.G.; Karoly, D. The spatial distribution of rainfall extremes and the influence of El Niño Southern Oscillation. Weather Clim. Extrem. 2017, 18, 17–28. [Google Scholar] [CrossRef]
- Shin, S.-I.; Sardeshmukh, P.D.; Newman, M.; Penland, C.; Alexander, M.A. Impact of Annual Cycle on ENSO Variability and Predictability. J. Clim. 2021, 34, 171–193. [Google Scholar] [CrossRef]
- Hao, Z.; Zhang, X.; Singh, V.P.; Hao, F. Joint modeling of precipitation and temperature under influences of El Niño Southern Oscillation for compound event evaluation and prediction. Atmos. Res. 2020, 245, 105090. [Google Scholar] [CrossRef]
- Park, C.-K.; Park, D.-S.R.; Ho, C.-H.; Park, T.-W.; Kim, J.; Jeong, S.-J.; Kim, B.-M. A Dipole Mode of Spring Precipitation between Southern China and Southeast Asia Associated with the Eastern and Central Pacific Types of ENSO. J. Clim. 2020, 33, 10097–10111. [Google Scholar] [CrossRef]
- Yan, Y.; Wu, H.; Gu, G.; Ward, P.J.; Luo, L.; Li, X.; Huang, Z.; Tao, J. Exploring the ENSO Impact on Basin-Scale Floods Using Hydrological Simulations and TRMM Precipitation. Geophys. Res. Lett. 2020, 47, e2020GL089476. [Google Scholar] [CrossRef]
- Chhin, R.; Shwe, M.M.; Yoden, S. Time-lagged correlations associated with interannual variations of pre-monsoon and post-monsoon precipitation in Myanmar and the Indochina Peninsula. Int. J. Clim. 2019, 40, 3792–3812. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, L.; Hao, Z.; Li, J.; Thorstensen, A.; Gao, H. A Framework for Exploring Joint Effects of Conditional Factors on Compound Floods. Water Resour. Res. 2018, 54, 2681–2696. [Google Scholar] [CrossRef]
- Qian, Q.F.; Wu, R.; Jia, X.J. Persistence and Nonpersistence of East and Southeast Asian Rainfall Anomaly Pattern From Spring to Summer. J. Geophys. Res. Atmos. 2020, 125, e2020JD033404. [Google Scholar] [CrossRef]
- Yulihastin, E.; Hadi, T.W.; Ningsih, N.S.; Syahputra, M.R. Early morning peaks in the diurnal cycle of precipitation over the northern coast of West Java and possible influencing factors. Ann. Geophys. 2020, 38, 231–242. [Google Scholar] [CrossRef] [Green Version]
- Amirudin, A.; Salimun, E.; Tangang, F.; Juneng, L.; Zuhairi, M. Differential Influences of Teleconnections from the Indian and Pacific Oceans on Rainfall Variability in Southeast Asia. Atmosphere 2020, 11, 886. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef]
- Schott, F.A.; Xie, S.-P.; McCreary, J.P. Indian Ocean circulation and climate variability. Rev. Geophys. 2009, 47, RG1002. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an Integrating Concept in Earth Science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Xie, S.-P.; Wu, L.; Kosaka, Y.; Lau, N.-C.; Vecchi, G.A. Seasonality and Predictability of the Indian Ocean Dipole Mode: ENSO Forcing and Internal Variability. J. Clim. 2015, 28, 8021–8036. [Google Scholar] [CrossRef]
- Aryal, Y.; Zhu, J. Multimodel ensemble projection of meteorological drought scenarios and connection with climate based on spectral analysis. Int. J. Clim. 2019, 40, 3360–3379. [Google Scholar] [CrossRef]
- Cai, W.; Van Rensch, P.; Cowan, T.; Hendon, H.H. Teleconnection Pathways of ENSO and the IOD and the Mechanisms for Impacts on Australian Rainfall. J. Clim. 2011, 24, 3910–3923. [Google Scholar] [CrossRef]
- Kurniadi, A.; Weller, E.; Min, S.; Seong, M. Independent ENSO and IOD impacts on rainfall extremes over Indonesia. Int. J. Clim. 2021, 41, 3640–3656. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Saji, N.H.; Yamagata, T. Individual and Combined Influences of ENSO and the Indian Ocean Dipole on the Indian Summer Monsoon. J. Clim. 2004, 17, 3141–3155. [Google Scholar] [CrossRef]
- Cha, E.-J. El Niño-Southern Oscillation, Indian Ocean Dipole Mode, a Relationship between the Two Phenomena, and Their Impact on the Climate over the Korean Peninsula. J. Korean Earth Sci. Soc. 2007, 28, 35–44. [Google Scholar] [CrossRef]
- Jourdain, N.C.; Lengaigne, M.; Vialard, J.; Izumo, T.; Gupta, A.S. Further Insights on the Influence of the Indian Ocean Dipole on the Following Year’s ENSO from Observations and CMIP5 Models. J. Clim. 2016, 29, 637–658. [Google Scholar] [CrossRef]
- Sang, Y.-F.; Singh, V.P.; Xu, K. Evolution of IOD-ENSO relationship at multiple time scales. Theor. Appl. Climatol. 2019, 136, 1303–1309. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, W.; Zhou, F.; Chai, F. Frontal variability and its impact on chlorophyll in the Arabian sea. J. Mar. Syst. 2021, 218, 103545. [Google Scholar] [CrossRef]
- Zhang, Z.; Moore, J.C. Empirical Orthogonal Functions, Mathematical and Physical Fundamentals of Climate Change; Elsevier: Amsterdam, The Netherlands, 2015; Chapter 6; pp. 161–197. [Google Scholar] [CrossRef]
- Ardiansyah, M.; Boer, R.; Situmorang, A.P. Typology of land and forest fire in South Sumatra, Indonesia Based on Assessment of MODIS Data. IOP Conf. Ser. Earth Environ. Sci. 2017, 54, 12058. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Li, L.; Wang, J.; Qi, W.; Xu, C.-Y.; Kim, J.-S. Evaluation of Multi-Satellite Precipitation Datasets and Their Error Propagation in Hydrological Modeling in a Monsoon-Prone Region. Remote Sens. 2020, 12, 3550. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 2003, 108, 4407. [Google Scholar] [CrossRef]
- Ferzali, W.; Proakis, J. Adaptive SVD algorithm for covariance matrix eigenstructure computation. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 2002; Volume 5, pp. 2615–2618. [Google Scholar] [CrossRef]
- Kaiser, A.; Schenck, W.; Möller, R. Coupled singular value decomposition of a cross-covariance matrix. Int. J. Neural Syst. 2010, 20, 293–318. [Google Scholar] [CrossRef]
- Perkins-Kirkpatrick, S.; Pitman, A.J.; Holbrook, N.; McAneney, J. Evaluation of the AR4 Climate Models’ Simulated Daily Maximum Temperature, Minimum Temperature, and Precipitation over Australia Using Probability Density Functions. J. Clim. 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Bosman, P.A.N.; Thierens, D. Negative Log–Likelihood and Statistical Hypothesis Testing as the Basis of Model Selection in IDEAs. In Genetic and Evolutionary Computation Conference GECCO-00; Utrecht University: Utrecht, The Netherlands, 2000; Available online: https://homepages.cwi.nl/~bosman/publications/2000_negativeloglikelihood.pdf (accessed on 29 June 2022).
- Chakrabarti, A.; Ghosh, J.K. AIC, BIC and Recent Advances in Model Selection. Philos. Stat. 2011, 7, 583–605. [Google Scholar] [CrossRef]
- Al-Noor, N.H.; Assi, N.K. Rayleigh-Rayleigh Distribution: Properties and Applications. In Journal of Physics: Conference Series; IOP Publishing: Hillah, Iraq, 2020; Volume 1591. [Google Scholar] [CrossRef]
- Muraleedharan., G.; Guedes, C.S.; Lucas, C. Characteristic and Moment Generating Functions of Generalised Extreme Value Distribution (GEV). In Sea Level Rise, Coastal Engineering, Shorelines and Tides; Wright, L.L., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2011; Chapter-14; pp. 269–276. ISBN 978-1-61728-655-1. [Google Scholar]
- Taylor, J.; Verbyla, A. Joint modelling of location and scale parameters of the t distribution. Stat. Model. 2004, 4, 91–112. [Google Scholar] [CrossRef]
- Wang, Y. Rapid surface defect detection based on singular value decomposition using steel strips as an example. AIP Adv. 2018, 8, 055209. [Google Scholar] [CrossRef] [Green Version]
- Björnsson, H.; Venegas, S. A Manual for EOF and SVD Analyses of Climate Data; McGill University: Quebec, QC, Canada, 1997. [Google Scholar]
- Chen, B.; Zhu, Y.; Hu, J.; Principe, J.C. System Identification Under Information Divergence Criteria. In System Parameter Identification; Elsevier: Amsterdam, The Netherlands, 2013; pp. 167–204. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Cavagnaro, D.R. Computational Approaches to Model Evaluation. In International Encyclopedia of the Social & Behavioral Sciences, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 475–479. [Google Scholar] [CrossRef]
- Chakrabarty, A.; De, A.; Gunasekaran, A.; Dubey, R. Investment horizon heterogeneity and wavelet: Overview and further research directions. Phys. A Stat. Mech. Appl. 2015, 429, 45–61. [Google Scholar] [CrossRef]
- Chang, X.; Wang, B.; Yan, Y.; Hao, Y.; Zhang, M. Characterizing effects of monsoons and climate teleconnections on precipitation in China using wavelet coherence and global coherence. Clim. Dyn. 2018, 52, 5213–5228. [Google Scholar] [CrossRef] [Green Version]
- Das, J.; Jha, S.; Goyal, M.K. On the relationship of climatic and monsoon teleconnections with monthly precipitation over meteorologically homogenous regions in India: Wavelet & global coherence approaches. Atmos. Res. 2020, 238, 104889. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P. Interdecadal Changes in the ESNO-Monsoon System. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef] [Green Version]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- GGWS. El Niño and La Niña Years and Intensities. Available online: https://ggweather.com/enso/oni.htm (accessed on 1 May 2021).
- BOM. Climate Drivers in the Pacific, Indian and Southern Oceans and the Tropics. Available online: http://www.bom.gov.au/climate/enso/ (accessed on 21 July 2022).
- Nur’Utami, M.N.; Hidayat, R. Influences of IOD and ENSO to Indonesian Rainfall Variability: Role of Atmosphere-ocean Interaction in the Indo-pacific Sector. Procedia Environ. Sci. 2016, 33, 196–203. [Google Scholar] [CrossRef] [Green Version]
- Toe, M.T.; Kanzaki, M.; Lien, T.-H.; Cheng, K.-S. Spatial and temporal rainfall patterns in Central Dry Zone, Myanmar—A hydrological cross-scale analysis. Terr. Atmos. Ocean. Sci. 2017, 28, 425–436. [Google Scholar] [CrossRef] [Green Version]
- Nounmusig, W. Analysis of rainfall in the eastern Thailand. Int. J. GEOMATE 2018, 46, 150–155. [Google Scholar] [CrossRef]
- Chhuon, K.; Botkosal, W.; Chanthou, C. The State of Climate Change in Cambodia. In Proceedings of the 5th AUN/SEED-Net Regional Conference on Global Environment, Bandung, Indonesia, 21–22 November 2012. [Google Scholar]
- Hamada, J.-I.; Yamanaka, M.D.; Matsumoto, J.; Fukao, S.; Winarso, P.A.; Sribimawati, T. Spatial and Temporal Variations of the Rainy Season over Indonesia and their Link to ENSO. J. Meteorol. Soc. Jpn. Ser. II 2002, 80, 285–310. [Google Scholar] [CrossRef] [Green Version]
- Villafuerte, M.Q.; Matsumoto, J. Significant Influences of Global Mean Temperature and ENSO on Extreme Rainfall in Southeast Asia. J. Clim. 2015, 28, 1905–1919. [Google Scholar] [CrossRef]
- Yuan, D.; Hu, X.; Xu, P.; Zhao, X.; Masumoto, Y.; Han, W. The IOD-ENSO precursory teleconnection over the tropical Indo-Pacific Ocean: Dynamics and long-term trends under global warming. J. Oceanol. Limnol. 2017, 36, 4–19. [Google Scholar] [CrossRef]
- Wang, B.; Luo, X.; Yang, Y.-M.; Sun, W.; Cane, M.A.; Cai, W.; Yeh, S.-W.; Liu, J. Historical change of El Niño properties sheds light on future changes of extreme El Niño. Proc. Natl. Acad. Sci. USA 2019, 116, 22512–22517. [Google Scholar] [CrossRef] [Green Version]
- Cai, W.; Sullivan, A.; Cowan, T. Climate change contributes to more frequent consecutive positive Indian Ocean Dipole events. Geophys. Res. Lett. 2009, 36, L23704. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Yamagata, T. A Look at the Relationship between the ENSO and the Indian Ocean Dipole. J. Meteorol. Soc. Jpn. Ser. II 2003, 81, 41–56. [Google Scholar] [CrossRef] [Green Version]
- Cai, W.; Hendon, H.H.; Meyers, G. Indian Ocean dipolelikevariability in the CSIRO Mark 3 coupled climate model. J. Clim. 2005, 18, 1449–1468. [Google Scholar] [CrossRef]
- Lohani, S.; Dilts, T.E.; Weisberg, P.J.; Null, S.E.; Hogan, Z.S. Rapidly Accelerating Deforestation in Cambodia’s Mekong River Basin: A Comparative Analysis of Spatial Patterns and Drivers. Water 2020, 12, 2191. [Google Scholar] [CrossRef]
- Yu, B.; Chen, F.; Li, W.; Wang, L.; Wu, M.; Mingquan, W.; Bo, Y.; Fang, C.; Bin, L. Fire Risk Prediction Using Remote Sensed Products: A Case of Cambodia. Photogramm. Eng. Remote Sens. 2017, 83, 19–25. [Google Scholar] [CrossRef]
- Biswas, S.; Vadrevu, K.P.; Lwin, Z.M.; Lasko, K.; Justice, C.O. Factors Controlling Vegetation Fires in Protected and Non-Protected Areas of Myanmar. PLoS ONE 2015, 10, e0124346. [Google Scholar] [CrossRef] [PubMed]
- Junpen, A.; Garivait, S.; Bonnet, S. Estimating emissions from forest fires in Thailand using MODIS active fire product and country specific data. Asia-Pac. J. Atmos. Sci. 2013, 49, 389–400. [Google Scholar] [CrossRef]
- Tata, H.L.; Narendra, B.H.; Mawazin, M. Forest and land fires in Pelalawan District, Riau, Indonesia: Drivers, pressures, impacts and responses. Biodiversitas J. Biol. Divers. 2018, 19, 494–501. [Google Scholar] [CrossRef]
- Adrianto, H.A.; Spracklen, D.V.; Arnold, S.R.; Sitanggang, I.S.; Syaufina, L. Forest and Land Fires Are Mainly Associated with Deforestation in Riau Province, Indonesia. Remote Sens. 2019, 12, 3. [Google Scholar] [CrossRef] [Green Version]
- Saharjo, B.H.; Yungan, A. Forest and Land Fires in Riau Province: A Case Study in Fire Prevention Policy Implementation with Local Concession Holders. In Land-Atmospheric Research Applications in South and Southeast Asia; Vadrevu, K., Ohara, T., Justice, C., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Kusumaningtyas, S.D.A.; Aldrian, E. Impact of the June 2013 Riau province Sumatera smoke haze event on regional air pollution. Environ. Res. Lett. 2016, 11, 075007. [Google Scholar] [CrossRef]
- McBride, J.L.; Sahany, S.; Hassim, M.E.; Nguyen, C.M.; Lim, S.Y.; Rahmat, R.; Cheong, W.K. The 2014 record dry spell at Singapore: An intertropical convergence zone (itcz) drought. Bull. Am. Met. Soc. 2015, 96, S126–S130. [Google Scholar] [CrossRef]
- Eguchi, N.; Kodera, K.; Nasuno, T. A global non-hydrostatic model study of a downward coupling through the tropical tropopause layer during a stratospheric sudden warming. Atmos. Chem. Phys. 2015, 15, 297–304. [Google Scholar] [CrossRef] [Green Version]
- Dafri, M.; Nurdiati, S.; Sopaheluwakan, A. Quantifying ENSO and IOD impact to hotspot in Indonesia based on Heterogeneous Correlation Map (HCM). J. Phys. Conf. Ser. 2021, 1869, 012150. [Google Scholar] [CrossRef]
- Nurdiati, S.; Sopaheluwakan, A.; Julianto, M.T.; Septiawan, P.; Rohimahastuti, F. Modelling and analysis impact of El Nino and IOD to land and forest fire using polynomial and generalized logistic function: Cases study in South Sumatra and Kalimantan, Indonesia. Model. Earth Syst. Environ. 2021, 1–16. [Google Scholar] [CrossRef]
- Rathinasamy, M.; Agarwal, A.; Parmar, V.; Khosa, R.; Bairwa, A. Partial wavelet coherence analysis for understanding the standalone relationship between Indian Precipitation and Teleconnection patterns. arXiv 2017, arXiv:1702.06568. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).