A Statistical-Based Model for Typhoon Rain Hazard Assessment
Abstract
:1. Introduction
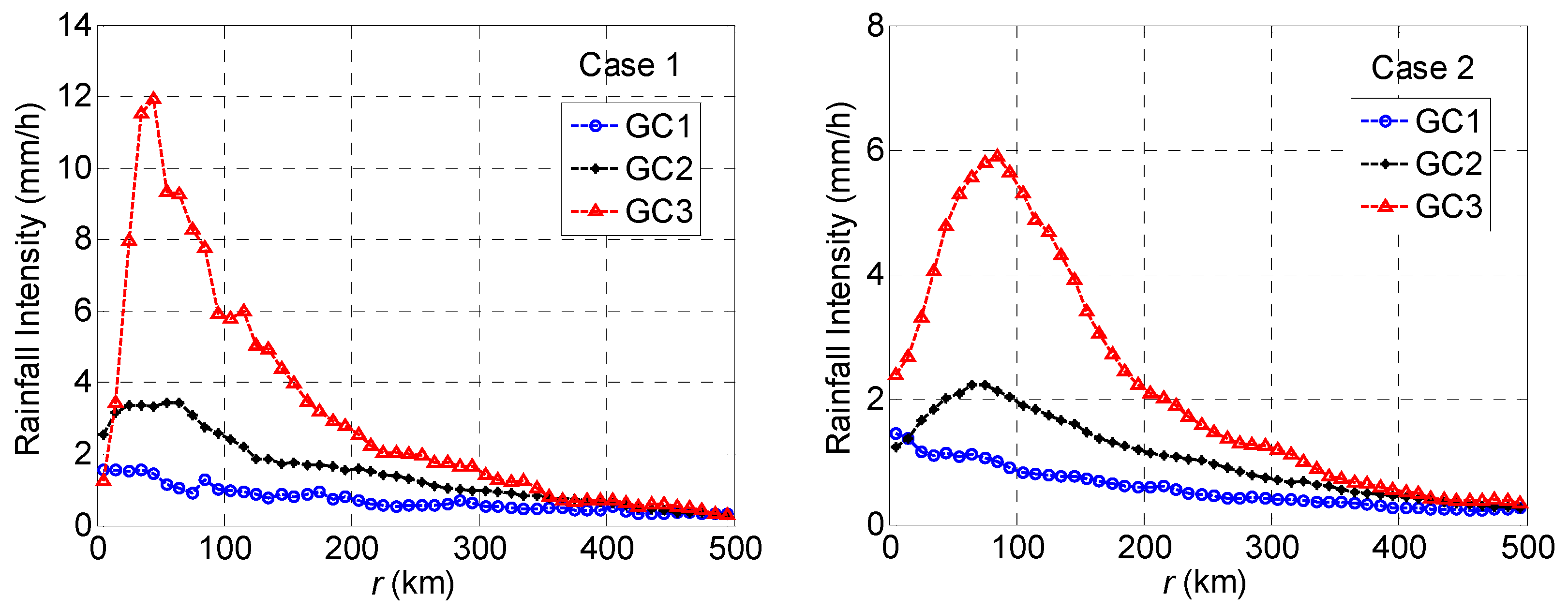
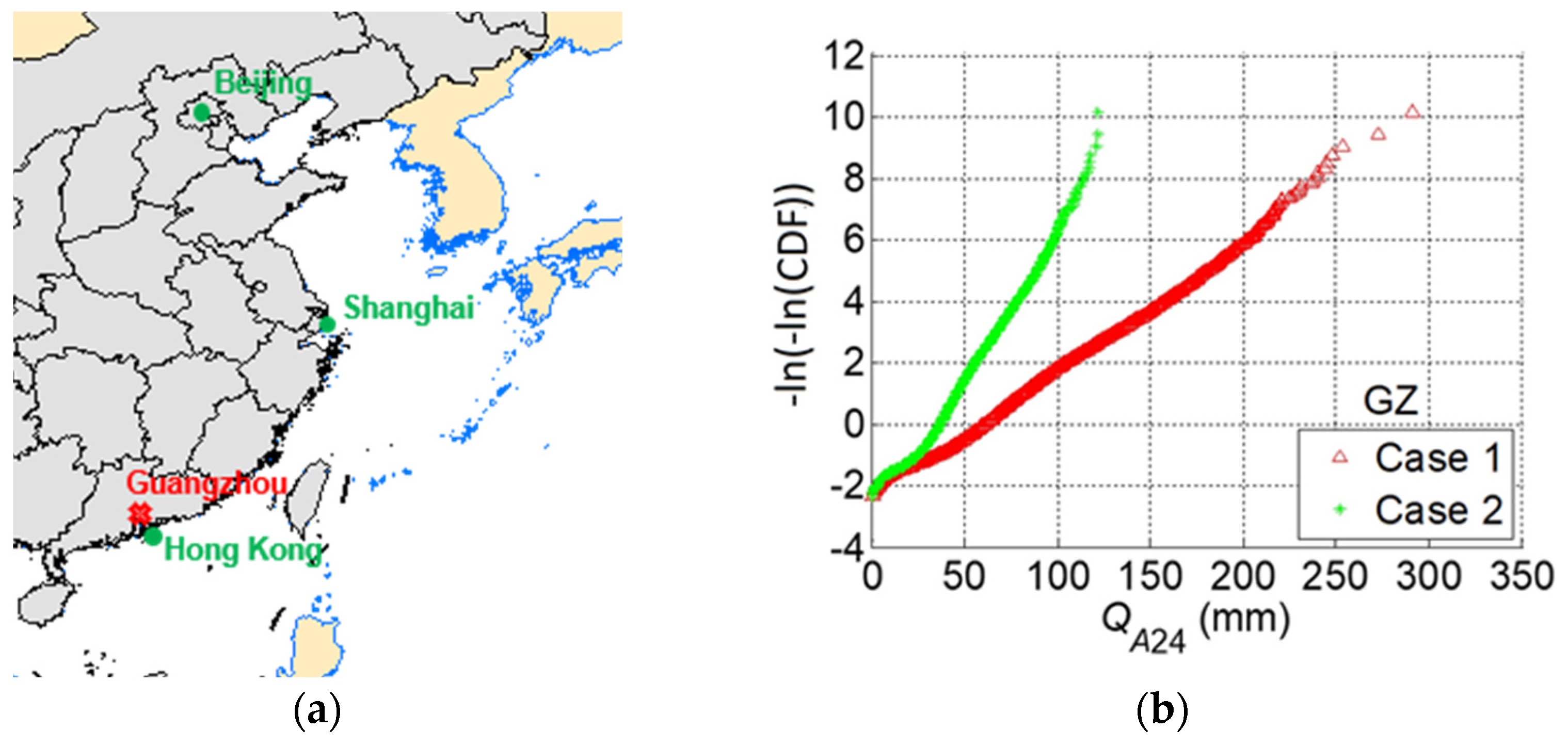
2. Considered TC Rainfall Intensity Snapshots
3. Calibrating PHRaM Using Snapshots of Rainfall Intensity Fields
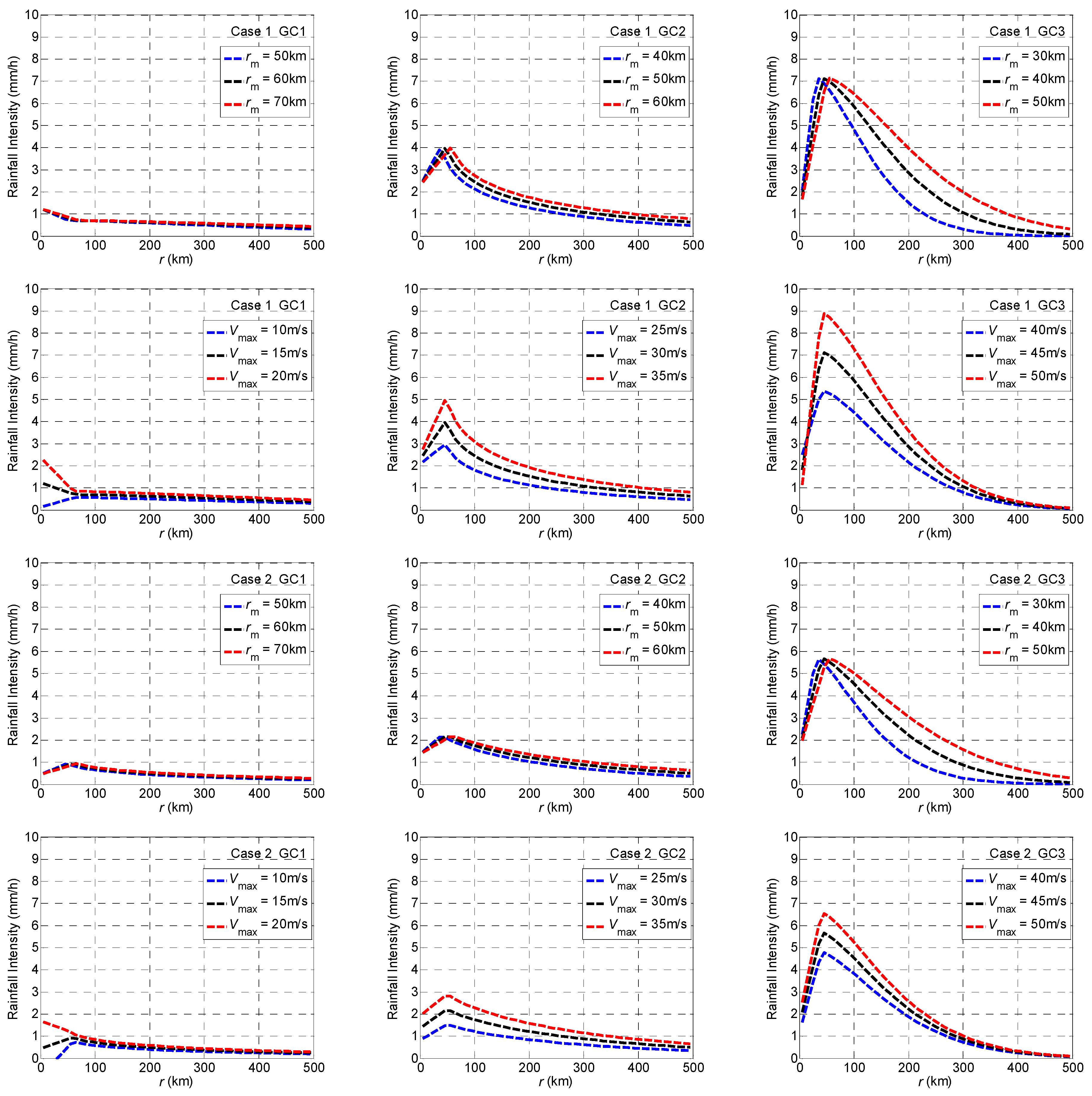
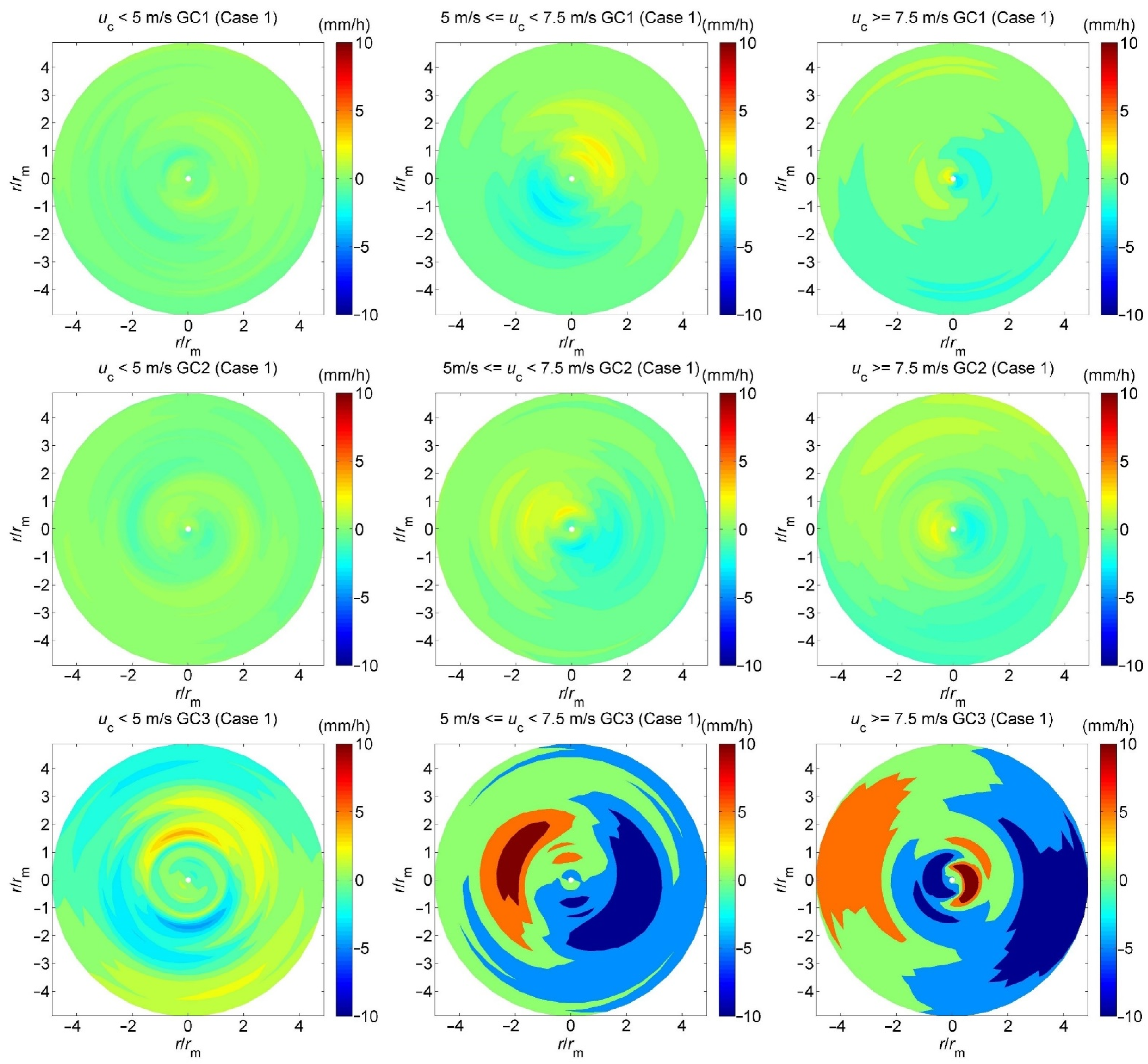
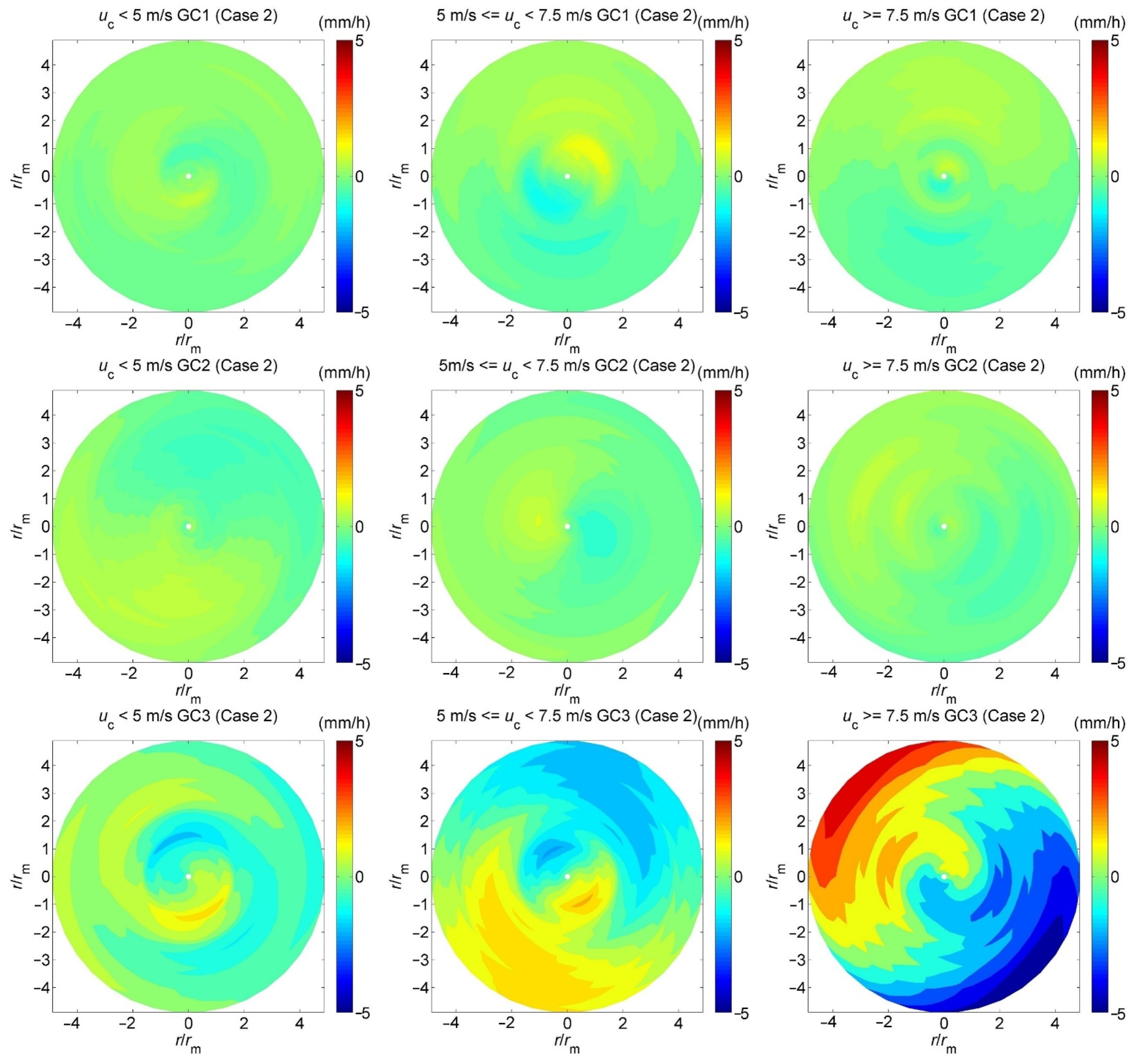
3.1. Modeling of the Rainfall Intensity
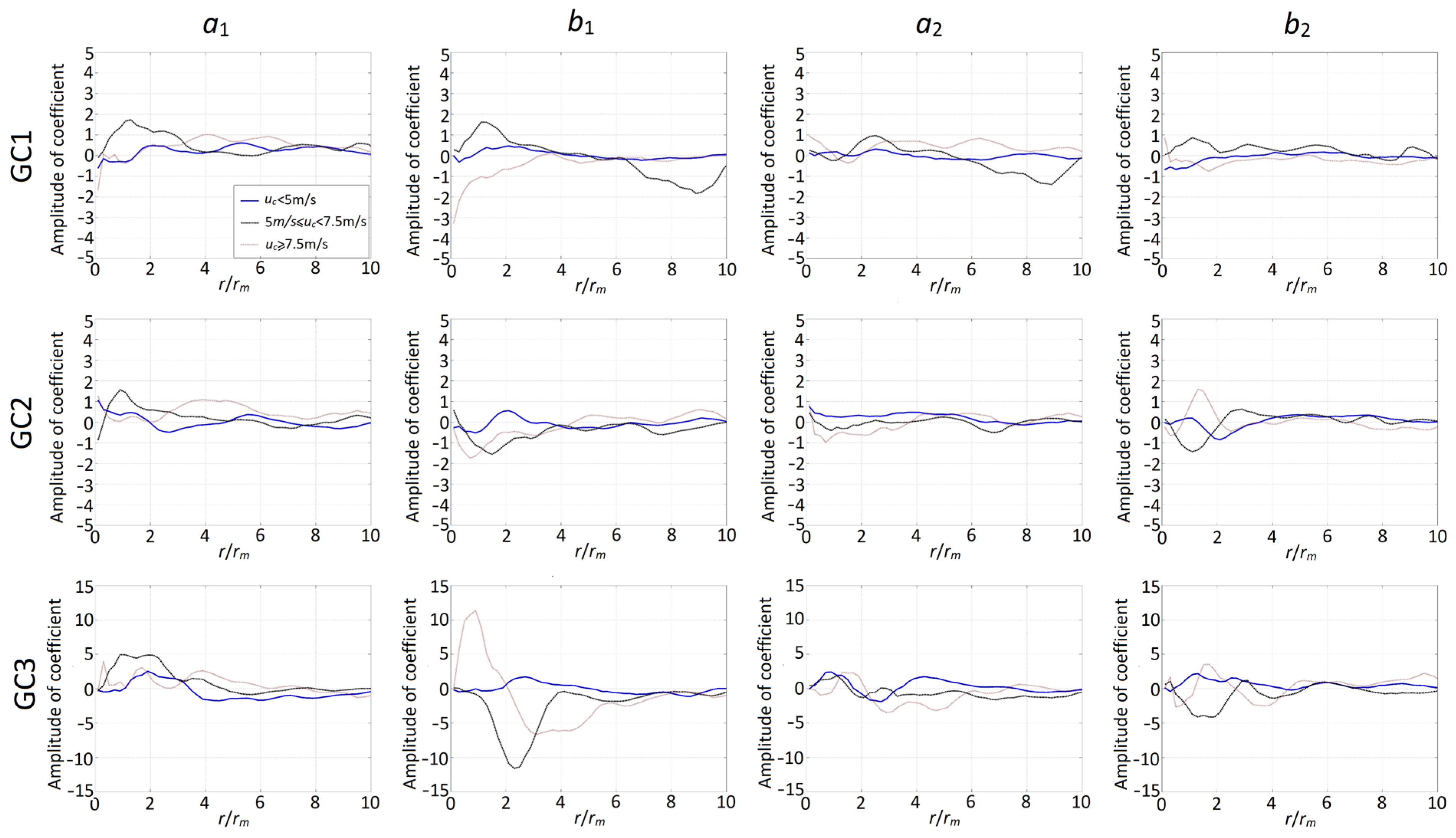
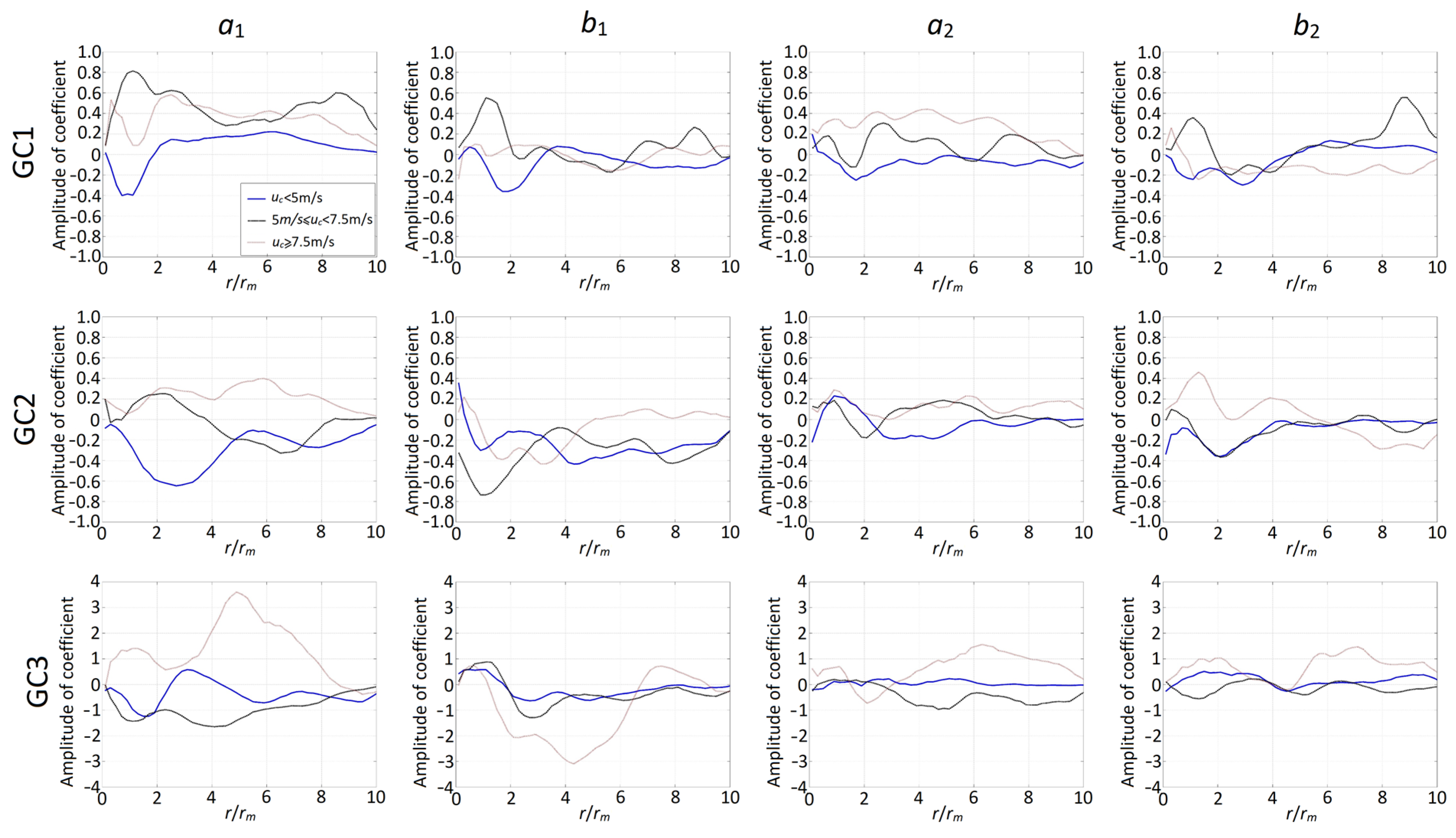
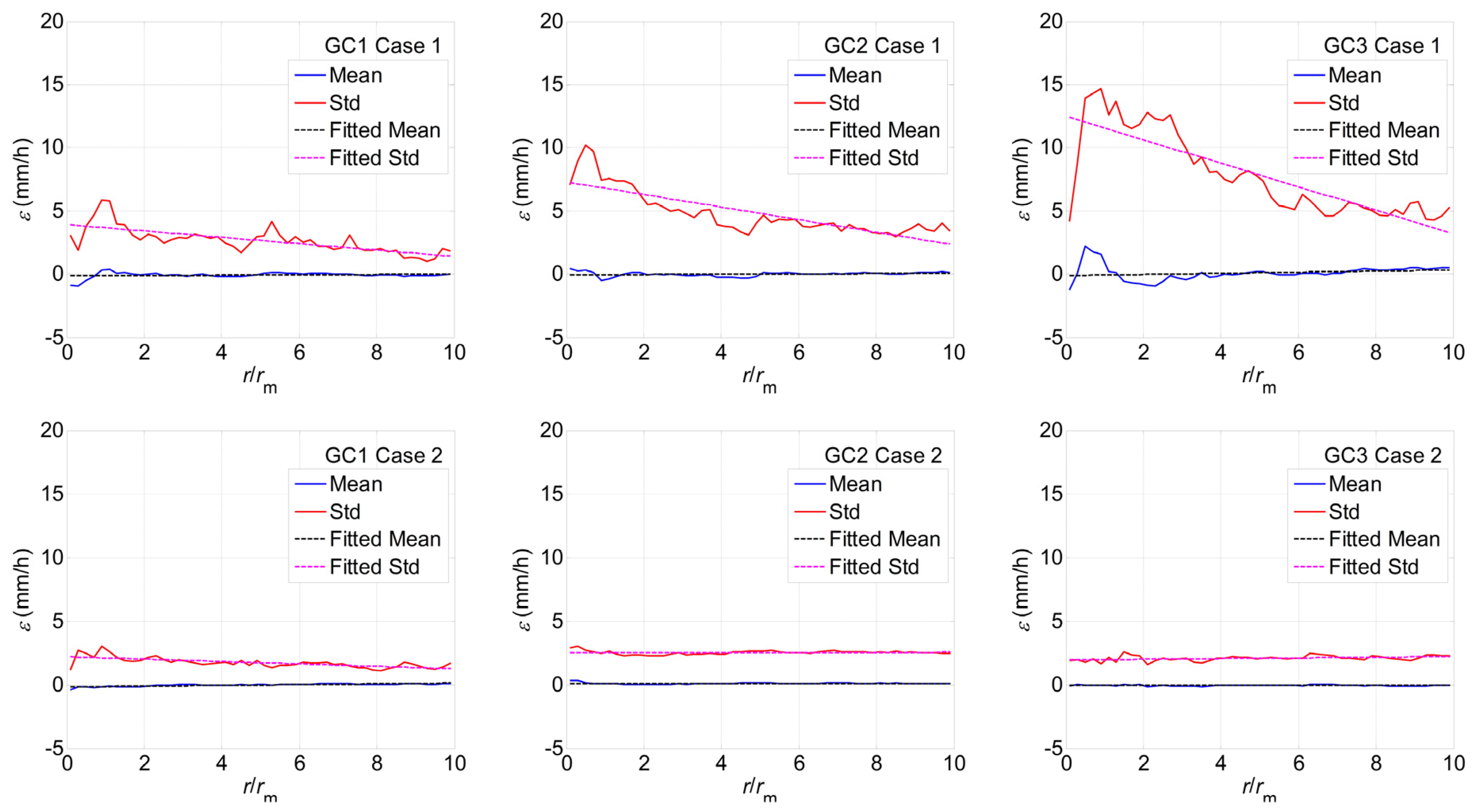
3.2. Estimating Model Parameters
4. Evaluation of the TC Rain Hazard
4.1. Procedure to Estimate the Accumulated Rainfall at a Single Site
4.2. TC Rain Hazard Mapping
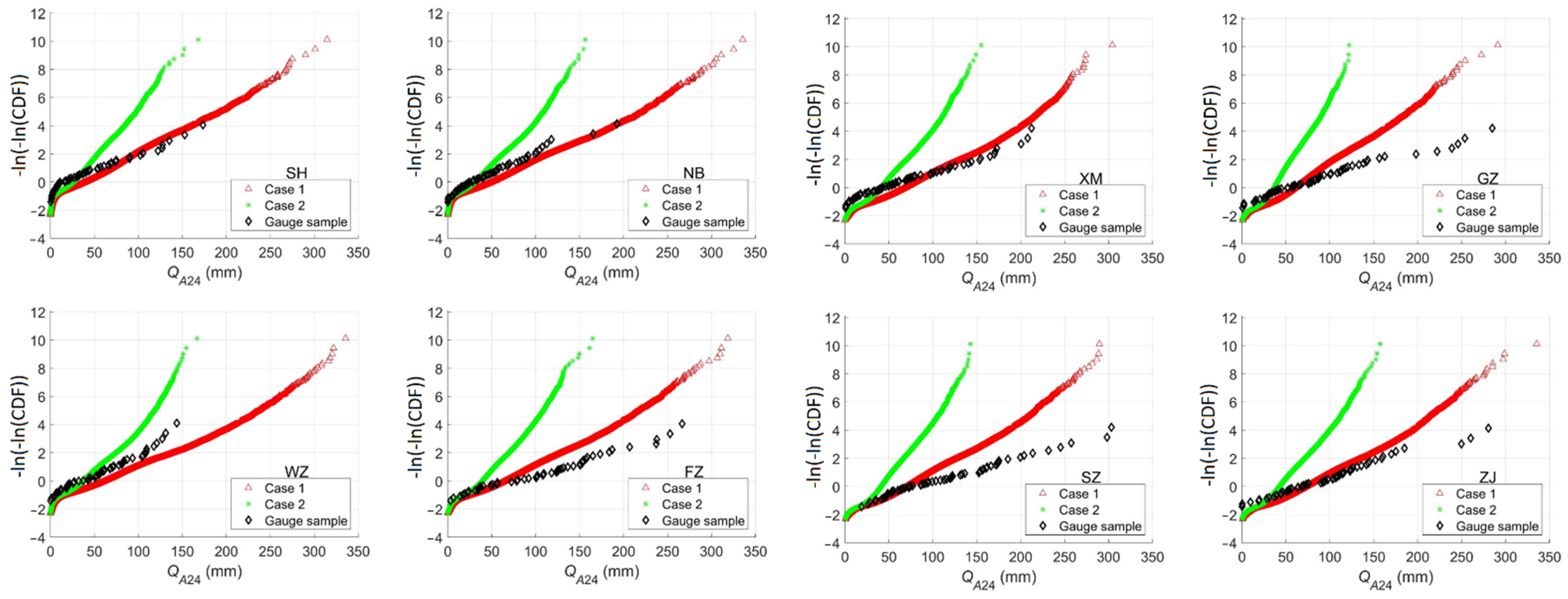
4.3. Comparison with Estimation from Gauge Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Luo, Y.; Sun, J.; Li, Y.; Xia, R.; Du, Y.; Yang, S.; Zhang, Y.; Chen, J.; Dai, K.; Shen, X.; et al. Science and prediction of heavy rainfall over China: Research progress since the reform and opening-up of new China. J. Meteorol. Res. 2020, 34, 427–459. [Google Scholar] [CrossRef]
- Chen, L.; Li, Y.; Cheng, Z. An overview of research and forecasting on rainfall associated with landfalling tropical cyclones. Adv. Atmos. Sci. 2010, 27, 967–976. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, L.; Liu, Q. Tropical cyclone damage in China: 1983–2006. Bull. Am. Meteorol. Soc. 2009, 90, 489–495. [Google Scholar] [CrossRef] [Green Version]
- Xiao, F.; Xiao, Z. Characteristics of tropical cyclones in China and their impacts analysis. Nat. Hazards 2010, 54, 827–837. [Google Scholar]
- Hong, H.P.; Li, S.H.; Duan, Z.D. Typhoon wind hazard estimation and mapping for coastal region in mainland China. Nat Hazards Rev. 2016, 17, 04016001. [Google Scholar] [CrossRef]
- Sun, J.H.; Qi, L.L.; Zhao, S.X. A study on mesoscale convective systems of the severe heavy rainfall in North China by “9608” typhoon. Acta Meteor. Sin. 2006, 64, 57–71. (In Chinese) [Google Scholar] [CrossRef]
- Xiao, Y.F.; Duan, Z.D.; Xiao, Y.Q.; Ou, J.P.; Chang, L.; Li, Q.S. Typhoon wind hazard analysis for southeast China coastal regions. Struct. Saf. 2011, 33, 286–295. [Google Scholar] [CrossRef]
- Li, S.H.; Hong, H.P. Typhoon wind hazard estimation for China using an empirical track model. Nat. Hazards 2016, 82, 1009–1029. [Google Scholar] [CrossRef]
- Sheng, C.; Hong, H.P. On the joint tropical cyclone wind and wave hazard. Struct. Saf. 2020, 84, 101917. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef] [Green Version]
- Frank, W.M.; Ritchie, E.A. Effects of vertical wind shear on the intensity and structure of numerically simulated hurricanes. Mon. Weather Rev. 2001, 129, 2249–2269. [Google Scholar] [CrossRef]
- DeMaria, M.; Tuleya, R.E. Evaluation of quantitative precipitation forecasts from the GFDL hurricane model. Preprints. In Proceedings of the Symposium on Precipitation of Extremes: Prediction, Impacts, and Responses, Alberquerque, NM, USA, 14–18 January 2001; pp. 340–343. [Google Scholar]
- Lonfat, M.; Marks, F.D., Jr.; Chen, S.S. Precipitation distribution in tropical cyclones using the Tropical Rainfall Measuring Mission (TRMM) Microwave Imager: A global perspective. Mon. Weather Rev. 2004, 132, 1645–1660. [Google Scholar] [CrossRef]
- Chen, S.S.; Knaff, J.A.; Marks, F.D., Jr. Effects of vertical wind shear and storm motion on tropical cyclone rainfall asymmetries deduced from TRMM. Mon. Weather Rev. 2006, 134, 3190–3208. [Google Scholar] [CrossRef]
- Ueno, M. Observational analysis and numerical evaluation of the effects of vertical wind shear on the rainfall asymmetry in the typhoon inner-core region. J. Meteorol. Soc. Japan. Ser. II 2007, 85, 115–136. [Google Scholar] [CrossRef] [Green Version]
- Tuleya, R.E.; DeMaria, M.; Kuligowski, R.J. Evaluation of GFDL and simple statistical model rainfall forecasts for US landfalling tropical storms. Weather Forecast. 2007, 22, 56–70. [Google Scholar] [CrossRef]
- Langousis, A.; Veneziano, D. Theoretical model of rainfall in tropical cyclones for the assessment of long-term risk. J. Geophys. Res. Atmos. 2009, 114, D02106. [Google Scholar] [CrossRef]
- Rogers, R.; Marks, F.; Marchok, T. Tropical cyclone rainfall. Encycl. Hydrol. Sci. J. 2009, 3, hsa030. [Google Scholar]
- Simpson, J.; Adler, R.F.; North, G.R. A proposed tropical rainfall measuring mission (TRMM) satellite. Bull. Am. Meteor. Soc. 1988, 69, 278–295. [Google Scholar] [CrossRef] [Green Version]
- Kummerow, C.; Simpson, J.; Thiele, O.; Barnes, W.; Chang, A.T.C.; Stocker, E.; Adler, R.F.; Hou, A.; Kakar, R.; Wentz, F.; et al. The status of the Tropical Rainfall Measuring Mission (TRMM) after two years in orbit. J. Appl. Meteorol. 2000, 39, 1965–1982. [Google Scholar] [CrossRef]
- Yamamoto, M.K.; Furuzawa, F.A.; Higuchi, A.; Nakamura, K. Comparison of diurnal variations in precipitation systems observed by TRMM PR, TMI, and VIRS. J. Clim. 2008, 21, 4011–4028. [Google Scholar] [CrossRef]
- Lonfat, M.; Rogers, R.; Marchok, T.; Marks, F.D., Jr. A parametric model for predicting hurricane rainfall. Mon. Weather Rev. 2007, 135, 3086–3097. [Google Scholar] [CrossRef]
- Brackins, J.T.; Kalyanapu, A.J. Evaluation of parametric precipitation models in reproducing tropical cyclone rainfall patterns. J. Hydrol. 2020, 580, 124255. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, Y.; Xu, H. Observed rainfall asymmetry in tropical cyclones making landfall over China. J. Appl. Meteorol. Climatol. 2015, 54, 117–136. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, Y.; Xu, H.; Davidson, N.; Chen, Y.; Chen, Y.; Yu, H. On the relationship between intensity and rainfall distribution in tropical cyclones making landfall over China. J. Appl. Meteorol. Climatol. 2017, 56, 2883–2901. [Google Scholar] [CrossRef]
- Lu, P.; Lin, N.; Emanuel, K.; Chavas, D.; Smith, J. Assessing hurricane rainfall mechanisms using a physics-based model: Hurricanes Isabel (2003) and Irene (2011). J. Atmos. Sci. 2018, 75, 2337–2358. [Google Scholar] [CrossRef]
- Xi, D.; Lin, N.; Smith, J. Evaluation of a physics-based tropical cyclone rainfall model for risk assessment. J. Hydrometeorol. 2020, 21, 2197–2218. [Google Scholar] [CrossRef]
- Marks, F.D.; Kappler, G.; DeMaria, M. Development of a tropical cyclone rainfall climatology and persistence (RCLIPER) model. Preprints. In Proceedings of the 25th Conference on Hurricanes and Tropical Meteorology, San Diego, CA, USA, 29 April–3 May.
- Gu, J.Y. Estimation of Tropical Cyclone Rain Hazard for Sites in Coastal Region of Mainland China. Ph.D. Thesis, The University of Western Ontario, London, ON, Canada, 2021. Available online: https://ir.lib.uwo.ca/etd/8175 (accessed on 22 April 2022).
- Grieser, J.; Jewson, S. The RMS TC-rain model. Meteorol. Z. 2012, 21, 79. [Google Scholar] [CrossRef]
- Willoughby, H.E.; Darling, R.W.R.; Rahn, M.E. Parametric representation of the primary hurricane vortex. Part II: A new family of sectionally continuous profiles. Mon. Weather Rev. 2006, 134, 1102–1120. [Google Scholar] [CrossRef] [Green Version]
- Holland, G.J. An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Georgiou, P.N.; Davenport, A.G.; Vickery, B.J. Design wind speeds in regions dominated by tropical cyclones. J. Wind Eng. Ind. Aerodyn. 1983, 13, 139–152. [Google Scholar] [CrossRef]
- Young, I.R. A review of parametric descriptions of tropical cyclone wind-wave generation. Atmosphere 2017, 8, 194. [Google Scholar] [CrossRef] [Green Version]
- Gu, J.Y.; Sheng, C.; Hong, H.P. Comparison of tropical cyclone wind field models and their influence on estimated wind hazard. Wind Struct. 2020, 31, 321–334. [Google Scholar]
- GB/T19201-2006; Classification of Tropical Cyclones. China Standard Press: Beijing, China, 2006. (In Chinese)
- Vickery, P.J.; Wadhera, D. Statistical models of Holland pressure profile parameter and radius to maximum winds of hurricanes from flight-level pressure and H* Wind data. J. Appl. Meteorol. Climatol. 2008, 47, 2497–2517. [Google Scholar] [CrossRef]
- Li, S.H.; Hong, H.P. Use of historical best track data to estimate typhoon wind hazard at selected sites in China. Nat. Hazards 2015, 76, 1395–1414. [Google Scholar] [CrossRef]
- Mo, H.M.; Hong, H.P.; Li, S.H.; Fan, F. Impact of Annual Maximum Wind Speed in Mixed Wind Climates on Wind Hazard for Mainland China. Nat. Hazards Rev. 2022, 23, 04021061. [Google Scholar] [CrossRef]



| Name, Intensity Category (IC) | Wind Speed (Representing the Near-Surface Maximum 2 min Mean Wind Speed Near the TC Center) (m/s) |
|---|---|
| Tropical depression, 1 | 10.8–17.1 |
| Tropical storm, 2 | 17.2–24.4 |
| Severe tropical storm, 3 | 24.5–32.6 |
| Typhoon, 4 | 32.7–41.4 |
| Severe typhoon, 5 | 41.5–50.9 |
| Super typhoon, 6 | ≥51.0 |
| Group | Case | Parameters | |||||
|---|---|---|---|---|---|---|---|
| aI0 | bI0 | aIm | bIm | n | ρe | ||
| GC1 | 1. PR-TRMM | −2.1462 | 0.2266 | 0.2818 | 0.0285 | 1.4047 | 26.1852 |
| 2. TMI-TRMM | −3.3118 | 0.2502 | 0.4321 | 0.0357 | 0.6310 | 2.5257 | |
| GC2 | 1. PR-TRMM | 1.0721 | 0.0401 | −2.3677 | 0.2169 | 0.5819 | 1.9059 |
| 2. TMI-TRMM | −1.9622 | 0.1110 | −1.8556 | 0.1361 | 0.8260 | 4.0765 | |
| GC3 | 1. PR-TRMM | 10.2792 | −0.2050 | −8.6572 | 0.3515 | 1.5275 | 9.0939 |
| 2. TMI-TRMM | −1.9554 | 0.0782 | −2.3464 | 0.1787 | 1.4319 | 7.7649 | |
| Case and Grouped Intensity Categories | Mean | ||||
|---|---|---|---|---|---|
| Case 1 | GC1 | −0.148 | 0.0154 | 3.927 | −0.2517 |
| GC2 | −0.049 | 0.0113 | 7.296 | −0.4970 | |
| GC3 | −0.112 | 0.0443 | 12.489 | −0.9281 | |
| Case 2 | GC1 | −0.159 | 0.0294 | 2.204 | −0.0940 |
| GC2 | 0.109 | 0.0000 | 2.510 | 0.0054 | |
| GC3 | −0.043 | −0.0011 | 1.956 | 0.0262 | |
| Latitude (°) | Longitude (°) | QA24-100 (mm) Case 1 | QA24-100 (mm) Case 2 | QA24-100 (mm) Gauge Sample | |
|---|---|---|---|---|---|
| Shanghai (SH) | 31.2333 | 121.4833 | 164.90 | 101.25 | 197.08 |
| Ningbo (NB) | 29.8667 | 121.5167 | 191.64 | 118.72 | 186.94 |
| Wenzhou (WZ) | 28.0167 | 120.65 | 218.09 | 135.55 | 185.55 |
| Fuzhou (FZ) | 26.0833 | 119.3 | 198.76 | 122.32 | 333.76 |
| Xiamen (XM) | 24.4833 | 118.1 | 198.02 | 123.00 | 266.96 |
| Guangzhou (GZ) | 23 | 113.2167 | 157.44 | 97.08 | 304.57 |
| Shenzhen (SZ) | 22.55 | 114.1167 | 189.72 | 117.79 | 343.69 |
| Zhanjiang (ZJ) | 21.2713 | 110.3608 | 200.58 | 125.71 | 299.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, J.; Cui, X.; Hong, H. A Statistical-Based Model for Typhoon Rain Hazard Assessment. Atmosphere 2022, 13, 1172. https://doi.org/10.3390/atmos13081172
Gu J, Cui X, Hong H. A Statistical-Based Model for Typhoon Rain Hazard Assessment. Atmosphere. 2022; 13(8):1172. https://doi.org/10.3390/atmos13081172
Chicago/Turabian StyleGu, Jiyang, Xizhong Cui, and Hanping Hong. 2022. "A Statistical-Based Model for Typhoon Rain Hazard Assessment" Atmosphere 13, no. 8: 1172. https://doi.org/10.3390/atmos13081172
APA StyleGu, J., Cui, X., & Hong, H. (2022). A Statistical-Based Model for Typhoon Rain Hazard Assessment. Atmosphere, 13(8), 1172. https://doi.org/10.3390/atmos13081172






