Abstract
In this study, ground observation data were selected from January 2016 to January 2020. First, six machine learning methods were used to predict visibility. We verified the accuracy of the method with and without principal components analysis (PCA) by combining actual examples with the European Centre for Medium-Range Weather Forecast (ECMWF) data and National Centers for Environmental Prediction (NECP) data. The results show that PCA can improve visibility prediction. Neural networks have high accuracy in machine learning algorithms. The initial visibility data plays an important role in the visibility forecast and can effectively improve forecast accuracy.
1. Introduction
Visibility is an indicator of atmospheric transparency. Visibility was first defined for meteorological purposes as a quantity to be estimated by a human observer, and observations made in that way are widely used [1]. The presence of atmospheric particles always causes a reduction of visibility [2]. As air pollution has become increasingly serious in recent years, visibility forecasts have directly affected work and life. On the morning of 27 December 2019, a plane of Kazakhstan Bek Airlines crashed after take-off at Almaty Airport because of the heavy fog. Therefore, the accuracy of low-visibility forecasts is directly related to aviation safety. The factors that affect visibility are complex, related to the degree of atmospheric aerosol pollution and atmospheric circulation, near-surface water vapor, temperature inversion, and human activities [3].
In the early days, visibility forecasts mainly used extrapolation methods to study the occurrence and development of weather systems. However, weather systems are nonlinear, and many important parameters are ignored after linearization. With the development of numerical weather prediction technology, researchers have gradually used numerical weather prediction technology to forecast visibility, but visibility changes have a strong locality. Numerical weather forecasting cannot meet airports’ need for high accuracy and high time resolution of visibility [4]. With the development of machine learning, researchers have increasingly used it to predict visibility [5].
Stewart and Essenwanger [6] studied the relative attenuations of visible wavelengths and divided fog into categories on the basis of objective criteria. Tuo [7] used the partial correlation method. The factors that have a greater impact on visibility were screened out, the data were unified by the regularization method, and the long- and short-term memory models were used to calculate and evaluate the visibility. This method was used to predict one-hour and three-hour visibility and was compared with the regression model. However, although the prediction accuracy was effectively improved by adjusting the model and resampling methods, the numerical results of the prediction were unsatisfactory owing to the limitations of the data and the model itself.
Kaipeng [8] introduced a weighted loss function and improved the accuracy of low-visibility prediction. For the regression model, a weighted loss function was constructed to improve the prediction accuracy of low-visibility data. It was found that the prediction results of the long-short-term memory regression model were better than those of the commonly used random forest and multilayer perceptron models.
Chong [9] conducted training modeling through statistical analysis of multi-dimensional data of different meteorological parameters and pollutants, and experiments showed that the improved random forest sea visibility spatial interpolation algorithm had a higher interpolation accuracy than the traditional spatial interpolation algorithm. Compared with the random forest spatial interpolation algorithm, the interpolation accuracy was improved by 15%. However, the disadvantage was that the distribution of weather stations was relatively discrete, and there was no unified standard for weather data sources and data attributes. Future research will focus on sea surface weather data collection and multisource data fusion to improve the quality of weather data.
Ji [10] used a Bayesian model to predict visibility on average; however, the sample used only 25 days of data, and the training sample was small. Hansen [11] used fuzzy logic algorithms to improve the 7–24 h accuracy of the WIND-3 forecasting system. Driss [12] used the data from 39 stations and obtained correlation coefficients from 20 influencing factors (MM5 mode as the initial field), selected them, and used neural network algorithms to predict the visibility. However, multiple algorithms were not used for comparison. Lu [4] used fuzzy C-means to establish historical data, screened out the influencing factors, and then used the hierarchical sparse representation algorithm to predict visibility and compared it with the BP neural network and BREMPS. Debashree [13] used decision trees and an ANN to make predictions about visibility. The advantage of this article lies in the addition of chemical elements such as NO2 and CO.
Hence, previous studies have mainly made limited forecasts of visibility from the perspective of machine learning. However, visibility is affected by various factors, such as moisture [14], condensation nuclei, weather phenomena, pollutant index [15], and inversion intensity [16]. Currently, there are several machine-learning methods available for visibility prediction. Numerical weather forecasting does not assimilate visibility into the forecast, and the results are relatively inaccurate. Therefore, it is necessary to compare the influencing factors, filter out the factors that do not have a very large influence on visibility, and select a method with a better prediction efficiency compared to that of the typical machine learning methods. In this study, various influencing factors based on the above-mentioned machine-learning methods were compared to predict visibility and screen out the most influential factors. In addition, because the existing methods cannot calculate the intensity of temperature inversion very effectively, this factor introduces a bias when determining visibility. Therefore, the temperature inversion layer was considered the influencing factor, and more typical machine-learning methods were compared. Finally, a weather process with poor visibility was used to compare the numerical weather forecast, actual visibility, and the methods selected in this study.
2. Data and Methods
2.1. Data
Ground observation and radiosonde data from Chengdu, Sichuan, were used in this study. Chengdu has a humid subtropical monsoon climate with rapid changes in visibility [17]. Li [18] discussed higher relative humidity as the typical meteorological characteristics of Chengdu due to the unique topography of Sichuan Basin and the unfavorable pollution problem; meteorological conditions also increase the seriousness of the air pollution problem. Heavy fog is prone to occur in winter, which affects aircraft take-off and landing. The heavy fog [19] in Chengdu usually occurs in winter mornings. If there is rain the previous day and there is no cloud behind the cold front, the probability of heavy fog will increase, mainly because of the colder winter temperatures and the condensation of water vapor into water droplets at lower altitudes. If it rained the day before and the groundwater vapor is humid, the cloudless weather will form a temperature inversion layer, preventing the water vapor from spreading outwards.
As shown in Table 1, historical meteorological data included ground observation data, and the time period considered was from January 2016 to January 2020. Ground observation data were obtained from a standardized automatic observation station; the basic elements were temperature, dew point temperature, local pressure, relative humidity, wind direction, wind speed, water vapor pressure, total cloud cover, and visibility. Visibility measurements were performed using a K/XYN02A laser-visibility tester. The interval between the ground observations collected was one hour.

Table 1.
The size of the datasets.
The verification data included meteorological elements to predict the visibility changes in the process of heavy foggy weather in Chengdu on 27 August 2021 after 2, 4, 8, 10, and 12 h. They were compared with the European Centre for Medium-Range Weather Forecasts (ECMWF), National Centers for Environmental Prediction (NECP), and actual observation data.
2.2. Method
The method used in this study is illustrated in Figure 1. First, principal component analysis (PCA) was used to filter out features. The selected meteorological elements were used by classification algorithms to predict visibility. Then, algorithms with higher accuracy were screened out, and a confusion matrix was used. A foggy weather process was used to compare with the selected algorithms and numerical weather forecasting. The process used to verify this method is as follows:
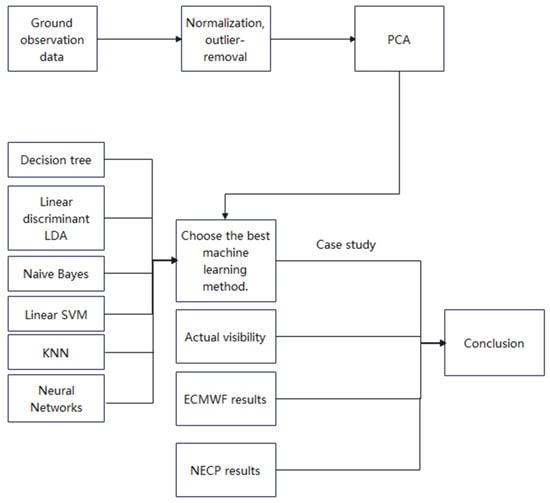
Figure 1.
Methodology employed to predict and compare visibility.
- Step 1: Data preprocessing for ground observation data from January 2016 to January 2020, such as normalization and outlier removal.
- Step 2: Data preprocessing using PCA.
- Step 3: Selected elements used as initial data and divided into two categories: data without PCA and data with PCA added.
- Step 4: Evaluation of the accuracy of the six intelligent classification algorithms. Confusion matrices used to pick out algorithms that are better at predicting low visibility.
- Step 5: Selection of classification algorithms with better effects. A weather process was used to predict the visibility and compare the predicted results with the actual visibility and numerical weather forecast results.
2.2.1. Principal Component Analysis (PCA)
Principal component analysis (PCA) [20] is a multivariate technique that analyzes a data table in which observations are described by several inter-correlated quantitative dependent variables. Its goal is to extract the important information from the table, represent it as a set of new orthogonal variables called principal components, and display the pattern of similarity as points in maps.
The algorithm steps of PCA:
- Step 1: Original data formed into a matrix X with m rows and n columns. Rows represent time series, and columns represent features.
- Step 2: Matrix X is converted to mean of zero.
- Step 3: Covariance matrix is calculated.
- Step 4: Eigenvalues of the covariance matrix and corresponding eigenvectors are calculated.
- Step 5: Eigenvalues are arranged from large to small and composed into a matrix in the order of eigenvalues. k eigenvectors form the matrix U.
- Step 6: Y = UTX is the new data reduced to k dimensions.
2.2.2. Machine Learning Classification Algorithm
The six common machine learning algorithms are: decision tree [21], linear discriminant analysis (LDA) [22], naive bayes [23], linear SVM [24], K-nearest neighbor (KNN) [25], and neural networks [26].
(1) Decision Tree
A decision tree is an algorithm used for classifying data; data characteristics are judged one by one to obtain the category to which the data belong. It can be regarded as a tree prediction model, which is a hierarchical structure comprising nodes and directed edges. The tree contains three nodes: root, internal, and leaf nodes. The decision tree has only one root node, which is a collection of all the training data. Each internal node in the tree is a split problem: a test for a certain attribute of the instance is specified, the samples arriving at the node are divided according to a specific attribute, and each subsequent branch of the node corresponds to a possible value for the attribute. Each leaf node is a data collection point with a classification label, indicating the category to which an instance belongs.
There are many decision tree algorithms such as ID3, C4.5, and CART. All these algorithms use a top-down greedy approach. Each internal node selects the attribute with the best classification effect to split and then continues this process until the decision tree can accurately classify all the training data or all attributes are used. The simplified version of the algorithm uses the assumptions of all samples to construct the decision tree. The specific steps are as follows:
Step 1: Suppose T is the training sample set.
Step 2: Select an attribute from the attribute set that best describes the sample in T.
Step 3: Create a tree node whose value is the selected attribute. The child nodes of this node are created. Each child chain represents a unique value (interval) for the selected attribute. The value of the child chain is used to further subdivide the sample into subcategories.
(2) Linear Discriminant
Linear discriminant analysis is a classic linear learning method that was first proposed by Fisher in 1936 on the two-classification problem, also known as the Fisher linear discriminant. The idea of linear discrimination is very simple: given a set of training samples, we project the examples onto a straight line so that the projection points of similar examples are as close as possible, and the projection points of different examples are as far away as possible. When classifying, they are projected onto the same straight line, and the class of the new sample is determined according to the position of the projection point.
Previously, we focused on analyzing the application of the LDA algorithm in dimensionality reduction. The LDA algorithm can also be used for classification. LDA assumes that various types of sample datasets conform to a normal distribution. After LDA reduces the dimensions of various types of sample data, we can calculate the mean and variance of each type of projection data through maximum likelihood estimation as follows:
Thereafter, the probability density function of samples from each class can be obtained as follows:
where is the sample after dimensionality reduction.
Therefore, the steps of LDA classification for an unlabeled input sample are:
- (1)
- LDA is used to reduce the dimensionality of the input sample.
- (2)
- According to the probability density function, the probability that the reduced dimensionality sample belongs to each class is calculated.
- (3)
- The category corresponding to the largest probability is identified as the predicted category.
(3) Naive Bayes
The naive Bayes classifier is a series of simple probability classifiers based on Bayes’ theorem under the assumption of strong (naive) independence between features. The classifier model assigns class labels represented by feature values to the problem instances, and the class labels are obtained from a limited set. It is not a single algorithm for training this classifier, but a series of algorithms based on the same principle: all naive Bayes classifiers assume that each sample feature is not related to other features.
Step 1: represents a data object with D-dimensional attributes. Training set S contains K categories, expressed as .
Step 2: The data object X to be classified predicts the category X, and the calculation method is as follows:
The obtained is in category X. The above formula indicates that when the data object X to be classified is known, the probabilities of X belonging to . are calculated and the maximum value of the probability is selected. The corresponding is category X.
Step 3: According to Bayes’ theorem, . is calculated as follows:
In the calculation process, is equivalent to the constant . Therefore, if the maximum value of . is to be obtained, only the maximum value of needs to be calculated. If the prior probability of the category is unknown, that is, s is unknown, it is usually assumed that these categories are equal in probability, that is, .
Step 4: Assuming that the attributes of data object X are independent of each other, is calculated as follows:
Step 5: is calculated as follows if the attribute is discrete or categorical. There are n data objects belonging to category in the training set with different attribute values under attribute ; in the training set, there are m data objects belonging to category and the attribute value under attribute . Therefore, is calculated as follows:
(4) Linear SVM
An SVM is a type of generalized linear classifier that classifies binary data in a supervised learning manner. Its decision boundary is the maximum margin hyperplane solved for the learning samples.
The SVM model makes the distance between all points and the hyperplane greater than a certain distance, such that all classification points are on both sides of the support vector of their respective categories. The mathematical formula is expressed as:
(5) KNN
The proximity algorithm, or the KNN classification algorithm, is one of the simplest methods in data-mining classification technology. Each sample can be represented by its KNNs. The nearest-neighbor algorithm classifies each record in the dataset.
In general, the KNN classification algorithm includes the following four steps:
Step 1: Data are prepared and preprocessed.
Step 2: The distance from the test sample point (i.e., the point to be classified) to every other sample point is calculated.
Step 3: Each distance is sorted, and the K points with the smallest distance are selected.
Step 4: The categories to which the K points belong are compared. According to the principle that the minority obeys the majority, the test sample points are classified into the category with the highest proportion among the K points.
(6) Neural Networks
The basic processing elements of artificial neural networks are called artificial neurons, simply neurons or nodes. In a simplified mathematical model of the neuron, the effects of the synapses are represented by connection weights that modulate the effect of the associated input signals, and the nonlinear characteristic exhibited by neurons is represented by a transfer function. The neuron impulse is then computed as the weighted sum of the input signals, transformed by the transfer function. The learning capability of an artificial neuron is achieved by adjusting the weights in accordance with the chosen learning algorithm.
The Artificial Neural Networks classification algorithm includes the following four steps:
- Step 1: Network structure is chosen.
- Step 2: Weights are randomly initialized.
- Step 3: Forward propagation FP algorithm is executed.
- Step 4: The cost function J is calculated through the code.
- Step 5: The backpropagation algorithm is executed.
- Step 6: Gradient check is performed.
- Step 7: Function J is minimized using the optimization and backpropagation algorithms.
3. Experiment Design
3.1. Accuracy Test
Because aircraft take-off and landing and highway closures are mainly affected by low visibility, low visibility was the focus of this study. This study belongs to the classification problem in machine learning. The visibility in the dataset was divided into 0–1 km, 1–2 km, 2–4 km, and >4 km.
Normalization and outlier removal were conducted on the dataset. This study used ten selected indicators as the initial data and six intelligent classification algorithms: decision tree, linear discriminant, Naive Bayes, linear SVM, KNN, and artificial neural networks to classify and learn visibility. To protect against overfitting, we used the -and set it as 10 folds. As shown in Table 2, the maximum number of splits of the decision tree was 100, and the split criterion was the Gini diversity index. The covariance structure of the linear discriminant was full. The distribution name for the numerical predictor of Naive Bayes was Gaussian. The kernel function of the linear SVM was linear, the kernel scale was automatic, the box constraint level was 1, and the multi-class method was one-to-one. The number of neighbors of KNN was 1, the distance metric was Euclidean, and the distance weight was equidistant. The number of fully connected layers of the neural network was 2, the size of the first layer was 10, the size of the second layer was 10, the activation function was ReLU, and the iteration limit was 1000.

Table 2.
Algorithms and key settings.
Figure 2 and Figure 3 show the accuracy rates of the six algorithms without and with the addition of the PCA; Table 3 is the exact number of Figure 2; Table 4 is the exact number of Figure 3. The accuracy rate represents the proportion of correctly classified samples to the total number of classified samples. The abscissa is the time from the initial data, and the ordinate is the accuracy of verification data.
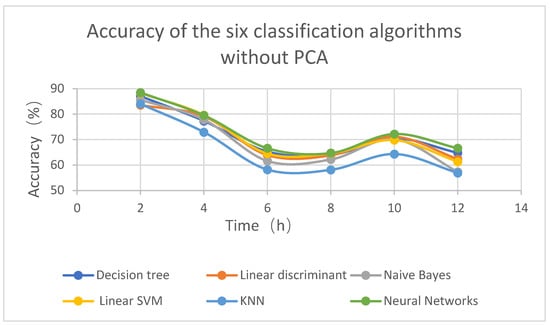
Figure 2.
Accuracy of the six classification algorithms without PCA.
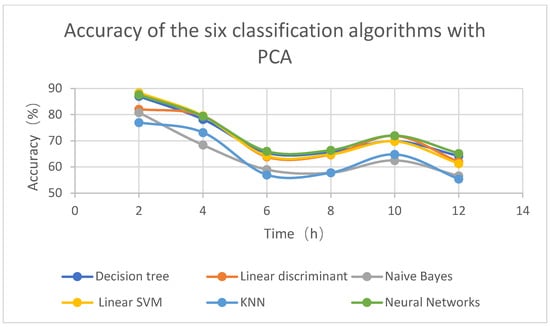
Figure 3.
Accuracy of the six classification algorithms with PCA.

Table 3.
Accuracy of the six classification algorithms without PCA.

Table 4.
Accuracy of the six classification algorithms with PCA.
As shown in Figure 2 and Table 3, the accuracy of visibility prediction gradually decreased over time, but prediction accuracy increased after ten hours. The accuracy rate was the highest after 2 h, the decline rate was larger from 2 to 6 h, and the accuracy rate decreased more smoothly after 6 h. The neural networks had higher accuracy than other machine learning classification algorithms, whereas linear discriminant and KNN had lower accuracy than the other machine classification learning algorithms. Figure 2 and Figure 3 show the accuracy of the six classification algorithms with and without PCA. It can be seen from the figure that the accuracy of the machine classification algorithm after adding PCA was higher than that without PCA. The average accuracy of Table 3 was 69.15, and the average accuracy of Table 4 was 70.22; thus, the average accuracy improved by 1.07 after adding PCA. However, for the linear SVM algorithm, the accuracy of adding PCA and not adding PCA did not change much.
In general, among the six machine classification learning algorithms, the neural network best predicted visibility, and the accuracy was slightly improved after adding PCA.
3.2. Confusion Matrix
The confusion matrix is a situation analysis table that summarizes the prediction results of the classification model in machine learning. TPR is the true positive rate, which represents the probability of predicting the positive class as a positive class, that is, predicting the correct probability. TNR is the probability that the true class of a sample is a negative class, and the model recognizes it as a negative class.
Table 5 is the confusion matrix of the six classification algorithms, from which we can see that the TPR gradually decreased as time increased. Naive Bayes predicted < 1 km better than the rest of the machine learning algorithms. Linear discriminant and linear SVM had weak prediction ability for visibility < 1 km. All six algorithms had better prediction ability for >4 km.

Table 5.
Confusion matrix of the six classification algorithms.
3.3. Case Analysis
A day with foggy weather in Chengdu, 27 August 2021, was selected, and the visibilities predicted by ECWMF and by NECP were compared with those predicted using the Neural Networks algorithm and in the actual situation. The ECWMF, NECP numerical weather forecast, and neural networks time steps were 3 h, 3 h, and 2 h. Table 6 shows the initial data collection times of the three methods were all 20:00 on 26 August 2021. Figure 4 shows the calculation results.

Table 6.
Time of initial data: 27 August 2021, at 02:00.
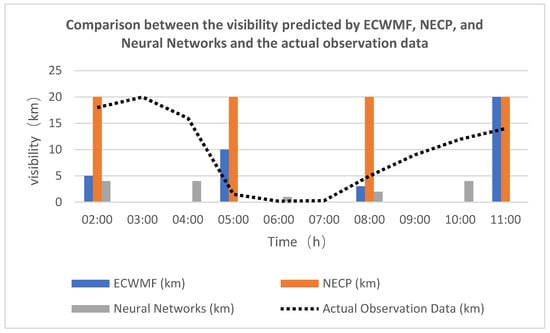
Figure 4.
Comparison between the visibility predicted by ECWMF, NECP, and neural networks and the actual observation data.
From the comparison in Figure 4, since the clustering method was used, the result predicted by the neural network was the range of <1 km, 1–2 km, 2–4 km, and >4 km. This is a typical heavy fog process. The visibility was greater than 10 km before 5:00 in the morning, but began to decline from 4:00 to 5:00 in the morning. The visibility at 6:00 and 7:00 in the morning was 0.2 km and 0.3 km, respectively, which reached the standard of heavy fog. The time resolution of the numerical weather forecast was 3 h, and the time resolution of the neural network was 2 h. As can be seen from the figure, the neural network predicted that the visibility was 4 km at 4:00 and 1–2 km at 6:00; thus, a trend of decreasing visibility was predicted. ECWMF predicted that the visibility was 10 km at 5:00 and 3 km at 8:00. It also predicted a decreasing trend of visibility, but the predicted value was larger than the actual value. If ECMWF is used in practical application, the purpose of early warning of heavy fog cannot be achieved. The NECP forecast visibility has always been greater than 20 km, which is quite different from the actual results. The reason why NECP and ECWMF forecasting results are not good is that in atmospheric science, initial data has a great influence on the forecasting results. Neither ECMWF nor NECP assimilated visibility as initial data into numerical weather prediction [27,28]. However, the neural network in this article added initial visibility data to the dataset; thus, adding initial visibility data to the neural network can effectively improve the accuracy of visibility forecasting.
4. Discussion
Aiming at the contradiction between the current visibility forecasting accuracy and the airport expressway’s demand for visibility forecasting, this study proposes a new forecasting method based on previous studies. The contributions of the manuscript are as follows:
- Ground observation and radiosonde data in Chengdu were used in the manuscript.
- Six representative machine learning algorithms were used to predict visibility. We compared six machine learning algorithms for visibility prediction.
- We judge the usefulness of PCA by comparing visibility accuracy with and without PCA.
- We compare ECWMF, NECP, and neural networks with actual observation data.
The discussions are as follows:
1. Comparing Figure 2 and Figure 3 and Table 3 and Table 4, the accuracy of the six classification algorithms with PCA was partially improved. For decision tree, linear discriminant, linear SVM, and neural networks, the improvement was not obvious because these algorithms have PCA-like pacing. For Naive Bayes and KNN, the improvement was more obvious. It is recommended to perform PCA before using Naive Bayes and KNN.
2. Comparing the accuracy of the six classification algorithms, neural networks, decision tree, and linear SVM had higher prediction accuracy at the initial moment. Accuracy decreased over time, but neural networks always had the highest accuracy.
3. For airports, we mainly focused on low-visibility events. According to Table 4, the confusion matrix of the six classification algorithms, we paid more attention to the algorithms that can classify a visibility of <1 km. As can be seen from the table, Naive Bayes showed better TPR compared to the six machine learning algorithms. However, linear discriminant and linear SVM had lower TPR.
4. We compared ECWMF, NECP, and neural networks with actual observation data. We found that the comparison between ECWMF and NECP for visibility prediction and neural networks was quite different from the actual visibility. The reason is that ECWMF and NECP do not add initial visibility to the calculation; the visibility of these two numerical forecasts is calculated by the model and other parameters. In order to better calculate the visibility, it is necessary to add the actual visibility to the initial data.
Deficiency of the proposed work:
1. This article compares six machine learning algorithms, in addition to which there are many algorithms that can be added.
2. This article uses data from January 2016 to January 2020. With more data, the accuracy of machine learning will be higher.
3. This paper does not include the impact of air pollution on visibility in the impact factor, and it is hoped that it can be improved in future research.
5. Conclusions
From the discussion, we draw the following conclusions:
1. The addition of PCA can improve the accuracy of Naive Bayes and KNN, but the accuracy of others is limited.
2. Neural networks have high accuracy in typical machine learning algorithms.
3. Naive Bayes predicts visibility at <1 km better than the rest of the machine learning algorithms. Linear discriminant and linear SVM have weak prediction ability for visibility <1 km.
4. The initial visibility data plays an important role in the visibility forecast and can effectively improve forecast accuracy.
Author Contributions
Conceptualization, Y.Z. (Yu Zhang) and Y.W.; methodology, Y.W.; software, L.Y.; validation, Y.Z. (Yu Zhang); formal analysis, C.L.; investigation, Y.W.; resources, Y.W.; data curation, Y.Z. (Yingqian Zhu); writing—original draft preparation, L.G. and Y.Z. (Yingqian Zhu); writing—review and editing, Y.Z. (Yu Zhang) and Y.W.; visualization, Y.Z. (Yu Zhang); supervision, Y.W.; project administration, C.L.; funding acquisition, L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by the Chinese National Natural Science Fund grant number 2021JJ40669 of Hunan Province.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- WHO. Guide to Meteorological Instruments and Methods of Observation, 8th ed.; WHO: Geneva, Switzerland, 2018. [Google Scholar]
- Horvath, H. Atmospheric visibility. Atmos. Environ. 1967, 15, 1785–1796. [Google Scholar] [CrossRef]
- Deng, J.; Wang, T.; Jiang, Z.; Xie, M.; Zhang, R.; Huang, X.; Zhu, J. Characterization of visibility and its affecting factors over Nanjing, China. Atmos. Res. 2011, 101, 681–691. [Google Scholar] [CrossRef]
- Zhenyu, L.; Bingjian, L.; Hengde, Z.; You, F.; Yunan, Q.; Tianming, Z. A method of visibility forecast based on hierarchical sparse representation. J. Vis. Commun. Image Represent. 2019, 58, 160–165. [Google Scholar]
- Stewart, D.A.; Essenwanger, O.M. A survey of fog and related optical propagation characteristics. Rev. Geophys. 1982, 20, 481–495. [Google Scholar] [CrossRef]
- Marzban, C.; Leyton, S.; Colman, B. Ceiling and Visibility Forecasts via Neural Networks. Weather. Forecast. 2007, 22, 466–479. [Google Scholar] [CrossRef]
- Deng, T. Visibility Forecast for Airport Operations by LSTM Neural Work. Master’s Thesis, Shandong University, Shandong, China, 2019. [Google Scholar]
- Kaipeng, Z. Study on Characteristics and Forecast of Visibility in Bohai Rim Region. Master’s Thesis, Lanzhou University, Lanzhou, China, 2019. [Google Scholar]
- Chong, L. The Research of Multi-Dimensional Visibility on Ocean Based on Machine Learning. Master’s Thesis, Nanjing University of Information Science and Technology, Nanjing, China, 2019. [Google Scholar]
- Luying, J.; Xiefei, Z.; Shoupeng, Z.; Klaus, F. Probabilistic Precipitation Forecasting over East Asia Using Bayesian Model Averaging. Weather. Forecast. 2019, 34, 377–392. [Google Scholar]
- Hansen, B. A Fuzzy Logic Based Analog Forecasting System for Ceiling and Visibility. Weather. Forecast. 2010, 22, 1319. [Google Scholar] [CrossRef]
- Bari, D.; Khlifi, M.E. LVP conditions at Mohamed V airport, Morocco: Local characteristics and prediction using neural networks. Int. J. Basic Appl. Sci. 2015, 4, 354. [Google Scholar] [CrossRef]
- Dutta, D.; Chaudhuri, S. Nowcasting visibility during wintertime fog over the airport of a metropolis of India: Decision tree algorithm and artificial neural network approach. Nat. Hazards 2015, 75, 1349–1368. [Google Scholar] [CrossRef]
- Cornejo-Bueno, S.; Casillas-Pérez, D.; Cornejo-Bueno, L.; Chidean, M.I.; Caamaño, A.J.; Sanz-Justo, J.; Casanova-Mateo, C.; Salcedo-Sanz, S. Persistence Analysis and Prediction of Low-Visibility Events at Valladolid Airport, Spain. Atmosphere 2020, 12, 1045. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S. Statistical Analysis and Machine Learning Prediction of Fog-Caused Low-Visibility Events at A-8 Motor-Road in Spain. Atmosphere 2021, 12, 679. [Google Scholar]
- Castillo-Botón, C.; Casillas-Pérez, D.; Casanova-Mateo, C.; Ghimire, S.; Cerro-Prada, E.; Gutierrez, P.A.; Deo, R.C.; Salcedo-Sanz, S. Machine learning regression and classification methods for fog events prediction. Atmos. Res. 2022, 272, 106157. [Google Scholar] [CrossRef]
- Chen, F.; Peng, Y.U.; Li, L.I. Preliminary Analysis of Chengdu Shuangliu Airport’s Prevailing Visibility Data over the Years and the Realization of R. Comput. Knowl. Technol. 2012, 27, 6428–6433. [Google Scholar]
- Li, L.; Tan, Q.; Zhang, Y.; Feng, M.; Qu, Y.; An, J.; Liu, X. Characteristics and source apportionment of PM2. 5 during persistent extreme haze events in Chengdu, southwest China. Environ. Pollut. 2017, 230, 718–729. [Google Scholar] [CrossRef]
- Roach, W.T.; Brown, R.; Caughey, S.J.; Garland, J.A.; Readings, C. The physics of radiation fog: I—A field study. Q. J. R. Meteorol. Soc. 1976, 102, 313–333. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Myles, A.J.; Feudale, R.N.; Liu, Y.; Woody, N.A.; Brown, S.D. An introduction to decision tree modeling. J. Chemom. A J. Chemom. Soc. 2004, 18, 275–285. [Google Scholar] [CrossRef]
- Balakrishnama, S.; Ganapathiraju, A. Linear discriminant analysis-a brief tutorial. Inst. Signal Inf. Process. 1998, 18, 1–8. [Google Scholar]
- Webb, G.I.; Keogh, E.; Miikkulainen, R.; Bayes, N. Encyclopedia of Machine Learning; Springer: Berlin/Heidelberg, Germany, 2010; Volume 15, pp. 713–714. [Google Scholar]
- Chauhan, V.K.; Dahiya, K.; Sharma, A. Problem formulations and solvers in linear SVM: A review. Artif. Intell. Rev. 2019, 52, 803–855. [Google Scholar] [CrossRef]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy k-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. 1985, 4, 580–585. [Google Scholar] [CrossRef]
- Priddy, K.L.; Keller, P.E. Artificial Neural Networks: An Introduction; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Bonavita, M.; Hólm, E.; Isaksen, L.; Fisher, M. The evolution of the ECMWF hybrid data assimilation system. Q. J. R. Meteorol. Soc. 2016, 142, 287–303. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, J.; Arsenault, K.; Brian, C.; Radakovich, J.; Entin, J.K.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).