Mesospheric Gravity Wave Potential Energy Density Observed by Rayleigh Lidar above Golmud (36.25° N, 94.54° E), Tibetan Plateau
Abstract
1. Introduction
2. Data and Analysis Method
2.1. Rayleigh Lidar and Data
2.2. Analysis Method
3. Results of the Analysis
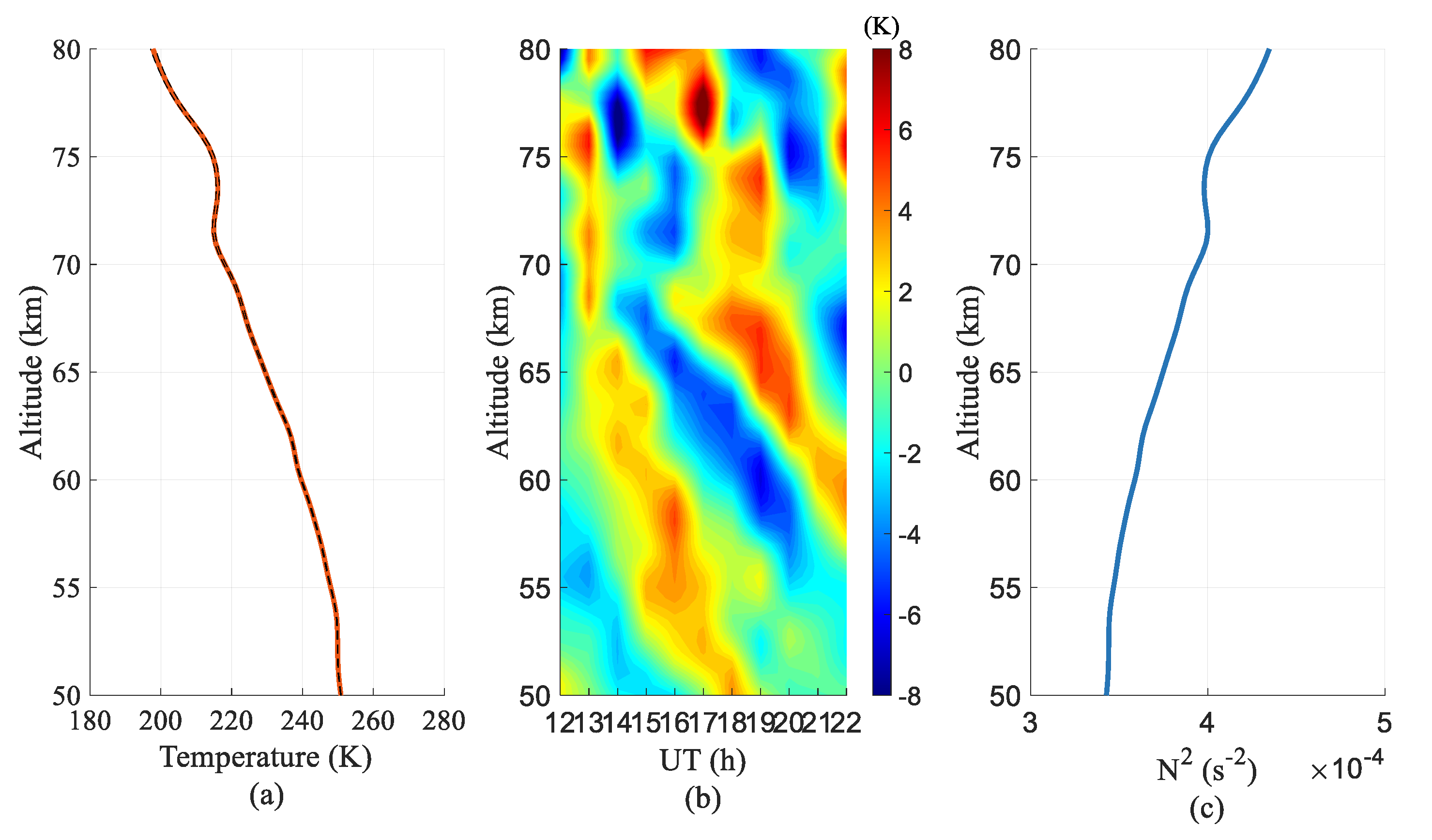
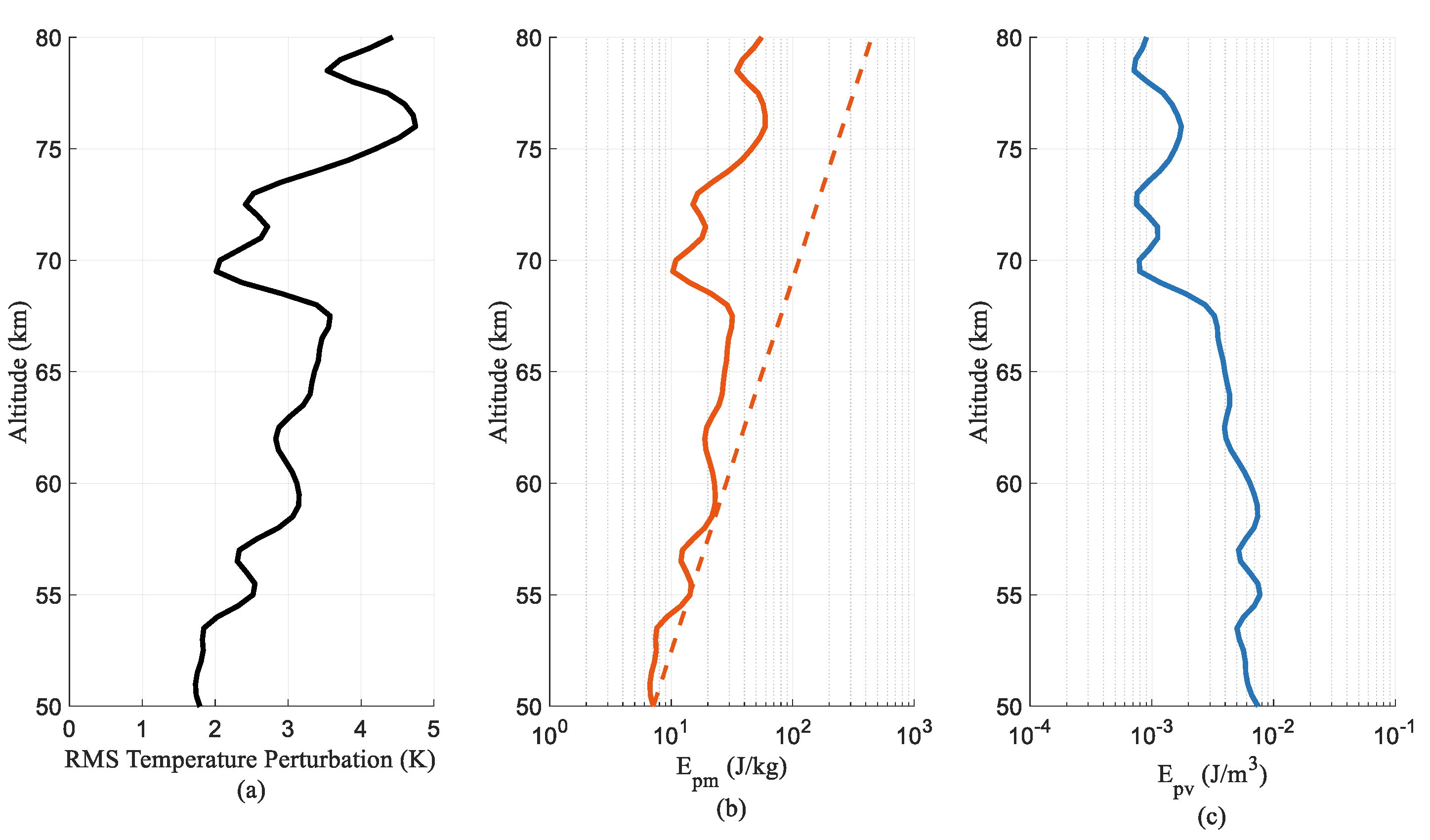
3.1. Example of the Gravity Waves
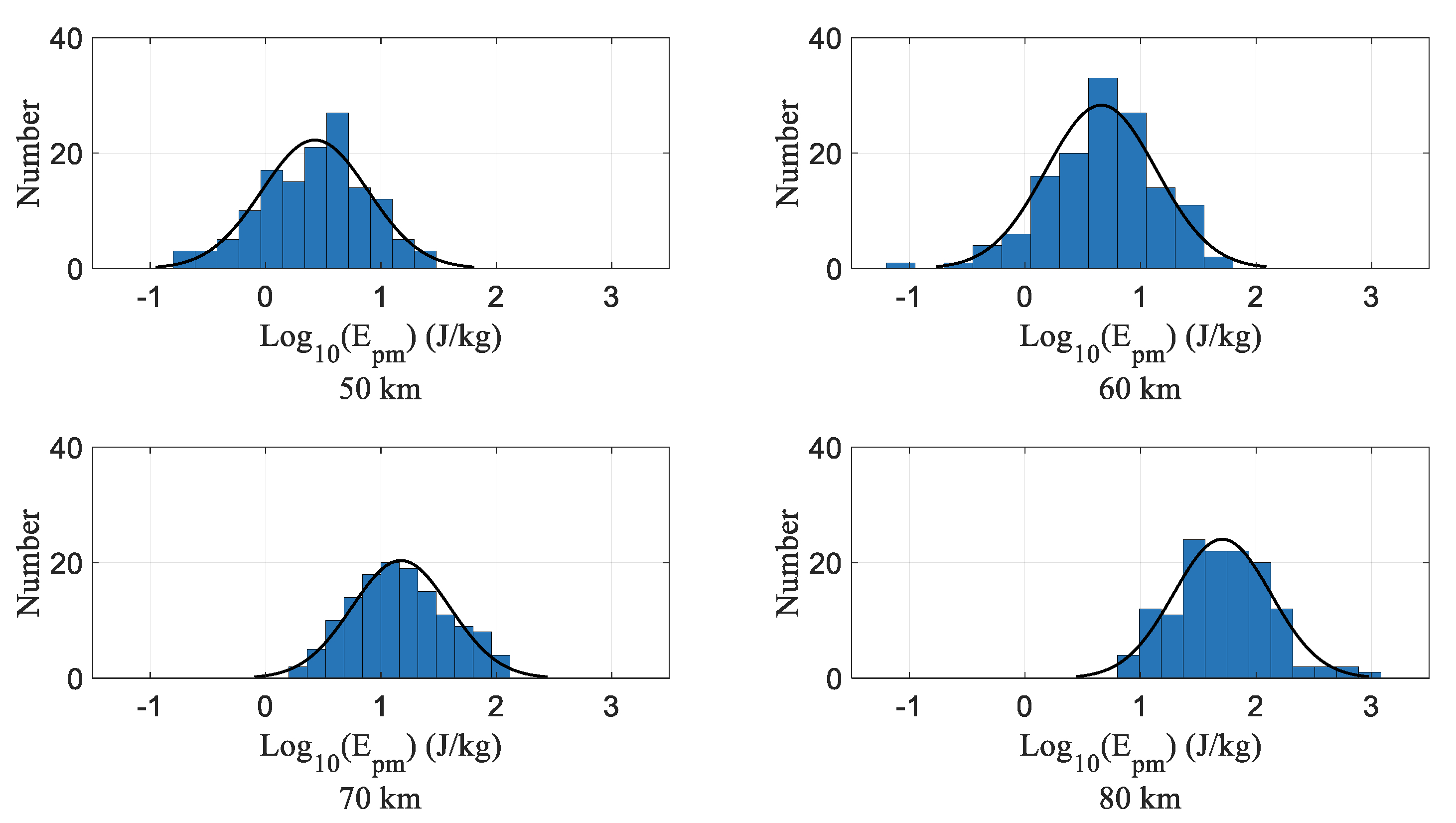
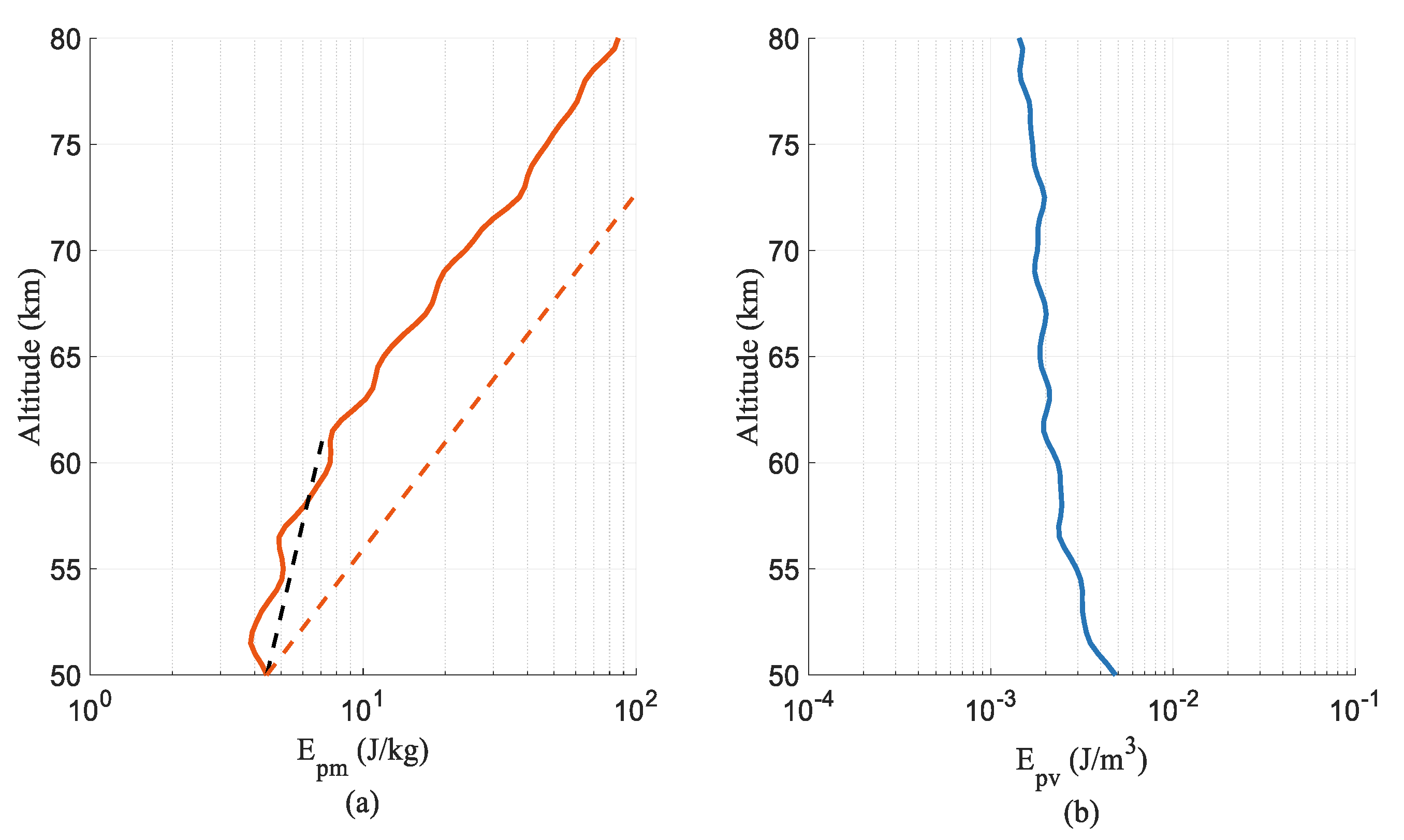
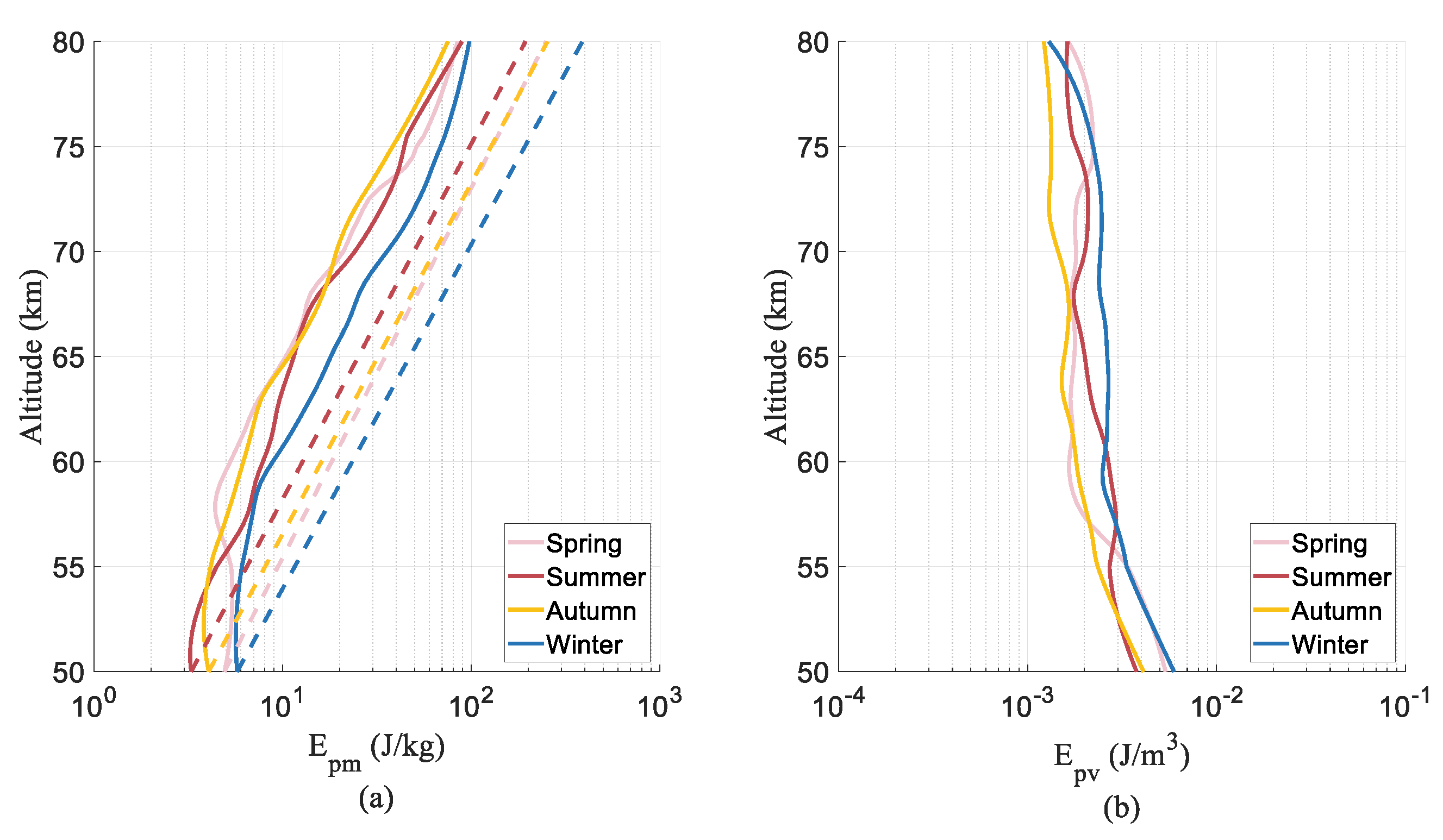
3.2. Characteristics of the GWPED
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Lindzen, R.S. Turbulence and stress owing to gravity wave and tidal breakdown. J. Geophys. Res. 1981, 86, 9707–9714. [Google Scholar] [CrossRef]
- Cai, X.; Yuan, T.; Eccles, J.V. A numerical investigation on tidal and gravity wave contributions to the summer time Na variations in the midlatitude E region. J. Geophys. Res. Space Phys. 2017, 122, 10577–10595. [Google Scholar] [CrossRef]
- Gardner, C.S. Role of wave-induced diffusion and energy flux in the vertical transport of atmospheric constituents in the mesopause region. J. Geophys. Res. Atmos. 2018, 123, 6581–6604. [Google Scholar] [CrossRef]
- Ba, J.; Hu, X.; Yan, Z.; Guo, S.; Cheng, Y.; Yang, J. Observation analysis on the characteristics of vertical dynamical transport of sodium atoms in the mesopause region over the Langfang area. Chin. J. Geophys. 2018, 61, 449–457. [Google Scholar]
- Alexander, M.J.; Geller, M.; McLandress, C.; Polavarapu, S.; Preusse, P.; Sassi, F.; Sato, K.; Eckermann, S.; Ern, M.; Hertzog, A.; et al. Recent developments in gavity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models. Q. J. R. Meteorol. Soc. 2010, 136, 1103–1124. [Google Scholar] [CrossRef]
- Geller, M.A.; Alexander, M.J.; Love, P.T.; Bacmeister, J.; Ern, M.; Hertzog, A.; Manzini, E.; Preusse, P.; Sato, K.; Scaife, A.A.; et al. A comparison between gravity wave momentum fluxes in observations and climate models. J. Clim. 2013, 26, 6383–6405. [Google Scholar] [CrossRef]
- Strelnikova, I.; Almowafy, M.; Baumgarten, G.; Baumgarten, K.; Ern, M.; Gerding, M.; Lübken, F. Seasonal Cycle of Gravity Wave Potential Energy Densities from Lidar and Satellite Observations at 54° and 69° N. J. Atmos. Sci. 2021, 78, 1359–1386. [Google Scholar] [CrossRef]
- Ern, M.; Trinh, Q.T.; Preusse, P.; Gille, J.C.; Mlynczak, M.G.; Russell, J.M., III; Riese, M. GRACILE. A comprehensive climatology of atmospheric gravity wave parameters based on satellite limb soundings. Earth Syst. Sci. Data 2018, 10, 857–892. [Google Scholar] [CrossRef]
- Alexander, M.J.; Gille, J.; Cavanaugh, C.; Coffey, M.; Craig, C.; Eden, T.; Francis, G.; Halvorson, C.; Hannigan, J.; Khosravi, R.; et al. Global estimates of gravity wave momentum flux from High Resolution Dynamics Limb Sounder observations. J. Geophys. Res. 2008, 113, D15S18. [Google Scholar] [CrossRef]
- Ern, M.; Preusse, P.; Alexander, M.J.; Warner, C.D. Absolute values of gravity wave momentum flux derived from satellite data. J. Geophys. Res. 2004, 109, D20103. [Google Scholar] [CrossRef]
- Bossert, K.; Fritts, D.C.; Heale, C.J.; Eckermann, S.D.; Plane, J.M.C.; Snively, J.B.; Williams, B.P.; Reid, I.M.; Murphy, D.J.; Spargo, A.J.; et al. Momentum flux spectra of a mountain wave event over New Zealand. J. Geophys. Res. Atmos. 2018, 123, 9980–9991. [Google Scholar] [CrossRef]
- Rauthe, M.; Gerding, M.; Höffner, J.; Lübken, F.J. Lidar temperature measurements of gravity waves over Kuhlungsborn (54° N) from 1 to 105 km: A winter-summer comparison. J. Geophys. Res. 2006, 111, D24108. [Google Scholar] [CrossRef]
- Alpers, M.; Eixmann, R.; Fricke-Begemann, C.; Gerding, M.; Höffner, J. Temperature lidar measurements from 1 to 105 km altitude using resonance, Rayleigh, and Rotational Raman scattering. Atmos. Chem. Phys. 2004, 4, 793–800. [Google Scholar] [CrossRef]
- Chanin, M.L.; Hauchecorne, A. Lidar observations of gravity and tidal waves in the stratosphere and mesosphere. J. Geophys. Res. 1981, 86, 9715–9721. [Google Scholar] [CrossRef]
- Gardner, C.S.; Miller, M.S.; Liu, C.H. Rayleigh lidar observations of gravity wave activity in the upper stratosphere at Urbana, Illinois. J. Atmos. Sci. 1989, 46, 1838–1854. [Google Scholar] [CrossRef]
- Zhao, J.; Chu, X.; Chen, C.; Lu, X.; Fong, W.; Yu, Z.; Jones, R.M.; Roberts, B.R.; Dörnbrack, A. Lidar observations of stratospheric gravity waves from 2011 to 2015 at McMurdo (77.84° S, 166.69° E), Antarctica: 1. Vertical wavelengths, periods, and frequency and vertical wave number spectra. J. Geophys. Res. Atmos. 2017, 122, 5041–5062. [Google Scholar] [CrossRef]
- Cai, X.; Yuan, T.; Liu, H.L. Large Scale Gravity Waves perturbations in mesosphere region above northern hemisphere mid-latitude during Autumn-equinox: A joint study by Na Lidar and Whole Atmosphere Community Climate Model. Ann. Geophys. 2017, 35, 181–188. [Google Scholar] [CrossRef]
- Sivakumar, V.; Rao, P.B.; Bencherif, H. Lidar observations of middle atmospheric gravity wave activity over a low-latitude site (Gadanki, 13.5° N, 79.2° E). Ann. Geophys. 2006, 24, 823–834. [Google Scholar] [CrossRef]
- Taori, A.; Raizada, S.; Ratnam, M.V.; Tepley, C.A.; Nath, D.; Jayaraman, A. Role of tropical convective cells in the observed middle atmospheric gravity wave properties from two distant low latitude stations. Earth Sci. Res. 2012, 1, 87–97. [Google Scholar] [CrossRef][Green Version]
- Kafle, D.N. Rayleigh-Lidar Observations of Mesospheric Gravity Wave Activity above Logan, Utah; Utah State University: Logan, UT, USA, 2009. [Google Scholar]
- Llamedo, P.; Salvador, J.; Torre, A.; Quiroga, J.; Alexander, P.; Hierro, R.; Schmidt, T.; Pazmiño, A.; Quel, E. 11 years of Rayleigh lidar observations of gravity wave activity above the southern tip of South America. J. Geophys. Res. Atmos. 2019, 124, 451–467. [Google Scholar] [CrossRef]
- McDonald, A.J.; Thomas, L.; Wareing, D.F. Night-to-night changes in the characteristics of gravity waves at stratospheric and lower-mesospheric heights. Ann. Geophys. 1998, 16, 229–237. [Google Scholar] [CrossRef][Green Version]
- Murayama, Y.; Tsuda, T.; Wilson, R.; Nakane, H.; Hayashida, S.A.; Sugimoto, N.; Matsui, I.; Sasano, Y. Gravity wave activity in the upper stratosphere and lower mesosphere observed with the Rayleigh lidar at Tsukuba, Japan. Geophys. Res. Lett. 1994, 21, 1539–1542. [Google Scholar] [CrossRef]
- Mzé, N.; Hauchecorne, A.; Keckhut, P.; Thétis, M. Vertical distribution of gravity wave potential energy from long-term Rayleigh lidar data at a northern middle-latitude site. J. Geophys. Res. Atmos. 2014, 119, 12069–12083. [Google Scholar] [CrossRef]
- Rauthe, M.; Gerding, M.; Lübken, F.-J. Seasonal changes in gravity wave activity measured by lidars at mid-latitudes. Atmos. Chem. Phys. Discuss. 2008, 8, 6775–6787. [Google Scholar] [CrossRef]
- Sica, R.J.; Argall, P.S. Seasonal and nightly variations of gravity-wave energy density in the middle atmosphere measured by the Purple Crow Lidar. Ann. Geophys. 2007, 25, 2139–2145. [Google Scholar] [CrossRef]
- Whiteway, J.A.; Carswell, A.I. Lidar observations of gravity wave activity in the upper stratosphere over Toronto. J. Geophys. Res. 1995, 100, 14113–14124. [Google Scholar] [CrossRef]
- Wilson, R.; Chanin, M.L.; Hauchecorne, A. Gravity waves in the middle atmosphere observed by Rayleigh lidar: 2. Climatology. J. Geophys. Res. 1991, 96, 5169–5183. [Google Scholar] [CrossRef]
- Thurairajah, B.; Collins, R.L.; Harvey, V.L.; Lieberman, R.S.; Mizutani, K. Rayleigh lidar observations of reduced gravity wave activity during the formation of an elevated stratopause in 2004 at Chatanika, Alaska (65° N, 147° W). J. Geophys. Res. 2010, 115, D13109. [Google Scholar] [CrossRef]
- Alexander, S.P.; Klekociuk, A.R.; Murphy, D.J. Rayleigh lidar observations of gravity wave activity in the winter upper stratosphere and lower mesosphere above Davis, Antarctica (69° S, 78° E). J. Geophys. Res. 2011, 116, D13109. [Google Scholar] [CrossRef]
- Blum, U.; Fricke, K.H.; Baumgarten, G.; Schöch, A. Simultaneous lidar observations of temperatures and waves in the polar middle atmosphere on the east and west side of the Scandinavian mountains: A case study on 19/20 January 2003. Atmos. Chem. Phys. Discuss. 2004, 4, 809–816. [Google Scholar] [CrossRef]
- Chu, X.; Zhao, J.; Lu, X.; Harvey, V.L.; Jones, R.M.; Becker, E.; Chen, C.; Fong, W.; Yu, Z.; Roberts, B.R.; et al. Lidar observations of stratospheric gravity waves from 2011 to 2015 at McMurdo (77.84° S, 166.69° E), Antarctica: 2. Potential energy densities, lognormal distributions, and seasonal variations. J. Geophys. Res. Atmos. 2018, 123, 7910–7934. [Google Scholar] [CrossRef]
- Ehard, B.; Achtert, P.; Gumbel, J. Long-term lidar observations of wintertime gravity wave activity over northern Sweden. Ann. Geophys. 2014, 32, 1395–1405. [Google Scholar] [CrossRef]
- Kaifler, B.; Lübken, F.-J.; Höffner, J.; Morris, R.J.; Viehl, T.P. Lidar observations of gravity wave activity in the middle atmosphere over Davis (69° S, 78° E), Antarctica. J. Geophys. Res. Atmos. 2015, 120, 4506–4521. [Google Scholar] [CrossRef]
- Li, Z.; Chu, X.; Harvey, V.L.; Jandreau, J.; Lu, X.; Yu, Z.; Zhao, J.; Fong, W. First lidar observations of Quasi-Biennial Oscillation-induced interannual variations of gravity wave potential energy density at McMurdo via a modulation of the Antarctic polar vortex. J. Geophys. Res. Atmos. 2020, 125, e2020JD032866. [Google Scholar] [CrossRef]
- Lu, X.; Chu, X.; Fong, W.; Chen, C.; Yu, Z.; Roberts, B.R.; McDonald, A.J. Vertical evolution of potential energy density and vertical wave number spectrum of Antarctic gravity waves from 35 to 105 km at McMurdo (77.8° S, 166.7° E). J. Geophys. Res. Atmos. 2015, 120, 2719–2737. [Google Scholar] [CrossRef]
- Whiteway, J.A.; Duck, T.J.; Donovan, D.P.; Bird, J.C.; Pal, S.R.; Carswell, A.I. Measurements of gravity wave activity within and around the arctic stratospheric vortex. Geophys. Res. Lett. 1997, 24, 1387–1390. [Google Scholar] [CrossRef]
- Yamashita, C.; Chu, X.; Liu, H.-L.; Espy, P.J.; Nott, G.J.; Huang, W. Stratospheric gravity wave characteristics and seasonal variations observed by lidar at the South Pole and Rothera, Antarctica. J. Geophys. Res. 2009, 114, D12101. [Google Scholar] [CrossRef]
- Dai, Y.; Pan, W.; Hu, X.; Bai, Z.; Ban, C.; Zhang, H.; Che, Y. An approach for improving the NRLMSISE-00 model using a radiosonde at Golmud of the Tibetan Plateau. Meteorol. Atmos. Phys. 2020, 132, 451–459. [Google Scholar] [CrossRef]
- Qiao, S.; Pan, W.; Ban, C.; Zhang, H. Mesospheric density measured by Rayleigh lidar over Golmud, Infrared and Laser Engineering. Infrared Laser Eng. 2018, 47, 23–28. [Google Scholar]
- Gardner, C.S.; Liu, A.Z. Seasonal variations of the vertical fluxes of heat and horizontal momentum in the mesopause region at Starfire Optical Range, New Mexico. J. Geophys. Res. Atmos. 2007, 112, D09113. [Google Scholar] [CrossRef]
- Forbes, J.M. Middle Atmosphere Tides and Coupling between Atmospheric Regions. J. Geomagn. Geoelectr. 1991, 43, 597–609. [Google Scholar] [CrossRef]
- Zhu, X.; Yee, J.H.; Strobel, D.F.; Wang, X.; Greenwald, R.A. On the numerical modelling of middle atmosphere tides. Q. J. R. Meteorol. Soc. 1999, 125, 1825–1857. [Google Scholar] [CrossRef]
- Lighthill, J. Waves in Fluids; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]

| 2013 | January | February | March | April | May | June | July | August | September | October | November | December | Total |
| Observations | 6 | 6 | |||||||||||
| hours/h | 61 | 61 | |||||||||||
| 2014 | January | February | March | April | May | June | July | August | September | October | November | December | Total |
| Observations | 5 | 2 | 11 | 9 | 10 | 17 | 14 | 18 | 86 | ||||
| hours/h | 45 | 14 | 83 | 71 | 82 | 156 | 134 | 180 | 765 | ||||
| 2015 | January | February | March | April | May | June | July | August | September | October | November | December | Total |
| Observations | 5 | 5 | 11 | 8 | 1 | 13 | 43 | ||||||
| hours/h | 34 | 39 | 82 | 60 | 8 | 125 | 348 |
| Scale Heights | Spring | Summer | Autumn | Winter | Total |
|---|---|---|---|---|---|
| (km) | 58.1 | 12.6 | 30.9 | 47.4 | 23.6 |
| H (km) | 7.6 | 7.3 | 7.3 | 7.1 | 7.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Hu, X.; Pan, W.; Yan, Z.; Guo, W. Mesospheric Gravity Wave Potential Energy Density Observed by Rayleigh Lidar above Golmud (36.25° N, 94.54° E), Tibetan Plateau. Atmosphere 2022, 13, 1084. https://doi.org/10.3390/atmos13071084
Zhao W, Hu X, Pan W, Yan Z, Guo W. Mesospheric Gravity Wave Potential Energy Density Observed by Rayleigh Lidar above Golmud (36.25° N, 94.54° E), Tibetan Plateau. Atmosphere. 2022; 13(7):1084. https://doi.org/10.3390/atmos13071084
Chicago/Turabian StyleZhao, Weibo, Xiong Hu, Weilin Pan, Zhaoai Yan, and Wenjie Guo. 2022. "Mesospheric Gravity Wave Potential Energy Density Observed by Rayleigh Lidar above Golmud (36.25° N, 94.54° E), Tibetan Plateau" Atmosphere 13, no. 7: 1084. https://doi.org/10.3390/atmos13071084
APA StyleZhao, W., Hu, X., Pan, W., Yan, Z., & Guo, W. (2022). Mesospheric Gravity Wave Potential Energy Density Observed by Rayleigh Lidar above Golmud (36.25° N, 94.54° E), Tibetan Plateau. Atmosphere, 13(7), 1084. https://doi.org/10.3390/atmos13071084






