Prediction of Air Pollutant Concentrations via RANDOM Forest Regressor Coupled with Uncertainty Analysis—A Case Study in Ningxia
Abstract
:1. Introduction
2. Area Description
Study Area
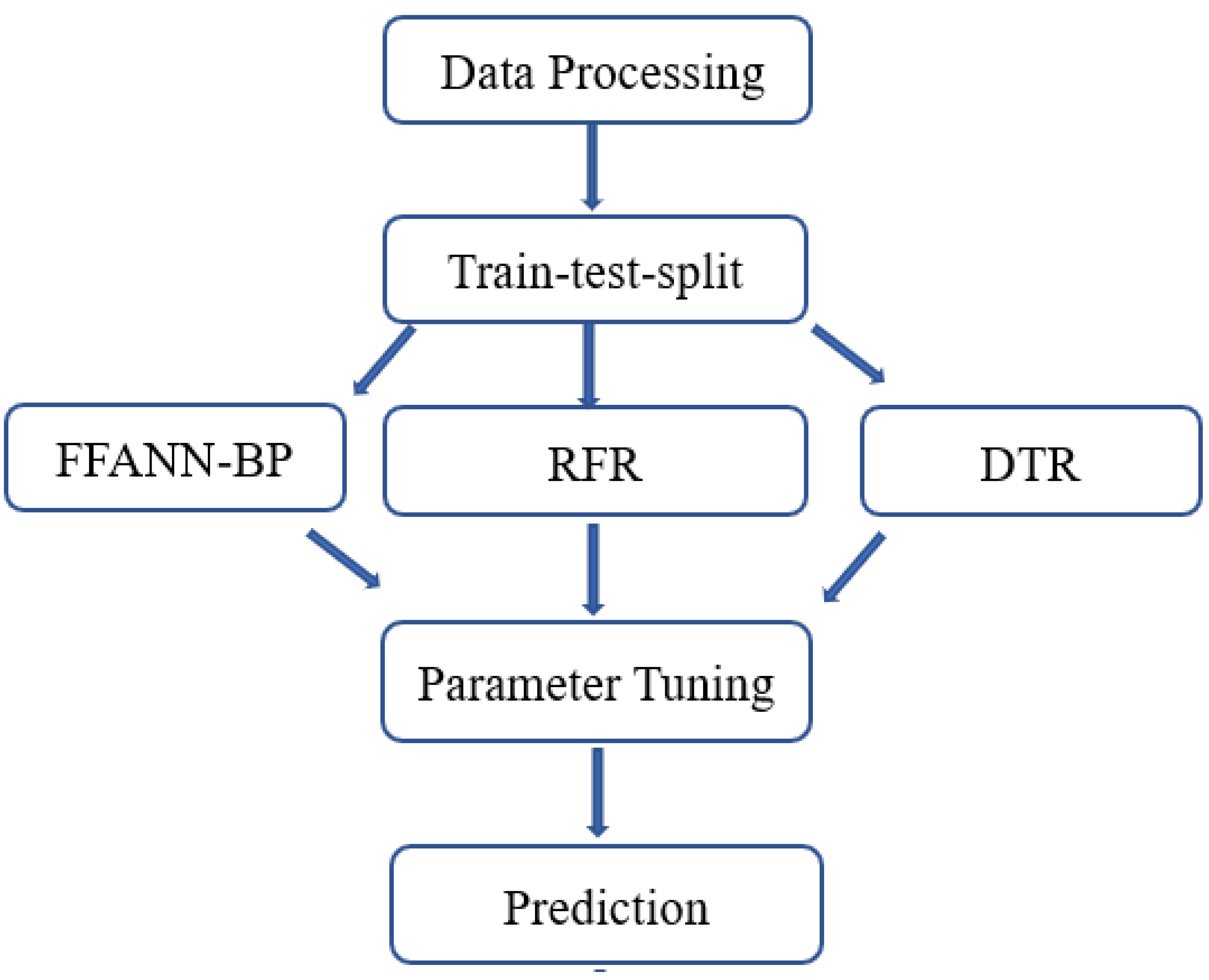
3. Methods
3.1. Data Preprocessing
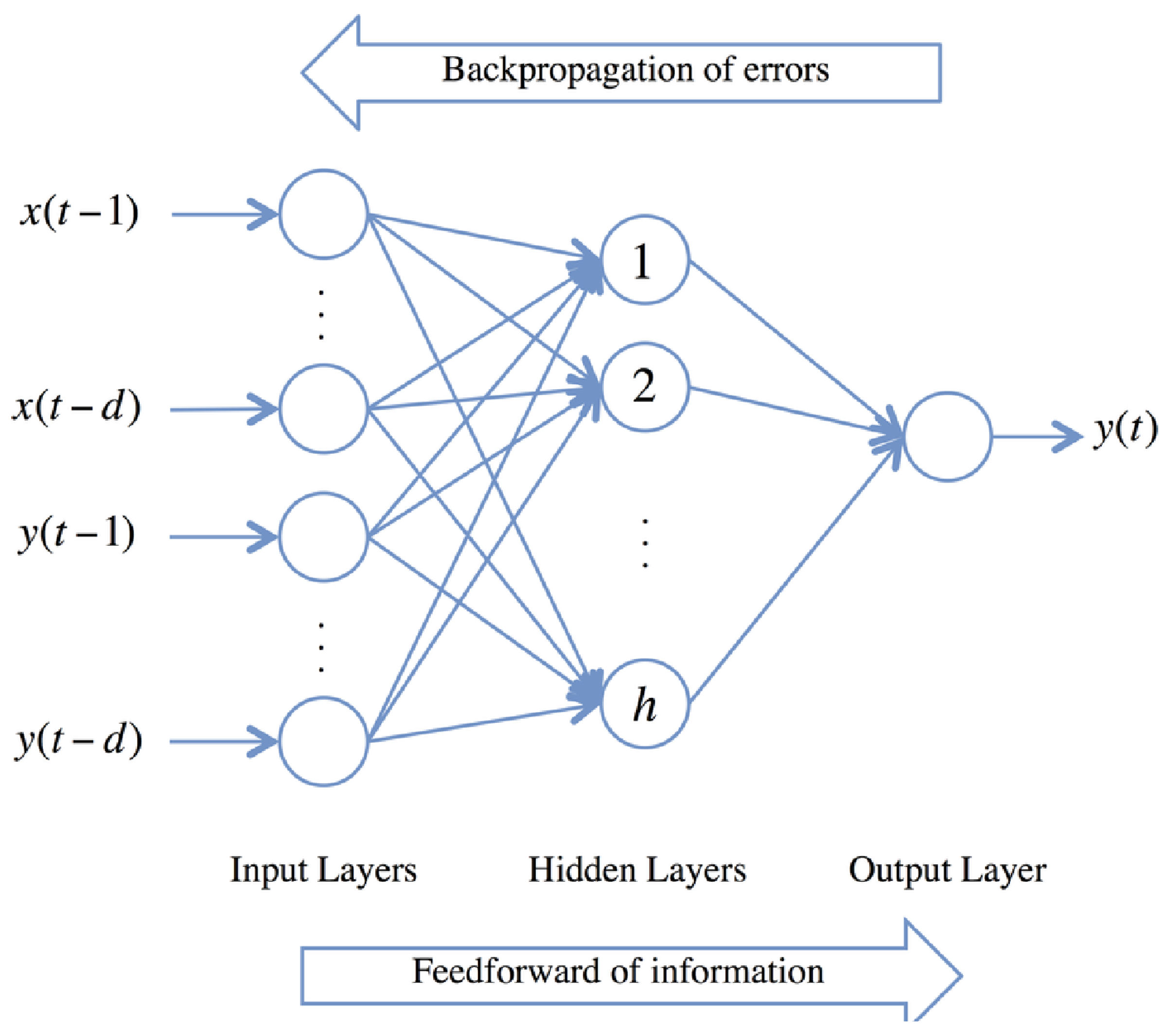
3.2. FFANN-BP
3.3. DTR
3.4. Random Forest Regression
3.5. Statistical Indexes
4. Results and Discussion
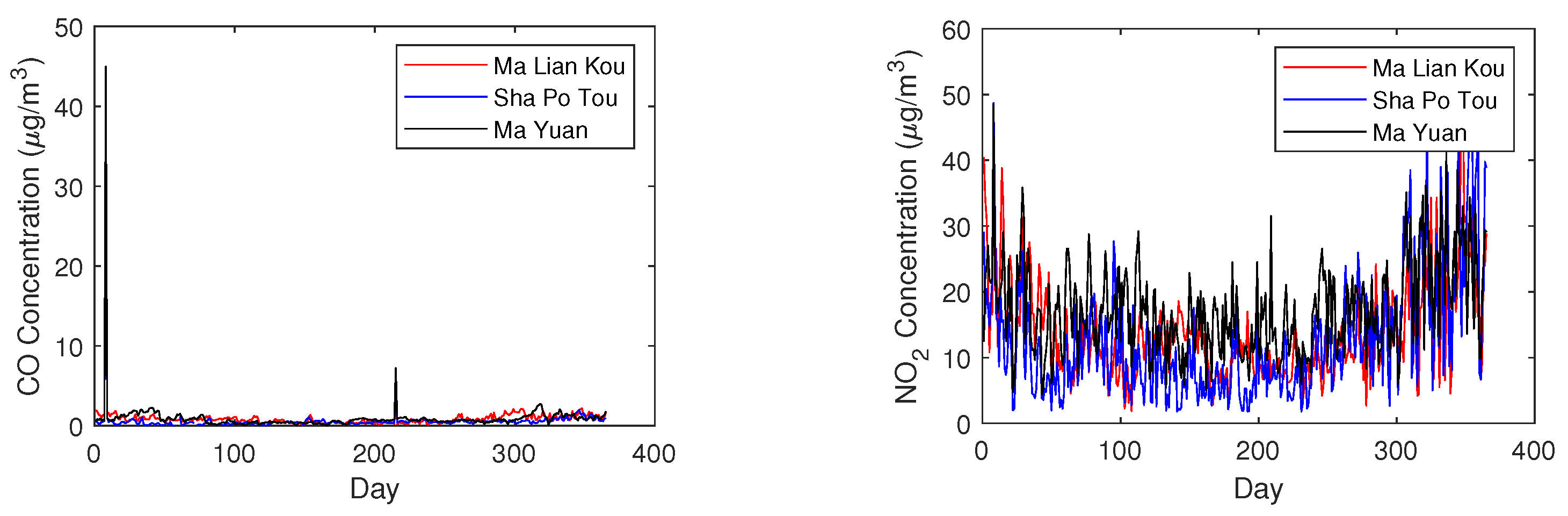
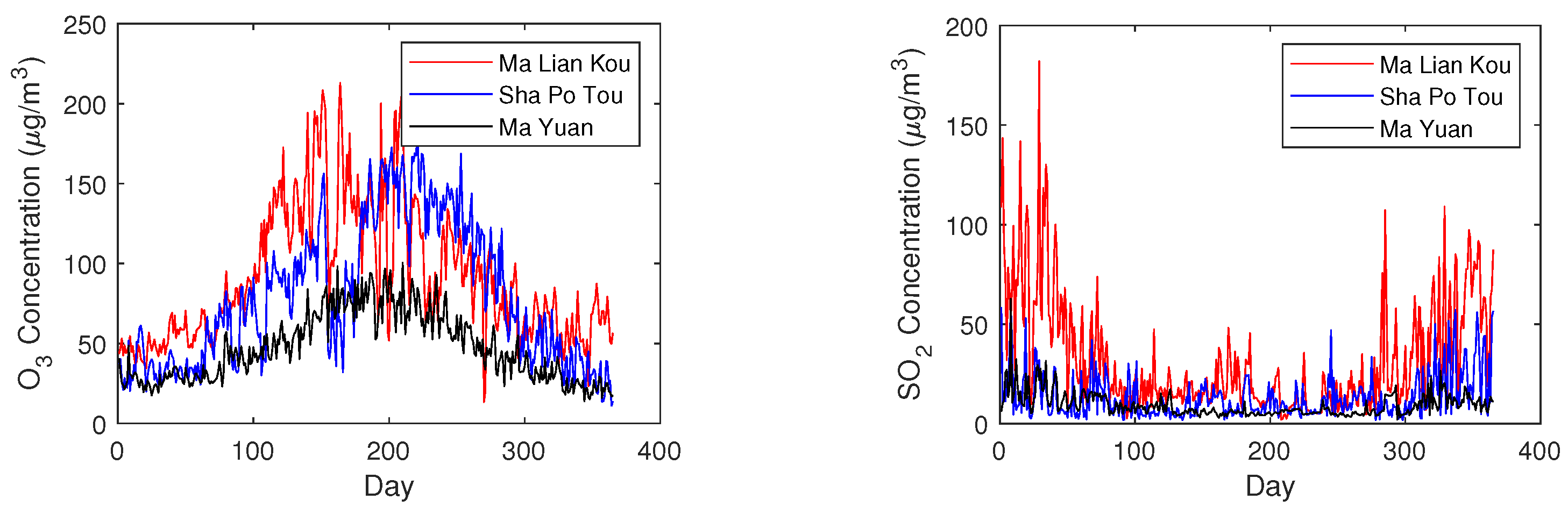
4.1. Data Used
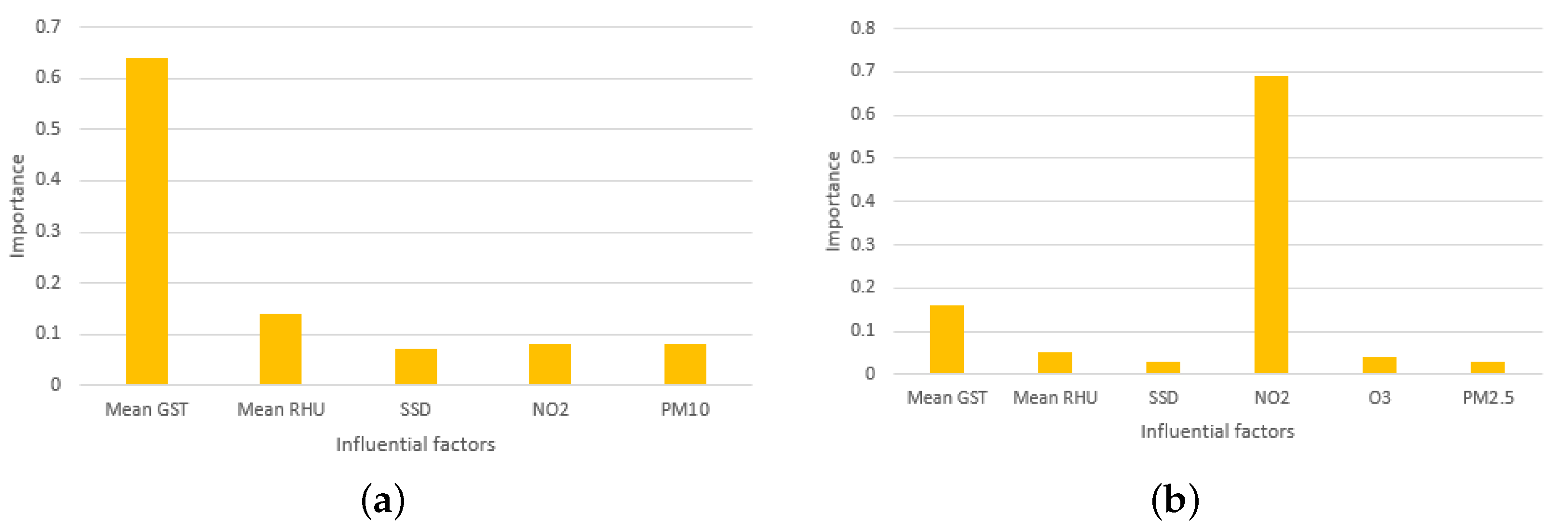
4.2. Selection of the Influential Factors
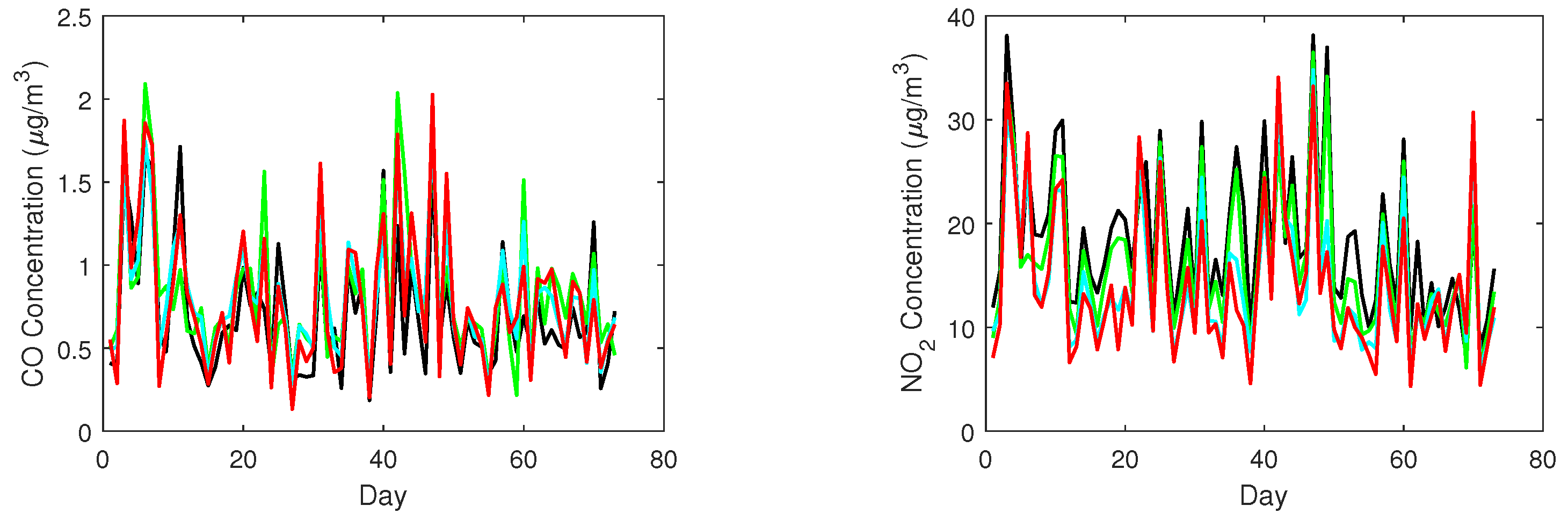
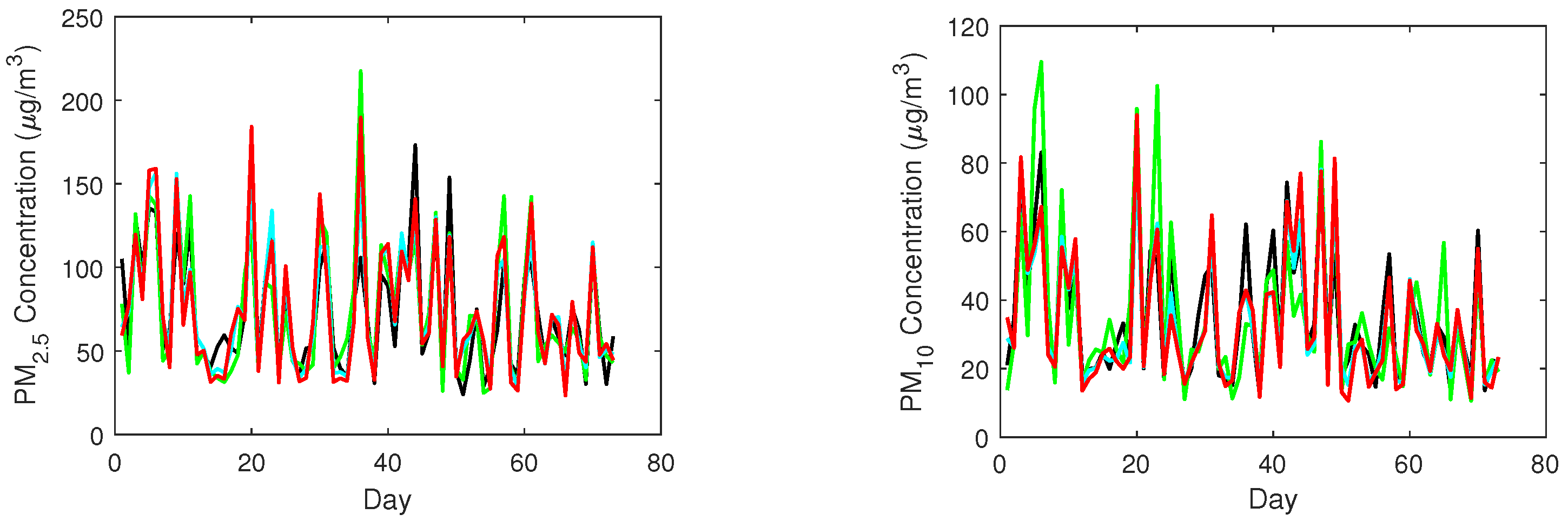
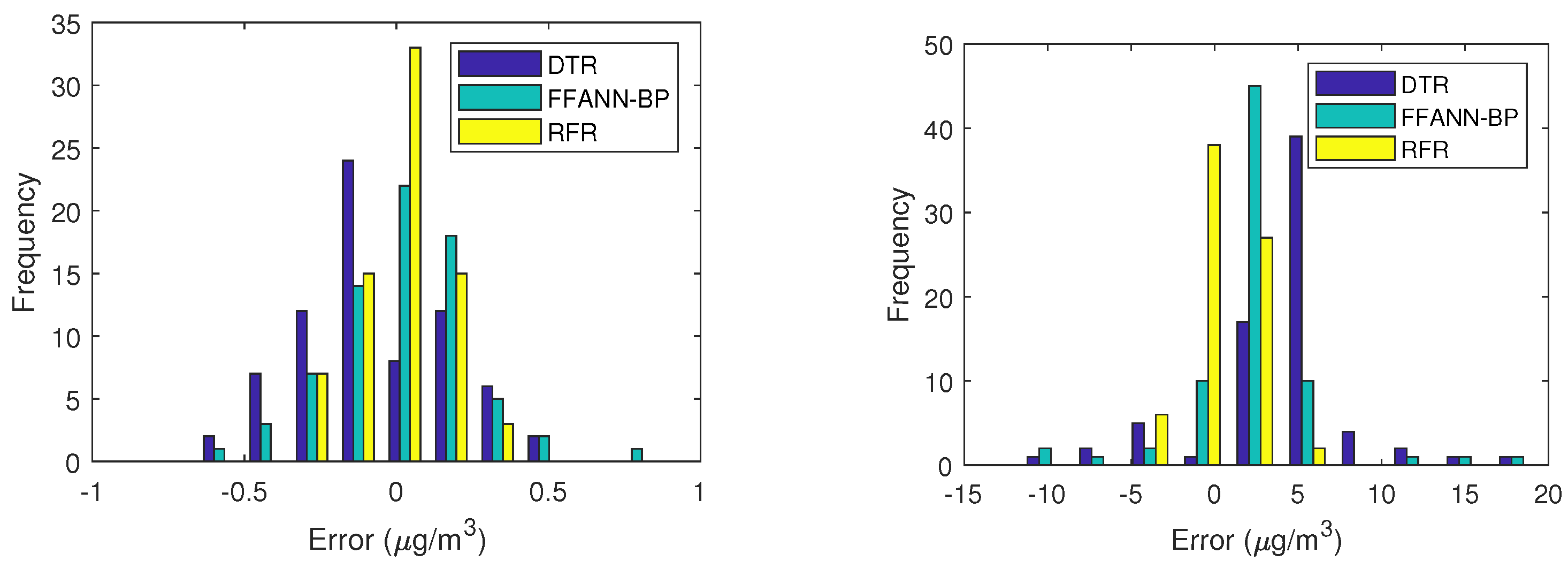
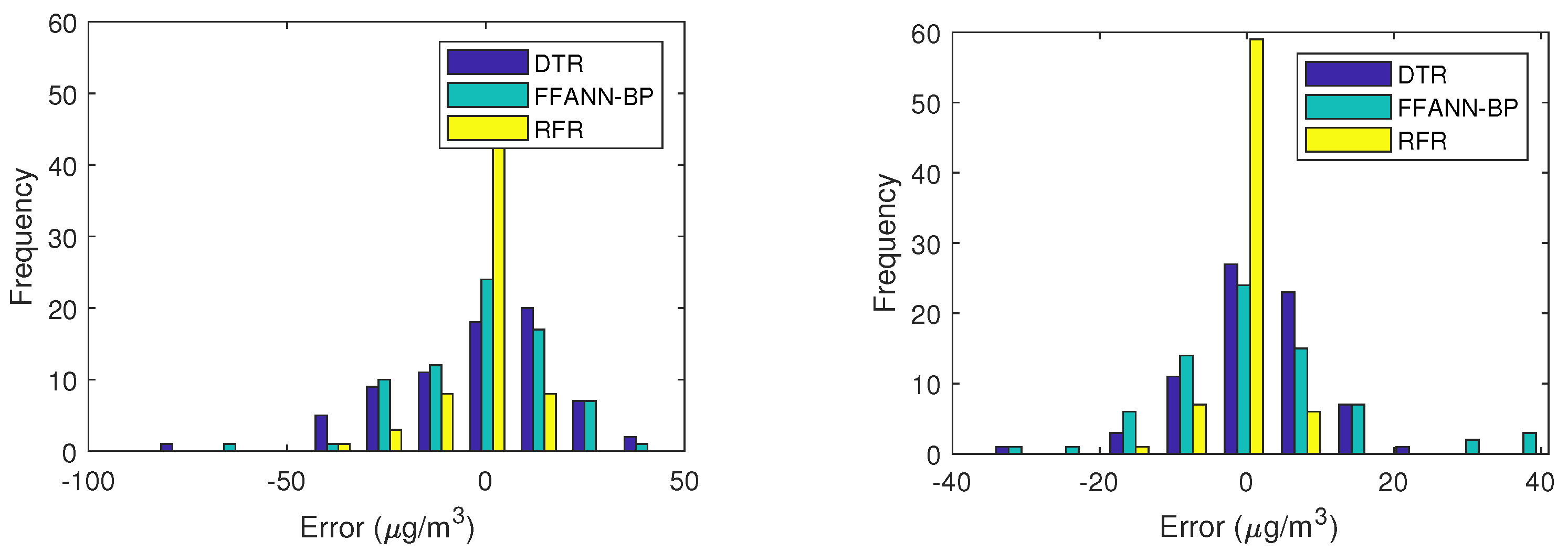
4.3. Experimental Results and Interpretations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Berg, A.; McColl, K.A. No projected global dry lands expansion under greenhouse warming. Nat. Clim. Chang. 2021, 11, 331–337. [Google Scholar] [CrossRef]
- Liao, Z.; Gao, M.; Sun, J.; Fan, S. The impact of synoptic circulation on air quality and pollution-related human health in the Yangtze River Delta region. Sci. Total Environ. 2017, 607, 838–846. [Google Scholar] [CrossRef]
- Pang, Y.; Huang, W.; Luo, X.; Chen, Q.; Zhan, Z.; Tang, M.; Hong, Y.; Chen, J.; Li, H. In-vitro human lung cell injuries induced by urban PM2.5 during a severe air pollution episode: Variations associated with particle components. Ecotoxicol. Environ. Saf. 2020, 206, 111406. [Google Scholar] [CrossRef]
- Shang, Y.; Sun, Z.; Cao, J.; Wang, X.; Zhong, L.; Bi, X.; Li, H.; Liu, W.; Zhu, T.; Huang, W. Systematic review of Chinese studies of short-term exposure to air pollution and daily mortality. Environ. Int. 2013, 54, 100–111. [Google Scholar] [CrossRef]
- Shaddick, G.; Thomas, M.L.; Amini, H. Data integration for the assessment of population exposure to ambient air pollution for global burden of disease assessment. Environ. Sci. Technol. 2018, 52, 9069–9078. [Google Scholar] [CrossRef]
- Zhang, J.S.; Ding, W.F. Prediction of air pollutants concentration based on extreme learning machine: The case of Hong Kong. Int. J. Environ. Sci. Public Health 2017, 7, 114. [Google Scholar] [CrossRef]
- Dennis, R.L.; Byun, D.W.; Novak, J.H. The next generation of integrated air quality modeling: EPA’s models-3. Atmos. Environ. 1996, 30, 1925–1938. [Google Scholar] [CrossRef]
- Wang, Z.F.; Xie, F.Y.; Wang, X.Q. Development and application of nested air quality prediction modeling system. Atmos. Sci. 2006, 31, 778–790. [Google Scholar]
- Batterman, S.A.; Zhang, K.; Kononowech, R. Prediction and analysis of near-road concentrations using a reduced-form emission/dispersion model. Environ. Health 2010, 9, 29. [Google Scholar] [CrossRef] [Green Version]
- Abal, G.; Aicardi, D.; Suarez, R.A.; Laguarda, A. Performance of empirical models for diffuse fraction in uruguay. Sol. Energy 2017, 141, 166–181. [Google Scholar] [CrossRef]
- Briant, R.; Seigneur, C.; Gadrat, M.; Bugajny, C. Evaluation of roadway gaussian plume models with large- scale measurement campaigns. Geosci. Model. 2013, 6, 445–456. [Google Scholar] [CrossRef] [Green Version]
- Mishra, D.; Goyal, P. Development of artificial intelligence based NO2 forecasting models at Taj Mahal, Agra centre for atmospheric sciences. Atmos. Pollut. Res. 2015, 6, 99–106. [Google Scholar] [CrossRef] [Green Version]
- Pahlavani, P.; Sheikhian, H.; Bigdeli, B. Assessment of an air pollution monitoring network to generate urban air pollution maps using Shannon information index, fuzzy overlay, and Dempster-Shafer theory, A case study: Tehran, Iran. Atmos. Environ. 2017, 167, 254–269. [Google Scholar] [CrossRef]
- Sayegh, A.S.; Munir, S.; Habeebullah, T.M. Comparing the performance of statistical models for predicting PM10 concentrations. Aerosol. Air Qual. Res. 2014, 14, 653–665. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zheng, W.; Li, W.; Huang, Y. Large group activity security risk assessment and risk early warning based on random forest algorithm. Pattern Recognit. Lett. 2021, 144, 1–5. [Google Scholar] [CrossRef]
- Danesh Yazdi, M.; Kuang, Z.; Dimakopoulou, K.; Barratt, B.; Suel, E.; Amini, H.; Schwartz, J. Predicting fine particulate matter (PM2.5) in the greater London area: An ensemble approach using machine learning methods. Remote Sens. 2020, 12, 914. [Google Scholar] [CrossRef] [Green Version]
- Ding, W.F.; Zhang, J.S. Prediction of air pollutant concentration based on sparse response backpropagation training feedforward neural networks. Environ. Sci. Pollut. Res. 2016, 23, 19481–19494. [Google Scholar] [CrossRef]
- Ding, W.; Leung, Y.; Zhang, J.; Fung, T. A hierarchical Bayesian model for the analysis of space-time air pollutant concentrations and an application to air pollution analysis in Northern China. Stoch. Environ. Res. Risk Assess. 2021, 35, 2237–2271. [Google Scholar] [CrossRef]
- Joharestani, M.Z.; Cao, C.; Ni, X.; Bashir, B.; Talebiesfandarani, S. PM2.5 Prediction based on random forest, XGBoost, and deep learning using multisource remote sensing data. Atmosphere 2019, 10, 373. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, A.B.; Ordóñez, C.; Lasheras, F.S.; de Cos Juez, F.J.; Roca-Pardias, J. Forecasting SO2 pollution incidents by means of elman artificial neural networks and ARIMA models. In Abstract and Applied Analysis; Hindawi: London, UK, 2013; pp. 1–6. [Google Scholar]
- Li, L.; Zhang, J.; Qiu, W.; Wang, J.; Fang, Y. An ensemble spatiotemporal model for predicting PM2.5 concentrations. Int. J. Environ. Res. Public Health 2017, 14, 549. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Zou, B.; Li, S.; Zhang, H.; Qin, K. Prediction of PM2.5 concentrations at unsampled points using multiscale geographically and temporally weighted regression. Environ. Pollut. 2021, 284, 117116. [Google Scholar] [CrossRef]
- Alimissis, A.; Philippopoulos, K.; Tzanis C, G. Spatial estimation of urban air pollution with the use of artificial neural network models. Atmos. Environ. 2018, 191, 205–213. [Google Scholar] [CrossRef]
- Bahari, R.A.; Abbaspour, R.A.; Pahlavani, P. Prediction of PM2.5 concentrations using temperature inversion effects based on an artificial neural network. In Proceedings of the ISPRS International Conference of Geospatial Information Research, Tehran, Iran, 15–17 November 2014; Volume 15, p. 17. [Google Scholar]
- Feng, X.; Li, Q.; Zhu, Y.; Hou, J.; Jin, L.; Wang, J. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Valentini, G. Ensemble Methods: A Review, in Advances in Machine Learning and Data Mining for Astronomy; Chapman & Hall Data Mining and Knowledge Discovery Series; CRC Press: London, UK, 2012; Volume 26, pp. 563–594. [Google Scholar]
- Calkins, C.; Ge, C.; Wang, J.; Anderson, M.; Yang, K. Effects of meteorological conditions on sulfur dioxide air pollution in the North China plain during winters of 2006–2015. Atmos. Environ. 2016, 147, 296–309. [Google Scholar] [CrossRef]
- Harishkumar, K.; Yogesh, K.; Gad, I. Forecasting air pollution particulate matter (PM2.5) using machine learning regression models. Procedia Comput. Sci. 2020, 171, 2057–2066. [Google Scholar]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46 (Suppl. 1), 234–240. [Google Scholar] [CrossRef]
- Ningxia Government. Overview of Ningxia. Available online: cn.nxcan.com/index.php?case=archive&act=show&aid=55 (accessed on 6 July 2015).
- Ningxia Government. Ningxia Meteorology. Available online: https://sthjt.nx.gov.cn (accessed on 8 August 2014).
- Sergey, I.; Christian, S. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Bishop, C. Neural Networks for Pattern Recognition, 3rd ed.; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Scikit-Learn: Machine Learning in Python. Available online: https://scikit-learn.org/stable/ (accessed on 9 September 2016).
- Hastie, T.; Tibshirani, R.; Friedman, J. The elements of statistical learning. J. R. Stat. Soc. 2004, 167, 192. [Google Scholar]
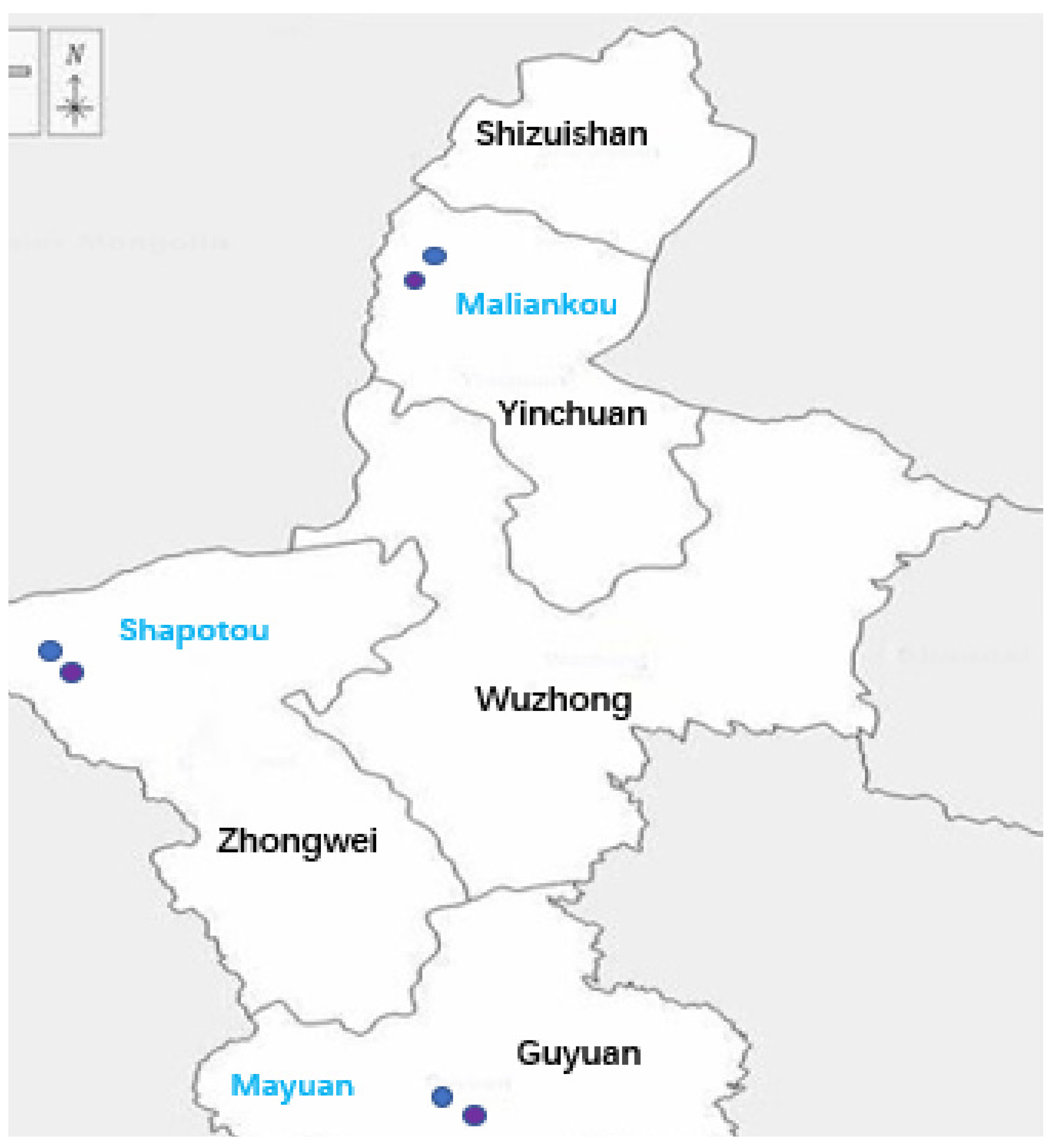
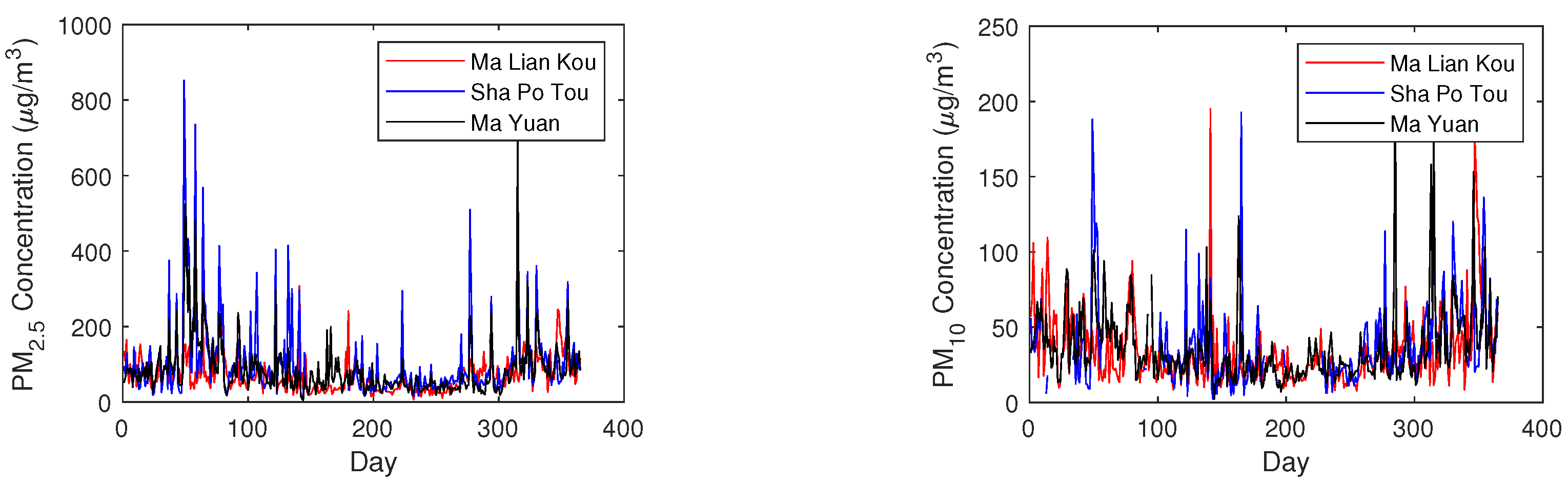




| Air Stations | Coordinates | |
|---|---|---|
| 1 | Ma Lian Kou | 105.95, 38.60 |
| 2 | Sha Po Tou | 105.02, 37.45 |
| 3 | Ma Yuan | 106.23, 36.14 |
| Air Pollutants | Station | Mean | Median | Range | SD |
|---|---|---|---|---|---|
| Ma Lian Kou | 0.88 | 0.70 | 0.67∼40.8 | 2.1 | |
| CO | Sha Po Tou | 0.62 | 0.52 | 0.01∼41.0 | 1.7 |
| Ma Yuan | 0.91 | 0.74 | 0.01∼45.0 | 1.90 | |
| Ma Lian Kou | 13.8 | 12.2 | 1.63∼53.6 | 7.3 | |
| Sha Po Tou | 16.6 | 14.5 | 1.8∼57.0 | 10.7 | |
| Ma Yuan | 21.4 | 20.3 | 4.4∼60.0 | 9.3 | |
| Ma Lian Kou | 95.6 | 90.1 | 13.4∼213 | 36.2 | |
| Sha Po Tou | 79.1 | 75.5 | 11.0∼189 | 38.8 | |
| Ma Yuan | 57.9 | 54.8 | 13.8∼137.4 | 26.8 | |
| Ma Lian Kou | 33.2 | 27.1 | 6.1∼195.2 | 22.4 | |
| Sha Po Tou | 35.1 | 28.0 | 2.1∼192.8 | 27.0 | |
| Ma Yuan | 34.3 | 29.0 | 2.3∼224.5 | 22.8 | |
| Ma Lian Kou | 75.4 | 62.6 | 3∼696 | 53.1 | |
| Sha Po Tou | 100.8 | 71.7 | 5.2∼1313.3 | 112.2 | |
| Ma Yuan | 86.5 | 71.9 | 5.4∼874.2 | 76.3 | |
| Ma Lian Kou | 31.2 | 20.3 | 2.0∼182.0 | 27.0 | |
| Sha Po Tou | 15.2 | 11.0 | 1.73∼91.6 | 12.1 | |
| Ma Yuan | 10.1 | 9.0 | 2.1∼62.8 | 5.3 |
| Meteorological | Station | Mean | Median | Range | SD |
|---|---|---|---|---|---|
| Variables | |||||
| Ma Lian Kou | 14.2 | 15.9 | −13.4∼40.2 | 14.7 | |
| Mean GST (°C) | Sha Po Tou | 13.7 | 15.5 | −12.9∼39.1 | 13.1 |
| Ma Yuan | 10.8 | 10.8 | −14.6∼34.5 | 11.2 | |
| Ma Lian Kou | 48.9 | 48.0 | 14.0∼94 | 15.40 | |
| Max RHU | Sha Po Tou | 52.6 | 52 | 19∼91 | 14.7 |
| Ma Yuan | 53.6 | 53 | 12∼93 | 17.3 | |
| Ma Lian Kou | 10.9 | 12.6 | −15.4∼30.3 | 11.4 | |
| Mean TEM (°C) | Sha Po Tou | 10.6 | 12.7 | −17.4∼29.8 | 11.0 |
| Ma Yuan | 8.4 | 8.8 | −18.1∼27.5 | 9.8 | |
| Ma Lian Kou | 40.4 | 37 | 17∼116 | 15.1 | |
| Mean WIN (m/s) | Sha Po Tou | 57.1 | 56 | 17∼150 | 20.9 |
| Ma Yuan | 55.0 | 52.5 | 25∼119 | 15.2 | |
| Ma Lian Kou | 7.9 | 8.3 | 0∼13.6 | 3.6 | |
| SSD (hr) | Sha Po Tou | 8.4 | 8.8 | 0∼13.9 | 3.5 |
| Ma Yuan | 6.9 | 7.9 | 0∼13.7 | 3.9 |
| 0.05 | 0.13 *** | *** | 0.15 *** | 0.07 | 0.16 *** | |
| 0.08 ** | 0.66 *** | *** | 0.52 *** | 0.27 *** | 0.56 *** | |
| −0.15 *** | −0.42 *** | 0.87 *** | −0.28 *** | −0.18 *** | −0.49 *** | |
| 0.05 | 0.42 *** | −0.32 *** | 0.57 *** | 0.44 *** | 0.39 *** | |
| 0.04 | 0.19 *** | −0.24 *** | 0.42 *** | 0.56 *** | 0.22 *** | |
| 0.12 *** | 0.57 *** | −0.46 *** | 0.45 *** | 0.28 *** | 0.69 *** | |
| −0.17 *** | −0.53 *** | 0.75 *** | −0.38 *** | −0.28 *** | −0.64 *** | |
| 0.04 | 0.25 *** | −0.20 *** | 0.20 *** | −0.09 | −0.04 | |
| −0.07 | −0.31 *** | 0.46 *** | −0.30 *** | −0.20 *** | −0.22 *** | |
| −0.17 *** | −0.52 *** | 0.73 *** | −0.36 *** | −0.26 *** | −0.64 *** | |
| −0.31 | −0.33 *** | 0.08 | −0.13 *** | 0.07 | −0.20 *** |
| Air Pollutants | Influential Factors |
|---|---|
| , , , , , | |
| , , , , , | |
| , , , , , | |
| , | |
| , , , , , |
| Air | Statistical | Ma Lian Kou | Sha Po Tou | Ma Yuan | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pollutants | Index | RMSE | MAE | MAPE | RMSE | MAE | MAPE | RMSE | MAE | MAPE | |||
| DTR | 0.70 | 0.25 | 0.21 | 0.31 | 0.61 | 0.47 | 0.33 | 0.38 | 0.46 | 0.63 | 0.51 | 0.66 | |
| CO | FFANN-BP | 0.71 | 0.24 | 0.18 | 0.31 | 0.70 | 0.23 | 0.16 | 0.19 | 0.61 | 0.32 | 0.24 | 0.33 |
| RFR | 0.90 | 0.15 | 0.12 | 0.20 | 0.91 | 0.14 | 0.10 | 0.11 | 0.62 | 0.45 | 0.20 | 0.21 | |
| DTR | 0.66 | 6.2 | 5.4 | 0.47 | 0.51 | 8.0 | 6.7 | 0.28 | 0.47 | 7.8 | 6.4 | 0.25 | |
| FFANN-BP | 0.72 | 4.5 | 3.4 | 0.29 | 0.76 | 5.3 | 4.2 | 0.17 | 0.75 | 5.3 | 4.4 | 0.17 | |
| RFR | 0.95 | 1.8 | 1.4 | 0.12 | 0.83 | 4.3 | 3.4 | 0.14 | 0.87 | 4.0 | 3.2 | 0.13 | |
| DTR | 0.54 | 23.9 | 16.1 | 0.17 | 0.70 | 16.3 | 13.4 | 0.24 | 0.52 | 20.2 | 16.5 | 0.37 | |
| FFANN-BP | 0.67 | 20.3 | 12.2 | 0.12 | 0.86 | 12.1 | 9.1 | 0.16 | 0.89 | 9.7 | 7.8 | 0.16 | |
| RFR | 0.89 | 12.2 | 8.6 | 0.09 | 0.95 | 7.3 | 5.6 | 0.11 | 0.94 | 8.4 | 6.8 | 0.15 | |
| DTR | 0.73 | 21.2 | 16.3 | 0.25 | 0.72 | 99.1 | 42.3 | 0.32 | 0.67 | 45.4 | 23.0 | 0.23 | |
| FFANN-BP | 0.81 | 18.1 | 13.9 | 0.21 | 0.44 | 126.7 | 50.5 | 0.35 | 0.76 | 43.0 | 22.6 | 0.23 | |
| RFR | 0.96 | 9.2 | 6.1 | 0.09 | 0.97 | 57.9 | 25.3 | 0.26 | 0.92 | 30.4 | 13.2 | 0.18 | |
| DTR | 0.82 | 8.6 | 6.5 | 0.22 | 0.79 | 17.8 | 12.4 | 0.32 | 0.88 | 8.6 | 6.3 | 0.20 | |
| FFANN-BP | 0.64 | 13.7 | 9.4 | 0.30 | 0.90 | 12.8 | 8.8 | 0.26 | 0.81 | 10.6 | 6.9 | 0.21 | |
| RFR | 0.98 | 3.5 | 2.4 | 0.09 | 0.94 | 12.2 | 7.7 | 0.23 | 0.97 | 4.9 | 3.9 | 0.14 | |
| DTR | 0.81 | 15.5 | 10.4 | 0.42 | 0.51 | 23.8 | 16.3 | 0.55 | 0.86 | 4.2 | 2.9 | 0.27 | |
| FFANN-BP | 0.76 | 16.3 | 11.7 | 0.55 | 0.83 | 14.5 | 9.6 | 0.34 | 0.61 | 8.8 | 4.5 | 0.38 | |
| RFR | 0.99 | 4.5 | 3.4 | 0.18 | 0.92 | 11.0 | 5.8 | 0.17 | 0.98 | 1.8 | 1.3 | 0.15 | |
| Pollutants | Index | Mean GST | Mean RHU | SSD | ||||
|---|---|---|---|---|---|---|---|---|
| CO | DTR | 0.01 | 0.0 | 0.0 | 0.99 | |||
| RFR | 0.16 | 0.1 | 0.12 | 0.63 | ||||
| DTR | 0.19 | 0.12 | 0.07 | 0.08 | 0.55 | |||
| RFR | 0.19 | 0.08 | 0.06 | 0.09 | 0.58 | |||
| DTR | 0.61 | 0.14 | 0.07 | 0.09 | 0.1 | |||
| RFR | 0.64 | 0.14 | 0.07 | 0.08 | 0.08 | |||
| DTR | 0.03 | 0.04 | 0.03 | 0.33 | 0.01 | 0.57 | ||
| RFR | 0.03 | 0.1 | 0.03 | 0.24 | 0.02 | 0.58 | ||
| DTR | 0.02 | 0.02 | 0.02 | 0.16 | 0.05 | 0.73 | ||
| RFR | 0.03 | 0.04 | 0.03 | 0.19 | 0.02 | 0.69 | ||
| DTR | 0.17 | 0.06 | 0.05 | 0.66 | 0.04 | 0.03 | ||
| RFR | 0.16 | 0.05 | 0.03 | 0.69 | 0.04 | 0.03 |
| FFANN-BP | DTR | RFR | |
|---|---|---|---|
| 0.058 | 0.002 | 0.032 | |
| 0.242 | 0.002 | 0.034 | |
| 0.303 | 0.002 | 0.034 | |
| 0.349 | 0.002 | 0.04 | |
| 0.206 | 0.002 | 0.038 | |
| 0.364 | 0.002 | 0.038 |
| Mean | Variance | |||
|---|---|---|---|---|
| 0.65 | 0.14 | 0.42 | 0.85 | |
| 4.4 | 0.73 | 3.1 | 6.8 | |
| 85.8 | 11.7 | 60.7 | 100.9 | |
| 33.9 | 8.5 | 28.8 | 34.1 | |
| 135.9 | 22.8 | 91.8 | 156.9 | |
| 1.9 | 0.8 | 1.2 | 6.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, W.; Qie, X. Prediction of Air Pollutant Concentrations via RANDOM Forest Regressor Coupled with Uncertainty Analysis—A Case Study in Ningxia. Atmosphere 2022, 13, 960. https://doi.org/10.3390/atmos13060960
Ding W, Qie X. Prediction of Air Pollutant Concentrations via RANDOM Forest Regressor Coupled with Uncertainty Analysis—A Case Study in Ningxia. Atmosphere. 2022; 13(6):960. https://doi.org/10.3390/atmos13060960
Chicago/Turabian StyleDing, Weifu, and Xueping Qie. 2022. "Prediction of Air Pollutant Concentrations via RANDOM Forest Regressor Coupled with Uncertainty Analysis—A Case Study in Ningxia" Atmosphere 13, no. 6: 960. https://doi.org/10.3390/atmos13060960
APA StyleDing, W., & Qie, X. (2022). Prediction of Air Pollutant Concentrations via RANDOM Forest Regressor Coupled with Uncertainty Analysis—A Case Study in Ningxia. Atmosphere, 13(6), 960. https://doi.org/10.3390/atmos13060960





