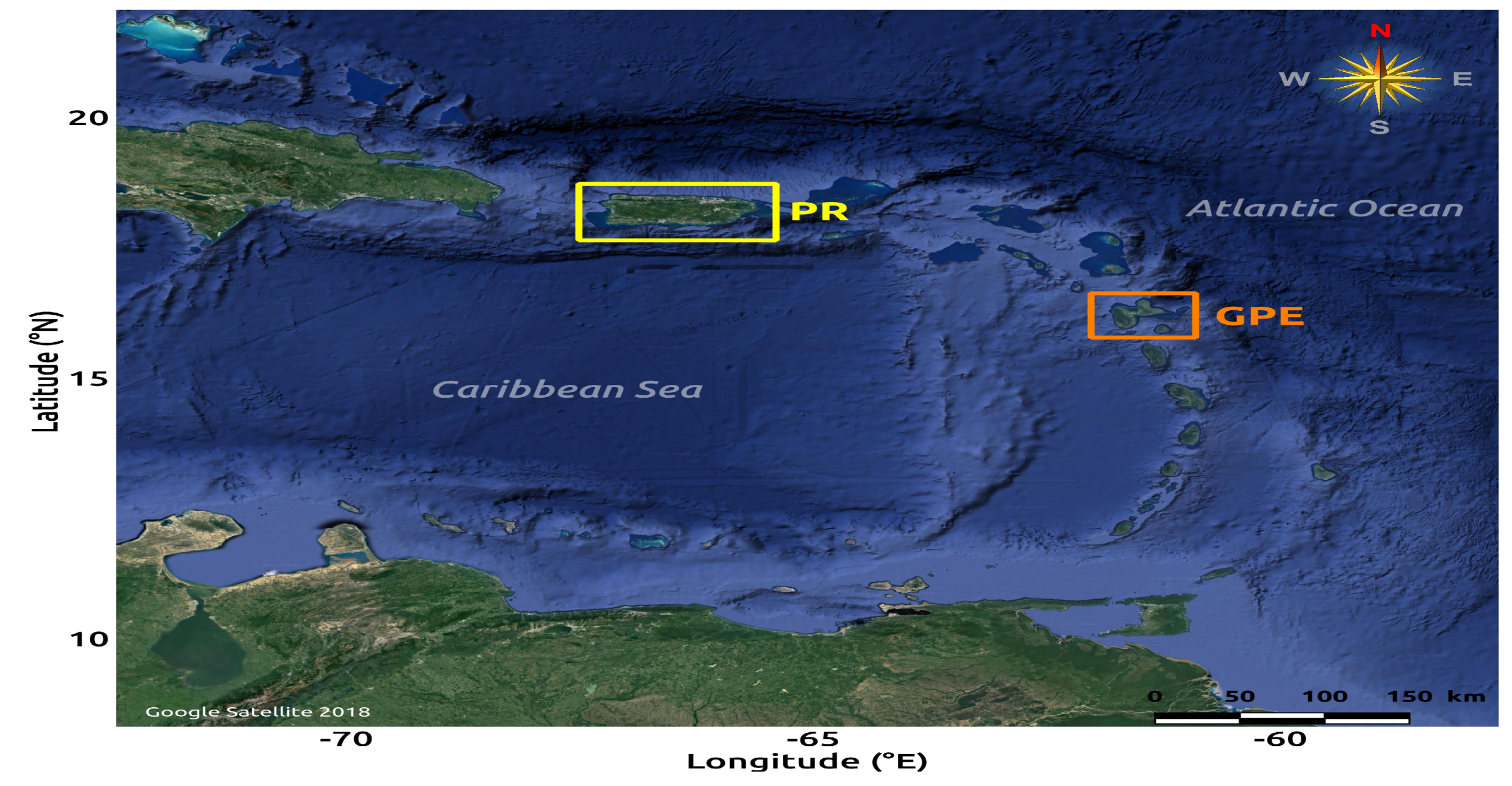
Figure 1.
Overview of the Caribbean area with the location of Guadeloupe archipelago (16.25° N, −61.58° E; GPE in orange) and Puerto-Rico (18.23° N, −66.50° E; PR in yellow).
Figure 1.
Overview of the Caribbean area with the location of Guadeloupe archipelago (16.25° N, −61.58° E; GPE in orange) and Puerto-Rico (18.23° N, −66.50° E; PR in yellow).
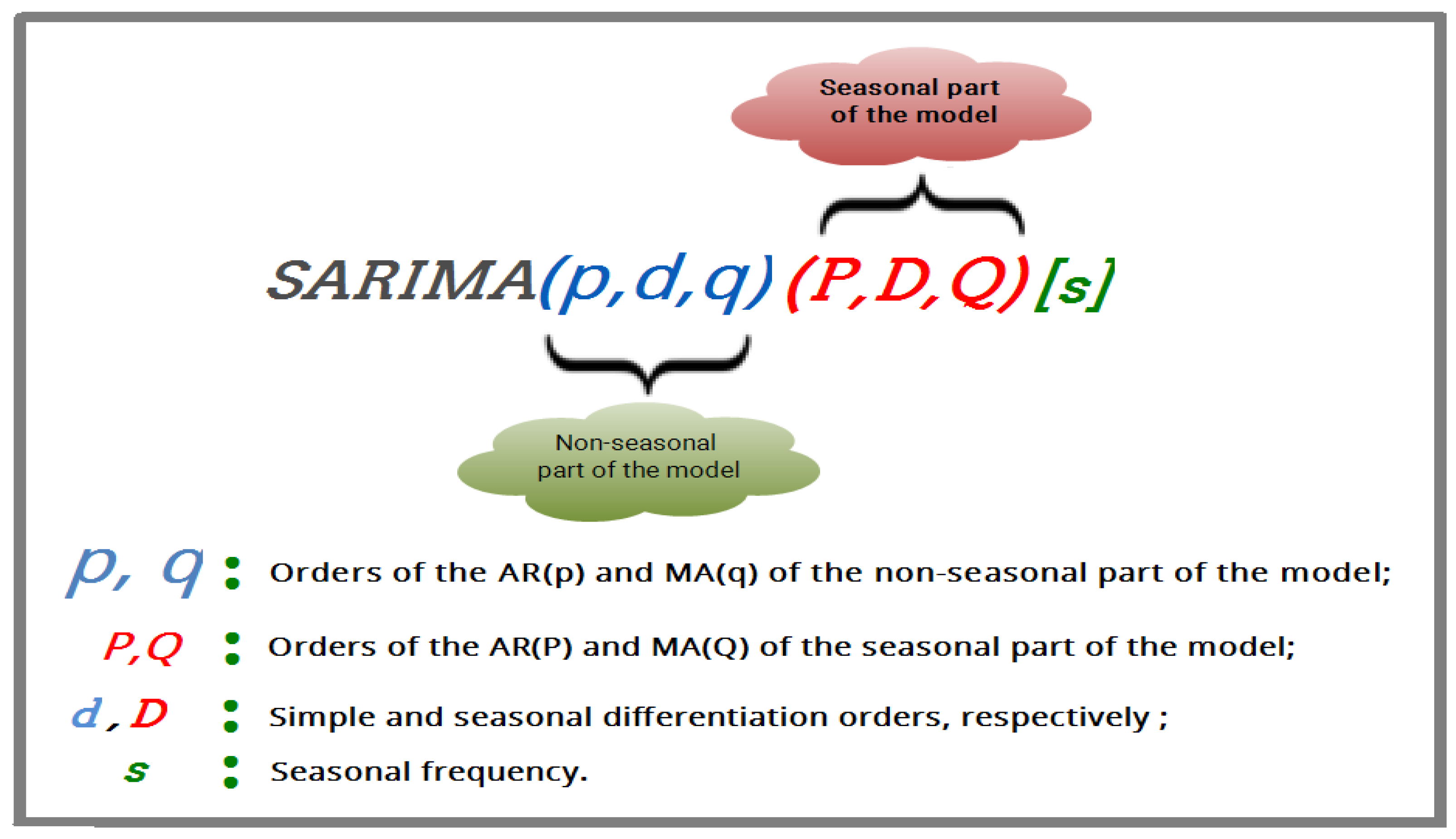
Figure 2.
Description of the Seasonal
ARIMA model [
53].
Figure 2.
Description of the Seasonal
ARIMA model [
53].
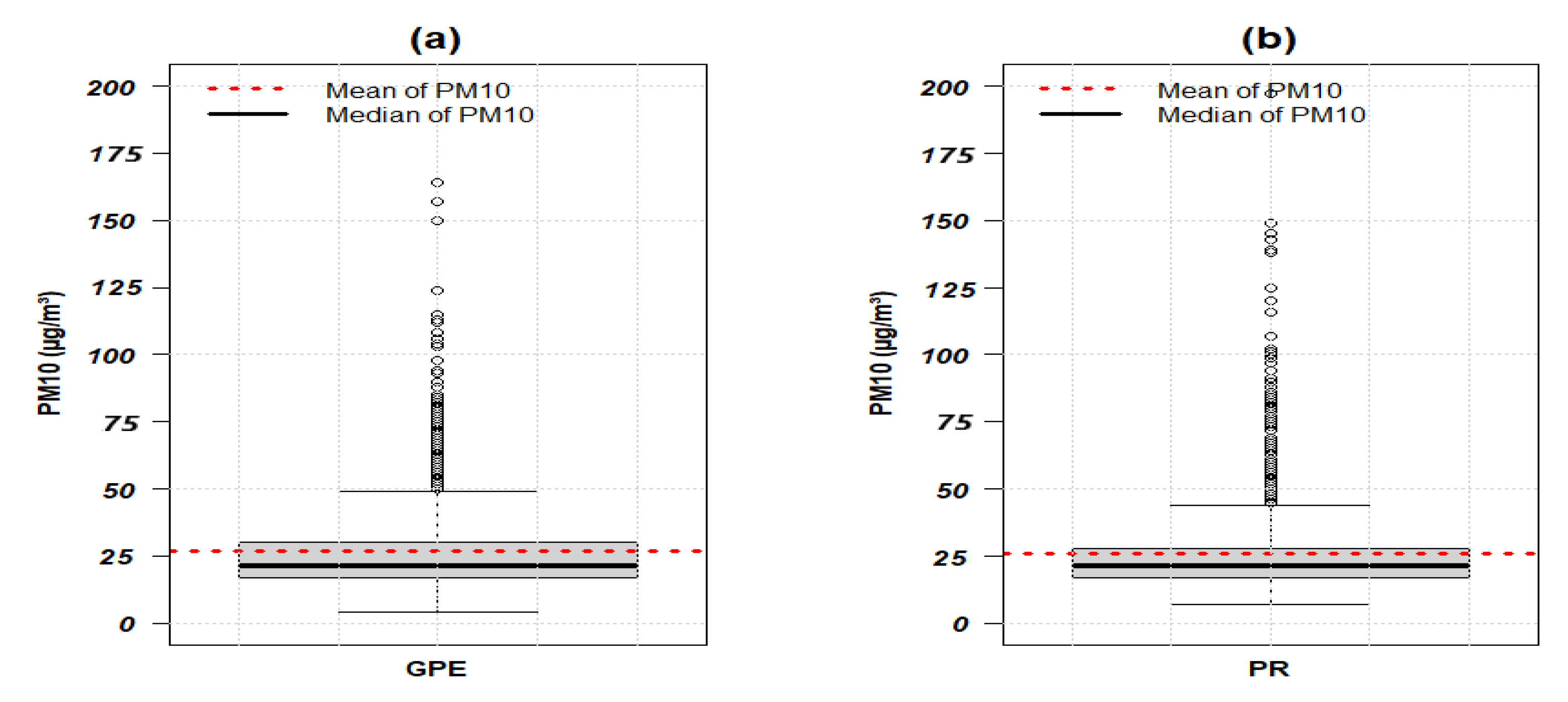
Figure 3.
Boxplot of PM10 data in GPE and PR from 2006 to 2010.
Figure 3.
Boxplot of PM10 data in GPE and PR from 2006 to 2010.
Figure 4.
Scatterplot and polynomial regression curve in the relationship where (a) (resp. (b)) PM10PR (resp. PM10GPE) is a function of PM10GPE (resp. PM10PR).
Figure 4.
Scatterplot and polynomial regression curve in the relationship where (a) (resp. (b)) PM10PR (resp. PM10GPE) is a function of PM10GPE (resp. PM10PR).
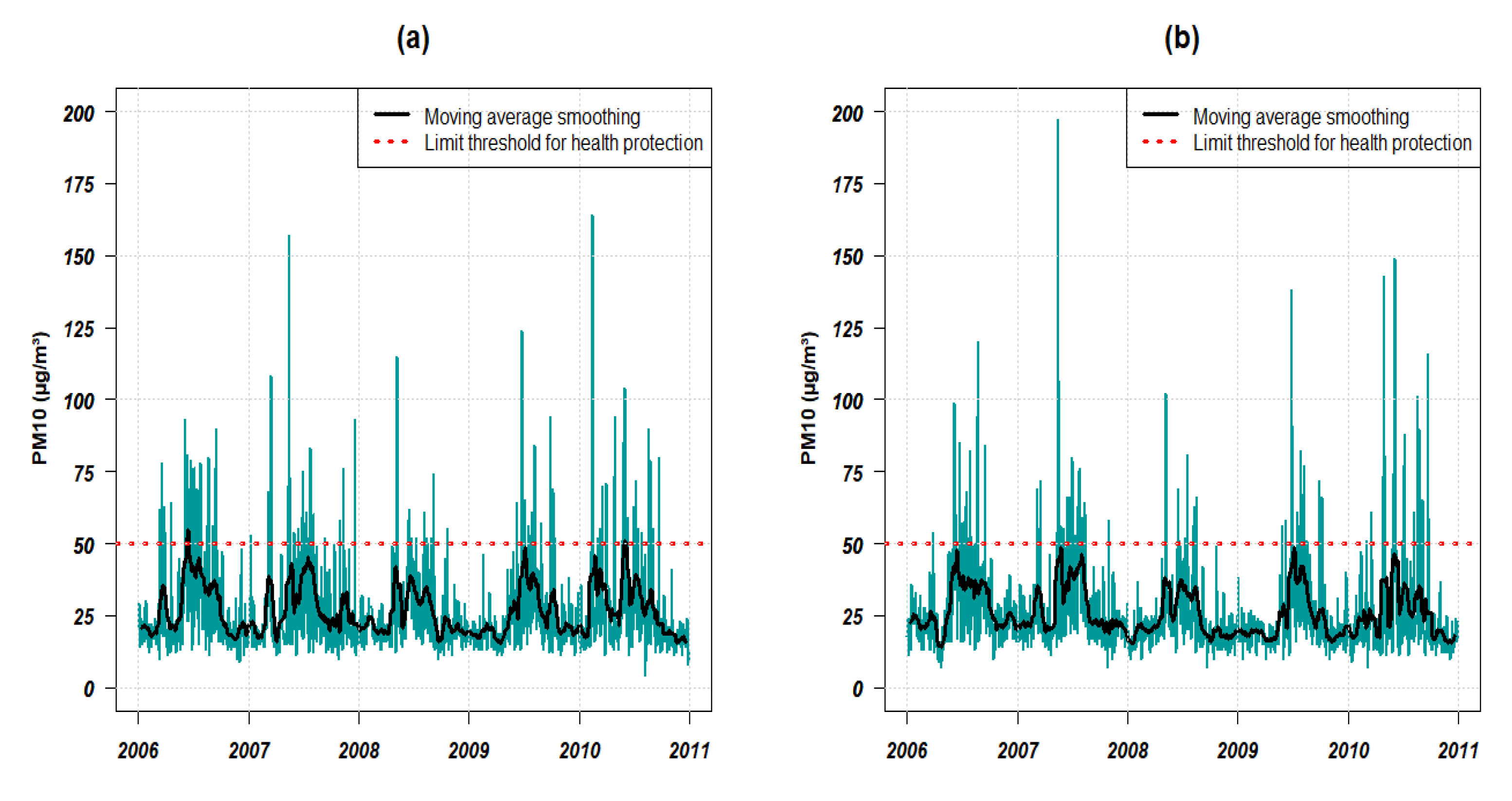
Figure 5.
Daily evolution of PM10 concentrations at (
a) GPE and (
b) PR from 2006 to 2010. The red horizontal dashed line shows the Air Quality Guideline for 24 h mean PM10 concentrations at 50
g/m
[
66]. The black curve represents the smoothed moving average series calculated by taking
.
Figure 5.
Daily evolution of PM10 concentrations at (
a) GPE and (
b) PR from 2006 to 2010. The red horizontal dashed line shows the Air Quality Guideline for 24 h mean PM10 concentrations at 50
g/m
[
66]. The black curve represents the smoothed moving average series calculated by taking
.
Figure 6.
Additive decomposition of the PM10 data series at (a) GPE and (b) PR from 2006 to 2010.
Figure 6.
Additive decomposition of the PM10 data series at (a) GPE and (b) PR from 2006 to 2010.
Figure 7.
Autocorrelation function (ACF) of PM10 data at (a) GPE and (b) PR from 2006 to 2010 before the Box–Cox transformation and the seasonal differentiation. The gray vertical lines of equation denote the offsets that are multiples of 365.
Figure 7.
Autocorrelation function (ACF) of PM10 data at (a) GPE and (b) PR from 2006 to 2010 before the Box–Cox transformation and the seasonal differentiation. The gray vertical lines of equation denote the offsets that are multiples of 365.
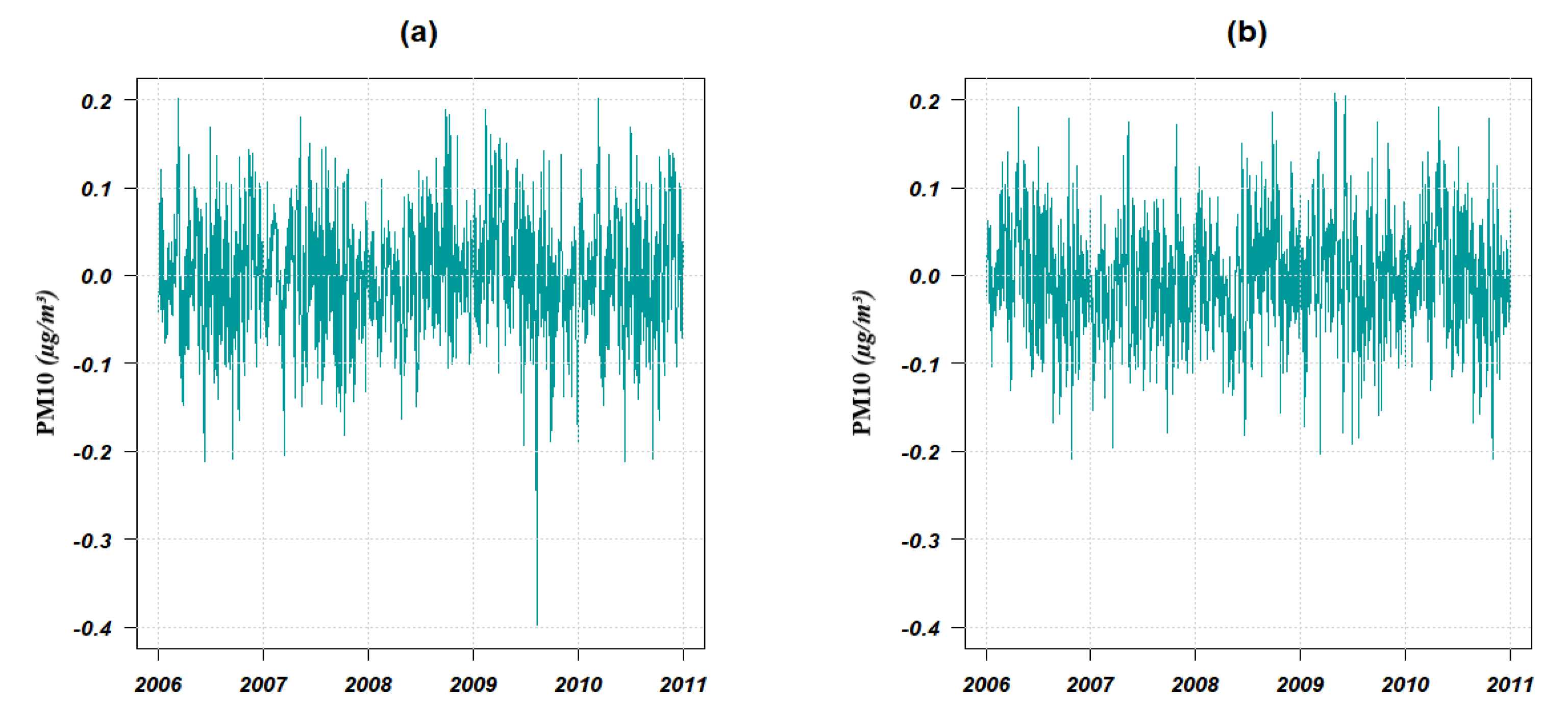
Figure 8.
Chronogram of PM10 data at (a) GPE and (b) PR from 2006 to 2010 after the Box–Cox transformation and the seasonal differentiation.
Figure 8.
Chronogram of PM10 data at (a) GPE and (b) PR from 2006 to 2010 after the Box–Cox transformation and the seasonal differentiation.
Figure 9.
Fitting of model computed values and transformed data of PM10 in (a) GPE and (b) PR.
Figure 9.
Fitting of model computed values and transformed data of PM10 in (a) GPE and (b) PR.
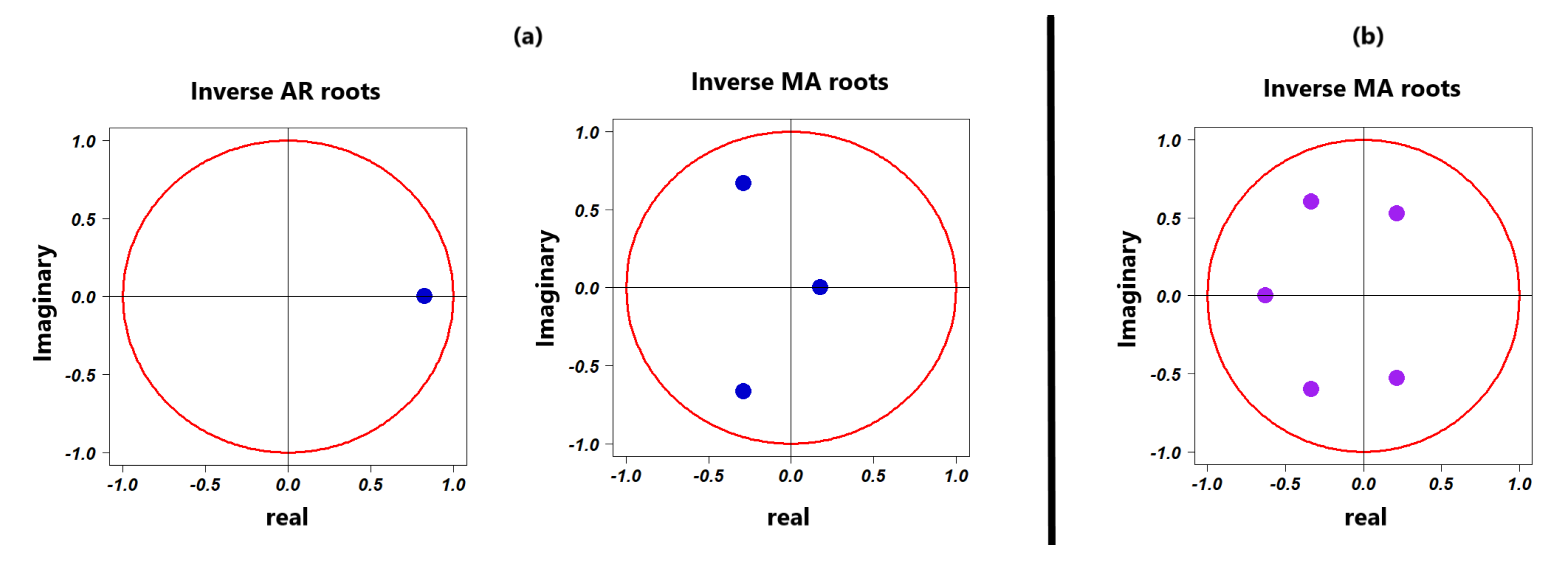
Figure 10.
Stationarity of the PM10 SARIMA model at (a) GPE and (b) PR from 2006 to 2010.
Figure 10.
Stationarity of the PM10 SARIMA model at (a) GPE and (b) PR from 2006 to 2010.
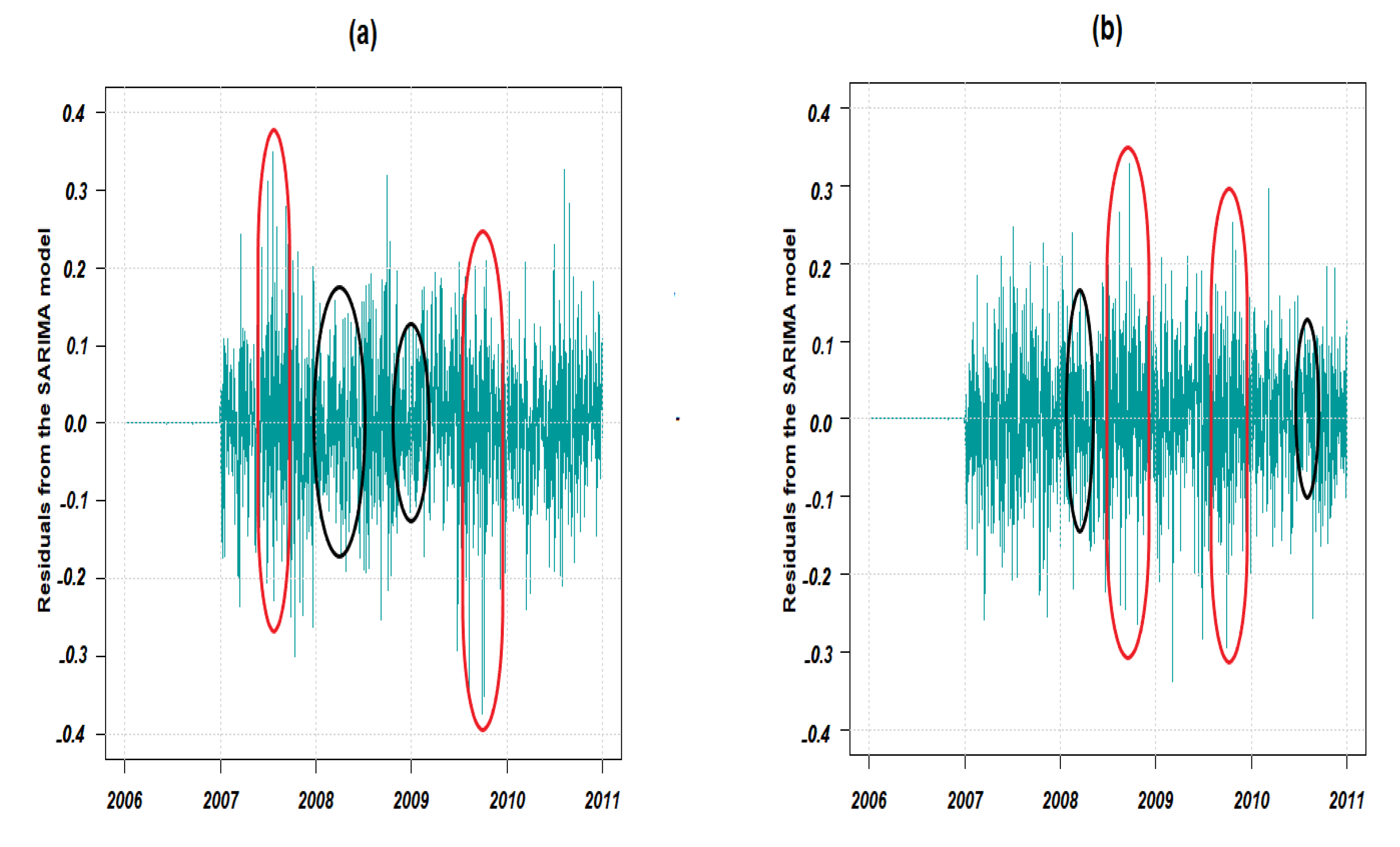
Figure 11.
Chronogram of PM10 SARIMA model residuals in (a) GPE and (b) PR from 2006 to 2010. Selected red and black portions denote locations with high and low residual error variability, respectively.
Figure 11.
Chronogram of PM10 SARIMA model residuals in (a) GPE and (b) PR from 2006 to 2010. Selected red and black portions denote locations with high and low residual error variability, respectively.
Figure 12.
Chronogram of squared residuals of the SARIMA model of PM10 in (a) GPE and (b) PR from 2006 to 2010.
Figure 12.
Chronogram of squared residuals of the SARIMA model of PM10 in (a) GPE and (b) PR from 2006 to 2010.
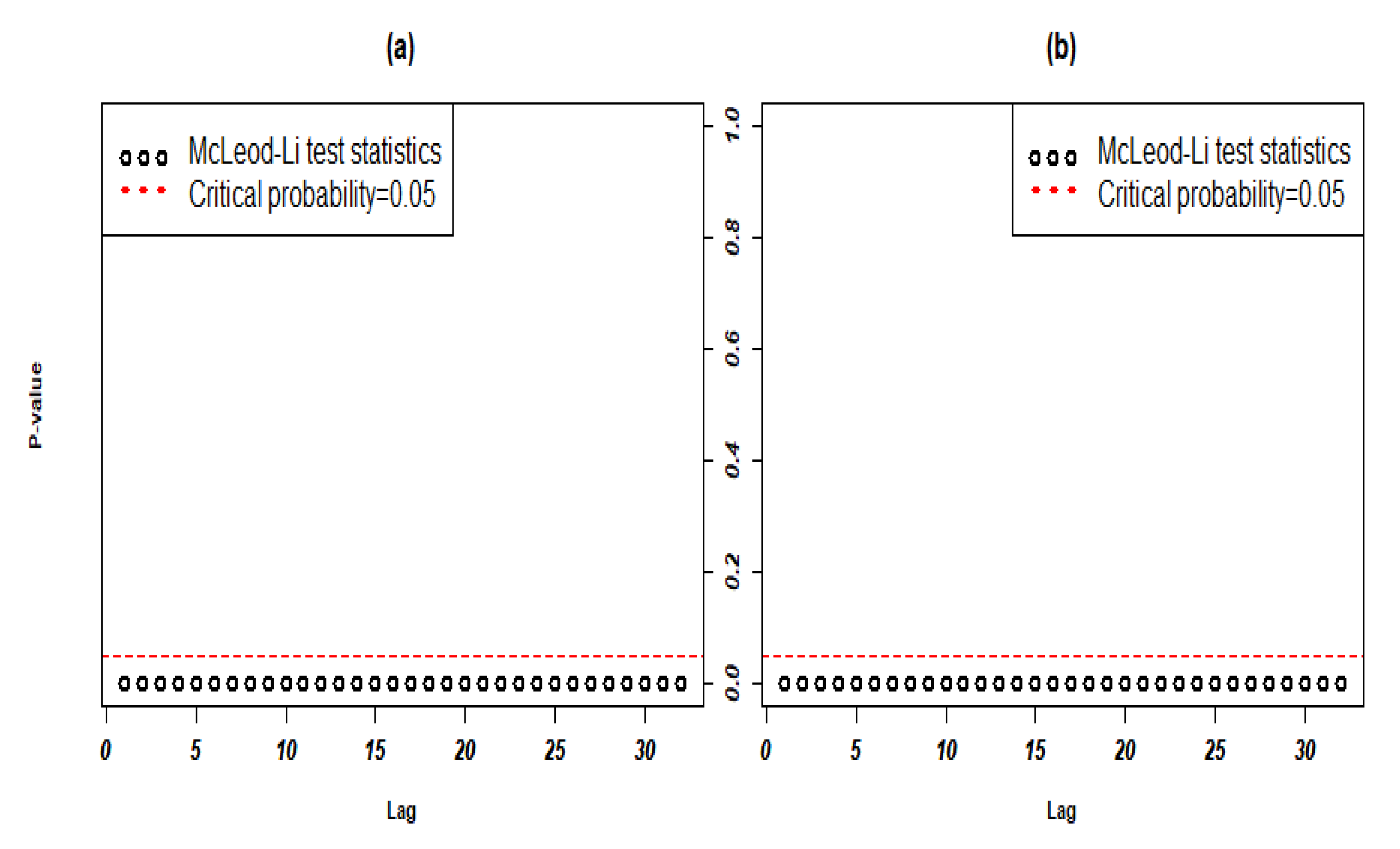
Figure 13.
McLeod–Li test for PM10 model residual errors in (a) GPE and (b) PR from 2006 to 2010.
Figure 13.
McLeod–Li test for PM10 model residual errors in (a) GPE and (b) PR from 2006 to 2010.
Figure 14.
Shape for distribution of PM10 model residuals at (a) GPE and (b) PR from 2006 to 2010. The red curve is the residual error density, while the green curve is the normal distribution.
Figure 14.
Shape for distribution of PM10 model residuals at (a) GPE and (b) PR from 2006 to 2010. The red curve is the residual error density, while the green curve is the normal distribution.
Figure 15.
Collinearity between variance of residuals from the SARIMA model and computed variance of the GARCH model in (a) GPE and (b) (PR).
Figure 15.
Collinearity between variance of residuals from the SARIMA model and computed variance of the GARCH model in (a) GPE and (b) (PR).
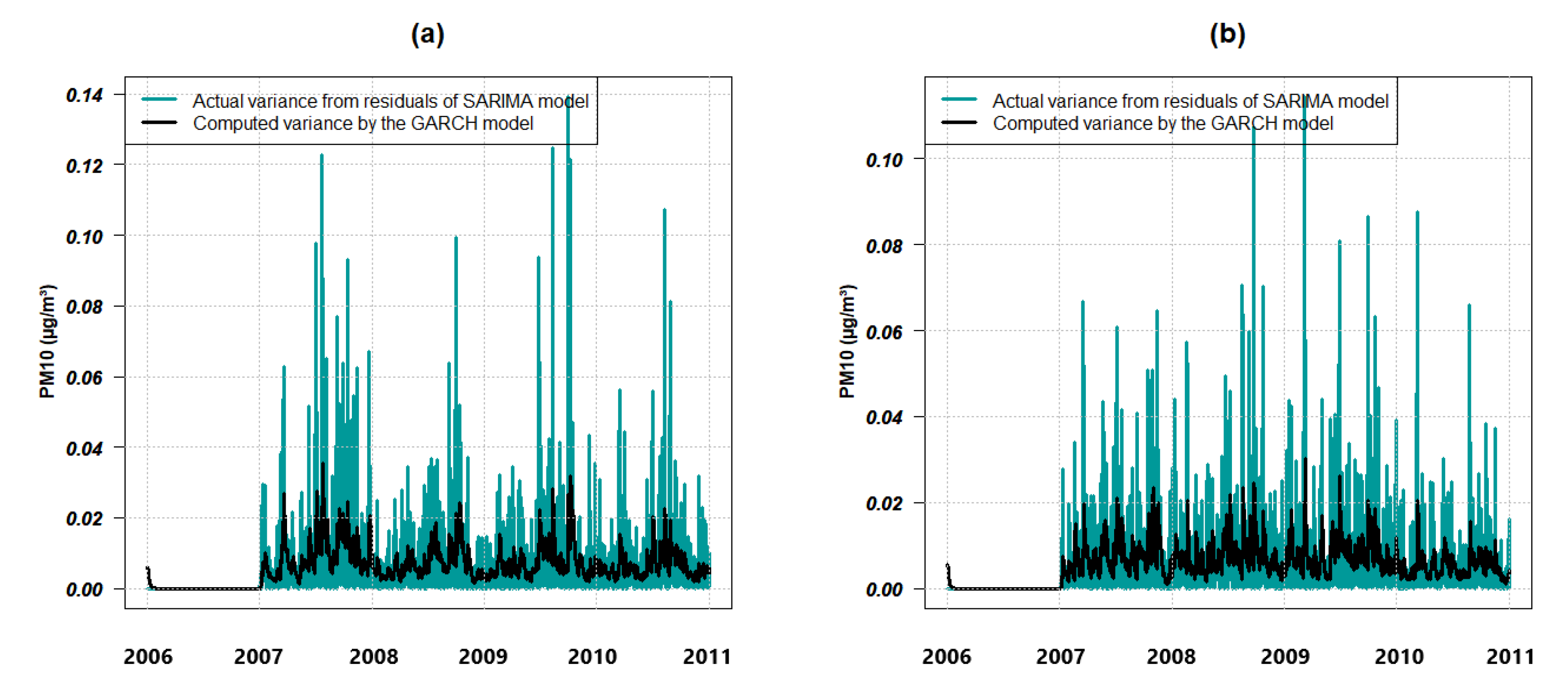
Figure 16.
Variance of residuals from the SARIMA model against computed variance by the GARCH model in (a) GPE and (b) PR.
Figure 16.
Variance of residuals from the SARIMA model against computed variance by the GARCH model in (a) GPE and (b) PR.
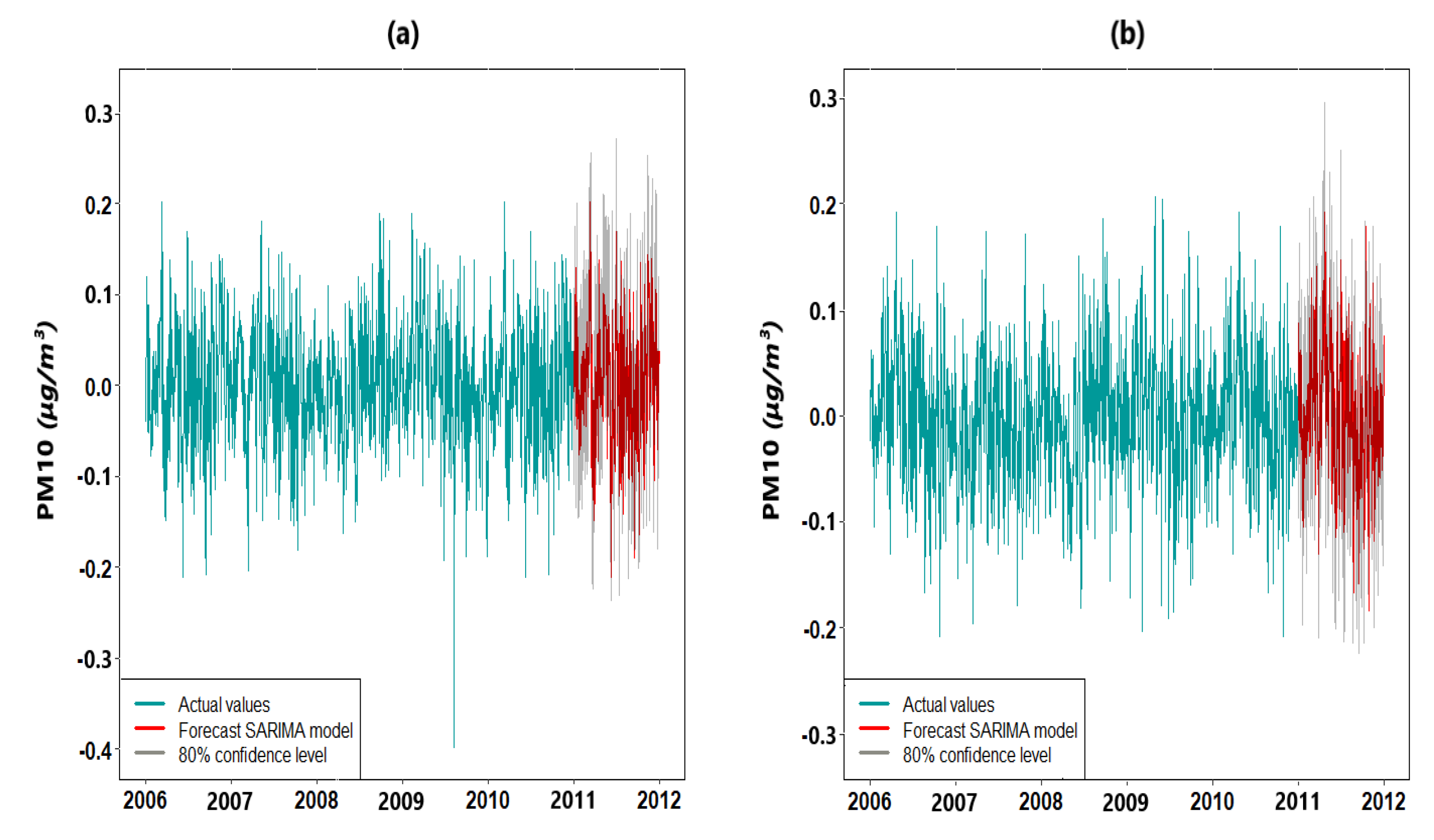
Figure 17.
Forecasts of PM10 data series in (a) GPE and (b) PR after the Box–Cox transformation and seasonal differentiation. The light gray band represents the 80% confidence interval. The red curves contained in this region are the forecasts beyond 2010.
Figure 17.
Forecasts of PM10 data series in (a) GPE and (b) PR after the Box–Cox transformation and seasonal differentiation. The light gray band represents the 80% confidence interval. The red curves contained in this region are the forecasts beyond 2010.
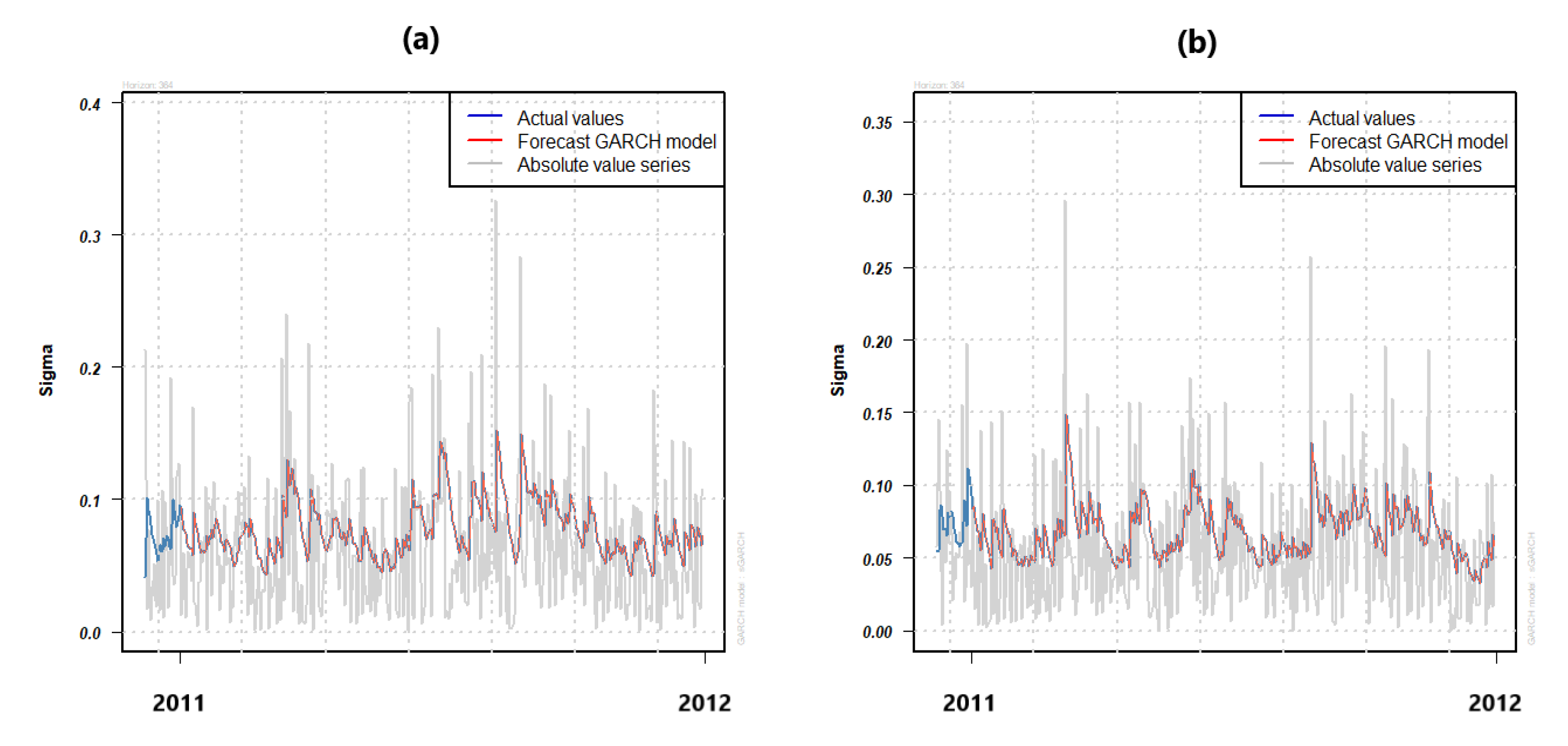
Figure 18.
365-day rolling forecast of PM10 variability from the GARCH model in (a) GPE and (b) PR.
Figure 18.
365-day rolling forecast of PM10 variability from the GARCH model in (a) GPE and (b) PR.
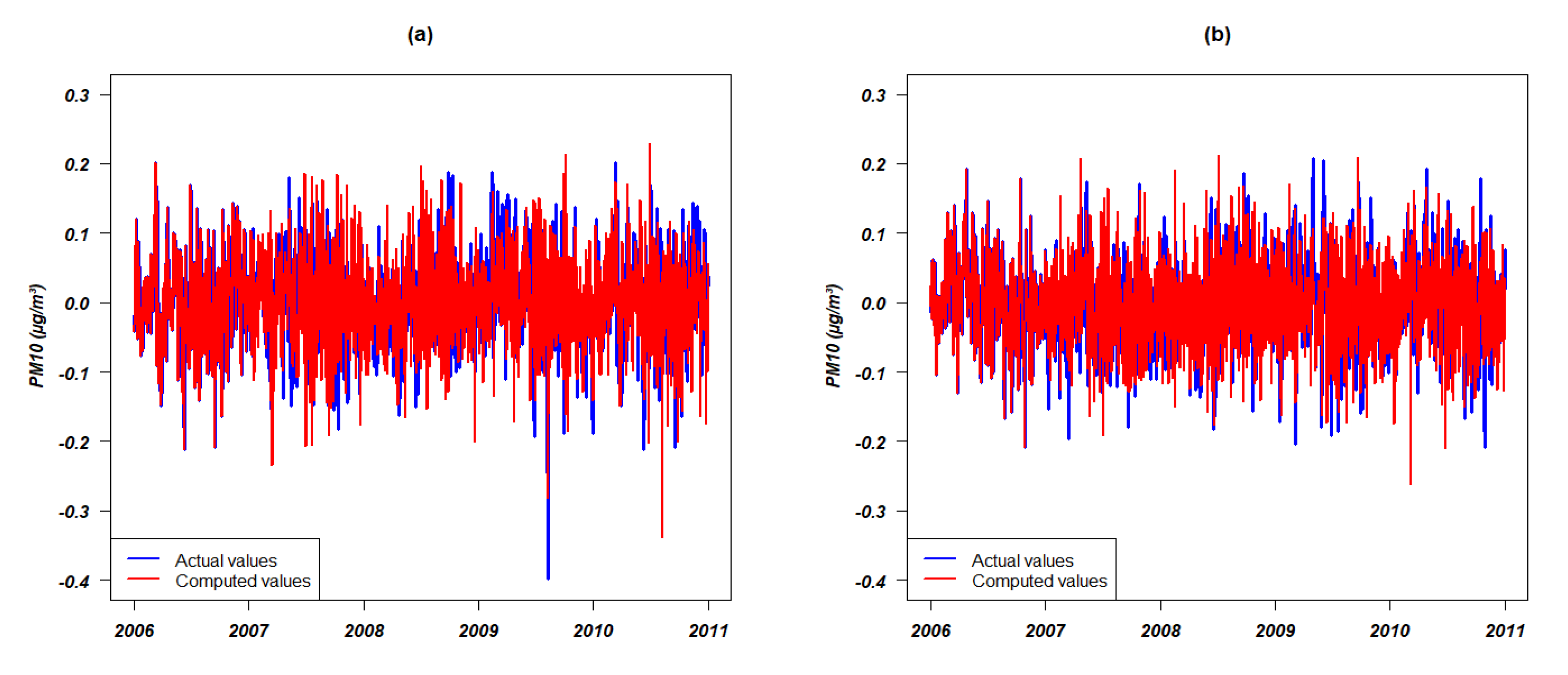
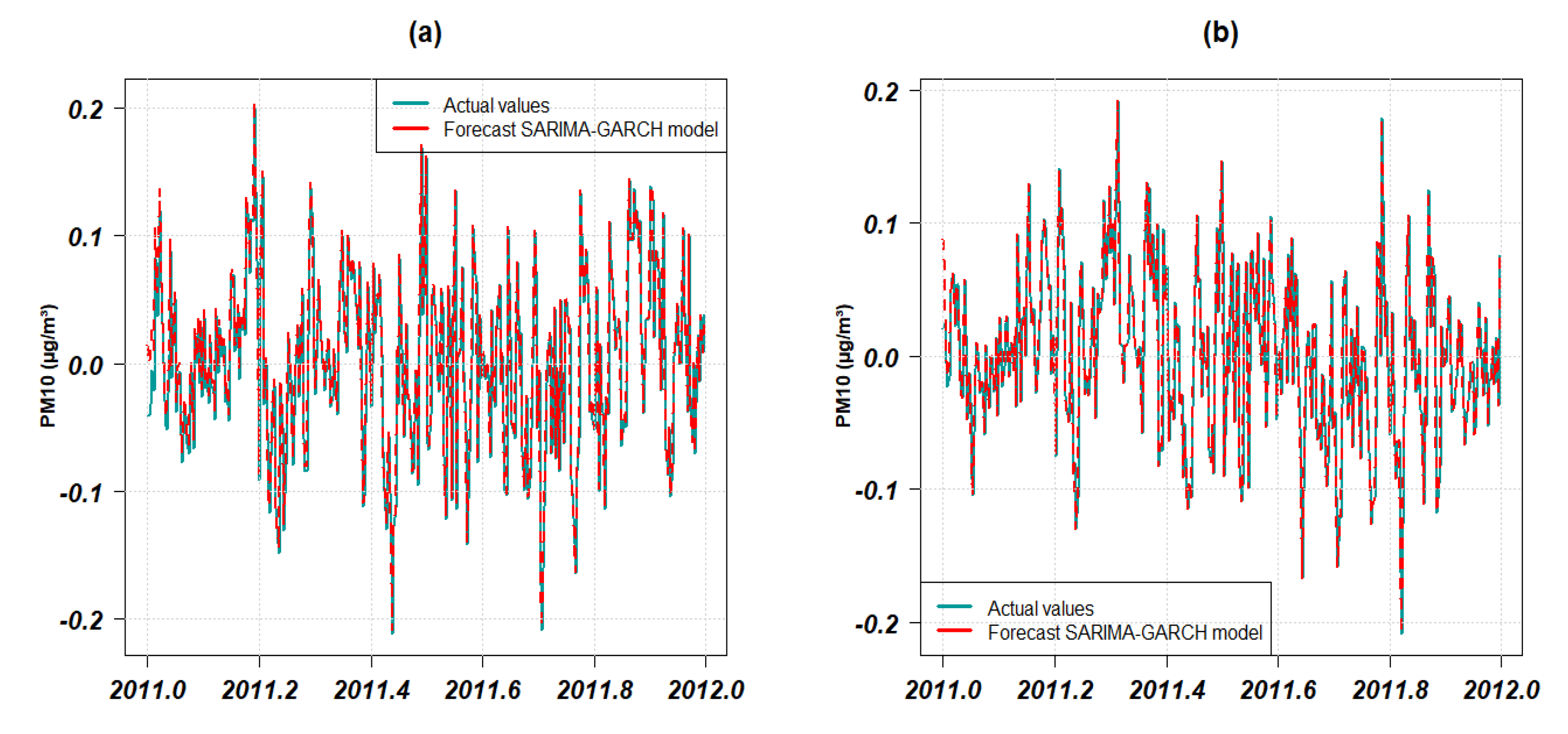
Figure 19.
Actual (blue curve) and predicted (red curve) values plot using the coupled SARIMA-GARCH model for PM10 data transformed in (a) GPE and (b) PR.
Figure 19.
Actual (blue curve) and predicted (red curve) values plot using the coupled SARIMA-GARCH model for PM10 data transformed in (a) GPE and (b) PR.
Table 1.
Some statistics of PM10 data in GPE and PR from 2006 to 2010.
Table 1.
Some statistics of PM10 data in GPE and PR from 2006 to 2010.
| Statistics | Before Correction | After Correction |
|---|
| | | |
|---|
| Minimum | | | | |
| First quartile | | | | |
| Median | | | | |
| Mean | | | | |
| Third quartile | | | | |
| Maximum | | | | |
| Missing data | | | − | − |
| Variance | | | | |
| Standard deviation | | | | |
| Coefficient of variation | | | | |
| Skewness | | | | |
| Kurtosis | | | | |
Table 2.
The results of the quadratic regression model.
Table 2.
The results of the quadratic regression model.
| Regression | Coefficients | Estimate | Std. Error | t Value | Pr(>|t|) |
|---|
| 1 | Intercept | | | | 3.71 × 10−14 |
| PM10GPE | | | | <2.00 × 10−16 |
| | | | × 10−4 |
| 2 | Intercept | | | | × 10−8 |
| PM10PR | | | | <2.00 × 10−16 |
| | | | × 10−15 |
Table 3.
Checking of the PM10 model information criteria in GPE and PR.
Table 3.
Checking of the PM10 model information criteria in GPE and PR.
| PM10GPE | PM10PR |
|---|
| Model | AIC | Model | AIC |
|---|
| | | |
| | | |
| | | |
| | | |
| −2965.30
| | −3114.69 |
Table 4.
Estimation and significance of PM10 model parameters in GPE and PR; C.I.: Confidence Interval.
Table 4.
Estimation and significance of PM10 model parameters in GPE and PR; C.I.: Confidence Interval.
| Model | Parameters | Estimate | Std. Error | t-Test | p-Value | Coefficient C.I. |
|---|
| 2.5% | 97.5% |
|---|
| | | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
Table 5.
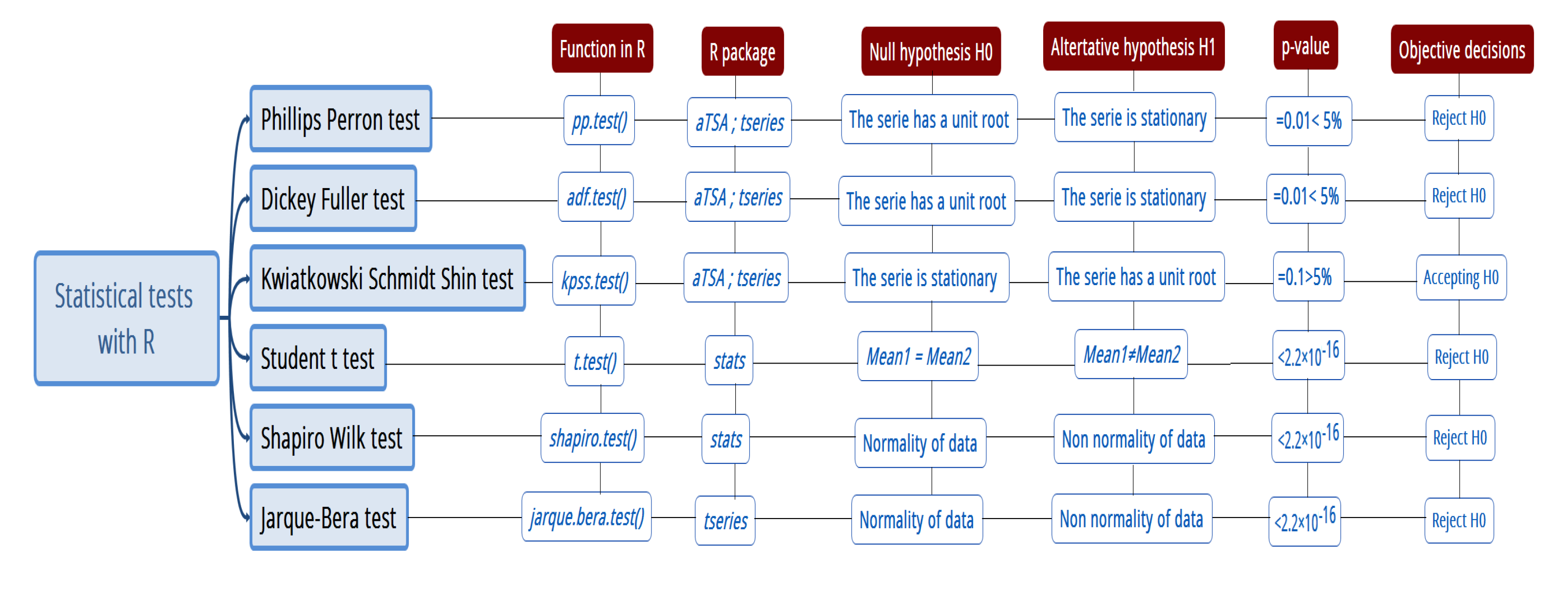
Normality, autocorrelation, and heteroskedasticity tests of residuals from the SARIMA model.
Table 5.
Normality, autocorrelation, and heteroskedasticity tests of residuals from the SARIMA model.
| | PM10GPE | PM10PR |
|---|
| Hypothesis Tests | Statistics | Df | p-Value | Statistics | Df | p-Value |
|---|
| Shapiro–Wilk | | NA | <2.2 | | NA | <2.2 |
| Jarque–Bera | | 2 | <2.2 | | 2 | <2.2 |
| ARCH LM-test | | 20 | <2.2 | | 20 | <3.0 |
Table 6.
Residual model information criteria for the PM10 process in GPE and PR.
Table 6.
Residual model information criteria for the PM10 process in GPE and PR.
| PM10GPE | PM10PR |
|---|
| Model | AIC | Model | AIC |
|---|
| | | |
| −3.3754 | | −3.8294 |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Table 7.
Residual model parameters from the process for PM10 at GPE and PR.
Table 7.
Residual model parameters from the process for PM10 at GPE and PR.
| | PM10GPE | PM10PR |
|---|
| Parameters | Estimate | Std. Error | t Value | Pr(>|t|) | Estimate | Std. Error | t Value | Pr(>|t|) |
|---|
| 8.652 | | | | 8.567 | | | |
| 1.622 | | | | 1.951 | | | |
| 8.368 | | | | 8.039 | | | |
Table 8.
Forecast accuracy of PM10 models in GPE and PR.
Table 8.
Forecast accuracy of PM10 models in GPE and PR.
| | PM10GPE | PM10PR |
|---|
| Models | | | MASE | | | | | MASE | | |
|---|
| SARIMA | 350 | | | | | 350 | | | | |
| GARCH | 365 | | | | | 365 | | | | |
| Coupled SARIMA-GARCH | 350 | | | | | 337 | | | | |
 was used. This function uses a variant of the Hyndman–Khandakar algorithm, which combines unit root tests, minimization, and the maximum likelihood estimator (MLE) to obtain an ARIMA model [53]. The orders d and D were obtained from the stationarity and periodicity criteria applied to the data series.
was used. This function uses a variant of the Hyndman–Khandakar algorithm, which combines unit root tests, minimization, and the maximum likelihood estimator (MLE) to obtain an ARIMA model [53]. The orders d and D were obtained from the stationarity and periodicity criteria applied to the data series.
![Atmosphere 13 00862 i002]()
 .
.