Evaluation of the Planetary Boundary Layer Height in China Predicted by the CMA-GFS Global Model
Abstract
1. Introduction
2. Data and Methods
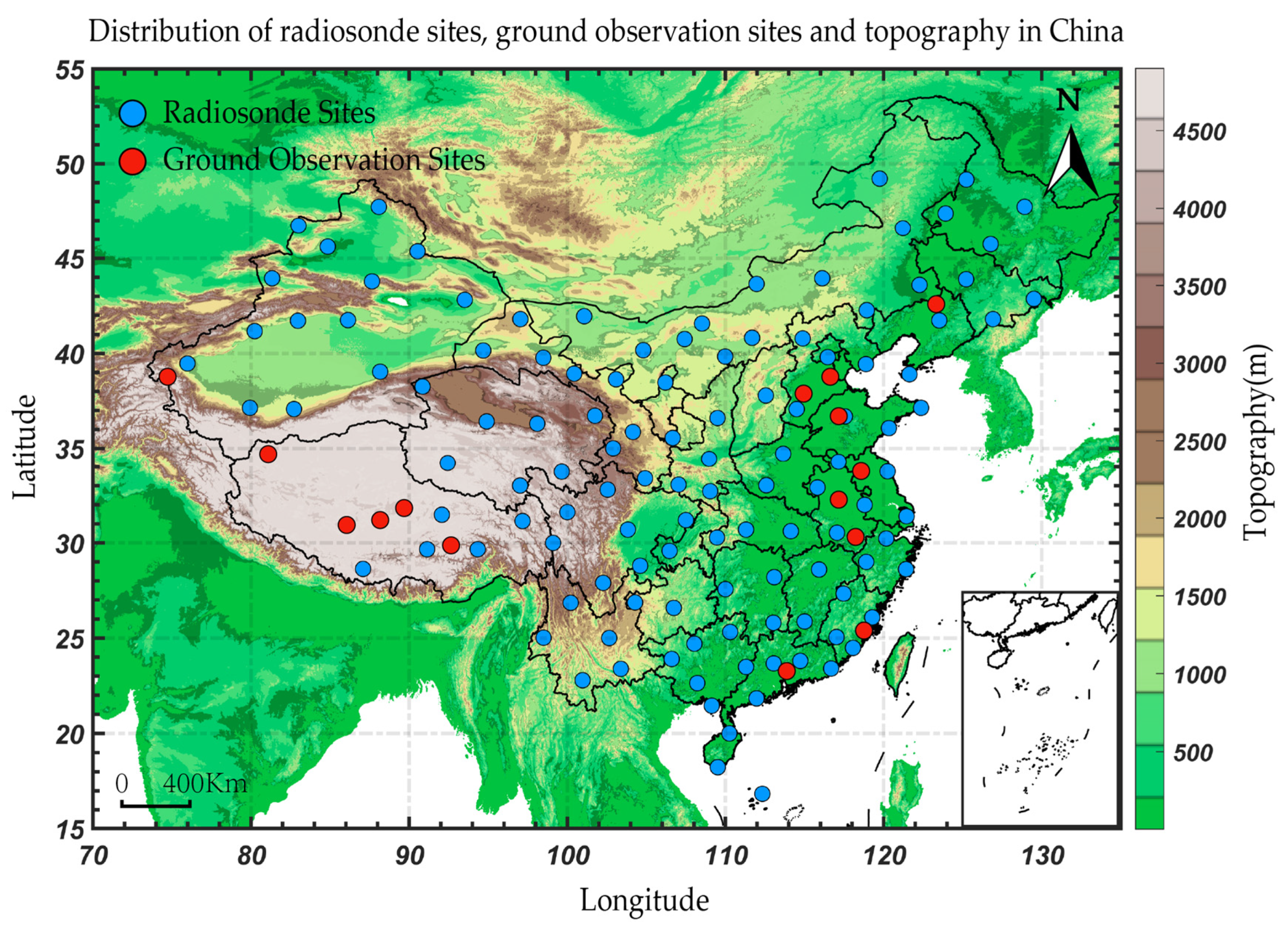
2.1. Data
2.2. PBLH Calculation Method
2.2.1. Bulk Richardson Method
2.2.2. Potential Temperature Gradient Method
3. Results
3.1. Seasonal Bias of the PBLH in the CMA-GFS Model
3.2. Diurnal Bias of the PBLH in the CMA-GFS Model
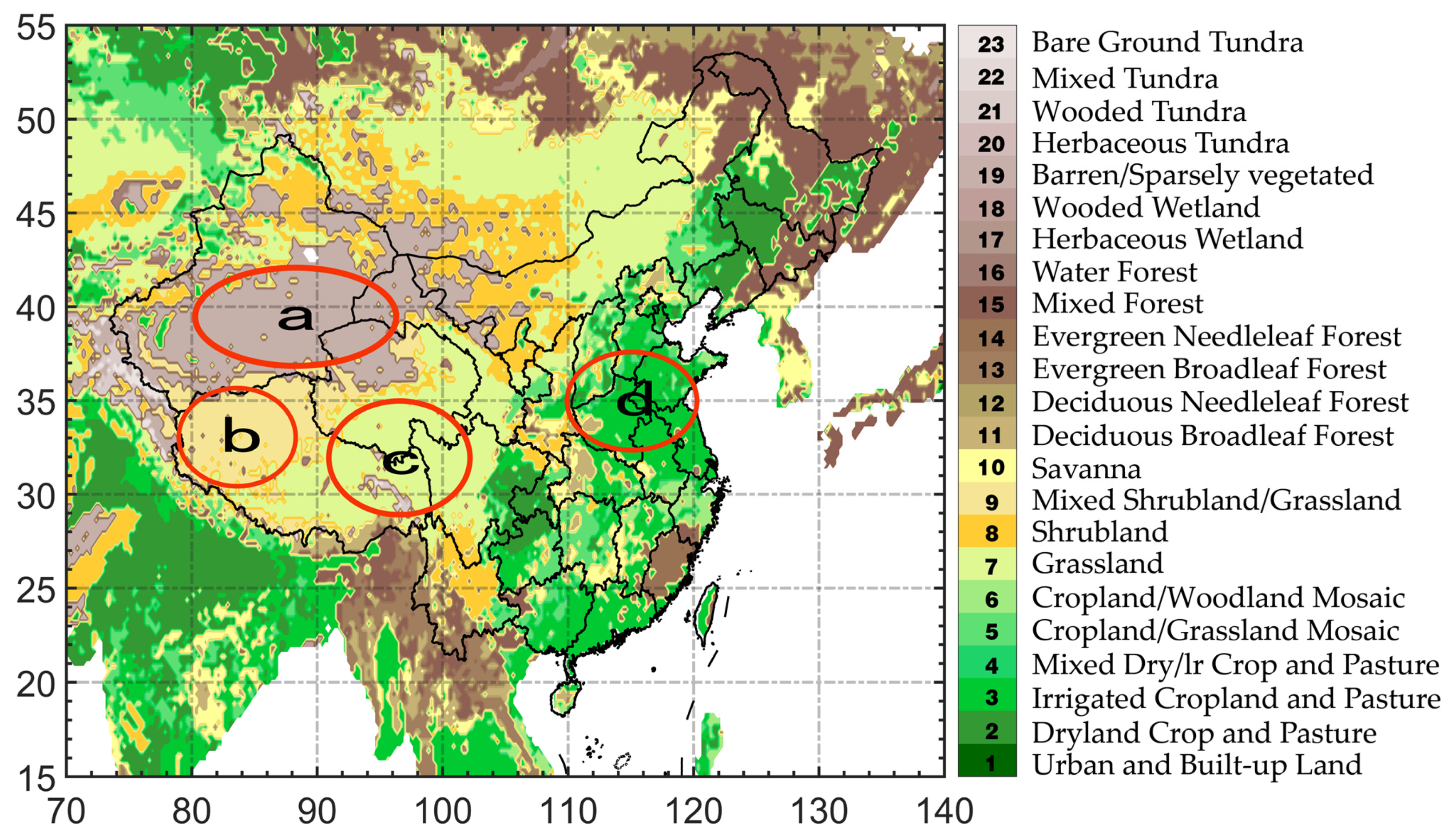
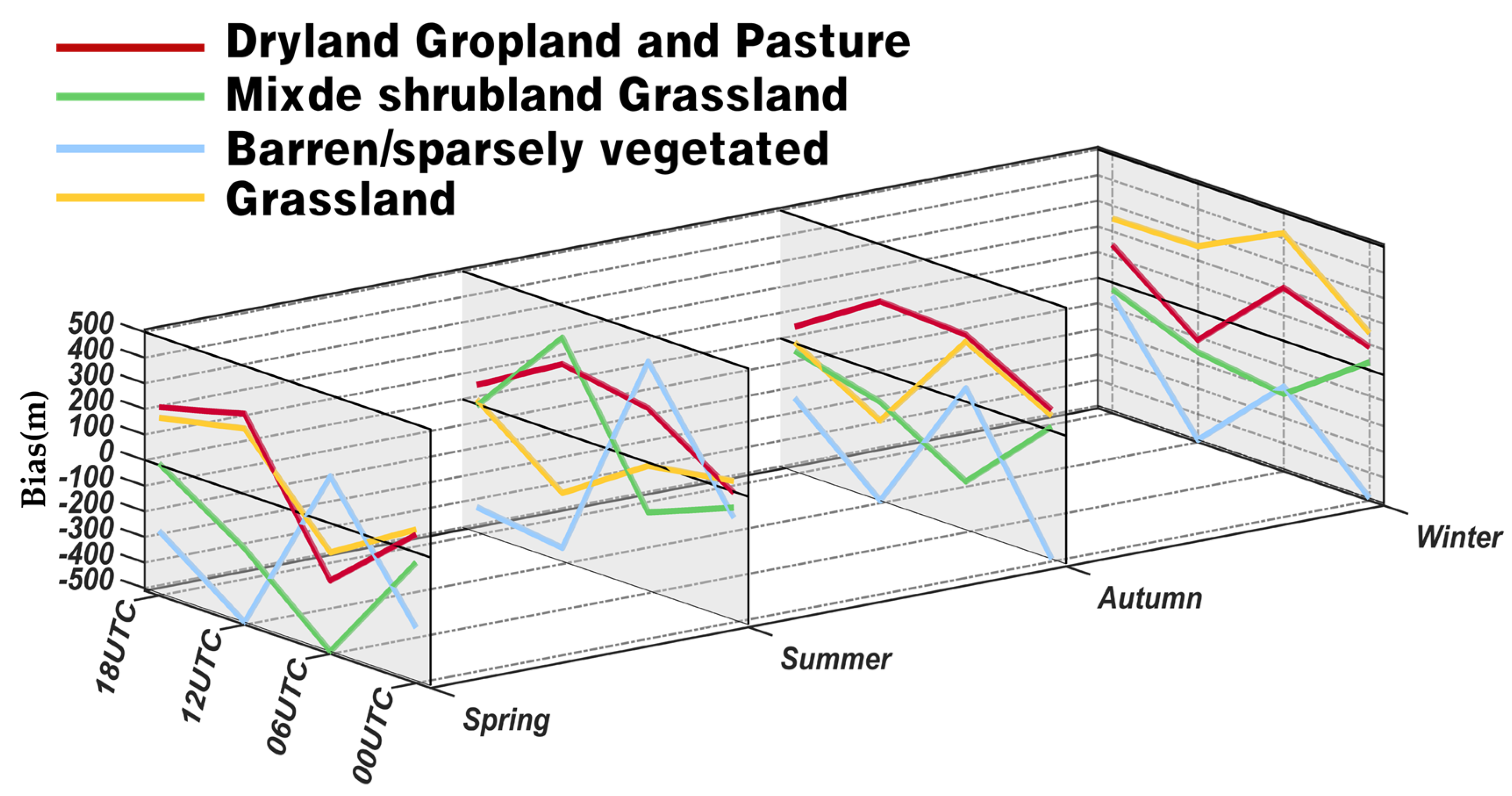
3.3. Different Underlying Surface
4. Discussion
4.1. Evaluation of the Model Bias
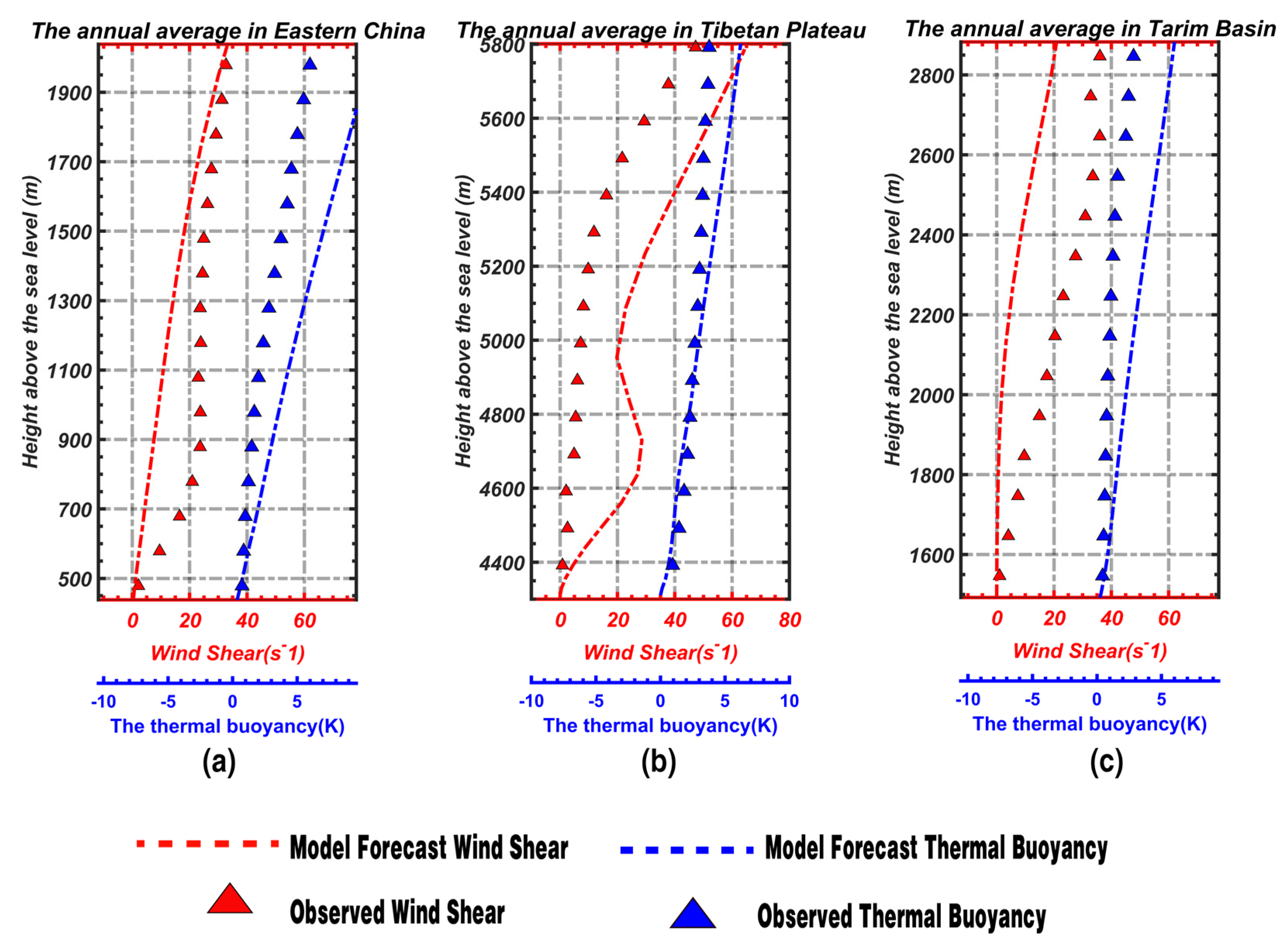
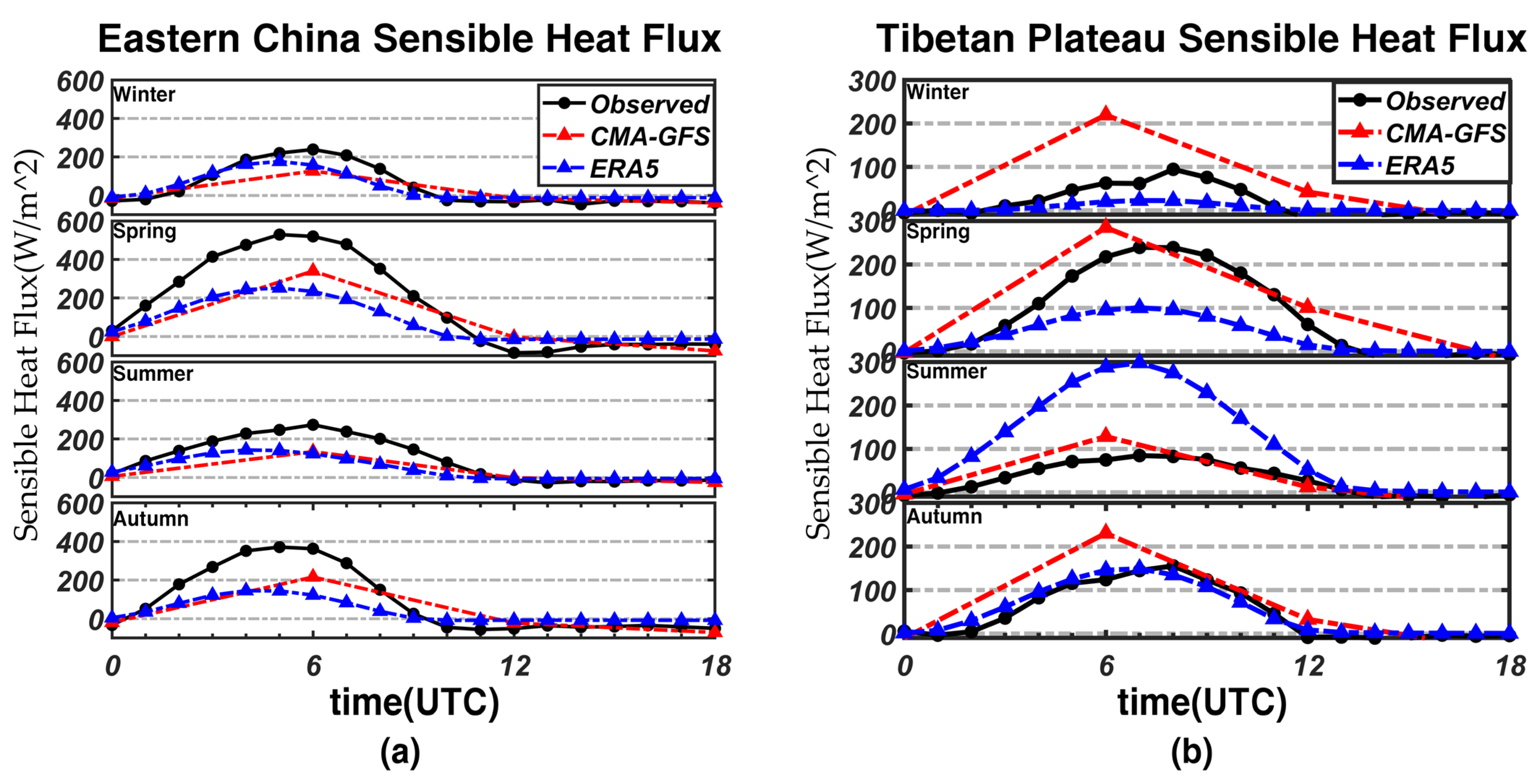
4.2. Bias in East China
4.3. Bias over the Qinghai–Tibetan Plateau and in the Tarim Basin
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; pp. 1–545. [Google Scholar]
- Cheng, S.Y.; Zhang, B.N.; Bai, T.X. Study on the height of atmospheric mixed layer and its meteorological characteristics in Beijing. J. Environ. Eng. 1992, 46, 52. (In Chinese) [Google Scholar]
- Suarez, M.J.; Arakawa, A.; Randall, D.A. The parameterization of the planetary layer in the UCLA general circulation model: Formulation and results. Mon. EeaRev. 1983, 111, 2224–2243. [Google Scholar] [CrossRef][Green Version]
- Konor, C.S.; Boezio, G.C.; Mechoso, C.R.; Arakawa, A. Parameterization of PBL Processes in an Atmospheric General Circulation Model: Description and Preliminary Assessment. Mon. Weather Rev. 2009, 137, 1061–1082. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H.; Wei, W.; Cai, X.; Song, Y.; Kang, L. A study on atmospheric turbulence structure and intermittency during heavy haze pollution in the Beijing area. Sci. China Earth Sci. 2019, 62, 2058–2068. [Google Scholar] [CrossRef]
- Garrat, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Vilà-Guerau de Arellano, J.; Van Heerwaarden, C.C.; Van Stratum, B.J. Atmospheric Boundary Layer: Integrating Air Chemistry and Land Interactions; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Zhong, J.T.; Zhang, X.Y.; Wang, Y.Q. Relative contributions of boundary-layer meteorological factors to the explosive growth of PM2.5 during the red-alert heavy pollution episodes in Beijing in December 2016. J. Meteor. Res. 2017, 31, 809–819. [Google Scholar] [CrossRef]
- Liu, H.Z.; Wang, L.; Du, Q. An overview of recent studies on atmospheric boundary layer physics (2012–2017). Chin. J. Atmos. Sci. 2018, 42, 823–832. (In Chinese) [Google Scholar] [CrossRef]
- Yang, F.Y. Comparison of Determination Methods and Characteristics of Boundary Layer Height in Semi-Arid Area; Lanzhou University: Lanzhou, China, 2018. (In Chinese) [Google Scholar]
- Gui, K.; Che, H.Z.; Wang, Y.Q.; Wang, H. Satellite-derived PM2.5 concentration trends over Eastern China from 1998 to 2016: Relationships to emissions and meteorological parameters. Environ. Pollut. 2019, 247, 1125–1133. [Google Scholar] [CrossRef]
- Zhang, H.S.; Zhang, X.Y.; Li, Q.H. Research progress on estimation of atmospheric boundary layer height. Acta Meteorol. Sin. 2020, 78, 522–536. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Z.; Cao, X.; Zhang, L.; Notholt, J.; Zhou, B.; Liu, R.; Zhang, B. Lidar measurement of planetary boundary layer height and comparison with microwave profiling radiometer observation. Atmos. Meas. Tech. 2012, 5, 1965–1972. [Google Scholar] [CrossRef]
- Saeed, U.; Rocadenbosch, F.; Crewell, S. Adaptive Estimation of the Stable Boundary Layer Height Using Combined Lidar and Microwave Radiometer Observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6895–6906. [Google Scholar] [CrossRef]
- Bravo-Aranda, J.A.; de Arruda Moreira, G.; Navas-Guzmán, F.; Granados-Muñoz, M.J.; Guerrero-Rascado, J.L.; Pozo-Vázquez, D.; Arbizu-Barrena, C.; Olmo Reyes, F.J.; Mallet, M.; Alados Arboledas, L. A new methodology for PBL height estimations based on lidar depolarization measurements: Analysis and comparison against MWR and WRF model-based results. Atmos. Chem. Phys. 2017, 17, 6839–6851. [Google Scholar] [CrossRef]
- Emeis, S.; Schäfer, K.; Münkel, C. Surface-based remote sensing of the mixinglayer height-A review. Meteorol. Z. 2008, 17, 621–630. [Google Scholar] [CrossRef] [PubMed]
- Kallistratova, M.A.; Petenko, I.V.; Kouznetsov, R.D.; Kulichkov, S.N.; Chkhetiani, O.G.; Chunchusov, I.P.; Lyulyukin, V.S.; Zaitseva, D.V.; Vazaeva, N.V.; Perepelkin, V.G.; et al. Sodar Sounding of the Atmospheric Boundary Layer: Review of Studies at the Obukhov Institute of Atmospheric Physics, Russian Academy of Sciences. Izv. Atmos. Ocean. Phys. 2018, 54, 242–256. [Google Scholar] [CrossRef]
- Liang, Z.H.; Wang, D.H.; Liang, Z.M. Spatio-temporal characteristics of boundary layer height Derived from Soundings. J. Appl. Meteorol. Sci. 2020, 31, 447–459. (In Chinese) [Google Scholar]
- Ao, C.O.; Waliser, D.E.; Chan, S.K. Planetary boundary layer heights from GPS radio occultation refractivity and humidity profiles, J. Geophys. Res. 2012, 117, D16117. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, N.J.; Yang, X.S. Height of atmospheric boundary layer top as detected by COSMIC GPS radio occultation data. J. Trop. Meteorol. 2015, 31, 43–50. (In Chinese) [Google Scholar]
- Angevine, W.M.; White, A.B.; Avery, S.K. Boundary-layer depth and entrainment zone characterization with a boundary-layer profiler. Bound.-Layer Meteorol. 1994, 68, 375–385. [Google Scholar] [CrossRef]
- Hu, M.B.; Zheng, G.G.; Zhang, P.C. The study of maximum entropy method user in wind profiler. Spectrosc. Spectr. Anal. 2012, 32, 1085–1089. (In Chinese) [Google Scholar]
- Ge, S.R.; Hu, N. Research on vertical air velocity and planetary boundary height detection by the wind profiler. Natl. Univ. Def. Technol. 2017 000916. (In Chinese) [Google Scholar]
- Sokolovskiy, S.V.; Rocken, C.; Lenschow, D.H.; Kuo, Y.-H.; Anthes, R.A.; Schreiner, W.S.; Hunt, D.C. Observing the moist troposphere with radio occultation signals from COSMIC. Geophys. Res. Lett. 2007, 34, L18802. [Google Scholar] [CrossRef]
- Seibert, P.; Beyrich, F.; Gryning, S.-E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review, and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 2000, 34, 1001–1027. [Google Scholar] [CrossRef]
- Holtslag, A.A.; Nieuwstadt, F.T. Scaling the atmospheric boundary layer Boundary-Layer Meteorol. Bound.-Layer Meteorol. 1986, 36, 201–209. [Google Scholar] [CrossRef]
- Su, T.N.; Li, Z.Q. Relationships between the planetary boundary layer height and surface pollutants derived from lidar observations over China: Regional pattern and influencing factors. Atmos. Chem. Phys. 2018, 18, 15921–15935. [Google Scholar] [CrossRef]
- Wu, H.K.; Chen, Q.Y.; Hua, W. A statistical study of Gravity Wave with Second-Level Radiosonde Data in Sichuan. J. Appl. Meteorol. Sci. 2019, 30, 491–501. (In Chinese) [Google Scholar]
- Li, F.F.; Chen, Q.Y.; Wu, H.K. A statistical study of Brunt-Vaisala frequency with Second-Level Radiosonde Data in China. J. Appl. Meteorol. Sci. 2019, 30, 629–640. (In Chinese) [Google Scholar]
- Chen, W.; Li, Y. Statistical Relationship between Gravity Waves over the Eastern Tibetan Plateau and the Southwest Vortex. Chin. J. Atmos. Sci. 2019, 43, 773–782. (In Chinese) [Google Scholar]
- Tsai, L.C.; Su, S.Y. Ionospheric electron density profiling and modeling of COSMIC follow-on simulations. J. Geod. 2016, 90, 129–142. [Google Scholar] [CrossRef]
- Hautecoeur, O.; Borde, R. Derivation of wind vectors from AVHRR/Metop at EUMETSAT. J. Atmos. Ocean. Technol. 2017, 34, 1645–1659. [Google Scholar] [CrossRef]
- Yan, B.; Chen, J.; Zou, C.-Z. Calibration and Validation of Antenna and Brightness Temperatures from Metop-C Advanced Microwave Sounding Unit-A (AMSU-A). Remote Sens. 2020, 12, 2978. [Google Scholar] [CrossRef]
- Ho, S.P.; Zhou, X.; Shao, X.; Zhang, B. Initial Assessment of the COSMIC-2/FORMOSAT-7 Neutral Atmosphere Data Quality in NESDIS/STAR Using In Situ and Satellite Data. Remote Sens. 2020, 12, 4099. [Google Scholar] [CrossRef]
- Ho, S.-P.; Peng, L.; Mears, C.; Anthes, R.A. Comparison of Global Observations and Trends of Total Precipitable Water Derived from Microwave Radiometers and COSMIC Radio Occultation from 2006 to 2013. Atmos. Chem. Phys. 2018, 18, 259–274. [Google Scholar] [CrossRef]
- Li, X.; Peng, X.; Li, X. An improved dynamic core for a non-hydrostatic model system on the Yin-Yang grid. Adv. Atmos. Sci 2015, 32, 648–658. [Google Scholar] [CrossRef]
- Yang, X.; Chen, J.; Hu, J.; Chen, D.; Shen, X.; Zhang, H. A semi-implicit semi-Lagrangian global nonhydrostatic model and the polar discretization scheme. Sci. China Ser. D-Earth Sci. 2007, 50, 1885–1891. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Q.; Zhao, C.; Shen, X.; Wang, Y.; Jiang, J.H.; Li, Z.; Yung, Y. Application and evaluation of an explicit prognostic cloud-cover scheme in GRAPES global forecast system. J. Adv. Modeling Earth Syst. 2018, 10, 652–667. [Google Scholar] [CrossRef]
- Charney, J.G.; Phillips, N.A. Numerical integration of the quasi-geostrophic equations for barotropic and simple baroclinic flows. J. Meteorol. 1953, 10, 71–99. [Google Scholar] [CrossRef]
- Chen, J.; Ma, Z.; Li, Z.; Shen, X.; Su, Y.; Chen, Q.; Liu, Y. Vertical diffusion and cloud scheme coupling to the Charney–Phillips vertical grid in GRAPES global forecast system. Q. J. R. Meteorol. Soc. 2020, 146, 2191–2204. [Google Scholar] [CrossRef]
- Morcrette, J.-J.; Barker, H.W. Impact of a new radiation package, McRad, in the ECMWF Integrated Forecast System. Mon. Weather Rev. 2008, 136, 4773–4798. [Google Scholar] [CrossRef]
- Arakawa, A.; Schubert, W.H. Interaction of a cumulus cloud ensemble with the large-scale environment, Part I. J. Atmos. Sci. 1974, 31, 674–701. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Q.; Sun, J. Modification of cumulus convection and planetary boundary layer schemes in the GRAPES global model. J. Meteorol. Res. 2015, 29, 806–822. [Google Scholar] [CrossRef]
- Hong, S.Y.; Pan, H.L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Han, J.; Pan, H.L. Revision of convection and vertical diffusion schemes in the NCEP global forecast system. Wea. Forecast. 2011, 26, 520–533. [Google Scholar] [CrossRef]
- Dai, Y.; Zeng, X. The Common Land Model, B. Am. Meteorol. Soc. 2003, 84, 1013–1023. [Google Scholar] [CrossRef]
- Chen, Q.Y.; Shen, X.S. Momentum Budget Diagnosis and the Parameterization of Subgrid-Scale Orographic Drag in Global GRAPES. J. Meteorol. Res. 2016, 30, 771–788. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteor. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Liu, S.Y.; Liang, X. Observed Diurnal Cycle Climatology of Planetary Boundary Layer Height. J. Clim. 2010, 23, 5790–5809. [Google Scholar] [CrossRef]
- Guo, J.P.; Miao, Y.C. The climatology of planetary boundary layer height in China derived from radiosonde and reanalysis data. Atmos. Chem. Phys. 2016, 16, 13309–13319. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Zhang, A.; Chen, Y.; Yang, M. Analysis on Atmosphere Boundary Layer Variation Characteristics and Their Impact Factors in Arid Region and Semi-Arid Region over Northwest China. Plateau Meteorol. 2016, 35, 385–396. (In Chinese) [Google Scholar]
- Hou, W.; Jin, L.L. Review on the Desert Land Surface Process and Regional Climate Effect. Desert Oasis Meteorol. 2016, 10, 87–94. (In Chinese) [Google Scholar]
- Liu, S.M.; Xu, Z.W. Multi-scale surface flux and meteorological elements observation dataset in the Hai River Basin (Huailai station-eddy covariance system-10m tower, 2020). Natl. Data Cent. Tibet. Plateau Sci. 2021. (In Chinese) [Google Scholar] [CrossRef]
- Sud, Y.C.; Smith, W.E. The influence of surface roughness of deserts on the July circulation. Bound.-Layer Meteorol. 1985, 33, 15–49. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, H.; Chen, Q.; Gong, X.; Zhu, K. Evaluation of the Planetary Boundary Layer Height in China Predicted by the CMA-GFS Global Model. Atmosphere 2022, 13, 845. https://doi.org/10.3390/atmos13050845
Long H, Chen Q, Gong X, Zhu K. Evaluation of the Planetary Boundary Layer Height in China Predicted by the CMA-GFS Global Model. Atmosphere. 2022; 13(5):845. https://doi.org/10.3390/atmos13050845
Chicago/Turabian StyleLong, Haichuan, Qiying Chen, Xi Gong, and Keyun Zhu. 2022. "Evaluation of the Planetary Boundary Layer Height in China Predicted by the CMA-GFS Global Model" Atmosphere 13, no. 5: 845. https://doi.org/10.3390/atmos13050845
APA StyleLong, H., Chen, Q., Gong, X., & Zhu, K. (2022). Evaluation of the Planetary Boundary Layer Height in China Predicted by the CMA-GFS Global Model. Atmosphere, 13(5), 845. https://doi.org/10.3390/atmos13050845




