Evaluation of Hydrological Simulation in a Karst Basin with Different Calibration Methods and Rainfall Inputs
Abstract
:1. Introduction
2. Materials
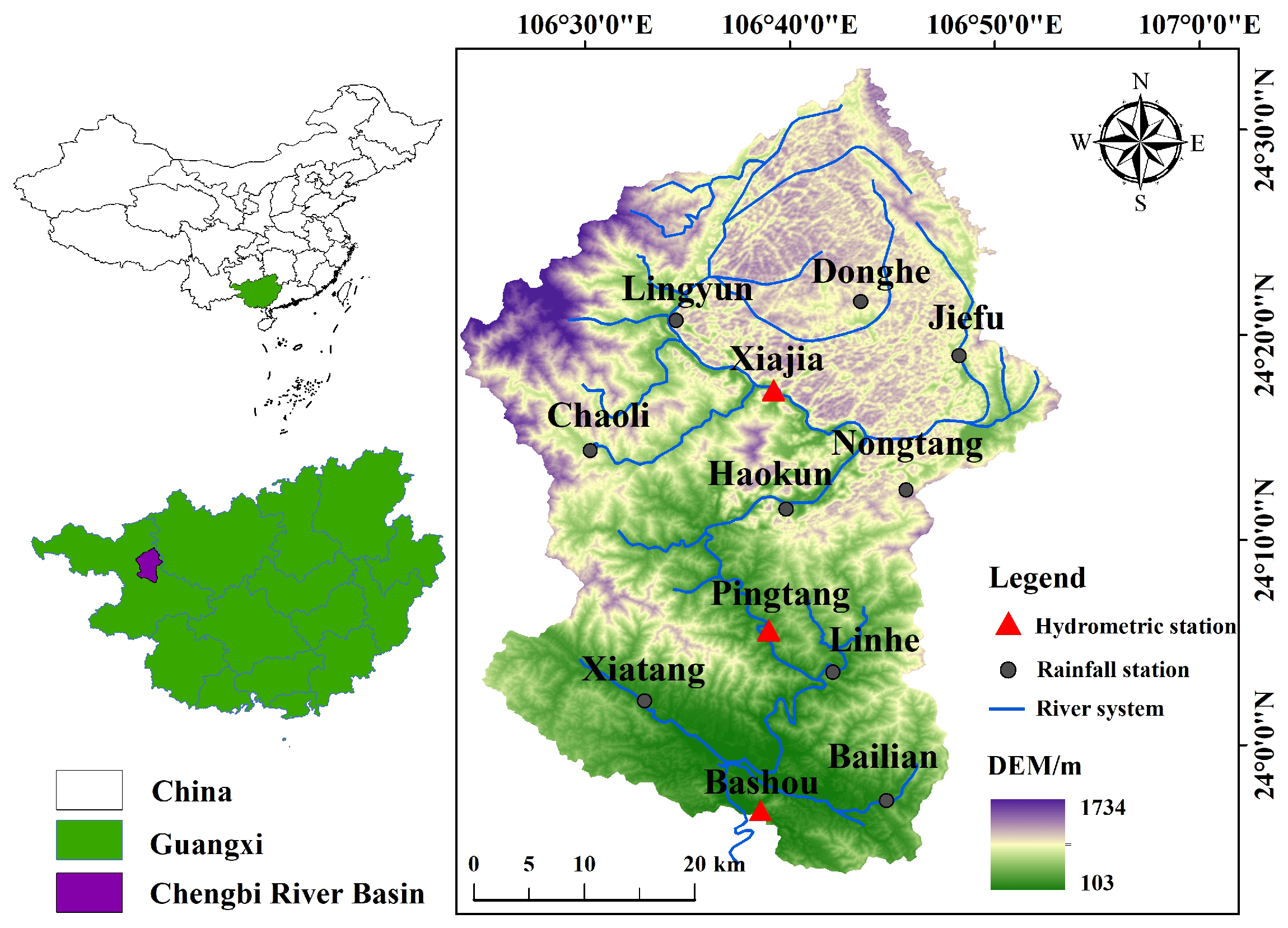
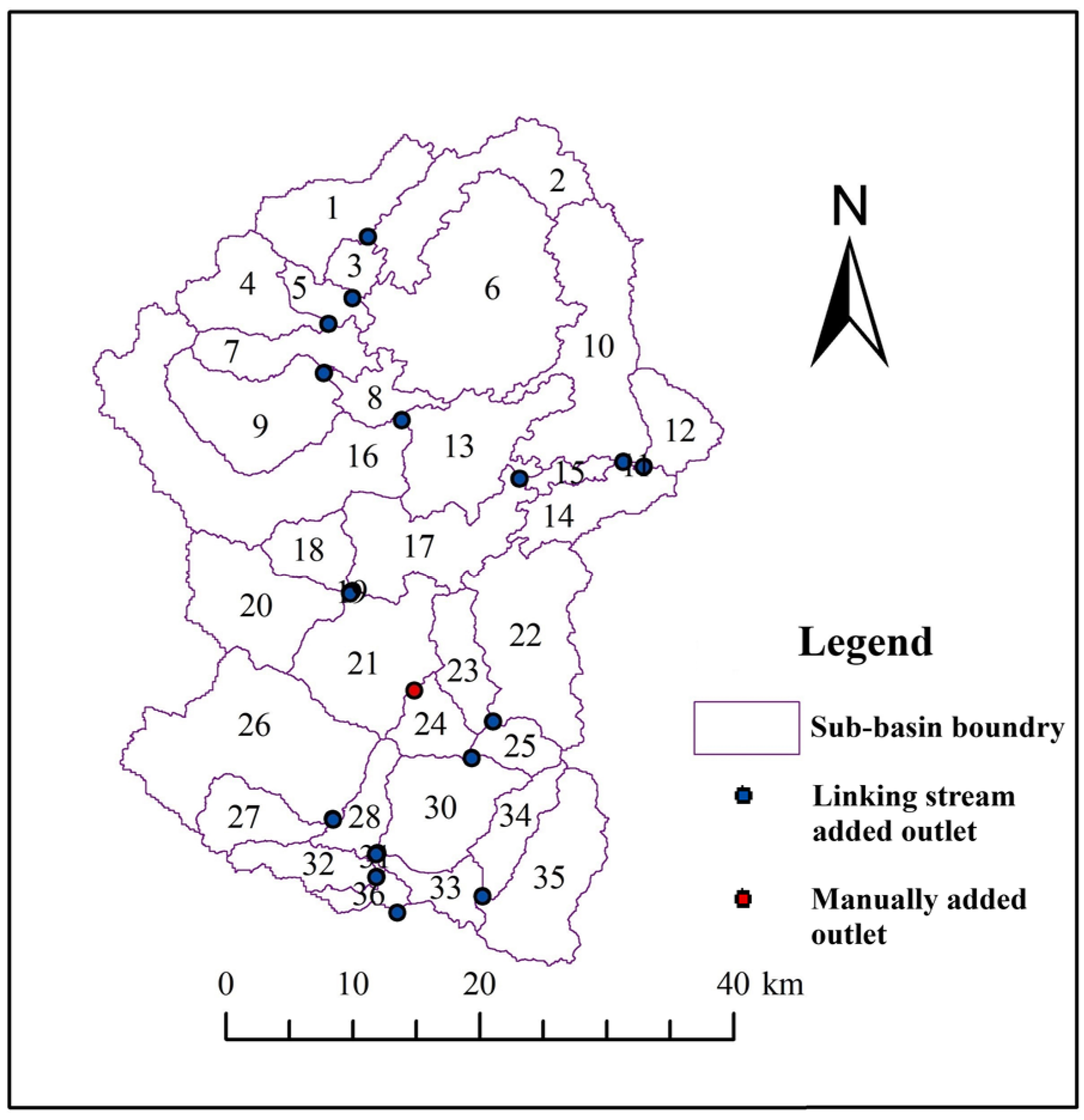
2.1. Overview of Study Area
2.2. Model and Data
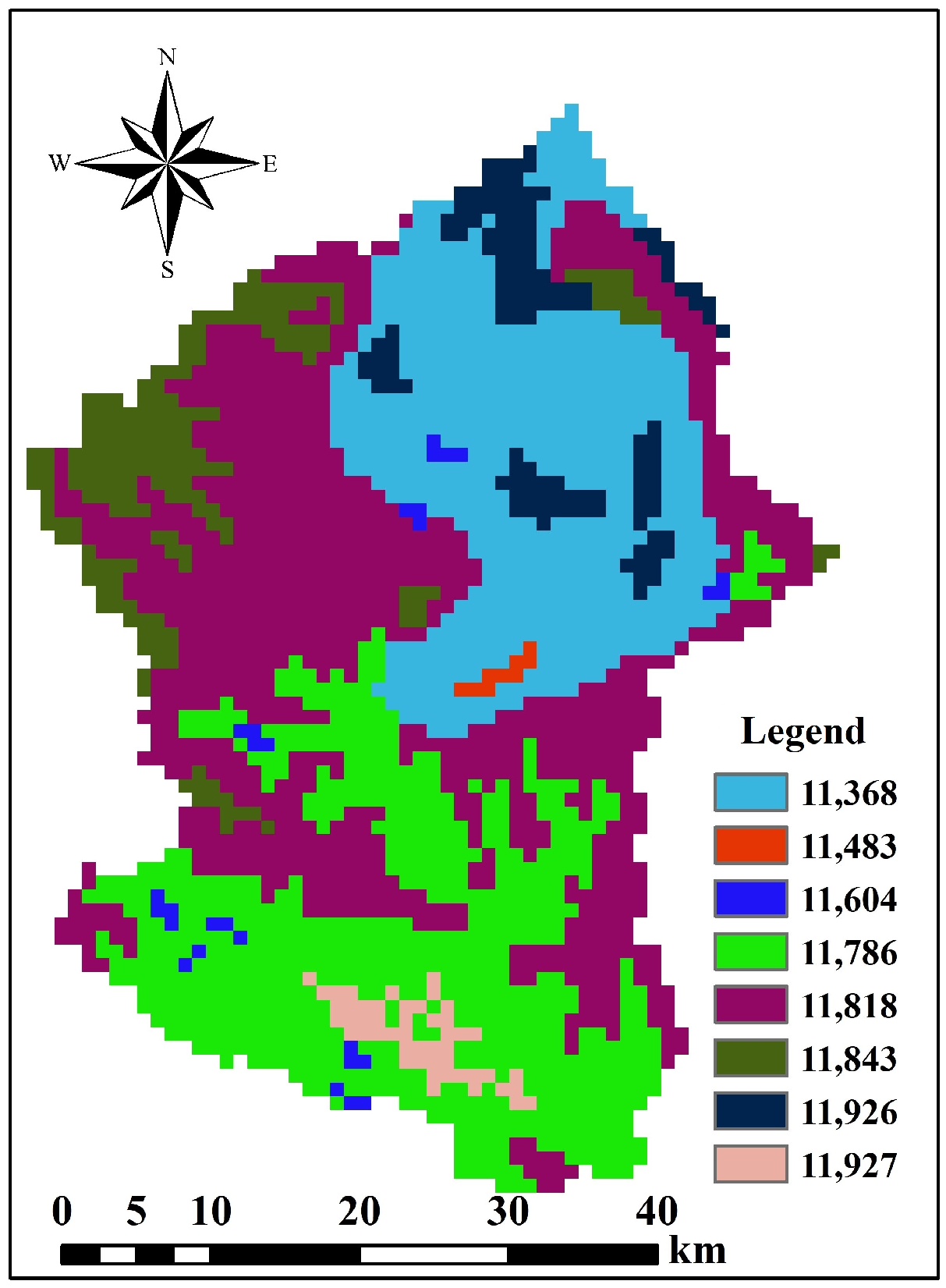
2.2.1. DEM Data
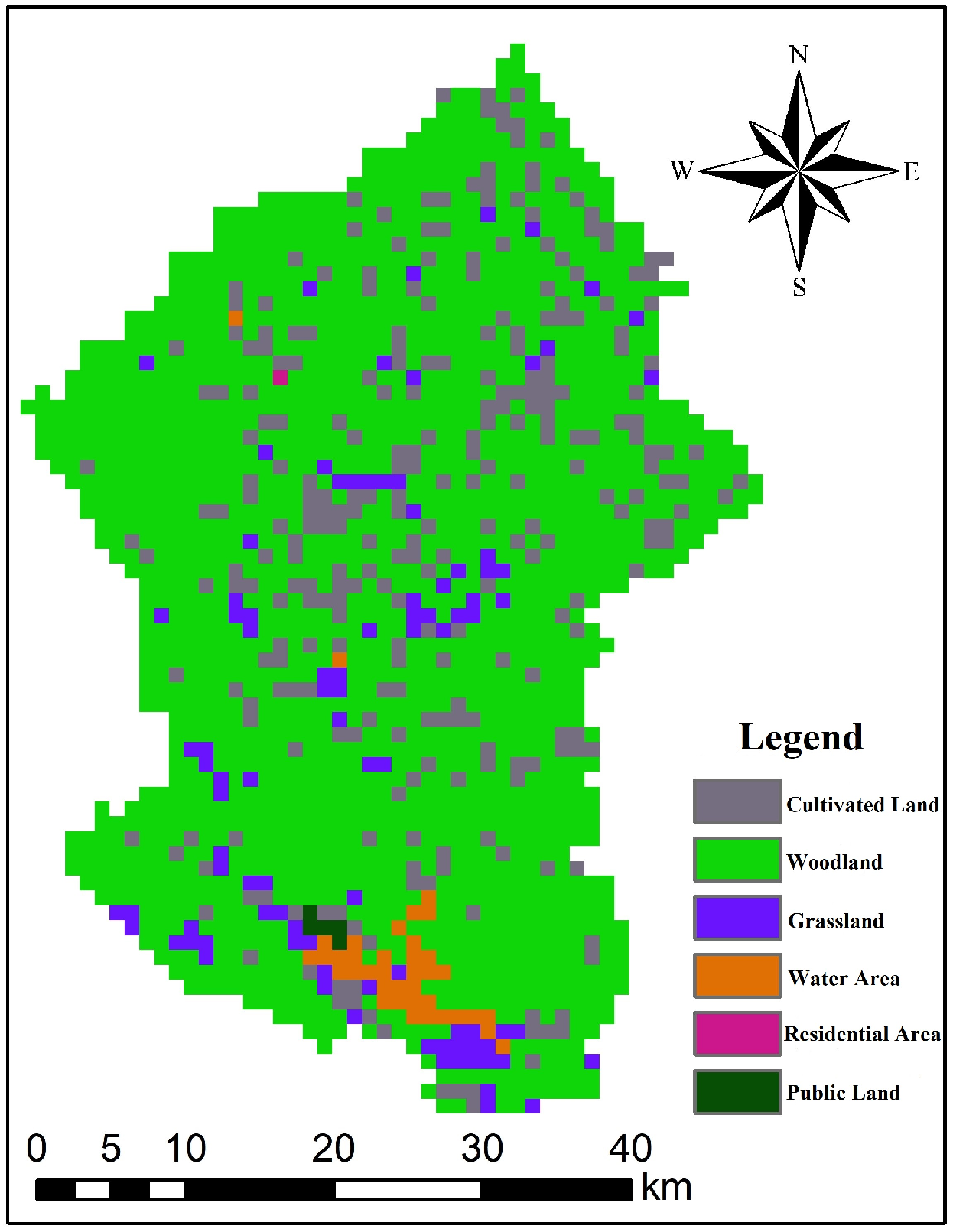
2.2.2. Land Cover Data
2.2.3. Soil Data
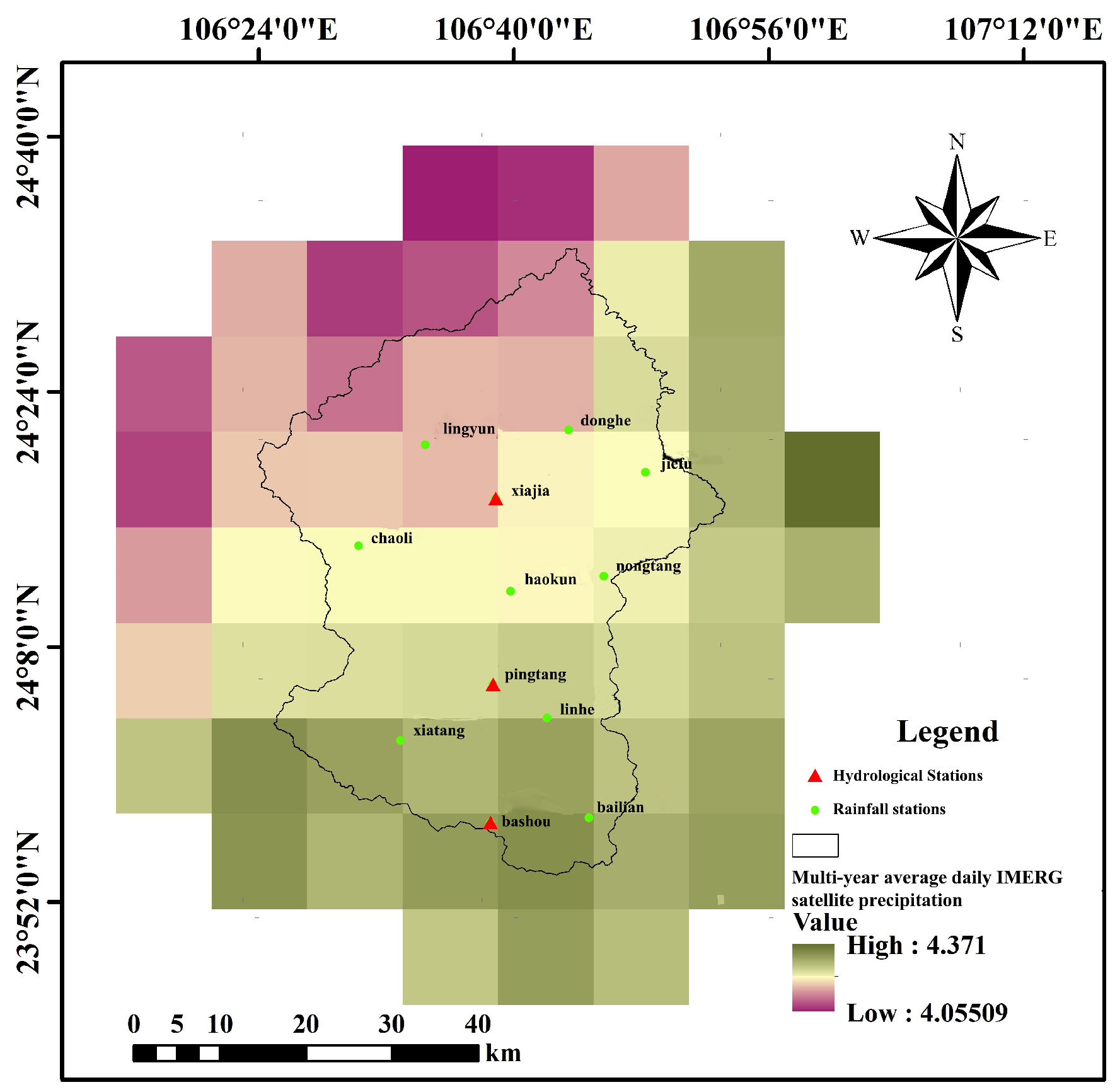
2.2.4. Meteorological and Hydrological Data
2.3. Evaluation Criteria
3. Methods
3.1. Construction and Calibration of Hydrological Model
3.1.1. Construction of the SWAT Model
3.1.2. Calibration of the SWAT Model
- (1)
- Firstly, the runoff result preliminarily simulated by the initial parameters of the SWAT model was loaded into a new SWAT-CUP project.
- (2)
- Secondly, the runoff of the upstream Xiajia station was calibrated. The four parameters given by the software, R__CN2, V__ALPHA_BF, V__GW_DELAY, and V__GWQMN, were calibrated in File Par_inf.txt of Calibration Inputs, and other inputs could refer to the handbook of SWAT-CUP2012. When these inputs were completed, the first calibration was conducted by clicking the Calibrate button.
- (3)
- Thirdly, R2 and NSE were checked in File Summary_Stat.txt of Calibration Outputs. If they did not meet the requirements, the value ranges of each parameter in File Best_Par.txt of Calibration Inputs were loaded in File Par_inf.txt for the second calibration, and the value ranges were kept within the recommended ranges from SWAT-CUP software. R2 and NSE were repeatedly checked until they met the requirements, and then the iteration ended.
- (4)
- Finally, after the above four parameters had been calibrated, a new parameter was added in File Par_inf.txt, and the above steps were repeated until all the 13 parameters had been calibrated. Based on the ranges for the 13 parameters, parameters were calibrated according to the above steps with Pingtang and Bashou in sequence.
3.2. Preparation of Multi-Source Rainfall Data
3.2.1. Fusion and Correction
- (1)
- At the m rainfall station, is the difference between the measured rainfall of this rainfall station and the satellite rainfall . at the corresponding location.
- (2)
- Based on the , the difference of the 1 × 1 km-resolution grid in the study area was calculated by GWR.
- (3)
- Add the to the corresponding 1 × 1 km-resolution-grid IMERG satellite rainfall, and the result is the GWR fusion rainfall .
3.2.2. Downscaling Method
- (1)
- Firstly, the proportional indexes of the original daily IMERG rainfall to the corresponding monthly IMERG rainfall from 2014 to 2018 were calculated:where is the original IMERG satellite rainfall of day i, the denominator is the cumulant of IMERG rainfall of the corresponding month. is the rainfall proportional index of each day i to the corresponding month ranging from 2014 to 2018, added up to 1 each month.
- (2)
- Then, the proportional index was multiplied to the monthly fusion rainfall for the corresponding daily fusion rainfall.
4. Results
4.1. Sensitivity Analysis
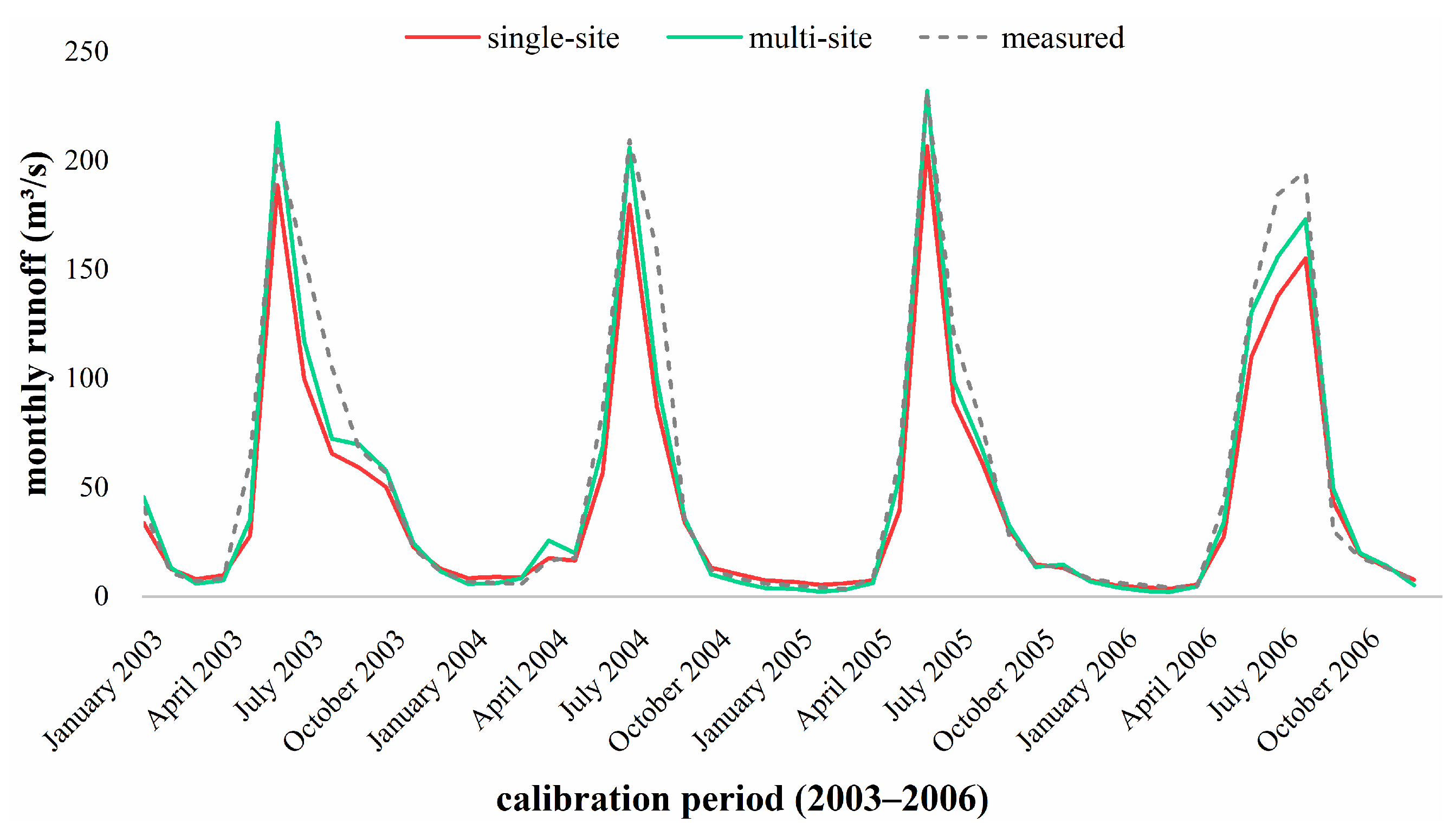
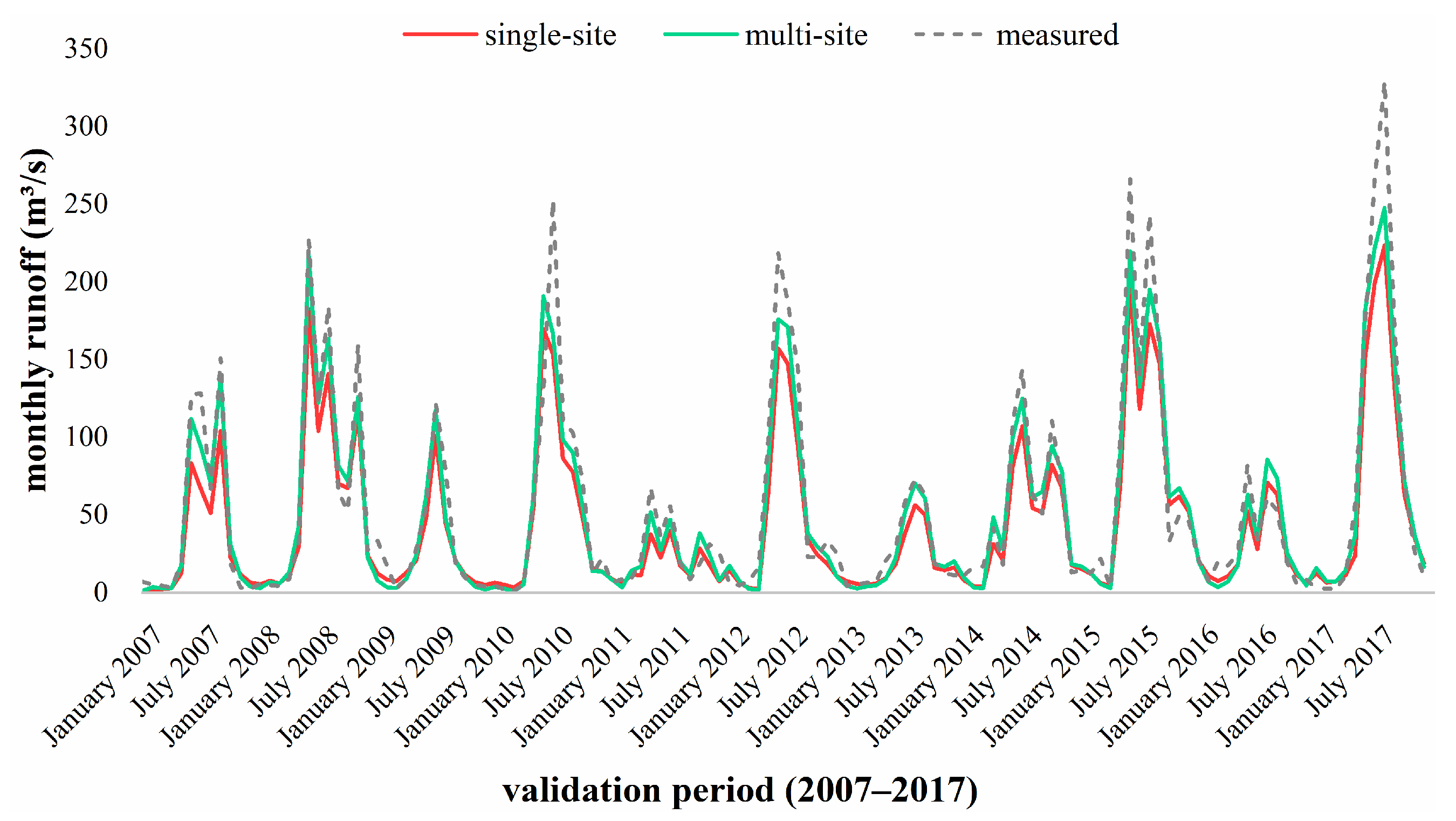
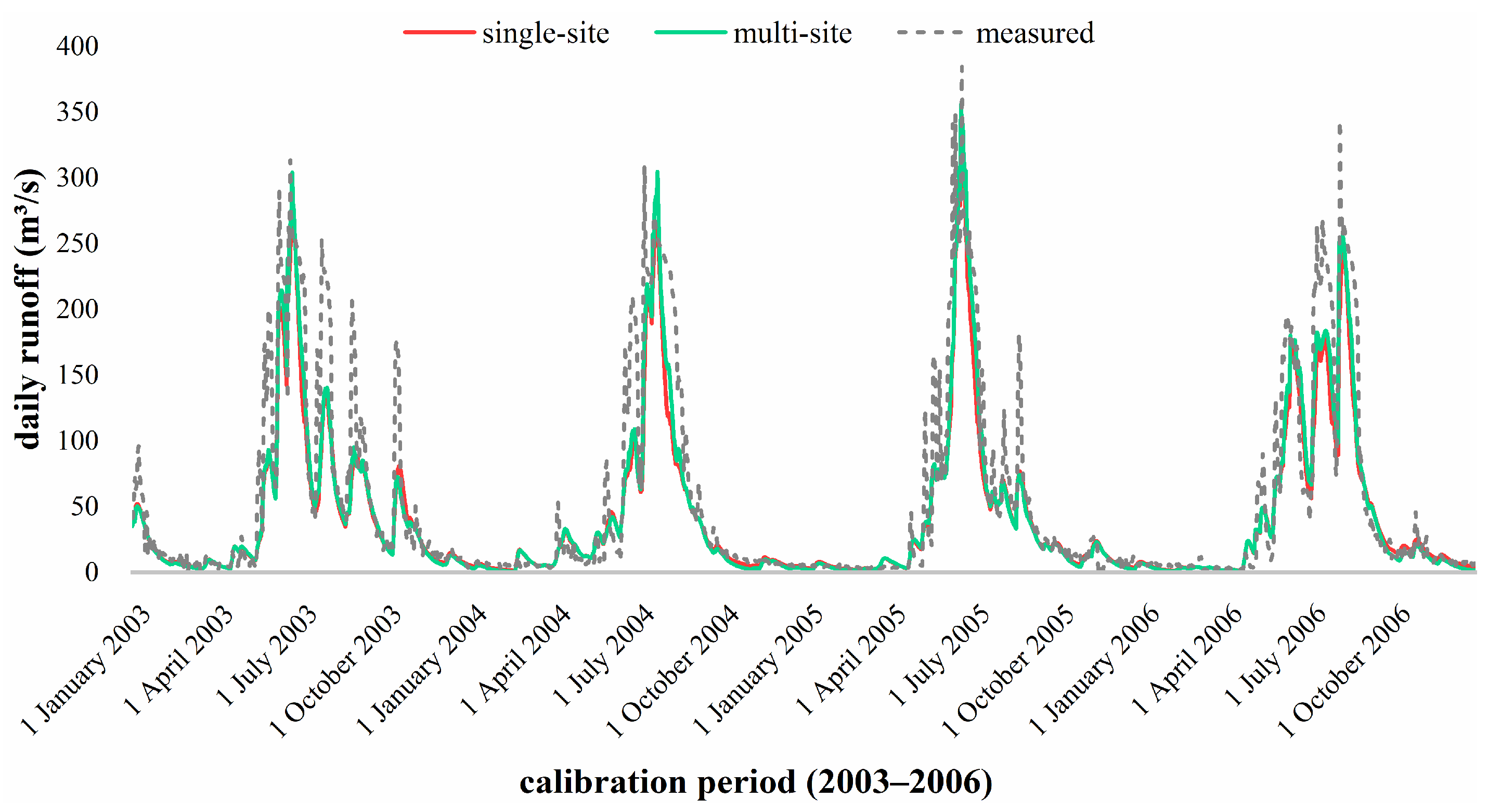
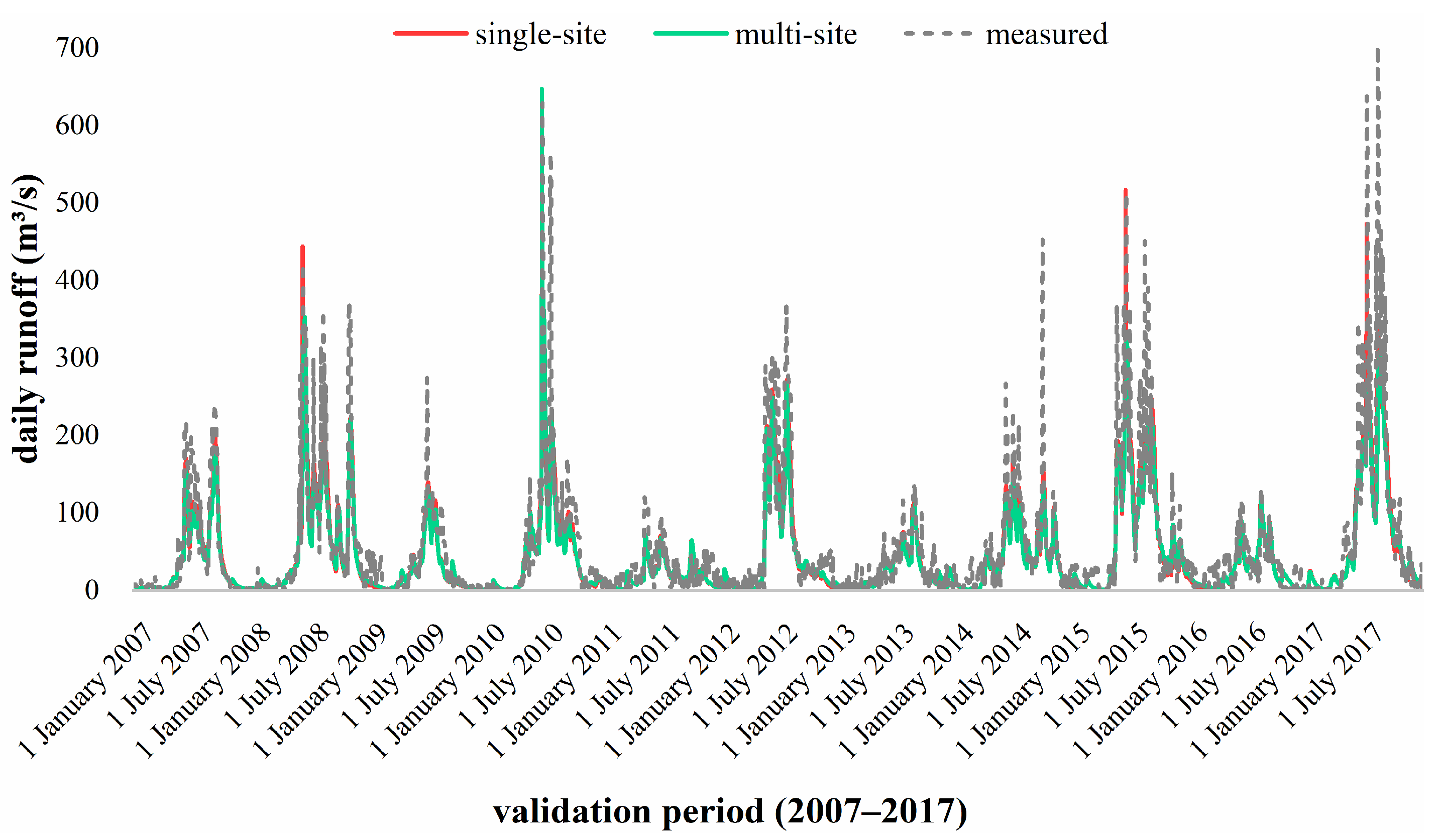
4.2. Comparison of Different Calibration Methods
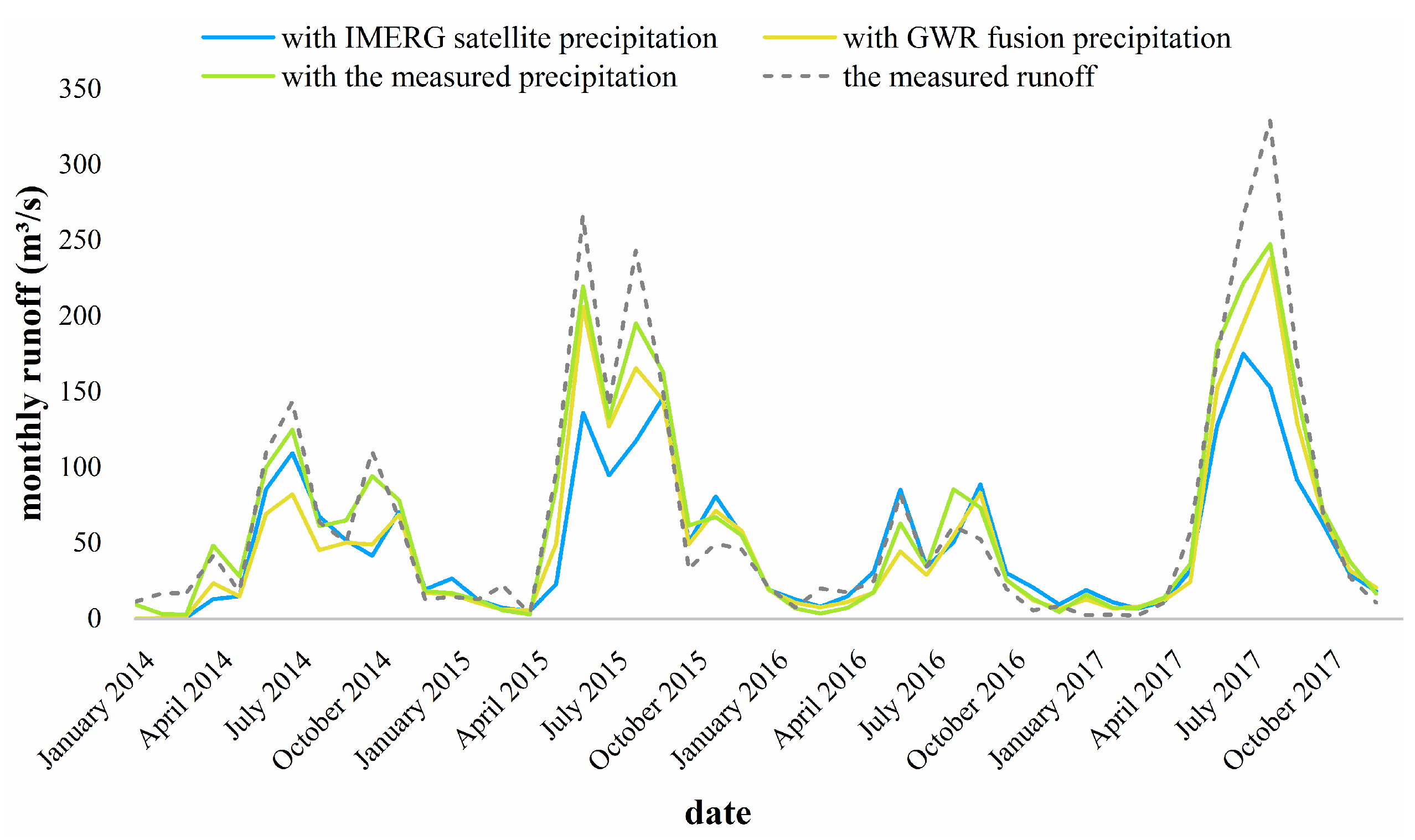
4.3. Comparison of Different Rainfall Inputs
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chawanda, C.J.; Arnold, J.; Thiery, W.; van Griensven, A. Mass balance calibration and reservoir representations for large-scale hydrological impact studies using SWAT. Clim. Change 2020, 163, 1307–1327. [Google Scholar] [CrossRef]
- Jakada, H.; Chen, Z.H. An approach to runoff modelling in small karst watersheds using the SWAT model. Arab. J. Geosci. 2020, 13, 1–18. [Google Scholar] [CrossRef]
- Gumindoga, W.; Rientjes, T.H.M.; Haile, A.T.; Dube, T. Predicting streamflow for land cover changes in the Upper Gilgel Abay River Basin, Ethiopia: A TOPMODEL based approach. Phys. Chem. Earth 2014, 76–78, 3–15. [Google Scholar] [CrossRef]
- Park, D.; Fan, H.J.; Zhu, J.J.; Oh, S.E.; Um, M.J.; Jung, K. Evaluation of reliable digital elevation model resolution for TOPMODEL in two mountainous watersheds, South Korea. Appl. Sci. 2019, 9, 3690. [Google Scholar] [CrossRef] [Green Version]
- Paparrizos, S.; Maris, F. Hydrological simulation of Sperchios River basin in Central Greece using the MIKE SHE model and geographic information systems. Appl. Water Sci. 2017, 7, 591–599. [Google Scholar] [CrossRef] [Green Version]
- Ramteke, G.; Singh, R.; Chatterjee, C. Assessing impacts of conservation measures on watershed hydrology using MIKE SHE model in the face of climate change. Water Resour. Manag. 2020, 34, 4233–4252. [Google Scholar] [CrossRef]
- Hengade, N.; Eldho, T.I.; Ghosh, S. Climate change impact assessment of a river basin using CMIP5 climate models and the VIC hydrological model. Hydrol. Sci. J. 2018, 63, 596–614. [Google Scholar] [CrossRef]
- Maza, M.; Srivastava, A.; Bisht, D.S.; Raghuwanshi, N.S.; Bandyopadhyay, A.; Chatterjee, C.; Bhadra, A. Simulating hydrological response of a monsoon dominated reservoir catchment and command with heterogeneous cropping pattern using VIC model. J. Earth Syst. Sci. 2020, 129, 1–16. [Google Scholar] [CrossRef]
- Krysanova, V.; White, M. Advances in water resources assessment with SWAT—An overview. Hydrol. Sci. J. 2015, 60, 771–783. [Google Scholar] [CrossRef] [Green Version]
- Khoi, D.N.; Suetsugi, T. Impact of climate and land-use changes on hydrological processes and sediment yield—A case study of the Be River catchment, Vietnam. Hydrol. Sci. J. 2014, 59, 1095–1108. [Google Scholar] [CrossRef]
- Akhavan, S.; Abedi-Koupai, J.; Mousavi, S.F.; Afyuni, M.; Eslamian, S.S.; Abbaspour, K.C. Application of SWAT model to investigate nitrate leaching in Hamadan-Bahar Watershed, Iran. Agric. Ecosyst. Environ. 2010, 139, 675–688. [Google Scholar] [CrossRef]
- Akoko, G.; Le, T.H.; Gomi, T.; Kato, T. A Review of SWAT model application in Africa. Water 2021, 13, 1313. [Google Scholar] [CrossRef]
- Dutta, P.; Sarma, A.K. Hydrological modeling as a tool for water resources management of the data-scarce Brahmaputra basin. J. Water Clim. Change 2021, 12, 152–165. [Google Scholar] [CrossRef] [Green Version]
- Dile, Y.T.; Ayana, E.K.; Worqlul, A.W.; Xie, H.; Srinivasan, R.; Lefore, N.; You, L.Z.; Clarke, N. Evaluating satellite-based evapotranspiration estimates for hydrological applications in data-scarce regions: A case in Ethiopia. Sci. Total Environ. 2020, 743, 140702. [Google Scholar] [CrossRef]
- Ji, G.X.; Lai, Z.Z.; Xia, H.B.; Liu, H.; Wang, Z. Future runoff variation and flood disaster prediction of the Yellow River Basin based on CA-Markov and SWAT. Land 2021, 10, 421. [Google Scholar] [CrossRef]
- Moges, E.; Demissie, Y.; Larsen, L.; Yassin, F. Review: Sources of Hydrological Model Uncertainties and Advances in Their Analysis. Water 2021, 13, 28. [Google Scholar] [CrossRef]
- Zhou, Q.; Chen, L.; Singh, V.P.; Zhou, J.; Chen, X.; Xiong, L. Rainfall-runoff simulation in karst dominated areas based on a coupled conceptual hydrological model. J. Hydrol. 2019, 573, 524–533. [Google Scholar] [CrossRef]
- Nikolaidis, N.P.; Bouraoui, F.; Bidoglio, G. Hydrologic and geochemical modeling of a karstic mediterranean watershed. J. Hydrol. 2013, 477, 129–138. [Google Scholar] [CrossRef]
- Geng, X.X.; Zhang, C.P.; Zhang, F.E.; Chen, Z.Y.; Nie, Z.L.; Liu, M. Hydrological modeling of karst watershed containing subterranean river using a modified SWAT model: A case study of the Daotian River Basin, southwest China. Water 2021, 13, 3552. [Google Scholar] [CrossRef]
- Hu, P.; Cai, T.J.; Sui, F.X.; Duan, L.L.; Man, X.L.; Cui, X.Q. Response of runoff to extreme land use change in the permafrost region of northeastern China. Forests 2021, 12, 1021. [Google Scholar] [CrossRef]
- Bai, J.W.; Shen, Z.Y.; Yan, T.Z. A comparison of single- and multi-site calibration and validation: A case study of SWAT in the Miyun Reservoir watershed, China. Front. Earth Sci. 2017, 11, 592–600. [Google Scholar] [CrossRef]
- Nkiaka, E.; Nawaz, N.R.; Lovett, J.C. Effect of single and multi-site calibration techniques on hydrological model performance, parameter estimation and predictive uncertainty: A case study in the Logone catchment, Lake Chad basin. Stoch. Environ. Res. Risk Assess. 2018, 32, 1665–1682. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.W.; Shen, Z.Y.; Liu, R.M.; Hong, Q.; Wu, X. A comparison of single- and multi-gauge based calibrations for hydrological modeling of the Upper Daning River watershed in China’s Three Gorges Reservoir Region. Hydrol. Res. 2012, 43, 822–832. [Google Scholar] [CrossRef]
- Azgin, S.T.; Celik, F.D. Evaluating surface runoff responses to land use changes in a data scarce basin: A case study in Palas Basin, Turkey. Water Resour. 2020, 47, 828–834. [Google Scholar] [CrossRef]
- Sadeghi, S.; Saghafian, B.; Najarchi, M. Assessment of impacts of change in land use and climatic variables on runoff in Tajan River Basin. Water Supply 2020, 20, 2779–2793. [Google Scholar] [CrossRef]
- Zhang, D.J.; Lin, Q.Y.; Chen, X.W.; Chai, T. Improved curve number estimation in SWAT by reflecting the effect of rainfall intensity on runoff generation. Water 2019, 11, 163. [Google Scholar] [CrossRef] [Green Version]
- Nepal, B.; Shrestha, D.; Sharma, S.; Shrestha, M.S.; Aryal, D.; Shrestha, N. Assessment of GPM-Era satellite products’ (IMERG and GSMaP) ability to detect precipitation extremes over mountainous country Nepal. Atmosphere 2021, 12, 254. [Google Scholar] [CrossRef]
- Lu, C.X.; Ye, J.; Fang, G.H.; Huang, X.F.; Yan, M. Assessment of GPM IMERG satellite precipitation estimation under complex climatic and topographic conditions. Atmosphere 2021, 12, 780. [Google Scholar] [CrossRef]
- Jiang, D.J.; Wang, K. The role of satellite-based remote sensing in improving simulated streamflow: A review. Water 2019, 11, 1615. [Google Scholar] [CrossRef] [Green Version]
- Setti, S.; Maheswaran, R.; Sridhar, V.; Barik, K.K.; Merz, B.; Agarwal, A. Inter-comparison of gauge-based gridded data, reanalysis and satellite precipitation product with an emphasis on hydrological modeling. Atmosphere 2020, 11, 1252. [Google Scholar] [CrossRef]
- Zhao, C.X.; Ren, L.L.; Yuan, F.; Zhang, L.M.; Jiang, S.H.; Shi, J.Y.; Chen, T.; Liu, S.Y.; Yang, X.L.; Liu, Y.; et al. Statistical and hydrological evaluations of multiple satellite precipitation products in the Yellow River Source Region of China. Water 2020, 12, 3082. [Google Scholar] [CrossRef]
- Jiang, L.G.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Nourani, V.; Gkeku, H.; Gichamo, T. Ensemble data-driven rainfall-runoff modeling using multi-source satellite and gauge rainfall data input fusion. Earth Sci. Inform. 2021, 14, 1787–1808. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Zhao, M.M. Quantitative evaluation of the impact of the number of different sub-basins on the flood simulation accuracy of the distributed hydrological model of the basin. Water Resour. Plan. Des. 2019, 5, 48–50. [Google Scholar]
- Xiao, J.C. Non-Point Source Pollution Model: SWAT User Application Guide; Geological Publishing House: Beijing, China, 2010. [Google Scholar]
- Lin, Y.T. Impact of Land Use Change on Waterdhed Runoff Based on SWAT Model; Guangxi University: Nanning, China, 2018. [Google Scholar]
- Zhu, X.R. Study on Response of Extreme Runoff under Changing Environment in the Karst Basin; Guangxi University: Nanning, China, 2019. [Google Scholar]
- Qin, J.K. Applicability of IMERG Satellite Precipitation Data in Runoff Simulation in Karst Area; Guangxi University: Nanning, China, 2019. [Google Scholar]
- Chen, F.R.; Li, X. Evaluation of IMERG and TRMM 3B43 monthly precipitation products over mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Wang, D.; Huang, C. Evaluating the applicability of GPM satellite precipitation data in Heihe River Basin. J. Nat. Resour. 2018, 33, 1847–1860. [Google Scholar]
- Jin, X.; Shao, H.; Zhang, C.; Yan, Y. The applicability evaluation of three satellite products in Tianshan Mountains. J. Nat. Resour. 2016, 31, 2074–2085. [Google Scholar]
- Ma, Z.Q.; Xu, J.T.; Zhu, S.Y.; Yang, J.; Tang, G.Q.; Yang, Y.J.; Shi, Z.; Hong, Y. AIMERG: A new Asian precipitation dataset (0.1 degrees/half-hourly, 2000–2015) by calibrating the GPM-era IMERG at a daily scale using APHRODITE. Earth Syst. Sci. Data 2020, 12, 1525–1544. [Google Scholar] [CrossRef]
- Tan, W.; Zeng, C.; Shen, H.; Tian, L. Gaussian process regression algorithm based method for merging daily-scale IMERG and gauge precipitation data:a case of Hubei Province. J. Cent. China Norm. Univ. Nat. Sci. Ed. 2020, 54, 439–446. [Google Scholar]
- Jin, C.P. Research on Space Downscaling Calibration and Application of TRMM Satellite Rainfall Data; Guangxi University: Nanning, China, 2018. [Google Scholar]
- Sun, L.; Hao, Z.; Wang, J.; Ioan, N.; Ousmane, S. Assessment and correction of TMPA products 3B42RT and 3B42V6. J. Hydraul. Eng. 2014, 45, 1135–1146. [Google Scholar]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef] [Green Version]
- Shi, P.; Zhou, M.; Qu, S.M.; Chen, X.; Qiao, X.Y.; Zhang, Z.C.; Ma, X.X. Testing a conceptual lumped model in Karst Area, southwest China. J. Appl. Math. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Sun, G.; Strauss, P.; Guo, J.; Tang, Y.; Yao, A. Multi-site calibration, validation, and sensitivity analysis of the MIKE SHE Model for a large watershed in northern China. Hydrol. Earth Syst. Sci. 2012, 16, 4621–4632. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Liu, X.; Chen, J.L.; Yu, Y.; Ma, X.Y. Overcoming equifinality: Time-varying analysis of sensitivity and identifiability of SWAT runoff and sediment parameters in an arid and semiarid watershed. Environ. Sci. Pollut. Res. 2022, 29, 31631–31645. [Google Scholar] [CrossRef]
- Vigiak, O.; Malago, A.; Bouraoui, F.; Vanmaercke, M.; Poesen, J. Adapting SWAT hillslope erosion model to predict sediment concentrations and yields in large Basins. Sci. Total Environ. 2015, 538, 855–875. [Google Scholar] [CrossRef]
- Luo, X.; Wu, W.Q.; He, D.M.; Li, Y.G.; Ji, X. Hydrological simulation using TRMM and CHIRPS precipitation estimates in the lower Lancang-Mekong River Basin. Chin. Geogr. Sci. 2019, 29, 13–25. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Tan, W.; Wang, C.; Chen, Z. Spatial downscaling of TRMM 3B43 precipitation data based on GWR model in Karst Mountainous Area of Guizhou Province. J. Arid. Meteorol. 2018, 36, 10. [Google Scholar]

| Station | Elevation (m) | Latitude (°) | Longitude (°) | Record Length (Year) |
|---|---|---|---|---|
| Donghe | 1004 | 24.360 | 106.724 | 2002–2018 |
| Lingyun | 689 | 24.345 | 106.574 | 2002–2018 |
| Jiefu | 689 | 24.316 | 106.804 | 2002–2018 |
| Xiajia | 592 | 24.289 | 106.648 | 2002–2018 |
| Chaoli | 801 | 24.239 | 106.504 | 2002–2018 |
| Nongtang | 883 | 24.207 | 106.761 | 2002–2018 |
| Haokun | 408 | 24.192 | 106.663 | 2002–2018 |
| Pingtang | 314 | 24.094 | 106.645 | 2002–2018 |
| Linhe | 245 | 24.059 | 106.701 | 2002–2018 |
| Xiatang | 206 | 24.036 | 106.548 | 2002–2018 |
| Bailian | 277 | 23.955 | 106.745 | 2002–2018 |
| Bashou | 263 | 23.950 | 106.642 | 2002–2018 |
| Data Types | Specific Types | Data Sources |
|---|---|---|
| Rainfall data | The station measured rainfall | Chengbi River Reservoir Authority |
| IMERG satellite rainfall | NASA | |
| The fusion rainfall data | GWR method, proportional index method | |
| Other meteorological data | Solar radiation, wind speed, air temperature, relative humidity | China Meteorological Data Service Center |
| Hydrological data | daily runoff | Chengbi River Reservoir Authority |
| Grades | Very Good | Good | Satisfactory | Unsatisfactory |
|---|---|---|---|---|
| Values | 1.0 ≥ NSE > 0.75 | 0.75 ≥ NSE > 0.65 | 0.65 ≥ NSE > 0.50 | NSE ≥ 0.50 |
| Parameter Name | Description | t-Stat | p-Value | Rank |
|---|---|---|---|---|
| R__SOL_AWC.sol | Available water capacity of the soil layer | −19.19 | 0.00 | 1 |
| V__ESCO.hru | Soil evaporation compensation factor | 14.61 | 0.00 | 2 |
| V__GW_DELAY.gw | Groundwater delay | −8.55 | 0.00 | 3 |
| V__ALPHA_BNK.rte | Baseflow alpha factor for bank storage | 4.31 | 0.00 | 4 |
| V__CH_K2.rte | Effective hydraulic conductivity in the main channel alluvium | 3.32 | 0.00 | 5 |
| V__GWQMN.gw | Threshold depth of water in the shallow aquifer required for return flow to occur | −2.75 | 0.01 | 6 |
| V__GW_REVAP.gw | Groundwater “revap” coefficient | −1.74 | 0.09 | 7 |
| R__SOL_BD(..).sol | Moist bulk density | 0.68 | 0.50 | 8 |
| R__CN2.mgt | SCS runoff curve number | 0.64 | 0.53 | 9 |
| V__ALPHA_BF.gw | Baseflow alpha factor | −0.62 | 0.54 | 10 |
| V__CH_N2.rte | Manning’s “n” value for the main channel | −0.54 | 0.59 | 11 |
| V__REVAPMN.gw | Threshold depth of water in the shallow aquifer for “revap” to occur | 0.41 | 0.68 | 12 |
| R__SOL_K(..).sol | Saturated hydraulic conductivity | 0.30 | 0.76 | 13 |
| Monthly Scale | Single-Site Calibration Method | Multi-Site Calibration Method | |
|---|---|---|---|
| Calibration period | R2 | 0.960 | 0.963 |
| NSE | 0.900 | 0.953 | |
| Re | −0.191 | −0.095 | |
| Validation period | R2 | 0.942 | 0.944 |
| NSE | 0.867 | 0.926 | |
| Re | −0.197 | −0.079 | |
| Daily Scale | Single-Site Calibration Method | Multi-Site Calibration Method | |
|---|---|---|---|
| Calibration period | R2 | 0.876 | 0.887 |
| NSE | 0.822 | 0.856 | |
| Re | −0.215 | −0.186 | |
| Validation period | R2 | 0.697 | 0.800 |
| NSE | 0.681 | 0.743 | |
| Re | −0.218 | −0.187 | |
| Time Scale | IMERG Satellite Rainfall | GWR Fusion Rainfall | The Measured Rainfall | |
|---|---|---|---|---|
| Monthly | R2 | 0.809 | 0.932 | 0.956 |
| NSE | 0.660 | 0.854 | 0.933 | |
| Re | −0.262 | −0.206 | −0.063 | |
| Daily | R2 | 0.679 | 0.791 | 0.821 |
| NSE | 0.534 | 0.717 | 0.740 | |
| Re | −0.325 | −0.238 | −0.223 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, C.; Chen, X.; Lei, X.; Wang, Y.; Ruan, Y.; Lai, S.; Xing, Z. Evaluation of Hydrological Simulation in a Karst Basin with Different Calibration Methods and Rainfall Inputs. Atmosphere 2022, 13, 844. https://doi.org/10.3390/atmos13050844
Mo C, Chen X, Lei X, Wang Y, Ruan Y, Lai S, Xing Z. Evaluation of Hydrological Simulation in a Karst Basin with Different Calibration Methods and Rainfall Inputs. Atmosphere. 2022; 13(5):844. https://doi.org/10.3390/atmos13050844
Chicago/Turabian StyleMo, Chongxun, Xinru Chen, Xingbi Lei, Yafang Wang, Yuli Ruan, Shufeng Lai, and Zhenxiang Xing. 2022. "Evaluation of Hydrological Simulation in a Karst Basin with Different Calibration Methods and Rainfall Inputs" Atmosphere 13, no. 5: 844. https://doi.org/10.3390/atmos13050844
APA StyleMo, C., Chen, X., Lei, X., Wang, Y., Ruan, Y., Lai, S., & Xing, Z. (2022). Evaluation of Hydrological Simulation in a Karst Basin with Different Calibration Methods and Rainfall Inputs. Atmosphere, 13(5), 844. https://doi.org/10.3390/atmos13050844







