Prediction of Fine Particulate Matter Concentration near the Ground in North China from Multivariable Remote Sensing Data Based on MIV-BP Neural Network
Abstract
:1. Introduction
2. Study Area and Data
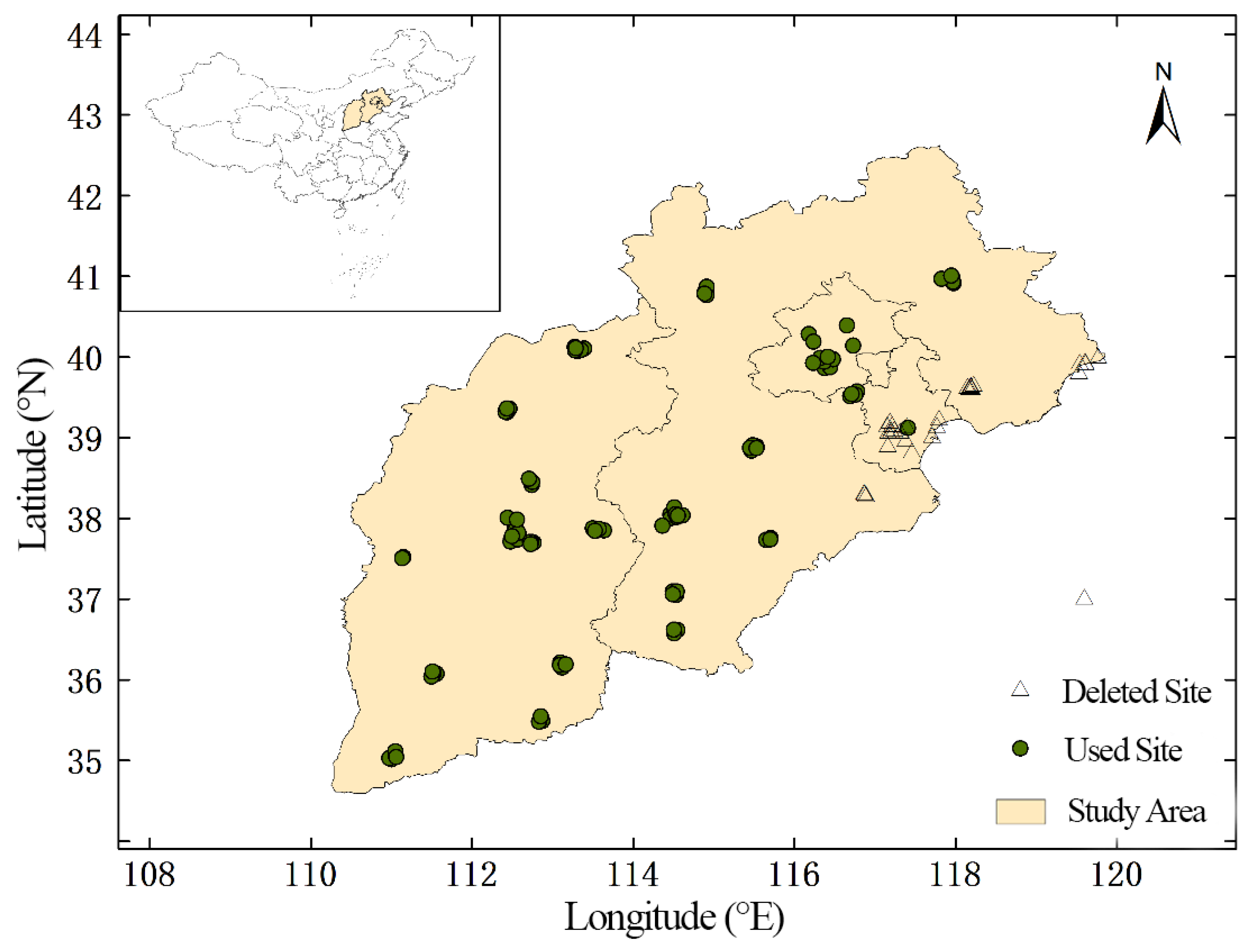
2.1. Study Area
2.2. Data
3. Methods and Experiment Design
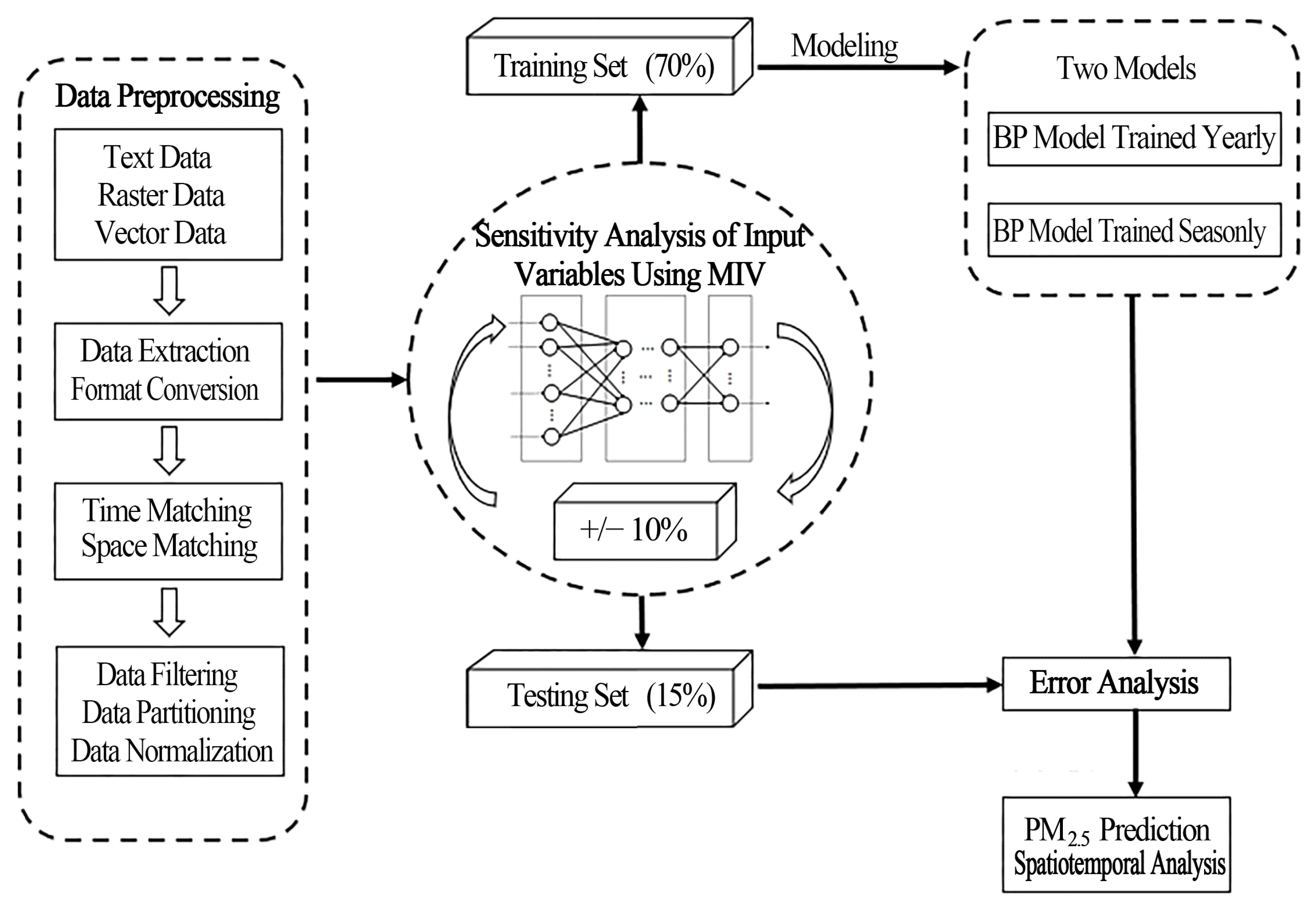
3.1. Data Preprocessing
3.2. MIV Algorithm to Analyze Remote Sensing Variables
- (1)
- After completing the BP neural network training, respectively add or subtract 10% of each variable in the training sample to form two new training samples;
- (2)
- Take them as simulation samples, respectively, and use the established network to carry out simulations and obtain two simulation results;
- (3)
- Calculate the difference between these two simulation results, and the obtained value is the impact value (IV) of the impact of the input variable change on the output;
- (4)
- Calculate the average value of the impact value (IV) of all samples, and then the mean impact value (MIV) corresponding to this input variable can be obtained;
- (5)
- Repeat the above steps, and calculate the MIV value of each variable in turn;
- (6)
- Sort the calculated MIV values of each variable to obtain the influence weight of each input parameter on the prediction result.
3.3. Network Construction
3.4. Experiment Design
4. Results
4.1. MIV of Input Variables
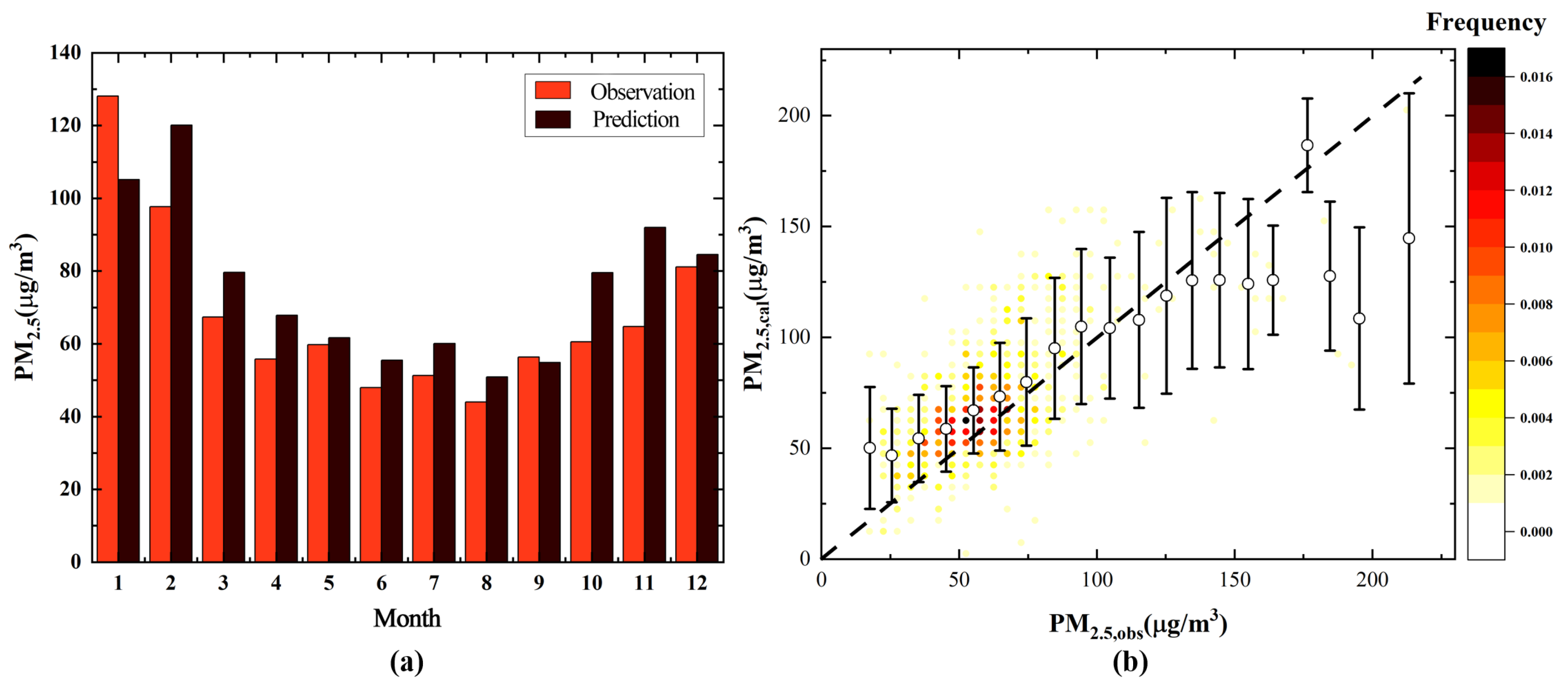
4.2. Evaluation of PM2.5 Models
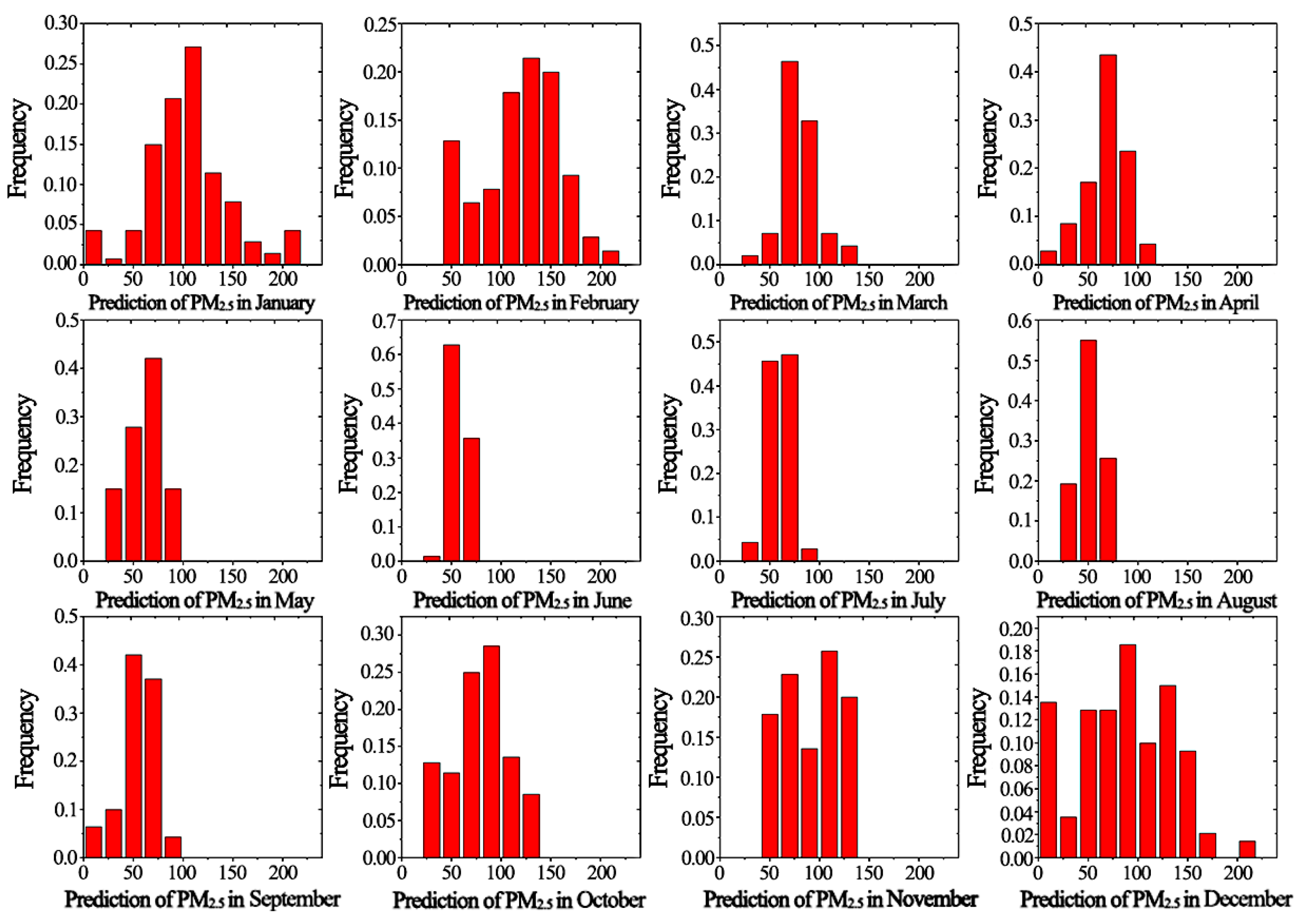
4.3. Intermonth Variation of PM2.5 Mass Concentration
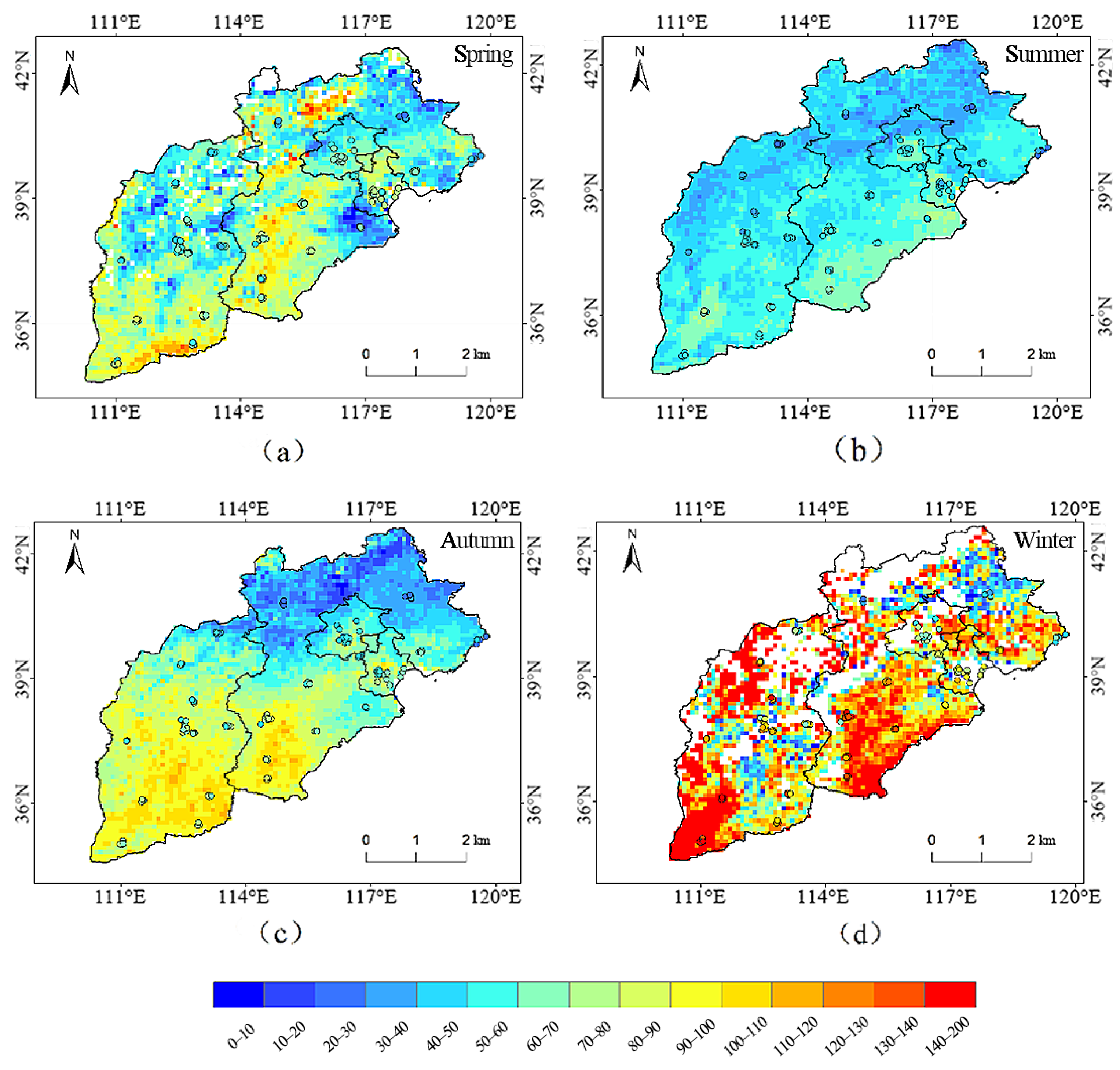
4.4. Spatial Distribution of PM2.5 Mass Concentration
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable Number | Variable | Description | Relative Contribution Rate (Full Year)/% |
|---|---|---|---|
| 1 | time | Day of the year | 0.73 |
| 2 | longitude | Longitude | 15.86 |
| 3 | latitude | Latitude | 8.19 |
| 4 | Land_Ocean_Quality_Flag | Quality flag for land and ocean Aerosol retrievals | 4.48 |
| 5 | Land_sea_Flag | Land_sea_Flag | 4.37 |
| 6 | Optical_Depth_Land_And_Ocean | AOT at 0.55 μm for both ocean and land | 17.85 |
| 7 | Image_Optical_Depth_Land_And_Ocean | AOT at 0.55 μm for both ocean and land with all quality data | 15.23 |
| 8 | Aerosol_Type_Land | Aerosol type | 8.25 |
| 9 | Fitting_Error_Land | Spectral fitting error for inversion over land | 9.28 |
| 10–12 | Corrected_Optical_Depth_Land 0.47, 0.55, 0.66 μm | Retrieved AOT at 0.47, 0.55, 0.66 μm | 13.36, 15.69, 16.37 |
| 13 | Corrected_Optical_Depth_Land_wav2p1 2.13 μm | Retrieved AOT at 2.13 μm | 16.75 |
| 14 | Optical_Depth_Ratio_Small_Land | Fraction of AOT contributed by fine dominated model | 15.38 |
| 15–16 | Number_Pixels_Used_Land 0.47 and 0.66μm | Number of pixels used for land retrieval at 0.47 and 0.66 μm | 2.25, 3.91 |
| 17–23 | Mean_Reflectance_Land 0.47, 0.55, 0.65, 0.86, 1.24, 1.63, 2.11μm | Mean reflectance of pixels used for land retrieval at 0.47, 0.55, 0.65, 0.86, 1.24, 1.63, 2.11 μm | 4.23, 3.61, 2.64, 6.12, 6.46, 4.84, 4.51 |
| 24–30 | STD_Reflectance_Land 0.47, 0.55, 0.65, 0.86, 1.24, 1.63, 2.11μm | Standard deviation of reflectance of pixels used for land retrieval at 0.47, 0.55, 0.65, 0.86, 1.24, 1.63, 2.11 μm | 8.48, 6.20, 4.67, 4.65, 6.61, 7.29, 5.08 |
| 31 | Mass_Concentration_Land | Estimated column mass (per area) using assumed mass extinction efficiency | 4.26 |
| 32 | Aerosol_Cloud_Fraction_Land | Cloud fraction from land aerosol cloud mask from retrieved and overcast pixels not including cirrus mask | 19.64 |
| 33–35 | Quality_Assurance_Land | Runtime QA flags | 4.70, 9.99, 15.04 |
| 36 | 10 m wind field (u) | 10 m wind field (u) | 6.54 |
| 37 | 10 m wind field (v) | 10 m wind field (v) | 6.93 |
| 38 | 2 m dew point temperature | 2 m dew point temperature | 5.97 |
| 39 | 2 m temperature | 2 m temperature | 3.85 |
| 40 | boundary layer dissipation | Boundary layer dissipation | 0.02 |
| 41 | Boundary layer height | Boundary layer height | 1.10 |
| 42 | surface pressure | Surface pressure | 0.07 |
| 43 | total precipitation | Total precipitation | 6.56 |

References
- Sicard, P.; Khaniabadi, Y.O.; Perez, S.; Gualtieri, M.; De Marco, A. Effect of O3, PM10 and PM2.5 on Cardiovascular and Respiratory Diseases in Cities of France, Iran and Italy. Environ. Sci. Pollut. Res. 2019, 26, 32645–32665. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Moran, A.E.; Coxson, P.G.; Yang, X.; Liu, F.; Cao, J.; Chen, K.; Wang, M.; He, J.; Goldman, L.; et al. Potential Cardiovascular and Total Mortality Benefits of Air Pollution Control in Urban China. Circulation 2017, 136, 1575–1584. [Google Scholar] [CrossRef] [PubMed]
- Geng, G.; Zhang, Q.; Martin, R.; van Donkelaar, A.; Huo, H.; Che, H.; Lin, J.; He, K. Estimating Long-Term PM2.5 Concentrations in China Using Satellite-Based Aerosol Optical Depth and a Chemical Transport Model. Remote Sens. Environ. 2015, 166, 262–270. [Google Scholar] [CrossRef]
- Huang, K.; Xiao, Q.; Meng, X.; Geng, G.; Wang, Y.; Lyapustin, A.; Gu, D.; Liu, Y. Predicting Monthly High-Resolution PM2.5 Concentrations with Random Forest Model in the North China Plain. Environ. Pollut. 2018, 242, 675–683. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.; Zhang, Q.; Chen, C.; Wang, L.; Wei, Z.; Zhou, S.; Parworth, C.; Zheng, B.; Canonaco, F.; et al. Wintertime Aerosol Chemistry and Haze Evolution in an Extremely Polluted City of the North China Plain: Significant Contribution from Coal and Biomass Combustion. Atmos. Chem. Phys. 2017, 17, 4751–4768. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Chen, D. A Semi-Empirical Model for Predicting Hourly Ground-Level Fine Particulate Matter (PM2.5) Concentration in Southern Ontario from Satellite Remote Sensing and Ground-Based Meteorological Measurements. Remote Sens. Environ. 2010, 114, 221–229. [Google Scholar] [CrossRef]
- Hoff, R.M.; Christopher, S.A. Remote Sensing of Particulate Pollution from Space: Have We Reached the Promised Land? J. Air Waste Manag. Assoc. 2009, 59, 645–675. [Google Scholar] [CrossRef]
- Xie, Z.Y.; Liu, H.; Tang, X.M. Correlation Analysis between Modis Aerosol Optical Depth and PM10 Concentration over Beijing. Acta Sci. Circumstantiae 2015, 35, 3292–3299. [Google Scholar]
- Zhang, Y.; Li, Z.; Bai, K.; Wei, Y.; Xie, Y.; Zhang, Y.; Ou, Y.; Cohen, J.; Zhang, Y.; Peng, Z.; et al. Satellite Remote Sensing of Atmospheric Particulate Matter Mass Concentration: Advances, Challenges, and Perspectives. Fundam. Res. 2021, 1, 240–258. [Google Scholar] [CrossRef]
- Lin, H.-F.; Xin, J.-Y.; Zhang, W.-Y.; Wang, Y.-S.; Liu, Z.-R.; Chen, C.-L. Comparison of Atmospheric Particulate Matter and Aerosol Optical Depth in Beijing City. Huan Jing Ke Xue Huanjing Kexue 2013, 34, 826–834. [Google Scholar]
- Xin, J.; Zhang, Q.; Wang, L.; Gong, C.; Wang, Y.; Liu, Z.; Gao, W. The Empirical Relationship between the PM2.5 Concentration and Aerosol Optical Depth over the Background of North China from 2009 to 2011. Atmos. Res. 2014, 138, 179–188. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z. Remote Sensing of Atmospheric Fine Particulate Matter (PM2.5) Mass Concentration near the Ground from Satellite Observation. Remote Sens. Environ. 2015, 160, 252–262. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Chang, W.; Zhang, Y.; de Leeuw, G.; Schauer, J.J. Satellite Observations of PM2.5 Changes and Driving Factors Based Forecasting over China 2000–2025. Remote Sens. 2020, 12, 2518. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Z.; Zhang, Y.; Chen, C.; Xie, Y.; Lv, Y.; Dubovik, O. Derivation of PM10 Mass Concentration from Advanced Satellite Retrieval Products Based on a Semi-Empirical Physical Approach. Remote Sens. Environ. 2021, 256, 112319. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Kahn, R.; Levy, R.; Verduzco, C.; Villeneuve, P.J. Global Estimates of Ambient Fine Particulate Matter Concentrations from Satellite-Based Aerosol Optical Depth: Development and Application. Environ. Health Perspect. 2010, 118, 847–855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Donkelaar, A.; Martin, R.V.; Li, C.; Burnett, R.T. Regional Estimates of Chemical Composition of Fine Particulate Matter Using a Combined Geoscience-Statistical Method with Information from Satellites, Models, and Monitors. Environ. Sci. Technol. 2019, 53, 2595–2611. [Google Scholar] [CrossRef] [Green Version]
- Van Donkelaar, A.; Martin, R.V.; Park, R.J. Estimating Ground-Level PM2.5 Using Aerosol Optical Depth Determined from Satellite Remote Sensing. J. Geophys. Res. Atmos. 2006, 111, 7436–7444. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Pasch, A.N.; Szykman, J.J.; Zhang, L.; Wang, Y.X.; Chen, D. Improving the Accuracy of Daily Satellite-Derived Ground-Level Fine Aerosol Concentration Estimates for North America. Environ. Sci. Technol. 2012, 46, 11971–11978. [Google Scholar] [CrossRef]
- van Donkelaar, A.; Martin, R.V.; Spurr, R.J.D.; Drury, E.; Remer, L.A.; Levy, R.C.; Wang, J. Optimal Estimation for Global Ground-Level Fine Particulate Matter Concentrations. J. Geophys. Res. Atmos. 2013, 118, 5621–5636. [Google Scholar] [CrossRef] [Green Version]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Boys, B.L. Use of Satellite Observations for Long-Term Exposure Assessment of Global Concentrations of Fine Particulate Matter. Environ. Health Perspect. 2015, 123, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Waller, L.A.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes, M.G., Jr.; Estes, S.M.; Quattrochi, D.A.; Sarnat, J.A.; Liu, Y. Estimating Ground-Level PM2.5 Concentrations in the Southeastern Us Using Geographically Weighted Regression. Environ. Res. 2013, 121, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, L. A Locally Weighted Neural Network Constrained by Global Training for Remote Sensing Estimation of PM2.5. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Li, L.; Chen, B.; Zhang, Y.; Zhao, Y.; Xian, Y.; Xu, G.; Zhang, H.; Guo, L. Retrieval of Daily PM2.5 Concentrations Using Nonlinear Methods: A Case Study of the Beijing–Tianjin–Hebei Region, China. Remote Sens. 2018, 10, 2006. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Tian, Y.; Xiao, Y.; Jiang, W.; Tian, L.; Liu, J. Study on the Spatial Distribution Characteristics and the Drivers of Aqi in North China. Acta Sci. Circumstantiae 2017, 8, 3085–3096. [Google Scholar]
- Deng, W.-Y.; Zheng, Q.-H.; Chen, L.; Xu, X.-B. Research on Extreme Learning of Neural Networks. Chin. J. Comput. 2010, 33, 279–287. [Google Scholar] [CrossRef]
- Sun, B.L.; Sun, H.; Zhang, C.N.; Shi, J.W.; Zhong, D.Q. Forecast of Air Pollutant Concentrations by Bp Neural Network. Acta Sci. Circumstantiae 2017, 37, 1864–1871. [Google Scholar]
- Guo, L.; Fan, B.; Zhang, F.; Jin, Z.; Lin, H. The Clustering of Severe Dust Storm Occurrence in China from 1958 to 2007. J. Geophys. Res. Atmos. 2018, 123, 8035–8046. [Google Scholar] [CrossRef]
- Li, Y.; Xue, Y.; Guang, J.; She, L.; Fan, C.; Chen, G. Ground-Level PM2.5 Concentration Estimation from Satellite Data in the Beijing Area Using a Specific Particle Swarm Extinction Mass Conversion Algorithm. Remote Sens. 2018, 10, 1906. [Google Scholar] [CrossRef] [Green Version]
- Yan, D.; Lei, Y.; Shi, Y.; Zhu, Q.; Li, L.; Zhang, Z. Evolution of the Spatiotemporal Pattern of Pm2. 5 Concentrations in China–a Case Study from the Beijing-Tianjin-Hebei Region. Atmos. Environ. 2018, 183, 225–233. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Li, Z.; Zhang, Y.; Chen, C.; Dubovik, O.; Xu, H.; Li, K.; Chen, J.; Wang, H.; Ge, B.; et al. Validation of Polder Grasp Aerosol Optical Retrieval over China Using Sonet Observations. J. Quant. Spectrosc. Radiat. Transf. 2020, 246, 106931. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Y.; Chen, M.; Wang, L.; Zhao, S.; Pu, X.; Chen, X. Estimation of Monthly 1 Km Resolution PM2.5 Concentrations Using a Random Forest Model over “2 + 26” Cities, China. Urban Clim. 2021, 35, 100734. [Google Scholar] [CrossRef]
- Zhan, Y.; Luo, Y.; Deng, X.; Chen, H.; Grieneisen, M.L.; Shen, X.; Zhu, L.; Zhang, M. Spatiotemporal Prediction of Continuous Daily PM2.5 Concentrations across China Using a Spatially Explicit Machine Learning Algorithm. Atmos. Environ. 2017, 155, 129–139. [Google Scholar] [CrossRef]
- Chen, J.; Yin, J.; Zang, L.; Zhang, T.; Zhao, M. Stacking Machine Learning Model for Estimating Hourly PM2.5 in China Based on Himawari 8 Aerosol Optical Depth Data. Sci. Total Environ. 2019, 697, 134021. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, X.; Zhang, L. Estimating Ground-Level PM2.5 by Fusing Satellite and Station Observations: A Geo-Intelligent Deep Learning Approach. Geophys. Res. Lett. 2017, 44, 11–985. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Weng, F.; Li, Z. Satellite-Based PM2.5 Estimation Directly from Reflectance at the Top of the Atmosphere Using a Machine Learning Algorithm. Atmos. Environ. 2019, 208, 113–122. [Google Scholar] [CrossRef]

| No. | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|
| 1 | Corrected_Optical_Depth_Land_wav2p1 2.13 μm (6.79%) | Optical_Depth_Land_And_Ocean 0.55 μm (4.62%) | Corrected_Optical_Depth_Land_wav2p1 2.13 μm (4.65%) | Optical_Depth_Ratio_Small_Land (5.15%) |
| 2 | Aerosol_Cloud_Fraction_Land (6.70%) | Corrected_Optical_Depth_Land 0.47 μm (4.38%) | Aerosol_Cloud_Fraction_Land (4.62%) | Longitude (5.13%) |
| 3 | Optical_Depth_Land_And_Ocean 0.55 μm (6.51%) | Longitude (4.36%) | Corrected_Optical_Depth_Land 0.66 μm (4.53%) | Quality_Assurance_Land (4.89%) |
| 4 | Quality_Assurance_Land (4.83%) | Aerosol_Type_Land (4.28%) | Quality_Assurance_Land (4.42%) | Corrected_Optical_Depth_Land 0.47 μm (4.74%) |
| 5 | Corrected_Optical_Depth_Land 0.66 μm (4.38%) | Image_Optical_Depth_Land_And_Ocean 0.55 μm (4.17%) | Corrected_Optical_Depth_Land 0.55 μm (4.25%) | Image_Optical_Depth_Land_And_Ocean 0.55 μm (4.37%) |
| Which Group | MAE | RMSE | R |
|---|---|---|---|
| Group 1 | 21.5 | 32.19 | 0.70 |
| Group 2 | 20.55 | 29.46 | 0.72 |
| Group 3_Spring | 21.05 | 30.50 | 0.85 |
| Group 3_Summer | 18.99 | 14.28 | 0.75 |
| Group 3_Autumn | 17.26 | 24.45 | 0.81 |
| Group 3_Winter | 32.86 | 45.84 | 0.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhang, Y.; Li, Z.; Wei, Y.; Peng, Z.; Luo, J.; Ou, Y. Prediction of Fine Particulate Matter Concentration near the Ground in North China from Multivariable Remote Sensing Data Based on MIV-BP Neural Network. Atmosphere 2022, 13, 825. https://doi.org/10.3390/atmos13050825
Wu H, Zhang Y, Li Z, Wei Y, Peng Z, Luo J, Ou Y. Prediction of Fine Particulate Matter Concentration near the Ground in North China from Multivariable Remote Sensing Data Based on MIV-BP Neural Network. Atmosphere. 2022; 13(5):825. https://doi.org/10.3390/atmos13050825
Chicago/Turabian StyleWu, Hailing, Ying Zhang, Zhengqiang Li, Yuanyuan Wei, Zongren Peng, Jie Luo, and Yang Ou. 2022. "Prediction of Fine Particulate Matter Concentration near the Ground in North China from Multivariable Remote Sensing Data Based on MIV-BP Neural Network" Atmosphere 13, no. 5: 825. https://doi.org/10.3390/atmos13050825
APA StyleWu, H., Zhang, Y., Li, Z., Wei, Y., Peng, Z., Luo, J., & Ou, Y. (2022). Prediction of Fine Particulate Matter Concentration near the Ground in North China from Multivariable Remote Sensing Data Based on MIV-BP Neural Network. Atmosphere, 13(5), 825. https://doi.org/10.3390/atmos13050825









