Influence of Relative Humidity on the Characteristics of Filter Cake Using Particle Flow Code Simulation
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
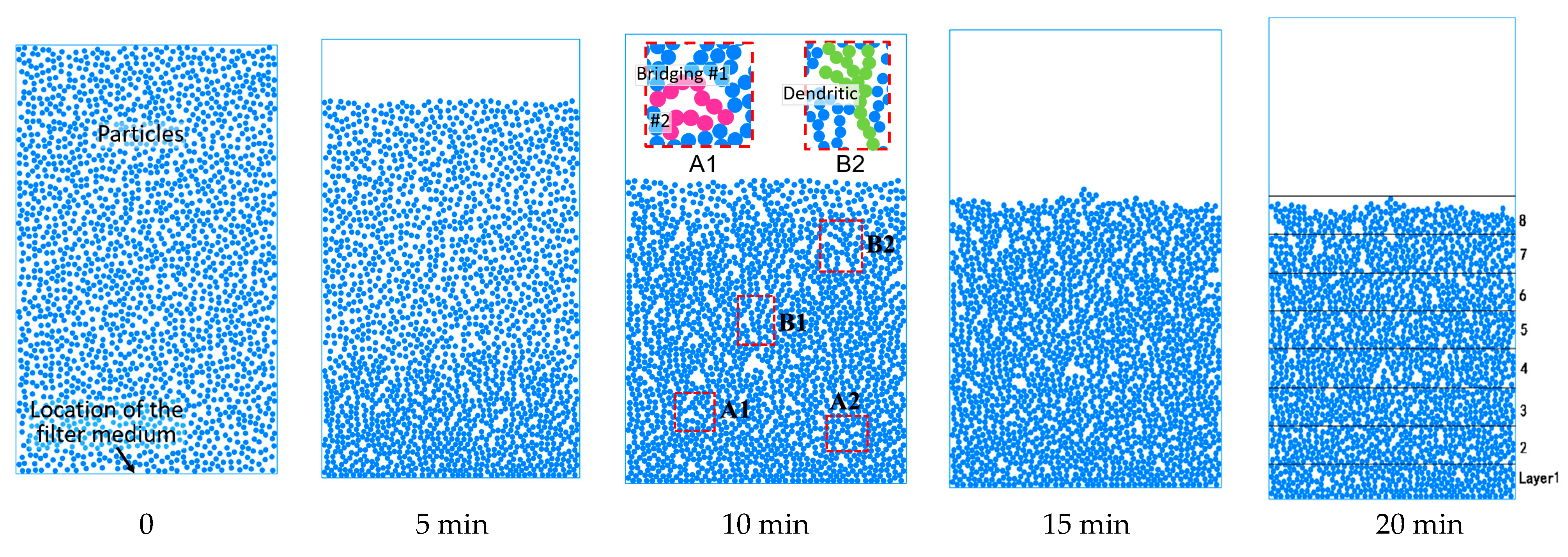
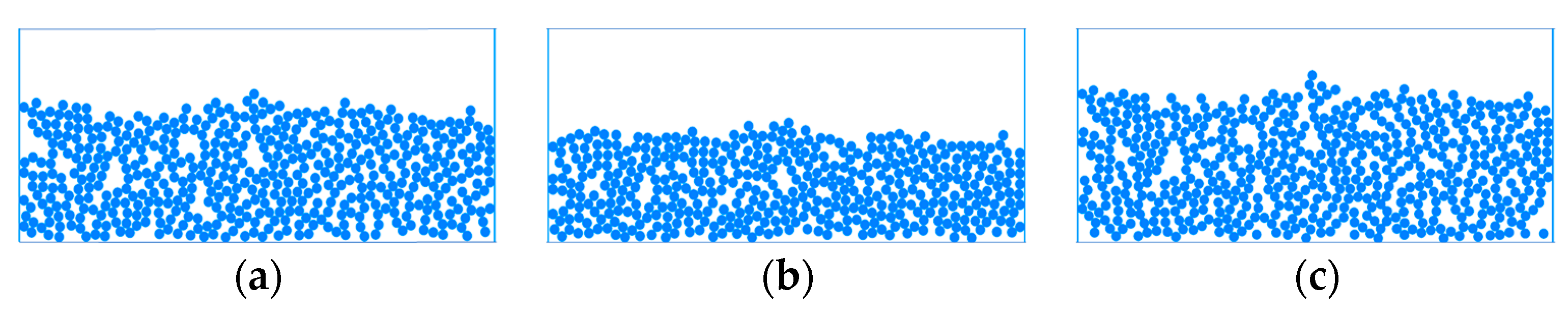
3.1. Deposition Morphology of Particles
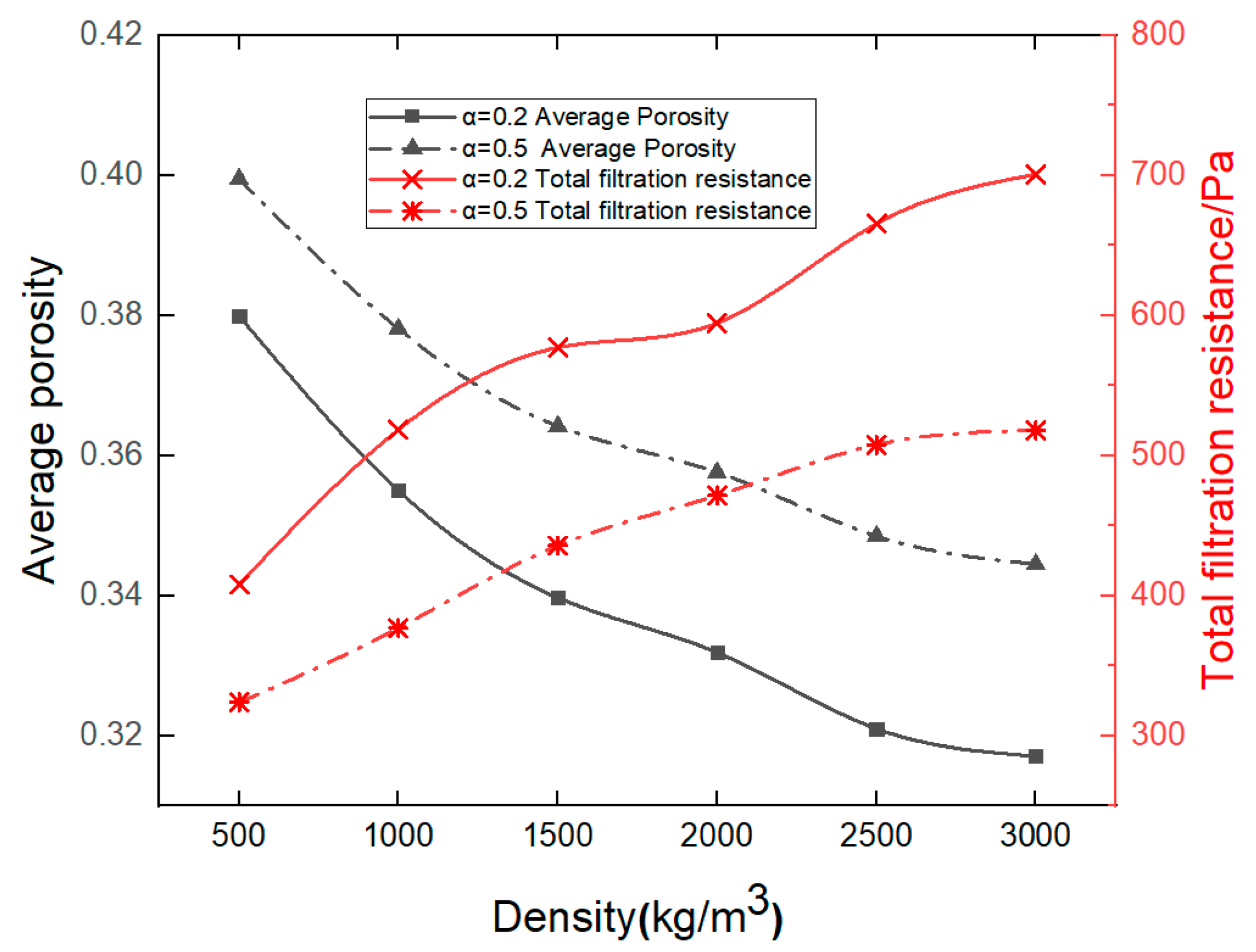
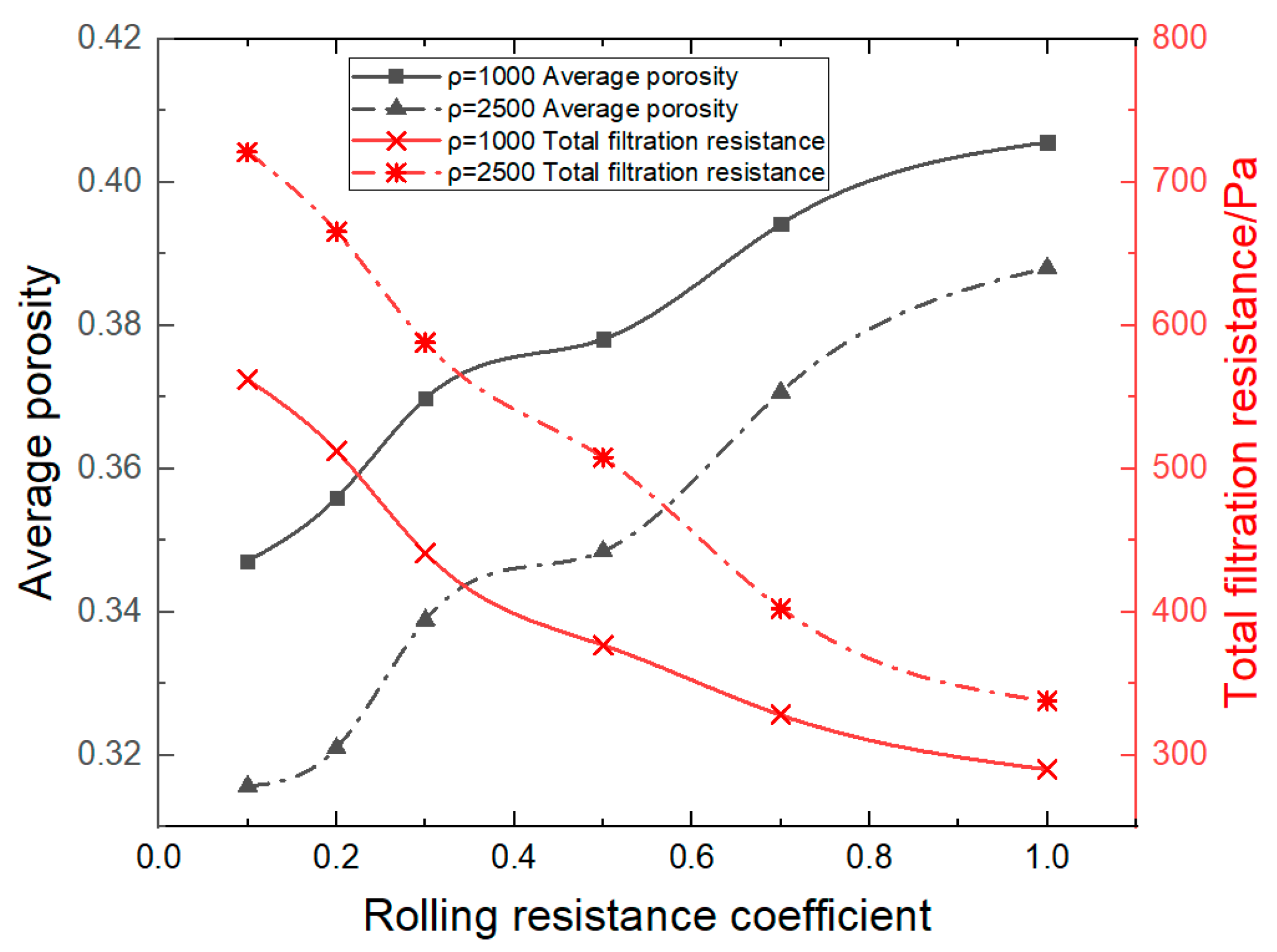
3.2. Effect of Particle Density on Filter Cake Properties
3.3. Influence of Particle Viscosity on Filter Cake Properties
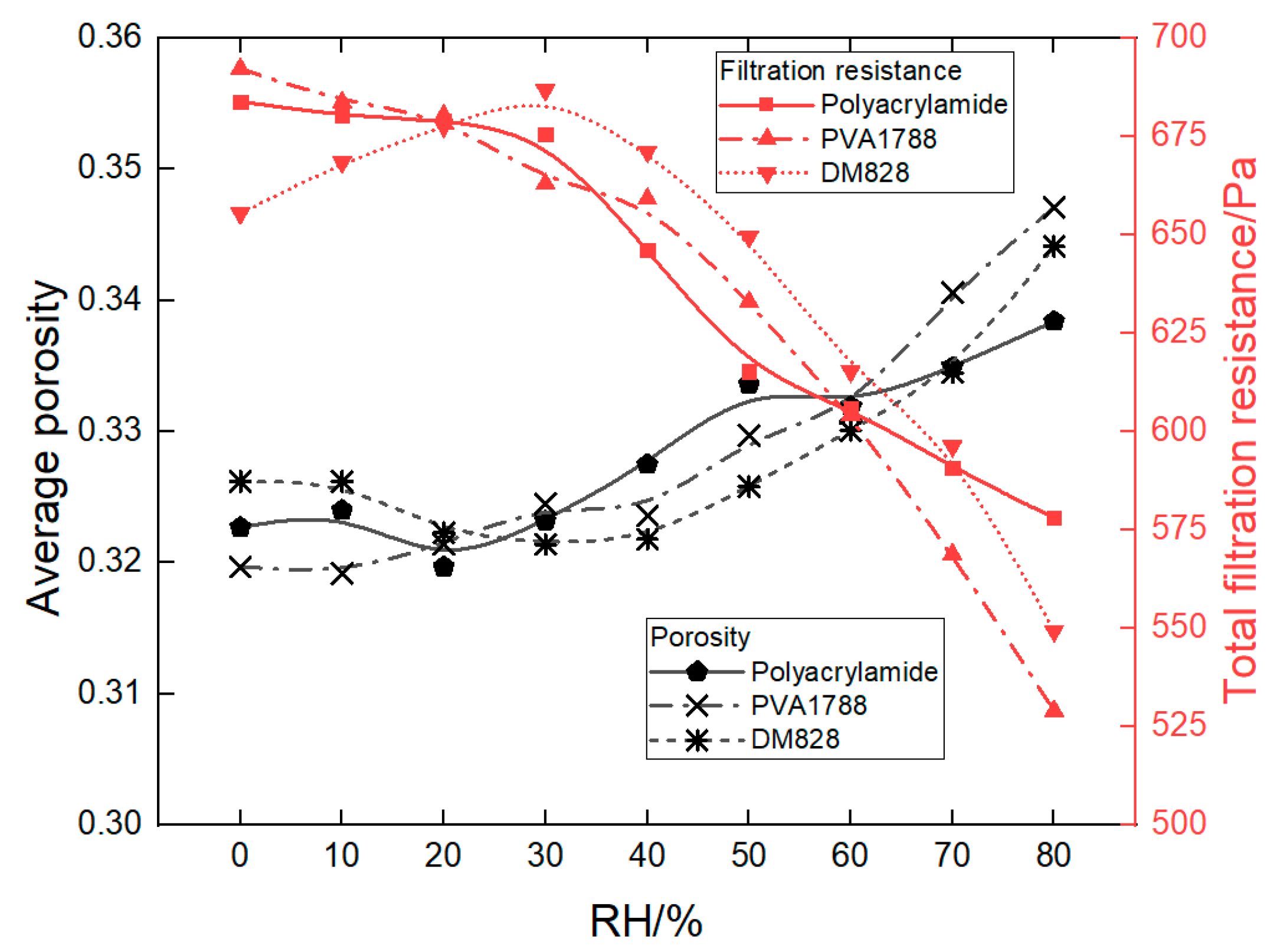
3.4. Influence of Air Humidity on Filter Cake Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pu, H.; Luo, K.; Wang, P.; Wang, S.; Kang, S. Spatial variation of air quality index and urban driving factors linkages: Evidence from Chinese cities. Environ. Sci. Pollut. Res. 2017, 24, 4457–4468. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wu, Q.; Huang, Y.; Sun, Z.; Li, J.; Wu, D. Particulate matters filtration by a filter medium with pin holes: Modeling and experimental verification. Process Saf. Environ. Prot. 2022, 158, 282–290. [Google Scholar] [CrossRef]
- Dentoni, V.; Grosso, B.; Pinna, F.; Lai, A.; Bouarour, O. Emission of Fine Dust from Open Storage of Industrial Materials Exposed to Wind Erosion. Atmosphere 2022, 13, 320. [Google Scholar] [CrossRef]
- Adamkiewicz, Ł.; Maciejewska, K.; Rabczenko, D.; Drzeniecka-Osiadacz, A. Ambient Particulate Air Pollution and Daily Hospital Admissions in 31 Cities in Poland. Atmosphere 2022, 13, 345. [Google Scholar] [CrossRef]
- Li, T.; Guo, Y.; Liu, Y.; Wang, J.; Wang, Q.; Sun, Z.; He, M.Z.; Shi, X. Estimating mortality burden attributable to short-term PM2.5 exposure: A national observational study in China. Environ. Int. 2019, 125, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Zanobetti, A.; Schwartz, J.; Dockery, D.W. Airborne particles are a risk factor for hospital admissions for heart and lung disease. Environ. Health Perspect. 2000, 108, 1071–1077. [Google Scholar] [CrossRef]
- Dominici, F.; Peng, R.D.; Bell, M.L.; Pham, L.; Mcdermott, A.; Zeger, S.L.; Samet, J.M. Fine particulate air pollution and hospital admission for cardiovascular and respiratory diseases. JAMA 2006, 295, 1127–1134. [Google Scholar] [CrossRef] [Green Version]
- Mazzeo, A.; Zhong, J.; Hood, C.; Smith, S.; Stocker, J.; Cai, X.; Bloss, W.J. Modelling the Impact of National vs. Local Emission Reduction on PM2.5 in the West Midlands, UK Using WRF-CMAQ. Atmosphere 2022, 13, 377. [Google Scholar] [CrossRef]
- Zaib, S.; Lu, J.; Bilal, M. Spatio-Temporal Characteristics of Air Quality Index (AQI) over Northwest China. Atmosphere 2022, 13, 375. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Q.; Chen, D.-R. Effect of pleat shape on reverse pulsed-jet cleaning of filter cartridges. Powder Technol. 2017, 305, 1–11. [Google Scholar] [CrossRef]
- Wang, J.; Ponting, M.; Zhang, C.; Olah, A.; Baer, E. Fuel filtration properties and mechanism of a novel fibrous filter produced by a melt-process. J. Membr. Sci. 2017, 526, 229–241. [Google Scholar] [CrossRef] [Green Version]
- Arunangshu, M.; Harshad, S.B. Emission of fine particles and ageing behavior of PTFE finished filter media during industrial pollution control. Environ. Pollut. 2015, 4, 58–68. [Google Scholar]
- Li, J.; Wang, A.; Fan, B.; Kuang, Q.; Li, J.; Wu, D. On the fractional dust emission features of the dust collector during the pulse-jet cleaning affected stage. J. Saf. Environ. 2018, 18, 315–319. [Google Scholar]
- Li, J.; Wang, P.; Wu, D.; Chen, D.-R. Numerical study of opposing pulsed-jet cleaning for pleated filter cartridges. Sep. Purif. Technol. 2019, 234, 116086. [Google Scholar] [CrossRef]
- Li, J.; Zhou, F.; Li, S. Experimental study on the dust filtration performance with participation of water mist. Process Saf. Environ. Prot. 2017, 109, 357–364. [Google Scholar] [CrossRef]
- Zhou, F.; Li, J.; Li, S.; Wang, F. Experimental investigation and application of dry-type filtering dust collection technology in fully mechanized excavation face. J. China Coal Soc. 2017, 42, 639–645. [Google Scholar]
- Wang, G. The Study of Behavior of ePTFE Membrane Filter in Air-Filtration Process; Beijing University of Chemical Technology: Beijing, China, 2004. [Google Scholar]
- Qing, T.; Shao, T.; Wen, S. Effects of relative humidity on surface adhesion. Tribology 2006, 26, 295–299. [Google Scholar]
- Xue, Z.; Qian, F.; Zhu, J. Numerical simulation of deposition characteristics for high moisture viscous particles on the surface of polytetrafluoroethylene microporous membrane filtration materials. Chin. J. Process Eng. 2020, 20, 521–530. [Google Scholar]
- Zhan, F. Modeling and Validation of Dust Particle Deposition on Fin-and-Tube Heat Exchangers; Shanghai Jiao Tong University: Shanghai, China, 2018. [Google Scholar]
- Gupta, A.; Novick, V.J.; Biswas, P.; Monson, P.R. Effect of humidity and particle hygroscopicity on the mass loading capacity of high efficiency particulate air (HEPA) filters. Aerosol Sci. Technol. 1993, 19, 94–107. [Google Scholar] [CrossRef]
- Ribeyre, Q.; Charvet, A.; Vallières, C.; Thomas, D. Impact of relative humidity on a nanostructured filter cake—Experimental and modelling approaches. Chem. Eng. Sci. 2017, 161, 109–116. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Li, X.; Wu, D.; Wu, Q.; Li, J. Dynamic simulation for depositive regularity of cohesive particles on surface of filter media. J. Saf. Environ. 2019, 19, 978–984. [Google Scholar]
- Boudhan, R.; Joubert, A.; Durécu, S.; Gueraoui, K.; Le Coq, L. Influence of air humidity on particle filtration performance of a pulse-jet bag filter. J. Aerosol Sci. 2019, 130, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Joubert, A.; Laborde, J.C.; Bouilloux, L.; Callé-Chazelet, S.; Thomas, D. Influence of Humidity on Clogging of Flat and Pleated HEPA Filters. Aerosol Sci. Technol. 2010, 44, 1065–1076. [Google Scholar] [CrossRef]
- Joubert, A.; Laborde, J.; Bouilloux, L.; Chazelet, S.; Thomas, D. Modelling the pressure drop across HEPA filters during cake filtration in the presence of humidity. Chem. Eng. J. 2011, 166, 616–623. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, X.; Yang, Z.; Yang, F.; Yang, J.; Zhang, W. Effects of humidity on dust removal intensification of bag filters. J. Chem. Eng. Chin. Univ. 2019, 33, 965–971. [Google Scholar]
- Li, J.; Li, S.; Zhou, F. Effect of moisture content in coal dust on filtration and cleaning performance of filters. Physicochem. Probl. Miner. Process. 2016, 52, 365–379. [Google Scholar]
- Shi, C.; Zhang, Q.; Wang, S. Particle Flow (PFC5.0) Numerical Simulation Technology and Application; China Construction Industry Press: Beijing, China, 2018. [Google Scholar]
- Ai, J.; Chen, J.; Rotter, J.M.; Ooi, J.Y. Assessment of rolling resistance models in discrete element simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- Chen, L.; Qian, F.; Ye, M.; Wei, M.; Han, Y.; Lu, J. Mathematical model of high-humidity dust peeling during pulse-jet cleaning. J. China. Coal Soc. 2019, 2, 683–690. [Google Scholar]
- Xie, H. Powder Mechanics and Engineering; Chemical Industry Press: Beijing, China, 2003. [Google Scholar]
- Payam, A.F.; Fathipour, M. A capillary force model for interactions between two spheres. Particuology 2011, 9, 381–386. [Google Scholar] [CrossRef]
- Xiong, G.; Gao, Z.; Hong, C.; Qiu, B.; Li, S. Effect of the rolling friction coefficient on particles’ deposition morphology on single fibre. Comput. Geotech. 2020, 121, 103450. [Google Scholar] [CrossRef]
- Liu, X.; Wu, C.; Sun, G.; Chen, B. Correlation analysis of blast furnace slag fly ash mixture of the macro micro mechanics parameter. J. Civ. Eng. Manag. 2015, 32, 1–7. [Google Scholar]
- Sun, Q.; Wang, G. Review on granular flow dynamics and its discrete element method. Adv. Mech. 2008, 38, 87–100. [Google Scholar]
- Shen, Z.; Jiang, M.; Zhu, F.; Hu, H. Influence of the micro parameters of discrete element on the macro parameters of sands. Northwestern Seismol. J. 2011, 33, 160–165. [Google Scholar]
- Zhou, B.; Wang, H.; Zhao, W.; Li, J.; Zhen, B. Analysis of relationship between particle mesoscopic and macroscopic mechanical parameters of cohesive materials. Rock Soil Mech. 2012, 33, 3171–3175. [Google Scholar]
- Carman, P.C. Fundamental principles of industrial filtration (A critical review of present knowledge). Trans. Inst. Chem. Eng. 1938, 16, 168–188. [Google Scholar]
- Wu, H.; Yao, Y.; Shen, Y. Moisture absorption and liberation regularities of textile sizes. Text. Res. J. 2016, 37, 72–77. [Google Scholar]



| Items | Values |
|---|---|
| Elastic modulus (Ec, Pa) | 1.0 × 108 |
| Stiffness ratio (kn/ks, -) | 2.0 |
| Friction coefficient (β, -) | 1.5 |
| Rolling resistance coefficient (α, -) | 0.0–1.0 |
| Particle radius (rp, μm) | 5 |
| Particle density (ρ, kg‧m−3) | 500–3000 |
| Number of particles (n, -) | 2000 |
| Particle Name | PVA1788 | Polyacrylamide | DM828 |
|---|---|---|---|
| Fitting formula | R = 0.1101RH – 0.4034 | R = 0.6595e0.0501RH | R = 0.2084RH – 0.1376 |
| Fitting degree R2 | 0.9081 | 0.9917 | 0.9918 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, D.; Li, J.; Du, Y.; Wu, Q.; Huang, S.; Huang, H.; Wu, D. Influence of Relative Humidity on the Characteristics of Filter Cake Using Particle Flow Code Simulation. Atmosphere 2022, 13, 770. https://doi.org/10.3390/atmos13050770
Shi D, Li J, Du Y, Wu Q, Huang S, Huang H, Wu D. Influence of Relative Humidity on the Characteristics of Filter Cake Using Particle Flow Code Simulation. Atmosphere. 2022; 13(5):770. https://doi.org/10.3390/atmos13050770
Chicago/Turabian StyleShi, Dinglian, Jianlong Li, Yongnan Du, Quanquan Wu, Shan Huang, Hong Huang, and Daishe Wu. 2022. "Influence of Relative Humidity on the Characteristics of Filter Cake Using Particle Flow Code Simulation" Atmosphere 13, no. 5: 770. https://doi.org/10.3390/atmos13050770
APA StyleShi, D., Li, J., Du, Y., Wu, Q., Huang, S., Huang, H., & Wu, D. (2022). Influence of Relative Humidity on the Characteristics of Filter Cake Using Particle Flow Code Simulation. Atmosphere, 13(5), 770. https://doi.org/10.3390/atmos13050770








