Abstract
Spectral analysis of terrain height variance is conducive to quantitatively study the terrain characteristics and grid-size selection for mesoscale models. Improved topographic resolutions can lead to the variations of terrain characteristics and the appropriate grid size for a fixed analyzed area. Spectral methods of one-dimensional weighted average and arithmetic mean were used to investigate the specific impact on the distribution of terrain spectra and grid-size selection for mesoscale models of the landslide-prone areas in western Sichuan. The results indicate that the maximum spectral energy (the variance of the terrain height series) of 30″ resolution (R1) is larger than that of 90 m resolution (R2), indicating a gentler undulation of terrain for R2. The spectral curve of R2 almost overlaps with that of R1 because the difference in topographic resolution does not change the dominant distribution of the topography. Their differing spectral energies at longer wavelengths are related to the majority of grid points of R2 distributed at shorter wavelength bands. A least squares fit in the form of was used to estimate the decreasing trend of the spectral distribution. The difference in spectral slope between R1 and R2 is mainly caused by the spectral energy of R2 at shorter wavelengths. The exponent b is connected with grid-size selection for mesoscale models. A universal horizontal grid size of 2.5 km for R1 and 1.9 km for R2 are required to resolve 95% of the terrain height variance for a mesoscale model application without a subgrid-scale parameterization. The simulation tests show that the improved topographic resolution appears to perform better in reproducing precipitation, which is probably related to the finer details of the terrain recognized by the model.
1. Introduction
Several years have passed since the Wenchuan earthquake, but secondary disasters caused by earthquakes pose another serious threat to local residents. Earthquakes result in mountain cracking, which is prone to forming a debris flow when a certain amount of precipitation occurs. Thus, it is crucial to focus on the study of rainfall in landslide-prone areas in western Sichuan, where terrain plays a very important role in triggering precipitation and affecting its spatial and temporal distribution. Major mountain barriers can significantly modulate precipitation over mountainous areas through dynamic processes, such as upslope ascent, leeside descent, and associated gravity wave activities [1,2,3,4,5,6,7,8]. Much of the previous research has found that even the gently rolling, small-scale terrain has an obvious effect on the distribution of the lower flows [9,10,11,12,13,14], thus affecting the distribution of precipitation. The ability to accurately capture the main features of atmospheric flows and rainfall distribution by the simulation relies heavily on resolving the primary terrain features over the focused region [15]. Since topography is a major driving force of the mesoscale atmospheric processes involved, the grid size and the domain of nested grids should be primarily influenced by local topography. However, accurate studies of the suitable model resolution for mesoscale models of the fixed domain are scant. An ultra-height model resolution for modeling will lead to typical numerical instability, making artificial rising of wave amplitudes for wave lengths between 2 and 4 distances of grid spacings. Suitable grid-size selection for filtering helps to retain major waves, filter out the short-wave disturbance in numerical integration, and effectively suppress the instability of nonlinear calculation [16]. The increase in model resolution also produces a significant calculation error of pressure gradient force, especially in steep terrain, though it helps the model to capture smaller-scale terrain and sharper topographic gradient. Thus, analysis of the terrain height variance is a necessary (although not sufficient) step in the process of establishing the suitable model resolution for a mesoscale model application [16].
Pielke and Kennedy (1980) [17] suggested that terrain characteristics can be truly represented in spectrum space, and terrain spectra can quantitatively reflect the effect of topographic dynamic forcing on atmosphere. Young and Pielke (1983) [18] found that the spectral analysis of terrain cross-sections can be used to investigate the terrain spectra. Since then, the one-dimensional operation along several adjacent terrain sections has been extensively used for the high computational efficiency [15,19,20,21,22]. Additionally, the spectral analysis of terrain height variance is associated with grid-size selection for mesoscale models [18,23]. The dominant wavelengths of terrain variance, represented by the terrain spectra in wavenumber (k) space or wavelength (λ = 1/k) space, facilitate the selection of the required grid size to resolve topographic perturbations without a subgrid-scale parameterization in mesoscale models. However, previous values of the grid spacing vary considerably due to different landscapes of differing focused areas [18,19,20,23,24]. It is essential to individually determine the required grid spacing for mesoscale models of each region (e.g., the landslide-prone areas).
The computed horizontal grid size relies on the domain length and the topographic resolution selected for the model. Related studies have suggested that the shorter model domain length corresponds to the smaller gird size under the same topographic resolution [18,20,23,24]. However, studies on the impact of the improved topographic resolution on the maximum grid size, which the majority of terrain can be resolved for mesoscale models of the fixed domain coverage, are scant. For example, terrain data with a 30″ resolution are usually used for mesoscale model applications. To investigate the fine detail of the terrain and, therefore, its effect on mesoscale atmospheric flows and precipitation distribution, the topographic resolution should be improved for mesoscale simulations in landslide-prone areas. How do the terrain spectra and the maximum grid size vary with the increased topographic resolution, and what causes these variances? The aim of this study was to explore the impact of the improved topographic resolution on the distribution of terrain spectra and grid-size selection for mesoscale models of the landslide-prone areas in western Sichuan. In this paper, the topographic data, the selected study area, and the spectral analysis method are presented in Section 2. The results of the impact of improved topographic resolution on the distribution of terrain spectra and grid-size selection for mesoscale models in the landslide-prone areas are presented in Section 3. The discussion and conclusions are summarized in Section 4.
2. Data and Methods
2.1. Data and Site
For this study, a region of landslide analysis with limits of 102.86°–104.16° E, 30.52°–31.72° N was selected. It covers an area of 123.6 × 133.6 km centered approximately in the epicenter (Wenchuan County), on the east border of the Tibetan Plateau in western Sichuan. Since the Wenchuan earthquake, several experimental campaigns have been carried out in this area for studying the slope runoff and infiltration [25,26,27,28] (Xu et al. 2012; Song et al. 2013; Gan et al. 2016; Li et al. 2016). Other works concerning landscape evolution and rainfall also have focused on this area [29,30,31,32,33,34] (Jiang and Li 2008; Yin et al. 2009; Fang et al. 2012; Li et al. 2018; Liu et al. 2018; Xie et al. 2018). The region is broadly considered to be a representative experimental site of the landslide-prone areas for investigating the influence of various aspects after the earthquake.
Two different topographic databases were used in this study. The gridded and quality-controlled global land base elevation database with 30″ resolution (R1) from the United States Geographical Data Center for its wide use for mesoscale modeling purposes, and the latest SRTM 90 m digital elevation database (R2), originally produced by National Aeronautics and Space Administration (NASA), were both used for the spectral algorithm. The topography distribution over the studied region in western Sichuan with the two topographic resolutions is shown in Figure 1. A region of landslide analysis with limits of 102.86°–104.16° E, 30.52°–31.72° N was selected. Although the topography distribution of R1 (Figure 1a) is basically the same as that of R2 (Figure 1b), a slight deviation exists in small areas (e.g., steep mountains). The increased topographic resolution produces a sharper topographic gradient and a finer terrain detail over transition zones between plains and mountains. The difference of the terrain characteristics affects the distribution of the terrain spectra and grid-size selection for mesoscale models, which will be described below in detail. In addition, the study region with 30″ resolution corresponds to the zonal and meridional grid points of 157 and 145, respectively. The actual topographic resolutions in the zonal and meridional directions are 792 and 928 m, respectively. For R2, the zonal grid points of 1561 and the meridional value of 1441 correspond to the approximate resolutions in the zonal and meridional directions of 79.2 and 92.8 m, respectively.
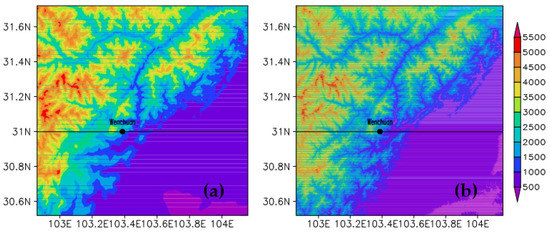
Figure 1.
The topography distribution over the studied region in western Sichuan with (a) 30″ resolution and (b) 90 m resolution (shaded, unit: m).The position of Wenchuan County is plotted as a dot. Black line indicates the cross-section along 31° N.
2.2. Methods
Since the terrain is two-dimensional, it is preferable to use a two-dimensional spectral analysis to depict the characteristic of a given terrain. However, it is computationally time-consuming to calculate the two-dimensional terrain spectra for a larger study region, in spite of the rapid development of computational resources. A quasi two-dimensional spectral algorithm for handling a large amount of topographic data greatly decreases the computational effort. Both the one-dimensional weighted average method and one-dimensional arithmetic mean were used to investigate the terrain spectra. The weighted average method, highlighting the weight contribution of each point to others when calculating, is more accurate in describing the terrain cross-section and the distribution of topographic disturbance spectra in the zonal and meridional directions. The arithmetic mean method, supposing the equal weight of each point, cancels out the large and small topographic spectral energy (the variance of the terrain height series). However, it is reliable in reflecting the intensity of the terrain effect, which can be used to reveal the amplitude difference of topographic perturbations between the zonal and meridional cross-sections in the same area.
The meridionally arithmetic mean zonal topographic profile () and zonally arithmetic mean meridional profile () are computed as follows:
where and represent the meridional and zonal grid, respectively, and M and N are the meridional and zonal grid points, respectively. The definition of the topographic energy, and the algorithm of the meridionally weighted average zonal topographic profile and zonally-weighted average meridional profile, can be found in Wang et al. (2019) [22]. Using the one-dimensional weighted average and arithmetic mean method, the meridionally averaged zonal topographic height series, and zonally-averaged meridional height series can be acquired, respectively. The terrain height variance spectra of the resulting series are determined by the algorithm of a discrete Fourier transform (DFT), and the resulting spectra (actually the mean-squared amplitude) depict the topographic distribution in k space or λ space.
For a model application, terrain height variations can be divided into two ranges: those with wavelengths greater than 2Δx (Δx is the grid size for mesoscale models) resolved by the model, and those with wavelengths less than 2Δx; the subgrid-scale terrain variations not resolvable [15]. Generally, the subgrid-scale terrain effect can be approximatively resolved by the parameterization of the subgrid-scale flux terms. However, for the uncertainty of the parameterization, a sufficiently small Δx is required to ignore the subgrid-scale effect. A least squares fit is used to estimate the relationship between the terrain height spectra (S) and variable λ in the form of . A two-dimensional spectrum analysis can be achieved using a two-dimensional fast Fourier transform (2DFFT). The minimum wavenumber (maximum wavelength) resolvable for a specific terrain is 1/L (L is the model domain length, Lx and Ly correspond to the zonal and meridional domain length, respectively), and the shortest wavelength (maximum wavenumber) in the measured spectra is 2δx (δx is the grid resolution of the terrain data). Assuming that a numerical model cannot resolve any characteristic with a length scale less than 2Δx, and that an acceptable representation may require 4Δx length scales, the ratio of the subgrid-scale terrain height variance to the model-resolved terrain height variance (r) is [23]
However, this method is computationally intensive, and is thus an inconvenient and uneconomical method for obtaining optimum model grid spacing [15]. Young and Pielke (1983) verified that spatial spectral analysis of a two-dimensional topographic profile can be replaced by a one-dimensional profile. The one-dimensional algorithm along several adjacent cross sections of terrain has been widely used for the convenience of calculation [15,19,20,24]. Based on the type of , r is
The expression (4) integrates to
where nΔx is the model domain length, and L = nΔx. The value of the exponent b is used to estimate the horizontal grid spacing for mesoscale models. When calculating the grid size, both the weighted-average method and the arithmetic mean can smooth out the small-scale terrain. It is not advisable to fit the power exponent based on the terrain height spectra obtained by these two methods. Accurate b and, therefore, computed grid spacings for each region can be obtained by investigating many zonal and meridional terrain cross sections with an appropriate interval [18,19]. The minimum grid spacing, not optimal for many mesoscale modeling, applies to study every case in a specific area.
3. Results
3.1. The Terrain Spectra with Different Resolutions
The zonal and meridional distributions of weighted-average terrain height variance spectra versus wavenumbers (km−1) with two topographic resolutions are represented in Figure 2. As the discreteness of terrain data results in the insignificance of the wavelengths less than twice the grid resolution, the minimum measured wavelength in spectrum space is twice the terrain resolution. In Figure 2a, the smallest wavelength is 1.59 km (k = 0.63 km−1) for R1 (black line) and 0.16 km (k = 6.3 km−1) for R2 (red line). The spectral energy for 1.59 km < λ < 10 km (R1) and 0.16 km < λ < 10 km (R2) is close to zero, implying that the terrain spectra energy in these wavelength bands is not dominant in the whole study region. It can be found that the maximum topographic spectral energy is 3.6 × 106 m2 km (R1) and 3.2 × 106 m2 km (R2) in the zonal direction, indicating that the increased topographic resolution produces a gentler undulation of terrain. The dominant wavelengths (DWs) corresponding to the topographic spectral peak are both 61.8 km for R1 and R2 in the zonal direction (Figure 2a), showing the most evident undulation of terrain and videlicet the maximum topographic dynamic forcing. When λ < DW, the spectral energy (the forcing) mainly declines with decreasing λ, in spite of several departures.
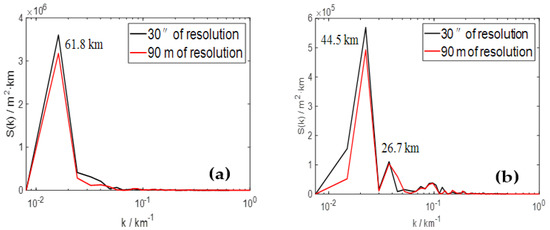
Figure 2.
The weighted-average terrain height variance spectra (a) in zonal direction and (b) in meridional direction. Black curve and red curve correspond to 30″ resolution and 90 m resolution, respectively.
Similarly, in the meridional direction (Figure 2b), the smallest resolvable wavelength is 1.86 km for R1 (black line) and 0.19 km for R2 (red line). The maximum topographic spectral energy is 5.7 × 105 m2 km (R1) and 4.8 × 105 m2 km (R2), corresponding to the same DW of 44.5 km. Moreover, as shown in Figure 2, the spectral peak in meridional direction is about an order of magnitude less than the value in zonal direction, indicating a weaker topographic dynamic forcing in meridional direction. When λ < 44.5 km, the topographic forcing weakens with decreasing λ, though there are sporadic departures (λ = 26.7 km) from this trend for the actual complex terrain.
The zonal and meridional distributions of arithmetic-mean terrain height variance spectra (Figure 3) are about the same as that of weighted-average terrain height variance spectra (Figure 2). The obtained DWs by these two methods are both 61.8 km in zonal direction and 44.5 km in meridional direction, and the spectral energy curves of R1 and R2 are basically the same. In addition, no matter in zonal direction or in meridional direction, the order of magnitude of the maximum spectral energy obtained by arithmetic mean is the same as that obtained by weighted average, and the maximum spectral energy of R1 is larger than that of R2. However, subtle differences between the arithmetic-mean terrain spectra and the weighted-average terrain spectra exist objectively, especially at DWs. As shown in Figure 3, the maximum topographic spectral energy is 3.3 × 106 m2 km (R1) and 2.5 × 106 m2 km (R2) in zonal direction (Figure 3a), less than the values obtained by weighted average. In meridional direction (Figure 3b), the maximum topographic spectral energy is 7 × 105 m2 km (R1) and 6.3 × 105 m2 km (R2), both larger than the values obtained by weighted average. The changes of the maximum spectral energy in the zonal and meridional directions by the two algorithms just show the different characteristics of these two methods.
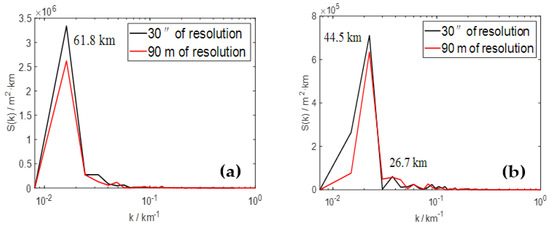
Figure 3.
The arithmetic-mean terrain height variance spectra (a) in the zonal direction and (b) in the meridional direction. Black curve and red curve correspond to 30″ resolution and 90 m resolution, respectively.
The distribution of the terrain spectra with these two topographic resolutions along 31° N is also shown in Figure 4. The cross-section region indicated by the black line in Figure 1 represents the complex terrain across the Wenchuan County. It can be seen that the distribution of the topographic spectral energy along 31° N is almost the same as the meridionally averaged zonal spectral energy (Figure 2a and Figure 3a). They correspond to the same DW of 61.8 km, and the maximum topographic spectral energy of R1 is always larger than that of R2. In addition, the maximum spectral energy is 15 × 106 m2 km (R1) and 11.5 × 106 m2 km (R2) (Figure 4), much larger than the values of the averaged zonal spectral energy, implying the significant differences of the topographic spectral energy in different zonal locations. Moreover, as shown in Figure 2, Figure 3 and Figure 4, the spectral energy of R2 almost overlaps with that of R1, no matter along 31° N or in zonal and meridional direction. It is understandable because the variation of topographic resolution basically does not change the dominant distribution of topography for the same region. Moreover, from a statistical standpoint, the total energy of the power spectrum defined in the spatial domain is exactly the variance of the terrain height series, from which a linear trend of the topographic profile has been subtracted. This total energy or total variance can be decomposed into the sum of energy or variance at each wavelength, which basically remains unchanged for the same domain when the topographic resolution changes, according to the definition of variance. So, under the same wavelengths (e.g., λ > 1.59 km in zonal direction), the spectral energy of R2 (the variance) changes little though the number of grid points increases compared to that of R1. On the other hand, although the spectral energy of R1 shows values that are much closer to R2 at λ > 1.59 km in zonal direction and λ > 1.86 km in meridional direction, the differences between them exist objectively, especially at DWs. As the mathematical expectation of the disturbed terrain height series is zero, the total energy or total variance is almost invariable for the same domain length, no matter how the topographic resolution changes. The higher resolution corresponds to more grid points, for example, the zonal number of grid points of R2 is 4801, 9 times more than that of R1, so the majority of grid points are scattered at the wavelength bands of λ < 1.59 km. The spectral energy at the wavelength bands of λ > 1.59 km decreases correspondingly compared to that of R1, thus causing the differences at each wavelength.
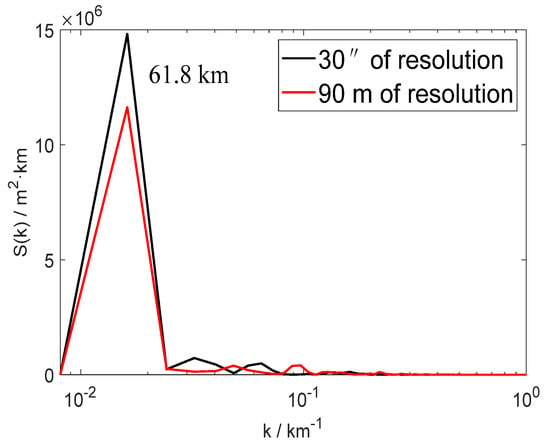
Figure 4.
Terrain height variance spectra for the cross section along 31° N. Black curve and red curve correspond to 30″ resolution and 90 m resolution, respectively.
A further analysis is undertaken on the relation between the terrain height spectra (S) and variable λ. As mentioned above, the longer wavelength presents a larger spectral energy, and the relatively short wavelength corresponds to the smaller spectral energy. The trend of the spectral distribution at the wavelength bands of λ < DW is basically downward with decreasing λ. A least squares fit in the form of is used to estimate the decreasing trend that is close to the exponential form. The parameter a in this equation represents the variance of the terrain height when λ = 1 km, and the exponent b is the spectral slope of the fitting curve in the log–log space. The smaller b shows the greater terrain variance at the shorter wavelength bands and videlicet the stronger small-scale topographic forcing. It is commonly reported that topographic spectra obey this power law relationship and considerable attention has been devoted to the exponent b [35,36,37,38,39,40,41].
As the distribution of the topographic spectral energy for the cross section along 31° N is almost the same as the weighted-average spectra and the arithmetic-mean spectra, the weighted-average terrain spectra are only selected to analyze the exponent b. In Figure 5a, zonal distribution of the weighted-average terrain height variance spectra in the log–log coordinate are represented. Each discrete point, representing the value of spectral energy, is an individual element from the one-dimensional DFT array. The dashed line is the fitting spectral slope of R1 and the solid line represents the slope of R2. In the log–log space, the relationship between the variables is transformed into the form of . Obviously, the fitting slope, which shows a downward spectral energy trend, is exactly the value of −b (Figure 5a). It can be found that the fitting slope of R1 is −2.2, corresponding to the exponent b of 2.2. In view of a similar roll-off in spectral energy between R1 and R2 at the wavelength bands of λ > 1.59 km (k < 0.63 km−1), the spectral slope of R2 is also approximately −2.2 at the same bands. Although the spectral slope (−2.2) is relatively gentle at k < 0.63 km−1, there is a marked steepening of the spectral slope of R2 at k > 0.63 km−1, thus causing the fitting spectral slope of −2.42 at the whole wavelength bands. Obviously, the difference of the slopes is mainly caused by the spectral energy of R2 at higher wavenumber bands. The deviation of the zonal spectral energy between R1 (the extension of the slope) and R2 at k > 0.63 km−1 is presented in Figure 5b. Conceivably, the positive deviation shows a smaller spectral slope of R2 (b > 2.2) and the negative deviation corresponds to the larger slope (b < 2.2). Therefore, the positive value shown in Figure 5b explains the decrease of the spectral slope of R2.
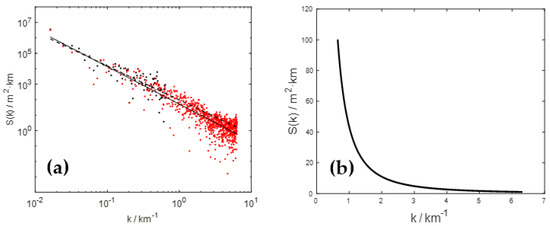
Figure 5.
(a) The zonal terrain height variance spectra in the log–log coordinate and (b) the deviation of the spectral energy between 30″ resolution and 90 m resolution above the wavenumber of 1.59 km−1. The dashed line is the fitting spectral slope of 30″ resolution based on the black dots and the solid line represents the slope of 90 m resolution based on the red dots.
Further insight into the positive deviation, which results in the decrease of the spectral slope (the increase of b), is gained. In general, the increased topographic resolution (R2) presents finer terrain features and, therefore, more actual topographic amplitudes at shorter wavelengths (the red dots at λ < 1.59 km in Figure 5a). These terrain spectra are less than the fitting values of R1, because the prominent terrain height variance at longer wavelengths (λ > 1.59 km) can result in larger amplitudes by lengthening the fitting least-squares regression line of R1. Therefore, the larger spectral energy of R1 at shorter wavelengths leads to the positive deviation between R1 and R2, and this deviation declines with increasing k (Figure 5b). Meanwhile, in consideration of the similar spectral energy of R1 and R2 at longer wavelengths, the spectral energy deviation of R2 between longer wavelengths and shorter wavelengths is more obvious than that of R1. Moreover, as mentioned before, the majority of discrete points of R2 are scattered at shorter wavelengths, where the roll-off in spectral energy is remarkable. The overwhelming advantage in number plays a leading role in fitting the spectral slope of R2, thus increasing the decrease of the spectral slope. For these reasons, the zonal spectral slope of R2 is much smaller than that of R1.
Similarly in meridional direction (Figure 6a), the fitting spectral slope of R1 is −2.29 and the slope of R2 is −2.44, corresponding to the exponent b of 2.29 and 2.44, respectively. The downward spectral energy trend of R2 at longer wavelengths (λ > 1.86 km) is more obvious compared to R1 at shorter wavelengths (λ < 1.86 km). This difference is mainly caused by the positive deviation of the meridional spectral energy between R1 and R2 at shorter wavelengths, shown in Figure 6b. In addition, the exponent b of R1 (or R2) in meridional direction is less than that in zonal direction, indicating a smoother terrain surface in meridional direction. Moreover, through numerous tests in different regions (figures not shown), the spectral slope of R2 is always less than that of R1, implying that the increased topographic resolution results in the decrease of the spectral slope (the increase of b) under the same domain length. This further affects the selection of grid size for mesoscale models, which will be analyzed in detail in the following section.
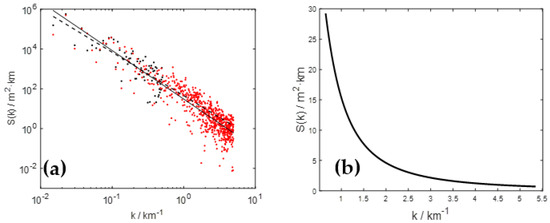
Figure 6.
(a) The meridional terrain height variance spectra in the log–log coordinate and (b) the deviation of the spectral energy between 30″ resolution and 90 m resolution above the wavenumber of 1.86 km−1. The dashed line is the fitting spectral slope of 30″ resolution based on the black dots and the solid line represents the slope of 90 m resolution based on the red dots.
3.2. The Relationship between the Grid Size and the Exponent b
Pielke and Kennedy (1980) [17] first obtained an upper bound of Δx for west-central Virginia by integrating the area under terrain height spectra and specifying a percentage of model-resolved terrain height variance to total terrain height variance. The same procedure can be used to estimate the grid spacing for mesoscale models of any terrain. For example, Young and Pielke (1983) [18] determined the suitable grid spacing of 2.75–7.5 km to resolve 90% of the terrain variance for different terrain cross sections. Salvador et al. (1999) [23] obtained a grid spacing of 10 km for the whole Iberian Peninsula, using a model-resolved terrain percentage of 95%.
As mentioned before, the value of the exponent b, which fits the terrain height variance spectra on a logarithmic scale, is used to determine the horizontal grid spacing for mesoscale models. Every terrain cross section is analyzed to obtain the exponent b and Δx, by computing Equation (5) with specified percentage of r in advance. It is troublesome to pick out the minimum Δx through calculating many different fitting exponents. Finding a mathematical relationship between Δx and b can improve calculation efficiency considerably. Wang et al. (2015) [15] proved that Δx is a monotonically increasing function with respect to b, indicating that the minimum Δx is determined by the minimum b. The result that Δx increases with increasing b can also be obtained by analyzing the distribution of the topographic spectral energy in the log–log coordinate (Figure 5a and Figure 6a). In Figure 5a, there is a similar distribution of the topographic spectral energy between R1 and R2 at the wavelength bands of λ > 1.59 km, whereas a significant reduction in spectral energy of R2 exists at shorter wavelengths (λ < 1.59 km) compared to R1. The positive deviation of the spectral energy between R1 and R2 (Figure 5b) indicates that the increased topographic resolution results in the decrease of the spectral energy at shorter wavelengths. It is assumed that the spectral slopes of R1 and R2 represent the terrain height variance for two cross sections of a fixed region under the same topographic resolution. In order to obtain the same r with R1, Δx must move along opposite direction of the X-axis (Figure 5a) to increase the subgrid-scale terrain height variance of R2, thus increasing the value of Δx.
3.3. Universal Grid Sizes for Mesoscale Models of the Landslide-Prone Areas with Different Topographic Resolutions
Since the value of Δx decreases with decreasing b, the universal grid spacing for the model domain is determined by the minimum b. The study region is divided into seven cross sections in zonal and meridional directions, respectively, each with an interval of 0.2°. The values of a and b for each of the fourteen cross sections of R1, based on the least squares best fit relation , are given in Table 1. The coefficient a, having a considerable difference among these cross sections, represents differing topographic forcing. The value b, varying from 1.80 to 3.01, reflects dissimilar terrain smoothness.

Table 1.
Parameters of the least squares fit relation , for fourteen terrain height variance spectra of 30″ resolution (R1) for the landslide-prone areas in western Sichuan.
In the zonal direction, the minimum b of 1.80 for R1 among seven terrain cross sections can be obtained. For the spectral relationship in the form of , the ratio of subgrid-scale terrain height variance to model resolved terrain height variance is . It integrates to
nΔx is 123.6 km for a zonal distance of the study region, and δx = 0.793 km. The values of percentages of resolved terrain height variance and computed model grid sizes, are tabulated in Table 2. Supposing that resolving 95% of the terrain variance of R1 gives adequate consideration in terrain effects of the model domain, a zonal grid size of 2.5 km is required without a subgrid-scale parameterization for the landslide-prone areas. A minimum b of 1.84 for R2 is also obtained among seven cross sections in the zonal direction (table not shown). For the same domain, nΔx = 123.6 km, but δx = 0.079 km for R2. Several calculated grid spacings, corresponding to the same percentages of resolved terrain height variance as in Table 2, are given in Table 3. A zonal Δx of 1.9 km or finer is appropriate to correctly consider the overall terrain effects of R2, which is smaller than the value of Δx for R1 (2.5 km). As mentioned above, Δx increases with increasing b under the same topographic resolution. The decrease of Δx for R2 is mainly caused by the improved topographic resolution (δx).

Table 2.
The resolved terrain height variance of R1 for model resolution and the ratios of unresolved/resolved topography (r) in mesoscale model. nΔx = 123.6 km and δx = 0.793 km.

Table 3.
The same as in Table 2, but for 90-m topographic resolution (R2). nΔx = 123.6 km and δx = 0.079 km.
Similarly, in the meridional direction, based on the minimum b of 2.0 (R1) and 2.09 (R2), values of computed grid resolutions are listed in Table 4 and Table 5, respectively. It is evident that 4.1 km (R1) and 4.2 km (R2) are likely maximum allowable values of meridional grid spacings to resolve the overwhelming majority of terrain height variance. Furthermore, both the grid sizes of R1 and R2 in the meridional direction (Table 4 and Table 5) are larger than that in the zonal direction (Table 2 and Table 3). The upper bounds of Δx for the whole study region, corresponding to different percentages of resolved terrain height variance, are actually the values given in Table 2 and Table 3, respectively. Thus, for every case study to resolve the vast majority (95%) of the terrain effects for a mesoscale model in the landslide-prone areas without a subgrid-scale parameterization, the required grid spacings are 2.5 km for R1 and 1.9 km for R2, respectively.


3.4. Model Sensitivity to Grid Sizes with Different Topographic Resolutions
To show the effect of differing grid sizes on a mesoscale model with different topographic resolutions and better illustrate the results obtained by the spectral method, several simulations using the advanced regional prediction system (ARPS) with different grid spacings were performed. In our previous study [15], the simulations under R2 with different grid resolutions (Table 3) showed that the model captured more features of the observed rainfall distribution as the grid size decreased. When the grid size was on the order of 4.1 km or less, the model improved only slightly in terms of the spatial distribution of precipitation. In order to show how the improved topographic resolution works on the grid sizes, the simulation of T-2.5, which corresponds to 95% of resolved terrain variance of R1, is added for the comparison with T-1.9 [15]. The model physics packages of T-2.5 are consistent with that of T-1.9. As shown in T-2.5 (Figure 7c), the simulated result roughly reproduces the shapes of precipitation areas and zones of maximum precipitation (Figure 7a). The extent and rain rates at some locations are highly overestimated (e.g., 30.75° N, 103.45° E, and 31.1° N, 103.5° E), and the false precipitation center at 30.9° N, 103.5° E arises compared to the observed location. The simulation of T-1.9 (Figure 7b) appropriately produces similar areas of precipitation as well as the maximum precipitation, despite a slight disparity in range compared to the observed precipitation centers. In addition, the maximum precipitation also shows values much closer to the observed maximum.
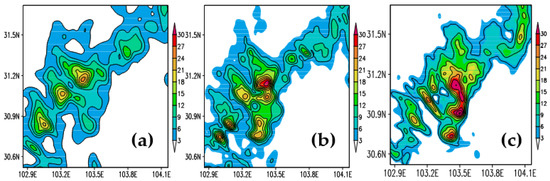
Figure 7.
The 1-h accumulated precipitation (shaded, unit: mm) at 1800 UTC 9 July, 2013; (a) observed precipitation; (b) simulated precipitation under R2 with 1.9-km grid size; (c) simulated precipitation under R1 with 2.5-km grid size.
Overall, although the simulation tests of T-2.5 and T-1.9 appear to perform well in estimating the observed precipitation, the model result in T-1.9 is better than the simulation of T-2.5 in terms of the spatial distribution and intensity. The result of the tests indicates that although the model using the selected grid spacings of 2.5 km for R1 and 1.9 km for R2 can both capture the majority (95%) of the terrain characteristics for a mesoscale modeling, the improved topographic resolution appears to obtain better simulation performance in precipitation and corresponding atmospheric flows (figure not shown).This is probably related to the finer detail of the terrain recognized by the model using the improved topographic resolution. Thus, it is recommended to drive the mesoscale modeling using the improved topographic resolution for better simulation results, especially in the regions of complex topography.
4. Discussion and Conclusions
The representation of the terrain height variance in spectrum space is conducive to quantitatively study the terrain characteristics of a fixed analyzed area (e.g., the landslide-prone areas in western Sichuan). This process can be accomplished by a spectral analysis of terrain heights using the DFT. Quasi two-dimensional algorithms of terrain height series are used to investigate the terrain spectra. The resulting spectra with two topographic resolutions (30″ and 90 m) are presented to depict their differences. The maximum spectral energy of R1 is larger than that of R2, indicating that the increased topographic resolution produces a gentler undulation of terrain. The spectral curve of R2 almost overlaps with that of R1 both in zonal and meridional direction because the difference of topographic resolution does not change the dominant distribution of topography. It can be also explained from a statistical standpoint—that the terrain height variance (exactly the spectral energy) basically remains unchanged at each wavelength for the same domain when the resolution changes. The differences between the spectral energy of R2 and that of R1 at longer wavelengths are mainly caused by part of spectral energy of R2 distributed at shorter wavelengths.
The trend of the spectral distribution at the wavelength bands of λ < DW is basically downward with decreasing λ. A least squares fit in the form of is used to estimate this decreasing trend. In logarithmic space, the fitting spectral slope, exactly the value of −b, shows the roll-off in spectral energy. The obvious difference in spectral slope between R1 and R2 is mainly caused by the spectral energy of R2 at shorter wavelengths. The positive deviation of the spectral energy between R1 and R2 at shorter wavelengths causes the decrease of the spectral slope of R2. Meanwhile, the majority of discrete points of R2 are scattered at shorter wavelengths where the roll-off in spectral energy is remarkable. The overwhelming advantage in number illustrates a major role these points play in fitting the spectral slope of R2, thus deepening the decrease.
The exponent b is related to the selection of grid spacing for mesoscale models. Different topographic resolutions correspond to dissimilar spectral slopes and therefore the discrepant horizontal grid spacings. The minimum grid spacing for the model domain is determined by the minimum b, by giving the fixed domain length and the percentage of resolved terrain height variance. The computed upper bound of grid spacing is greater in the meridional direction than that in the zonal direction. A universal horizontal grid size of 2.5 km for R1 and 1.9 km for R2 are necessary to resolve 95% of the terrain height variance for mesoscale models of the landslide-prone areas, without resorting to the parameterization of subgrid-scale terrain effects. The effect of differing grid sizes on a mesoscale model with the two topographic resolutions is analyzed by several simulation tests. The improved topographic resolution appears to perform better in reproducing precipitation and corresponding atmospheric flows, which is probably related to the finer detail of the terrain identified by the model. It is recommended to drive the mesoscale modeling using the improved topographic resolution for better simulation results, especially in the regions of complex topography.
We should note that a designated domain coverage should be large enough to include the majority of terrain features, which might influence the atmospheric flows. When the model domain is determined in advance, the horizontal grid size depends only on the selected terrain resolution. Although the inclusion of 95% of the terrain height variance should be good enough to capture the majority of terrain influence on the basic flows, it does not mean that the subgrid-scale terrain effect is fully resolved. A small proportion of unresolved topography (5%), corresponding to the negligible topographic spectral energy, indicates weak dynamic forcing that can be ignored. It is hard to assure whether resolving 95% of the terrain variance is adequate for an application of mesoscale models. However, the study provides a method to calculate the terrain variance. In addition, the spectral analysis of terrain height variance for the selection of the grid size is not, of course, the only prior analysis that should be made in any mesoscale model application. There are other more important considerations on the numerical resolution for mesoscale models, for example, the needs to resolve convection (the most important element for precipitation modeling), and numerical diffusion that often renders the effective resolution to a factor five to seven times larger than actual model grid spacing. However, the terrain spectra provide some constraint on the required horizontal grid spacing and a reference for others simulating the orographic flow without resorting to the parameterization of subgrid-scale terrain variance for mesoscale models.
Author Contributions
Conceptualization, C.W.; methodology, C.W., L.L. and W.Z.; formal analysis, C.W.; investigation, C.W.; data curation, C.W. and L.L.; writing—original draft, C.W.; writing—review and editing, C.W., L.L., W.Z., S.G. and S.Y.; supervision, S.G. and S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Science Foundation for Young Scientists of China (grant no. 41905048), the National Key Research and Development Program of China (grant no. 2018YFC1505705), and the Basic Research Fund of Chinese Academy of Meteorological Sciences (grant no. 2019Z008).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The research data related to this study can be made available for scientifific purposes upon request to the corresponding author.
Acknowledgments
The authors thank the anonymous reviewers for their suggestions, which helped to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scorer, R.S. Theory of waves in the lee of mountains. Q. J. R. Meteorol. Soc. 1949, 75, 41–56. [Google Scholar] [CrossRef]
- Mclntyre, M.E. On Long’s hypothesis of no upstream influence in uniformly stratified or rotating flow. J. Fluid Mech. 1972, 52, 209–243. [Google Scholar] [CrossRef]
- Klemp, J.B.; Lilly, D.K. Numerical simulation of hydrostatic mountain waves. J. Atmos. Sci. 1978, 35, 78–107. [Google Scholar] [CrossRef]
- Tucker, D.F.; Reiter, E.R. Modeling heavy precipitation in complex terrain. Meteorol. Atmos. Phys. 1988, 39, 119–131. [Google Scholar] [CrossRef]
- Johnson, G.L.; Hanson, C.L. Topographic and atmospheric influences on precipitation variability over a mountainous watershed. J. Appl. Meteor. 1995, 34, 68–87. [Google Scholar] [CrossRef]
- Aebischer, U.; Schar, C. Low-level potential vorticity and cyclogenesis to the lee of the Alps. J. Atmos. Sci. 1998, 55, 186–207. [Google Scholar] [CrossRef]
- Jiang, Q.F. Precipitation over concave terrain. J. Atmos. Sci. 2006, 63, 2269–2288. [Google Scholar] [CrossRef]
- Jiang, Q.F. Precipitation over multiscale terrain. Tellus 2007, 59, 321–335. [Google Scholar] [CrossRef]
- Queney, P. The problem of air flow over mountains: A summary of theoretical studies. Bull. Amer. Meteor. Soc. 1948, 29, 16–26. [Google Scholar] [CrossRef]
- Lu, J.H. The Panorama of South-West Vortex; Meteorology Press: Beijing, China, 1986; p. 270. [Google Scholar]
- Ding, Y.H. The Research of Mesoscale Weather and Dynamics; Meteorology Press: Beijing, China, 1996; p. 322. [Google Scholar]
- Schar, C.; Durran, D.R. Vortex formation and vortex shedding in continuously stratified flows past isolated topography. J. Atmos. Sci. 1997, 54, 534–554. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Sang, J.G.; Liu, H.Z.; Liu, S.H. Wave drag and form drag induced by small scale terrain in the nocturnal stable boundary layer. Chin. J. Geophys. 2007, 50, 43–50. [Google Scholar] [CrossRef]
- Steeneveld, G.J.; Holtslag, A.A.M.; Nappo, C.J.; van de Wiel, B.J.H.; Mahrt, L. Exploring the possible role of small-scale terrain drag on stable boundary layers over land. J. Appl. Meteor. Climatol. 2008, 47, 2518–2530. [Google Scholar] [CrossRef]
- Wang, C.X.; Gao, S.T.; Ran, L.K.; Liang, L. Proof of the monotonicity of grid size and its application in grid-size selection for mesoscale models. Adv. Atmos. Sci. 2015, 32, 1005–1015. [Google Scholar] [CrossRef]
- Pielke, R.A. Mesoscale Meteorological Modeling; Academic Press: San Diego, CA, USA, 1984; p. 599. [Google Scholar]
- Pielke, R.A.; Kennedy, E. Mesoscale Terrain Features. Report UVA-ENV SCI-MESO-1980-1; University of Virginia: Charlottesville, VA, USA, 1980; p. 19. [Google Scholar]
- Young, G.S.; Pielke, R.A. Application of terrain height variance spectra to mesoscale modeling. J. Atmos. Sci. 1983, 40, 2555–2560. [Google Scholar] [CrossRef][Green Version]
- Young, G.S.; Pielke, R.A.; Kessler, R.C. A comparison of the terrain height variance spectra of the Front Range with that of a hypothetical mountain. J. Atmos. Sci. 1984, 41, 1249–1252. [Google Scholar] [CrossRef]
- Ramanathan, N.; Srinivasan, K. An estimation of optimum grid size for Kashmir Valley by spectral method. J. Appl. Meteor. 1995, 34, 2783–2786. [Google Scholar] [CrossRef][Green Version]
- Wang, W.T.; Wang, Y. A spectral analysis of satellite topographic profile: A coincident pattern between latitudinal topographic and westerly perturbation on the lee side of Qinghai-Tibet Plateau. J. Nanjing Univ. 2004, 40, 304–317. (In Chinese) [Google Scholar]
- Wang, C.X.; Gao, S.T.; Ran, L.K.; Liang, L.; Chen, Y.L. Effect of topographic perturbation on the precipitation distribution in Sichuan. J. Appl. Meteor. Sci. 2019, 30, 586–597. (In Chinese) [Google Scholar]
- Salvador, R.; Calbo, J.; Millan, M.M. Horizontal grid size selection and its influence on mesoscale model simulations. J. Appl. Meteor. 1999, 38, 1311–1329. [Google Scholar] [CrossRef]
- Srinivasan, K.; Ramanathan, N. Terrain variance spectra for Indian Western Ghats. Proc. Indian Natn. Sci. Acad. 1994, 60, 133–138. [Google Scholar]
- Xu, X.J.; He, B.H.; Hu, H.; Xiong, M.B.; Yang, W.B.; Li, Z.L. Effect on Soil Infiltration of Water and Soil Loss Made by Earthquake in Wenchuan Area. Sci. Agric. Sinica 2012, 45, 2520–2529. (In Chinese) [Google Scholar]
- Song, G.H.; Cui, P.; Guo, X.J. Infiltration Characteristics Experiment in Wenchuan Earthquake Zone. Bulletion Soil Water Conserv. 2013, 33, 248–252. (In Chinese) [Google Scholar]
- Gan, F.L.; He, B.H.; Wang, T. Study on the characteristics of rainfall infiltration runoff using artificial simulation experiment in Wenchuan Earthquake Area. J. Hydraul. Eng. 2016, 47, 780–788. (In Chinese) [Google Scholar]
- Li, T.Y.; He, B.H.; Chen, Z.P.; Zhang, Y.; Liang, C.; Wang, R.X. Effects of gravel on infiltration, runoff, and sediment yield in landslide deposit slope in Wenchuan earthquake area, China. Environ. Sci. Pollut. Res. 2016, 23, 12075–12084. [Google Scholar] [CrossRef]
- Jiang, X.W.; Li, Y.Q. The Statistical Analysis of Earthquake and Precipitation in Sichuan Province. Plateau Mt. Meteorol. Res. 2008, 28, 33–36. (In Chinese) [Google Scholar]
- Yin, Y.P.; Wang, F.W.; Sun, P. Landslide hazards triggered by the 2008 Wenchuan earthquake, Sichuan, China. Landslides 2009, 6, 139–152. [Google Scholar] [CrossRef]
- Fang, H.; Cui, P.; Pei, L.Z.; Zhou, X.J. Model testing on rainfall-induced landslide of loose soil in Wenchuan earthquake region. Nat. Hazards Earth Syst. Sci. 2012, 12, 527–533. [Google Scholar] [CrossRef]
- Li, C.R.; Wang, M.; Liu, K.; Xie, J. Topographic changes and their driving factors after 2008 Wenchuan earthquake. Geomorphology 2018, 311, 27–36. [Google Scholar] [CrossRef]
- Liu, L.; Ran, L.K.; Gao, S.T. Analysis of the Characteristics of Inertia-Gravity Waves during an Orographic Precipitation Event. Adv. Atmos. Sci. 2018, 35, 604–620. [Google Scholar] [CrossRef]
- Xie, J.; Wang, M.; Liu, K.; Coulthard, T.J. Modeling sediment movement and channel response to rainfall variability after a major earthquake. Geomorphology 2018, 320, 18–32. [Google Scholar] [CrossRef]
- Steyn, D.G.; Ayotte, K.W. Application of two-dimensional terrain height spectra to mesoscale modeling. J. Atmos. Sci. 1985, 42, 2884–2887. [Google Scholar] [CrossRef]
- Mulla, D.J. Using geostatistics and spectral analysis to study spatial patterns in the topography of southeastern Washington State, U.S.A. Earth Surf. Proc. Land. 1988, 13, 389–405. [Google Scholar] [CrossRef]
- Ouchi, S.; Matsushita, M. Measurement of self-affinity on surfaces as a trial application of fractal geometry to landform analysis. Geomorphology 1992, 5, 115–130. [Google Scholar] [CrossRef]
- Xu, T.B.; Moore, I.D.; Gallant, J.C. Fractals, fractal dimensions and landscapes—A review. Geomorphology 1993, 8, 245–262. [Google Scholar] [CrossRef]
- Gallant, J.C.; Moore, I.D.; Hutchinson, M.F.; Gessler, P. Estimating fractal dimension of profiles: A comparison of methods. Math. Geol. 1994, 26, 455–481. [Google Scholar] [CrossRef]
- Wilson, T.H.; Dominic, J. Fractal interrelationships between topography and structure. Earth Surf. Proc. Land. 1998, 23, 509–525. [Google Scholar] [CrossRef]
- Perron, J.T.; Kirchner, J.W.; Dietrich, W.E. Spectral signatures of characteristic spatial scales and nonfractal structure in landscapes. J. Geophys. Res. 2008, 113, F04003. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).