Abstract
High-spatial-resolution air quality (AQ) mapping is important for identifying pollution sources to facilitate local action. Some of the most populated cities in the world are not equipped with the infrastructure required to monitor AQ levels on the ground and must rely on other sources, such as satellite derived estimates, to monitor AQ. Current satellite-data-based models provide AQ mapping on a kilometer scale at best. In this study, we focus on producing hundred-meter-scale AQ maps for urban environments in developed cities. We examined the feasibility of an image-based object-detection analysis approach using very high-spatial-resolution (2.5 m) commercial satellite imagery. We fed the satellite imagery to a deep neural network (DNN) to learn the association between visual urban features and air pollutants. The developed model, which solely uses satellite imagery, was tested and evaluated using both ground monitoring observations and land-use regression modeled PM2.5 and NO2 concentrations over London, Vancouver (BC), Los Angeles, and New York City. The results demonstrate a low error with a total RMSE < 2 µg/m3 and highlight the contribution of specific urban features, such as green areas and roads, to continuous hundred-meter-scale AQ estimations. This approach offers promise for scaling to global applications in developed and developing urban environments. Further analysis on domain transferability will enable application of a parsimonious model based merely on satellite images to create hundred-meter-scale AQ maps in developing cities, where current and historical ground data are limited.
1. Introduction
Air quality (AQ) in urban environments results from a complex interaction between environmental conditions and natural and anthropogenic sources. The air we breathe has a strong impact on our health and life expectancy [1,2]. Poor air quality has been consistently ranked among the top risk factors for death and disability worldwide. In 2017, air pollution was the fifth-highest mortality risk factor globally and was associated with about 4.9 million deaths [3]. Fine particulate matter (PM2.5) and nitrogen dioxide (NO2) are common urban air pollutants [4,5]. Whereas NO2 is especially important in urban areas and a marker for traffic-related air pollution, mainly affected by local sources (e.g., transportation), PM2.5 is most relevant for health impacts and has a regional effect with numerous contributors [6,7].
Many epidemiological studies examining the health effects of air pollution have measures of air pollutant concentrations collected from sparse networks of stationary ground monitors as their main exposure metric. Continuous, high-spatial-resolution air AQ estimates will help with source identification, facilitate local awareness, improve the accuracy and specificity of health effects studies, and be useful for tracking impacts of air quality management.
Over the past several decades, different models have been used to estimate air quality, with improved spatial coverage and reduced bias. These include dispersion modeling [8], regression kriging [9], land-use regression (LUR) [10,11,12,13,14], and satellite-based models [15,16,17]. The satellite-based models use retrieved variables such as aerosol optical depth (AOD) as explanatory variables. Satellite-based estimates are increasingly being used to determine continuous exposure metrics in health studies at coarse resolutions (1 km–10 km) and with limitations related to column-surface calibration. Assessments of long-term air pollution exposure in environmental health studies have commonly employed LUR or chemical transport modeling (CTM) techniques. Whereas CTM requires local emissions data, LUR is a commonly used algorithm for urban regions that require substantial local (measured) data such as traffic, meteorology, and spatially disaggregated population data. LUR requires gathering many datasets on a specific location and therefore is usually performed on an annual basis [11,13]. Due to large input data requirements of LUR models, coverage cannot easily be scaled up. As a result, we currently lack high-spatial-resolution estimates of pollutant levels in many cities around the world, especially in low- and middle-income countries.
LUR modeling uses multiple regression equations to describe the relationship between sample locations and environmental variables. Resulting models can predict pollution concentrations at unmeasured locations, usually with relatively high spatial resolution. In addition, satellite-based retrieved data (e.g., AOD, temperature) have been used for estimating concentrations of air pollutants mostly combined with additional explanatory variables [18,19,20,21]. The great allure of satellite data is their global coverage. These models perform well where historical ground monitoring data and ancillary data are available, and calibration is possible, which facilitates the production of continuous air pollutant concentration maps at a relatively coarse spatial resolution (i.e., on the kilometer scale).
The spatial resolution of available satellite imagery has increased significantly due to the existence of commercial satellites that obtain daily images of the globe at a meter-scale resolution. Current developments in applying deep learning methods to satellite imagery, and not only to satellite-borne retrieved variables as AOD, have recently been used to improve capabilities of estimating air quality [22,23] and socioeconomic and environmental factors [24,25,26]. Visual features in high-spatial-resolution satellite imagery contain significant information relevant to urban air quality. This will allow the next generation of AQ models to estimate hundred-meter-scale air quality concentrations in urban environments, potentially without requiring any locally collected ground data.
This study demonstrates a novel deep learning approach based on very high-spatial-resolution satellite imagery (2.5 m) to estimate PM2.5 and NO2 annual mean concentrations in urban environments. The analysis was conducted on Greater London, UK; Vancouver, Canada; and Los Angeles (LA), USA and evaluated on an unseen city—New York City (NYC), USA in 2010 (datasets and methodology are detailed in the ‘Data and Methods’ section and in the Supplementary Material). Results from the multi-location model are validated with ground measurements and with 2010 LUR models (which serve as our target data). Furthermore, spatial error analysis and model interpretability are discussed.
2. Data and Methods
2.1. Data
- Satellite Imagery
We used Maxar Technologies (formerly DigitalGlobe, USA) WorldView2 (WV2) images available over Greater London, Vancouver, LA, and NYC for the year 2010. WV2 was launched on 8 October 2009, as part of the Maxar satellite constellation. It is a Sun-synchronous satellite with a 10:30 a.m. descending node overpass, located 770 km from Earth. Images are produced in 8 spectral bands in the VIS–NIR range (400 nm–1040 nm) with a spatial resolution of 50 cm (for the panchromatic imagery) and 2.5 m (for the multi-spectral imagery) [27]. The latter have been used in this study. Access to the Maxar imagery archive was completed under the ‘NextView’ license framework. Over the study period, we obtained and pre-processed raw imagery over all study areas, including radiometric correction and cloud cleaning, resulting in a total of 717 non-overlapping 2.5 m spatial-resolution satellite images that cover all the studied cities for 2010. These images were used to construct a total of 612,248 100 m × 100 m (40 pixels × 40 pixels) image patches that were then used as input to the model. Table 1 shows the number of available images and constructed patches for each individual city (more details in the “Data Preparation” section).

Table 1.
Summary details of data availability over the study areas (2010).
- LUR data
We obtained annual mean LUR-modeled PM2.5 and NO2 concentrations (for 2010) with 100 m and 200 m spatial resolution, respectively, for all studied cities [11,13,28,29,30]. These continuous surfaces served as the target data for training, testing, and validating the model. An example list of variables included in a LUR can be found in Table S1, with more details in [11].
To efficiently use the meter-scale satellite images with the ability to have a target dataset for testing and validating the developed model, we looked for a reliable continuous surface that is commonly used. Since a ground monitoring network is not a continuous mapping surface, it does not provide a sufficient amount of labeled data to train deep learning models. As an alternative, we propose to use land-use regression model (LUR) outputs, which are developed based on real data, e.g., air quality monitors, traffic density, distance from roads and rails, and population density, among others (Table S1). LURs require much effort in obtaining the data and are limited for regions that have those data available. It has been used in environmental health and urban planning studies as a valid exposure metrics [31,32,33]. For further evaluation, we calculated annual concentrations for each available ground monitoring site for all study regions. The correlations between 2010 LUR PM2.5/NO2 models and the annual mean ground monitoring concentrations, from available ground monitoring sites at the study metropolitan areas range from 0.262 in London to 0.44 in New York for PM2.5 and 0.1 in London to 0.78 in Vancouver for NO2. These calculated correlations are in agreement with published results in Europe between LUR model outputs and AQ concentrations from ground monitoring sites [11].
In this study, we are mapping AQ in the 100 m–200 m scale, defined by the target data (i.e., LUR) resolution. This finer spatial resolution expresses human exposure. It addresses local AQ distribution and AQ spatial variation that cannot be captured in lower spatial resolutions. These high spatial resolutions are key for detecting pollution sources and are a proxy for human activity and urban planning. We use information from 2.5 m spatial-resolution satellite imagery to understand the relationship between PM2.5/NO2 and surface reflectance (in a broader look). The advantage of using very high-spatial-resolution satellite images is the ability to capture urban features that are known to influence pollution levels (e.g., roads, buildings, trees) that are often used as inputs to LUR models but not visible at lower resolutions. This approach helps our proposed model to account for more than a single pixel (2.5 × 2.5 m2 area) but understand the urban composition causing that pollution level.
This study introduces an opportunity to use meter-scale images that are globally available to develop a more parsimonious model for estimating AQ. This approach can then be applicable in developed and developing urban environments that lack the data required for developing LUR models.
- Ground monitoring data
Ground monitoring data of PM2.5 and NO2 concentrations in ug/m3 were obtained for 2010 at all study areas and annual concentrations were calculated. For London, daily ground monitoring data were used to calculate annual means of measured pollution over ground stations that had at least one measured value every month. For the other cities, annual means of measured data were used for the ground monitoring sites that had collected data for over 50% of the year. Only sites that had co-located model-estimated values within a distance less than 500 m were included. We used a total of 33 (31) ground PM2.5 (NO2) sites, for evaluation, with 11 (7), 8 (12), 8 (10), and 6 (2) sites in London, Vancouver, LA, and NYC, respectively (Table 1). Data were obtained from the following sources: London [34,35], Vancouver [36], LA [37], and NYC [28,37].
2.2. Methodology
In this study, we used over 700 Maxar satellite images to train, validate, and test our air quality estimation models. The imagery had a spatial resolution of 2.5 m, covering 4 cities, and came from the year 2010 (see details in Table 1).
In the first stage, the model was trained and validated on combined data from three urban environments: London, Vancouver, and LA. This multi-location model was then tested to predict PM2.5 and NO2 concentrations in the same three locations, on a subset of 10% of the data unseen by the model. In the second stage, we validated the same trained model on NYC: an urban region completely unseen by the model.
The same two-stage process was used to produce separate models for each air pollutant, and both models were trained and evaluated with LUR estimates as their target data (more details in the ‘Data and Methods’ section). Root mean squared error (RMSE), residuals (defined as the difference between the predicted values and the target data), and normalized RMSE (NRMSE, defined as RMSE divided by the difference between the 25th and 75th percentiles of the target PM2.5/NO2 concentrations) were calculated to quantify model prediction errors. In addition, we compared our results to available ground monitoring stations’ annual concentrations for PM2.5 and NO2.
- Model Architecture
We used a deep learning approach to develop a new model for estimating PM2.5 and NO2 concentrations. We modified a VGG16 model (developed by [38]), which is a deep convolutional neural network (CNN) originally tasked to classify objects in the ImageNet dataset. CNNs are a type of neural networks that are popular for their effective and efficient performances in dependent data structures such as time series and images [39]. CNNs consist of a stack of convolutional layers that will understand data patterns using internal data dependency. For instance, in images, each pixel is dependent on its neighboring pixels, and the image patterns are linked to not just a pixel but a collection of pixels in a neighborhood. Hence, CNNs are capable of learning spatial features, such as roads, buildings, trees, etc., in urban environments from satellite images. The aim of this study is to train a CNN that efficiently and effectively learns urban features and finds their relations to the PM2.5 and NO2 pollution level. To adapt the VGG16 model to our objective, we changed the original architecture from a classification model to a regression model by removing the final softmax activation function (resulting in a neuron with linear output). This enabled us to estimate continuous PM2.5 and NO2 concentration levels. We also removed some of the convolutional layers to account for the difference in size of our input imagery. The new model is trained to learn urban reflectance patterns and estimate their corresponding PM2.5 and NO2 concentrations (Figure 1 and Figure S1). This approach was feasible due to the computational resources of the NASA Ames Research Center High-End Computing Capability GPU nodes. The proposed model is set up to take Maxar images with a spatial resolution of 2.5 m as input and output AQ maps with 100–200 m scale. The model will take a high-spatial-resolution image (meter-scale) as input and output a corresponding value with 100–200 m scale. Thus, we will not see the local pixelated behavior, and the model output will have the same resolution/detail level as the LUR target data.
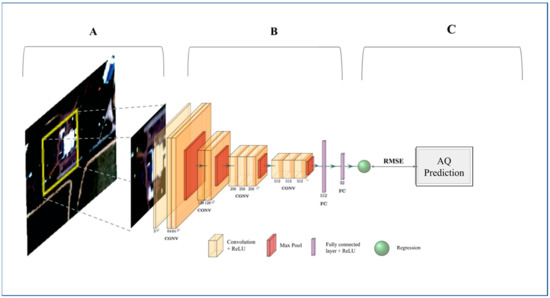
Figure 1.
Methodology Flowchart. (A) Single satellite imagery patches are input to the CNN 40 × 40 pixels (100 m × 100 m) for PM2.5 and 80 × 80 pixels (200 m × 200 m) for NO2, each patch corresponds to one target value from a continuous LUR surface. (B) The satellite images are applied to a CNN, which consists of stacked layers of convolution and nonlinear activation functions (rectified linear unit (ReLU); yellow blocks), followed by max pooling layers (red blocks) to spatially down-sample the features at the end of each convolutional block. Lastly, the convolutional features are flattened and fed into fully connected layers (showed in purple) and (C) regressed to the LUR training data to predict continuous PM2.5/NO2 estimates. RMSE was used to measure the error and evaluate the model. (Further details: Section S1 of Supplementary Material). (This figure was developed using the PlotNeuralNet package [40]).
- Data Preparation
To prepare our data for model training, we aligned our satellite imagery from the study areas with the LUR models and partitioned the imagery into patches that matched the grid resolution of the LUR-modeled data. This resulted in 100 m (200 m), 40 × 40 (80 × 80) pixel patches, for the PM2.5 (NO2) data. Some locations in our study area have multiple overlapping satellite images, which produces multiple patches for the same target data point. We randomly selected one of these patches for each point so that our dataset has only one patch corresponding to each target data point. Our imagery dataset has a disproportionate number of image patches for some cities over others, with LA having over three times as many patches as London. To prevent the model from favoring the image distribution of one city, we balanced the dataset by oversampling patches proportionally from the under-represented cities. We also used a city-stratified, randomly selected 80/10/10 split for our training/validation/testing datasets.
The model output resolution is limited by the spatial resolution of the target data we have for validating the model. LUR models have the finest spatial resolution for this purpose. The aim of this study is to leverage the meter-scale land surface information to map pollution. However, instead of pixel-to-pixel mapping, we used a broader land surface area that will allow us to accurately understand the pollution distribution in the area. To achieve this, we designed a patch sampling to collect a 40 × 40-pixel image centered over the LUR pollution point (Figure 1). The input to the model is a single patch of satellite imagery, i.e., 40 × 40 pixels of 2.5 m spatial-resolution imagery, which corresponds to a real-world image patch of 100 m × 100 m in size (for PM2.5; NO2 patches are twice as big). Each patch corresponds to one LUR value from a continuous LUR surface. The model is learning to engineer features from the imagery and associate those features with the corresponding AQ measurement.
The dataset of imagery patches for London, LA, and Vancouver was split into three portions: 80% of the patches were used to train the model, 10% of the patches were used to examine performance between models, adjust model hyperparameters, and evaluate overfitting, and the last 10% were held out until the end and only used to evaluate performance of the final model. All numbers in the results section used the latter.
- Validation
Stage 1: We used the trained model to predict on NYC—a location completely unseen by the model during training—to examine generalizability. Stage 2: We examined the association between the model predictions and available ground monitoring site concentrations in all study regions.
3. Results
- Air Quality Data
All studied regions are urban environments that have available coverage of satellite imagery, ground monitoring sites, and LUR-modeled target data at high spatial resolution. LUR models require substantial time and effort, mainly in obtaining a large number of input datasets, and while they are used for planning and decision-making purposes, LUR-modeled data are not commonly available.
The continuous LUR-modeled PM2.5 concentrations in all our case study regions are more heterogeneously spread, while NO2 concentrations demonstrate a clearer spatial trend, following roads as the main contributor (Figure 2 and Figure 3). It is clear from the target data surfaces that PM2.5 annual concentrations are much lower in Vancouver than in LA and London, especially related to the city centers’ density (Details in Table 1).
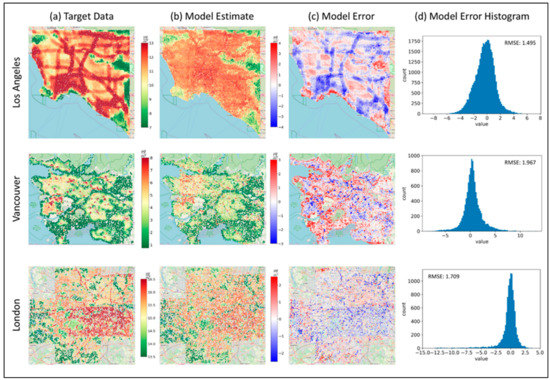
Figure 2.
PM2.5 target data, model estimates and errors. PM2.5 target data (a), based on 2010 LUR data in Los Angeles, Vancouver, and London. Column (b) shows the 100 m model estimates of PM2.5 annual concentrations using the testing dataset (10% of the available data for all 3 cities), and column (c) shows the model residuals calculated by the difference between the predicted concentrations and the target data. The residuals’ distributions are shown in column (d).
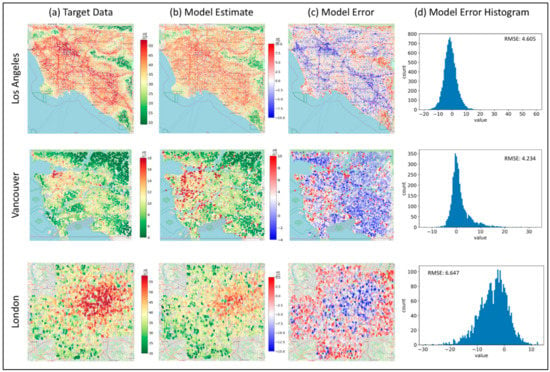
Figure 3.
NO2 target data, model estimates and errors. NO2 target data (a), based on 2010 LUR data in Los Angeles, Vancouver, and London. Column (b) shows the 200 m model estimates of NO2 annual concentrations using the testing dataset (10% of the available data for all cities). Column (c) shows the model residuals calculated by the difference between the predicted concentrations and the target data, and the residuals’ distributions are shown in column (d).
In particular, the spatial distribution of PM2.5/NO2 in LA is dominated by highways and roads. Particularly high PM2.5/NO2 levels are observed in the downtown area and at the border of Los Angeles and Orange counties. Low pollution concentrations are spotted at recreation areas such as Angeles National Forest in Northeastern LA. Vancouver demonstrates lower PM2.5/NO2 concentrations compared to LA and is mainly dominated by recreational areas with low pollution levels. Downtown Vancouver and areas close to the Vancouver International Airport are regions with relatively higher pollution levels. The PM2.5/NO2 concentrations over London are mostly moderate with distinct high-pollution areas close to roads. Low pollution levels are observed in the southern and western regions co-located with South Downs National Park and North Wessex Downs Area of Outstanding Natural Beauty, respectively. NYC has a high concentration of pollutants in the densely populated Manhattan region, as well as Queens and Brooklyn Heights.
- Estimating PM2.5 Concentrations
Table 2 presents the model results for each individual city and for all cities combined. The model was trained for 100 iterations and showed a Pearson correlation between the target data and the model-predicted PM2.5 concentrations in the testing subset of R = 0.93, and an RMSE of 1.64 µg/m3, for all locations trained by the model. The model explained 87% of the variance in the multi-location testing dataset using solely images as input to the model, and the model outcomes for validation and testing phases result in a relatively low RMSE < 2 µg/m3 for all study regions (Figure 2; Table 2).

Table 2.
PM2.5 and NO2 model performance.
The model captures most of the coarser spatial trends, such as greenery spaces and populated areas, with fairly small residuals spanning mostly from −4 to +4 µg/m3. It also captures some of the spatial trends of larger road features in LA. However, it tends to underestimate pollution levels over roads (more dominant in LA) and overestimate over green areas (seen in all locations). All validation residuals are distributed fairly evenly around zero µg/m3 for all locations (Figure 2).
- Estimating NO2 Concentrations
Here, we used the same imagery input from all study regions with an adjusted patch size of 200 m × 200 m, derived from the target data resolution, to estimate NO2 annual concentrations. We obtained results with a reasonably strong Pearson correlation between the predicted concentrations and target data (LUR) NO2 concentrations for all training locations of R = 0.95, and a low RMSE < 6.7 µg/m3 (Figure 3; Table 2). These results demonstrate a robust model. The model explained 91% of the variance in the data using solely the satellite imagery as input to the model.
The model clearly captured patterns in the spatial distribution of NO2, which are largely affected by local sources, such as traffic, as seen in the results (Figure 3). However, the model underestimates highly polluted roads, and overestimates green areas with very low pollution—similar to the PM2.5 model results. Although London city center is well captured by the model, its surrounding road networks are underestimated to a level of 15 µg/m3. This may reflect the greater proportion of diesel vehicles and higher levels of congestion in London compared to the other training cities [41]. LA and Vancouver show better results with more evenly distributed model residuals.
- Validation
Stage 1: The model performed well (see Figure 4 and Table 2) but lacks some of the feature specificity the trained cities have.
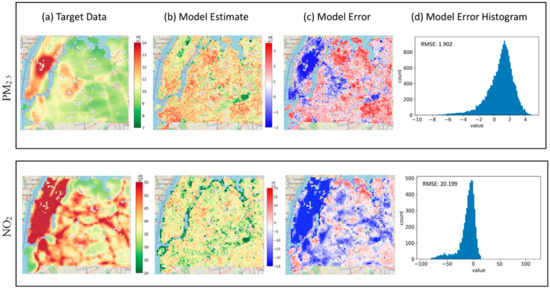
Figure 4.
PM2.5 and NO2 target data, model estimates and errors for NYC. Target data (a), based on 2010 LUR data in New York City. Column (b) shows the 100 m, and 200 m model estimates of PM2.5 and NO2 annual concentrations, respectively. Column (c) shows the model residuals calculated by the difference between the predicted concentrations and the target data, and the residuals’ distributions are shown in column (d).
The model clearly underestimates pollution over Central Park, which is an atypically large ‘green lung’ located in the middle of Manhattan—a bustling and densely populated borough of NYC. In the satellite images, these ‘green lungs’, which are large, green areas surrounded by high levels of human activity, look virtually indistinguishable from green areas outside the city, especially for small patch sizes.
Stage 2: Figure 5 shows the correlations between the estimated annual PM2.5 and NO2 concentrations and the observed annual mean concentrations at co-located ground monitoring sites with a total R2 of 0.86, 0.43 and RMSE of 1.78, 16.68 µg/m3, respectively. We obtained data from 33 sites for PM2.5 and 31 sites for NO2.
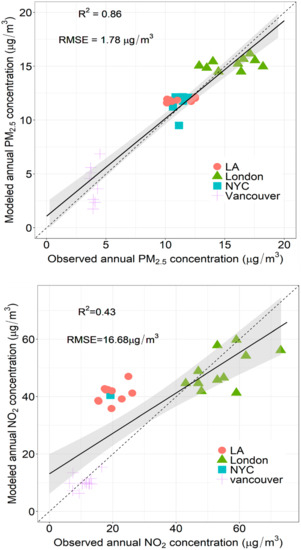
Figure 5.
Correlations between observed and predicted PM2.5 and NO2 concentrations. Correlations between observed PM2.5 (upper panel) and NO2 (lower panel) concentrations at ground monitoring sites and predicted values based on our model; the dashed line is the 1:1 line and the black line is the regression line with 95% confidence intervals (R2 = 0.86, 0.43, and RMSE = 1.78, 16.68 μg/m3, respectively). Only sites that had co-located model-estimated values within a distance less than 500 m were included. For London, daily station data was used to calculate annual means of measured pollution over ground stations that had at least one measured value every month. For the other cities, annual means of measured data were used for the stations that had collected data for over 50% of the year.
- Model Interpretability
To further examine the main hypothesis that urban features visible from high-spatial-resolution satellite images directly correlate with pollution levels, we analyzed the effect of different urban features on the value of the prediction. We wanted to investigate whether inputs (e.g., roads, trees) to the LUR models (whose outputs were used as labels) are being captured by the deep learning models. Neural networks are known to often be black-box models with learned features that cannot be interpreted easily [42,43,44]. However, recent advances in machine learning have made it possible to gain insights into some types of neural networks, such as CNNs. We know that certain urban features, such as roads and industrial objects, are correlated with high pollution levels. Conversely, green areas and residential blocks are associated with lower pollution levels [45]. To test the effect these urban features have on the pollution estimate, we created synthesized images by adding urban features on top of existing imagery, and we used these synthesized images to examine how these added features affected the model estimate (Figure 6b).

Figure 6.
Feature contribution analysis (a) Hypothesis of expected changes in PM2.5 concentrations (μg/m3) when adding different urban features to original imagery; (b) Confusion table following the hypothesize in subfigure (a) using satellite images with and without synthesized residential, greenery, and road features. The columns represent the original satellite images of greenery, road, industrial, and residential from left to right. From top to bottom, the rows are partial residential, greenery and road images to be overlayed on original images. We demonstrate the differences of PM2.5 levels between the original and synthesized images on the right hand of each subplot. The results in subfigure (b) are in line with our hypothesis demonstrated in subfigure (a) and support the conclusion that our model is learning the non-linear relations between urban objects and air pollution concentrations.
We started by randomly selecting different images that have urban features consisting of greenery, road, industrial and residential objects. Then, we synthesized satellite images with urban features associated with low and high pollution levels (i.e., artificially adding image features over existing images) with examples in Figure 6b. Each row/column in Figure 6b represents an urban feature category and the intersection of each row and column shows a synthesized image combining those features. The differences between pollution concentrations of original and synthesized images predicted by the model are indicated on the right hand of each subplot in Figure 6b. We fed the original and synthesized images into the trained model and analyzed the difference in pollution levels predicted by the model.
In Figure 6a, we hypothesize the expected changes in PM2.5 concentrations between the original imagery and the synthesized imagery. For example, we expect that, for all categories of features, adding greenery features will lower the concentration. The correspondence between the expected changes (Figure 6a) and the interpretability of the results (Figure 6b) supports the hypothesis that our model learns the non-linear relations between visual urban features and their corresponding pollution levels. The overall results indicate the trained model successfully learns correlations between visual urban features and pollution levels and are in line with our physics-backed understanding of urban feature compositions.
4. Discussion
The goal of our study is to estimate hundred-meter-scale PM2.5 and NO2 concentrations in different urban environments. Our approach advances the science by (i) introducing a novel approach to the earth science community by applying deep learning to solely very high-spatial-resolution satellite imagery for AQ estimation, (ii) developing fine-scale continuous AQ maps, and (iii) creating an efficient approach for high-spatial-resolution AQ monitoring independent of ground monitoring and ancillary data. Although we have compelling results, we recognize some of the limitations of our model and discuss methods to address them.
The existing literature on satellite-based AQ estimation incorporates many variables in the modeling scheme, including meteorology, traffic, topography, and distance from emission source [15,16,18]. The model by [46] reported 36% explained variation in PM2.5 in NYC, with a coarser (kilometer-scale) spatial resolution. Other models reported a PM2.5 prediction RMSE of 3.1 µg/m3 in the LA region [47], and PM2.5 (NO2) hourly prediction RMSE of 6.7 (43.5) µg/m3 in London [48]. Our model results, trained and validated on modeled LUR data, improve current modeling efforts in all study areas (Table 3). The models exhibit reduced error and produce high-spatial-resolution predictions, while significantly decreasing the amount of input datasets required.

Table 3.
Baseline model performance.
Certain features of the urban environment demonstrated a clear effect on the air quality prediction (e.g., greenery, roads). Nevertheless, changes in air pollution can be related to urban features that cannot be recognized by the image-analysis model (e.g., the use of electric cars, winds, and temperature). These features may also affect the physical relationship between the measured air quality variables and the image reflectance values. Furthermore, the model underestimates PM2.5 and NO2 concentrations in certain urban areas that lack context—the aforementioned ‘Central Park problem’. The model perceives Central Park only as a green area, without any context of the human activity in the areas surrounding it. This causes it to under-predict air pollution over that area. Incorporating the “bigger picture” context into the model is expected to resolve this issue. We examined the use of satellite-based night-time light data retrieved from the Visible Infrared Imaging Radiometer Suite (VIIRS) instrument onboard the Suomi-NPP satellite [49] as a means for incorporating context-based on human activity into the model. The VIIRS night-time light product over NYC was analyzed as a potential additional input to the model. This dataset can detect the large, bright areas around Central Park that represent its location with context (i.e., in the heart of urban activity) (Figure S2).
Apart from adding larger-scale context to the model, it was also observed that the VIIRS night-time light data demonstrated a high pixel-to-pixel Pearson correlation coefficient of R = 0.64 with PM2.5 over NYC. This shows promise for night-time light data to also be used as a feature co-located with the satellite images. Moreover, the VIIRS data are available globally, which could help facilitate the process of transferring the model to different urban regions around the globe. Although we have demonstrated generalizability to a completely unseen city, we need to explore how well the model generalizes to a wide range of global urban environments in developed and developing locations with different distributions of both urban features and AQ. This study sets the standard for future work applying this model to other developed urban environments as well as examining the transferability of the model to developing cities that lack ground measurements. The ability to exclusively use satellite images to infer AQ on a local scale is novel to the AQ-modeling research community and can address some of the shortcomings of current modeling approaches, particularly in areas where historical ground data do not exist. The reason we were able to use an image taken on a single day to predict the annual mean is because larger scale objects (e.g., buildings, roads, cars) do not change drastically from day to day or even over the course of months. Changes in larger features would generally happen on the scale of years. Therefore, contributions such as urban density and buildings correlated with industry, or infrastructure correlated with driving, would not change substantially over the imagery taken within a year. We recognize the need to train our model on additional years to be able to pick up changes from year to year and test the sensitivity of the model to annual changes. The scope of our project and funding is primarily to demonstrate a proof of concept that a CNN model can infer some types of air pollutants solely from satellite imagery.
This paper presents a strong and feasible methodology to work with for future AQ-modeling efforts. Although satellite images are a promising source of data for generating estimates at high spatial resolution on a local scale, as they do capture some spatial variability, they are limited to generalize in certain areas. Future work should focus on combining additional datasets readily available globally (e.g., additional bands of satellite data, Normalized difference vegetation index (NDVI)/ Enhanced Vegetation Index (EVI), meteorology, Digital Elevation Model (DEM)) that can be combined with meter-scale satellite images to generate better estimates. In addition, future efforts will need to assess the sensitivity of image-based models to images collected with different temporal aspects such as time of day and season.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/atmos13050696/s1, Figure S1: Deep Learning Model Architecture, Table S1: Common variables used in LUR models, Figure S2: VIIRS Night-Time Light over Manhattan [50,51].
Author Contributions
Conceptualization, M.S.-H., M.V.P., A.S., A.A.A. and K.D.; Data curation, M.S.-H. and M.V.P.; Formal analysis, M.V.P., A.S. and A.A.A.; Methodology, M.S.-H., M.V.P., A.S. and A.A.A.; Resources, M.S.-H.; Supervision, M.S.-H.; Validation, M.V.P., A.S. and A.A.A.; Visualization, M.V.P., A.S., A.A.A., E.D. and V.L.; Writing—original draft, M.S.-H., M.V.P., A.S. and A.A.A.; Writing—review and editing, M.S.-H., E.S., N.C.O., M.E. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Wellcome Trust grant number (209376/Z/17/Z), as well as the APC.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Publicly available datasets, code, and maps resulting from this project will be archived for free download at NASA Ames Research Center (ARC) on the NASA Earth Exchange (NEX) platform website/data repository, and NASA GitHub, uploaded and archived in NASA PubSpace. Manuscripts will be deposited to PubSpace within one year of completion of the (manuscript) peer review process, according to NASA requirements. Commercial Satellite images are not publicly available and cannot be shared.
Acknowledgments
This work was supported by the Pathways to Equitable Healthy Cities grant from the Wellcome Trust (209376/Z/17/Z), NASA ARC ARIA Award, and USRA IRAD Award. We thank the Pathways to Equitable Healthy Cities team and Wellcome Trust, NASA, and USRA, for the financial and professional support, the NEX group at NASA ARC for supporting our work, Michael Jerrett (UCLA) for the data and Jason Su (UC Berkeley) who helped develop the land use regression model in LA, as well as Maxar for providing access to their images.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pope, C.A.; Lefler, J.S.; Ezzati, M.; Higbee, J.D.; Marshall, J.D.; Kim, S.-Y.; Bechle, M.; Gilliat, K.S.; Vernon, S.E.; Robinson, A.L.; et al. Mortality risk and fine particulate air pollution in a large, representative cohort of U.S. adults. Environ. Health Perspect. 2019, 127, 77007. [Google Scholar] [CrossRef] [PubMed]
- Brauer, M. Air quality and health: Looking forward. Air Qual. Clim. Chang. 2017, 51, 23–26. [Google Scholar]
- HEI. State of Global Air Special Report. Health Effects Institute. 2019. Available online: http://www.stateofglobalair.org/sites/default/files/soga_2019_report.pdf (accessed on 1 March 2022).
- Wang, Y.; Bechle, M.J.; Kim, S.-Y.; Adams, P.J.; Pandis, S.N.; Pope, C.A.; Robinson, A.L.; Sheppard, L.; Szpiro, A.A.; Marshall, J.D. Spatial decomposition analysis of NO2 and PM2.5 air pollution in the United States. Atmos. Environ. 2020, 241, 117470. [Google Scholar] [CrossRef]
- Kotchenruther, R.A. Source apportionment of PM2.5 at multiple Northwest U.S. sites: Assessing regional winter wood smoke impacts from residential wood combustion. Atmos. Environ. 2016, 142, 210–219. [Google Scholar] [CrossRef]
- Nguyen, C.; Soulhac, L.; Salizzoni, P. Source apportionment and data assimilation in urban air quality modelling for NO2: The lyon case study. Atmosphere 2018, 9, 8. [Google Scholar] [CrossRef] [Green Version]
- Karagulian, F.; Belis, C.A.; Dora, C.F.C.; Prüss-Ustün, A.M.; Bonjour, S.; Adair-Rohani, H.; Amann, M. Contributions to cities’ ambient particulate matter (PM): A systematic review of local source contributions at global level. Atmos. Environ. 2015, 120, 475–483. [Google Scholar] [CrossRef]
- Isakov, V.; Arunachalam, S.; Baldauf, R.; Breen, M.; Deshmukh, P.; Hawkins, A.; Kimbrough, S.; Krabbe, S.; Naess, B.; Serre, M.; et al. Combining Dispersion Modeling and Monitoring Data for Community-Scale Air Quality Characterization. Atmosphere 2019, 10, 610. [Google Scholar] [CrossRef] [Green Version]
- Van Zoest, V.; Osei, F.B.; Hoek, G.; Stein, A. Spatio-temporal regression kriging for modelling urban NO2 concentrations. Int. J. Geogr. Inf. Sci. 2020, 34, 851–865. [Google Scholar] [CrossRef] [Green Version]
- Jin, L.; Berman, J.D.; Warren, J.L.; Levy, J.I.; Thurston, G.; Zhang, Y.; Xu, X.; Wang, S.; Zhang, Y.; Bell, M.L. A land use regression model of nitrogen dioxide and fine particulate matter in a complex urban core in Lanzhou, China. Environ. Res. 2019, 177, 108597. [Google Scholar] [CrossRef]
- De Hoogh, K.; Gulliver, J.; Donkelaar, A.; van Martin, R.V.; Marshall, J.D.; Bechle, M.J.; Cesaroni, G.; Pradas, M.C.; Dedele, A.; Eeftens, M.; et al. Development of West-European PM2.5 and NO2 land use regression models incorporating satellite-derived and chemical transport modelling data. Environ. Res. 2016, 151, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Bertazzon, S.; Johnson, M.; Eccles, K.; Kaplan, G.G. Accounting for spatial effects in land use regression for urban air pollution modeling. Spat. Spatiotemporal. Epidemiol. 2015, 14–15, 9–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beelen, R.; Hoek, G.; Vienneau, D.; Eeftens, M.; Dimakopoulou, K.; Pedeli, X.; Tsai, M.-Y.; Künzli, N.; Schikowski, T.; Marcon, A.; et al. Development of NO2 and NOx land use regression models for estimating air pollution exposure in 36 study areas in Europe—The ESCAPE project. Atmos. Environ. 2013, 72, 10–23. [Google Scholar] [CrossRef]
- Ross, Z.; Jerrett, M.; Ito, K.; Tempalski, B.; Thurston, G. A land use regression for predicting fine particulate matter concentrations in the New York City region. Atmos. Environ. 2007, 41, 2255–2269. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Hsu, N.C.; Kahn, R.A.; Levy, R.C.; Lyapustin, A.; Sayer, A.M.; Winker, D.M. Global Estimates of Fine Particulate Matter using a Combined Geophysical-Statistical Method with Information from Satellites, Models, and Monitors. Environ. Sci. Technol. 2016, 50, 3762–3772. [Google Scholar] [CrossRef] [PubMed]
- Kloog, I.; Sorek-Hamer, M.; Lyapustin, A.; Coull, B.; Wang, Y.; Just, A.C.; Schwartz, J.; Broday, D.M. Estimating daily PM2.5 and PM10 across the complex geo-climate region of Israel using MAIAC satellite-based AOD data. Atmos. Environ. 2015, 122, 409–416. [Google Scholar] [CrossRef] [Green Version]
- Engel-Cox, J.A.; Holloman, C.H.; Coutant, B.W.; Hoff, R.M. Qualitative and quantitative evaluation of MODIS satellite sensor data for regional and urban scale air quality. Atmos. Environ. 2004, 38, 2495–2509. [Google Scholar] [CrossRef]
- Hammer, M.S.; van Donkelaar, A.; Li, C.; Lyapustin, A.; Sayer, A.M.; Hsu, N.C.; Levy, R.C.; Garay, M.J.; Kalashnikova, O.V.; Kahn, R.A.; et al. Global Estimates and Long-Term Trends of Fine Particulate Matter Concentrations (1998–2018). Environ. Sci. Technol. 2020, 54, 7879–7890. [Google Scholar] [CrossRef]
- Sorek-Hamer, M.; Franklin, M.; Chau, K.; Garay, M.; Kalashnikova, O. Spatiotemporal Characteristics of the Association between AOD and PM over the California Central Valley. Remote Sens. 2020, 12, 685. [Google Scholar] [CrossRef] [Green Version]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Kahn, R.; Levy, R.; Verduzco, C.; Villeneuve, P.J. Global estimates of ambient fine particulate matter concentrations from satellite-based aerosol optical depth: Development and application. Environ. Health Perspect. 2010, 118, 847–855. [Google Scholar] [CrossRef] [Green Version]
- Franklin, M.; Chau, K.; Kalashnikova, O.; Garay, M.; Enebish, T.; Sorek-Hamer, M. Using Multi-Angle Imaging SpectroRadiometer Aerosol Mixture Properties for Air Quality Assessment in Mongolia. Remote Sens. 2018, 10, 1317. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Zang, Z.; Luo, N.; Jiang, Y.; Li, Z. New Interpretable Deep Learning Model to Monitor Real-Time PM2.5 Concentrations from Satellite Data. Environ. Int. 2020, 144, 106060. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Zang, Z.; Jiang, Y.; Shi, W.; Guo, Y.; Li, D.; Zhao, C.; Husi, L. A Spatial-Temporal Interpretable Deep Learning Model for Improving Interpretability and Predictive Accuracy of Satellite-based PM2.5. Environ. Pollut. 2021, 273, 116459. [Google Scholar] [CrossRef] [PubMed]
- Suel, E.; Polak, J.W.; Bennett, J.E.; Ezzati, M. Measuring social, environmental and health inequalities using deep learning and street imagery. Sci. Rep. 2019, 9, 6229. [Google Scholar] [CrossRef]
- Maharana, A.; Nsoesie, E.O. Use of deep learning to examine the association of the built environment with prevalence of neighborhood adult obesity. JAMA Netw. Open 2018, 1, e181535. [Google Scholar] [CrossRef] [PubMed]
- Jean, N.; Burke, M.; Xie, M.; Davis, W.M.; Lobell, D.B.; Ermon, S. Combining satellite imagery and machine learning to predict poverty. Science 2016, 353, 790–794. [Google Scholar] [CrossRef] [Green Version]
- DigitalGlobe. WorldView2-DS-WV2-rev2. 2016. Available online: https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/98/WorldView2-DS-WV2-rev2.pdf (accessed on 1 March 2022).
- NYCCAS. The New York City Community Air Survey: Neighborhood Air Quality. NYC Health. 2018. Available online: https://www1.nyc.gov/ (accessed on 15 January 2022).
- Bechle, M.J.; Millet, D.B.; Marshall, J.D. National Spatiotemporal Exposure Surface for NO2: Monthly Scaling of a Satellite-Derived Land-Use Regression, 2000–2010. Environ. Sci. Technol. 2015, 49, 12297–12305. [Google Scholar] [CrossRef]
- Henderson, S.B.; Beckerman, B.; Jerrett, M.; Brauer, M. Application of land use regression to estimate long-term concentrations of traffic-related nitrogen oxides and fine particulate matter. Environ. Sci. Technol. 2007, 41, 2422–2428. [Google Scholar] [CrossRef]
- Gulliver, J.; Morley, D.; Dunster, C.; McCrea, A.; van Nunen, E.; Tsai, M.Y.; Probst-Hensch, N.; Eeftens, M.; Imboden, M.; Ducret-Stich, R.; et al. Land use regression models for the oxidative potential of fine particles (PM2.5) in five European areas. Environ. Res. 2017, 160, 247–255. [Google Scholar] [CrossRef] [Green Version]
- Hoek, G. Methods for Assessing Long-Term Exposures to Outdoor Air Pollutants. Curr. Environ. Health Rep. 2017, 4, 450–462. [Google Scholar] [CrossRef]
- Xie, D.; Liu, Y.; Chen, J. Mapping Urban Environmental Noise: A Land Use Regression Method. Environ. Sci. Technol. 2011, 45, 7358–7364. [Google Scholar] [CrossRef]
- Lang, P.E.; Carslaw, D.C.; Moller, S.J. A trend analysis approach for air quality network data. Atmos. Environ. 2019, X2, 100030. [Google Scholar] [CrossRef]
- Kings College. London Air Quality Network. 2022. Available online: https://www.londonair.org.uk/london/asp/reportdetail.asp?ReportID=lars2010 (accessed on 1 January 2022).
- Government of Canada. Environment and Climate Change Canada Data. 2022. Available online: https://open.canada.ca/en (accessed on 1 January 2022).
- US EPA. Air Quality Download Data. 2022. Available online: https://www.epa.gov/outdoor-air-quality-data (accessed on 15 January 2022).
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In The Handbook of Brain Theory and Neural Networks; The MIT Press: Cambridge, MA, USA, 1998; p. 3361. [Google Scholar]
- Iqbal, H. HarisIqbal88/PlotNeuralNet v1.0.0. 2018. Available online: https://zenodo.org/record/2526396 (accessed on 2 March 2022).
- O’Driscoll, R.; Stettler, M.E.J.; Molden, N.; Oxley, T.; ApSimon, H.M. Real world CO2, and NOx emissions from 149 Euro 5 and 6 diesel, gasoline and hybrid passenger cars. Sci. Total Environ. 2018, 621, 282–290. [Google Scholar] [CrossRef] [PubMed]
- Fong, R.C.; Vedaldi, A. Interpretable Explanations of Black Boxes by Meaningful Perturbation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 3449–3457. [Google Scholar]
- Yosinski, J.; Clune, J.; Nguyen, A.; Fuchs, T. Understanding neural networks through deep visualization. arXiv 2015, arXiv:1506.06579. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Guo, Y.; Su, J.G.; Dong, Y.; Wolch, J. Application of land use regression techniques for urban greening: An analysis of Tianjin, China. Urban For. Urban Green. 2019, 38, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Gupta, P.; Christopher, S.A.; Wang, J.; Gehrig, R.; Lee, Y.; Kumar, N. Satellite remote sensing of particulate matter and air quality assessment over global cities. Atmos. Environ. 2006, 40, 5880–5892. [Google Scholar] [CrossRef]
- Wang, M.; Sampson, P.D.; Hu, J.; Kleeman, M.; Keller, J.P.; Olives, C.; Szpiro, A.A.; Vedal, S.; Kaufman, J.D. Combining Land-Use Regression and Chemical Transport Modeling in a Spatiotemporal Geostatistical Model for Ozone and PM2.5. Environ. Sci. Technol. 2016, 50, 5111–5118. [Google Scholar] [CrossRef] [Green Version]
- Carslaw, D.; ApSimon, H.; Beevers, S.; Brookes, D.; Carruthers, D.; Cooke, S.; Kitwiroon, N.; Oxley, T.; Stedman, J.; Stocker, J. Defra Phase 2 Urban Model Evaluation (Kings College London). 2013. Available online: http://uk-air.defra.gov.uk/assets/documents/reports/cat20/1312021020_131031urbanPhase2.pdf (accessed on 1 March 2022).
- Stokes, E.C.; Román, M.O.; Wang, Z. Urban Applications of Nasa’s Black Marble Product Suite. In Proceedings of the 2019 Joint Urban Remote Sensing Event (JURSE), Vannes, France, 22–24 May 2019; pp. 1–4. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- ESRI. Open Street Map (OSM). 2018. Available online: https://www.esri.com/arcgis-blog/products/arcgis-living-atlas/mapping/new-osm-vector-basemap/ (accessed on 7 January 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).