Abstract
In this study, a polarimetric radar forward model operator was developed for the Weather Research and Forecasting (WRF) model that was based on a scattering algorithm using the T-matrix methodology. Three microphysics schemes—Thompson, Morrison 2-moment, and Milbrandt-Yau 2-moment—were supported in the operator. This radar forward operator used the microphysics, thermodynamic, and wind fields from WRF model forecasts to compute horizontal reflectivity, radial velocity, and polarimetric variables including differential reflectivity (ZDR) and specific differential phase (KDP) for S-band radar. A case study with severe convective storms was used to examine the accuracy of the radar operator. Output from the radar operator was compared to real radar observations from the Weather Surveillance Radar–1988 Doppler (WSR-88D) radar. The results showed that the radar forward operator generated realistic polarimetric signatures. The distribution of polarimetric variables agreed well with the hydrometer properties produced by different microphysics schemes. Similar to the observed polarimetric signatures, radar operator output showed ZDR and KDP columns from low-to-mid troposphere, reflecting the large amount of rain within strong updrafts. The Thompson scheme produced a better simulation for the hail storm with a ZDR hole to indicate the existence of graupel in the low troposphere.
1. Introduction
Ground-based Doppler weather radars have been routinely used by the national weather agencies of different countries to monitor hazardous weather and related precipitation [1]. With advances in radar technology during the last few decades, it has been shown that radar-derived estimates of precipitation can be greatly improved using polarimetric techniques. Polarimetric Doppler radars transmit and receive both horizontal and vertical polarized signals. From the two different reflected power returns, more information on the convective storm dynamics, kinematics, and precipitation within the developing storms can be obtained. In addition to variables from the regular Doppler radar (horizontal reflectivity ZH and radial velocity VR), variables derived from polarimetric radars typically include some of the following: differential reflectivity (ZDR), differential phase (ΦDP), specific differential phase (KDP), correlation coefficient (ρHV), and linear depolarization ratio (LDR). These variables contain additional information that can be used to estimate the type, shape, size, density, and orientation of hydrometeor precipitation particles within the storms [2,3,4]. Of these observables, ZDR and KDP are two major polarimetric radar variables. ZDR represents the ratio of the backscattered horizontal-to-vertical power return. Large ZDR values normally indicate the presence of oblate particles or horizontally oriented particles. ΦDP is the difference in the phase shift between horizontal and vertical signals. KDP is one-half the range derivative of ΦDP. High values of KDP indicate significant amounts of liquid water content.
Polarimetric radar observations have broad applications in convective storm forecasting. Studies have shown that when ZDR and KDP information are combined with ZH, the accuracy of precipitation rate, accumulation, and mass content estimates within the cloud are improved [5,6,7,8,9,10,11,12,13,14,15]. In addition, polarimetric radar signatures provide important information in precipitation particle classification [4,16,17,18,19,20,21,22]. They can also be used to discriminate the non-meteorological particles and objects from the liquid and ice precipitation particles [4,23,24]. ZDR columns (vertical columns of large values of ZDR above the freezing 0 °C level) generally indicate the existence of supercooled raindrops of large size and water-coated hail or ice [4,25,26]. ZDR and KDP can provide important information in identifying the presence of hail and for estimating its size [16,17,18,19,27,28,29,30,31]; computing the freezing layer height [32]; and helping to detect tornado-lofted non-hydrometeor debris and lightning activities [33,34,35,36,37].
Ground-based S-, C-, and X-band Doppler weather radars (single- or dual-polarization) usually provide measurements every few minutes, and rapid-scan radars with a single or limited set of elevation angles can provide measurements every few seconds to help detect tornadoes, hail, and storm-scale processes [38,39,40,41,42,43,44,45,46,47,48,49]. However, these radar observations are usually not sufficient to fully describe the convective and precipitation processes and their variations within the developing clouds. Radar observations also lack information about thermodynamic conditions, and the gaps in spatial coverage and the limited domain often constrain the value of the radar observation in studying the key processes during the development of convective storms.
Numerical simulations from high-resolution model systems are important components used to forecast and analyze severe storms as well as other atmospheric phenomena, providing continuous temporal and spatial coverage of the atmospheric conditions and their variation on a regular grid. In addition, numerical simulations contain more variables that can be used to describe the dynamics, physics, microphysics, and precipitation processes as well as cross-scale processes when compared to observational data. By comparing the numerical simulations with real observations, a deeper understanding of the phenomena and the mechanisms of and factors affecting them can be obtained. On the other hand, real observations play an essential role in validating and assessing forecast accuracy, hence helping to optimize the numerical models [50].
For many instruments (e.g., radar, lidar, satellite, as well as some unconventional instruments such as telescopes) that are currently used in the field to monitor atmospheric phenomena from the large-scale systems to turbulence, numerical models often do not provide the variables that the instruments observe. Therefore, a simulator or observational operator is needed to achieve the comparison and validation [51,52,53,54,55,56,57,58]. Specifically, in most numerical models, radar quantities, especially the polarimetric variables, are not considered as standard model output variables. In order to use such model data for verification or to understand physical processes, a radar forward operator is needed to convert the model variables into simulated radar measurements. The polarimetric radar forward operator is a vibrant research area. Pfeifer et al. [51] created a simulator using the T-matrix method to provide synthetic polarimetric parameters ZH, ZDR, and LDR for the bulk microphysics scheme with the Consortium for Small-scale Modeling (COSMO-DE) model. Ryzhkov et al. [52] presented a radar emulator to estimate polarimetric radar variables for the Hebrew University Cloud Model with spectral microphysics. The polarimetric variables were calculated with the scattering amplitudes for hydrometeors using T-matrix codes for resonance-sized particles and Rayleigh formulas for smaller particles. This emulator has been implemented in numerous studies such as Snyder et al. [59], Ilotoviz et al. [60], and Shpund et al. [61] to examine the characteristic of polarimetric signatures for a better understanding and forecast of updraft and graupel or hail. Jung et al. [53] developed a polarimetric radar forward operator to compute ZH, vertical reflectivity ZV and ZDR, reflectivity difference ZDP, and KDP for the single-moment Milbrandt and Yau microphysics scheme for the Advanced Regional Prediction System (ARPS) model. In a later study by Jung et al. [62], the radar forward operator was updated and the double-moment Milbrandt and Yau microphysics scheme was adopted to form an improved simulation of polarimetric signatures. The application of this radar operator includes a number of studies focused on assimilation of polarimetric radar observations for deep convective systems such as supercell [63,64,65,66]. In Snyder et al. [67,68], a three-moment microphysics scheme was built upon Jung et al. [62] to examine differences in simulated polarimetric signatures for radars at different wavelengths (X-band vs. S-band). A recent study by Oue et al. [69] demonstrated their Cloud-resolving model Radar SIMulator (CR-SIM) that could be used to compute polarimetric radar variables for multiple instruments (multi-wavelength radars and lidars) with input from multiple cloud and convective storm resolving models. Although all of the above-mentioned radar operators used the T-matrix algorithm to compute radar variables, there were differences among the operators due to the focuses of implementation and parameters used in the operator as well as the microphysics schemes. It is desired to develop different radar forward operators in the research community to provide techniques for validation of different numerical models, evaluate the accuracy and sensitivity of different assumptions in microphysics schemes for various weather systems, assess the radar retrieval methods, and provide more tools that can be used in data assimilation. This served the motivation of the current study.
The community Weather Research and Forecasting (WRF) model [70] is commonly used to simulate and analyze weather systems of different regimes and scales [71,72,73,74,75,76,77]. The above-mentioned studies demonstrate the capability of the WRF model to successfully simulate convective storms. At the same time, it was also shown that the model simulations are quite sensitive to the physics parameterizations. In this study, we developed a stand-alone polarimetric radar forward operator for three 2-moment microphysics schemes by Morrison et al. [78], Milbrandt and Yau [79,80], and Thompson et al. [81] that are commonly adopted in simulations of convective storms. This operator read in the WRF output files and computed polarimetric radar variables on the WRF model grid. The main purpose of this paper was to introduce of the polarimetric radar forward operator and demonstrate its capability. Another component of this study involved the analysis of observations from the National Weather Service (NWS) Weather Surveillance 1988 Doppler (WSR-88D) radar system for a severe convective storm. By comparing the simulated radar variables with the real observations, this analysis enabled us to understand more about the differences and limitations of the WRF model and the microphysics schemes.
This paper is organized as follows: Section 2 introduces the radar operator. In addition, a brief discussion is given on the observational data used, the model configuration, and the experiment design. In Section 3, the output from the polarimetric radar operator is discussed. A severe thunderstorm event was used as a case study to demonstrate the radar forward operator, and the output from the radar operator was compared with the real WSR-88D radar observations. Section 4 provides a summary and addresses some unresolved questions.
2. Materials and Methods
2.1. Polarimetric Radar Forward Operator
In this research study, we developed a portable polarimetric radar forward model operator coded in Fortran-90. This radar operator used output from WRF model simulations to compute idealized polarimetric radar observables for a S-band radar. The operator contained the following steps, as shown in Figure 1. In the first step, the hydrometeor mixing ratios, number concentrations, and atmosphere conditions including temperature, moisture, pressure, 3-D wind (speed and direction), air density, and model grid information were collected from the WRF output files. The radar location (longitude, latitude, and height above sea level) could be defined in the parameter file. The second step started with a module to compute the radar scan coordinates (elevation angle, range, and azimuth angle) for each model Cartesian grid (x, y, and z). The T-matrix algorithm was used to calculate scattering properties. The T-matrix scattering was calculated using look-up tables by numerically integrating forward and backward scattering amplitudes with hydrometeor sizes ranging from zero to the maximum sizes for each hydrometeor. Look-up tables of forward and backward scattering amplitudes were created based on Mishchenko’s T-matrix code [82] for different hydrometeors with various sizes and shapes. The radar variables were thus computed for each individual type of hydrometeor. Finally, the radar variables for all types of hydrometeors were added together and the final variables were derived for each model grid box.
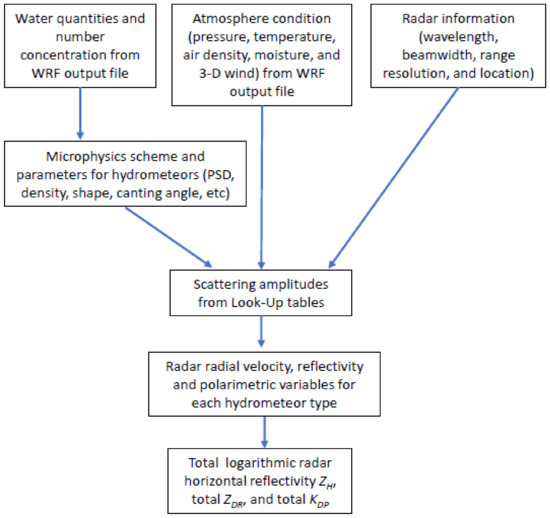
Figure 1.
Flow chart of the radar forward operator.
The hydrometeors in the radar operator included cloud, rain, ice, snow, and graupel and/or hail. The output variables from the radar operator included radial velocity (VR), horizontal reflectivity (ZH), vertical reflectivity (ZV), differential reflectivity (ZDR), and specific differential phase (KDP). This operator could be used for radars at different frequencies (S-, C-, X-, etc.). For the particular example shown in this paper, we used S-band radar with a wavelength of 10 cm and a frequency of 3 GHz. The radar beamwidth was set as 0.91° and radar range resolution was 250 m.
Radar reflectivity factors were computed as the total of different hydrometeor species with an integration over the particle size distribution using the following equations as given by Ryzhkov et al. [52]:
Here, Zhh, Zvv, and Zvh are expressed in mm6 m−3, and KDP is in degrees per kilometer. The corresponding logarithmic scale values of ZH in dBZ and ZDR in dB were obtained by:
In the above equations, λ is radar wavelength, |Kw|2 = 0.92 is the dielectric factor of water, Ni (D) gives the number of particles within the diameter interval between D and D + dD for the specific hydrometeor type i, M is the number of different species in the volume, and D is the equivalent volume diameter for the hydrometeor size bin. Re represents the real part of the complex number, and | | is its magnitude. The coefficients A1–A7 represent the angular moments of orientation distribution. fa,b(π) and fa,b(0) represent the complex backward and forward scattering amplitudes along the major (a) and minor (b) axes, respectively. The subscript * represents conjugation. The scattering amplitudes of each hydrometeor with different diameters were pre-computed and stored in the look-up tables using Mishchenko’s T-matrix code (available online on http://www.giss.nasa.gov/staff/mmishchenko/t_matrix.html, accessed on 15 April 2022). The look-up tables were built for each hydrometeor type as a function of particle size, density, aspect ratio, and air temperature. It was assumed that all hydrometeor particle types have a two-dimensional axisymmetric Gaussian distribution of particle orientations. As in Ryzhkov et al. [52], it was assumed that the mean canting angle is 0° and the standard deviation σ is 10° for cloud, rain, and ice, and 40° for snow and graupel or hail. Cloud particles were assumed to have a spherical shape, whereas the other hydrometeor types were assumed to be oblate spheroids. The aspect ratio for rain particles was a function of drop size following Brandes et al. [14], and the aspect ratio for graupel or hail followed the equations given by Ryzhkov et al. [52]. The scattering amplitudes were calculated for particles with equivolume diameters of 0.1–9 mm with bin widths of 10 μm for rain, 5 μm–50 mm with bin width of 10 μm for graupel, 5 μm–70 mm with bin width of 10 μm for hail, and 0.1–50 mm with bin width of 10 μm for snow.
The operator supported three 2-moment microphysics schemes: Milbrandt and Yau, Thompson, and Morrison. The related parameters of the hydrometeor particles were defined based on the specific microphysics scheme. For the Morrison scheme, a Gamma distribution with a fixed shape factor was assumed for particle size:
where N0, μ, and λ are the intercept, shape, and slope parameters of the size distribution, respectively. D is the particle diameter. For ice, rain, snow, and graupel, μ = 0. The number concentration of cloud droplet was set as a fixed value of 250 cm−1.
The slope was given by:
where is the gamma function, Q is the hydrometeor mass mixing ratio, and NT is the total number concentration of the specific hydrometeor. Parameters c and d were given by the power law mass–diameter relationship assuming fixed densities (500 kg m−3 for ice, 100 kg m−3 for snow, and 400 kg m−3 for graupel) for the hydrometeors.
The intercept was given by:
The Milbrandt and Yau scheme contains six hydrometeors: cloud, rain, ice, snow, graupel, and hail. The Gamma distribution was assumed for the particle size:
where NT is the total number concentration, and are dispersion parameters, and λ is the slope. For cloud droplets, = 1 and = 3. For other hydrometeors, = 1, so a more commonly used Gamma distribution was applied:
where the intercept parameter N0 was defined as:
The slope was given by:
where Q is hydrometeor mass mixing ratio. Parameters c and d were given by the power law mass–diameter relationship . In the Milbrandt and Yau scheme, hydrometeor density is defined as 100 kg m−3 for spherical snow, 400 kg m−3 for graupel, and 900 kg m−3 for hail.
The Thompson scheme contains five hydrometeors: cloud, rain, ice, snow, graupel, and hail. It predicts the mixing ratio for each hydrometeor species but the number concentrations for rain and ice only. The scheme also assumes a generalized Gamma distribution similar to Equation (8) for cloud droplets, cloud ice, and rain. The slope and intercept for these species were defined as in Equations (9) and (10).
For snow, the number density distribution was:
where is the nth moment of the snow size distribution. , , , , and .
For graupel, a generalized gamma distribution was assumed with the slope and intercept as:
where is the air density, and the particle density is defined as kg m−3 for graupel. Further details of the microphysics schemes are contained in Morrison et al. [78], Milbrandt and Yau [79,80], and Thompson et al. [81]. In these microphysics schemes, the particles are either liquid or solid. Therefore, melting or mixed-phased hydrometeors were not considered when developing the radar simulator package.
2.2. Numerical Experiments
A severe convective storm event in the afternoon of 29 May 2018 was used for a case study as a means of comparing simulated to real polarimetric radar fields. Simulations for this event were conducted with the WRF model version 3.8.1. Three nested domains were centered on the location of the event (Figure 2). The model domains had horizontal resolutions of 6.25, 1.25, and 0.25-km with 46 vertical levels, in order to adequately resolve the detailed storm scale structures with an affordable computational cost.
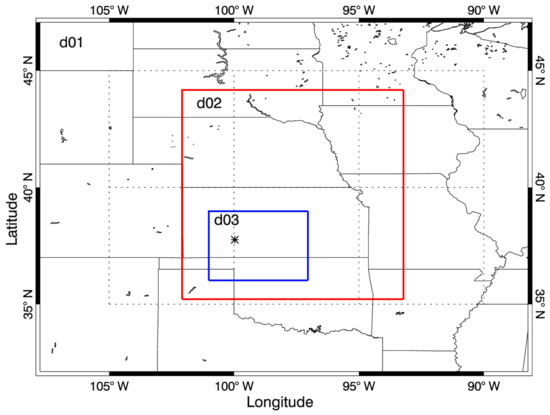
Figure 2.
WRF model nested domains for the case study. The black star shows the location of the KDDC radar.
The following physical schemes were used: the rapid radiative transfer model (RRTM; Mlawer et al. [83]) long-wave radiation, Dudhia short-wave radiation [84], Betts-Miller-Janjic cumulus parameterization [85], Mellor-Yamada_Janjic (MYJ) planetary boundary layer (PBL) schemes [85], and the Unified Noah land-surface model [86]. The cumulus scheme was only used for the outermost domain. The model top was set as 50 hPa. Three WRF model experiments were conducted using different microphysics schemes: WRF_Morr used the Morrison scheme, WRF_MY used the Milbrandt and Yau scheme, and WRF_Th used the Thompson scheme. All three experiments were initialized at 1200 UTC 29 May 2018 and ended at 12 UTC 30 May 2018. The initial and boundary conditions were interpolated from the NCEP 12-km resolution North American Mesoscale (NAM) analysis (https://rda.ucar.edu/datasets/ds609.0/#!description, accessed on 15 April 2022).
The WRF model outputs were saved every 5 min and were used as inputs for the radar forward operator. In this paper, the result focused on the simulation for the innermost domain. The radar operator was applied for all horizontal grids and for vertical levels from the lowest to the highest levels. Polarimetric variables were simulated for the S-band WSR-88D radar KDDC (the black star in Figure 2, 99.969° W in longitude, 37.761° N in latitude, and 813 m in altitude) in Dodge City, KS.
3. Results
To demonstrate the capability of the radar forward operator, it was applied to the WRF model simulation for the case study, as described above. In this section, we discuss the results from the radar operator, and compare the result with the real observation from the WSR-88D radar to evaluate the performance of the microphysics schemes used in the WRF model simulations.
3.1. Case Event and WSR-88D Radar Observation
On the afternoon of 29 May 2018, several multicell clusters and small-line-type convective storms formed in association with a dry-line boundary that extended from Colorado Front Range to Nebraska and Kansas where mixed layer convective available potential energy (MLCAPE) values of 1500–2000 J kg−1 were present. Starting at 2000 UTC, several isolated storms quickly intensified into severe thunderstorms. Supercell-type convection developed as the storms moved eastward across Kansas. Multiple reports of large hail with isolated regions of hail reaching up to 4 inches in diameter and severe gusts over 70 miles per hour were observed in central Kansas and near the Oklahoma and Kansas border. From 2100 UTC 29 May to 0100 UTC 30 May, three tornadoes were reported, one in Oklahoma and two in Kansas (https://www.spc.noaa.gov/exper/archive/event.php?date=20180529, accessed on 15 April 2022).
The Level II radar base data from the WSR-88D KDDC was obtained from the NOAA National Center for Environmental Information (NCEI; https://www.ncdc.noaa.gov/nexradinv/choosesite.jsp, accessed on 15 April 2022) and processed and analyzed for the severe storms simulated by the WRF model. In order to make comparisons with the model simulations, the Level 2 radar data were interpolated into the Cartesian coordinates (latitude, longitude, and height) with 250 m horizontal grid spacing and 500 m vertical spacing using the software Py-ART [87]. Figure 3 displays radar horizontal reflectivity at 1 km (where most particles were liquid water), 3 km (where mixed-phase and melting occurred), and 8 km (where most particles were solid) height at 2346 UTC 29 May when the storm reached its mature stage. As in Figure 3, a line of deep convective cells was developing in Oklahoma to Kansas with maximum reflectivity above 55 dBZ throughout the lower to upper troposphere. Within 10 min of this time, large hail with diameters up to 2.5 inches was reported at more than 10 places within this domain.
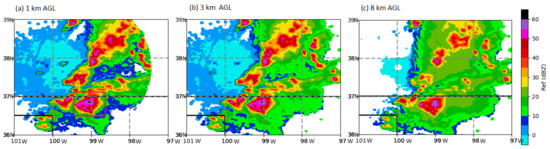
Figure 3.
ZH at (a) 1 km, (b) 3 km, and (c) 8 km height collected by KDDC radar on 2346 UTC 29 May 2018. The red box in the left panel shows the location of the hail storm that is discussed further in Section 3.3.
3.2. Radar Operator Result
Figure 4 shows the WRF model output for the mixing ratio and number concentration of rain and graupel or hail at 1 km altitude when the simulated storm reached the mature stage at 2345 UTC 29 May. Since both graupel and hail are predicted by the Milbrandt and Yau scheme, the sum of the two species was plotted in Figure 4e,k. The Thompson scheme does not provide number concentration for graupel, so it was not plotted here. The three microphysics schemes performed quite differently at this time. WRF_Morr produced a broader area of rainwater above 0.1 g kg−1 when compared to the other schemes. In WRF_MY, the storm area indicated by rainwater was narrower than WRF_Morr, but had comparable or even larger values of rain number concentration. WRF_Th produced the largest value for the maximum rainwater mixing ratio (7.2 g kg−1 vs. 3.5 in WRF_MY, and 3.2 in WRF_Morr) but the storm area indicated by rainwater was much narrower. In terms of rain number concentration, WRF_Th produced much higher values than the other two experiments (106 vs. 104 kg−1). WRF_MY produced graupel or hail in the lower troposphere with a maximum mixing ratio of 1.3 g kg−1 and WRF_Th produced graupel in the lower troposphere with a larger maximum amount of 2.8 g kg−1. In WRF_Morr, the graupel amount was quite small (10−4 g kg−1) during the entire simulation period.
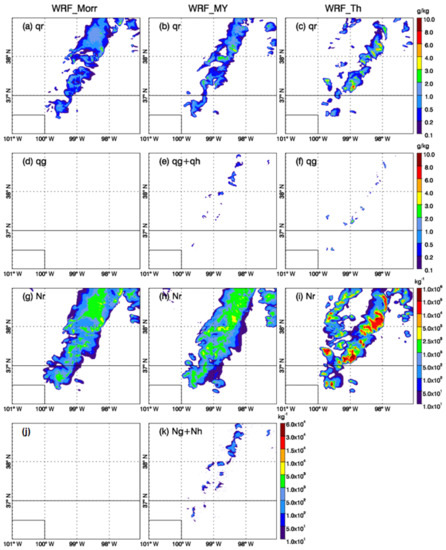
Figure 4.
Mixing ratio of rainwater (a–c) and graupel or hail (d–f) for WRF_Morr, WRF_MY, and WRF_Th, respectively. Total number concentration of rainwater (g–i) for WRF_Morr, WRF_MY, and WRF_Th, respectively. Graupel or hail number concentration for (j) WRF_Morr and (k) WRF_MY. All plots are for the fields at 2345 UTC 29 May 2018 at 1 km altitude.
Figure 5 shows ZH as produced by the radar operator corresponding to the WRF model output shown in Figure 4. Consistent with Figure 4a–c, ZH in WRF_Morr displayed a broader storm area than the other two experiments. WRF_Th predicted higher reflectivity convective cores than the other two with the maximum ZH of 60 dBZ. WRF_MY produced a narrower storm area but with the maximum ZH greater than WRF_Morr and a larger area of reflectivity >50 dBZ. For differential reflectivity, WRF_MY generated much smaller ZDR values for regions with ZH lower than 45 dBZ, indicating smaller rain particles. In WRF_Morr, ZDR was typically greater than 1.5 dB at most rainy areas with ZH above 30 dBZ, indicating the existence of large rain particles. A few areas of ZDR greater than 3 dB with the maximum value of 4.4 dB were also found to the east of strong convective regions. For example, the area near 36.4° N, 99.4° W was located to the east of the strong convection with ZH > 45 dBZ. This indicates that this location contained a small number of large drops of rain and lacked small drops. WRF_Th behaved differently when compared to WRF_Morr and WRF_MY. ZDR was generally 2–3 dB for regions with ZH over 30 dBZ except for the locations where graupel existed (Figure 4f). For example, ZDR was lower than 0.5 dB near 37.2° N, 99.0° W where ZH was above 40 dBZ, which is examined further in Section 3.3. Specific differential phase is sensitive to the amount of liquid water. Therefore, the locations of large KDP values (>0.4) agreed well with high ZH and high rainwater mixing ratio.
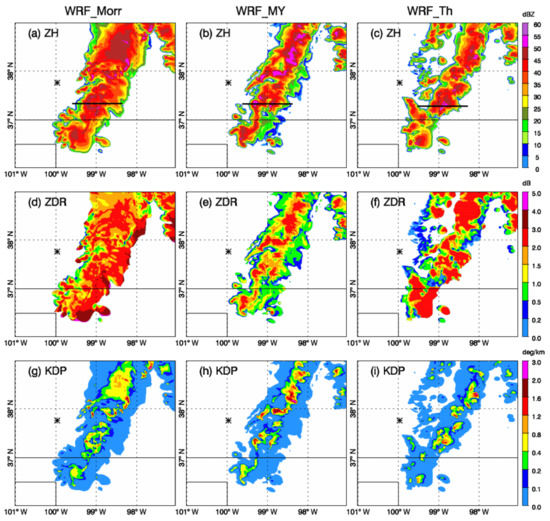
Figure 5.
ZH (a–c), ZDR (d–f), and KDP (g–i) for WRF_Morr, WRF_MY, and WRF_Th, respectively. All plots are for the fields at 2345 UTC 29 May 2018 at 1 km height. The black star shows the location of the KDDC radar. The black lines show the location of the cross-section discussed in Section 3.3.
The mean mass diameter (MMD) is a parameter that can be used to easily evaluate the particle size distribution. Since the ZDR field is largely proportional to the median diameter of the rain particles within the detected volume, the MMD of rain could help us understand the behavior of ZDR in the three simulations. The MMD in the unit volume for a Gamma distribution was defined as:
where is the air density and is density of liquid water, qr is rainwater mixing ratio, and NTr is the total number concentration of rain droplets. As shown in Figure 6, the overall pattern of MMDr at 1 km height generally agreed with ZDR shown in Figure 5d–f. For example, rain particles WRF_Morr showed the diameter as large as 0.8 mm over the southern end of the storm near 36.4° N, 99.4° W where the ZDR value was larger than 3 dB. WRF_MY had rain hydrometeors with MMDr generally lower than 0.2 mm except for the convective core regions, corresponding to the lower ZDR values (Figure 5e). For the Thompson scheme, MMDr was uniformly 0.2–0.3 mm for rainy areas which may explain ZDR values of 2–3 dB spreading over the region (Figure 5f).
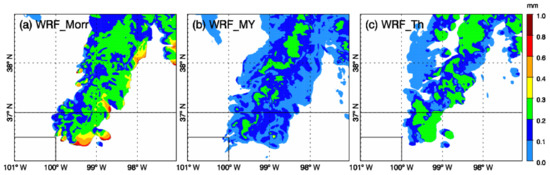
Figure 6.
Mean mass diameter of rain particles at 1 km height for (a) WRF_Morr, (b) WRF_MY and (c), WRF_Th at 2345 UTC 29 May 2018.
Figure 7 shows the mixing ratios for rainwater, snow, and graupel and/or hail in the mid-troposphere (3 km) where liquid water and ice coexist. At 3 km height, liquid water still dominated the precipitation. Similar to Figure 4, rainwater at mid-level in WRF_Morr expanded over a much broader area than the rest of the experiments. WRF_Th produced the largest maximum value (7–8 g kg−1), but it was concentrated over small areas. WRF_MY produced the smallest amount of rainwater with maximum value of 4.5 g kg−1. At 3 km, the snow mixing ratio (<0.5 g kg−1) was much smaller than rain and graupel or hail (both >1 g kg−1). Among all three experiments, WRF_Th produced the least amount of snow. WRF_Morr produced more snow for the northern part of the storm, while WRF_MY produced more snow for the southern part of the storm. For graupel and hail, WRF_MY produced a larger amount than WRF_Morr within the convective centers. WRF_Th generated the largest maximum value of 7.8 g kg−1 in graupel in the convective core near 37.2° N, 98.97° W.
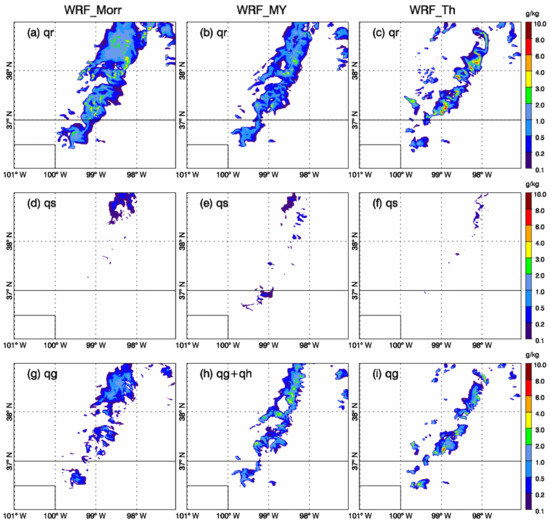
Figure 7.
Mixing ratio of rainwater (a–c), snow (d–f), and graupel and/or hail (g–i) for WRF_Morr, WRF_MY, and WRF_Th, respectively. All plots are for the fields at 2345 UTC 29 May 2018 at 3 km height.
Figure 8 shows the output from the radar operator for the WRF model output displayed in Figure 7. In the mid-troposphere where both liquid and frozen water exist, ZH over the convective centers became stronger than at lower levels due to the existence of graupel or hail. This could be seen in all three experiments. ZDR values were smaller here than at lower levels due to the same reason and the existence of snow. KDP values were generally smaller than Figure 5 except in the convective cores in WRF_Morr where larger amount of rainwater was predicted at mid-level than low level. Among all three experiments, WRF_MY produced the smallest values in ZDR, which was consistent with the patterns in the lower troposphere (Figure 5e) and the smaller amount of rainwater (Figure 7b) than the other experiments. In WRF_Morr, ZDR was generally greater than 0.5 dB at locations where there was more rain than graupel and below 0.5 dB at locations where graupel dominated, which was also the case for WRF_Th. In areas where the rainwater amount was large (Figure 7c), ZDR was around 2 dB and KDP values were above 0.4 deg km−1. For regions with a large amount of graupel (Figure 7i), ZDR was below 0.5 dB and KDP was less than 0.1 deg km−1.
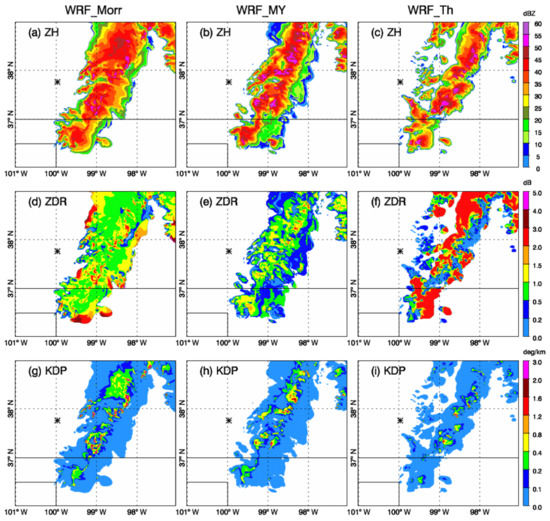
Figure 8.
ZH (a–c), ZDR (d–f), and KDP (g–i) for WRF_Morr, WRF_MY, and WRF_Th, respectively. All plots are for the fields at 2345 UTC 29 May 2018 at 3 km height. The star signs in the plots show the location of the KDDC radar.
One of the major benefits of this forward operator package was to provide polarimetric radar variables for each hydrometeor. Therefore, we had the opportunity to check the contribution from each individual hydrometeor species to the radar properties. Figure 9 shows ZH and ZDR at 3 km height for rain, snow, and graupel from WRF_Morr. It was seen that strong reflectivity (>40 dBZ) and large ZDR (>1 dB) appeared in convective storms from rain. Reflectivity from snow was quite small (<25 dBZ in most areas) and ZDR was near zero. For graupel, the horizontal reflectivity exceeded 40 dBZ over the northeastern part of the storm where graupel mixing ratio was larger than 1 g kg−1. ZDR from graupel was small (below 0.2 dB).
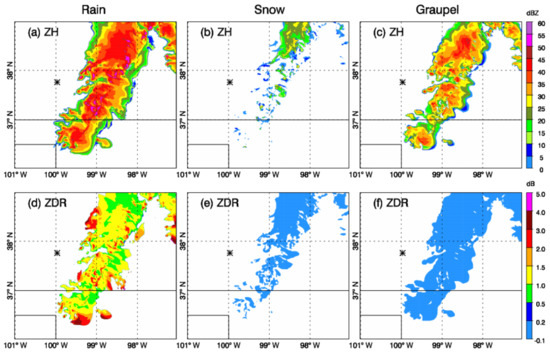
Figure 9.
ZH in (a–c) and ZDR in (d–f) from WRF_Morr contributed by rain, snow, and graupel, respectively. All plots are for 2345 UTC 29 May 2018 at 3 km height. The star signs in the plots show the location of the KDDC radar.
Figure 10 shows the mixing ratio and number concentration of snow and graupel and/or hail at 8 km height (near 350 hPa). Since the number concentration of snow and graupel are not predicted in Thompson scheme, these were not included here. The total of graupel and hail were plotted for Milbrandt and Yau scheme in Figure 10e,j. With a large area of snow >2 g kg−1 and a smaller area of graupel >1 g kg−1, WRF_Th overall predicted the most snow and the least graupel at high-level troposphere among the three experiments. WRF_MY produced comparable amounts of snow and graupel and hail as WRF_Morr but with larger maximum values (9.4 vs. 8.2 g kg−1) in graupel and hail over the convective centers. The overall number concentration of snow in WRF_MY was about two times higher than WRF_Morr. However, the number concentration of graupel and/or hail in WRF_Morr was generally larger than in WRF_MY.
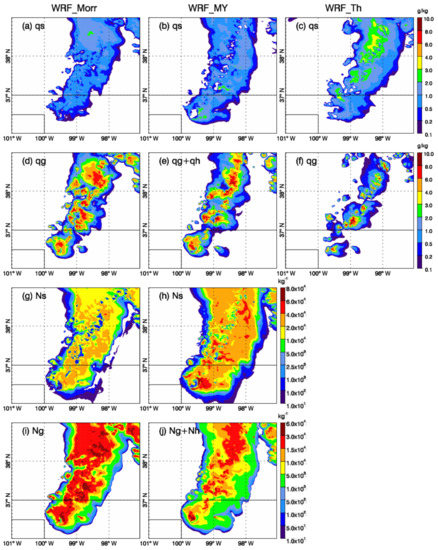
Figure 10.
Mixing ratios of snow (a–c) and graupel and/or hail (d–f) for WRF_Morr, WRF_MY, and WRF_Th, respectively. Total number concentrations of snow (g–h) and graupel and/or hail (i,j) for WRF_Morr and WRF_MY, respectively. All plots are for the fields at 2345 UTC 29 May 2018 at 8 km height.
Figure 11 shows the output from the radar operator for the WRF model fields shown in Figure 10. In the upper troposphere, ZH became smaller than mid-level due to the existence of large amounts of snow and ice. Among all three experiments, WRF_Th produced the strongest echo in convective centers with the maximum ZH exceeding 60 dBZ due to the large amount of graupel (Figure 8f). ZDR in all three experiments was generally less than 0.2 dB due to the dominance of frozen particles. KDP values in high tropospheric levels were generally below 0.1 deg km−1. Note that there were two areas with KDP above 0.2 deg km−1 in WRF_Morr, indicating the existence of supercooled water (red contour lines shown in Figure 11g) brought upward by strong updrafts.
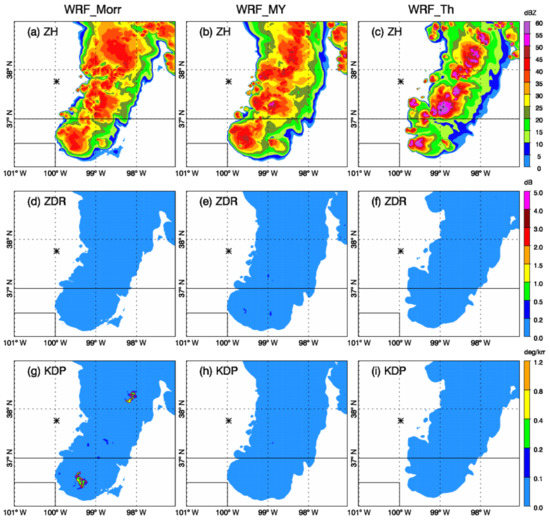
Figure 11.
ZH (a–c), ZDR (d–f), and KDP (g–i) for WRF_Morr, WRF_MY, and WRF_Th, respectively. Red contour lines in KDP plot show the rain water mixing ratio of 0.5 g kg−1. All plots are for the fields at 2345 UTC 29 May 2018 at 8 km height. The star signs in the plots show the location of the KDDC radar.
3.3. Observation and Simulated Variables for a Hail Storm
Figure 12 plots the NDDC radar measured reflectivity and differential reflectivity of a hail storm within the region of 36.5–37.3° N and 98.6–99.6° W at 2321 UTC (see the red box in Figure 3). The Level II radar data were interpolated into Cartesian coordinates by Py-ART using a Cressman function with the radius of influence increasing with distance from the radar. Storm reports indicated that hail with diameter up to 6 cm at five different places were produced by this storm from 2250 to 2330 UTC. From Figure 12a, two high ZH (>55 dBZ) areas were produced. One was in the convective core near 36.85° N, 99.34° W, and the other was around 36.9° N, 99.3–99.0° W. The vertical cross-section of ZH along the longitude of 99.34° W (Figure 12b) showed high ZH (above 40 dBZ) extending from the surface to 10 km altitude. In Figure 12c, a small area of low ZDR (“ZDR hole”) appeared near 36.85° N, 99.34° W surrounded by high ZDR values. This is a typical polarimetric signature to indicate the existence of hail in the lower troposphere. Another area of low ZDR values was found within the high ZH area near 36.8–36.93° N, 99.3–99.0° W, coincident with the hail reported near 36.82° N, −99.12° W. From the vertical cross section plot (Figure 12d), the ZDR hole could be seen from the surface up to the mid-troposphere. On both sides of the ZDR hole, ZDR columns (large ZDR up to 3.0 dB from surface to ~4 km height) were found, indicating large particles of rainwater in the lower atmosphere.
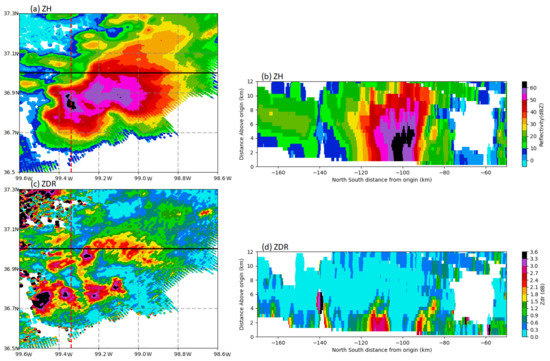
Figure 12.
(a) ZH and (c) ZDR at 1 km height collected by KDDC radar at 2321 UTC 29 May 2018. Vertical cross-section of (b) ZH and (d) ZDR along the longitude of 99.34° W.
Figure 13 shows the west-east vertical cross-section (the black lines shown in Figure 5a–c) of the simulated storm from different experiments. For the storm in WRF_Morr, three strong updrafts were created along the latitude line with ZH up to 55 dBZ from the low- to mid-level troposphere. In general, large values of ZDR (>2 dB) concentrated at the surface to 2 km height with extremely large ZDR values (>3 dB) appearing below 1 km height. At the updraft centers, ZDR columns (ZDR values above 2 dB from surface to 3–4 km height) were found, which indicated large rain particles brought upward by the updrafts. The location of 0.2 dB agreed well with the 0 °C isotherm, indicating the separation of frozen and liquid precipitation particles. KDP corresponded well with the ZH field. KDP columns (large KDP up to 3 deg km−1 from surface to mid-level) were found in the convective centers with ZH > 50 dBZ. Supercooled water was seen from 9 to 12 km which caused KDP exceeding 0.2 deg km−1 (red contour line in Figure 13g). For WRF_MY, Figure 13b captures two major updrafts with ZH near 60 dBZ. The sizes of the convective centers in both horizontal and vertical directions were larger in WRF_MY than WRF_Morr. However, the ZDR columns in WRF_MY were generally smaller than in WRF_Morr with 2–3 dB confined below 2.5 km height. Again, KDP columns were also found in WRF_MY but with smaller maximum values. In Figure 13h, small areas of total KDP up to 0.4 deg km−1 were found around 10 km height. This was largely due to the supercooled water drops (contribution indicated by the red contour line of 0.2 deg km−1) carried up by the strong updrafts. WRF_Th produced a storm that had graupel at the surface and low troposphere. There was only one strong updraft in the center of the storm with ZH above 60 dBZ from the mid- to upper-troposphere. Beneath the strong updraft, downdraft and ZH of 55 dBZ were found from the surface to 2 km height. The ZDR plot in Figure 13f shows a ZDR hole (small ZDR less than 0.2 dB surrounded by larger values of ZDR) in the low levels. The small ZDR with large ZH near 98.9° W indicated the existence of graupel from the surface to the upper troposphere (confirmed by Figure 5i, Figure 7i, and Figure 10f).
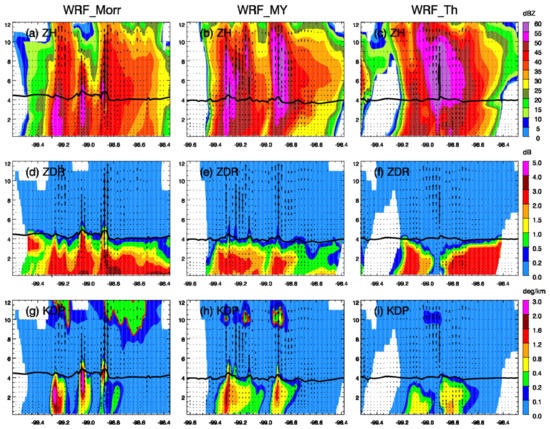
Figure 13.
Vertical cross-sections of ZH in (a–c), ZDR in (d–f), and KDP in (g–i) for WRF_Morr, WRF_MY, and WRF_Th, respectively. Vertical cross-sections are plotted along the black lines shown in Figure 5a–c. The vectors are vertical velocity and the black curves show the height of the 0 °C isotherms. The red contours in the upper level of (g–i) show KDP of 0.2 deg km−1 from rain water only.
Comparing with the simulated storms shown in Figure 13, the observed hail storm shown in Figure 12 had a smaller horizontal span with strong echoes (55–65 dBZ) existing mostly below 6 km height. The strong echoes in the simulated storms (Figure 13b,c) reached 9 km height and above, indicating much stronger updrafts and a larger amount of graupel or hail in the upper atmosphere of the simulated storms. The observed storm showed ZDR columns (ZDR > 2 dB) in the low- to mid-troposphere in regions with ZH exceeding 35 dBZ, which was also found in all simulated storms reflecting the large amount of large rain drops. The above results showed that the radar forward operator was developed properly and demonstrated value by the ability to produce representative polarimetric radar fields. To note, specific differential phase was not Level II base data from NWS WSR-88D radar; therefore, no comparison between observations and predictions was made for KDP.
In order to better understand the existence of the ZDR column and KDP column, scatterplots with qr were generated for the three experiments. In Figure 14a–c, large ZDR values (≥1.5 dB for grid points below freezing level) and their corresponding qr values were plotted. In WRF_Morr, large ZDR ranged from 1.5 to 3.8 dB with qr up to 8.5 g kg−1. For qr above 4 g kg−1, a large portion of the grid points had ZDR of 2.1–2.3 dB. For grid point with ZDR > 3 dB, qr was generally less than 1 g kg−1. For WRF_MY, ZDR was between 1.5 and 2.8 dB with qr almost evenly distributed within 0–4 g kg−1. In addition, most of the grid points with ZDR > 2.3 dB had qr lower than 2.0 g kg−1. For WRF_Th, ZDR values were between 1.5 and 2.5 dB with qr up to 8.2 g kg−1. For larger qr (>6 g kg−1), ZDR values were typically lower than 1.8 dB. Figure 14d–f plots large KDP values (≥1.0 deg km−1 for grid points below freezing level) and their corresponding qr. In WRF_Morr and WRF_MY, KDP increased with qr. Therefore, the largest KDP agreed with the largest value in qr. In WRF_Th, such increasing trend of KDP was not apparent. For high qr values (>6 g kg−1), KDP spread out between 1.0 and 3.8 deg km−1.
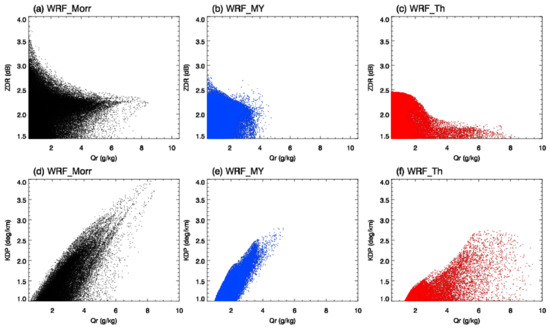
Figure 14.
Scatterplots of large ZDR vs. qr in (a–c) and KDP vs. qr in (d–f) for WRF_Morr, WRF_MY, and WRF_Th, respectively, when temperature was equal to or above 0 °C.
4. Discussion
In this paper, we introduced a new polarimetric radar forward operator for three different microphysics schemes: 2-moment Morrison, 2-moment Milbrandt and Yau, and Thompson. The radar forward operator was developed based on scattering calculations using the T-matrix algorithm. The radar forward operator used thermodynamic, microphysics, and wind information from WRF model simulations as input and produced polarimetric radar variables including VR, ZH, ZDR, and KDP. A case study for a severe thunderstorm on 29–30 May 2018 was examined to demonstrate the capability of the radar forward operator.
High-resolution WRF simulations for the severe thunderstorms showed that the microphysics schemes performed significantly different in terms of the type, mass, and number concentration of different hydrometeors. The Morrison scheme produced a broader area with a large amount of rain in the low- to mid-troposphere. The Thompson scheme produced a much larger rain number concentration than both the Milbrandt and Yau scheme and Morrison scheme. In addition, the significant difference in the Thompson scheme from the other schemes was the presence of a much larger amount of graupel from the surface into the lower troposphere over the convective core. In the upper troposphere, the Thompson scheme produced the largest amount of snow and the least amount of graupel among all experiments. The snow number concentration from the Milbrandt and Yau scheme was about two times larger than that in the Morrison scheme, while the graupel and hail number concentration from the Milbrandt and Yao scheme was smaller than the Morrison scheme.
The output from the radar forward operator followed the distribution of the microphysics properties. From ZH, it was shown that the Morrison scheme produced a broader storm area at low- to mid-levels than the other two experiments. At upper levels, the Milbrandt and Yau showed stronger ZH at convective centers than the Morrison scheme, but the Thompson scheme generated the strongest radar echo among all three schemes. Regarding ZDR, the Milbrandt and Yau scheme produced generally smaller ZH values, which could be explained by the much smaller mean mass diameter of rain drops. Since each hydrometeor was processed separately in the radar forward operator, it was convenient to examine the contributions from different hydrometeors. This was especially useful in mid-levels where liquid and solid or ice particles coexist. This was seen in the polarimetric variables at 3 km height for the Morrison scheme, which showed that a major part of the high reflectivity and high ZDR values were contributed by rain. For KDP, all three experiments indicated a good correlation between large KDP values and the large amount of rain. KDP could also indicate the supercooled water at high altitudes. ZDR columns and KDP columns were found in all three model simulations corresponding to the large amount of rain within the strong updrafts in the low- to mid-troposphere. The ZDR hole was found to spatially closely correspond with the existence of graupel in the lower troposphere as produced by the Thompson scheme.
The results confirmed that the radar operator was properly built for the three microphysics schemes. Since these schemes do not allow mixed-phase particles, melting was not considered in the current operator. However, melting is an important process for snow and graupel or hail in the real atmosphere. The absence of melting processes may cause errors in polarimetric variables. For future developments, the melting process is a key component to add. In addition, two other polarimetric variables, the correlation coefficient ρHV and the linear depolarization ratio (LDR), are still under development. ρHV is the correlation coefficient between the horizontal and vertical polarized echoes. LDR is the ratio of the vertical power return from a horizontal pulse or the horizontal power return from a vertical pulse, which is sensitive to the existence of mixed types of precipitation particles. Both variables can bring important information on the characteristics of mixed-phase precipitation particles. We must also compare the output from our operator with other publicly available radar operators (e.g., pyDualPol software available from http://arps.ou.edu/downloadpyDualPol.html, accessed on 15 April 2022). The comparison would be toward an assessment of scheme accuracy relative to radar-observed storms to gain confidence in how well our method simulates polarimetric variables. Comparing results from the pyDualPol operator to the operator developed here would help the research community evaluate the overall value of such operators.
For future work, it is our plan to produce simulated polarimetric observables and compare them with the real radar observations to validate and evaluate the microphysics schemes. Currently, our case studies (besides the event shown in the paper, we are also investigating two other heavy precipitation cases in 2018) only focus on S-band radars. Since many C- or X-band radars are also available for both research and operational communities, it is valuable to expand the present examination and include these higher frequency radars. The current forward operator was developed for WRF model output, yet with modifications in the interface modules, this operator can be adapted for other regional forecast models as well. The comparisons shown here between KDDC WSR-88D radar and WRF model simulations are only from one case study, which may not represent the general behavior of different microphysics schemes. More case studies for different precipitation regimes (light, moderate, and heavy) need to be conducted for a thorough understanding of the microphysics properties and polarimetric signatures produced by the different schemes.
In addition, as an idealized research tool, the errors that occur in the model forecast is passed to the radar operator. The impact of these errors is two-fold: (1) the errors provide a great opportunity to explore the uncertainties in the WRF model microphysics schemes through sensitivity studies, which may be an important component of our future research; (2) they allow for the validation of the WRF-model-simulated radar variables against real observations since attenuations, errors, and noise are expected in real observations. In future studies, the community should explore techniques to enhance the simulator toward creating data closer to the real radar observations.
Author Contributions
Conceptualization, X.L. and J.R.M.; methodology, X.L. and J.R.M.; software, X.L. and J.S.; validation, X.L.; formal analysis, X.L.; writing—original draft preparation, X.L., J.R.M., J.A.O. and D.S.H.; writing—review and editing, X.L., J.R.M., J.A.O., D.S.H. and J.S.; visualization, X.L. and J.S.; supervision, J.R.M. and J.A.O.; project administration, J.R.M. and J.A.O.; funding acquisition, J.R.M. and J.A.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science Foundation grants AGS-1746119 and AGS-1746475.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The storm report data can be obtained from https://www.spc.noaa.gov/exper/archive, accessed on 15 April 2022. The WSR-88D radar level II base data can be downloaded from the NOAA National Center for Environmental Information (NCEI; https://www.ncdc.noaa.gov/nexradinv/choosesite.jsp, accessed on 15 April 2022). The NCEP 12 km resolution North American Mesoscale (NAM) analysis is available from https://rda.ucar.edu/datasets/ds609.0/#!description (accessed on 15 April 2022). The WRF model data presented in this study are available via request to the corresponding author.
Acknowledgments
The authors would like to acknowledge the support of NSF Grants AGS-1746119 and AGS-1746475 and the comments from the anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rinehart, R.E. Radar for Meteorologists, 4th ed.; Rinehart: Columbia, MO, USA, 2004; p. 482. ISBN 0965800210. [Google Scholar]
- Seliga, T.A.; Bringi, V.N. Potential Use of Radar Differential Reflectivity Measurements at Orthogonal Polarizations for Measuring Precipitation. J. Appl. Meteor. 1976, 15, 69–76. [Google Scholar] [CrossRef]
- Sachidananda, M.; Zrnić, D.S. Rain rate estimates from differential polarization measurements. J. Atmos. Ocean. Technol. 1987, 4, 588–598. [Google Scholar] [CrossRef]
- Straka, J.M.; Zrnić, D.S.; Ryzhkov, A.V. Bulk Hydrometeor Classification and Quantification Using Polarimetric Radar Data: Synthesis of Relations. J. Appl. Meteorol. 2000, 39, 1341–1372. [Google Scholar] [CrossRef]
- Seliga, T.A.; Bringi, V.N.; AI-Khatib, H.H. A preliminary study of comparative measurements of rainfall rate using the differential reflectivity radar technique and a raingage network. J. App. Meteorol. 1981, 20, 1362–1368. [Google Scholar] [CrossRef]
- Seliga, T.A.; Aydin, K.; Direskeneli, H. Disdrometer measurements during an intense rainfall event in central Illinois: Implications for differential reflectivity radar observations. J. Appl. Meteorol. 1986, 25, 835–846. [Google Scholar] [CrossRef][Green Version]
- Ulbrich, C.W.; Atlas, D. Assessment of the contribution of differential polarization to improved rainfall measurements. Radio Sci. 1984, 19, 49–57. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Zrnić, D. Comparison of dual-polarization radar estimators of rain. J. Atmos. Ocean. Technol. 1995, 12, 249–256. [Google Scholar] [CrossRef]
- Hall, M.; Goddard, J.; Cherry, S. Identification of hydrometeors and other targets by dual-polarization radar. Radio Sci. 1984, 19, 132–140. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Bringi, V.; Balakrishnan, N.; Zrnić, D. Error structure of multiparameter radar and surface measurements of rainfall: Part III. Specific differential phase. J. Atmos. Ocean. Technol. 1990, 7, 621–629. [Google Scholar] [CrossRef]
- Zrnić, D.; Ryzhkov, A. Advantages of rain measurements using specific differential phase. J. Atmos. Ocean. Technol. 1996, 13, 454–464. [Google Scholar] [CrossRef]
- Carey, L.; Rutledge, S.; Ahijevych, D.; Keenan, T. Correcting propagation effects in C-band polarimetric radar observations of tropical convection using differential propagation phase. J. Appl. Meteorol. 2000, 39, 1405–1433. [Google Scholar] [CrossRef]
- Zhang, G.; Vivekanandan, J.; Brandes, E. A method for estimating rain rate and drop size distribution from polarimetric radar measurements. IEEE Trans. Geosci. Remote Sens. 2001, 39, 830–841. [Google Scholar] [CrossRef]
- Brandes, E.; Zhang, G.; Vivekanandan, J. Experiments in rainfall estimation with a polarimetric radar in a subtropical environment. J. Appl. Meteorol. 2002, 41, 674–685. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Zhang, G.; Brandes, E. Polarimetric radar estimators based on a constrained gamma drop size distribution model. J. Appl. Meteorol. 2004, 43, 217–230. [Google Scholar] [CrossRef]
- Aydin, K.; Zhao, Y.; Seliga, T. A differential reflectivity radar hail measurement technique: Observations during the Denver hailstorm of 13 June 1984. J. Atmos. Ocean. Technol. 1990, 7, 104–113. [Google Scholar] [CrossRef]
- Aydin, K.; Seliga, T.; Balaji, V. Remote sensing of hail with a dual linear polarization radar. J. Clim. Appl. Meteorol. 1986, 25, 1475–1484. [Google Scholar] [CrossRef]
- Carey, L.; Rutledge, S. Electrical and multiparameter radar observations of a severe hailstorm. J. Geophys. Res. 1998, 103, 13979–14000. [Google Scholar] [CrossRef]
- Hubbert, J.; Bringi, V.; Carey, L. CSU-CHILL polarimetric radar measurements from a severe hail storm in Eastern Colorado. J. Appl. Meteorol. 1998, 37, 749–775. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Kernen, R.; Lim, S.; Moisseev, D. Recent advances in classification of observations from dualpolarization weather radars. Atmos. Res. 2013, 119, 97–111. [Google Scholar] [CrossRef]
- Thompson, E.; Rutledge, S.; Dolan, B.; Chandrasekar, V.; Cheong, B. A dual-polarization radar hydrometeor classification algorithm for winter precipitation. J. Atmos. Ocean. Technol. 2014, 31, 1457–1481. [Google Scholar] [CrossRef]
- Wen, G.; Protat, A.; May, P.; Wang, X.; Moran, W. A cluster-based method for hydrometeor classification using polarimetric variables. Part I: Interpretation and analysis. J. Atmos. Ocean. Technol. 2015, 32, 1320–1340. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Ellis, S.; Oye, R.; Zrnić, D.; Ryzhkov, A.; Straka, J. Cloud microphysics retrieval using S-band dual-polarization radar measurements. Bull. Am. Meteorol. Soc. 1999, 80, 381–388. [Google Scholar] [CrossRef]
- Deierling, W. The Relationship between Total Lightning and Ice Fluxes. Ph.D. Thesis, University of Alabama in Huntsville, Huntsville, AL, USA, 2006. [Google Scholar]
- Kumjian, M.R.; Khain, A.P.; Benmoshe, N.; Ilotoviz, E.; Ryzhkov, A.V.; Phillips, V. The anatomy and physics of ZDR columns: Investigating a polarimetric radar signature with a spectral bin microphysical model. J. Appl. Meteorol. Climatol. 2014, 53, 1820–1843. [Google Scholar] [CrossRef]
- Kuster, C.M.; Schuur, T.J.; Lindley, T.T.; Snyder, J.C. Using ZDR Columns in Forecaster Conceptual Models and Warning Decision-Making. Weather Forecast. 2020, 35, 2507–2522. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Kumjian, M.R.; Ganson, S.M.; Khain, A.P. Polarimetric radar characteristics of melting hail. Part I: Theoretical simulations using spectral microphysical modeling. J. Appl. Meteorol. Climatol. 2013, 52, 2849–2870. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Kumjian, M.R.; Ganson, S.M.; Khain, A.P. Polarimetric radar characteristics of melting hail. Part II: Practical implication. J. Appl. Meteorol. Climatol. 2013, 52, 2871–2886. [Google Scholar] [CrossRef]
- Ortega, K.L.; Krause, J.M.; Ryzhkov, A.V. Polarimetric radar characteristics of melting hail. Part III: Validation of the algorithm for hail size discrimination. J. Appl. Meteorol. Climatol. 2016, 55, 829–848. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Zrnić, D. Use of polarization to characterize precipitation and discriminate large hail. J. Atmos. Sci. 1990, 47, 1525–1540. [Google Scholar] [CrossRef]
- Holler, H.; Bringi, V.; Hubbert, J.; Hagen, M.; Meischner, P. Life cycle and precipitation formation in a hybridtype hailstorm revealed by polarimetric and Doppler radar measurements. J. Atmos. Sci. 1994, 51, 2500–2522. [Google Scholar] [CrossRef]
- Brandes, E.; Ikeda, K. Freezing-level estimation with polarimetric radar. J. Appl. Meteor. 2004, 43, 1541–1553. [Google Scholar] [CrossRef]
- Bluestein, H.; French, M.; Tanamachi, R.; Frasier, S.; Hardwick, K.; Junyent, F.; Pazmany, A. Close-Range observations of tornadoes in supercells made with a dual-polarization, X-band, mobile Doppler radar. Mon. Weather Rev. 2007, 135, 1522–1543. [Google Scholar] [CrossRef]
- Deierling, W.; Petersen, W.; Latham, J.; Ellis, S.; Christian, H. The relationship between lightning activity and ice fluxes in thunderstorms. J. Geophys. Res. 2008, 113, D15210. [Google Scholar] [CrossRef]
- Payne, C.; Schuur, T.; MacGorman, D.; Biggerstaff, M.; Kuhlman, K.; Rust, W. Polarimetric and electrical characteristics of a lightning ring in a supercell storm. Mon. Weather Rev. 2010, 138, 2405–2425. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S.; Jauernic, S.T. Spatial and temporal characteristics of polarimetric tornadic debris signatures. J. Appl. Meteorol. Climatol. 2014, 53, 2217–2231. [Google Scholar] [CrossRef][Green Version]
- Snyder, J.; Ryzhkov, A. Automated Detection of Polarimetric Tornadic Debris Signatures Using a Hydrometeor Classification Algorithm. J. Appl. Meteorol. Climatol. 2015, 54, 1861–1870. Available online: https://journals.ametsoc.org/view/journals/apme/54/9/jamc-d-15-0138.1.xml (accessed on 15 April 2022). [CrossRef]
- Bluestein, H.B.; French, M.M.; Popstefanija, I.; Bluth, R.T.; Knorr, J.B. A mobile, phased-array doppler radar for the study of severe convective storms: The MWR-05XP. Bull. Am. Meteorol. Soc. 2010, 91, 579–600. [Google Scholar] [CrossRef]
- Bluestein, H.B.; Thiem, K.J.; Snyder, J.C.; Houser, J.B. Tornadogenesis and early Tornado evolution in the El Reno, Oklahoma, supercell on 31 May 2013. Mon. Weather. Rev. 2019, 147, 2045–2066. [Google Scholar] [CrossRef]
- Pazmany, A.L.; Mead, J.B.; Bluestein, H.B.; Snyder, J.C.; Houser, J.B. A mobile rapid-scanning X-band polarimetric (RaXPol) Doppler radar system. J. Atmos. Ocean. Technol. 2013, 30, 1398–1413. [Google Scholar] [CrossRef]
- French, M.M.; Bluestein, H.B.; PopStefanija, I.; Baldi, C.A.; Bluth, R.T. Reexamining the vertical development of tornadic vortex signatures in supercells. Mon. Weather Rev. 2013, 141, 4576–4601. [Google Scholar] [CrossRef]
- Griffin, C.B.; Bodine, D.J.; Kurdzo, J.M.; Mahre, A.; Palmer, R.D. High-temporal resolution observations of the 27 May 2015 Canadian, Texas, Tornado using the Atmospheric Imaging Radar. Mon. Weather Rev. 2019, 147, 873–891. [Google Scholar] [CrossRef]
- Houser, J.L.; Bluestein, H.B.; Snyder, J.C. Rapid-scan, polarimetric, doppler radar observations of tornadogenesis and tornado dissipation in a tornadic supercell: The “El Reno, Oklahoma” storm of 24 May 2011. Mon. Weather Rev. 2015, 143, 2685–2710. [Google Scholar] [CrossRef]
- Kosiba, K.A.; Wurman, J. The three-dimensional structure and evolution of a tornado boundary layer. Weather Forecast. 2013, 28, 1552–1561. [Google Scholar] [CrossRef]
- Kuster, C.M.; Snyder, J.C.; Schuur, T.J.; Lindley, T.T.; Heinselman, P.L.; Furtado, J.C.; Brogden, J.W.; Toomey, R. Rapid-update radar observations of ZDR column depth and its use in the warning decision process. Weather Forecast. 2019, 34, 1173–1188. [Google Scholar] [CrossRef]
- Kurdzo, J.M.; Nai, F.; Bodine, D.J.; Bonin, T.A.; Isom, B.; Palmer, R.D.; Cheong, B.L.; Lujan, J.; Mahre, A.; Byrd, A. Observations of severe local storms and tornadoes with the Atmospheric Imaging Radar. Bull. Amer. Meteorol. Soc. 2017, 98, 915–935. [Google Scholar] [CrossRef]
- Snyder, J.C.; Bluestein, H.B. Some considerations for the use of high-resolution mobile radar data in tornado intensity determination. Weather Forecast. 2014, 29, 799–827. [Google Scholar] [CrossRef]
- Witt, A.; Burgess, D.W.; Seimon, A.; Allen, J.T.; Snyder, J.C.; Bluestein, H.B. Rapid-scan radar observations of an Oklahoma tornadic hailstorm producing giant hail. Weather Forecast. 2018, 33, 1263–1282. [Google Scholar] [CrossRef]
- Wurman, J.; Kosiba, K.; Robinson, P.; Marshall, T. The role of multiple-vortex tornado structure in causing storm researcher fatalities. Bull. Amer. Meteorol. Soc. 2014, 95, 31–45. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Snyder, J.; Carlin, J.T.; Khain, A.; Pinsky, M. What polarimetric weather radars offer to cloud modelers: Forward radar operators and microphysical/thermodynamic retrievals. Atmosphere 2020, 11, 362. [Google Scholar] [CrossRef]
- Pfeifer, M.; Craig, G.; Hagen, M.; Keil, C. A polarimetric radar forward operator for model evaluation. J. Appl. Meteor. Climatol. 2008, 47, 3202–3220. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Pinsky, M.; Pokrovsky, A.; Khain, A. Polarimetric Radar Observation Operator for a Cloud Model with Spectral Microphysics. J. Appl. Meteor. Climatol. 2011, 50, 873–894. [Google Scholar] [CrossRef]
- Jung, Y.; Xue, M.; Zhang, G.; Straka, J. Assimilation of simulated polarimetric radar data for a convective storm using the ensemble Kalman filter. Part I: Observation operators for reflectivity and polarimetric variables. Mon. Wea. Rev. 2008, 136, 2228–2245. [Google Scholar] [CrossRef]
- Pincus, R.; Platnick, S.; Ackerman, S.A.; Hemler, R.S.; Hofmann, R.J.P. Reconciling Simulated and Observed Views of Clouds: MODIS, ISCCP, and the Limits of Instrument Simulators. J. Clim. 2012, 25, 4699–4720. [Google Scholar] [CrossRef]
- Botygina, N.N.; Kovadlo, P.G.; Kopylov, E.A.; Lukin, V.P.; Tuev, M.V.; Shikhovtsev, A.Y. Estimation of the astronomical seeing at the large solar vacuum telescope site from optical and meteorological measurements. Atmos. Ocean. Opt. 2014, 27, 142–146. [Google Scholar] [CrossRef]
- Kovadlo, P.G.; Shikhovtsev, A.Y.U.; Kopylov, E.A.; Kiselev, A.V.; Russkikh, I.V. Study of the Optical Atmospheric Distortions using Wavefront Sensor Data. Russ. Phys. J. 2021, 63, 1952–1958. [Google Scholar] [CrossRef]
- Avila, R.; Carrasco, E.; Ibañez, F.; Vernin, J.; Prieur, J.-L.; Cruz, D.X. Generalized SCIDAR Measurements at San Pedro Mártir. II. Wind Profile Statistics. Publ. Astron. Soc. Pac. 2006, 118, 503–515. [Google Scholar] [CrossRef]
- Voyez, J.; Robert, C.; Conan, J.-M.; Mugnier, L.M.; Samain, E.; Ziad, A. First on-sky results of the CO-SLIDAR Cn2 profiler. Opt. Express 2014, 22, 10948–10967. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Snyder, J.C.; Ryzhkov, A.V.; Kumjian, M.R.; Khain, A.P.; Picca, J. A ZDR column detection algorithm to examine convective storm updrafts. Weather Forecast. 2015, 30, 1819–1844. [Google Scholar] [CrossRef]
- Ilotoviz, E.; Khain, A.; Ryzhkov, A.V.; Snyder, J.C. Relationship between aerosols, hail microphysics, and ZDR columns. J. Atmos. Sci. 2018, 75, 1755–1781. [Google Scholar] [CrossRef]
- Shpund, J.; Khain, A.; Lynn, B.; Fan, J.; Han, B.; Ryzhkov, A.; Snyder, J.; Dudhia, J.; Gill, D. Simulating a mesoscale convective system using WRF with a new spectral bin microphysics: 1: Hail vs graupel. J. Geophys. Res. Atmos. 2019, 124, 14072–14101. [Google Scholar] [CrossRef]
- Jung, Y.; Xue, M.; Zhang, G.; Straka, J. Simulations of polarimetric radar signatures of a supercell storm using a two-moment bulk microphysics scheme. J. Appl. Meteor. Climatol. 2010, 49, 146–163. [Google Scholar] [CrossRef]
- Jung, Y.; Xue, M.; Zhang, G.; Straka, J.M. Assimilation of Simulated Polarimetric Radar Data for a Convective Storm Using the Ensemble Kalman Filter. Part II: Impact of Polarimetric Data on Storm Analysis. Mon. Weather Rev. 2008, 136, 2246–2260. Available online: https://journals.ametsoc.org/view/journals/mwre/136/6/2007mwr2288.1.xml (accessed on 15 April 2022). [CrossRef]
- Snook, N.; Xue, M.; Jung, Y. Analysis of a Tornadic Mesoscale Convective Vortex Based on Ensemble Kalman Filter Assimilation of CASA X-Band and WSR-88D Radar Data. Mon. Weather Rev. 2011, 139, 3446–3468. [Google Scholar] [CrossRef]
- Jung, Y.; Xue, M.; Tong, M. Ensemble Kalman Filter Analyses of the 29–30 May 2004 Oklahoma Tornadic Thunderstorm Using One- and Two-Moment Bulk Microphysics Schemes, with Verification against Polarimetric Radar Data. Mon. Weather Rev. 2012, 140, 1457–1475. Available online: https://journals.ametsoc.org/view/journals/mwre/140/5/mwr-d-11-00032.1.xml (accessed on 15 April 2022). [CrossRef]
- Putnam, B.; Xue, M.; Jung, Y.; Snook, N.; Zhang, G. Ensemble Kalman Filter Assimilation of Polarimetric Radar Observations for the 20 May 2013 Oklahoma Tornadic Supercell Case. Mon. Weather Rev. 2019, 147, 2511–2533. Available online: https://journals.ametsoc.org/view/journals/mwre/147/7/mwr-d-18-0251.1.xml (accessed on 15 April 2022). [CrossRef]
- Snyder, J.; Bluestein, H.; Dawson, D., II; Jung, Y. Simulations of Polarimetric, X-Band Radar Signatures in Supercells. Part I: Description of Experiment and Simulated ρhv Rings. J. Appl. Meteor. Climatol. 2017, 56, 1977–1999. [Google Scholar] [CrossRef]
- Snyder, J.; Bluestein, H.; Dawson, D., II; Jung, Y. Simulations of Polarimetric, X-Band Radar Signatures in Supercells. Part II: ZDR Columns and Rings and KDP Columns. J. Appl. Meteor. Climatol. 2017, 56, 2001–2026. [Google Scholar] [CrossRef]
- Oue, M.; Tatarevic, A.; Kollias, P.; Wang, D.; Yu, K.; Vogelmann, A. The Cloud-resolving model Radar SIMulator (CR-SIM) Version 3.3: Descriptin and applications of a virtual observatory. Geosci. Model Dev. 2020, 13, 1975–1998. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D.; Duda, M.; Huang, X.-Y.; Wang, W.; Powers, J.A. Description of the Advanced Research WRF Version 3; NCAR Tech. Note, NCAR/TN-4751STR; University Corporation for Atmospheric Research: Boulder, CO, USA, 2008; p. 113. [Google Scholar] [CrossRef]
- Davis, C.; Wang, W.; Chen, S.S.; Chen, Y.; Corbosiero, K.; DeMaria, M.; Dudhia, J.; Holland, G.; Klemp, J.; Michalakes, J.; et al. Prediction of Landfalling Hurricanes with the Advanced Hurricane WRF Model. Mon. Weather Rev. 2008, 136, 1990–2005. [Google Scholar] [CrossRef]
- Karan, H.; Fitzpatrick, P.; Hill, C.; Li, Y.; Xiao, Q.; Lim, E. The Formation of Multiple Squall Lines and the Impacts of WSR-88D Radial Winds in a WRF Simulation. Weather Forecast. 2010, 25, 242–262. [Google Scholar] [CrossRef][Green Version]
- Gray, K.; Frame, J. Investigating the Transition from Elevated Multicellular Convection to Surface-Based upercells during the Tornado Outbreak of 24 August 2016 Using a WRF Model Simulation. Weather Forecast. 2019, 34, 1051–1079. [Google Scholar] [CrossRef]
- Zhang, F.; Li, M.; Ross, A.; Lee, S.; Zhang, D. Sensitivity Analysis of Hurricane Arthur (2014) Storm Surge Forecasts to WRF Physics Parameterizations and Model Configurations. Weather Forecast. 2017, 32, 1745–1764. [Google Scholar] [CrossRef]
- Bao, J.-W.; Michelson, S.; Grell, E. Microphysical Process Comparison of Three Microphysics Parameterization Schemes in the WRF Model for an Idealized Squall-Line Case Study. Mon. Weather Rev. 2019, 147, 3093–3120. [Google Scholar] [CrossRef]
- McCaul, E., Jr.; Priftis, G.; Case, J.; Chronis, T.; Gatlin, P.; Goodman, S.; Kong, F. Sensitivities of the WRF Lightning Forecasting Algorithm to Parameterized Microphysics and Boundary Layer Schemes. Weather Forecast. 2020, 35, 1545–1560. [Google Scholar] [CrossRef]
- Sunny Lim, K.; Chang, E.; Sun, R.; Kim, K.; Tapiador, F.J.; Lee, G. Evaluation of Simulated Winter Precipitation Using WRF-ARW during the ICE-POP 2018 Field Campaign. Weather Forecast. 2020, 35, 2199–2213. [Google Scholar] [CrossRef]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of cloud micrpohysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one- and two-moment schemes. Mon. Weather Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef]
- Milbrandt, J.; Yau, M. A multimoment bulk microphysics parameterization. Part I: Analysis of the role of the spectral shape parameter. J. Atmos. Sci. 2005, 62, 3051–3064. [Google Scholar] [CrossRef]
- Milbrandt, J.; Yau, M. A multimoment bulk microphysics parameterization. Part II: A proposed three–moment closure and scheme description. J. Atmos. Sci. 2005, 62, 3065–3081. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Mon. Weather Rev. 2008, 136, 5095–5155. [Google Scholar] [CrossRef]
- Mishchenko, M.I. Calculation of the amplitude matrix for a nonspherical particle in a fixed orientation. Appl. Opt. 2000, 39, 1026–1031. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmosphere: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Janjic, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Helmus, J.J.; Collis, S.M. The Python ARM Radar Toolkit (Py-ART), a Library for Working with Weather Radar Data in the Python Programming Language. J. Open Res. Softw. 2016, 4, e25. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).