Next Article in Journal
Risks for Public Health and Social Infrastructure in Russian Arctic under Climate Change and Permafrost Degradation
Next Article in Special Issue
Response of Population Canopy Color Gradation Skewed Distribution Parameters of the RGB Model to Micrometeorology Environment in Begonia Fimbristipula Hance
Previous Article in Journal
No-Tillage Improvement of Nitrogen Absorption and Utilization in a Chinese Mollisol Using 15N-Tracing Method
Previous Article in Special Issue
Evaluation of Ground-Based Models for Estimating Surface Albedo with In-Situ Radiometric Measurements across China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 13
Issue 4
10.3390/atmos13040531
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Quantifying Agricultural Drought Severity for Spring Wheat Based on Response of Leaf Photosynthetic Features to Progressive Soil Drying

by
Kai Zhang
1,2,
Bo Zhang
1,* and
Funian Zhao
2,*
1
College of Geography and Environmental Science, Northwest Normal University, Lanzhou 730070, China
2
Key Laboratory of Arid Climatic Change and Disaster Reduction of Gansu Province/Key Laboratory of Arid Climate Change and Disaster Reduction of CMA, Lanzhou Institute of Arid Meteorology, China Meteorological Administration, Lanzhou 730020, China
*
Authors to whom correspondence should be addressed.
Atmosphere 2022, 13(4), 531; https://doi.org/10.3390/atmos13040531
Submission received: 2 March 2022 / Revised: 23 March 2022 / Accepted: 25 March 2022 / Published: 28 March 2022
(This article belongs to the Special Issue Agrometeorology)
Browse Figures
Versions Notes

Abstract

:
Agricultural drought definition focuses on the effect of water deficit during the crop growth period on the final crop yield. However, it is difficult to quantify the dynamic process for agricultural drought precisely during the crop growing season and then relate its impact to the final crop yield. This study was conducted to quantify agricultural drought severity for spring wheat (Triticum aestivum L.) at the jointing stage based on the response of leaf physiological parameters to progressive soil drying. The leaf potential and gas exchange parameters were observed daily using a DewPoint Potential Meter (WP4) and portable photosynthetic apparatus (LI-6400) at the jointing stage of spring wheat for two different water treatments: well water supply and natural drought, respectively. The results showed that the leaf photosynthetic features’ response to available soil water could be classified into five main stages, as the available soil water thresholds were at 0.41, 0.2, 0.12, and 0.04, respectively. We defined those five stages as no agricultural drought, mild agricultural drought, moderate agricultural drought, severe agricultural drought, and extremely severe agricultural drought based on the different mechanisms of the net photosynthesis rate’s response to progressive soil drying. The parameters of three stomatal conductance models, i.e., Ball–Berry, Leuning, and Medlyn, had two apparently different groups of values divided by moderate agricultural drought. This study combined atmosphere–soil–crop as a unit to quantify agricultural drought severity during the crop growth period could be used to model crop growth and development under water deficit conditions and calculate agricultural drought indices in drought research and management.

1. Introduction

Drought, resulting in great losses in economic sectors worldwide, especially in agriculture, can occur in every region of the world, whether under arid or humid climates [1]. However, drought is one of the most complex natural disasters due to its creeping and reoccurring characteristics [2]. At present, it even still lacks a universally accepted definition. For quantifying the dynamic processes of drought, such as the onset, termination, intensity, duration, and severity of drought, it becomes much more difficult [3].
Researchers have made great efforts to understand drought [4]. They classified drought into four main categories based on the affected sectors: meteorological drought, hydrological drought, agricultural drought, and economic drought [5]. Meteorological drought always relates to a deviation of precipitation in a specific period from the mean value during the long term [6]. Hydrological drought focuses on the shortage of water in the forms of streams, lakes, and ground water. Agricultural drought is defined as lacking enough water in soil for crop growth and development during the crop growth period, resulting in great final yield reduction. Economic drought is related to the three kinds of drought mentioned above, and related research has been about the effects of drought on society. Generally, the dynamic process for meteorological drought and hydrological drought can be easily quantified because of the obtainable long-term records, amount of precipitation in the research area, and water levels in various reservoirs, for instance [7]. However, the onset, termination, intensity, duration, and severity of agricultural drought are always difficult to define and monitor precisely due to limited quantitative data and methods in agriculture sectors [8]. Furthermore, to understand drought fully, the quantification of drought parameters is necessary. These drought parameters, such as onset, termination, intensity, and duration, are mainly based on precise estimates of drought severity, which are also directly related to the effect of agricultural drought on crop growth and the final yield [9]. Hence, quantifying agricultural drought severity plays a central role in understanding the dynamic process of agricultural drought.
Crop features could respond to water stress directly and sensitively, and could be used to define and monitor agricultural drought severity. These crop features includes morphological indices, leaf potential, photosynthesis parameters, leaf temperature, and the final yield [10]. However, we could not use most of the morphological indices quantitatively to define agricultural drought and relate these indices to the final crop yield owing to the various crop types and crop varieties. Meanwhile, monitoring the final yield can not give a timely quantification of agricultural drought severity during the crop growing season. Fortunately, some of the crop features, such as the leaf potential, leaf temperature, and photosynthesis parameters, could be monitored quantitatively with the rapid development of various techniques [11]. The leaf potential is frequently used as an indicator for water stress [12]. However, this index is not easy to relate to the crop final yield. Idso and Jackson developed a crop water stress index based on the difference between the leaf temperature and air temperature and related it to the final crop yield [13]. It has been widely used in many arid and semi-arid climates, and even in humid climates. This type of index focuses on stomatal conductance, which has a close relationship with the photosynthesis process. Meanwhile, to relate agricultural drought effects and definition to the crop final yield, it has clearly been shown that the photosynthesis parameters are the main process that produces crop biomass and the final yield. Furthermore, many crop models have used the photosynthesis process to calculate crop yield, and most of these crop models just accounted for the drought’s effect on crop growth based on a stress coefficient originating from the ratio of actual evapotranspiration and potential evapotranspiration [14]. Nevertheless, at present, the photosynthetic features are seldom used to define and monitor agricultural drought severity [15].
Soil water is the final water supply resource for crops, and soil water plays a key role in the action of the atmosphere, plant, and soil on the water balance and the dynamics of the water flux on plants [16]. Hence, the soil water content can be used to monitor the agricultural drought severity related to the atmosphere and plant. There are different methods to quantify soil water, such as the volume soil water content, gravity soil water content, relative soil water content, available soil water content, and soil water potential [17]. Due to the different soil textures of various soil types, most methods representing the soil water content could not be compared with each other. However, the available soil water content with relation to the soil water potential is a commonly used variable that could be compared with various soil types.
The crop water demand and usage for its growth, development, and final yield are mainly controlled by atmospheric conditions, crop characteristics, and soil features, which interact with each other and have different effects on the crop water status [18]. Therefore, we could use the available soil water based on the response of leaf physiological features to progressive soil drying to quantify agricultural drought severity in the soil–plant–atmosphere (SPA) unit [19].
The stomatal conductance model has been frequently used to predict stomatal behavior and gas exchange between plants and the atmosphere [20]. Some commonly used models were proven under well water conditions [21]. However, whether the parameters of those stomatal conductance models would change or not under different agricultural drought severities has not been quantified [22,23]. In order to understand the dynamic process of agricultural drought and its impact on plant gas exchange precisely, this study was conducted to: (1) monitor the response of leaf physiological features to progressive soil drying and quantify agricultural drought severity in the form of available soil water; and (2) compare the parameters of three stomatal conductance models under different soil water conditions. The results of this study could be used to monitor and define agricultural drought clearly and model crop growth precisely as agricultural drought occurs during the crop growth period.

2. Materials and Methods

2.1. Experimental Site Description

This study was conducted in 2014 at the Dingxi Arid Meteorology and Ecological Environment Experimental Station (35°33′ N, 104°35′ E, 1896.7 m elevation), located in Dingxi County, Gansu Province, Northwest China. The region is subjected to a typical semi-arid climate with a highly erratic precipitation pattern. The average annual precipitation is about 386 mm in this region, and most of the precipitation falls from July to September [24]. The soil type in the experimental site is a typical loessal soil, with the texture of sandy silt.

2.2. Experimental Design

Spring wheat was grown outdoors in pots (29 cm diameter, 45 cm height). The test variety was Dingxi 40. Soil was carried from the surface of the field, ranging from 0 to 30 cm, and added to each pot (14 kg dry soil for each pot). The average soil bulk density, field capacity, and wilting point of the soil used in the pots were 1.21 g cm−3, 25.4 cm3 cm−3, and 5.8 cm3 cm−3, respectively. We established two treatments, well water (WW) and drought (DR). Each treatment had 10 pots. Spring wheat was sowed on 26 March 2014. Two treatments were irrigated with the same amount of water until the beginning of the jointing stage (Day 65 after sowing). After the two treatments were irrigated to field capacity, the drought treatment was not irrigated until it wilted (day 73), and the well water treatment was irrigated to field capacity, while its soil water content reached 60% of the field capacity.

2.3. Field Data Collection

2.3.1. Available Soil Water Content

The weight of each pot was measured daily by using an electronic scale (with a minimum weight of 1 g) for different water treatments. The soil water content was calculated as the weight of each pot minus the sum weight of the dry soil, empty pot, and fresh plant material. The mass of the fresh plant material was weighed at the end of soil drying while the plant was wilted. The daily change in plant material in each pot was negligible due to the short soil drying duration (length at ten days). The available soil water content was obtained by the ratio between the difference in the actual soil water content and wilting point of soil and difference in the field capacity and wilting point of soil.
A S W C = θ a − θ w θ f − θ w
In Equation (1), ASWC is the available soil water content, and θa, θw, and θf are the actual soil water content, wilting point of soil and field capacity, respectively.

2.3.2. Leaf Water Potential

The leaf water potential was measured using a DewPoint Potential Meter (WP4) at 7:00 a.m. and 11:00 a.m. during the experiment period. Three leaf samples were selected for each treatment. We used the average value to obtain the daily leaf water potential for each treatment at 7:00 a.m. and 11:00 a.m.

2.3.3. Photosynthetic Parameters (Gas Exchange Measurements)

To obtain the daily max photosynthetic parameters, we measured the light response curve for each treatment with three replicates under the daily soil water conditions. We measured the fully developed young leaves of two different treatments using a portable gas-exchange system (Li-6400, Li-Cor, Lincoln, NE, USA) equipped with a light source (6200-02 B LED). We fixed the leaf temperature at 25 °C and ambient CO2 concentration at 400 μmol CO2 mol−1 air. Photosynthetically active radiation was set as a sequence of 2100, 1800, 1500, 1200, 900, 600, 300, 200, 120, 60, 30, 15, and 0 μmol m−2 s−1. Leaves were acclimated in the chamber for more than 40 min at a photosynthetically active radiation of 1500 μmol mol−1 before taking measurements. The vapor pressure deficit (VPD) ranged from 1.5 to 2.5 kPa during the gas exchange measurements. The light saturation point is about 1500 μmol m−2 s−1; therefore, the photosynthesis parameters at 1500 μmol m−2 s−1 were used for analysis in this study. Meanwhile, the value for analysis was the mean of the three replicates Furthermore, the data collected from drought treatment were used to simulate stomatal conductance.

2.4. Stomatal Conductance Models

2.4.1. Ball–Berry Model

Wong [25] found that the net photosynthesis rate had a relation to the stomatal conductance. Using this relation, Ball [26,27] developed a model to calculate stomatal conductance based on the net photosynthesis rate (An), relative humidity (RHs), and CO2 concentration at the leaf’s surface (Cs).
g s = a 1 A n R H s / C s + b 1
In Equation (2), a1 and b1 are parameters. An can be measured directly by LI 6400. RHs at leaf surface can be calculated as follows:
e i = 0.6108 × exp [ 17.27 T L / ( T L + 237.3 ) ]
g s ( e i − e s ) = g b ( e s − e a )
R H s = e s e i = ( e a / e i + g s / g b ) ( 1 + g s / g b )
where ei is the saturated water vapor in the internal stomata calculated by the leaf temperature; TL is the temperature at the leaf’s surface; es is the partial pressure of water vapor at the leaf’s surface; ea is the partial pressure of water vapor in the air, which was obtained during gas exchange measurement; and gb is the boundary layer conductance for water vapor, which was 2.84 in this study.
Cs could be calculated as:
C s = C a − A n 1.35 g b
gb for water vapor flux is 2.84, and that for carbon is gb/1.37 [28].

2.4.2. Leuning Model

For the consideration that the stomata aperture responds to vapor pressure deficit rather than relative humidity, Leuning [29] invented a modification relation between gs and An.
g s = a 2 A n / ( C s − Γ ) ( 1 + V P D a / b 2 ) + c 2
where a2, b2, and c2 are parameters; Γ is the CO2 compensation point, supposed as 60 μmol CO2 mol−1 air from other research [29]; and VPDa is the vapor pressure deficit in the atmosphere, which was obtained during the gas exchange measurement.

2.4.3. Medlyn Model

Using the theory of optimal stomatal conductance, Medlyn [30] proposed a simple theoretical model, which was closely analogous to the empirical models above.
g s = ( 1 + a 3 / V P D L ) A n / C a + b 3
where a3 and b3 are parameters and VPDL is the vapor pressure deficit in the leaf’s surface, obtained directly during the gas exchange measurement.

2.5. Statistical Analysis and Data Processing

Hierarchical clustering with the agglomerative approach was used to determine the thresholds of the leaf physiological parameters’ response to drying soil. Hierarchical clustering, which seeks to build a hierarchy of clusters, was one of the clustering analysis methods.
In this study, five steps were conducted to obtain the precise thresholds of the leaf physiological parameters’ responses to decreasing available soil water. Firstly, to obtain a large number of samples, we used the exponential function obtained from the simulation result of the leaf physiological parameters’ response to decreasing available soil water. The variable was the available soil water content, ranging from 0 (wilting point) to 1 (field capacity). The step was set as 0.1. Hence, 101 samples were obtained for the data cluster. Secondly, we used hierarchical clustering to obtain 3 thresholds and divided the leaf physiological parameters’ response to progressive soil drying into 4 clusters. From previous research [31], the response of leaf physiological features to drying soil has two apparent stages. The first stage is characterized as a small range of leaf physiological features change, in a horizontal line at a great value with decreasing soil water. However, the leaf physiological features decrease sharply in a linear relationship with the water remaining in the soil after water loss. Therefore, for the third step, we regressed the 6 physiological features against the available water when the available soil water was less than the maximum threshold obtained in the second step, which was taken as the first leaf physiological feature beginning to decrease as soil dries. The lines we obtained would interact with the horizontal line obtained from the average value before the first threshold. Fourthly, we used the two lines’ interaction to verify the first threshold of the response to drying soil. Finally, if the first threshold obtained from the two methods was not identical, there would be four thresholds for each leaf physiological parameter’s response to drying soil. Therefore, we used hierarchical clustering again to obtain five clusters, and then compared those results to the results obtained above.
We used SPSS 13.0 for hierarchical clustering and RStudio to estimate the parameters for 3 stomatal conductance models. Linear regression and other statistical analyses in this study were performed using Origin 8.1.

3. Results

3.1. Response of Physiological Features to Soil Drying

Figure 1 shows the response of six physiological features to progressive soil drying. The leaf physiological features of spring wheat varied in a small range until the available soil water fell to specific values, and then the leaf physiological features decreased sharply as the soil was dried. There were thresholds for each physiological feature to decreasing available soil water. The leaf water potential at 11:00 a.m. had the most apparent threshold response, and it also had the lowest threshold. The net photosynthesis rate, transpiration rate, and stomatal conductance had higher thresholds, and they seemed to be more sensitive to changes in the available soil water. However, the intercellular CO2 concentration decreased at the threshold of available soil water, but increased sharply as the available soil water decreased to 0 (point P in Figure 1f).
The leaf physiological features of spring wheat’s response to progressive drying in this study could be described by the exponential function (Table 1). By using the hierarchical clustering approach for four parts, we obtained three thresholds for each physiological feature. Table 1 shows that the thresholds for each physiological feature were not identical to those of the others. The first, second, and third thresholds of leaf potential at 11:00 a.m. were 0.16, 0.08, and 0.02, respectively, apparently lower than those of the others. The stomatal conductance had the highest first, second, and third thresholds of 0.36, 0.20, and 0.08, respectively. The results indicate that the stomatal conductance might be more sensitive to water deficit under a quickly developed agricultural drought with a high water loss rate from the soil in pot environments.
The six physiological features were regressed against the available water when the available water was less than 0.36, which was taken as the first physiological feature; the stomatal conductance began to decrease as the soil dried (Table 2). Table 2 shows that the water potential at 7:00 and the intercellular CO2 concentration had no significant relationship with the available water under the sharply decreasing stage (p > 0.1). However, the water potential at 11:00, net photosynthesis rate, transpiration rate, and stomatal conductance had a significant relationship with the available soil water. We prolonged those lines and drew horizontal lines of those three features at the average value when those values changed at a small range as the soil water decreased (Figure 1). We found that the interactions of the two lines for each feature in the formation of available soil water were 0.22, 0.41, 0.57, and 0.69 for the water potential at 11:00 a.m., net photosynthesis rate, transpiration rate, and stomatal conductance, respectively. Figure 1 shows that the water potential at 11:00 a.m. and net photosynthesis rate interacted at a point as the observational data were apparently divided into two parts. However, the interaction points of the transpiration rate and stomatal conductance could not divide the parts correctly, and many data points still did not change when the available water was less than the obtained interaction point. Furthermore, the net photosynthesis rate was the main factor determining the final crop biomass and, hence, the yield of crop, which was related to the traditional agricultural drought definition. Therefore, we used the net photosynthesis rate to divide the different stages of agricultural drought.
We obtained five thresholds by using the net photosynthesis rate to quantify the agricultural drought of spring wheat based on hierarchical clustering and two linear interactions. However, the statistical method of clustering could also divide the response of the net photosynthesis rate to soil drying into five parts. Therefore, we used hierarchical clustering again to analyze the response. The four thresholds were 0.44, 0.2, 0.12, and 0.04. The latter three were the same as the results in Table 1 by dividing the response of the net photosynthesis rate to drying soil into four parts. The first threshold, 0.44, was not the same as that when two different lines interacted with each other. In Figure 1c, we found that the net photosynthesis rate did not change until the available water approached 0.41; therefore, we deemed 0.41 as the first threshold at which the net photosynthesis rate began to decrease as the soil dried, and the five different stages are shown in Figure 1c, A, B, C, D, and E, respectively.

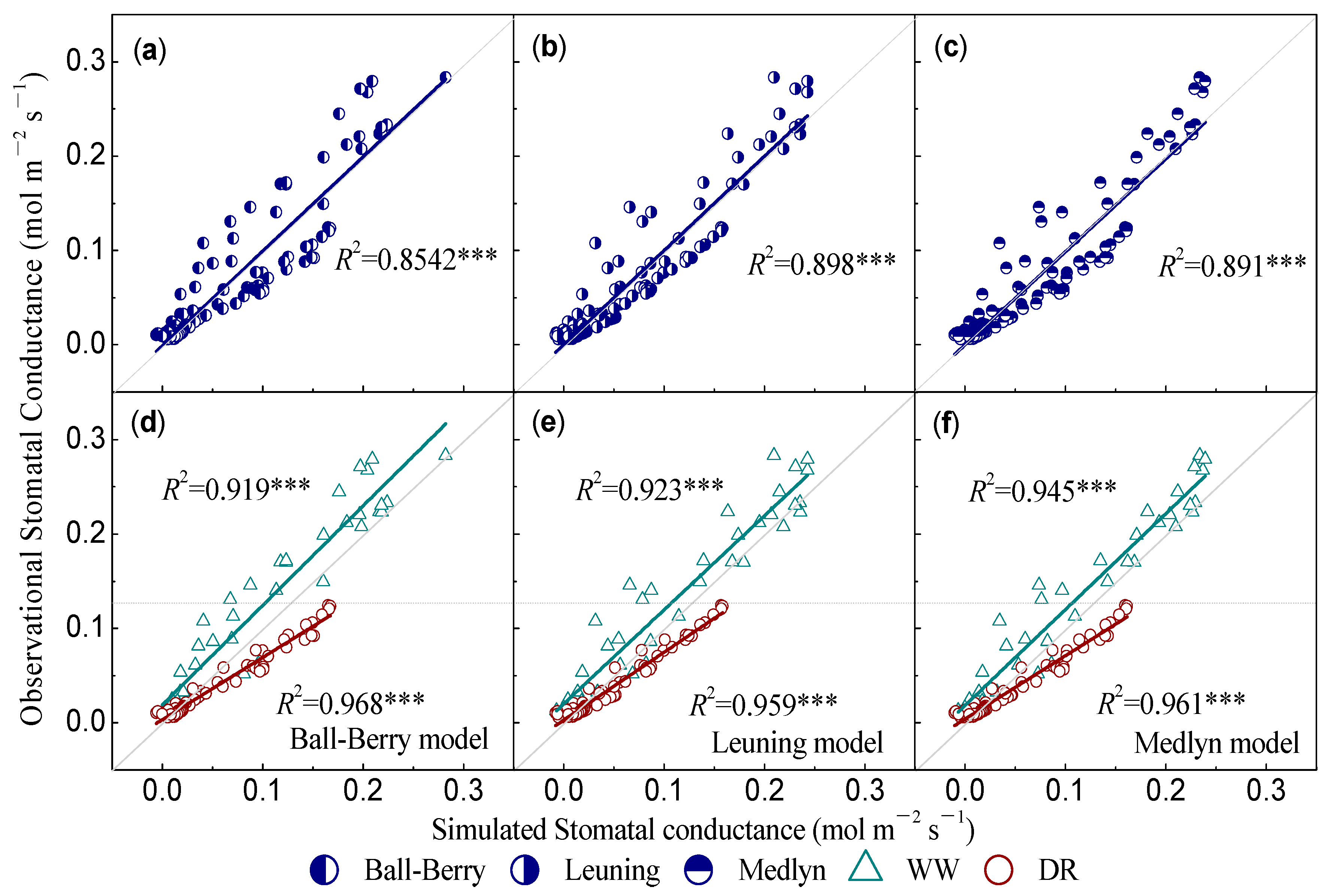
3.2. Stomatal Conductance Models

The simulated stomatal conductance and observational stomatal conductance had highly significant linear relationships with each other for three different stomatal conductance models (Figure 2a–c). The Leuning model and Medlyn model simulated the stomatal conductance better than the Ball–Berry model, with R2 at 0.898 and 0.891, respectively, compared 0.854 for the Ball–Berry model. This indicates that the effect of VPD on water transport from the stoma to the atmosphere was more important than the relative humidity. Meanwhile, the optimal water usage of leaves could be used to explain stomatal movement.
In Figure 2a–c, two apparently different linear relationships between the simulated stomatal conductance and observational stomatal conductance for each stomatal conductance model, divided by the regression line, are shown. We found that the two relationships were different from each other when the maximum net photosynthesis rate in the midmorning was less than 14 μmol m−2 s−1 and the stomatal conductance was 0.14 mol m−2 s−1 (Figure 2d–f). This value was identical to the value obtained from the threshold at stage (Figure 1c). Furthermore, the parameters for stomatal conductance models of the two different stages were calculated, as shown in Table 3. As the available soil water decreased to stages C, D, and E, a1, a2, and a3 reduced sharply, almost half of the value and one third for the Leuning model, as the available soil water was higher at stages A and B. The results indicate that the relationship between the net photosynthesis rate and stomatal conductance changed as the available soil water fell below a specific value.

4. Discussion

The goal of this analysis was to understand the dynamic process of agricultural drought for spring wheat during its growing season as the soil drying. The results suggest that the responses of most of the leaf physiological parameters for spring wheat to the available soil water were in a universal pattern that could be divided into five stages (A, B, C, D, and E) based on the change of net photosynthesis rate with soil drying. The parameters of the three stomatal conductance models at stages C, D, and E were apparently different from the values at stages A and B.

4.1. Feature Chosen to Quantify Agricultural Drought Severity

The leaf physiological features remained essentially unchanged until the available soil water approached 0.4 and then decreased linearly. This response could be determined by an exponential function and two interactive lines, respectively. The exponential equations obtained in this study were similar to the results of Sadras and Milroy [32], although we used the reverse formation as we regressed the observational photosynthetic parameters against the available soil water compared to the relative value in Sinclair. Furthermore, many researchers have demonstrated the universal response of the daily transpiration rates to the available soil water [33,34]. However, the main reason for this is unclear. One possible reason is that the water flux in the SPA unit is driven by the water potential difference [35]. The formation of the soil water content in the available soil water relates to a universal threshold for the soil water potential, which starts to decrease substantially with progressive soil drying and results in a sharp water exchange decrease between the atmosphere and the plant. With the formation of available soil water to the soil water content, the soil water potential is normalized into the same expression of the soil water content [36]. Therefore, the leaf physiological parameters respond to soil drying in a universal pattern.
Although the leaf water potential and leaf water content are usually used as crop water deficit indices, we found that the gas exchange process was more sensitive than the leaf potential to soil drying. Some studies have shown that plants could keep their leaf potential at a specific level during decreased soil water to reduce the harm of water stress [36]. Therefore, the photosynthesis parameters may decrease earlier than the leaf water potential by sensing some chemical signaling from roots, such as abscisic acid (ABA). Meanwhile, the gas exchange process related to photosynthesis is the central part of crop yield formation. Hence, the gas exchange parameters could be used to define agricultural drought severity.

4.2. Classification of Agricultural Drought Severity Based on Response of Net Photosynthesis Rate to Available Soil Water Decrease

The five different stages during the response process of the net photosynthesis rate to available soil water (Figure 1), A, B, C, D, and E, could be used to quantify agricultural drought severity phases as no agricultural drought, mild agricultural drought, moderate agricultural drought, severe agricultural drought, and extreme agricultural drought, respectively.
The leaf gas exchange dynamic process during soil drying is always determined by stomatal and non-stomatal factors. Stomatal conductance did not change as the soil water decreased below a threshold, 0.41 in this study, because of the acclimation of the crop to water stress, and this is also the principle of limited irrigation techniques. This phase, which could be labeled as no drought, was characterized by a small fluctuation in the net photosynthesis rate as the available soil water decreased.
The stomatal conductance then decreased slowly with a great reduction in the available soil water, and the stomatal conductance was the main reason that affected the decrease in the assimilation rate under such water stress conditions; the available soil water ranged from 0.41 to 0.2. This could be defined as mild agricultural drought.
As the available soil water decreased to 0.2, other factors began to dominate the effects on the assimilation rate. Pellegrino [37] found that the net photosynthesis rate decreased as the available soil water was less than 0.2 for grapevine, which was almost identical to our analysis. The relationship between the net photosynthesis and stomatal conductance also was affected, and the slope of the three stomatal conductance models decreased sharply (Table 3). This phase could be defined as moderate agricultural drought, with the available soil water ranging from 0.2 to 0.12.
The place of assimilation would be impaired when the available soil water was less than 0.04 in this study, and the intercellular CO2 concentration did not decrease with decreasing available soil water, but increased sharply. This indicates that the decrease of ribulose bisphosphate (RuBP) led to the inhibition of metabolic processes [38,39]. The stomata0 could not control the CO2 concentration at this stage, which could be defined as extremely severe agricultural drought [39]. During this phase, the leaf gas exchange process could not recover fully after rewatering [35]. Between moderate agricultural drought and extreme agricultural drought, the available soil water varied from 0.12 to 0.04, and this stage could be defined as severe agricultural drought.
Therefore, the agricultural drought could be divided into five stages: no agricultural drought, mild agricultural drought, moderate agricultural drought, severe agricultural drought, and extremely severe agricultural drought. Flexas [39] used the maximum stomatal conductance as a reference to label the water stress severity level. The stomatal conductance at 0.15, 0.10, and 0.05 were the thresholds of mild drought, moderate drought, severe drought, and extreme drought, respectively. These were very similar to our results, with the available soil water at 0.41, 0.2, 0.12, and 0.04, and stomatal conductance at 0.21, 0.14, 0.09, and 0.02 for no agricultural drought, mild agricultural drought, moderate agricultural drought, severe agricultural drought, and extreme agricultural drought, respectively.

4.3. Parameters of Stomatal Conductance Models under Different Agricultural Drought Severities

Many studies determined stomatal conductance with Ball–Berry model slope values around nine for well water C3 species [40,41,42], which was identical to the result in this study for spring wheat—8.9 under well water conditions. The slope of the Medlyn model in this study was 2.3 under well water conditions, which was at the range of 1.9 to 7.5 for 22 species [10]. As the parameters of the stomatal conductance models were not divided by different groups by the agricultural drought level, the b2 for the Leuning model was 369.7, and the values were 0.99 and 6.66, respectively, under well water conditions and drought conditions. The values of parameter b2 for the Leuning model obtained under different conditions were not the same. This might suggest that the great change in the value of b2 under different conditions would affect a2 in Equation (7). Therefore, we could not compare the slope in our study with that of others. However, we still found that the parameters of the Leuning model in our study under well water conditions were close to the values of some other studies [43].
As soil water deficits develop, there is controversy as to whether the parameters of the stomatal conductance model change or not [44]. The parameters of the three stomatal models in this study under different soil water statuses could be divided into two apparently different groups by the moderate agricultural drought level. Xu [23] found the same relationship between the net photosynthesis rate and stomatal conductance during drought development for the Ball–Berry model. However, many researchers suggested that the slope of the relationship between the net photosynthesis rate and stomatal conductance decreased as drought developed [45,46]. Liu [28] reported that the slope of the Ball–Berry model decreased in an exponential reduction function. This may be complicated a model as we used it to determine the agricultural drought process. Therefore, we believe agricultural drought could be modeled by two different stages based on the leaf physiological characteristics of the crop under water stress. The slope of the three stomatal conductance models can be taken in the formation of the derivative ratio between the stomatal conductance and net photosynthesis rate, dgs/dAn. The decrease in the slopes for the three stomatal conductance models indicated that each unit of stomatal conductance induced a much greater decrease in the net photosynthesis rate. This suggests that another factor resulted in the net photosynthesis rate decrease as the available soil water approached a specific value, 0.2 in this research. The other factor might be non-stomatal factors.
The thresholds of the available soil water content based on the response of the net photosynthesis rate to progressive soil drying could be used to quantitatively determine the dynamic process for agricultural drought [47]. Generally, gas exchange parameters are not easy to observe in many areas lacking equipment, and those parameters may fluctuate daily and diurnally because of environmental factor variations, resulting in difficulty in monitoring agricultural drought in a timely manner using gas exchange parameters [48]. In this study, we related the available soil water content to gas exchange parameters as agricultural drought developed, and it would be more useful to apply available soil water content for agricultural drought monitoring and management in any place with different soil textures.

Author Contributions

Conceptualization, K.Z., B.Z. and F.Z.; methodology, K.Z. and F.Z.; software, K.Z. and F.Z.; formal analysis, K.Z. and F.Z.; investigation, K.Z. and F.Z.; resources, K.Z.; data curation, K.Z. and F.Z.; writing—original draft preparation, K.Z.; writing—review and editing, B.Z. and F.Z.; visualization, K.Z.; supervision, B.Z. and F.Z.; project administration, K.Z.; funding acquisition, K.Z. and F.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was jointly supported by the National Natural Science Foundation of China (42005097, 42175192, and 41775107).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Data are available upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ojima, D.S. Climate resilient management in response to flash droughts in the US Northern Great Plains. Curr. Opin. Environ. Sust. 2021, 48, 125–131. [Google Scholar] [CrossRef]
  2. Nguyen, H.; Wheeler, M.C.; Hendon, H.H.; Lim, E.P.; Otkin, J.A. The 2019 flash droughts in subtropical eastern Australia and their association with large-scale climate drivers. Weather Clim. Extrem. 2021, 32, 100321. [Google Scholar] [CrossRef]
  3. Osman, M.; Zaitchik, B.F.; Badr, H.S.; Christian, J.I.; Tadesse, T.; Otkin, J.A.; Anderson, M.C. Flash drought onset over the contiguous United States: Sensitivity of inventories and trends to quantitative definitions. Hydrol. Earth. Syst. Sci. 2021, 25, 565–581. [Google Scholar] [CrossRef]
  4. Chen, L.G.; Gottschalck, J.; Hartman, A.; Miskus, D.; Tinker, R.; Artusa, A. Flash drought characteristics based on US drought monitor. Atmosphere 2019, 10, 498. [Google Scholar] [CrossRef] [Green Version]
  5. Panu, U.S.; Sharma, T.C. Challenges in drought research: Some perspectives and future directions. Hydrolog. Sci. J. 2002, 47, S19–S30. [Google Scholar] [CrossRef] [Green Version]
  6. American Meteorological Society. Statement on meteorolgical drought. Bull. Am. Meteorol. Soc. 2004, 85, 771–773. [Google Scholar]
  7. Heim, R.R. A Review of Twentieth-Century Drought Indices Used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1165. [Google Scholar] [CrossRef] [Green Version]
  8. Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
  9. Zhou, H.L.; Zhou, G.S.; He, Q.J.; Zhou, L.; Ji, Y.H.; Lv, X.M. Capability of leaf water content and its threshold values in reflection of soil-plant water status in maize during prolonged drought. Ecol. Indic. 2021, 124, 107395. [Google Scholar] [CrossRef]
  10. Zhou, S.X.; Duursma, R.A.; Medlyn, B.E.; Kelly, J.W.; Prentice, I.C. How should we model plant responses to drought? An analysis of stomatal and non-stomatal responses to water stress. Agric. For. Meteorol. 2013, 182, 204–214. [Google Scholar] [CrossRef]
  11. Soltani, A.; Khooie, F.; Ghassemi, G.K.; Moghaddam, M. Thresholds for chickpea leaf expansion and transpiration response to soil water deficit. Field Crops Res. 2000, 68, 205–210. [Google Scholar] [CrossRef]
  12. Yang, X.L.; Wang, B.F.; Chen, L.; Li, P.; Cao, C.G. The different influences of drought stress at the flowering stage on rice physiological traits, grain yield, and quality. Sci. Rep. 2019, 9, 3742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Chen, J.W.; Zhang, Q.; Li, X.S.; Cao, K.F. Gas exchange and hydraulics in seedlings of Hevea brasiliensis during water stress and recovery. Tree Physiol. 2010, 30, 876–885. [Google Scholar] [CrossRef] [PubMed]
  14. Jin, Z.N.; Zhuang, Q.L.; Tan, Z.L.; Dukes, J.S.; Zheng, B.Y.; Melillo, J.M. Do maize models capture the impacts of heat and drought stresses on yield? Using algorithm ensembles to identify successful approaches. Glob. Change Biol. 2016, 22, 3112–3126. [Google Scholar] [CrossRef] [PubMed]
  15. Chaves, M.; Flexas, J.; Pinheiro, C. Photosynthesis under drought and salt stress, Regulation mechanisms from whole plant to cell. Ann. Bot. 2009, 103, 551–560. [Google Scholar] [CrossRef] [Green Version]
  16. Zhang, Y.Q.; Kendy, E.; Yu, Q.; Liu, C.M.; Shen, Y.J.; Sun, H.Y. Effect of soil water deficit on evapotranspiration, crop yield, and water use efficiency in the North China Plain. Agric. Water Manag. 2004, 64, 107–122. [Google Scholar] [CrossRef]
  17. Moene, A.F.; Dam, J.C. Transport in the Atmosphere-Vegetation-Soil Continuum; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
  18. Xu, Z.Z.; Zhou, G.S.; Shi, M.Z. Plant responses to drought and rewatering. Plant Signal. Behav. 2010, 5, 649–654. [Google Scholar] [CrossRef] [Green Version]
  19. Williams, M.; Rastetter, E.B.; Fernandes, D.N.; Goulden, M.L.; Wofsy, S.C.; Shaver, G.R.; Melillo, J.M.; Munger, J.W.; Fan, S.M.; Nadelhoffer, K.J. Modelling the soil-plant-atmosphere continuum in a Quercus-Acer stand at Harvard Forest, the regulation of stomatal conductance by light, nitrogen and soil/plant hydraulic properties. Plant Cell Environ. 1996, 19, 911–927. [Google Scholar] [CrossRef] [Green Version]
  20. Beeck, M.O.D.; Low, M.; Deckmyn, G.; Ceulemans, R. A comparison of photosynthesis-dependent stomatal models using twig cuvette field data for adult beech (Fagus sylvatica L.). Agric. For. Meteorol. 2010, 150, 531–540. [Google Scholar] [CrossRef]
  21. Bonan, G.B.; Williams, M.; Fisher, R.A.; Oleson, K.W. Modeling stomatal conductance in the Earth system, linking leaf water-use efficiency and water transport along the soil-plant-atmosphere continuum. Geosci. Model Dev. 2014, 7, 2193–2222. [Google Scholar] [CrossRef] [Green Version]
  22. Manzoni, S.; Vico, G.; Katul, G.; Fay, P.A.; Polley, W.; Palmroth, S.; Porporato, A. Optimizing stomatal conductance for maximum carbon gain under water stress: A meta-analysis across plant functional types and climates. Funct. Ecol. 2011, 25, 456–467. [Google Scholar] [CrossRef]
  23. Xu, L.K.; Baldocchi, D.D. Seasonal trends in photosynthetic parameters and stomatal conductance of blue oak (Quercus douglasii) under prolonged summer drought and high temperature. Tree Physiol. 2003, 23, 865–877. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Zhao, F.N.; Lei, J.; Wang, R.Y.; Zhang, Q.; Qi, Y.; Zhang, K.; Guo, Q.; Wang, H.L. Environmental determination of spring wheat yield in a climatic transition zone under global warming. Int. J. Biometeorol. 2022, 66, 481–491. [Google Scholar] [CrossRef] [PubMed]
  25. Wong, S.C.; Cowan, I.R.; Farquhar, G.D. Stomatal conductance correlates with photosynthetic capacity. Nature 1979, 282, 424–426. [Google Scholar] [CrossRef]
  26. Ball, J.T.; Woodrow, I.E.; Berry, J.A. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. In Progress in Photosynthesis Research, Proceedings of the VIIth International Congress on Photosynthesis, Providence, RI, USA, 10–15 August 1986; Martinus Nijhoff Publishers: Dordrecht, The Netherlands, 1987; pp. 221–224. [Google Scholar]
  27. Ball, J.T. An Analysis of Stomatal Conductance; Stanford University: Stanford, CA, USA, 1988. [Google Scholar]
  28. Liu, F.L.; Andersen, M.N.; Jensen, C.R. Capability of the ‘Ball-Berry’ model for predicting stomatal conductance and water use efficiency of potato leaves under different irrigation regimes. Sci. Horticul. 2009, 122, 346–354. [Google Scholar] [CrossRef]
  29. Leuning, R. A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant Cell Environ. 1995, 18, 339–355. [Google Scholar] [CrossRef]
  30. Medlyn, B.E.; Duursma, R.A.; Eamus, D.; Ellsworth, D.S.; Prentice, I.C.; Barton, C.V.M.; Crous, K.Y.; Angelis, P.D.; Freeman, M.; Wingate, L. Reconciling the optimal and empirical approaches to modelling stomatal conductance. Glob. Change Biol. 2011, 17, 2134–2144. [Google Scholar] [CrossRef] [Green Version]
  31. Casadebaig, P.; Debaeke, P.; Jérémie, L. Thresholds for leaf expansion and transpiration response to soil water deficit in a range of sunflower genotypes. Eur. J. Agron. 2008, 28, 646–654. [Google Scholar] [CrossRef]
  32. Sadras, V.O.; Milroy, S.P. Soil-water thresholds for the responses of leaf expansion and gas exchange: A review. Field Crops Res. 1996, 47, 253–266. [Google Scholar] [CrossRef]
  33. Medrano, H.; Escalona, J.M.; Bota, J.; Flexas, J. Regulation of photosynthesis of C3 plants in response to progressive drought: Stomatal conductance as a reference parameter. Ann. Bot. 2002, 89, 895–906. [Google Scholar] [CrossRef]
  34. Baker, J.T.; Gitz, D.C.; Payton, P.; Wanjura, D.F.; Upchurch, D.R. Using leaf gas exchange to quantify drought in cotton irrigated based on canopy temperature measurements. Agron. J. 2007, 99, 637–644. [Google Scholar] [CrossRef]
  35. Flexas, J.; Bota, J.; Cifre, J.; Escalona, J.M.; Galmes, J.; Gulias, J.; Lefi, E.K.; Martinez, S.F.; Moreno, M.T.; Ribas, M.; et al. Understanding down-regulation of photosynthesis under water stress, future prospects and searching for physiological tools for irrigation management. Ann. Appl. Biol. 2004, 144, 273–283. [Google Scholar] [CrossRef]
  36. Misson, L.; Limousin, J.M.; Rodriguez, R.; Letts, M.G. Leaf physiological responses to extreme droughts in Mediterranean Quercus ilex forest. Plant Cell Environ. 2010, 33, 1898–1910. [Google Scholar] [CrossRef] [PubMed]
  37. Pellegrino, A.; Lebon, E.; Simonneau, T.; Wery, J. Towards a simple indicator of water stress in grapevine (Vitis vinifera L.) based on the differential sensitivities of vegetative growth components. Aust. J. Grape Wine R. 2005, 11, 306–315. [Google Scholar] [CrossRef]
  38. Brodribb, T. Dynamics of changing intercellular CO2 concentration (Ci) during drought and determination of minimum functional Ci. Plant Physiol. 1996, 111, 179–185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  39. Flexas, J.; Medrano, H. Drought-inhibition of photosynthesis in C3 plants: Stomatal and non-stomatal limitations revisited. Ann. Bot. 2002, 89, 183–189. [Google Scholar] [CrossRef] [Green Version]
  40. Yu, Q.; Xu, S.; Wang, J.; Lee, X.H. Influence of leaf water potential on diurnal changes in CO2 and water vapour fluxes. Bound. Lay. Meteorol. 2007, 124, 161–181. [Google Scholar] [CrossRef]
  41. Egea, G.; Verhoef, A.; González-Real, M.M.; Baille, A.; Nortes, P.A.; Domingo, R. Comparison of several approaches to modelling stomatal conductance in well-watered and drought-stressed almond trees. Acta Hortic. Sin. 2011, 922, 285–294. [Google Scholar] [CrossRef]
  42. Seidel, S.J.; Rachmilevitch, S.; Schütze, N.; Lazarovitch, N. Modelling the impact of drought and heat stress on common bean with two different photosynthesis model approaches. Environ. Modell. Softw. 2016, 81, 111–121. [Google Scholar] [CrossRef]
  43. Barnard, D.M.; Bauerle, W.L. The implications of minimum stomatal conductance on modeling water flux in forest canopies. J. Geophys. Res. Biogeosci. 2013, 118, 1322–1333. [Google Scholar] [CrossRef]
  44. Miner, G.L.; Bauerle, W.L.; Baldocchi, D.D. Estimating the sensitivity of stomatal conductance to photosynthesis: A review. Plant Cell Environ. 2016, 40, 1214–1238. [Google Scholar] [CrossRef] [PubMed]
  45. Egea, G.; Verhoef, A.; Vidale, P.L. Towards an improved and more flexible representation of water stress in coupled photosynthesis–stomatal conductance models. Agric. For. Meteorol. 2011, 151, 1370–1384. [Google Scholar] [CrossRef]
  46. Zhao, F.N.; Zhou, S.X.; Wang, R.Y.; Zhang, K.; Wang, H.L.; Yu, Q. Quantifying key model parameters for wheat leaf gas exchange under different environmental conditions. J. Integr. Agric. 2020, 19, 2188–2205. [Google Scholar] [CrossRef]
  47. Raab, N.; Meza, F.J.; Franck, N.; Bambach, N. Empirical stomatal conductance models reveal that the isohydric behavior of an Acacia caven Mediterranean Savannah scales from leaf to ecosystem. Agric. For. Meteorol. 2015, 213, 203–216. [Google Scholar] [CrossRef]
  48. Niinemets, Ü.; Keenan, T. Photosynthetic responses to stress in Mediterranean evergreens: Mechanisms and models. Environ. Exp. Bot. 2014, 103, 24–41. [Google Scholar] [CrossRef]
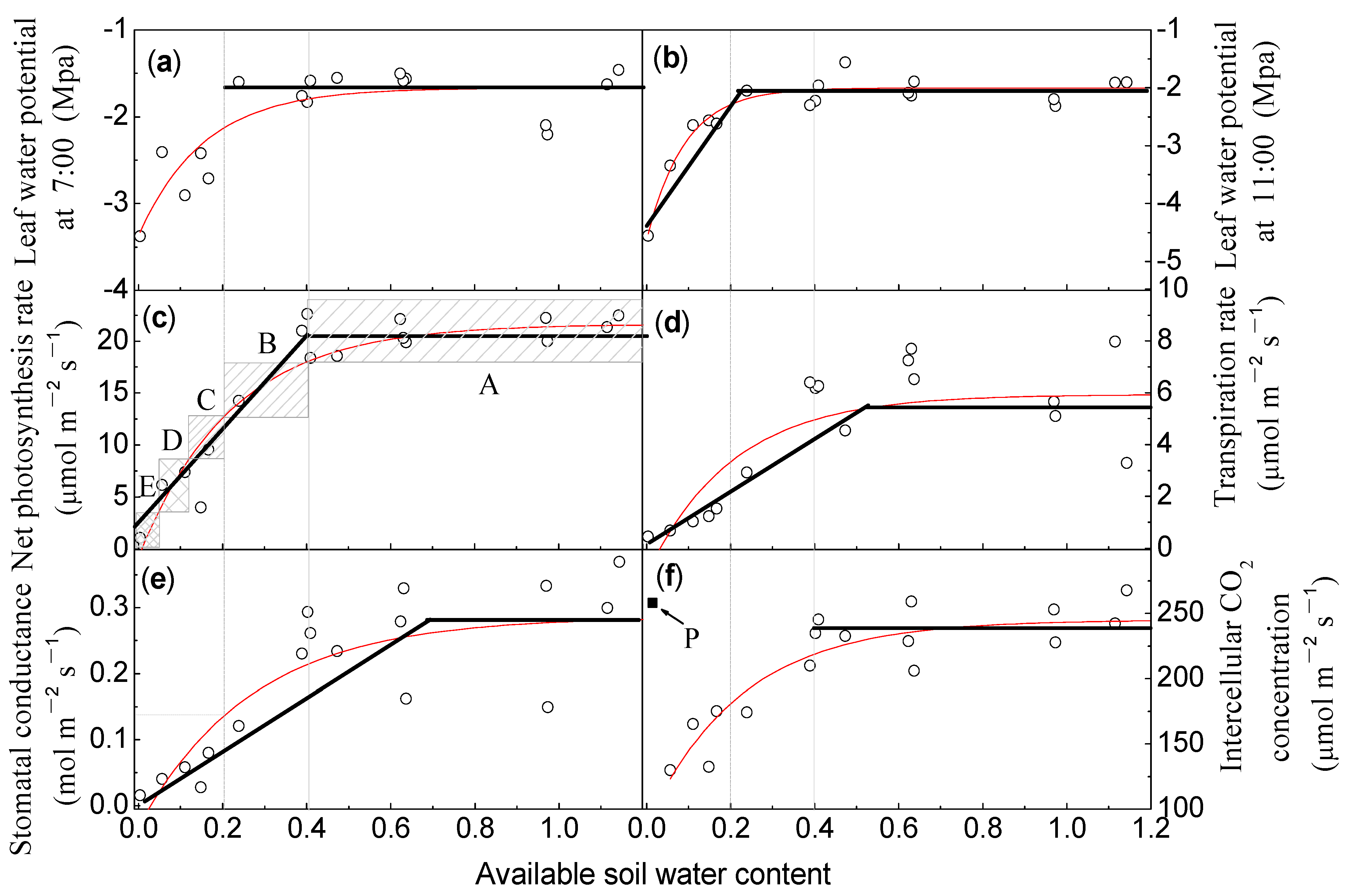
Atmosphere 13 00531 g001 550
Figure 1. Relationships between available soil water content and physiological indices for spring wheat, including (a) leaf water potential at 7:00, (b) leaf water potential at 11:00, (c) net photosynthetic rate, (d) transpiration rate, (e) stomatal conductance and (f) intercellular CO2 concentration. Note: Red lines indicate the fitted curves of response of physiological indices to soil water. Black bold lines indicate trend of change for physiological indices. Vertical solid line and vertical dotted line indicate the available soil water content for the first threshold and second threshold respectively based on net photosynthesis rate of spring wheat; A, B, C, D and E indicates the different drought stages based on response of photosynthetic features to available soil water content for spring wheat during jointing stage.
Figure 1. Relationships between available soil water content and physiological indices for spring wheat, including (a) leaf water potential at 7:00, (b) leaf water potential at 11:00, (c) net photosynthetic rate, (d) transpiration rate, (e) stomatal conductance and (f) intercellular CO2 concentration. Note: Red lines indicate the fitted curves of response of physiological indices to soil water. Black bold lines indicate trend of change for physiological indices. Vertical solid line and vertical dotted line indicate the available soil water content for the first threshold and second threshold respectively based on net photosynthesis rate of spring wheat; A, B, C, D and E indicates the different drought stages based on response of photosynthetic features to available soil water content for spring wheat during jointing stage.
Atmosphere 13 00531 g001
Atmosphere 13 00531 g002 550
Figure 2. Relationships between observational stomatal conductance and simulated stomatal conductance by three different models, including (a) Ball-Berry model for whole data, (b) Leuning model for whole data, (c) Medlyn model for whole data, (d) Ball-Berry model under different water conditions, (e) Leuning model under different water conditions, and (f) Medlyn model under different water conditions. *** indicate significant level at 0.001. Ball-Berry, Leuning and Medlyn indicates the three typical stomatal conductance models. WW indicates leaf stomatal conductance for spring wheat under well-water condition. DR indicates leaf stomatal conductance for spring wheat when light-saturated stomatal conductance is smaller than 0.14 mol m−2 s−1.
Figure 2. Relationships between observational stomatal conductance and simulated stomatal conductance by three different models, including (a) Ball-Berry model for whole data, (b) Leuning model for whole data, (c) Medlyn model for whole data, (d) Ball-Berry model under different water conditions, (e) Leuning model under different water conditions, and (f) Medlyn model under different water conditions. *** indicate significant level at 0.001. Ball-Berry, Leuning and Medlyn indicates the three typical stomatal conductance models. WW indicates leaf stomatal conductance for spring wheat under well-water condition. DR indicates leaf stomatal conductance for spring wheat when light-saturated stomatal conductance is smaller than 0.14 mol m−2 s−1.
Atmosphere 13 00531 g002
Table
Table 1. Relationship between the water content and physiological indices for spring wheat and their thresholds.
Table 1. Relationship between the water content and physiological indices for spring wheat and their thresholds.
Physiological ParametersEquationsR2First Threshold/Second Threshold/Third ThresholdIntercept
Water potential at 7:00y = − 1.667 − 1.702 * exp(−6.415x)0.696 **0.28/0.12/0.02/
Water potential at 11:00y = − 2.002 − 2.634 * exp(−11.072x)0.901 **0.16/0.08/0.02/
Net photosynthesis ratey = 21.642 − 22.444 * exp(−4.535x)0.866 **0.2/0.12/0.040.008
Transpiration ratey = 5.936 − 6.957 * exp(−4.912x)0.577 **0.28/0.12/0.080.03
Stomatal conductancey = 0.285 − 0.310 * exp(−3.700x)0.658 **0.36/0.20/0.080.023
Intercellular CO2 concentrationy = 245.090 − 157.000 * exp(−4.466x)0.785 **0.2/0.12/0.040.1
Note: ** indicates significance at the 0.01 probability level.
Table
Table 2. Relationship between the water content and physiological indices for spring when the available water content was less than 0.36.
Table 2. Relationship between the water content and physiological indices for spring when the available water content was less than 0.36.
Physiological ParametersEquationsR2Value Under Well-Water ConditionsPoint of Intersection with the Value under Well-Water Conditions
Water potential at 7:00/0.643−1.699/
Water potential at 11:00y = 9.847 * x − 4.1550.867 **−1.9870.22
Net photosynthesis ratey = 46.998 * x + 1.3760.741 *20.490.41
Transpiration ratey = 9.899 * x + 0.10920.727 **5.760.57
Stomatal conductancey = 0.394 * x + 0.0100.873 *0.2860.69
Intercellular CO2 concentration/0.444238/
Note: * indicates significance at the 0.05 probability level, ** indicates significance at the 0.01 probability level.
Table
Table 3. Coefficients of the three stomatal conductance models for spring wheat under different water statuses, well water (WW), drought (DR), and all combined data (N).
Table 3. Coefficients of the three stomatal conductance models for spring wheat under different water statuses, well water (WW), drought (DR), and all combined data (N).
ModelsClassa1b1a2b2c2a3b3
Ball–Berry (1987)N8.46190.0119/////
WW8.9330.031/////
DR5.58280.011/////
Leuning (1995)N//3.297369.70.0085//
WW//10.59680.994380.0256//
DR//2.97466.6630.00935//
Medlyn (2011)N/////2.1120.008
WW/////2.2840.025
DR/////1.0190.009
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhang, K.; Zhang, B.; Zhao, F. Quantifying Agricultural Drought Severity for Spring Wheat Based on Response of Leaf Photosynthetic Features to Progressive Soil Drying. Atmosphere 2022, 13, 531. https://doi.org/10.3390/atmos13040531

AMA Style

Zhang K, Zhang B, Zhao F. Quantifying Agricultural Drought Severity for Spring Wheat Based on Response of Leaf Photosynthetic Features to Progressive Soil Drying. Atmosphere. 2022; 13(4):531. https://doi.org/10.3390/atmos13040531

Chicago/Turabian Style

Zhang, Kai, Bo Zhang, and Funian Zhao. 2022. "Quantifying Agricultural Drought Severity for Spring Wheat Based on Response of Leaf Photosynthetic Features to Progressive Soil Drying" Atmosphere 13, no. 4: 531. https://doi.org/10.3390/atmos13040531

APA Style

Zhang, K., Zhang, B., & Zhao, F. (2022). Quantifying Agricultural Drought Severity for Spring Wheat Based on Response of Leaf Photosynthetic Features to Progressive Soil Drying. Atmosphere, 13(4), 531. https://doi.org/10.3390/atmos13040531

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop