Exploring the Sensitivity of Visibility to PM2.5 Mass Concentration and Relative Humidity for Different Aerosol Types
Abstract
:1. Introduction
2. Data and Methods
2.1. The Online Observation of PM2.5 Chemical Composition and Meteorological Factors
2.2. Parameterization Scheme of Atmospheric Visibility
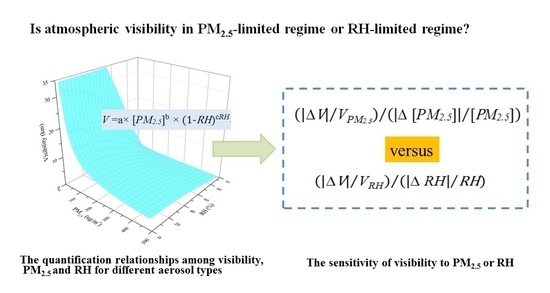
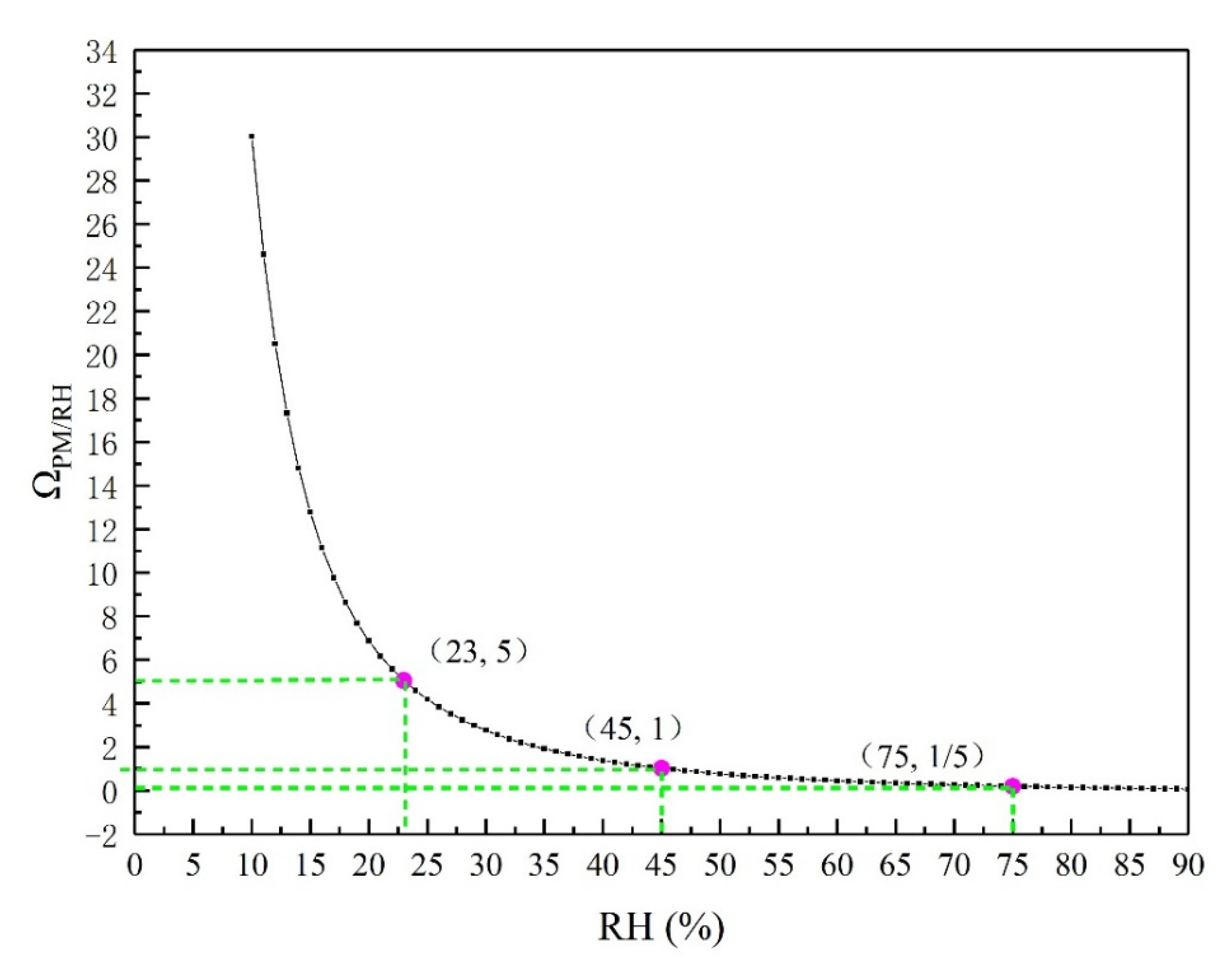
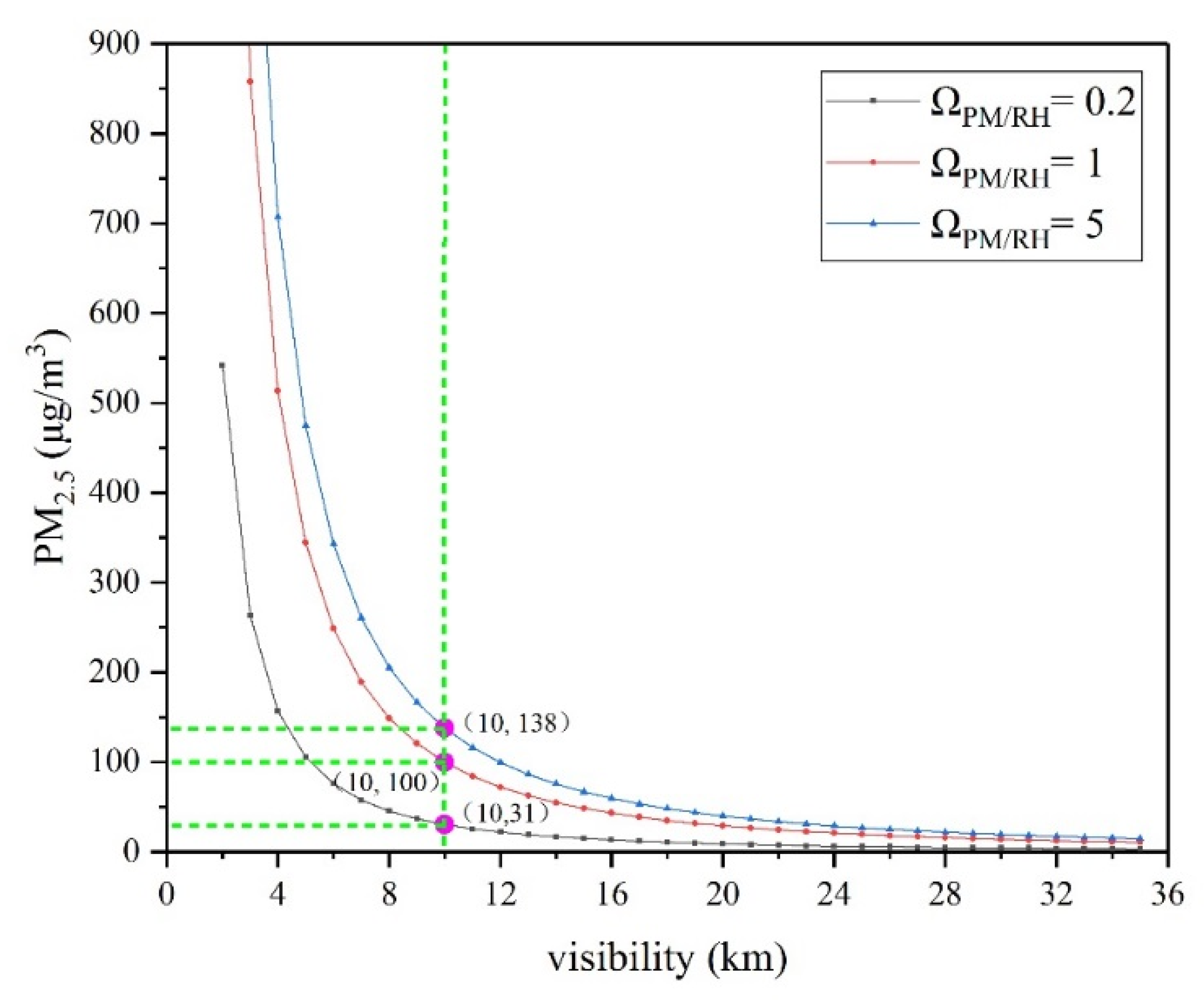
2.3. Classification Method of Visibility-Sensitive Regime, Depending on the Sensitivity of Visibility to PM2.5 Concentration and RH
2.4. IMPROVE Equations
3. Results and Discussion
3.1. Application of Visibility Control Category Classification Method
3.1.1. Quantification of Relationships among Visibility, PM2.5 Concentration, and RH in Tianjin, 2015
3.1.2. Sensitivity of Visibility to PM2.5 Concentration and RH
3.2. Sensitivity of Visibility to PM2.5 Concentration and RH for Different Aerosol Types
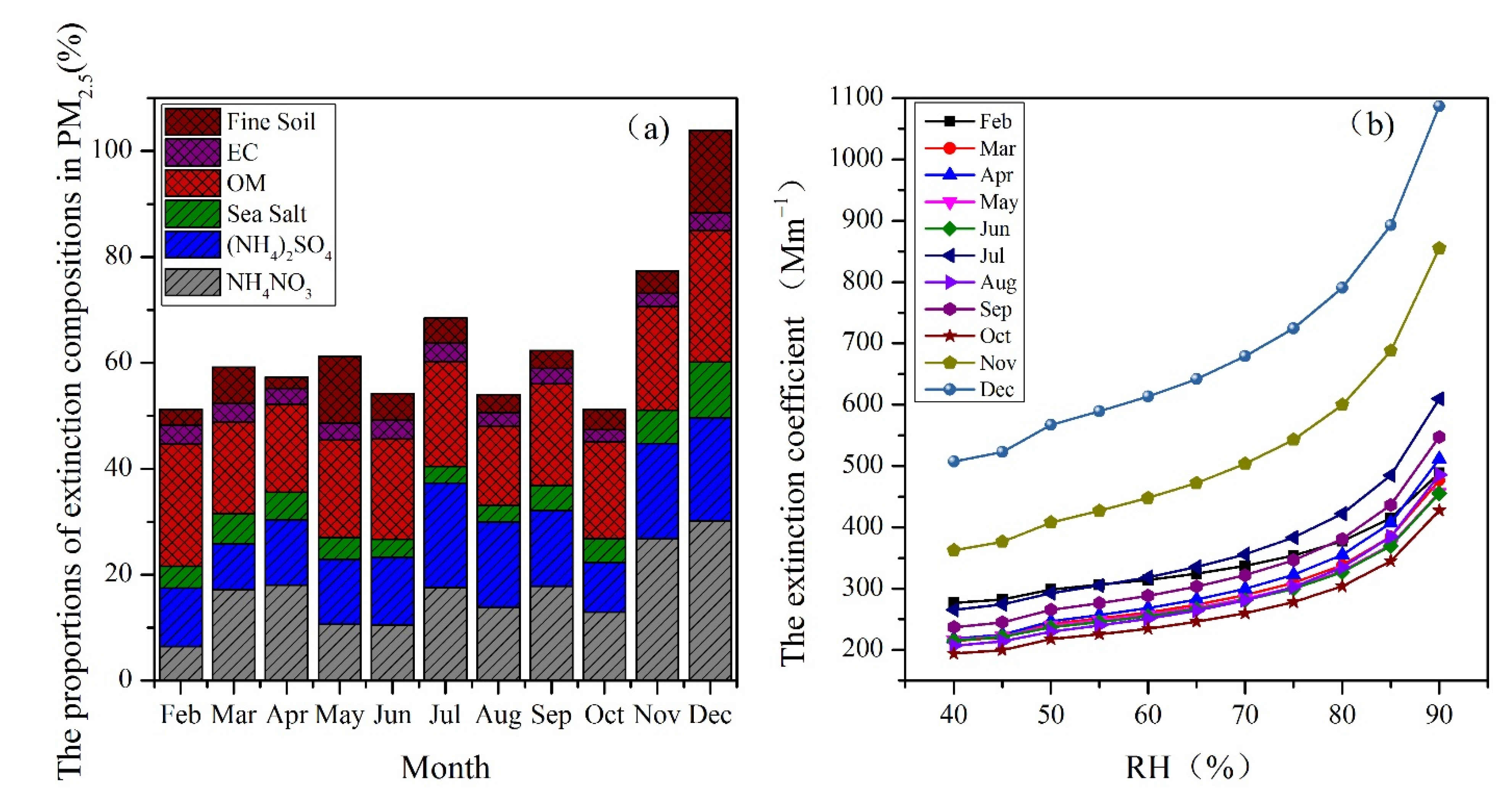
3.2.1. Constituents and Extinction Characteristics of Chemical Composition in PM2.5
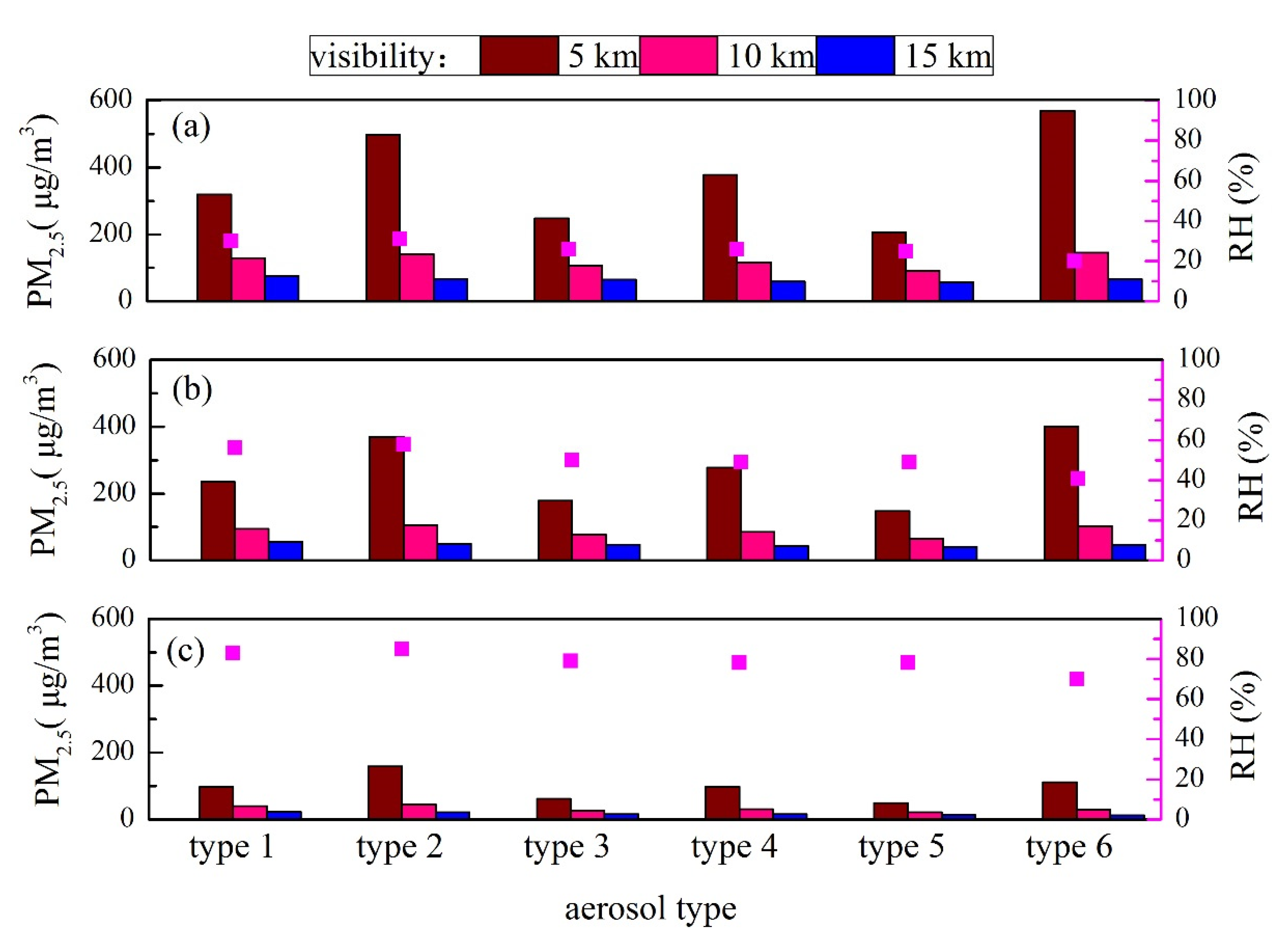
3.2.2. Classification of Aerosol Types
3.2.3. Impacts of Chemical Compositions on the Sensitivity of Visibility to PM2.5 and RH
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watson, J.G. Critical review discussion-visibility, Science and regulation. J. Air Waste Manag. Assoc. 2002, 52, 973–999. [Google Scholar] [CrossRef] [Green Version]
- Doyle, M.; Dorling, S. Visibility trends in the UK 1950–1997. Atmos. Environ. 2002, 36, 3161–3172. [Google Scholar] [CrossRef]
- Hu, Y.; Yao, L.; Cheng, Z.; Wang, Y. Long-term atmospheric visibility trends in megacities of China, India and the United States. Environ. Res. 2017, 159, 466–473. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, C.; Zhao, C.; Su, T. Changes in surface aerosol extinction trends over China during 1980–2013 inferred from quality-controlled visibility data. Geophys. Res. Lett. 2016, 43, 8713–8719. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Xu, L.; Chen, J.; Yu, Y.; Niu, Z.; Yin, L. Chemical compositions and extinction coefficients of PM2.5 in peri-urban of Xiamen, China, during June 2009–May 2010. Atmos. Res. 2012, 106, 150–158. [Google Scholar] [CrossRef]
- Founda, D.; Kazadzis, S.; Mihalopoulos, N.; Gerasopoulos, E.; Lianou, M.; Raptis, P.I. Long-term visibility variation in Athens (1931–2013): A proxy for local and regional atmospheric aerosol loads. Atmos. Chem. Phys. 2016, 16, 11219–11236. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Sun, Z.; He, J.; Hao, Y.; Tang, Q.; Zhang, X.; Zheng, C.; Miao, S. Seasonal variation in health impacts associated with visibility in Beijing, China. Sci. Total Environ. 2020, 730, 139149. [Google Scholar] [CrossRef]
- Singh, A.; Dey, S. Influence of aerosol composition on visibility in megacity Delhi. Atmos. Environ. 2012, 62, 367–373. [Google Scholar] [CrossRef]
- Shen, X.; Sun, J.; Zhang, X.; Zhang, Y.; Zhang, L.; Che, H.; Ma, Q.; Yu, X.; Yue, Y. Characterization of submicron aerosols and effect on visibility during a severe haze-fog episode in Yangtze River Delta, China. Atmos. Environ. 2015, 120, 307–316. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Bloss, W.J.; Pope, F.D. 60 years of UK visibility measurements: Impact of meteorology and atmospheric pollutants on visibility. Atmos. Chem. Phys. 2017, 17, 2085–2101. [Google Scholar] [CrossRef] [Green Version]
- Cao, J.-J.; Wang, Q.-Y.; Chow, J.C.; Watson, J.; Tie, X.-X.; Shen, Z.-X.; Wang, P.; An, Z.-S. Impacts of aerosol compositions on visibility impairment in Xi’an, China. Atmos. Environ. 2012, 59, 559–566. [Google Scholar] [CrossRef]
- Shen, Z.X.; Cao, J.J.; Arimoto, R.; Han, Z.; Zhang, R.; Han, Y.; Liu, S.; Okuda, T.; Nakao, S.; Tanaka, S. Ionic composition of TSP and PM2.5 during dust storms and air pollution episodes at Xi’an, China. Atmos. Environ. 2009, 43, 2911–2918. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Zhang, M.; Yang, Y.; Shen, X.; Wang, Y.; Chen, D.; Guo, J. A study of the meteorological causes of a prolonged and severe haze episode in January 2013 over central-eastern China. Atmos. Environ. 2014, 98, 146–157. [Google Scholar] [CrossRef]
- Zhang, Q.; Quan, J.N.; Tie, X.X.; Li, X.; Liu, Q.; Gao, Y.; Zhao, D.L. Effects of meteorology and secondary particle formation on visibility during heavy haze events in Beijing, China. Sci. Total Environ. 2015, 502, 578–584. [Google Scholar] [CrossRef] [PubMed]
- Luan, T.; Guo, X.L.; Guo, L.J.; Zhang, T. Quantifying the relationship between PM2.5 concentration, visibility and planetary boundary layer height for long-lasting haze and fog-haze mixed events in Beijing. Atmos. Chem. Phys. 2018, 18, 203–225. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Zhang, X.; Xu, X.; Zhao, X. Long-term visibility trends and characteristics in the region of Beijing, Tianjin, and Hebei, China. Atmos. Res. 2011, 101, 711–718. [Google Scholar] [CrossRef]
- Huang, K.; Zhuang, G.; Lin, Y.; Wang, Q.; Fu, J.S.; Zhang, R.; Li, J.; Deng, C.; Fu, Q. Impact of anthropogenic emission on air quality over a megacity-revealed from an intensive atmospheric campaign during the Chinese Spring Festival. Atmos. Chem. Phys. 2012, 12, 11631–11645. [Google Scholar] [CrossRef] [Green Version]
- Kong, L.; Xin, J.; Liu, Z.; Zhang, K.; Tang, G.; Zhang, W.; Wang, Y. The PM2.5 threshold for aerosol extinction in the Beijing megacity. Atmos. Environ. 2017, 167, 458–465. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, R.; Yu, W. The Effects of PM2.5 Concentrations and Relative Humidity on Atmospheric Visibility in Beijing. J. Geophys. Res. Atmos. 2019, 124, 2235–2259. [Google Scholar] [CrossRef]
- Deng, H.; Tan, H.; Li, F.; Cai, M.; Chan, P.W.; Xu, H.; Huang, X.; Wu, D. Impact of relative humidity on visibility degradation during a haze event: A case study. Sci. Total Environ. 2016, 569–570, 1149–1158. [Google Scholar] [CrossRef]
- Malm, W.C.; Day, D.E. Estimates of aerosol species scattering characteristics as a function of relative humidity. Atmos. Environ. 2001, 35, 2845–2860. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, C.S.; Ma, N.; Liu, P.F.; Göbel, T.; Hallbauer, E.; Deng, Z.Z.; Ran, L.; Xu, W.Y.; Liang, Z.; et al. A parameterization of low visibilities for hazy days in the North China Plain. Atmos. Chem. Phys. 2012, 12, 4935–4950. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Wang, X.; Yan, P.; Zhang, L.; Tao, J.; Liu, X.; Tian, P.; Han, Z.; Zhang, R. Investigation of hygroscopic growth effect on aerosol scattering coefficient at a rural site in the southern North China Plain. Sci. Total Environ. 2017, 599–600, 76–84. [Google Scholar] [CrossRef]
- Covert, D.S.; Charlson, R.J.; Ahlquist, N.C. A Study of the Relationship of Chemical Composition and Humidity to Light Scattering by Aerosols. J. Appl. Meteorol. 1972, 11, 968–976. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Huang, H.X.; Griffith, S.M.; Wu, C.; Lau, A.K.; Yu, J.Z. Quantifying the relationship between visibility degradation and PM2.5 constituents at a suburban site in Hong Kong: Differentiating contributions from hydrophilic and hydrophobic organic compounds. Sci. Total Environ. 2017, 575, 1571–1581. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.-C.; Yeh, H.-H. Comparative influences of airborne pollutants and meteorological parameters on atmospheric visibility and turbidity. Atmos. Res. 2010, 96, 496–509. [Google Scholar] [CrossRef]
- Schichtel, B.A.; Husar, R.B.; Falke, S.R.; Wilson, W.E. Haze trends over the United States, 1980–1995. Atmos. Environ. 2001, 35, 5205–5210. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, C.; Zhang, Y.; Xu, W.; Zhou, L.; Cheng, X.; Zheng, H.; Ji, D.; Li, J.; Tang, X.; et al. Rapid formation and evolution of an extreme haze episode in Northern China during winter 2015. Sci. Rep. 2016, 6, 27151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Day, D.E.; Malm, W.C. Aerosol light scattering measurements as a function of relative humidity: A comparison between measurements made at three different sites. Atmos. Environ. 2001, 35, 5169–5176. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Y.; Zhou, S.; Li, H.; Wang, F.; Yang, T. The influence of terrestrial transport on visibility and aerosol properties over the coastal East China Sea. Sci. Total Environ. 2018, 649, 652–660. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Zhang, L.; Engling, G.; Zhang, R.; Yang, Y.; Cao, J.; Zhu, C.; Wang, Q.; Luo, L. Chemical composition of PM2.5 in an urban environment in Chengdu, China: Importance of springtime dust storms and biomass burning. Atmos. Res. 2012, 122, 270–283. [Google Scholar] [CrossRef]
- Ye, B.M.; Ji, X.L.; Yang, H.Z.; Yao, X.; Chan, K.C.; Cadle, S.H.; Chan, T.; Mulawa, P.A. Concentration and chemical composition of PM2.5 in Shanghai for a 1-year period. Atmos. Environ. 2003, 37, 499–510. [Google Scholar] [CrossRef]
- Ma, N.; Zhao, C.; Chen, J.; Xu, W.; Yan, P.; Zhou, X. A novel method for distinguishing fog and haze based on PM2.5, visibility, and relative humidity. Sci. China Earth Sci. 2014, 57, 2156–2164. [Google Scholar] [CrossRef]
- Liu, B.; Yang, J.; Yuan, J.; Wang, J.; Dai, Q.; Li, T.; Bi, X.; Feng, Y.; Xiao, Z.; Zhang, Y.; et al. Source apportionment of atmospheric pollutants based on the online data by using PMF and ME2 models at a megacity, China. Atmos. Res. 2017, 185, 22–31. [Google Scholar] [CrossRef]
- Li, Y.F.; Liu, B.S.; Xue, Z.G.; Zhang, Y.F. Chemical characteristics and source apportionment of PM2.5 using PMF modelling coupled with 1-h resolution online air pollutant dataset for Linfen, China. Environ. Pollut. 2020, 263, 114532. [Google Scholar] [CrossRef]
- Song, M.; Han, S.Q.; Zhang, M.; Yao, Q.; Zhu, B. Relationship between visibility and relative humidity, PM10, PM2.5 in Tianjin. J. Meteor. Environ. 2013, 29, 34–41. (In Chinese) [Google Scholar]
- Randriamiarisoa, H.; Chazette, P.; Couvert, P.; Sanak, J.; Mégie, G. Relative humidity impact on aerosol parameters in a Paris suburban area. Atmos. Chem. Phys. 2006, 6, 1389–1407. [Google Scholar] [CrossRef] [Green Version]
- Carrico, C.M.; Rood, M.J.; Ogren, J.A.; Neusüss, C.; Wiedensohler, A.; Heintzenberg, J.; Neusüß, C. Aerosol Optical properties at Sagres, Portugal during ACE-2. Tellus B Chem. Phys. Meteorol. 2000, 52, 694–715. [Google Scholar] [CrossRef]
- Chitnis, N.; Hyman, J.; Cushing, J. Determining Important Parameters in the Spread of Malaria through the Sensitivity Analysis of a Mathematical Model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef] [PubMed]
- Aguilar-Canto, F.J.; de León, U.A.-P.; Avila-Vales, E. Sensitivity theorems of a model of multiple imperfect vaccines for COVID-19. Chaos Solitons Fractals 2022, 156, 111844. [Google Scholar] [CrossRef] [PubMed]
- Malm, W.C.; Gebhart, K.A.; Molenar, J.; Cahill, T.; Eldred, R.; Huffman, D. Examining the relationship between atmospheric aerosols and light extinction at Mount-Rainier-National-Park and North-Cascades-National-Park. Atmos. Environ. 1994, 28, 347–360. [Google Scholar] [CrossRef]
- Pitchford, M.; Malm, W.; Schichtel, B.; Kumar, N.; Lowenthal, D.; Hand, J. Revised algorithm for estimating light extinction from IMPROVE particle speciation data. J. Air Waste Manag. Assoc. 2007, 57, 1326–1336. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, Y.-F.; Feng, Y.-C.; Zheng, X.-J.; Jiao, L.; Hong, S.-M.; Shen, J.-D.; Zhu, T.; Ding, J.; Zhang, Q. Characterization and source apportionment of aerosol light extinction with a coupled model of CMB-IMPROVE in Hangzhou, Yangtze River Delta of China. Atmos. Res. 2016, 178–179, 570–579. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, Y.; Jiang, Q.; Du, W.; Sun, C.; Fu, P.; Wang, Z. Chemical composition of aerosol particles and light extinction apportionment before and during the heating season in Beijing, China. J. Geophys. Res. Atmos. 2015, 120, 12708–12722. [Google Scholar] [CrossRef]
- Turpin, B.J.; Lim, H.J. Species Contributions to PM2.5 Mass Concentrations: Revisiting Common Assumptions for Estimating Organic Mass. Aerosol. Sci. Technol. 2001, 35, 602–610. [Google Scholar] [CrossRef]
- Zou, J.; Liu, Z.; Hu, B.; Huang, X.; Wen, T.; Ji, D.; Liu, J.; Yang, Y.; Yao, Q.; Wang, Y. Aerosol chemical compositions in the North China Plain and the impact on the visibility in Beijing and Tianjin. Atmos. Res. 2018, 201, 235–246. [Google Scholar] [CrossRef]
- Tao, J.; Zhang, L.; Gao, J.; Wang, H.; Chai, F.; Wang, S. Aerosol chemical composition and light scattering during a winter season in Beijing. Atmos. Environ. 2015, 110, 36–44. [Google Scholar] [CrossRef]
- Aldabe, J.; Elustondo, D.; Santamaría, C.; Lasheras, E.; Pandolfi, M.; Alastuey, A.; Querol, X.; Santamaría, J.M. Chemical characterisation and source apportionment of PM2.5 and PM10 at rural, urban and traffic sites in Navarra (North of Spain). Atmos. Res. 2011, 102, 191–205. [Google Scholar] [CrossRef]
- Fu, X.; Wang, X.; Hu, Q.; Li, G.; Ding, X.; Zhang, Y.; He, Q.; Liu, T.; Zhang, Z.; Yu, Q.; et al. Changes in visibility with PM2.5 composition and relative humidity at a background site in the Pearl River Delta region. J. Environ. Sci. 2016, 40, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Ma, J.; An, J.; Yuan, L.; Zhu, B.; Liu, D.; Wang, J.; Yang, Y.; Cui, H. Impacts of meteorological condition and aerosol chemical compositions on visibility impairment in Nanjing, China. J. Clean. Prod. 2016, 131, 112–120. [Google Scholar] [CrossRef]

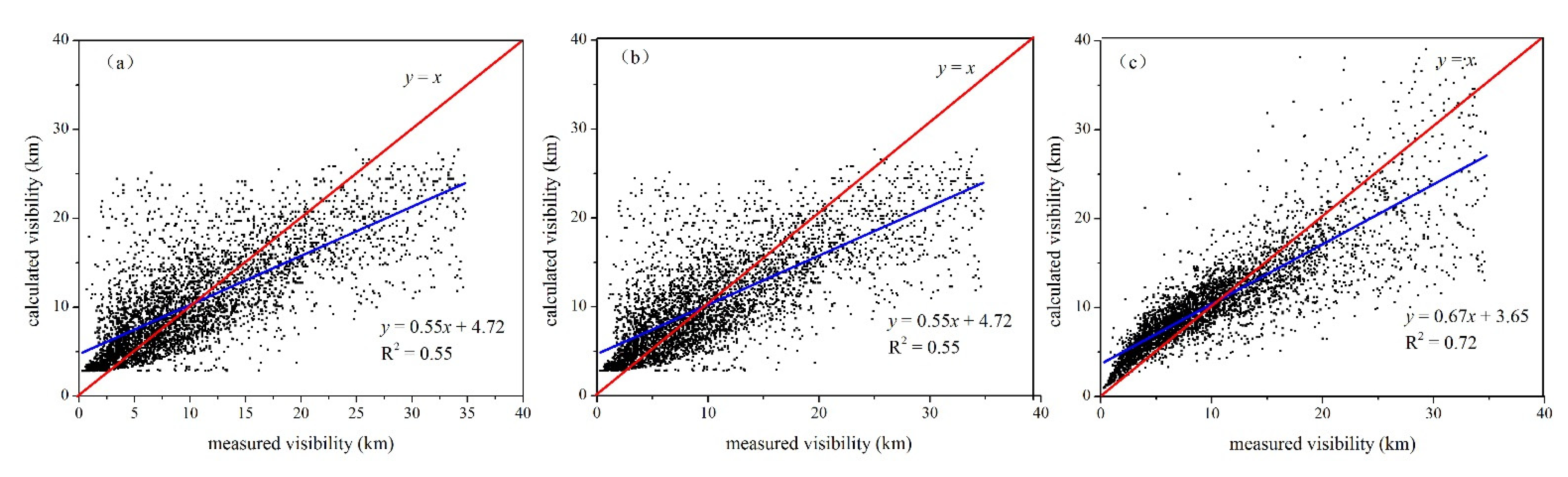


| Type | Fitting Equation | Relationship between Measured and Calculated Visibility | R2 |
|---|---|---|---|
| 1 | y = 0.62x + 4.66 | 0.65 | |
| 2 | y = 0.64x + 5.83 | 0.66 | |
| 3 | y = 0.75x + 1.93 | 0.76 | |
| 4 | y = 0.61x + 4.58 | 0.64 | |
| 5 | y = 0.84x + 0.65 | 0.84 | |
| 6 | y = 0.72x + 1.90 | 0.76 | |
| annual | y = 0.67x + 3.65 | 0.72 |
| Aerosol Types | PM2.5-Sensitive Regime | Transition Regime Dominated by PM2.5 | Transition Regime Dominated by RH | RH-Sensitive Regime |
|---|---|---|---|---|
| 1 | 27 | 48 | 23 | 2 |
| 2 | 47 | 47 | 6 | 0 |
| 3 | 6 | 31 | 59 | 3 |
| 4 | 9 | 31 | 54 | 6 |
| 5 | 1 | 13 | 77 | 9 |
| 6 | 3 | 8 | 46 | 44 |
| annual | 13 | 31 | 47 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wu, J.; Liu, B.; Liu, X.; Gao, H.; Zhang, Y.; Feng, Y.; Han, S.; Gong, X. Exploring the Sensitivity of Visibility to PM2.5 Mass Concentration and Relative Humidity for Different Aerosol Types. Atmosphere 2022, 13, 471. https://doi.org/10.3390/atmos13030471
Wang J, Wu J, Liu B, Liu X, Gao H, Zhang Y, Feng Y, Han S, Gong X. Exploring the Sensitivity of Visibility to PM2.5 Mass Concentration and Relative Humidity for Different Aerosol Types. Atmosphere. 2022; 13(3):471. https://doi.org/10.3390/atmos13030471
Chicago/Turabian StyleWang, Jiao, Jianhui Wu, Baoshuang Liu, Xiaohuan Liu, Huiwang Gao, Yufen Zhang, Yinchang Feng, Suqin Han, and Xiang Gong. 2022. "Exploring the Sensitivity of Visibility to PM2.5 Mass Concentration and Relative Humidity for Different Aerosol Types" Atmosphere 13, no. 3: 471. https://doi.org/10.3390/atmos13030471
APA StyleWang, J., Wu, J., Liu, B., Liu, X., Gao, H., Zhang, Y., Feng, Y., Han, S., & Gong, X. (2022). Exploring the Sensitivity of Visibility to PM2.5 Mass Concentration and Relative Humidity for Different Aerosol Types. Atmosphere, 13(3), 471. https://doi.org/10.3390/atmos13030471