Simulation of Arctic Thin Ice Clouds with Canadian Regional Climate Model Version 6: Verification against CloudSat-CALIPSO
Abstract
:1. Introduction
2. CRCM6
2.1. Model Description
2.2. Modifications of CRCM6 Model Physics
2.3. Model Configuration
3. Reanalysis and Satellite-Based Data
3.1. Reanalysis Data
3.2. Satellite-Based Observation Data
3.2.1. C-ICE Products
3.2.2. 2B-FLXHR-LIDAR Products
3.2.3. 2B-FLXHR-LIDAR Algorithm
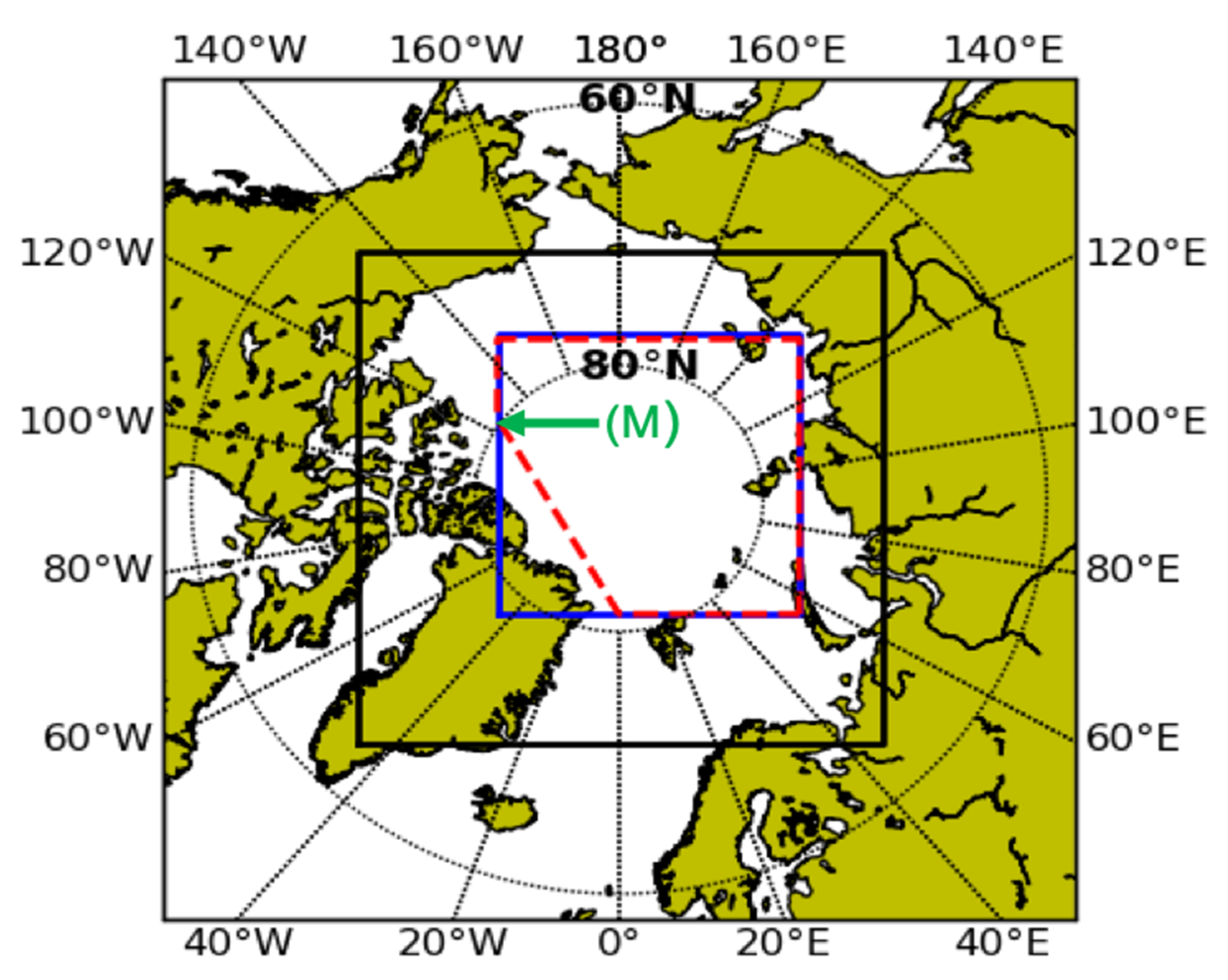
4. Methodological Considerations
4.1. CRCM6 Product vs. A-Train Product Comparisons
4.2. Comparative Analysis Strategies
5. Results
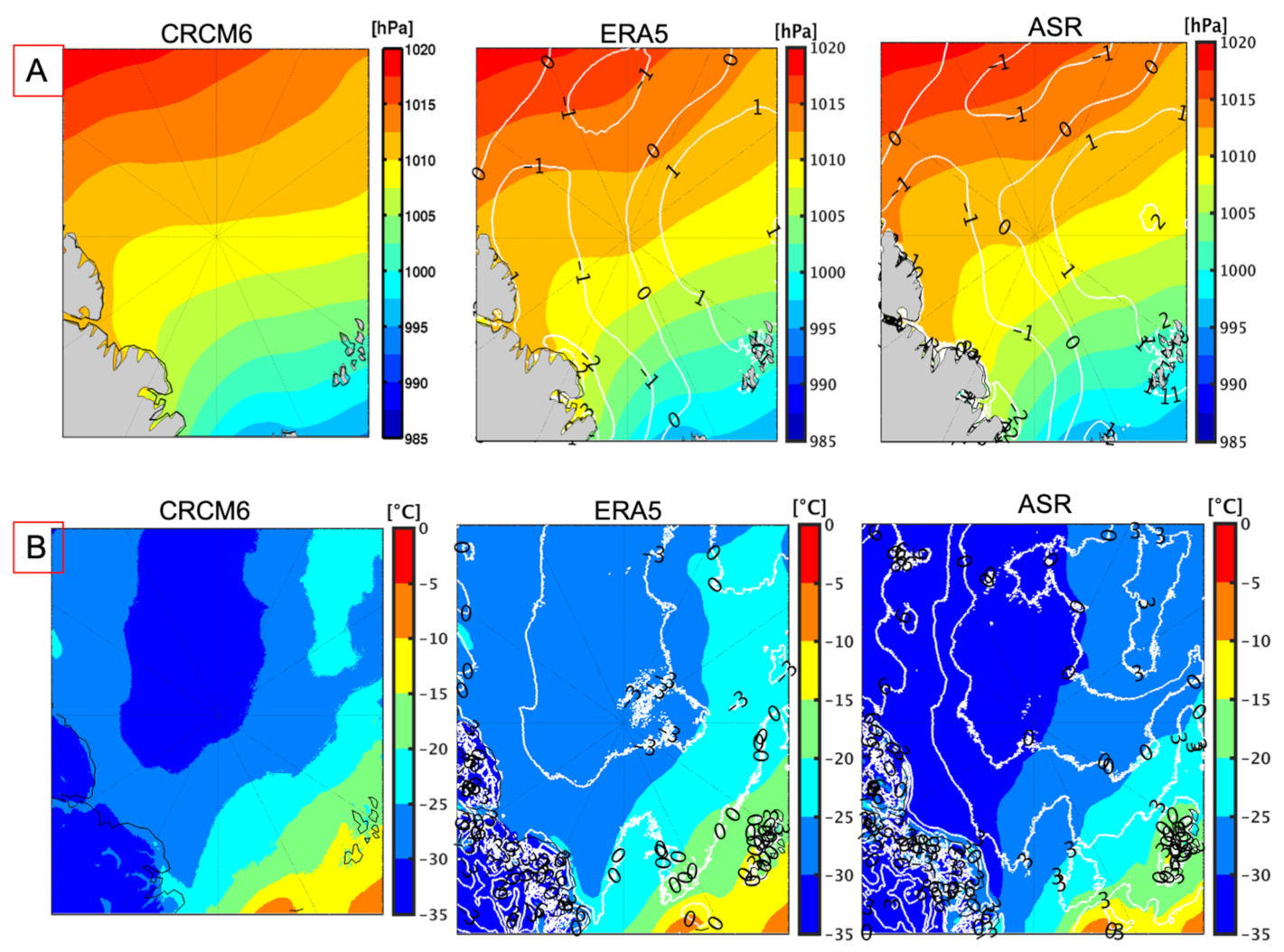
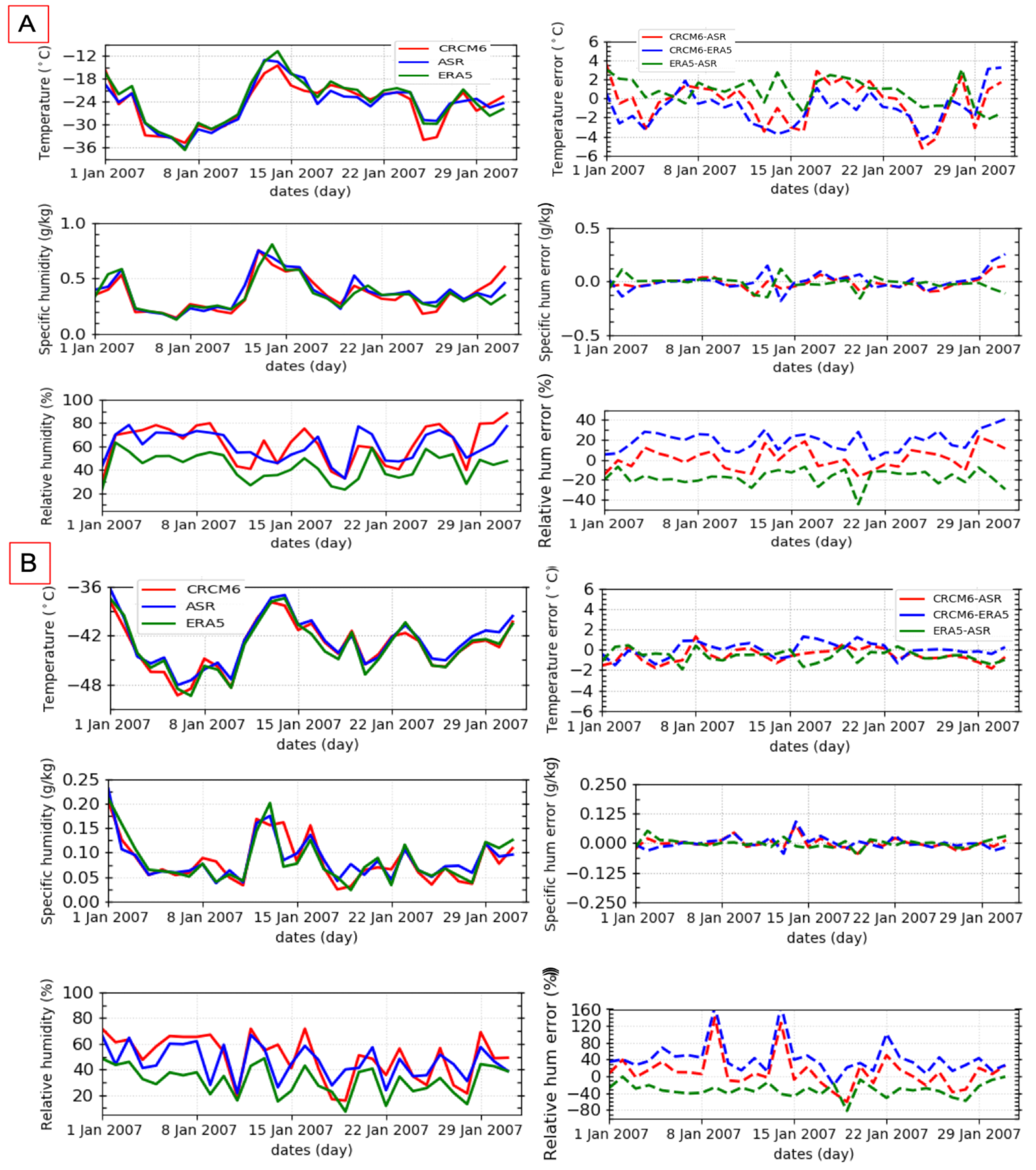
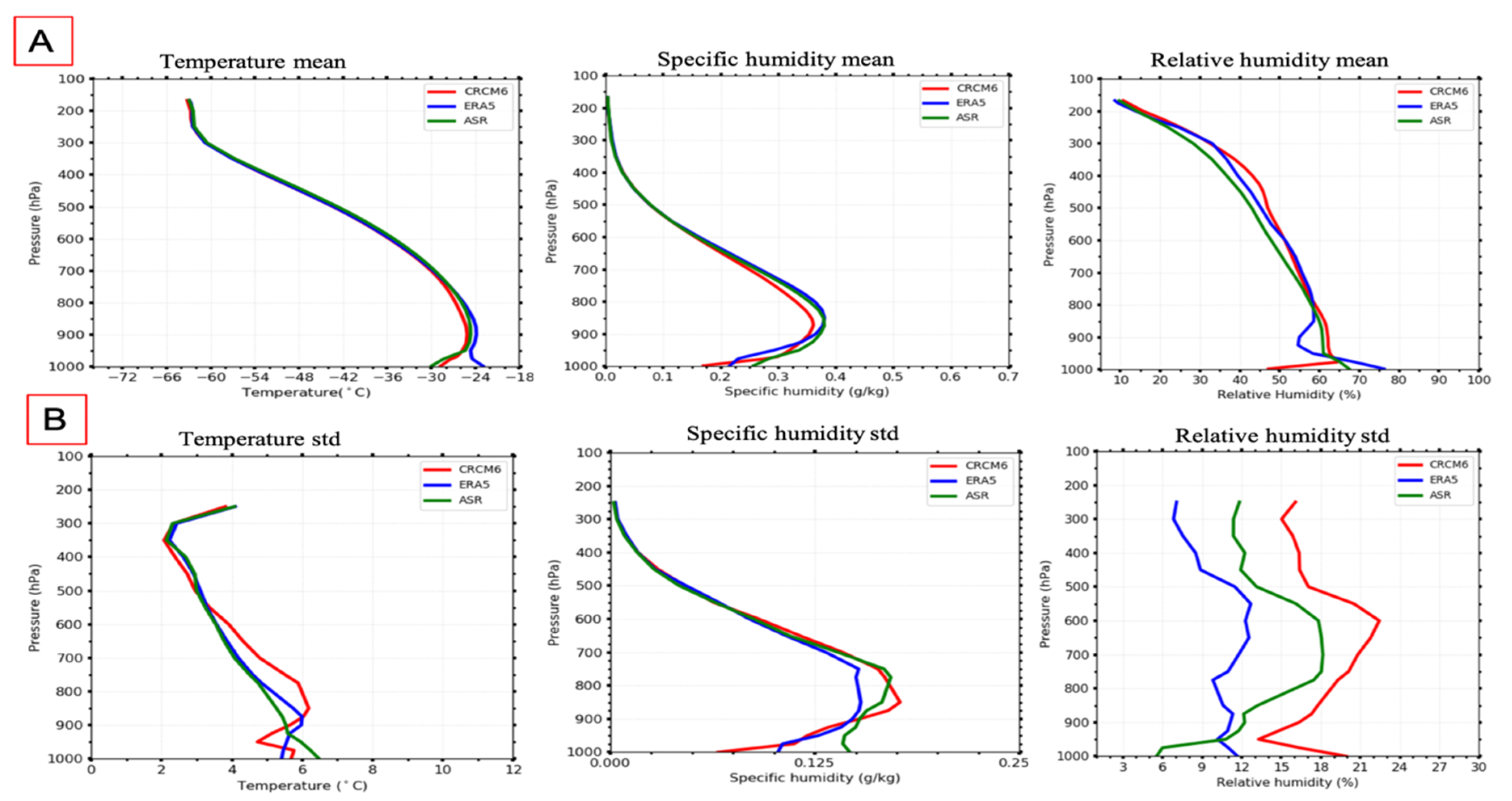
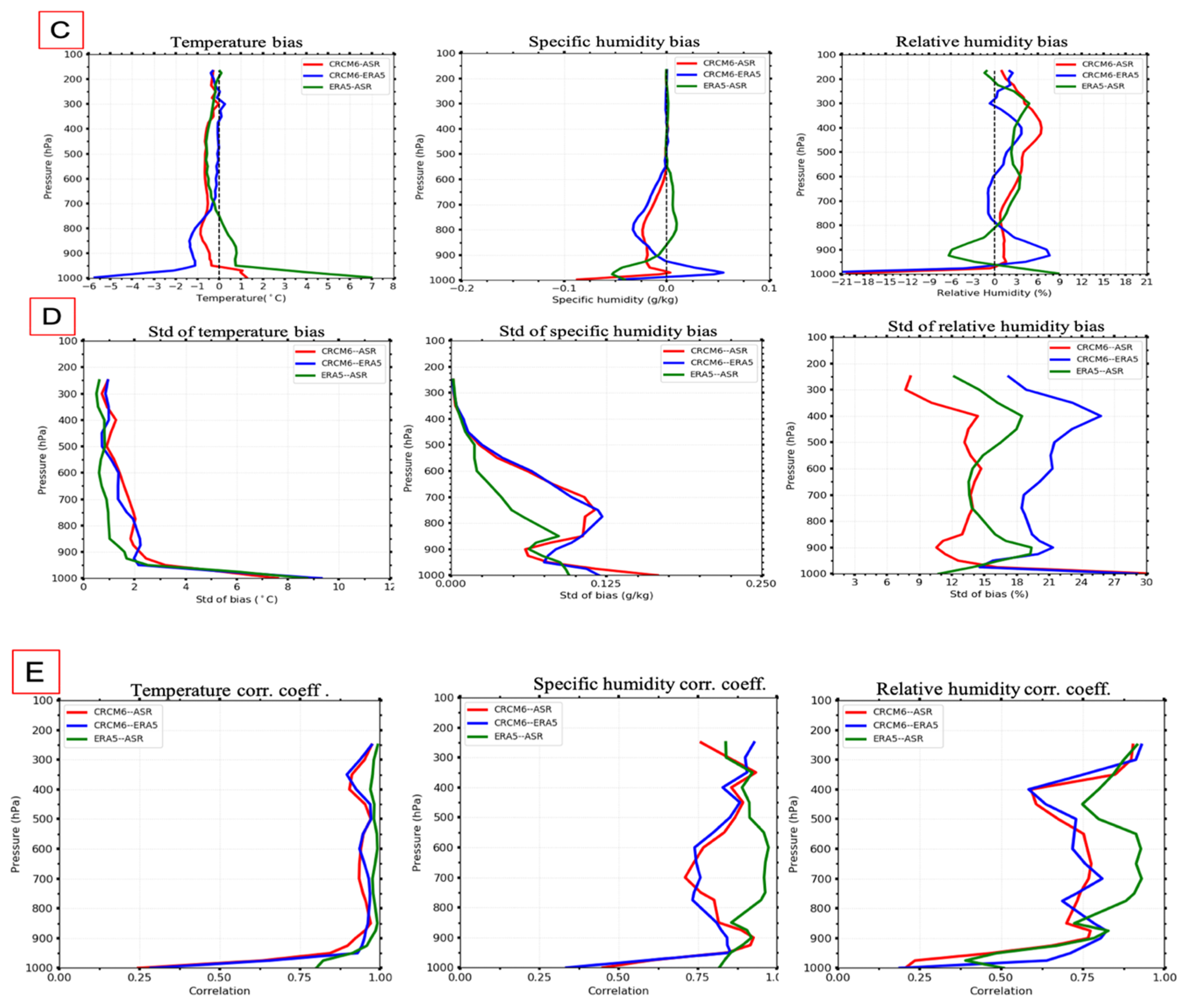
5.1. Meteorological Field Validation
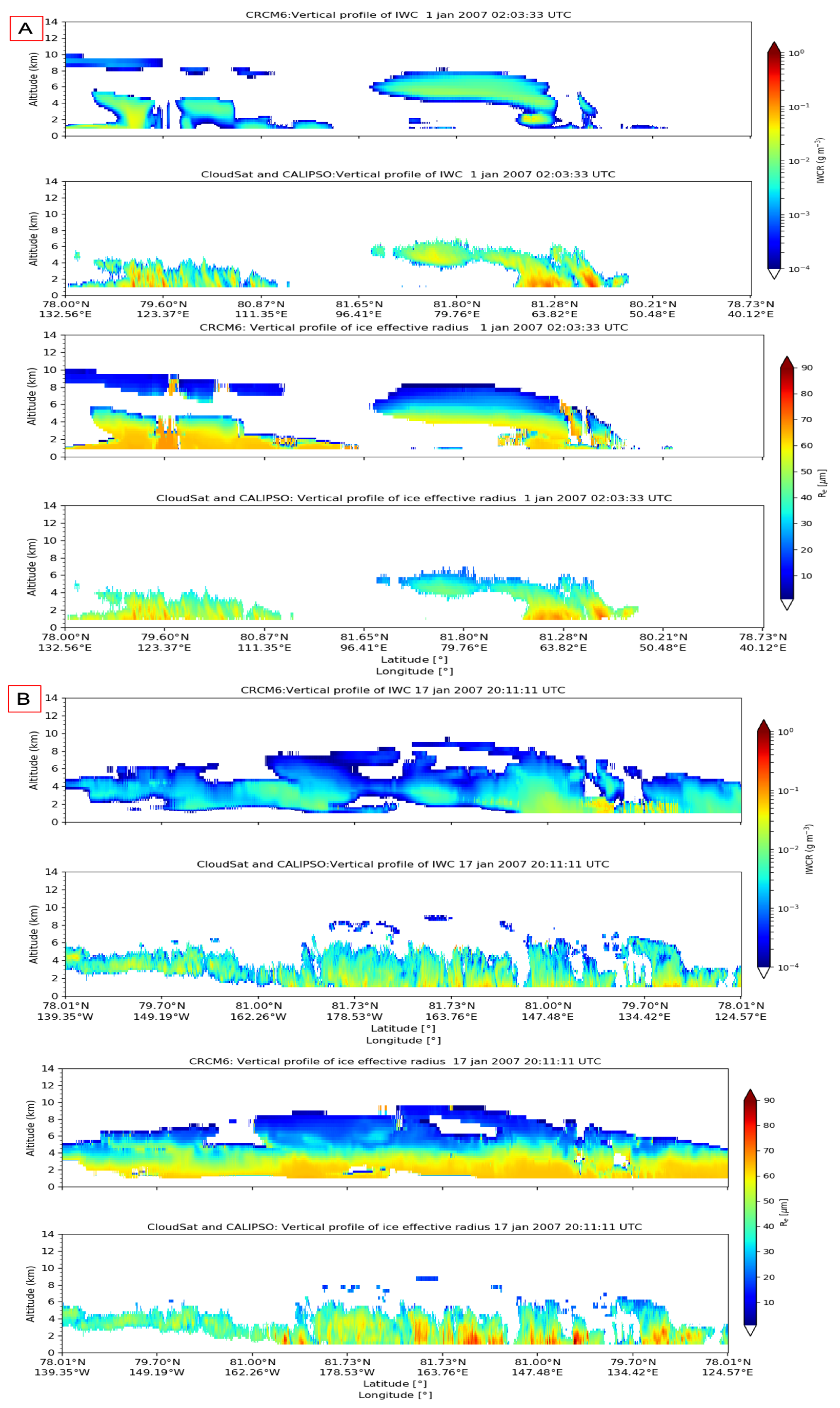
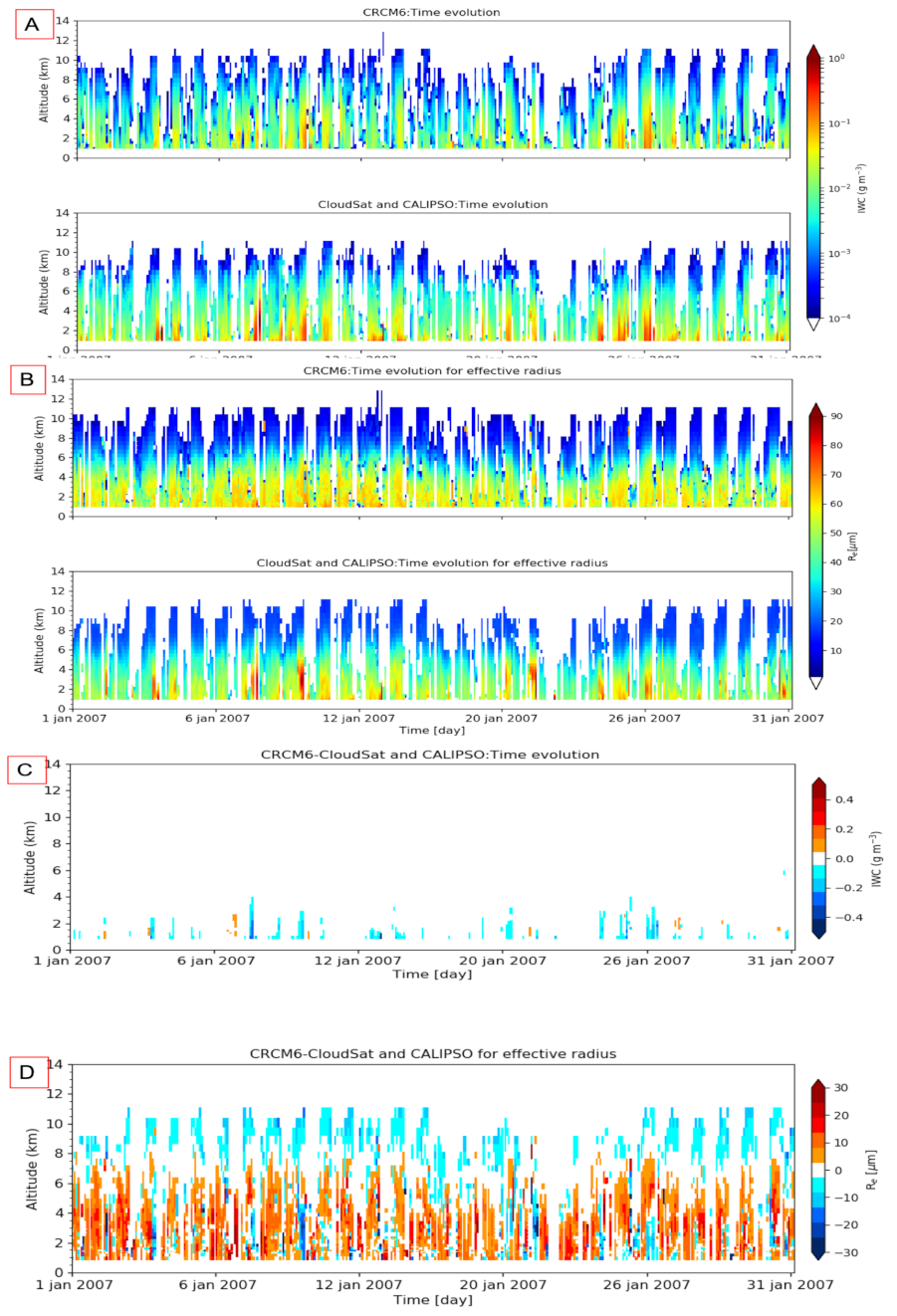
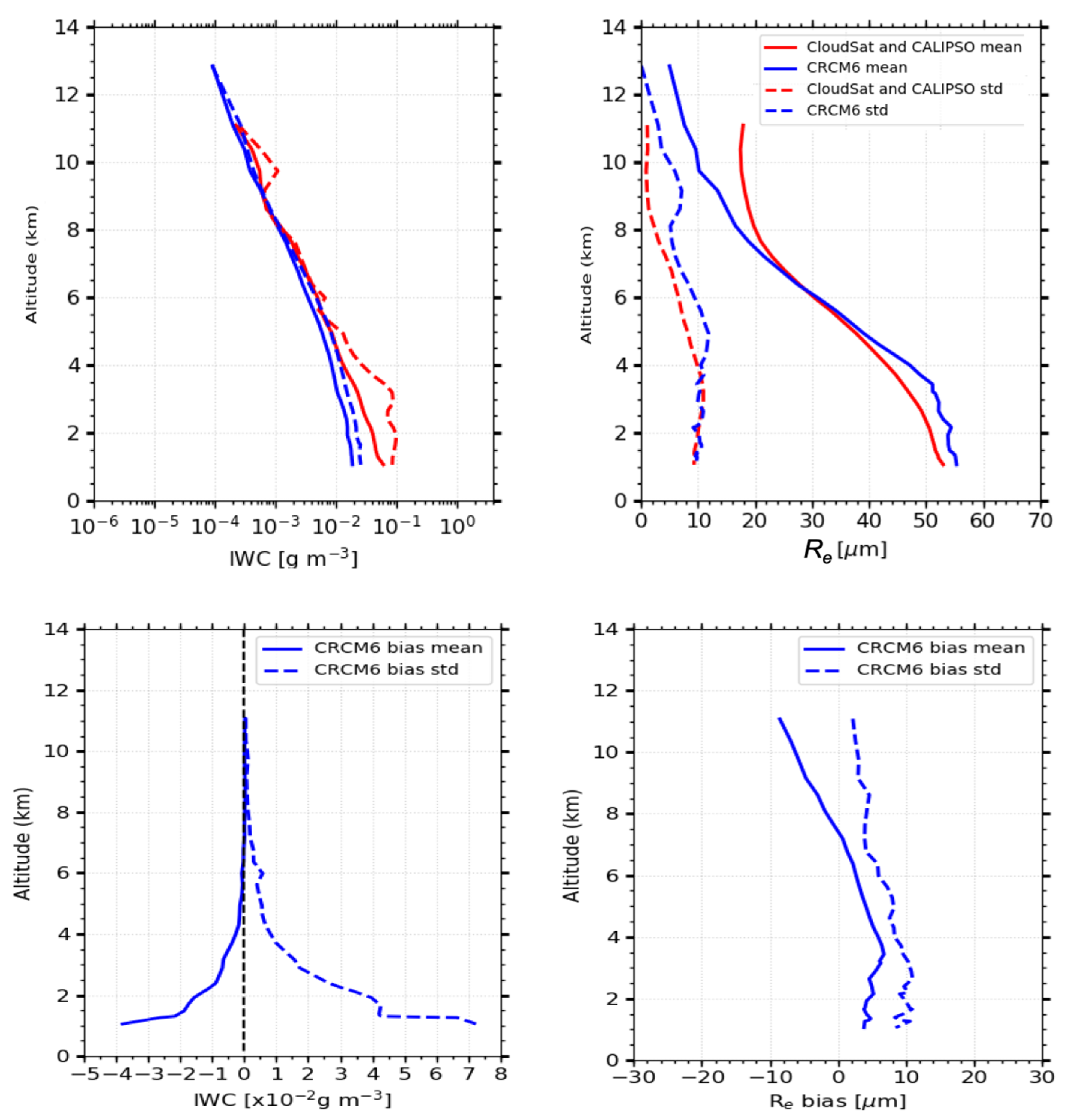
5.2. Optical Property Simulation of TICs
5.3. Cloud Heating Rates
6. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hassol, S.J. Impacts of a Warming Arctic-Arctic Climate Impact Assessment; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2004. [Google Scholar]
- Alexander, L.V. Global observed long-term changes in temperature and precipitation extremes: A review of progress and limitations in IPCC assessments and beyond. Weather Clim. Extrem. 2016, 11, 4–16. [Google Scholar] [CrossRef] [Green Version]
- Comiso, J.C. Warming trends in the Arctic from clear sky satellite observations. J. Clim. 2003, 16, 3498–3510. [Google Scholar] [CrossRef] [Green Version]
- Comiso, J.C. Arctic warming signals from satellite observations. Weather 2006, 61, 70–76. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Key, J.R.; Wang, X. The influence of changes in cloud cover on recent surface temperature trends in the Arctic. J. Clim. 2008, 21, 705–715. [Google Scholar] [CrossRef]
- Liu, Y.; Key, J.R.; Wang, X. Influence of changes in sea ice concentration and cloud cover on recent Arctic surface temperature trends. Geophys. Res. Lett. 2009, 36, 705–715. [Google Scholar] [CrossRef] [Green Version]
- Keita, S.A.; Girard, E. Importance of Chemical Composition of Ice Nuclei on the Formation of Arctic Ice Clouds. Pure Appl. Geophys. 2016, 173, 3141–3163. [Google Scholar] [CrossRef]
- Intrieri, J.M.; Shupe, M.D. Characteristics and radiative effects of diamond dust over the western Arctic Ocean region. J. Clim. 2004, 17, 2953–2960. [Google Scholar] [CrossRef]
- Libois, Q.; Blanchet, J.P. Added value of far-infrared radiometry for remote sensing of ice clouds. J. Geophys. Res. Atmos. 2017, 122, 6541–6564. [Google Scholar] [CrossRef] [Green Version]
- Curry, J.A.; Schramm, J.L.; Rossow, W.B.; Randall, D. Overview of Arctic cloud and radiation characteristics. J. Clim. 1996, 9, 1731–1764. [Google Scholar] [CrossRef] [Green Version]
- Blanchet, J.-P.; Royer, A.; Châteauneuf, F.; Bouzid, Y.; Blanchard, Y.; Hamel, J.-F.; de Lafontaine, J.; Gauthier, P.; O’Neill, N.T.; Pancrati, O. TICFIRE: A far infrared payload to monitor the evolution of thin ice clouds. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XV, Prague, Czech Republic, 19–22 September 2011; p. 81761K. [Google Scholar]
- Chen, T.; Rossow, W.B.; Zhang, Y. Radiative effects of cloud-type variations. J. Clim. 2000, 13, 264–286. [Google Scholar] [CrossRef]
- Kahl, J.D. Characteristics of the low-level temperature inversion along the Alaskan Arctic coast. Int. J. Climatol. 1990, 10, 537–548. [Google Scholar] [CrossRef]
- Kahl, J.D.; Serreze, M.C.; Schnell, R.C. Tropospheric low-level temperature inversions in the Canadian Arctic. Atmos.-Ocean. 1992, 30, 511–529. [Google Scholar] [CrossRef]
- Persson, P.; Uttal, T.; Intrieri, J.; Fairall, C.; Andreas, E.; Guest, P. Observations of large thermal transitions during the Arctic night from a suite of sensors at SHEBA. In Proceedings of the Preprints, Fifth Conference on Polar Meteorology and Oceanography, Virtual, 1–4 June 2021; pp. 10–15. [Google Scholar]
- Persson, P.O.G.; Fairall, C.W.; Andreas, E.L.; Guest, P.S.; Perovich, D.K. Measurements near the Atmospheric Surface Flux Group tower at SHEBA: Near-surface conditions and surface energy budget. J. Geophys. Res. Ocean. 2002, 107, SHE 21-1–SHE 21-35. [Google Scholar] [CrossRef] [Green Version]
- L’Ecuyer, T.S.; Wood, N.B.; Haladay, T.; Stephens, G.L.; Stackhouse, P.W., Jr. Impact of clouds on atmospheric heating based on the R04 CloudSat fluxes and heating rates data set. J. Geophys. Res. Atmos. 2008, 113, D00A15. [Google Scholar] [CrossRef] [Green Version]
- Oreopoulos, L.; Cho, N.; Lee, D.; Kato, S.; Huffman, G.J. An examination of the nature of global MODIS cloud regimes. J. Geophys. Res. Atmos. 2014, 119, 8362–8383. [Google Scholar] [CrossRef] [Green Version]
- Girard, E.; Blanchet, J.-P.; Dubois, Y. Effects of arctic sulphuric acid aerosols on wintertime low-level atmospheric ice crystals, humidity and temperature at Alert, Nunavut. Atmos. Res. 2005, 73, 131–148. [Google Scholar] [CrossRef]
- Girard, E.; Dueymes, G.; Du, P.; Bertram, A.K. Assessment of the effects of acid-coated ice nuclei on the Arctic cloud microstructure, atmospheric dehydration, radiation and temperature during winter. Int. J. Climatol. 2013, 33, 599–614. [Google Scholar] [CrossRef]
- Dufresne, J.-L.; Bony, S. An assessment of the primary sources of spread of global warming estimates from coupled atmosphere–ocean models. J. Clim. 2008, 21, 5135–5144. [Google Scholar] [CrossRef] [Green Version]
- Shupe, M.D.; Walden, V.P.; Eloranta, E.; Uttal, T.; Campbell, J.R.; Starkweather, S.M.; Shiobara, M. Clouds at Arctic atmospheric observatories. Part I: Occurrence and macrophysical properties. J. Appl. Meteorol. Climatol. 2011, 50, 626–644. [Google Scholar] [CrossRef] [Green Version]
- Uttal, T.; Curry, J.A.; McPhee, M.G.; Perovich, D.K.; Moritz, R.E.; Maslanik, J.A.; Guest, P.S.; Stern, H.L.; Moore, J.A.; Turenne, R. Surface heat budget of the Arctic Ocean. Bull. Am. Meteorol. Soc. 2002, 83, 255–276. [Google Scholar] [CrossRef] [Green Version]
- Shupe, M.D. Clouds at Arctic atmospheric observatories. Part II: Thermodynamic phase characteristics. J. Appl. Meteorol. Climatol. 2011, 50, 645–661. [Google Scholar] [CrossRef]
- Nikiéma, O.; Laprise, R. An approximate energy cycle for inter-member variability in ensemble simulations of a regional climate model. Clim. Dyn. 2013, 41, 831–852. [Google Scholar] [CrossRef] [Green Version]
- Blanchet, J.-P.; Girard, E. Arctic ‘greenhouse effect’. Nature 1994, 371, 383. [Google Scholar] [CrossRef]
- Grenier, P.; Blanchet, J.P.; Muñoz-Alpizar, R. Study of polar thin ice clouds and aerosols seen by CloudSat and CALIPSO during midwinter. J. Geophys. Res. Atmos. 2009, 114, D09201. [Google Scholar] [CrossRef] [Green Version]
- Jouan, C.; Girard, E.; Pelon, J.; Gultepe, I.; Delanoë, J.; Blanchet, J.P. Characterization of Arctic ice cloud properties observed during ISDAC. J. Geophys. Res. Atmos. 2012, 117, D23. [Google Scholar] [CrossRef] [Green Version]
- Keita, S.A.; Girard, E.; Raut, J.-C.; Leriche, M.; Blanchet, J.-P.; Pelon, J.; Onishi, T.; Cirisan, A. A new parameterization of ice heterogeneous nucleation coupled to aerosol chemistry in WRF-Chem model version 3.5. 1: Evaluation through ISDAC measurements. Geosci. Model Dev. 2020, 13, 5737–5755. [Google Scholar] [CrossRef]
- Keita, S.A.; Girard, E.; Raut, J.-C.; Pelon, J.; Blanchet, J.-P.; Lemoine, O.; Onishi, T. Simulating Arctic Ice Clouds during Spring Using an Advanced Ice Cloud Microphysics in the WRF Model. Atmosphere 2019, 10, 433. [Google Scholar] [CrossRef] [Green Version]
- Grenier, P.; Blanchet, J.P. Investigation of the sulphate-induced freezing inhibition effect from CloudSat and CALIPSO measurements. J. Geophys. Res. Atmos. 2010, 115, D22. [Google Scholar] [CrossRef] [Green Version]
- Cirisan, A.; Girard, E.; Blanchet, J.-P.; Keita, S.A.; Gong, W.; Irish, V.; Bertram, A.K. CNT Parameterization Based on the Observed INP Concentration during Arctic Summer Campaigns in a Marine Environment. Atmosphere 2020, 11, 916. [Google Scholar] [CrossRef]
- Jouan, C.; Pelon, J.; Girard, E.; Ancellet, G.; Blanchet, J.-P.; Delanoë, J. On the relationship between Arctic ice clouds and polluted air masses over the North Slope of Alaska in April. Atmos. Chem. Phys. 2014, 14, 1205–1224. [Google Scholar] [CrossRef] [Green Version]
- Morrison, H.; Milbrandt, J.A. Parameterization of cloud microphysics based on the prediction of bulk ice particle properties. Part I: Scheme description and idealized tests. J. Atmos. Sci. 2015, 72, 287–311. [Google Scholar] [CrossRef]
- Milbrandt, J.; Morrison, H. Parameterization of cloud microphysics based on the prediction of bulk ice particle properties. Part III: Introduction of multiple free categories. J. Atmos. Sci. 2016, 73, 975–995. [Google Scholar] [CrossRef]
- Milbrandt, J.A.; Bélair, S.; Faucher, M.; Vallée, M.; Carrera, M.L.; Glazer, A. The Pan-Canadian high resolution (2.5 km) deterministic prediction system. Weather Forecast. 2016, 31, 1791–1816. [Google Scholar] [CrossRef]
- Yang, J.; Jones, K.F.; Yu, W.; Morris, R. Simulation of in-cloud icing events on Mount Washington with the GEM-LAM. J. Geophys. Res. Atmos. 2012, 117, D17. [Google Scholar] [CrossRef] [Green Version]
- Côté, J.; Gravel, S.; Méthot, A.; Patoine, A.; Roch, M.; Staniforth, A. The operational CMC–MRB global environmental multiscale (GEM) model. Part I: Design considerations and formulation. Mon. Weather Rev. 1998, 126, 1373–1395. [Google Scholar] [CrossRef]
- Girard, C.; Plante, A.; Desgagné, M.; McTaggart-Cowan, R.; Côté, J.; Charron, M.; Gravel, S.; Lee, V.; Patoine, A.; Qaddouri, A. Staggered vertical discretization of the Canadian Environmental Multiscale (GEM) model using a coordinate of the log-hydrostatic-pressure type. Mon. Weather Rev. 2014, 142, 1183–1196. [Google Scholar] [CrossRef]
- Laprise, R. The Euler equations of motion with hydrostatic pressure as an independent variable. Mon. Weather Rev. 1992, 120, 197–207. [Google Scholar] [CrossRef]
- Bélair, S.; Mailhot, J.; Girard, C.; Vaillancourt, P. Boundary layer and shallow cumulus clouds in a medium-range forecast of a large-scale weather system. Mon. Weather Rev. 2005, 133, 1938–1960. [Google Scholar] [CrossRef]
- Bélair, S.; Mailhot, J.; Strapp, J.W.; MacPherson, J.I. An examination of local versus nonlocal aspects of a TKE-based boundary layer scheme in clear convective conditions. J. Appl. Meteor. 1999, 38, 1499–1518. [Google Scholar] [CrossRef]
- Takhsha, M.; Nikiéma, O.; Lucas-Picher, P.; Laprise, R.; Hernández-Díaz, L.; Winger, K. Dynamical downscaling with the fifth-generation Canadian regional climate model (CRCM5) over the CORDEX Arctic domain: Effect of large-scale spectral nudging and of empirical correction of sea-surface temperature. Clim. Dyn. 2018, 51, 161–186. [Google Scholar] [CrossRef]
- Li, J.; Barker, H. A radiation algorithm with correlated-k distribution. Part I: Local thermal equilibrium. J. Atmos. Sci. 2005, 62, 286–309. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef] [Green Version]
- Kuo, E. Wave scattering and transmission at irregular surfaces. J. Acoust. Soc. Am. 1964, 36, 2135–2142. [Google Scholar] [CrossRef]
- Sundqvist, H.; Berge, E.; Kristjansson, J. Condensation and cloud parameterization studies with a mesoscale numerical weather prediction model. Mon. Weather Rev. 1989, 117, 1641–1657. [Google Scholar] [CrossRef]
- Verseghy, D. The Canadian Land Surface Scheme: Technical Documentation—Version 3.4. 2008. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.614.4315&rep=rep1&type=pdf (accessed on 17 November 2021).
- Verseghy, D.L. The Canadian land surface scheme (CLASS): Its history and future. Atmos.-Ocean. 2000, 38, 1–13. [Google Scholar] [CrossRef]
- Cholette, M.; Morrison, H.; Milbrandt, J.A.; Thériault, J.M. Parameterization of the bulk liquid fraction on mixed-phase particles in the predicted particle properties (P3) scheme: Description and idealized simulations. J. Atmos. Sci. 2019, 76, 561–582. [Google Scholar] [CrossRef]
- Milbrandt, J.; Yau, M. A multimoment bulk microphysics parameterization. Part I: Analysis of the role of the spectral shape parameter. J. Atmos. Sci. 2005, 62, 3051–3064. [Google Scholar] [CrossRef] [Green Version]
- Sankaré, H.; Thériault, J.M. On the relationship between the snowflake type aloft and the surface precipitation types at temperatures near 0 °C. Atmos. Res. 2016, 180, 287–296. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Miloshevich, L.M. Parameterizations for the cross-sectional area and extinction of cirrus and stratiform ice cloud particles. J. Atmos. Sci. 2003, 60, 936–956. [Google Scholar] [CrossRef]
- Morrison, H.; Grabowski, W.W. A novel approach for representing ice microphysics in models: Description and tests using a kinematic framework. J. Atmos. Sci. 2008, 65, 1528–1548. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Dee, D.; Horányi, A.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I. The ERA5 Global Atmospheric Reanalysis at ECMWF as a comprehensive dataset for climate data homogenization, climate variability, trends and extremes. Geophys. Res. Abstr. 2019, 21, EGU2019-10826-1. [Google Scholar]
- Bromwich, D.H.; Wilson, A.B.; Bai, L.S.; Moore, G.W.; Bauer, P. A comparison of the regional Arctic System Reanalysis and the global ERA-Interim Reanalysis for the Arctic. Q. J. R. Meteorol. Soc. 2016, 142, 644–658. [Google Scholar] [CrossRef] [Green Version]
- Deng, M.; Mace, G.G.; Wang, Z.; Okamoto, H. Tropical Composition, Cloud and Climate Coupling Experiment validation for cirrus cloud profiling retrieval using CloudSat radar and CALIPSO lidar. J. Geophys. Res. Atmos. 2010, 115, D00J15. [Google Scholar] [CrossRef] [Green Version]
- Henderson, D.S.; L’Ecuyer, T.; Stephens, G.; Partain, P.; Sekiguchi, M. A multisensor perspective on the radiative impacts of clouds and aerosols. J. Appl. Meteorol. Climatol. 2013, 52, 853–871. [Google Scholar] [CrossRef]
- Deng, M.; Mace, G.G.; Wang, Z.; Lawson, R.P. Evaluation of several A-Train ice cloud retrieval products with in situ measurements collected during the SPARTICUS campaign. J. Appl. Meteorol. Climatol. 2013, 52, 1014–1030. [Google Scholar] [CrossRef] [Green Version]
- Mace, G.G.; Zhang, Q. The CloudSat radar-lidar geometrical profile product (RL-GeoProf): Updates, improvements, and selected results. J. Geophys. Res. Atmos. 2014, 119, 9441–9462. [Google Scholar] [CrossRef]
- Stephens, G.L.; Tsay, S.-C.; Stackhouse, P.W., Jr.; Flatau, P.J. The relevance of the microphysical and radiative properties of cirrus clouds to climate and climatic feedback. J. Atmos. Sci. 1990, 47, 1742–1754. [Google Scholar] [CrossRef]
- Stephens, G.L.; Gabriel, P.M.; Partain, P.T. Parameterization of atmospheric radiative transfer. Part I: Validity of simple models. J. Atmos. Sci. 2001, 58, 3391–3409. [Google Scholar] [CrossRef]
- Beare, R.J.; Macvean, M.K.; Holtslag, A.A.; Cuxart, J.; Esau, I.; Golaz, J.-C.; Jimenez, M.A.; Khairoutdinov, M.; Kosovic, B.; Lewellen, D. An intercomparison of large-eddy simulations of the stable boundary layer. Bound.-Layer Meteorol. 2006, 118, 247–272. [Google Scholar] [CrossRef] [Green Version]
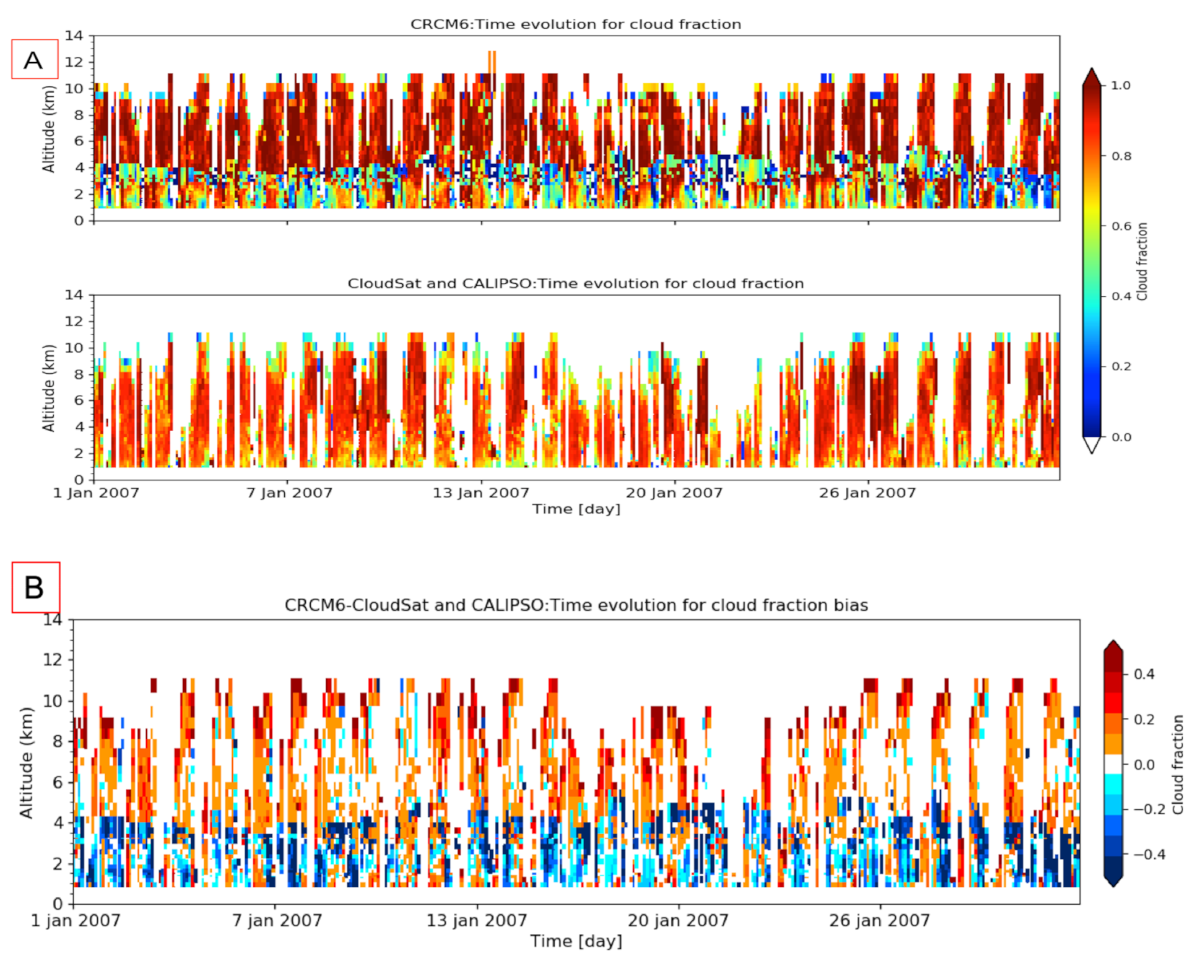
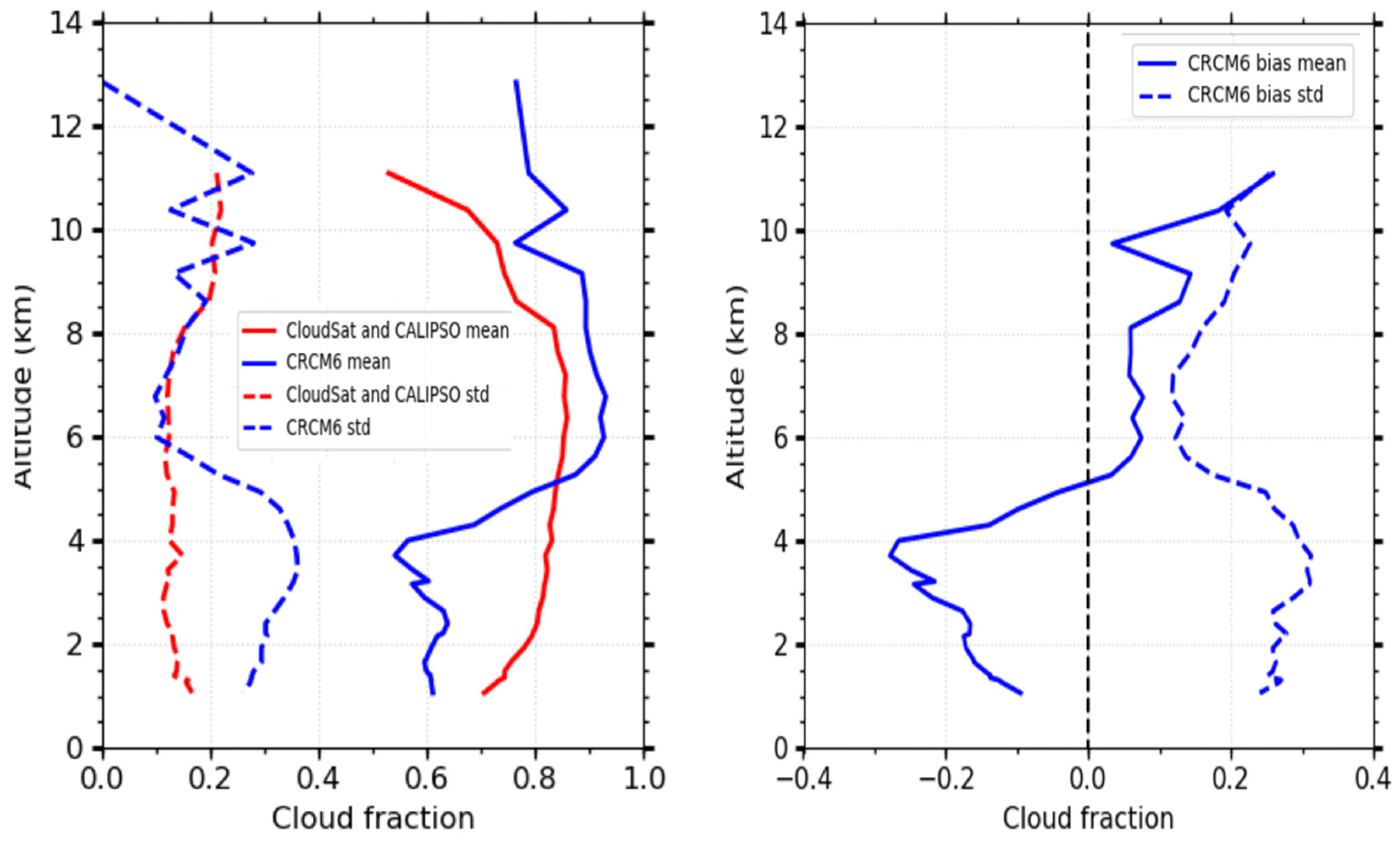
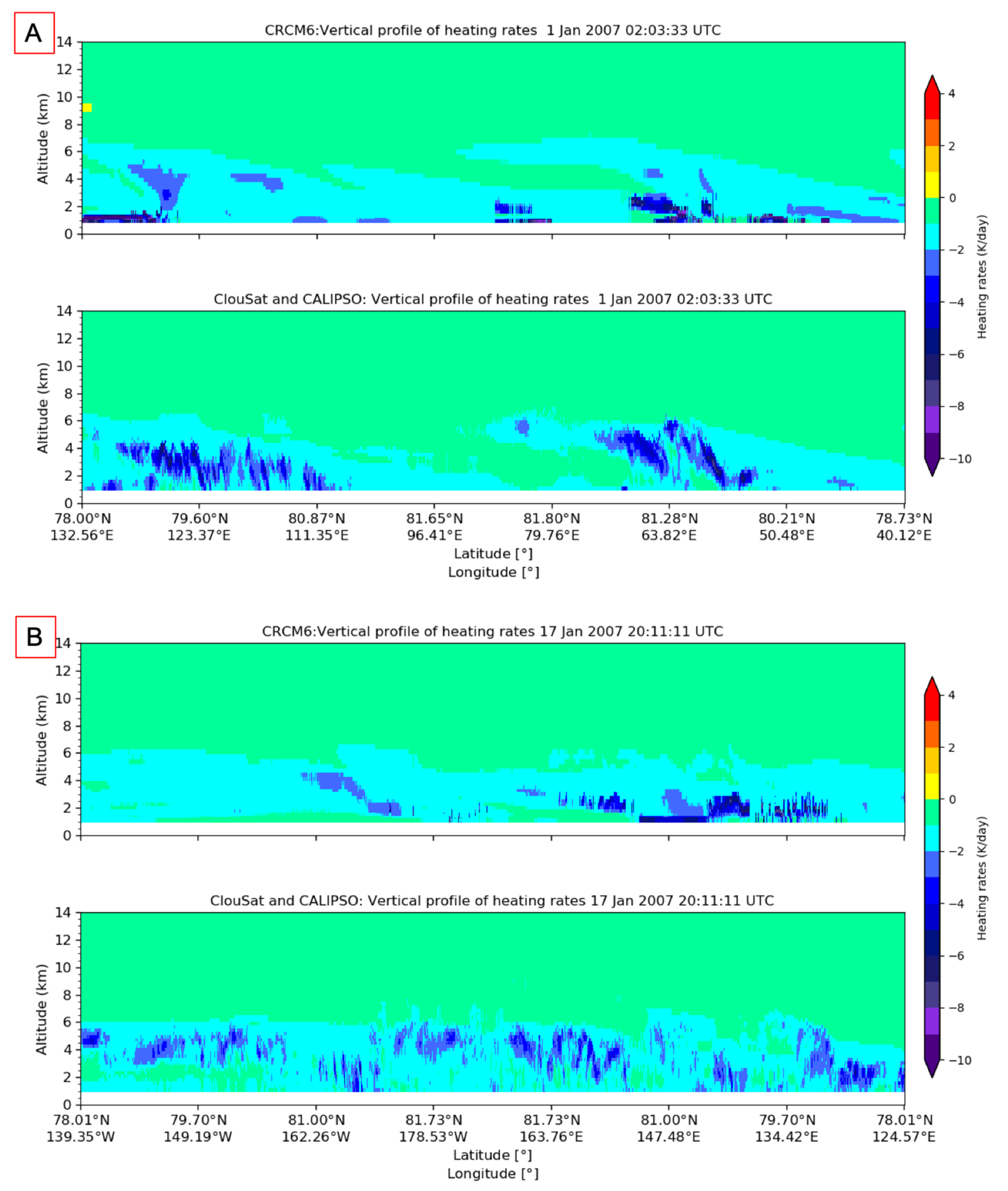

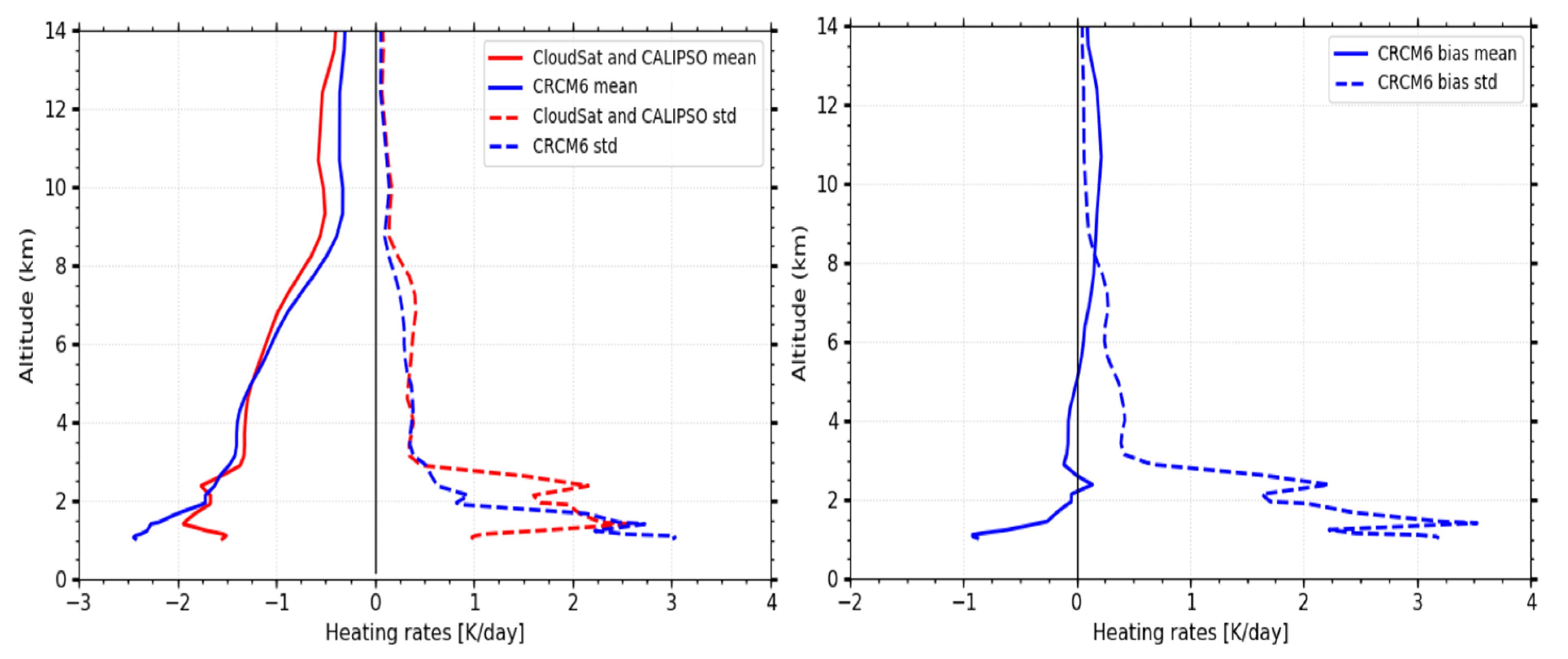
| Products | Instruments | Output Variables | References |
|---|---|---|---|
| 2C-ICE | Radar LiDAR | IWC, effective radius, extinction coefficient | Deng et al. [57]. |
| 2B-FLXHR | Radar | CPR-derived radiative fluxes, diabatic heating rate | L’Ecuyer et al. [17]. |
| 2B-FLXHR-LIDAR | Radar LiDAR | A-train derived, radiative fluxes, diabatic heating rate | Henderson et al. [58] |
| 2B-GEOPROF-LIDAR | Radar LiDAR | Cloud fraction, cloud top, and base | Mace and Zhang [58] |
| Models | ASR | ERA5 | Bias (CRCM6-ASR) | Bias (CRCM6-ERA5) | Bias (ERA5-ASR) | |||||
| Variables | mean | std | mean | std | mean | std | mean | std | mean | std |
| Temperature (°C) | −41.56 | 3.45 | −41.94 | 3.63 | −1.59 | 5.65 | −0.39 | 0.82 | −1.18 | 5.63 |
| Specific humidity (g/Kg) | 0.10 | 0.06 | 0.10 | 0.06 | −0.03 | 0.09 | −0.01 | 0.03 | −0.02 | 0.09 |
| Relative humidity (%) | 47.75 | 15.99 | 33.50 | 17.01 | 0.06 | 23.44 | −1.52 | 12.73 | 1.43 | 21.65 |
| Models | ASR | ERA5 | Bias (CRCM6-ASR) | Bias (CRCM6-ERA5) | Bias (ERA5-ASR) | |||||
| Variables | mean | std | mean | std | mean | std | mean | std | mean | std |
| Temperature (°C) | −25.45 | 4.93 | −21.76 | 4.76 | −5.06 | 6.77 | −0.78 | 1.96 | 0.76 | 6.66 |
| Specific humidity (g/Kg) | 0.56 | 0.33 | 0.56 | 0.29 | −0.11 | 0.51 | −0.05 | 0.18 | −0.07 | 0.49 |
| Relative humidity (%) | 65.55 | 18.36 | 57.61 | 16.06 | −1.67 | 25.73 | −19.71 | 24.02 | −0.19 | 21.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sankaré, H.; Blanchet, J.-P.; Laprise, R.; O’Neill, N.T. Simulation of Arctic Thin Ice Clouds with Canadian Regional Climate Model Version 6: Verification against CloudSat-CALIPSO. Atmosphere 2022, 13, 187. https://doi.org/10.3390/atmos13020187
Sankaré H, Blanchet J-P, Laprise R, O’Neill NT. Simulation of Arctic Thin Ice Clouds with Canadian Regional Climate Model Version 6: Verification against CloudSat-CALIPSO. Atmosphere. 2022; 13(2):187. https://doi.org/10.3390/atmos13020187
Chicago/Turabian StyleSankaré, Housseyni, Jean-Pierre Blanchet, René Laprise, and Norman T. O’Neill. 2022. "Simulation of Arctic Thin Ice Clouds with Canadian Regional Climate Model Version 6: Verification against CloudSat-CALIPSO" Atmosphere 13, no. 2: 187. https://doi.org/10.3390/atmos13020187
APA StyleSankaré, H., Blanchet, J.-P., Laprise, R., & O’Neill, N. T. (2022). Simulation of Arctic Thin Ice Clouds with Canadian Regional Climate Model Version 6: Verification against CloudSat-CALIPSO. Atmosphere, 13(2), 187. https://doi.org/10.3390/atmos13020187





