Detecting the Causal Nexus between Particulate Matter (PM10) and Rainfall in the Caribbean Area
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Data
2.2. Coherence Function
2.3. Causality Framework
2.3.1. Convergent Cross Mapping
2.3.2. Information Transfer
3. Results and Discussion
3.1. Coherence Function Analysis
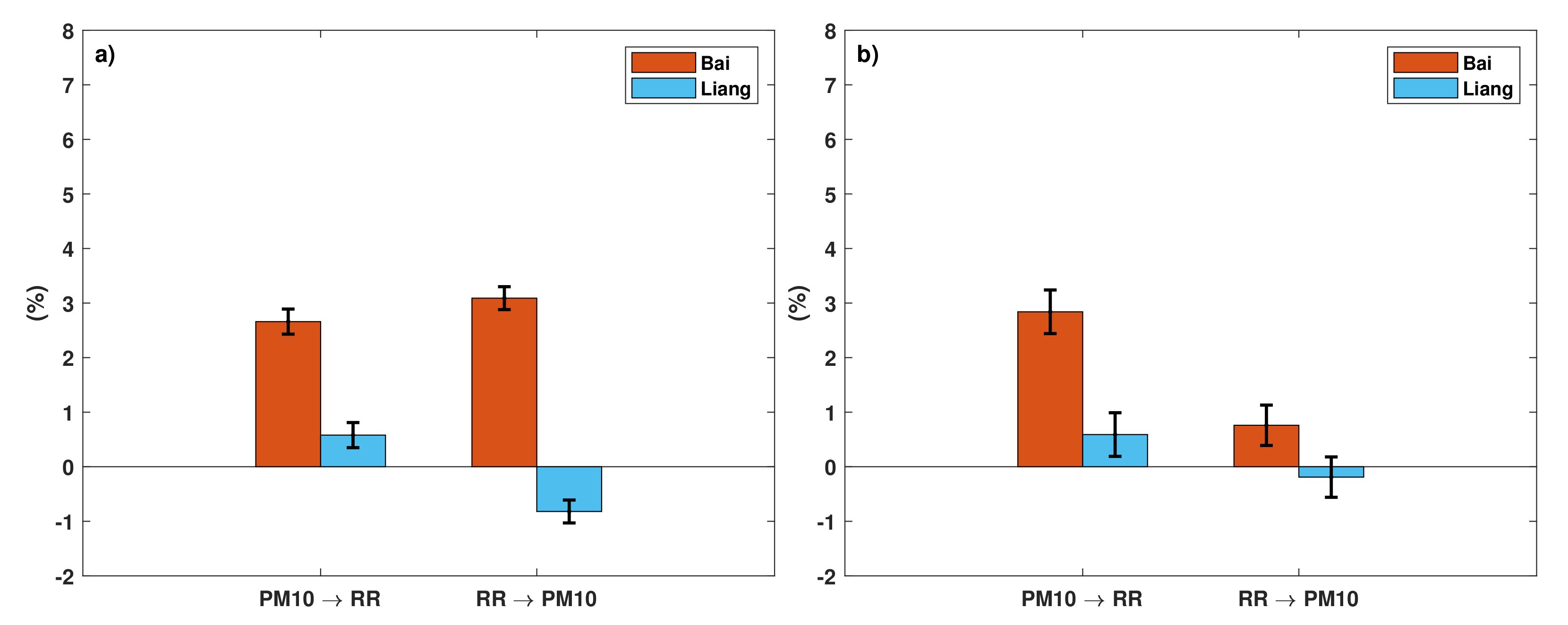
3.2. Causality Analysis
3.2.1. Overall Analysis
3.2.2. Seasonal Analysis
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaufman, Y.J.; Tanré, D.; Boucher, O. A satellite view of aerosols in the climate system. Nature 2002, 419, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Koch, D.; Menon, S.; Del Genio, A.; Ruedy, R.; Alienov, I.; Schmidt, G.A. Distinguishing aerosol impacts on climate over the past century. J. Clim. 2009, 22, 2659–2677. [Google Scholar] [CrossRef][Green Version]
- Rosenfeld, D.; Sherwood, S.; Wood, R.; Donner, L. Climate effects of aerosol-cloud interactions. Science 2014, 343, 379–380. [Google Scholar] [CrossRef] [PubMed]
- Dickerson, R.; Kondragunta, S.; Stenchikov, G.; Civerolo, K.; Doddridge, B.; Holben, B. The impact of aerosols on solar ultraviolet radiation and photochemical smog. Science 1997, 278, 827–830. [Google Scholar] [CrossRef] [PubMed]
- Moosmüller, H.; Chakrabarty, R.; Arnott, W. Aerosol light absorption and its measurement: A review. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 844–878. [Google Scholar] [CrossRef]
- Albrecht, B.A. Aerosols, cloud microphysics, and fractional cloudiness. Science 1989, 245, 1227–1230. [Google Scholar] [CrossRef] [PubMed]
- Andreae, M.; Rosenfeld, D. Aerosol–cloud–precipitation interactions. Part 1. The nature and sources of cloud-active aerosols. Earth-Sci. Rev. 2008, 89, 13–41. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Y.; Rosenfeld, D.; Liu, X. Review of aerosol–cloud interactions: Mechanisms, significance, and challenges. J. Atmos. Sci. 2016, 73, 4221–4252. [Google Scholar] [CrossRef]
- Li, Z.; Lau, W.M.; Ramanathan, V.; Wu, G.; Ding, Y.; Manoj, M.; Liu, J.; Qian, Y.; Li, J.; Zhou, T.; et al. Aerosol and monsoon climate interactions over Asia. Rev. Geophys. 2016, 54, 866–929. [Google Scholar] [CrossRef]
- Twomey, S. The influence of pollution on the shortwave albedo of clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef]
- Rosenfeld, D. TRMM observed first direct evidence of smoke from forest fires inhibiting rainfall. Geophys. Res. Lett. 1999, 26, 3105–3108. [Google Scholar] [CrossRef]
- Prospero, J.M.; Collard, F.X.; Molinié, J.; Jeannot, A. Characterizing the annual cycle of African dust transport to the Caribbean Basin and South America and its impact on the environment and air quality. Glob. Biogeochem. Cycles 2014, 28, 757–773. [Google Scholar] [CrossRef]
- Clergue, C.; Dellinger, M.; Buss, H.; Gaillardet, J.; Benedetti, M.; Dessert, C. Influence of atmospheric deposits and secondary minerals on Li isotopes budget in a highly weathered catchment, Guadeloupe (Lesser Antilles). Chem. Geol. 2015, 414, 28–41. [Google Scholar] [CrossRef]
- Rastelli, E.; Corinaldesi, C.; Dell’Anno, A.; Martire, M.L.; Greco, S.; Facchini, M.C.; Rinaldi, M.; O’Dowd, C.; Ceburnis, D.; Danovaro, R. Transfer of labile organic matter and microbes from the ocean surface to the marine aerosol: An experimental approach. Sci. Rep. 2017, 7, 11475. [Google Scholar] [CrossRef]
- Euphrasie-Clotilde, L.; Plocoste, T.; Feuillard, T.; Velasco-Merino, C.; Mateos, D.; Toledano, C.; Brute, F.N.; Bassette, C.; Gobinddass, M. Assessment of a new detection threshold for PM10 concentrations linked to African dust events in the Caribbean Basin. Atmos. Environ. 2020, 224, 117354. [Google Scholar] [CrossRef]
- Artíñano, B.; Salvador, P.; Alonso, D.G.; Querol, X.; Alastuey, A. Anthropogenic and natural influence on the PM10 and PM2.5 aerosol in Madrid (Spain). Analysis of high concentration episodes. Environ. Pollut. 2003, 125, 453–465. [Google Scholar] [CrossRef]
- Lewis, E.R.; Schwartz, S.E. Sea Salt Aerosol Production: Mechanisms, Methods, Measurements, and Models—A Critical Review; American Geophysical Union: Washington, DC, USA, 2004; Volume 152. [Google Scholar]
- Schulz, M.; de Leeuw, G.; Balkanski, Y. Sea-salt aerosol source functions and emissions. In Emissions of Atmospheric Trace Compounds; Springer: Berlin/Heidelberg, Germany, 2004; pp. 333–359. [Google Scholar]
- Prospero, J.M.; Delany, A.C.; Delany, A.C.; Carlson, T.N. The Discovery of African Dust Transport to the Western Hemisphere and the Saharan Air Layer: A History. Bull. Am. Meteorol. Soc. 2021, 102, E1239–E1260. [Google Scholar] [CrossRef]
- Prospero, J.M.; Carlson, T.N. Vertical and areal distribution of Saharan dust over the western equatorial North Atlantic Ocean. J. Geophys. Res. 1972, 77, 5255–5265. [Google Scholar] [CrossRef]
- Tsamalis, C.; Chédin, A.; Pelon, J.; Capelle, V. The seasonal vertical distribution of the Saharan Air Layer and its modulation by the wind. Atmos. Chem. Phys. 2013, 13, 11235–11257. [Google Scholar] [CrossRef]
- Petit, R.; Legrand, M.; Jankowiak, I.; Molinié, J.; Asselin de Beauville, C.; Marion, G.; Mansot, J. Transport of Saharan dust over the Caribbean Islands: Study of an event. J. Geophys. Res. Atmos. 2005, 110, D18S09. [Google Scholar] [CrossRef]
- Jury, M.R.; Jiménez, A.T.N. Tropical Atlantic dust and the zonal circulation. Theor. Appl. Climatol. 2021, 143, 901–913. [Google Scholar] [CrossRef]
- Schepanski, K. Transport of mineral dust and its impact on climate. Geosciences 2018, 8, 151. [Google Scholar] [CrossRef]
- Does, M.V.D.; Korte, L.F.; Munday, C.I.; Brummer, G.J.A.; Stuut, J.B.W. Particle size traces modern Saharan dust transport and deposition across the equatorial North Atlantic. Atmos. Chem. Phys. 2016, 16, 13697–13710. [Google Scholar] [CrossRef]
- Mahowald, N.; Albani, S.; Kok, J.F.; Engelstaeder, S.; Scanza, R.; Ward, D.S.; Flanner, M.G. The size distribution of desert dust aerosols and its impact on the Earth system. Aeolian Res. 2014, 15, 53–71. [Google Scholar] [CrossRef]
- Velasco-Merino, C.; Mateos, D.; Toledano, C.; Prospero, J.M.; Molinie, J.; Euphrasie-Clotilde, L.; González, R.; Cachorro, V.E.; Calle, A.; Frutos, A.M.d. Impact of long-range transport over the Atlantic Ocean on Saharan dust optical and microphysical properties based on AERONET data. Atmos. Chem. Phys. 2018, 18, 9411–9424. [Google Scholar] [CrossRef]
- Plocoste, T.; Calif, R.; Jacoby-Koaly, S. Temporal multiscaling characteristics of particulate matter PM10 and ground-level ozone O3 concentrations in Caribbean region. Atmos. Environ. 2017, 169, 22–35. [Google Scholar] [CrossRef]
- Cujia, A.; Agudelo-Castañeda, D.; Pacheco-Bustos, C.; Teixeira, E.C. Forecast of PM10 time-series data: A study case in Caribbean cities. Atmos. Pollut. Res. 2019, 10, 2053–2062. [Google Scholar] [CrossRef]
- Mauger, G.S.; Norris, J.R. Meteorological bias in satellite estimates of aerosol-cloud relationships. Geophys. Res. Lett. 2007, 34, 16. [Google Scholar] [CrossRef]
- Myhre, G.; Stordal, F.; Johnsrud, M.; Kaufman, Y.; Rosenfeld, D.; Storelvmo, T.; Kristjansson, J.E.; Berntsen, T.K.; Myhre, A.; Isaksen, I.S. Aerosol-cloud interaction inferred from MODIS satellite data and global aerosol models. Atmos. Chem. Phys. 2007, 7, 3081–3101. [Google Scholar] [CrossRef]
- Costantino, L.; Bréon, F.M. Analysis of aerosol-cloud interaction from multi-sensor satellite observations. Geophys. Res. Lett. 2010, 37, 11. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Bretherton, C.; Carslaw, K.S.; Coe, H.; DeMott, P.J.; Dunlea, E.J.; Feingold, G.; Ghan, S.; Guenther, A.B.; Kahn, R.; et al. Improving our fundamental understanding of the role of aerosol- cloud interactions in the climate system. Proc. Natl. Acad. Sci. USA 2016, 113, 5781–5790. [Google Scholar] [CrossRef]
- Wehbe, Y.; Tessendorf, S.A.; Weeks, C.; Bruintjes, R.; Xue, L.; Rasmussen, R.; Lawson, P.; Woods, S.; Temimi, M. Analysis of aerosol–cloud interactions and their implications for precipitation formation using aircraft observations over the United Arab Emirates. Atmos. Chem. Phys. 2021, 21, 12543–12560. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.h.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef]
- San Liang, X. Unraveling the cause-effect relation between time series. Phys. Rev. E 2014, 90, 052150. [Google Scholar] [CrossRef]
- Bai, C.; Zhang, R.; Bao, S.; San Liang, X.; Guo, W. Forecasting the tropical cyclone genesis over the Northwest Pacific through identifying the causal factors in cyclone–climate interactions. J. Atmos. Ocean. Technol. 2018, 35, 247–259. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Plocoste, T.; Calif, R.; Jacoby-Koaly, S. Multi-scale time dependent correlation between synchronous measurements of ground-level ozone and meteorological parameters in the Caribbean Basin. Atmos. Environ. 2019, 211, 234–246. [Google Scholar] [CrossRef]
- Bertin, A.; Frangi, J. Contribution to the study of the wind and solar radiation over Guadeloupe. Energy Convers. Manag. 2013, 75, 593–602. [Google Scholar] [CrossRef]
- Plocoste, T.; Pavón-Domínguez, P. Multifractal detrended cross-correlation analysis of wind speed and solar radiation. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 113109. [Google Scholar] [CrossRef]
- Winstanley, D. Rainfall patterns and general atmospheric circulation. Nature 1973, 245, 190–194. [Google Scholar] [CrossRef]
- Johnson, R.H.; Ciesielski, P.E. Rainfall and radiative heating rates from TOGA COARE atmospheric budgets. J. Atmos. Sci. 2000, 57, 1497–1514. [Google Scholar] [CrossRef]
- Plocoste, T.; Carmona-Cabezas, R.; Gutiérrez de Ravé, E.; Jimnez-Hornero, F.J. Wet scavenging process of particulate matter (PM10): A multivariate complex network approach. Atmos. Pollut. Res. 2021, 12, 101095. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; Tata McGraw-Hill Education: New York, NY, USA, 2002. [Google Scholar]
- Calif, R.; Schmitt, F.G. Multiscaling and joint multiscaling description of the atmospheric wind speed and the aggregate power output from a wind farm. Nonlinear Process. Geophys. 2014, 21, 379–392. [Google Scholar] [CrossRef]
- Liu, H.; Lei, M.; Zhang, N.; Du, G. The causal nexus between energy consumption, carbon emissions and economic growth: New evidence from China, India and G7 countries using convergent cross mapping. PLoS ONE 2019, 14, e0217319. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Sugihara, G.; May, R.M. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 1990, 344, 734–741. [Google Scholar] [CrossRef] [PubMed]
- Clark, A.T.; Ye, H.; Isbell, F.; Deyle, E.R.; Cowles, J.; Tilman, G.D.; Sugihara, G. Spatial convergent cross mapping to detect causal relationships from short time series. Ecology 2015, 96, 1174–1181. [Google Scholar] [CrossRef] [PubMed]
- San Liang, X. Information flow within stochastic dynamical systems. Phys. Rev. E 2008, 78, 031113. [Google Scholar] [CrossRef] [PubMed]
- San Liang, X. The Liang-Kleeman information flow: Theory and applications. Entropy 2013, 15, 327–360. [Google Scholar] [CrossRef]
- Plocoste, T.; Calif, R. Is there a causal relationship between Particulate Matter (PM10) and air Temperature data? An analysis based on the Liang–Kleeman information transfer theory. Atmos. Pollut. Res. 2021, 12, 101177. [Google Scholar] [CrossRef]
- San Liang, X. Normalizing the causality between time series. Phys. Rev. E 2015, 92, 022126. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, B.; Cai, J.; Gao, B. Understanding temporal patterns and characteristics of air quality in Beijing: A local and regional perspective. Atmos. Environ. 2016, 127, 303–315. [Google Scholar] [CrossRef]
- Ye, H.; Deyle, E.R.; Gilarranz, L.J.; Sugihara, G. Distinguishing time-delayed causal interactions using convergent cross mapping. Sci. Rep. 2015, 5, 14750. [Google Scholar] [CrossRef]
- Wallot, S.; Mønster, D. Calculation of Average Mutual Information (AMI) and False-Nearest Neighbors (FNN) for the estimation of embedding parameters of multidimensional time series in Matlab. Front. Psychol. 2018, 9, 1679. [Google Scholar] [CrossRef]
- Pillai, P.S.; Babu, S.S.; Moorthy, K.K. A study of PM, PM10 and PM2.5 concentration at a tropical coastal station. Atmos. Res. 2002, 61, 149–167. [Google Scholar] [CrossRef]
- Bayraktar, H.; Turalioğlu, F.S.; Tuncel, G. Average mass concentrations of TSP, PM10 and PM2.5 in Erzurum urban atmosphere, Turkey. Stoch. Environ. Res. Risk Assess. 2010, 24, 57–65. [Google Scholar] [CrossRef]
- Sonwani, S.; Kulshrestha, U.C. PM10 carbonaceous aerosols and their real-time wet scavenging during monsoon and non-monsoon seasons at Delhi, India. J. Atmos. Chem. 2019, 76, 171–200. [Google Scholar] [CrossRef]
- Tiwari, S.; Chate, D.; Pragya, P.; Ali, K.; Bisht, D.S. Variations in mass of the PM10, PM2.5 and PM 1 during the monsoon and the winter at New Delhi. Aerosol Air Qual. Res. 2012, 12, 20–29. [Google Scholar]
- Murakami, M.; Kimura, T.; Magono, C.; Kikuchi, K. Observations of precipitation scavenging for water-soluble particles. J. Meteorol. Soc. Jpn. Ser. II 1983, 61, 346–358. [Google Scholar] [CrossRef][Green Version]
- Schumann, T. Large discrepancies between theoretical and field-determined scavenging coefficients. J. Aerosol Sci. 1989, 20, 1159–1162. [Google Scholar] [CrossRef]
- McClintock, M.; McDowell, W.; González, G.; Schulz, M.; Pett-Ridge, J. African dust deposition in Puerto Rico: Analysis of a 20-year rainfall chemistry record and comparison with models. Atmos. Environ. 2019, 216, 116907. [Google Scholar] [CrossRef]
- Plocoste, T.; Calif, R.; Euphrasie-Clotilde, L.; Brute, F.N. Investigation of local correlations between particulate matter (PM10) and air temperature in the Caribbean basin using Ensemble Empirical Mode Decomposition. Atmos. Pollut. Res. 2020, 11, 1692–1704. [Google Scholar] [CrossRef]
- Plocoste, T.; Pavón-Domínguez, P. Temporal scaling study of particulate matter (PM10) and solar radiation influences on air temperature in the Caribbean basin using a 3D joint multifractal analysis. Atmos. Environ. 2020, 222, 117115. [Google Scholar] [CrossRef]
- Plocoste, T. Multiscale analysis of the dynamic relationship between particulate matter (PM10) and meteorological parameters using CEEMDAN: A focus on “Godzilla” African dust event. Atmos. Pollut. Res. 2022, 13, 101252. [Google Scholar] [CrossRef]
- Sherwood, S.C. Aerosols and ice particle size in tropical cumulonimbus. J. Clim. 2002, 15, 1051–1063. [Google Scholar] [CrossRef]
- Kristensen, T.B.; Müller, T.; Kandler, K.; Benker, N.; Hartmann, M.; Prospero, J.M.; Wiedensohler, A.; Stratmann, F. Properties of cloud condensation nuclei (CCN) in the trade wind marine boundary layer of the western North Atlantic. Atmos. Chem. Phys. 2016, 16, 2675–2688. [Google Scholar] [CrossRef]
- Plocoste, T.; Calif, R. Spectral Observations of PM10 Fluctuations in the Hilbert Space. In Functional Calculus; IntechOpen: London, UK, 2019; pp. 1–13. [Google Scholar]
- Plocoste, T.; Calif, R.; Euphrasie-Clotilde, L.; Brute, F.N. The statistical behavior of PM10 events over guadeloupean archipelago: Stationarity, modelling and extreme events. Atmos. Res. 2020, 241, 104956. [Google Scholar] [CrossRef]
- Plocoste, T.; Carmona-Cabezas, R.; Jiménez-Hornero, F.J.; Gutiérrez de Ravé, E.; Calif, R. Multifractal characterisation of particulate matter (PM10) time series in the Caribbean basin using visibility graphs. Atmos. Pollut. Res. 2021, 12, 100–110. [Google Scholar] [CrossRef]
- Martinez, C.; Goddard, L.; Kushnir, Y.; Ting, M. Seasonal climatology and dynamical mechanisms of rainfall in the Caribbean. Clim. Dyn. 2019, 53, 825–846. [Google Scholar] [CrossRef]
- Martinez, C.; Kushnir, Y.; Goddard, L.; Ting, M. Interannual variability of the early and late-rainy seasons in the Caribbean. Clim. Dyn. 2020, 55, 1563–1583. [Google Scholar] [CrossRef]
- Windsor, H.; Toumi, R. Scaling and persistence of UK pollution. Atmos. Environ. 2001, 35, 4545–4556. [Google Scholar] [CrossRef]
- Plocoste, T.; Dorville, J.F.; Monjoly, S.; Jacoby-Koaly, S.; André, M. Assessment of Nitrogen Oxides and Ground-Level Ozone behavior in a dense air quality station network: Case study in the Lesser Antilles Arc. J. Air Waste Manag. Assoc. 2018, 68, 1278–1300. [Google Scholar] [CrossRef]
- Euphrasie-Clotilde, L.; Plocoste, T.; Brute, F.N. Particle Size Analysis of African Dust Haze over the Last 20 Years: A Focus on the Extreme Event of June 2020. Atmosphere 2021, 12, 502. [Google Scholar] [CrossRef]
- Gavrouzou, M.; Hatzianastassiou, N.; Gkikas, A.; Korras-Carraca, M.B.; Mihalopoulos, N. A global climatology of dust aerosols based on satellite data: Spatial, seasonal and inter-annual patterns over the period 2005–2019. Remote. Sens. 2021, 13, 359. [Google Scholar] [CrossRef]
- Rosenfeld, D. Smoke and desert dust stifle rainfall, contribute to drought and desertification. Arid. News Lett. 2001, 49, 265. [Google Scholar]
- Rosenfeld, D.; Rudich, Y.; Lahav, R. Desert dust suppressing precipitation: A possible desertification feedback loop. Proc. Natl. Acad. Sci. USA 2001, 98, 5975–5980. [Google Scholar] [CrossRef]
- Tartaglione, C.A.; Smith, S.R.; O’Brien, J.J. ENSO impact on hurricane landfall probabilities for the Caribbean. J. Clim. 2003, 16, 2925–2931. [Google Scholar] [CrossRef]
- Dunion, J.P. Rewriting the climatology of the tropical North Atlantic and Caribbean Sea atmosphere. J. Clim. 2011, 24, 893–908. [Google Scholar] [CrossRef]
- Karyampudi, V.M.; Palm, S.P.; Reagen, J.A.; Fang, H.; Grant, W.B.; Hoff, R.M.; Moulin, C.; Pierce, H.F.; Torres, O.; Browell, E.V.; et al. Validation of the Saharan dust plume conceptual model using lidar, Meteosat, and ECMWF data. Bull. Am. Meteorol. Soc. 1999, 80, 1045–1076. [Google Scholar] [CrossRef]
- Plocoste, T.; Carmona-Cabezas, R.; Jiménez-Hornero, F.J.; Gutiérrez de Ravé, E. Background PM10 atmosphere: In the seek of a multifractal characterization using complex networks. J. Aerosol Sci. 2021, 155, 105777. [Google Scholar] [CrossRef]
- Zuidema, P.; Alvarez, C.; Kramer, S.J.; Custals, L.; Izaguirre, M.; Sealy, P.; Prospero, J.M.; Blades, E. Is summer African dust arriving earlier to Barbados? The updated long-term in situ dust mass concentration time series from Ragged Point, Barbados, and Miami, Florida. Bull. Am. Meteorol. Soc. 2019, 100, 1981–1986. [Google Scholar] [CrossRef]
- Negral, L.; Moreno-Grau, S.; Moreno, J.; Querol, X.; Viana, M.; Alastuey, A. Natural and anthropogenic contributions to PM10 and PM2.5 in an urban area in the western Mediterranean coast. Water Air Soil Pollut. 2008, 192, 227–238. [Google Scholar] [CrossRef]
- Perez, L.; Tobias, A.; Querol, X.; Künzli, N.; Pey, J.; Alastuey, A.; Viana, M.; Valero, N.; González-Cabré, M.; Sunyer, J. Coarse particles from Saharan dust and daily mortality. Epidemiology 2008, 19, 800–807. [Google Scholar] [CrossRef] [PubMed]
- Vanderstraeten, P.; Lénelle, Y.; Meurrens, A.; Carati, D.; Brenig, L.; Delcloo, A.; Offer, Z.Y.; Zaady, E. Dust storm originate from Sahara covering Western Europe: A case study. Atmos. Environ. 2008, 42, 5489–5493. [Google Scholar] [CrossRef]
- Yao, X.; Fang, M.; Chan, C.K.; Ho, K.; Lee, S. Characterization of dicarboxylic acids in PM2.5 in Hong Kong. Atmos. Environ. 2004, 38, 963–970. [Google Scholar] [CrossRef]
- Huang, G.; Cheng, T.; Zhang, R.; Tao, J.; Leng, C.; Zhang, Y.; Zha, S.; Zhang, D.; Li, X.; Xu, C. Optical properties and chemical composition of PM2.5 in Shanghai in the spring of 2012. Particuology 2014, 13, 52–59. [Google Scholar] [CrossRef]
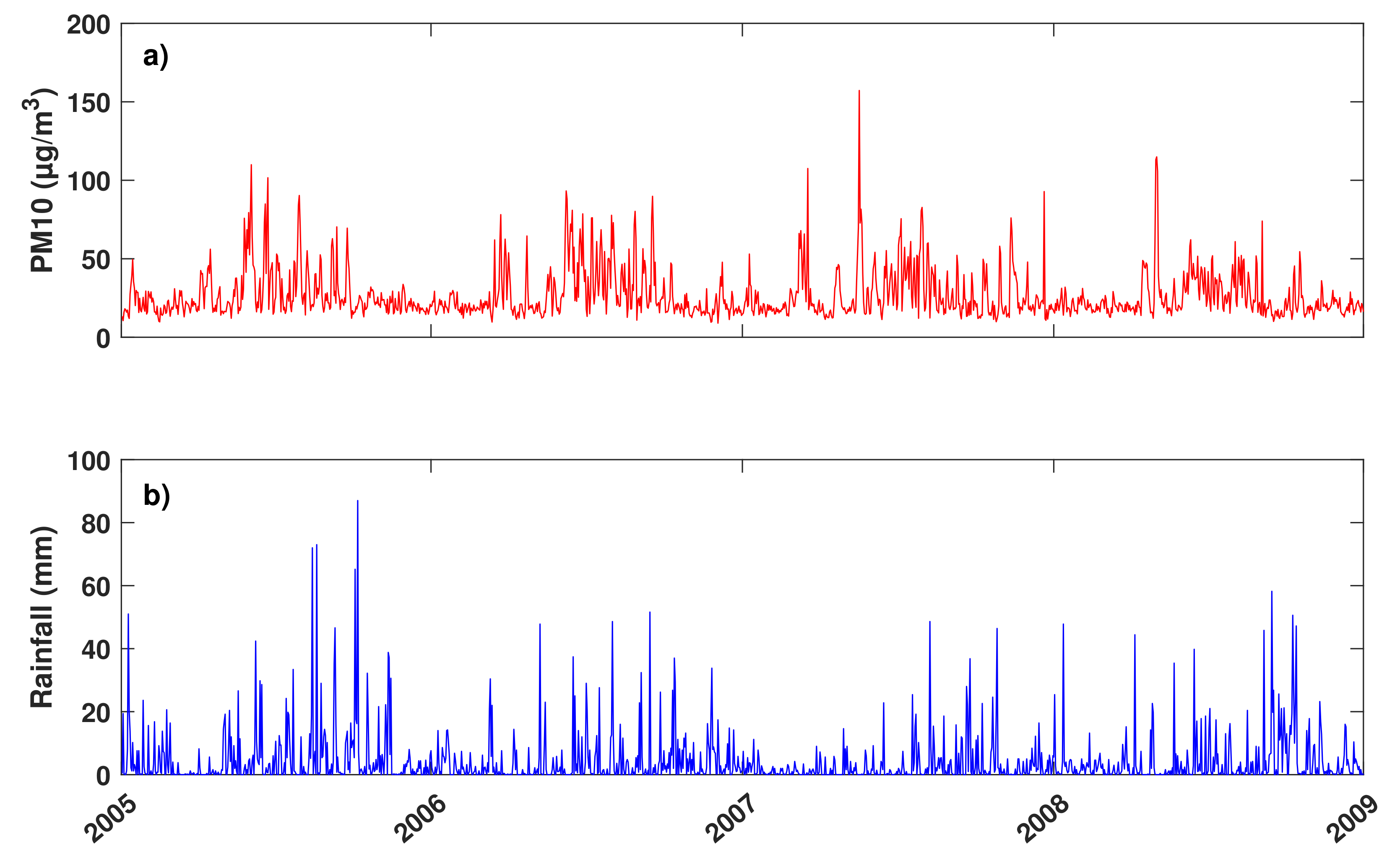






| Study Period | (g/m) | (g/m) | (mm) | (mm) | ||
| Overall (N = 3847) | 26.5 | 16.1 | 11.8 | 4.3 | 9.9 | 102.9 |
| Low dust season (N = 2250) | 22.0 | 12.2 | 33.9 | 3.8 | 8.3 | 59.0 |
| High dust season (N = 1597) | 32.8 | 18.5 | 5.9 | 5.0 | 11.8 | 103.3 |
| Dry season (N = 2244) | 25.8 | 16.2 | 13.9 | 3.3 | 8.9 | 231.4 |
| Wet season (N = 1603) | 27.5 | 15.9 | 9.09 | 5.6 | 11.1 | 25.6 |
| High dust dry season (N = 652) | 35.0 | 21.0 | 6.1 | 4.4 | 12.4 | 180.0 |
| High dust wet season (N = 945) | 31.4 | 16.5 | 4.0 | 5.4 | 11.3 | 28.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plocoste, T. Detecting the Causal Nexus between Particulate Matter (PM10) and Rainfall in the Caribbean Area. Atmosphere 2022, 13, 175. https://doi.org/10.3390/atmos13020175
Plocoste T. Detecting the Causal Nexus between Particulate Matter (PM10) and Rainfall in the Caribbean Area. Atmosphere. 2022; 13(2):175. https://doi.org/10.3390/atmos13020175
Chicago/Turabian StylePlocoste, Thomas. 2022. "Detecting the Causal Nexus between Particulate Matter (PM10) and Rainfall in the Caribbean Area" Atmosphere 13, no. 2: 175. https://doi.org/10.3390/atmos13020175
APA StylePlocoste, T. (2022). Detecting the Causal Nexus between Particulate Matter (PM10) and Rainfall in the Caribbean Area. Atmosphere, 13(2), 175. https://doi.org/10.3390/atmos13020175






