Correction to a Simple Biosphere Model 2 (SiB2) Simulation of Energy and Carbon Dioxide Fluxes over a Wheat Cropland in East China Using the Random Forest Model

Abstract

Modeling the heat and carbon dioxide (CO₂) exchanges in agroecosystems is critical for better understanding water and carbon cycling, improving crop production, and even mitigating climate change, in agricultural regions. While previous studies mainly focused on simulations of the energy and CO₂ fluxes in agroecosystems on the North China Plain, their corrections, simulations and driving forces in East China are less understood. In this study, the dynamic variations of heat and CO₂ fluxes were simulated by a standalone version of the Simple Biosphere 2 (SiB2) model and subsequently corrected using a Random Forest (RF) machine learning model, based on measurements from 1 January to 31 May 2015–2017 in eastern China. Through validation with direct measurements, it was found that the SiB2 model overestimated the sensible heat flux (H) and latent heat flux (LE), but underestimated soil heat flux (G₀) and CO₂ flux (F_c). Thus, the RF model was used to correct the results modeled by SiB2. The RF model showed that disturbances in temperature, net radiation, the G₀ output of SiB2, and the F_c output of SiB2 were the key driving factors modulating the H, LE, G₀, and F_c. The RF model performed well and significantly reduced the biases for H, LE, G₀, and F_c simulated by SiB2, with higher R² values of 0.99, 0.87, 0.75, and 0.71, respectively. The SiB2 and RF models combine physical mechanisms and mathematical correction to enable simulations with both physical meaning and accuracy.

1. Introduction

Land surface processes modulate the weather and climate primarily through the exchange of energy, momentum, water, and carbon dioxide (CO₂) across the atmospheric boundary layer [1,2,3,4,5]. Climate simulations are especially sensitive to the temporal characteristics in the energy partitioning of available energy into sensible heat (H) and latent heat (LE) fluxes [6,7,8]. Therefore, investigating the diurnal and seasonal variations of land-atmosphere interactions is important for improving boundary layer parameterization schemes and the precision of weather predictions [7].

To deepen our understanding of the surface–atmosphere exchanges of water, surface energy, and CO₂ fluxes, numerous measurement methods [e.g., the Bowen ratio–energy balance method, the eddy covariance (EC) method, and the scintillometer method] have been applied [2]. Among them, the EC technique is considered to be the most direct and trustworthy method to obtain data on soil–plant–atmosphere carbon, water, and energy fluxes [9,10]. However, rainy days and power outages can cause data losses [11]. Accordingly, a powerful way to obtain accurate flux variations is to model the fluxes using reliable surface models, while evaluating the outputs against observed data [12,13].

Land surface process models have broadly experienced four main stages of development [14,15,16]. To begin with, the simple “bucket” model was proposed by Manabe [17], in which all the land surface parameters were set to fixed values. Next, the biosphere transfer scheme [18] and the simple biosphere (SiB) model [19] were proposed, which took into account the role of vegetation in the land surface process. Then, version two of the SiB model (SiB2) was developed [20,21] which introduced a vegetation biochemical process, including photosynthesis and respiration. Finally, in the most recent stage of development, models that can simulate the process of dynamic vegetation changes have emerged [22], such as the dynamic land ecosystem model [23], albeit there have as yet been relatively fewer applications of them in these types of models owing to their reliance on extremely highly complex physical inner mechanisms [16]. Furthermore, there are also models used to investigate and evaluate the environmental impact of energy production or consumption processes, such as life cycle assessment [24,25]. SiB2, a widely used land surface model, is expected to continue to gain importance as a surface flux simulation method. Previous studies have used SiB2 to investigate the water, energy, and CO₂ fluxes over different underlying surfaces, and verified them with observations [4,7,12,14,26,27,28,29,30]. Most such investigations found that the processes of dynamic vegetation changes could not be reflected. There has also been some research carried out into revising SiB2 by correcting its fixed parameters [2,3] and physical equations [31] to address biases that arise from the model’s complexity and diversity of study area and vegetation. However, few studies have used machine learning algorithms to correct the outputs of SiB2.

With the development of machine learning, more and more researchers have used this approach to correct the biases of models [32]. For example, the European Center for Medium-Range Weather Forecasts model [33,34,35,36], the Weather Research and Forecasting model [37], land surface models such as ORCHIDEE (organising carbon and hydrology in dynamic ecosystems) [38], and that of Abramowitz et al. [39]. Recently, the random forest (RF) model has become a popular machine learning technique owing to its success in selecting and ranking numerous predictor variables [40]. Several works have investigated land surface processes with the RF model, such as the exchange of energy [41] and CO₂ [42,43], and obtained satisfactory results. Accordingly, there is reason to believe that the RF model could also be a promising method to correct SiB2 outputs. In addition, the energy and CO₂ exchanges simulated by SiB2 have tended to focus on forests and grasslands, with relatively less concern for agroecosystems, especially plains regions and different species of wheat [1,4,12,14,44]. In China, the only simulations of agroecosystems have focused on North and Northeast China [45]. Considerable uncertainty remains as to the current performance of simulations in East China.

East China is one of the country’s main grain-producing areas, with wheat and rice being the primary crops. The wheat-field ecosystem, as a key component of the broader terrestrial ecosystem, is important for investigating global-scale ecology, energy balances, and regional climate [46]. At the same time, rapid urbanization and economic development are prominent features in East China, both of which can modify nearby surface energy exchanges and the boundary layer structure [47,48]. Consequently, accurate simulation of the fluxes of surface energy and CO₂ for the wheat-field ecosystem in East China will help to better understand energy and carbon budgets, more accurately assess the influence of climate change, and increase crop production [31]. The objectives of the present work were to: (1) quantify the seasonal and diurnal variations in radiation, H, LE, and CO₂ fluxes; (2) compare the radiation, turbulence, soil heat, and CO₂ fluxes modeled by SiB2 against direct measurements; and (3) correct the outputs of the SiB2 model using RF machine learning algorithms.

2. Materials and Methods

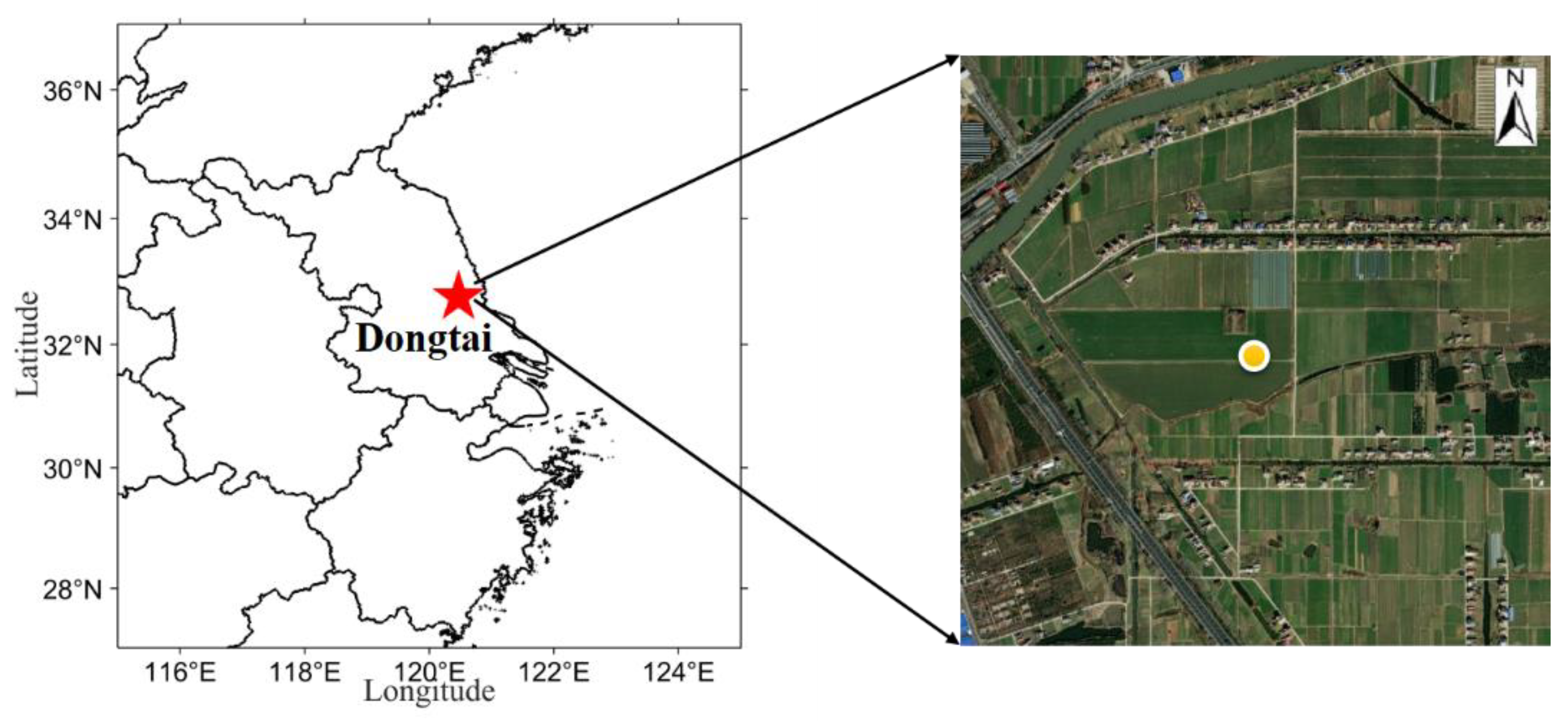
2.1. Site Description

The experiment was conducted at a 300 m × 300 m wheat field in Dongtai County, Jiangsu Province, China (32.76° N, 120.47° E; 2 m above sea level; Figure 1) from January to May 2015–2017. The site was relatively flat and homogeneous, with a clay soil texture. The climate is classed as “subtropical monsoon”, with an annual mean (1951–2015) air temperature of approximately 14.8 °C and rainfall of 1063 mm [49]. Meanwhile, the average annual sunshine duration and frost-free period are 2213 h and 220 days, respectively [50]. During the observation period, the “Yangmai 16” variety of winter wheat was planted around the EC tower. The wheat grew in good drainage and no silt soil conditions. Nitrogen fertilizer (urea) was applied at 180 kg ha⁻¹. The wheat growing season was divided into the vegetative stage (15 December–28 February), reproductive stage (1 March–15 April), and ripening stage (16 April–31 May) [10].

2.2. Instruments and Data Processing

The H, LE, and CO₂ fluxes were collected from an EC tower at 10-m above ground level (AGL), which consisted of a three-dimensional sonic anemometer (Campbell Scientific, Inc., UT, USA, CSAT3) and a CO₂/H₂O open path gas analyzer (LI-COR Biosciences, Inc., NE, USA, LI-7500). Downward shortwave/longwave and upward shortwave/longwave radiation measurements were obtained from a four-component net radiometer (Kipp and Zonen, Inc., CNR-4) at 3-m AGL. The air temperature, humidity (Vaisala, Inc., Helsinki, HMP45A), and wind speed (Met One, Inc., 034B) were measured at 3, 5, 8, and 10-m AGL. The soil heat flux (Hukseflux Thermal Sensors, Netherlands, HFP01), soil temperature (Campbell Scientific PT100), and soil water content (Campbell Scientific CS616) observations were collected at depths of 0.05, 0.1, 0.2, and 0.4-m. The data were averaged over 30-min intervals. In addition, the surface atmospheric pressure (Vaisala, Helsinki, PTB110) and precipitation (Campbell Scientific TE525MM) were also measured. More details about the instruments can be found in Duan et al. [10] and Li et al. [51].

Firstly, the Campbell Scientific LoggerNet 4.2.1 software was used to transform the raw 10-Hz EC data into the 30-min binaries. Then, the LI-COR EddyPro 5.2.1 software was applied to process the EC 30-min binaries, with the main steps involving averaging and statistical tests [52], time delay compensation, double rotation, spectral corrections [53], and compensation of density fluctuations [54]. The quality flags in EddyPro consist of “excellent” (flag 0), “moderate” (flag 1), and “exclude” (flag 2). The EC data on rainy or foggy days were discarded [10,47].

The 16-day Normalized Difference Vegetation Index (NDVI) data for the period 2015–2017, available from the 250-m resolution MODIS MOD13Q1 product (https://ladsweb.modaps.eosdis.nasa.gov/search/), were employed (accessed: 13 September 2022). The leaf area index (LAI), a fraction of photosynthetically active radiation (FPAR), green leaf fraction (N), and vegetation cover fraction (V) data were calculated based on the NDVI data following Sellers et al. [20] and Zhang et al. [11].

2.3. Methods

2.3.1. The SiB2 Model

The SiB2 model is a widely used and biophysics-based land surface model developed by Sellers et al. [20,21]. SiB2 contains a set of physics-based equations that couple the water balance, energy balance, and vegetation biochemical processes to simulate the exchanges of water, carbon, momentum, and energy fluxes among the atmosphere, a single canopy layer, and three soil layers (surface soil layer, root zone layer, and deep soil layer) [2,12,21,55]. As a parameterization scheme describing the processes of exchange between land and atmosphere, it simulates a more realistic vegetation physiological process owing to the incorporation of a canopy photosynthesis conductance submodel [3,30].

The SiB2 model requires soil, land-surface properties, initial conditions, and meteorological forcing data as inputs. The soil in the wheat field studied here consisted of clay, and thus parameter type 5 (Clay→clay loam) was selected from Table 4 in Sellers et al. [20]. In addition, the land surface category was defined as “agriculture or C3 grassland” (biome type 9) (Table 2 in Sellers et al. [20]). The parameter settings in the model for Dongtai are listed in

Table A1. Parameter settings in the SiB2 model for Dongtai.

Parameter		Value	Parameter		Value
Z2	Canopy-top height (m)	0.15, 0.58, 0.86	S6	Half-inhibition high temperature, respiration (K)	328
Z1	Canopy-base height (m)	0.1	Topt	Optimum temperature for vegetation growth (K)	298
χL	Leaf-angle distribution factor	−0.02	S3	Low temperature stress factor, photosynthesis (K−1)	0.2
Dr	Root depth (m)	0.1, 0.14, 0.21	S4	Half-inhibition low temperature, photosynthesis (K)	281
ψc	One-half inhibition water potential	−200	S1	High temperature stress factor, photosynthesis (K−1)	0.3
δV,l	Leaf transmittance, visible, live	0.07	S2	Half-inhibition high temperature, photosynthesis (K)	308
δV,d	Leaf transmittance, visible, dead	0.25	DT	Total soil depth (m)	0.4
δN,l	Leaf transmittance, near IR, live	0.22	αsV	Soil reflectance, visible	0.1
δN,d	Leaf transmittance, near IR, dead	0.38	αsN	Soil reflectance, near IR	0.15
αv,l	Leaf reflectance, visible, live	0.105	B	Soil wetness exponent	8.52
αv,d	Leaf reflectance, visible, dead	0.58	ψs	Soil tension at saturation (m)	−0.36
αN,l	Leaf reflectance, near IR, live	0.36, 0.18	Ks	Hydraulic conductivity at saturation (m s−1)	2.5 × 10−6
αN,d	Leaf reflectance, near IR, dead	0.58, 0.4	θs	Soil porosity (volume fraction)	0.48
ε	Intrinsic quantum efficiency (mol mol−1)	0.08	∅s	Mean topographic slope (radians)	0.176
M	Stomatal slope factor	13.0	Vmax0	Maximum rubisco capacity, top leaf (mol m−2 s−1)	1.5 × 10−4
b	Minimum stomatal conductance (mol m−2 s−1)	0.01	G(μ)/μ	Time-mean leaf projection	1.0
fd	Leaf respiration factor	0.015	G1	Augmentation factor for momentum transfer coefficient	1.449
βce	Photosynthesis coupling coefficient	0.98	G4	Transition height factor for momentum transfer coefficient	11.785
βps	Photosynthesis coupling coefficient	0.95	zwind	Wind observation height (m)	10.0
S5	High temperature stress factor, respiration (K−1)	1.3	zmet	Air temperature and humidity observation height (m)	10.0

. Six meteorological forcing variables—downward shortwave radiation, downward longwave radiation, vapor pressure, air temperature, wind speed, and precipitation—are shown in Figure 2. From January to May, the daily maximum radiation, vapor pressure, and air temperature increased substantially, with values of 1020 W m⁻², 442 W m⁻², 6 hPa, and 301 K, respectively. The daily average wind speed fluctuated between 1 and 6 m s⁻¹ during the observation period. The seasonal cumulative precipitation was 247 mm, with a maximum daily value of 35 mm on 17 March 2015.

2.3.2. The RF Model

The RF algorithm is an extensively used machine learning method that excels at classification and regression owing to its efficiency and flexibility [56]. Multidimensional and multicollinear data can be dealt with satisfactorily, and there is less sensitivity to overfitting [57]. The method’s feature selection tool can be used to pass judgement on how significant a predictor is, with the definition of feature importance being the weight of each of the model’s input factors, and significant variables having a stronger influence on the outcomes of the model evaluation [58].

In this study, we applied the RF framework to correct heat and carbon fluxes simulated by the SiB2 model (Figure 3). First, a set of explanatory variables (

Table A2. Variables selected to train the RF model.

Variable	Unit	Description	Variable	Unit	Description
NDVI	–	Normalized difference vegetation index	RH3	%	Relative humidity at 3 m
LAI	–	Leaf area index	P	hPa	Pressure
FPAR	–	Fraction of photosynthetically active radiation	q	g g−1	Specific humidity at 3 m
T3	K	Air temperature observed at 3 m	VPD	hPa	Vapor pressure deficit at 3 m
Tg	K	Temperature of land surface	u*	m s−1	Friction velocity
Tm	K	Average temperature of air at 3 m and ground	T*	K	Disturbances in temperature
G5	W m−2	Soil heat flux at the depth of 5 cm	WS	m s−1	Wind speed at 3 m
dT	K	Bias of temperature for canopy air space and observation height	WDir	degrees from north	Wind direction at 3 m
Ts5	K	Temperature of soil at the depth of 5 cm	Rn	W m−2	Net radiation
Ts10	K	Temperature of soil at the depth of 10 cm	SiB2H	W m−2	The H modeled by SiB2
Ts20	K	Temperature of soil at the depth of 20 cm	SiB2LE	W m−2	The LE modeled by SiB2
Ts40	K	Temperature of soil at the depth of 40 cm	SiB2G0	W m−2	The G0 modeled by SiB2
Es0	hPa	Saturated vapor pressure of land surface	SiB2Fc	μmol m−2 s−1	The Fc modeled by SiB2

) were selected based on previous research [43,59,60,61,62] and currently available in situ measurements. Second, 90% of the outputs of the SiB2 model and explanatory variables (Table A2) from January to May 2016–2017 were used to train the RF model, with the remaining 10% of them and 100% of the data in 2015 used to validate estimation performance of the model. A 10-fold cross-validation method was applied in the RF model to find the best hyperparameters and avoid the issue of overfitting. Two statistical metrics, the coefficient of determination (R²) and root-mean-square error (RMSE), were used to evaluate the performance of the 10-fold cross-validation results.

2.3.3. Radiation and Surface Energy Fluxes

Solar radiation is the key driver of surface energy, momentum, carbon, and water fluxes [4]. The Rn consists of DSR, USR, DLR, and ULR [7]:

$$Rn=\mathrm{DSR}+\mathrm{DLR}-\mathrm{USR}-\mathrm{ULR}.$$

(1)

where Rn is the net radiation, DSR is the downward shortwave radiation, DLR is the downward longwave radiation, USR is the upward shortwave radiation, and ULR is the upward longwave radiation. The surface energy balance can be estimated by [10]

$$Rn=H+LE+G_0+\epsilon ,$$

(2)

where H is the sensible heat flux, LE is the latent heat flux, G₀ is the soil surface heat flux, and ε is the residual energy term, such as canopy heat storage or the energy consumption of photosynthesis and respiration. The soil surface heat flux (G₀) can be estimated according to the formula given by Liu et al. [63].

2.3.4. Statistical Analysis

In this study, the traditional statistical analysis indexes (the standard deviation, R², and RMSE) were used to evaluate the accuracy of SiB2 and RF models. The comparison statistics were calculated as follows:

The standard deviation (S), R², and RMSE:

$$S=\sqrt{\frac{{{\displaystyle \sum }}_{i-1}^n{\left(x_i-\overline{x}\right)}^2}{n-1}},$$

(3)

where $x_i$ is the value of the ith point in the data set, $\overline{x}$ is the mean value of the data set, and n is the number of the data points in the data set. The standard deviation is the average amount of variability in the data set.

$$R^2=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left(M_i-O_i\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(O_i-\overline{O}\right)}^2},$$

(4)

where $M_i$ are the values modeled by the SiB2/RF model, $O_i$ are the observed values, and $\overline{O}$ is the mean value of the observation. When the R² is high, the simulations of the SiB2/RF model are close to the observations.

$$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{i-1}^n{\left(M_i-O_i\right)}^2}{n}}.$$

(5)

The discrete situation between the simulation and observation is indicated by RMSE.

3. Results

3.1. Radiation, Turbulence, and CO₂ Fluxes

Figure 4 shows remarkable diurnal variations in the median Rn, H, LE, G₀, and F_c in the vegetative, reproductive, and ripening stages. Rn, H, LE, and G₀ began to increase after sunrise (around 05:00–07:00 LST), reached their highest values of 280–615, 59–77, 98–406, and 34–107 W m⁻², respectively, in the middle of the day (11:00–14:00 LST), and then gradually decreased to stable values at around 17:00–19:00 LST. F_c had an opposite trend of variation to the surface energy fluxes. The positive nocturnal values of 0.4–3.9 μmol m⁻² s⁻¹ would have mainly been associated with the respiration of wheat [47], a lower boundary layer height [64], and poor atmospheric mixing [65], whilst the negative daytime (07:30–17:30 LST) values of approximately −18.5 to −0.4 μmol m⁻² would have been closely related to the strong photosynthesis of wheat and favorable dispersion conditions [66].

In addition, the Rn, H, LE, G₀, and F_c showed significant seasonal variations in the vegetative, reproductive, and ripening stages. The middle-of-the-day maximum Rn, LE, and G₀ increased from the vegetative stage (280, 98, and 34 W m⁻²) to the ripening stage (615, 406, and 107 W m⁻²); the H in the ripening stage (59 W m⁻²) was slightly lower than that in the vegetative and reproductive stage (77 and 60 W m⁻²; Figure 4a); and the F_c varied with the wheat phenology. The wheat field served as a carbon sink in the vegetative stage, with a mean value of −0.4 μmol m⁻² despite the low photosynthetic rate. The wheat field then became a CO₂ sink in the reproductive and ripening stages, with mean values of −4.2 and −3.7 μmol m⁻² s⁻¹, indicating stronger biological activities of the wheat (i.e., photosynthetic rate) during these stages.

3.2. SiB2 Evaluation

The diurnal variations in Rn, H, LE, G₀, and F_c modeled by SiB2 were consistent with the results obtained by direct measurements (Figure 4). The simulation of Rn depended largely on the simulation of USR and ULR, since DSR and DLR were given as inputs. As can be seen in Figure 4a, Rn was simulated very well, with both its peak together and diurnal variation being closely captured. In addition, the R² and RMSE of the overall growth period were 1.00 and 18.73 W m⁻², respectively. However, the biases indicated that the SiB2 model overestimated Rn, and this was slightly more apparent at nighttime, similar to the findings of Jing et al. [2], which may have been caused by underestimated values of the surface effective radiative temperature at night in the simulation. In addition, the median bias values in the different growth stages, in ascending order, were 11 W m⁻² for the ripening stage, 18 W m⁻² for the reproductive stage, and 21 W m⁻² for the vegetative stage; and the median (mean) values of observed and simulated Rn were −13 (82) and 3 (98) W m⁻², respectively. The mean bias and standard deviation for bias of observed and simulated Rn were 16 W m⁻² and 6 W m⁻². Overall, the SiB2 model overestimated Rn by 13%.

Figure 4b compares the H between the SiB2 simulation and observation. The diurnal variation that was again captured by SiB2 reason well, especially in the vegetative stage, however, its pattern was less regular than that of Rn. In addition, the R² and RMSE of the overall growth period were 0.59 and 32.92 W m⁻², respectively. As we can see, the simulation of H at night was better than during the daytime, especially around the middle of the day in the reproductive and ripening stages, when SiB2 overestimated the H. Further, a small part of the biases was attributable to underestimation in the reproductive and ripening stages. The median (average) values of the observed and simulated H were −4 (13) and −1 (20) W m⁻², respectively. The mean bias and standard deviation for bias of observed and simulated H were 4 W m⁻² and 12 W m⁻². In general, the SiB2 model overestimated H by 25%.

It can be seen from Figure 4c that the simulation of LE was better than that of H and closer to that of Rn, with R² and RMSE values that reached 0.75 and 72.87 W m⁻², respectively. The simulation of LE in the vegetative stage was much better than in the later stages. SiB2 basically overestimated LE, with only a slight underestimation in the daytime during the reproductive and ripening stages. In addition, the median (average) values of the observed and simulated LE were 11 (75) and 39 (92) W m⁻², respectively. The mean bias and standard deviation for bias of observed and simulated LE were 24 W m⁻² and 14 W m⁻². Overall, the SiB2 model overestimated LE by 36%.

The observed and simulated G₀ are compared in Figure 4d, which reveals less consistent temporal changes than for Rn. The R² and RMSE of the overall growth period for G₀ were 0.60 and 34.33 W m⁻², respectively. It is apparent that SiB2 overestimated the soil heat flux after sunrise in the vegetative and reproductive stages and mainly underestimated it at nighttime. The simulation of G₀ in the ripening stage was relatively better. In addition, the median (mean) values of the observed and simulated G₀ were −19 (0.4) and −34 (−12) W m⁻², respectively. The mean bias and standard deviation for bias of observed and simulated G₀ were −11 W m⁻² and 21 W m⁻². Overall, the SiB2 model underestimated G₀ by 37%. The negative mean value may have resulted from underestimation, especially at nighttime, in the ripening stage. This would be regarded as a simulation error when less than −100 W m⁻². The reason why SiB2 overestimated G₀ in the daytime of the vegetative stage may be the lower vegetation cover fraction set in the parameters resulting in higher absorption of radiation by the ground surface.

Significant diurnal variation is a well-known characteristic of CO₂ flux in cropland, in which the crop absorbs CO₂ by photosynthesis and emits it into the atmosphere. As shown in Figure 4e (in which positive values of biases between the simulation and observation represent emission and negative values indicate absorption), SiB2 estimated the CO₂ fluxes well, capturing the temporal variations accurately. The R² and RMSE were 0.62 and 6.82 μmol m⁻² s⁻¹, respectively; and the median (mean) values of CO₂ in the observation and simulation were 0.7 (−2) and 0.2 (−5) μmol m⁻² s⁻¹, respectively. The mean bias and standard deviation for bias of observed and simulated F_c were −2 μmol m⁻² s⁻¹ and 2 μmol m⁻² s⁻¹. In general, the SiB2 model underestimated F_c by 40%. In addition, the simulation in the vegetative stage was the best among the three stages, and the ripening stage was the worst. The simulation of F_c was predominantly underestimated, with only a slight overestimation in the reproductive stage. There were some daytimes when SiB2 overestimated F_c, which may have been caused a weaker photosynthesis resulting from less DSR and lower temperatures before and after rainfall. Additionally, the simulation of photosynthesis increased and decreased as the winter wheat grew and died following higher and lower LAI, FPAR, and V.

3.3. Driving Factors of Turbulence and CO₂ Fluxes

As demonstrated in Section 3.2, SiB2 captured the diurnal variation in H, LE, G₀, and F_c well, albeit with the simulation results still showing certain errors. Given that the R² of Rn reached 1.00, there was less possibility to improve its simulation accuracy. Therefore, we constructed the RF model to correct the SiB2 model outputs and improve the simulation accuracies of H, LE, G₀, and F_c. The RF model examined the potential drivers and assessed their relative contributions to H, LE, G₀, and F_c (Figure 5). Correlations among the turbulence and CO₂ fluxes and input variables were calculated with all the training data from the Dongtai site (Figure 6).

As we can see from Figure 5a, T* showed the greatest importance in the modulation of H, with a weight of 81% of all variables. Moreover, Figure 6a shows that H correlated most strongly with T*, consistent with the variable weighting value in Figure 5a, whose Pearson correlation coefficient (r) was 0.82. Apart from T*, there were two other critical variables, u* and SiB2_H, with weights of 11% and 8%, respectively. T* and u* have been mentioned previously as significant variables in the calculation of H in EC observations [10]. Comparatively speaking, the influence of the remaining variables was negligible, with importance values of less than 1%. Moreover, u* was microcorrelated with H despite its high importance in the RF model, while SiB2_H correlated closely with H even though its importance was lower than that of u*.

Figure 5b shows that Rn was the most essential variable in modulating LE, accounting for 21% of the importance of all variables. Although the r of Rn reached 0.82, the strongest positive correlation with LE was not Rn but SiB2_LE (Figure 6b), with the highest r of 0.83. Besides Rn, three other variables, SiB2_LE, T_g, and Es₀, impacted strongly on LE, with importance values of 17%, 13%, and 13%, respectively, since Es₀ and T_g play important roles in calculating LE in EC measurements. In contrast, the remaining variables were less important in modulating LE, with importance values ranging from 7% down to values approaching 0.

As illustrated in Figure 5c, SiB2_G0 had the strongest influence in modulating G₀, accounting for 60% of the total variable importance. SiB2_G0 had the greatest positive correlation with G₀, with the highest r of 0.76 in Figure 6c. Additionally, Rn was the second most important variable, with a weighting of 17%, and also had the second highest correlation with G₀ (r = 0.74). Both SiB2_G0 and Rn had close consistency in their variable weighting and correlation. Aside from SiB2_G0 and Rn, the remaining variables showed weaker influences in modulating G₀, with importance values ranging from 4% down to values approaching 0.

Figure 5d shows that SiB2_Fc played the most critical role in modulating F_c, with an importance weighting of 39% of all variables. SiB2_Fc had the greatest positive correlation with F_c, with the highest r of 0.63 in Figure 6d. In addition, as the second most significant variable, the weighting of Rn was 27% and its r was −0.56, which was the second highest negative correlation. These results were similar to those of SiB2_G0 and Rn in their modulation of G₀, being consistent in both variable weighting and correlation. In contrast, there was no apparent influence of VPD, T₃, FPAR, LAI, NDVI, and RH₃ on F_c, showing lower relative weights, with importance values of 8%, 7%, 5%, 5%, 5%, and 4%, respectively. Note that Rn, VPD, T₃, LAI, FPAR, and NDVI all correlated negatively with F_c.

3.4. RF Model Evaluation

It is clear that the RF model performed excellently in correcting the H (Figure 7a) in all three stages. The degree of overestimation in the daytime was slightly reduced, especially in the reproductive stage. It also resolved the problem of underestimation in the ripening stage. Accordingly, the estimation with the RF model was consistent with the observation, basically catching both the peak and diurnal variation. The mean bias and standard deviation for bias of observed and simulated H were 5 W m⁻² and 5 W m⁻², respectively. The R² of the RF model for H was 0.99, larger than that of 0.59 from SiB2 alone. Likewise, the RMSE was 4.73 W m⁻², which was smaller than that of 32.92 W m⁻² with SiB2.

The simulation of LE with the RF model (Figure 7b) was relatively less consistent with the observaton and worse than it was for H. It was able to capture the diurnal variation but failed to catch the peak, especially in the ripening stage. The mean bias and standard deviation for bias of observed and simulated LE were −4 W m⁻² and 28 W m⁻², respectively. The correction by the RF model did alleviate the degree of overestimation, especially in the ripening stage. However, there was a relatively greater underestimation than the SiB2 model in the ripening stage. Nonetheless, the results indicated that the correction still worked, with the R² reaching 0.85 and the RMSE reduced to 54.92 W m⁻².

It can be seen from Figure 7c that the simulation of G₀ after correction with the RF model was more consistent with the observation. Although the bias of the simulation for G₀ after the correction was still dominated by underestimation, more peaks were captured. The mean bias and standard deviation for bias of observed and simulated G₀ were −14 W m⁻² and 15 W m⁻², respectively. The biases, in terms of both overestimation and underestimation, became much smaller in the vegetative and reproductive stages, resulting in the simulation by SiB2 in these two stages improving. The R² reached 0.78 and the RMSE reduced to 25.53 W m⁻². Compared with the results of SiB2 alone, an improvement was still apparent after correction with the RF model.

Figure 7d shows a better simulation of CO₂ following correction with the RF model. It also displays a better consistency with the observation, especially at nighttime, with the overall biases at night becoming smaller. The mean bias and standard deviation for bias of observed and simulated F_c were −4 μmol m⁻² s⁻¹ and 28 μmol m⁻² s⁻¹. It is apparent that the simulation values became larger after correction, which were close to 0 originally, making the simulation more reasonable. Meanwhile, the biases of F_c in the vegetative and ripening stage decreased and the biases (overestimation) in the reproductive stage increased. In other words, the correction of the biases in the vegetative and ripening stages was better. Moreover, the R² increased from 0.62 to 0.71 and the RMSE decreased from 6.82 μmol m⁻² s⁻¹ to 4.70 μmol m⁻² s⁻¹.

3.5. Comparison of SiB2 and RF

Figure 8a shows the R² values for H, LE, G₀, and F_c in the different growth stages for the SiB2 and RF-corrected outputs (hereafter referred to simply as RF). During the vegetative stage, for the simulation of SiB2 and RF, H had the largest R², followed by G₀, LE, and then F_c. The H improved significantly in the vegetative stage, reaching 41%, followed by F_c (33%), G₀ (23%), and LE (13%). In the reproductive stage, for the simulation of SiB2, the largest R² was that of LE, followed by H, F_c, and then G₀; while for RF, the largest R² was that of H, followed by LE, G₀, and F_c. In addition, the degree of improvement for G₀ was the highest, reaching 63%, followed by 46% for H, 17% for LE, and then 9% for F_c. During the ripening stage, for the simulation of SiB2, F_c had the largest R², followed by G₀, LE, and then H; while for RF, H also had the largest R², followed by LE, G₀, and then F_c. Additionally, the degree of improvement for H was the highest, reaching 111%, followed by G₀ (33%), LE (23%), and then F_c (23%). For the simulation of SiB2, for H, the R² in the vegetative stage performed better; while for RF, the best performing R² was in the vegetative stage along with the reproductive stage. The effect of correction was better in the ripening stage. For the R² of the simulated LE, both SiB2 and RF performed best in the reproductive stage. For the simulation of G₀, the R² of SiB2 and RF were also best in the same stage, namely the ripening stage. However, the effect of correction in the reproductive stage was the best. For the F_c simulated by SiB2, the best performance in terms of R² was in the reproductive stage; for RF, the R² in the ripening stage performed better. Overall, the mean R² of SiB2 (RF) for the reproductive (ripening) stage was the largest, and the effect of correction in the ripening stage was better. During the whole growth period, the R² for H, LE, G₀, and F_c all improved greatly (68%, 13%, 30%, and 15%) (

Table 1. The values of R² and RMSE for the overall growth period in the SiB2 and RF-corrected model outputs.

Flux	SiB2		RF
	R2	RMSE	R2	RMSE
H	0.59	32.92	0.99	4.73
LE	0.75	72.87	0.85	54.92
G0	0.60	34.33	0.78	25.53
Fc	0.62	6.82	0.71	4.70

Note: H, sensible heat flux; LE, latent heat flux; G₀, soil heat flux; F_c, CO₂ flux.

).

Figure 8b shows the RMSE for H, LE, G₀, and F_c in the different growth stages as simulated by SiB2 and RF. For the simulation of SiB2, the RMSE of H, LE, and F_c became increasingly larger as the wheat grew. In other words, the order of RMSE values for H, LE, and F_c was vegetative stage < reproductive stage < ripening stage, which was similar to the RMSE of RF for H, LE, and G₀. Meanwhile, the RMSE of SiB2 for G₀ was lowest in the ripening stage, while that of RF for F_c was lowest in the vegetative stage. For the vegetative stage, the best degree of correction was for H, reaching −78%, and the worst was for F_c, at only −12%. For the reproductive stage, the correction for H also performed best, while for F_c it was worst. For the ripening stage, the correction with RF also performed best for H, and for G₀ it was negative. Furthermore, the best effect of the correction for H, LE, G₀, and F_c was in the reproductive, reproductive, vegetative, and ripening stages, respectively. Overall, the best mean correction effect was in the vegetative stage. During the whole growth period, all the RMSEs for H, LE, G₀, and F_c were reduced (Table 1).

4. Discussion

We have evaluated the turbulence and CO₂ fluxes with the in situ observations and remote sensing data. H, LE, G₀, and F_c simulated by SiB2 have standard deviations of 12 W m⁻², 14 W m⁻², 21 W m⁻² and 2 μmol m⁻² s⁻¹, respectively. H estimation has a 25% positive bias, which was similar to those reported by Chu et al. [14], Gao et al. [7], Lei et al. [31], Li et al. [3], and Xue et al. [29]. The positive H bias can be attributed to the higher initial input canopy temperature, which was set to the canopy air space temperature. The estimated LE has a 36% positive bias, which was consistent with the results of Gao et al. [7], Yan et al. [30], and Yuan et al. [67]. The soil moisture sensors were not mounted directly in the wheat field, resulting a in higher soil wetness fraction and measured LE. G₀ was underestimated by 37%, which was similar to the results reported by Zhang et al. [5]. The SiB2 model underestimated F_c by 40% and most simulated values were concentrated near to the value of 0, which was also found in Chu et al. [14], and Yuan et al. [4,67]. The soil respiration (R_soil) was set to 0 by default (R_soil = 0) in SiB2, leading to a relatively lower simulation of respiration in the wheat field, which can be regarded as a kind of model error. In other words, SiB2 has a tendency to underestimate ecosystem respiration at night during the growth period [26].

Given the bias of simulation by SiB2, the RF model was used to correct the results modeled by SiB2 and made great improvements to H, LE, G₀, and F_c with values of 68%, 13%, 30%, and 15%, respectively, during the whole growth period. There has also been some research carried out into revising SiB2 to address biases that arise from the model’s complexity and diversity of study area and vegetation. Lei et al. [31] adjusted the physical equation of soil respiration and calibrated the Ball-Berry stomatal conductance model. Li et al. [3] adjusted optimum growth and inhibition temperature parameters. Jing et al. [2] revised the SiB2 model by adding an irrigation module and adjusting parameters. The previous research mentioned above made improvements to the output of the SiB2 model, nevertheless their corrections, based on the observation, only applied to specific study regions. It is important to take into consideration the interactions among parameters and the physical implications of the parameters. Otherwise, there would be great overall uncertainty for the results of the SiB2 model.

This study only investigated the wheat field in Dongtai County for one growth season. In the next study, we will make an effort to extend the simulation of the combined SiB2 model and RF model from Dongtai County to the whole of East China, extend the species studied from wheat to a rotation of summer rice and winter wheat, and extend the study period from one growing season to several crop years. Additionally, investigating land surface processes and improving the accuracy of simulation are of great importance in future work.

5. Conclusions

In this study, radiation, turbulence, and CO₂ fluxes were observed with an EC system in a winter wheat field in eastern China from 1 January to 31 May 2015–2017. The Rn, H, LE, G₀, and F_c modeled by SiB2 showed obvious diurnal and seasonal variations during the whole winter wheat growing season, with R² values of 1.00, 0.59, 0.81, 0.60, and 0.62 against the direct observations, respectively. The SiB2 model overestimated the Rn, H, and LE (13%, 25%, and 36%) and underestimated the G₀ (−37%) and F_c (−40%). Thus, an RF model was designed to correct the results modeled by SiB2. The RF-corrected model showed that T*, Rn, SiB2_G0, and SiB2_Fc were the key driving factors in the modulation of H, LE, G₀, and F_c. Compared with the results modeled by SiB2, the RF model performed well and made great improvements to H, LE, G₀, and F_c with values of 68%, 13%, 30%, and 15% during the whole growth period.

The input parameters in SiB2 were dynamically updated every week to reflect the process of vegetation phenology, making the simulated turbulence and CO₂ fluxes more reasonable and realistic.