The Dynamic Impacts of COVID-19 Pandemic Lockdown on the Multifractal Cross-Correlations between PM2.5 and O3 Concentrations in and around Shanghai, China
Abstract
1. Introduction
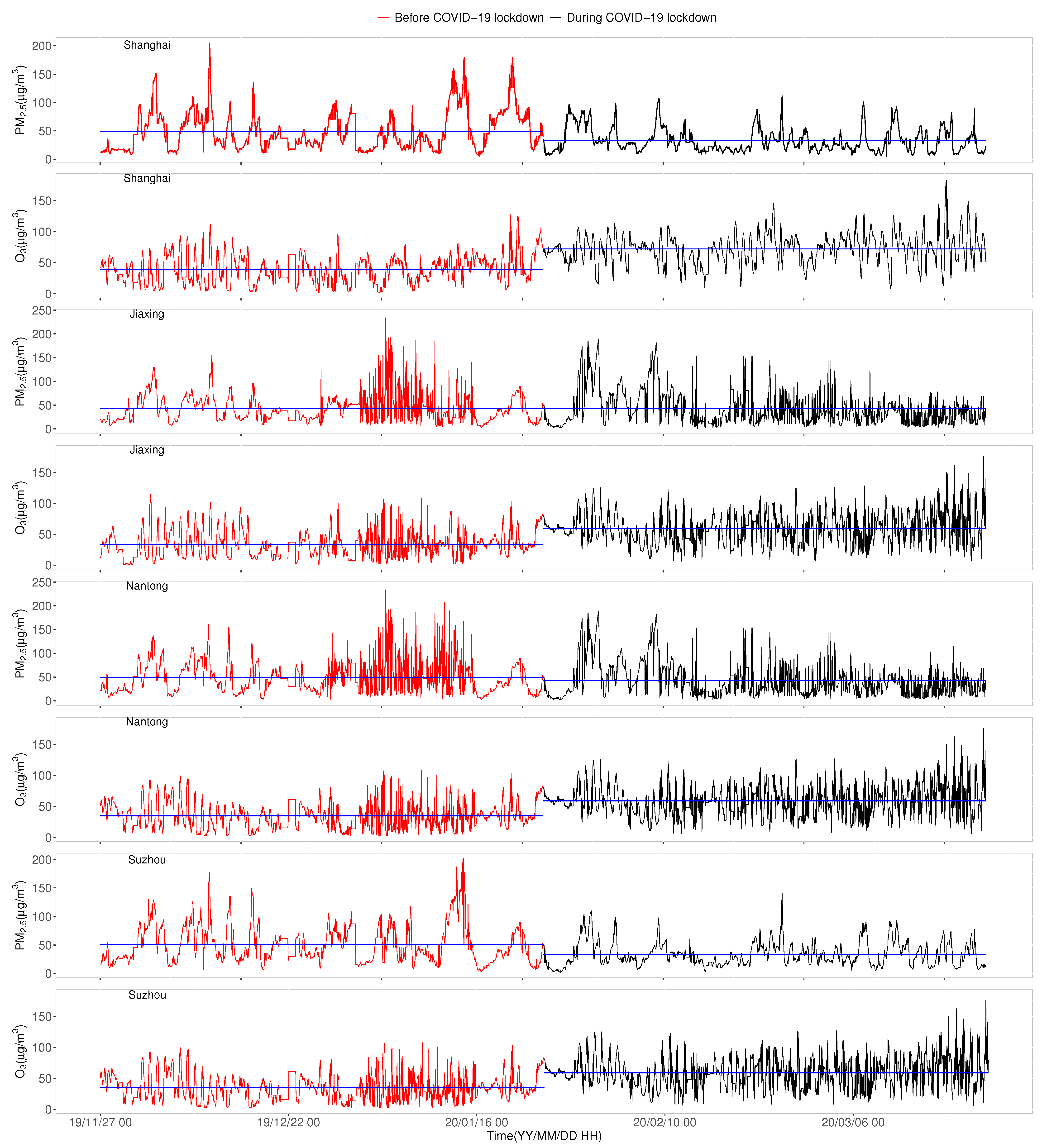
2. Data Description and Preprocessing Method
3. Methodology
3.1. Mf-Dcca Method
3.2. Multifractal Cause Analysis
- Step 1
- The original series is shuffled to remove any potential correlations. The MF-DCCA analysis is conducted on the shuffled series and the multifractal characteristic is determined.
- Step 2
- The surrogate series are constructed by phase-randomizing the original series using the IAAFT algorithm. The MF-DCCA analysis is carried out on the surrogate series and are calculated;
- Step 3
- Steps 1–2 are repeated until 80,000 sets of {, } of the hourly PM and O series in and around Shanghai, China, before and during the COVID-19 partial lockdown are accumulated.
- Step 4
- The differences between are checked to determine the components of the multifractality and intrinsic multifractality of the hourly PM and O series in four cities before and during the COVID-19 partial lockdown, respectively.
- Step 5
- Finally, the comparisons between the above multifractality parameters are applied to determine the dynamic impacts of the COVID-19 pandemic on the intrinsic multifractality hourly PM and O series in and around Shanghai, China.
3.3. Formation of a New Index
4. Results and Discussion
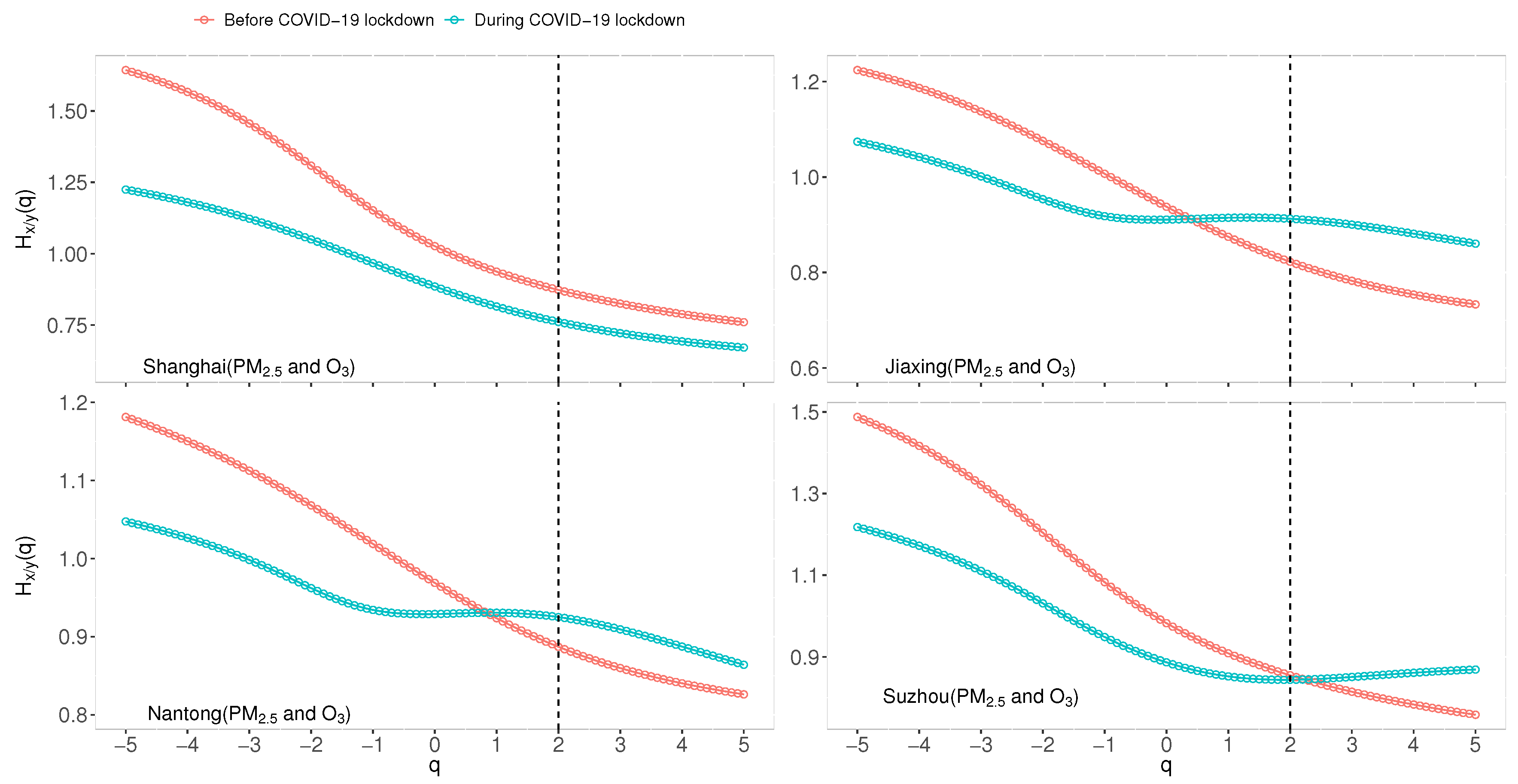
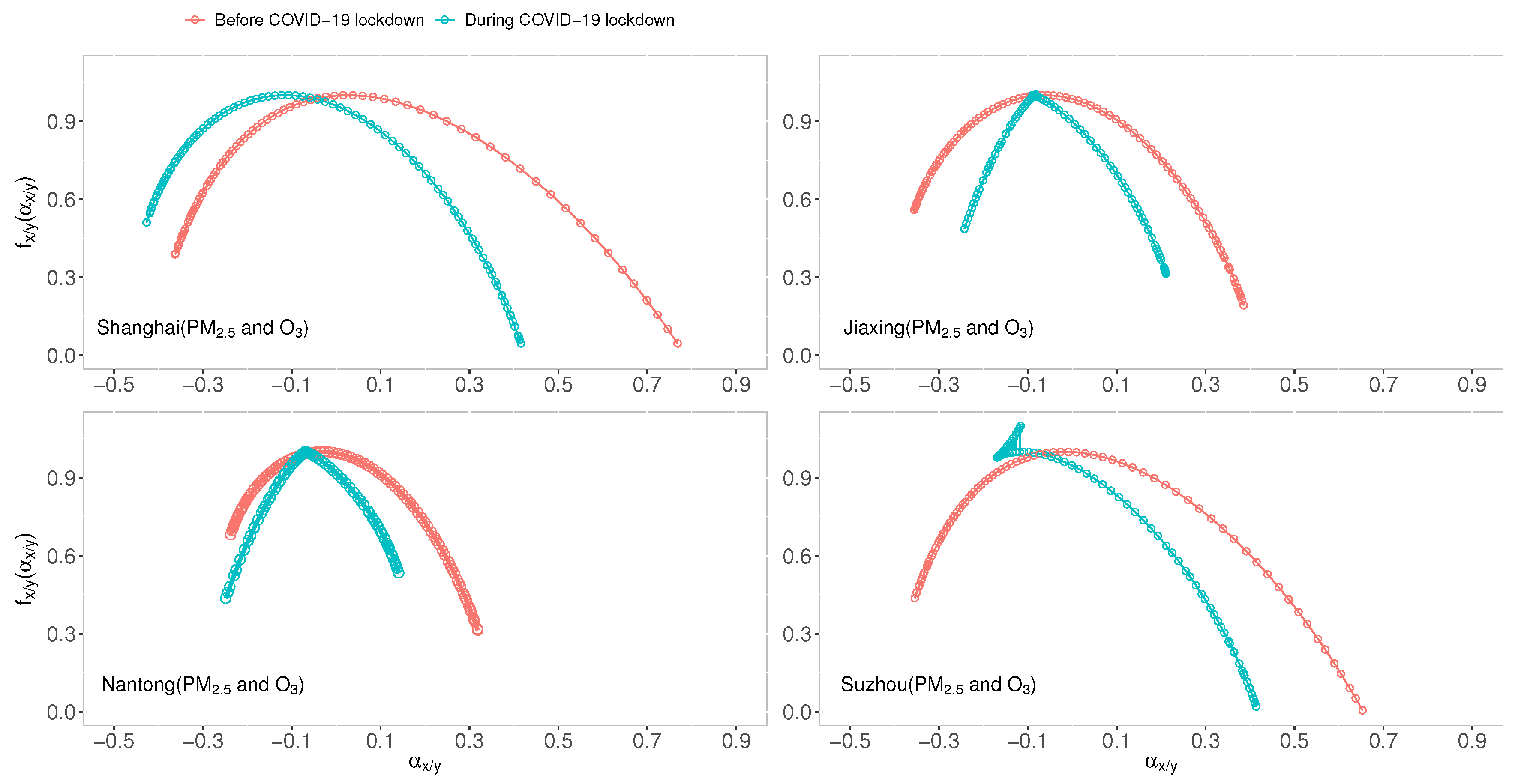
4.1. Multifractal Cross-Correlations of PM-O
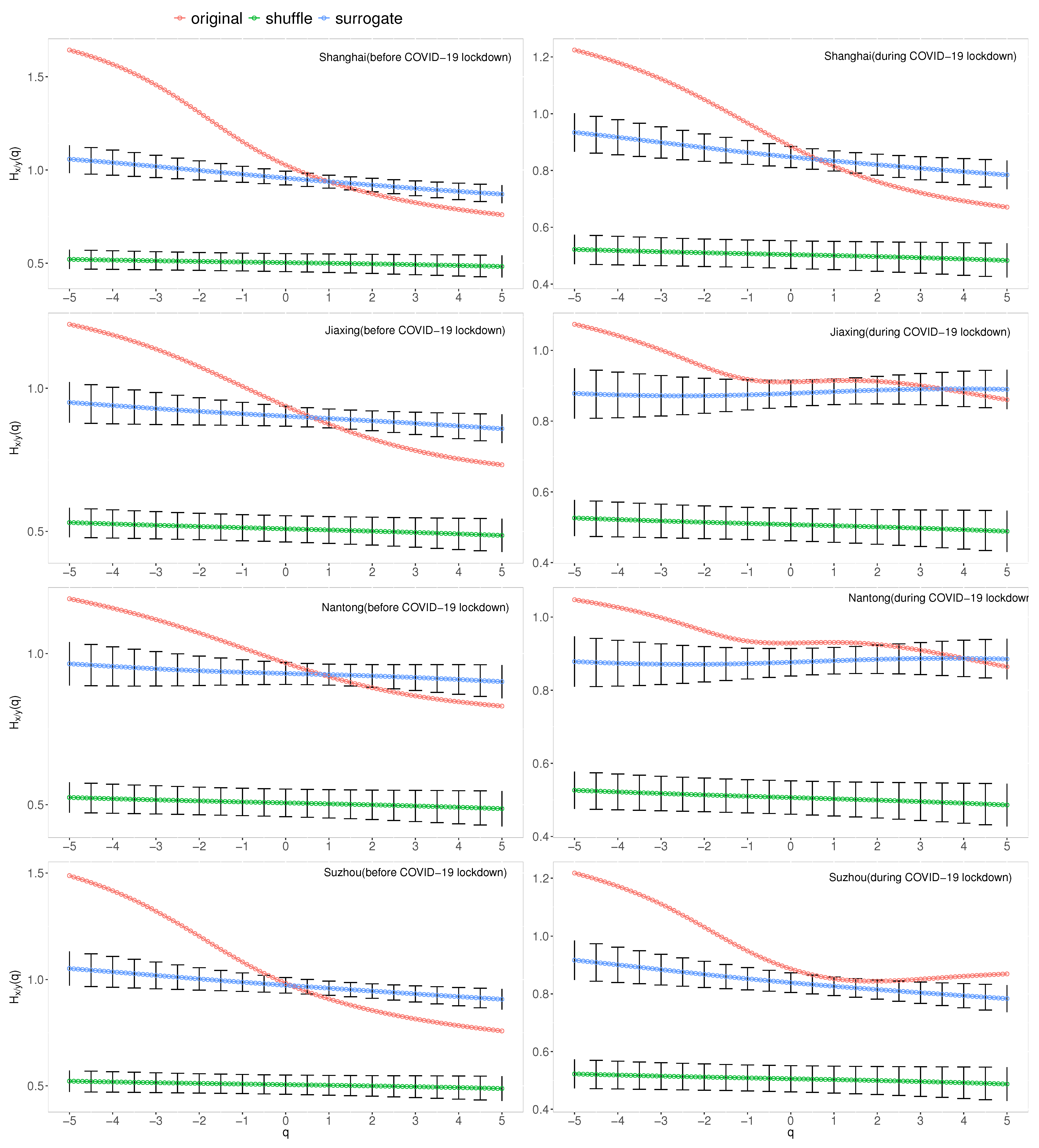
4.2. Causes of Cross-Correlations between PM and O
4.3. The Coordinated Control Degree of PM-O
4.4. Disscussion
5. Conclusions
- (1)
- The cross-correlations between PM and O in and around Shanghai both before and during the COVID-19 partial lockdown have multifractal characteristics. Moreover, there are weaker multifractal cross-correlation degrees of PM-O in four cities during the COVID-19 partial lockdown.
- (2)
- The impacts of multifractality due to the nonlinear correlation part in and around Shanghai are greater than the linear correlation part and the fat-tailed probability distribution part. The intrinsic multifractal cross-correlations between PM and O decreased in all cities during the COVID-19 partial lockdown.
- (3)
- Although the COVID-19 lockdown contributes to the improvement of multifractal cross-correlations between PM and O, their effects are limited from the perspective of intrinsic multifractality.
- (4)
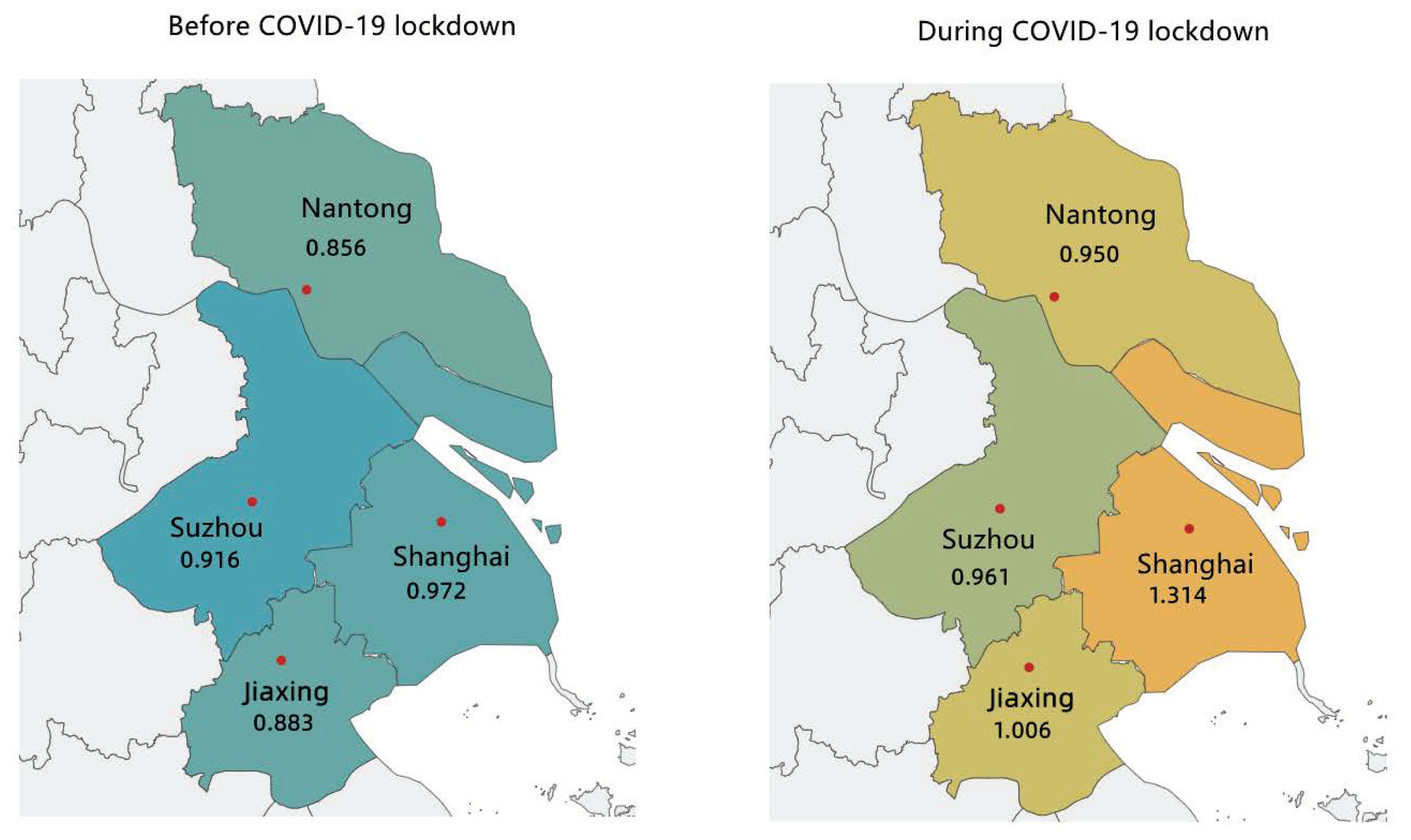
- The mean values of in and around Shanghai all increased during the COVID-19 partial lockdown. This indicates that the PM-O coordinated control degrees in all four cities become weaker. Among these four cities, the added value of in Shanghai is the maximum.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, K.; Jacob, D.J.; Liao, H.; Zhu, J.; Shah, V.; Shen, L.; Bates, K.H.; Zhang, Q.; Zhai, S. A two-pollutant strategy for improving ozone and particulate air quality in china. Nat. Geosci. 2019, 12, 906–910. [Google Scholar] [CrossRef]
- Wu, B.; Liu, C.; Zhang, J.; Du, J.; Shi, K. The multifractal evaluation of PM2.5-O3 coordinated control capability in China. Ecol. Indic. 2021, 129, 107877. [Google Scholar] [CrossRef]
- Wang, P.; Guo, H.; Hu, J.; Kot, S.H.; Ying, Q.; Zhang, H. Responses of PM2.5 and O3 concentrations to changes of meteorology and emissions in China. Sci. Total. Environ. 2019, 662, 297–306. [Google Scholar] [CrossRef] [PubMed]
- Kroll, J.H.; Heald, C.L.; Cappa, C.D.; Farmer, D.K.; Fry, J.L.; Murphy, J.G.; Steiner, A.L. The complex chemical effects of COVID-19 shutdowns on air quality. Nat. Chem. 2020, 12, 777–779. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Jacob, D.J.; Liao, H.; Shen, P.; Zhang, Q.; Bates, K.H. Anthropogenic drivers of 2013–2017 trends in summer surface ozone in China. Proc. Natl. Acad. Sci. USA 2019, 116, 422–427. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlind, S.; Bunde, A.; Stanley, H. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Lee, C.K.; Juang, L.C.; Wang, C.C.; Liao, Y.Y.; Yu, C.C.; Liu, Y.C.; Ho, D.S. Scaling characteristics in ozone concentration time series (OCTS). Chemosphere 2006, 62, 934–946. [Google Scholar] [CrossRef]
- Diosdado, A.M.; Coyt, G.G.; Lopez, J.B.; del Rio Correab, J. Multifractal analysis of air pollutants time series. Rev. Mex. Fis. 2013, 59, 7–13. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, L.; Zhu, H. Time–scaling property of air pollution indices: A case study of Shanghai, China. Atmos. Pollut. Res. 2015, 6, 886–892. [Google Scholar] [CrossRef]
- Shen, C.; Huang, Y.; Yan, Y. An analysis of multifractal characteristics of API time series in Nanjing, China. Phys. A Stat. Mech. Its Appl. 2016, 451, 171–179. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, Y.; Li, P. Multifractal behavior of an air pollutant time series and the relevance to the predictability. Environ. Pollut. 2017, 222, 444–457. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q. Multifractal characterization of air polluted time series in China. Phys. A Stat. Mech. Its Appl. 2019, 514, 167–180. [Google Scholar] [CrossRef]
- Li, X. On the multifractal analysis of air quality index time series before and during COVID-19 partial lockdown: A case study of Shanghai, China. Phys. A Stat. Mech. Its Appl. 2021, 565, 125551. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Chen, S.; Zou, L.; Zhang, X.; Tang, C. A study on daily PM2.5 concentrations in Hong Kong using the EMD-based MFDFA method. Phys. A Stat. Mech. Its Appl. 2019, 530, 121182. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Liu, C.; Wu, B.; Shi, K. A study of cross-correlations between PM2.5 and O3 based on Copula and Multifractal methods. Phys. A Stat. Mech. Its Appl. 2022, 589, 126651. [Google Scholar] [CrossRef]
- Zhou, W.X. Multifractal detrended cross-correlation analysis for two nonstationary signals. Phys. Rev. E 2008, 77, 066211. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Liu, C.; Shi, K.; Liu, Y. Multifractal detrended cross-correlation analysis on NO, NO2 and O3 concentrations at traffic sites. Phys. A Stat. Mech. Its Appl. 2018, 502, 605–612. [Google Scholar] [CrossRef]
- Rak, R.; Grech, D. Quantitative approach to multifractality induced by correlations and broad distribution of data. Phys. A Stat. Mech. Its Appl. 2018, 508, 48–66. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Potters, M.; Meyer, M. Apparent multifractality in financial time series. Eur. Phys. J. B—Condens. Matter Complex Syst. 2000, 13, 595–599. [Google Scholar] [CrossRef]
- von Hardenberg, J.; Thieberger, R.; Provenzale, A. A box-counting red herring. Phys. Lett. A 2000, 269, 303–308. [Google Scholar] [CrossRef]
- Saichev, A.; Sornette, D. Generic multifractality in exponentials of long memory processes. Phys. Rev. E 2006, 74, 011111. [Google Scholar] [CrossRef] [PubMed]
- Drożdż, S.; Kwapień, J.; Oświecimka, P.; Rak, R. Quantitative features of multifractal subtleties in time series. Europhys. Lett. 2009, 88, 60003. [Google Scholar] [CrossRef]
- Buonocorea, R.; Aste, T.; Matteo, T. Measuring multiscaling in financial time-series. Chaos Solitons Fractals 2016, 88, 38–47. [Google Scholar] [CrossRef]
- Kwapień, J.; Oświecimka, P.; Drożdż, S. Components of multifractality in high-frequency stock returns. Phys. A Stat. Mech. Its Appl. 2005, 350, 466–474. [Google Scholar] [CrossRef]
- Zhou, W.X. Finite-size effect and the components of multifractality in financial volatility. Chaos Solitons Fractals 2012, 45, 147–155. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Xie, W.J.; Zhou, W.X.; Sornetted, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 635. [Google Scholar] [CrossRef]
- Chen, F.; Miao, Y.; Tian, K.; Ding, X.; Li, T. Multifractal cross-correlations between crude oil and tanker freight rate. Phys. A Stat. Mech. Its Appl. 2017, 474, 344–354. [Google Scholar] [CrossRef]
- Almond, D.; Du, X.; Zhang, S. Did COVID-19 Improve Air Quality Near HuBei? National Bureau of Economic Research: Cambridge, MA, USA, 2020; No. W27086. [Google Scholar]
- Zhao, X.; Shen, N.; Li, L.; Wu, J.; Tao, J.; Zhao, W. Analysis on changes and influencing factors of air pollutants in Beijing-Tianjin-Hebei region during COVID-19 epidemic. Environ. Sci. 2021, 42, 1–15. [Google Scholar]

| City | Pollutant | Mean | Std. | Median | Skewness | Kurtosis | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Period | Period | Ratio | Period | Period | Period | Period | Period | Period | Period | Period | ||
| I(A) | II(B) | (B−A)/A | I | II | I | II | I | II | I | II | ||
| Shanghai | PM (μg/m) | 49.26 | 32.89 | −33.2% | 34.75 | 21.07 | 39.75 | 27.15 | 1.19 | 1.18 | 1.28 | 0.76 |
| O (μg/m) | 39.26 | 72.33 | 84.2% | 22.73 | 24.07 | 38.37 | 73.58 | 0.52 | 0.23 | 0.16 | 0.98 | |
| Jiaxing | PM (μg/m) | 42.99 | 42.87 | −0.3% | 30.75 | 35.99 | 37.19 | 32.7 | 1.62 | 1.51 | 3.92 | 2.24 |
| O (μg/m) | 33.58 | 59.34 | 76.7% | 22.04 | 25.73 | 31 | 58.22 | 0.87 | 0.45 | 0.43 | 0.25 | |
| Nantong | PM (μg/m) | 49.62 | 43.2 | −12.9% | 34.92 | 35.81 | 43.12 | 33.6 | 1.26 | 1.51 | 2.02 | 2.29 |
| O (μg/m) | 34.93 | 58.99 | 68.9% | 21.24 | 25.3 | 32.66 | 57.59 | 0.72 | 0.46 | 0.13 | 0.25 | |
| Suzhou | PM (μg/m) | 51.49 | 33.99 | −34.0% | 33.86 | 21.31 | 42.62 | 28.85 | 1.1 | 1.11 | 1.25 | 1.23 |
| O (μg/m) | 29.42 | 67.9 | 130.8% | 21.95 | 26.19 | 26.06 | 67.12 | 0.92 | 0.38 | 0.58 | 0.4 |
| City | Pollutant | ||||||
|---|---|---|---|---|---|---|---|
| Period I | Period II | Period I | Period II | Period I | Period II | ||
| Shanghai | PM-O | 1.321 | 0.843 | 0.112 | 0.115 | 0.349 | 0.292 |
| (0.062) | (0.064) | (0.132) | (0.122) | ||||
| Jiaxing | PM-O | 0.741 | 0.454 | 0.125 | 0.119 | 0.218 | 0.145 |
| (0.071) | (0.067) | (0.112) | (0.084) | ||||
| Nantong | PM-O | 0.556 | 0.389 | 0.116 | 0.120 | 0.189 | 0.142 |
| (0.066) | (0.082) | (0.103) | (0.082) | ||||
| Suzhou | PM-O | 1.146 | 0.583 | 0.113 | 0.113 | 0.292 | 0.269 |
| (0.066) | (0.123) | (0.135) | (0.123) |
| City | Pollutant | INTR Ratio | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Period I | Period II | Period I | Period II | Period I | Period II | Period I | Period II | Period I | Period II | ||
| Shanghai | PM-O | 0.237 | 0.177 | 0.972 | 0.550 | 0.112 | 0.115 | 0.972 | 0.550 | 73.59% | 65.32% |
| (0.146) | (0.138) | (0.132) | (0.122) | (0.062) | (0.064) | (0.132) | (0.122) | (9.98%) | (14.46%) | ||
| Jiaxing | PM-O | 0.093 | 0.026 | 0.523 | 0.309 | 0.125 | 0.119 | 0.523 | 0.309 | 70.58% | 68.16% |
| (0.132) | (0.108) | (0.112) | (0.084) | (0.071) | (0.067) | (0.112) | (0.084) | (15.10%) | (18.60%) | ||
| Nantong | PM-O | 0.073 | 0.023 | 0.368 | 0.247 | 0.116 | 0.120 | 0.368 | 0.247 | 66.10% | 63.41% |
| (0.122) | (0.106) | (0.103) | (0.082) | (0.066) | (0.082) | (0.103) | (0.082) | (18.49%) | (20.94%) | ||
| Suzhou | PM-O | 0.179 | 0.156 | 0.854 | 0.314 | 0.113 | 0.113 | 0.854 | 0.314 | 74.53% | 53.86% |
| (0.149) | (0.138) | (0.135) | (0.123) | (0.066) | (0.123) | (0.135) | (0.123) | (11.74%) | (21.01%) |
| City | Pollutant | (INTR ratio) | |||||
|---|---|---|---|---|---|---|---|
| Period I(A) | Period II(B) | Change(B−A)/A | Period I(C) | Period II(D) | Change(D-C) | ||
| Shanghai | PM-O | 1.321 | 0.843 | −36.2% | 73.59% | 65.32% | −8.3% |
| Jiaxing | PM-O | 0.741 | 0.454 | −38.8% | 70.58%) | 68.16% | −2.4% |
| Nantong | PM-O | 0.556 | 0.389 | −30.0% | 66.10% | 63.41% | −2.7% |
| Suzhou | PM-O | 1.146 | 0.583 | −49.1% | 74.53% | 53.86% | −20.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Su, F. The Dynamic Impacts of COVID-19 Pandemic Lockdown on the Multifractal Cross-Correlations between PM2.5 and O3 Concentrations in and around Shanghai, China. Atmosphere 2022, 13, 1964. https://doi.org/10.3390/atmos13121964
Li X, Su F. The Dynamic Impacts of COVID-19 Pandemic Lockdown on the Multifractal Cross-Correlations between PM2.5 and O3 Concentrations in and around Shanghai, China. Atmosphere. 2022; 13(12):1964. https://doi.org/10.3390/atmos13121964
Chicago/Turabian StyleLi, Xing, and Fang Su. 2022. "The Dynamic Impacts of COVID-19 Pandemic Lockdown on the Multifractal Cross-Correlations between PM2.5 and O3 Concentrations in and around Shanghai, China" Atmosphere 13, no. 12: 1964. https://doi.org/10.3390/atmos13121964
APA StyleLi, X., & Su, F. (2022). The Dynamic Impacts of COVID-19 Pandemic Lockdown on the Multifractal Cross-Correlations between PM2.5 and O3 Concentrations in and around Shanghai, China. Atmosphere, 13(12), 1964. https://doi.org/10.3390/atmos13121964






