Abstract
Volcanoes can be extremely damaging to the environment, human society, and also impact climate change. During volcanic eruption, massive amounts of gases and dust particles are thrown into the atmosphere and propagated instantaneously by the stratospheric circulation, resulting in a huge impact on the interactive pattern of the atmosphere. Here, we develop a climate network-based framework to study the temporal evolution of lower stratospheric atmosphere conditions in relation to a volcanic eruption, the Hunga Tonga-Hunga Ha’apai (HTHH) volcano, which erupted on 20 December 2021. Various spatial-temporal topological features of the climate network are introduced to analyze the nature of the HTHH. We show that our framework has the potential to identify the dominant eruption events of the HTHH and reveal the impact of the HTHH eruption. We find that during the eruption periods of the HTHH, the correlation behaviors in the lower stratosphere became much stronger than during normal periods. Both the degree and clustering coefficients increased significantly during the dominant eruption periods, and could be used as indications for the eruption of HTHH. The underlying mechanism for the observed cooperative mode is related to the impact of a volcanic eruption on global mass circulations. The study on the network topology of the atmospheric structure during a volcanic eruption provides a fresh perspective to investigate the impact of volcanic eruptions. It can also reveal how the interactive patterns of the atmosphere respond to volcanic eruptions and improve our understanding regarding the global impacts of volcanic eruptions.
1. Introduction
An undersea volcano at Hunga Tonga-Hunga Ha’apai (HTHH, 20.54 S, 175.38 W, as shown in Figure 1) began eruption on 20 December 2021 and reached a violent climax on 15 January 2022. The eruption intensity, represented by volcanic explosivity index (VEI), is estimated approximately as a level 5–6 and is one of the largest volcanic activities since the 1991 eruption of Mount Pinatubo [1,2]. It has been reported that about 0.4 million tons of emissions were sent into the stratosphere by this eruption [3]. Due to its massive eruption, extensive discussions have been aroused and focused on its climate impacts [4].
Figure 1.
The location of the Hunga Tonga-Hunga Ha’api volcano (HTHH, 20.54 S, 175.38 W).
Massive volcanic eruptions have significant impacts on weather and climate variability [4]. For example, during massive volcanic eruptions, large amounts of emissions are ejected. Once these emissions enter the stratosphere, they rapidly get distributed around the globe and influence the radiation balance immediately. As a result, precipitation and temperature patterns may be influenced on a global scale. Super-powerful eruptions can even trigger long-lasting climate disruptions and corresponding societal impacts [5,6,7,8,9,10]. For example, the 1815 Tambora eruption produced the “year without a summer” in 1816. Since volcanic eruptions are an important natural cause of changes in climate variability on many time scales, a lot of studies have focused on the different impacts of these events. Based on historical climate records, effects such as decreased temperature [11] and reduction of the diurnal cycle [12,13] following the large explosive volcanic eruptions are observed. Together with remote sensing measurements, related chemical and dynamical processes are studied and simulated in climate models to discuss the long-term responses in the climate system. By applying numerical modeling methods, phenomena such as suppressed global water cycle [4,14] and anomalous winter Eurasian warming [4,15] are identified. In recent studies, the long-term impact of the HTHH eruption on the global mean surface air temperature is also quantitatively estimated by climate models [16]. Since the ejection of unprecedented water vapor into the stratosphere is a significant feature of this eruption, the potential trajectory and long-term impact of ejected water vapor is also the focus of researchers [17] and is estimated in climate models [18].
Although numerical models can give good predictions about future scenarios under the background of volcanic eruptions, they usually contain a huge number of coupled dynamical equations. This makes the models extremely complex and time consuming. Most importantly, it is inconvenient and impractical in such models to figure out how climate variables cooperate to respond to the external forcing by volcanic eruptions. In the process by which a volcanic eruption propagates its emissions and spreads its influence, it is thus necessary to consider how atmospheric variables in different regions negotiate in response to the influence. This requires a new perspective, such as climate network, to analyze the collective behaviors of the atmosphere. However, as far as we know, there is still lack of the framework required to study the impact of volcanic eruptions from such a point of view. To fill this gap, we apply the complex networks approach to focus on the atmospheric correlation patterns, which formed during the massive eruption of the HTHH.
Network theory is a powerful tool used to study and understand the collective behavior of complex systems [19,20,21]. During the past decades, network theory has demonstrated its power and potential in the study of a wide range of real-world complex systems for both nature and society [19,22,23,24,25,26,27], e.g., the Internet, ecological network, power grid systems, science collaboration networks, disease spread, etc.
Recently, network theory has also been successfully applied towards the understanding of complex climate phenomena [28]. Climate networks are constructed from spatio-temporal datasets, where the spatial locations are regarded as nodes, and connections are established between nodes that exhibit significant statistical similarity [29,30,31,32,33,34,35,36,37]. This way, the climate network becomes a very effective tool to detect significant teleconnection patterns and identify critical nodes in the climate system. In particular, it is a very promising approach used to identify and predict large scale climate phenomena such as El Niño [36,38,39], the Indian Summer Monsoon [37,40,41], and tropical cyclones [42].
In climate networks, the local and global structural properties of climate phenomena are characterized by a variety of network measures. For instance, the local clustering coefficient can be associated with the spatial homogeneity of a rainfall field [43,44]. The regions of high betweenness centrality can reveal a flow of energy and information that can be related to transport phenomena such as global surface ocean currents and winds [33,44]. The degree and clustering coefficients can exhibit signatures for the occurrence of tropical cyclones and show their tracks [42].
However, as far as we know, the climate network framework has not yet been applied to measure the impacts of volcanic eruptions. In this study, we apply the climate networks approach to investigate the impacts of the massive eruption of the HTHH on the atmosphere. Climate networks that evolve in time during the eruption of the HTHH, are constructed on a global scale. Network measures such as degree and clustering coefficient are adopted to characterize the influence of volcanic eruptions on atmospheric variability. Our analyses show that the cooperative mode of the lower stratosphere atmosphere is exhibited in the degree field and clustering coefficient field as a response to the eruption of the HTHH.
2. Data and Methodology
2.1. Data
In this study, we use the ERA5 reanalysis temperature data with 3-hourly temporal resolution at 200 hPa [45] to construct the climate network. Since the massive eruption began on 20 December 2021 and ended on 15 January 2022, we chose the period spanning from 15 November 2021 to 15 February 2022 as the focused period. This period starts about one month ahead of the eruption and ends about one month after the eruption. Considering that the impact of the eruption may not be localized, we take the region between 45 S–45 N as the focused area. A spatial (zonal and meridional) resolution of is used, which proves to be sufficient for our analysis and results in N = 46 × 180 = 8280 nodes in the network.
2.2. Methods
We consider overlapping short time windows and construct the climate network for each given window. The length of the time window is taken to be 10 days. The climate network evolves in daily steps, which means that the successive time windows have 9 days of overlap. The link strength between each pair of nodes, i and j for time window t is measured by the maximum value of the absolute cross-correlation between the two nodes. The cross-correlation between i and j is defined by
where t indicates the middle date of the time window with 0 day shift, is the time lag, with 5 days. Therefore, the link strength is defined as
We use the average of the top 5% thresholds of link strengths for all sliding windows as
where indicates the top 5% threshold of link strengths for the sliding window t. Only links whose link strengths exceed are considered as significant links, and the adjacency matrix for each sliding window t is defined as
2.3. Network Measures
In this study, the topology of the interaction patterns in the climate network are defined as network measures such as the degree and clustering coefficient. The degree of a node i in a network is the number of connections attached to it from all other nodes:
where N is the total number of nodes in the network, and is the adjacency matrix. Regions with higher connectivity have larger values of degree and indicate more interactivity with other regions; while regions of low degree values are isolated and have little interaction with the surrounding area.
The clustering coefficient is the measure of degree to which nodes in a network tend to cluster together. The local clustering coefficient [46] of a node i in a network quantifies how close its neighbors are to being a clique (i.e., the nodes are all connected to each other), that is, the average probability that a pair of node i’s connected neighbors, j and h, are also connected. Mathematically, we calculate the number of connected pairs among a node i’s neighbors, and divide it by the total number of possible pairs between these neighbors,
The local clustering coefficient, measures the interactive relationship among node i’s neighbors. If the local clustering coefficient of a node i is high, then its neighbors are also closely coupled.
The global clustering coefficient C, also known as transitivity [19], measures the average probability that two neighbors of a node are themselves neighbors for the whole network. It measures the density of connection triangles in the network and is defined as the fraction of paths of length two in the network that are closed. This is equivalent to the number of closed triplets over the total number of triplets. For an undirected network with an adjacency matrix , the global clustering coefficient is mathematically expressed as
This global clustering coefficient gives an indication of the clustering in the whole network. If C = 1, perfect transitivity occurs in the network, i.e., all nodes of the network are connected. The global clustering coefficient is of interest because a higher C than expected by chance indicates the formation of structures of high connectivity in a network, e.g., the presence of tightly-knit groups characterized by a high density of ties in a social network.
3. Results
In the following, we show how the massive volcanic eruption at the HTHH (from 20 December 2021 to 15 January 2022) impacts the atmosphere system by using our network-based approach. There are two main dominant eruptive activities during this period. The first dominant one began on 20 December 2021 and ended on 21 December 2021. The second one began on 13 January 2022 and ended on 15 January 2022. The evolution of the average temperature around the eruption location at lower stratosphere (200hPa level) and surface level (2 m) are shown in Figure 2a,b, respectively. The averaged region is centered at the eruption location (20.54 S, 175.38 W) and extends from 177.88 W to 172.88 W and from 23.04 S to 18.04 S. The two dominant eruptions’ staring dates are marked by red dashed lines. We find that local temperature series at the 200 hPa level exhibits a more significant response to the dominant eruptive events compared to the surface level. Remarkable declining trends that last for several days are observed after the dominant eruptive events for the local 200 hPa temperature series (Figure 2a), while for the local surface temperature series, these responses are not so sensitive as the diurnal cycle plays a major role. This result is consistent with the fact that a huge amount of volcanic emissions was blasted into the lower stratosphere, which led to transient cooling due to an increase of planetary albedo. Due to the higher sensitivity to the volcanic eruptions, the temperature field at the 200 hPa level is used to construct the climate network, which can thus better reveal the volcanic eruptions’ transient impacts on the atmosphere.
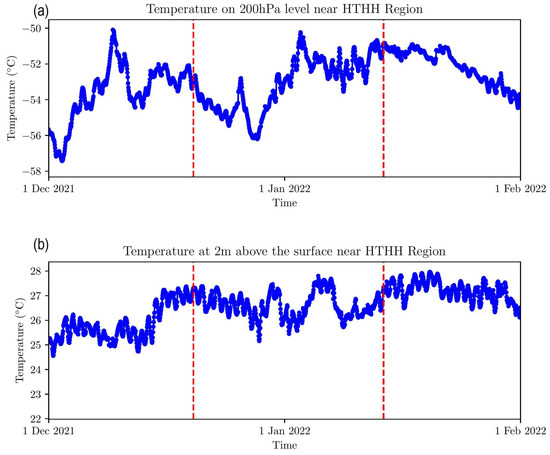
Figure 2.
The average temperature series at (a) 200 hPa and (b) 2 m around the HTHH. The averaged region is centered at the eruption location (20.54 S, 175.38 W) and extends from 177.88 W to 172.88 W and from 23.04 S to 18.04 S. The start dates (20 December 2021 and 13 January 2022) of the two dominant eruptions of the HTHH are highlighted by two dashed vertical red lines.
We first examine how link strength r (before setting the threshold ) evolves with the volcanic eruptions. The probability density function (PDF) of link strength r for different climate networks (with different periods) are presented in Figure 3a. We find that the average link strength is higher during the dominant eruption periods (16–25 December 2021 and 9–18 January 2022) than other normal periods, as shown in Figure 3b. Our results indicate that during the eruption periods of the HTHH, the correlation behaviors between each pair of nodes become stronger than during normal periods.
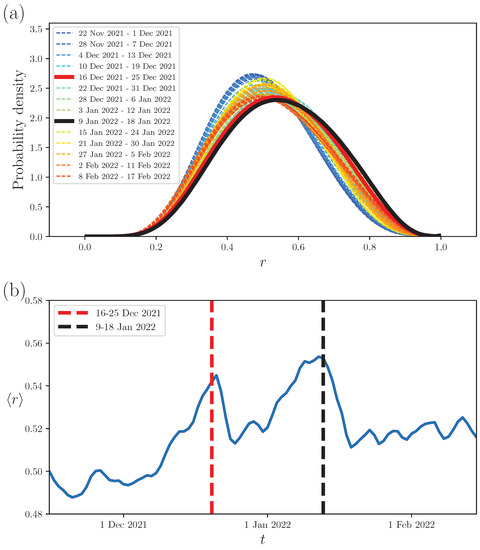
Figure 3.
(a) The probability density distribution function of link strength r for all climate networks (with different periods). The distribution for the dominant eruptions of the HTHH are remarked by red and black solid lines, respectively. The distribution for the other periods are shown in dashed lines. (b) The average link strength as a function of time is presented by the blue line. Here, the start dates of the two dominant eruptions correspond to the middle day of the two periods.
In the following, we construct climate networks by setting a fixed threshold for all sliding periods, i.e., if the link strength , then the nodes i and j are connected by an edge; otherwise, i and j are disconnected. In this study, the average of the top 5% thresholds of link strengths for all sliding windows is defined as , and the value of is 0.765 for the constructed networks.
For each constructed climate network, we consider the degree and the clustering coefficient as the measures to analyze the topology and correlation patterns of the networks and reveal the impacts of the HTHH eruption. Figure 4a,b depict the average degree and global clustering coefficient C(t), Equation (7), as a function of time, respectively. Here, the time t corresponds to the middle date of each time window. We observe that both and C(t) are increasing during the dominant eruption periods compared to the normal times, which indicates a large-scale cooperative mode—linking the HTHH and the rest during the volcanic events. The underlying mechanism for the observed cooperative mode is due to the volcanic eruptions potentially affecting the global/localized regions through teleconnection/short-range paths.
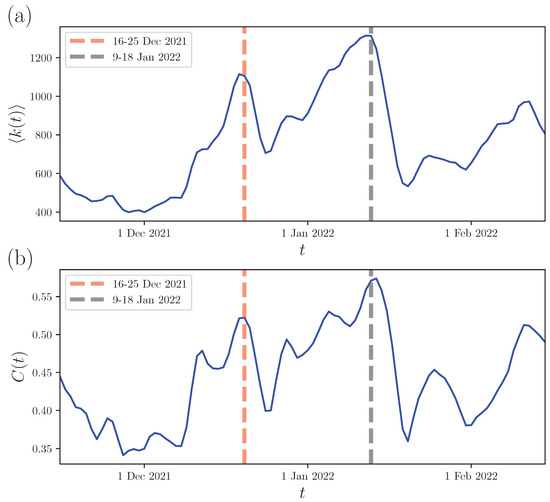
Figure 4.
(a) The average degree and (b) the global clustering coefficient for each evolving climate network are presented.
In order to analyze the spatial cooperative pattern of the climate network, we consider the spatial features of the degree and the local clustering coefficient fields, which can reveal the cooperation pattern of the temperature filed at the lower stratosphere as a response to the massive eruption of the HTHH. Figure 5 depicts the evolution of the spatial structure of the degree fields before (Figure 5a), during (Figure 5b,c), and after (Figure 5d) the eruption events of the HTHH. Compared with normal periods, we find that the intensity of the degree fields exhibit an enhanced modality during the eruption periods. In particular, these enhanced regions are spreading widely over the extratropical region for both hemispheres and exhibit roughly zonal symmetry (see Figure 5b,c). This corresponds to the downward transport area of the global mass circulation in the stratosphere. Our results indicate that the interaction of the nodes in these regions become more enhanced due to the impact of the volcanic eruption, and we associate the underlying mechanism with the impacts of the volcanic eruption through global mass circulations.
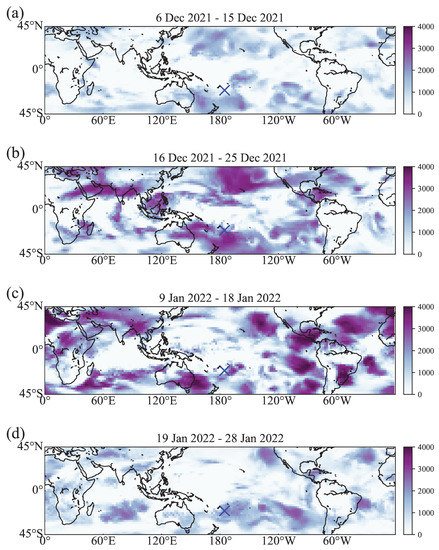
Figure 5.
Network degree fields over the period (a) before the eruption, (b) the first dominant eruption, (c) the second dominant eruption, and (d) after the eruption of HTHH are presented. The corresponding periods are marked at the top of each subplot. The degree of nodes in the extratropics increases greatly during the eruption periods, which may be related to the impacts of volcanic eruption on global mass circulation.
In addition, we present the evolution of the local clustering coefficient fields before (Figure 6a), during (Figure 6b,c), and after (Figure 6d) the eruption events of HTHH. In similarity, we uncover that the intensity of the local clustering coefficients becomes prominent almost throughout the entire focused region (45 S–45 N) during the dominant eruption periods. The areas with a smaller clustering coefficient (cavity in Figure 6) that are located near the equator also shrunk remarkably. It indicates that due to the effect of the volcanic eruptions, the nodes become more coherent. Notably, we find that the density of the local clustering coefficient in the west side of the HTHH is slightly higher than the east during the dominant eruption periods. The underlying mechanism may be related to the constantly westward force in the stratosphere.
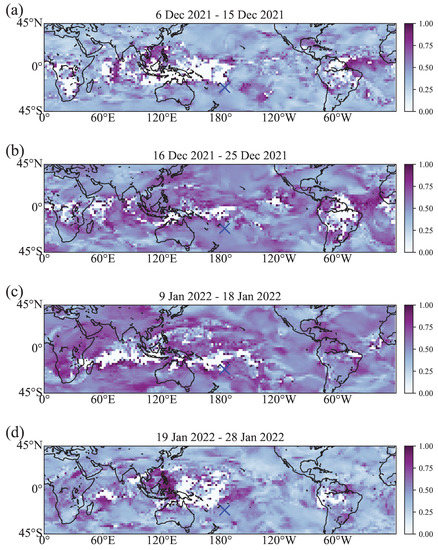
Figure 6.
Network local clustering coefficient fields over the period (a) before eruption, (b) the first dominant eruption, (c) the second dominant eruption, and (d) after the eruption of the HTHH. The corresponding periods are marked at the top of each subplot.
4. Discussion
The eruption of the HTHH in early 2022 ejected enormous quantities of ash, volcanic gases, and water vapor into the stratosphere. According to remote sensing measurements, about 0.4 million tons of emissions were sent into the stratosphere and propagated rapidly around the globe. These processes influenced the radiation balance and resulted in changes in the atmospheric dynamics.
Most previous studies estimated the impact of the HTHH by using climate models. For example, Zhang et al., used the radiation equilibrium model to give a quantitative estimation of the decrease in global average temperature [16]. The possible trajectory and potential climate impact of water vapor are also simulated and estimated [17,18]. Although numerical models can give good predictions about future scenarios under the background of a volcanic eruption, the extremely coupled dynamical equations in these models makes it difficult to figure out how atmospheric variables in different regions cooperate in response to the eruption of the HTHH. Since the propagation of volcanic emissions and the spread of volcanic influence are not a localized isolated process, the dynamic correlation patterns and its cooperative modes could provide a fresh perspective to understand the impacts of volcanic eruptions.
In this study, the climate network paradigm is introduced to study the temporal evolution of lower stratospheric atmosphere conditions in relation to the eruption of the HTHH. The cooperative mode and interactive patterns are investigated. We found that the correlation behaviors in the lower stratosphere become much stronger in the eruption periods of the HTHH. The network structure acts more interactive and transitive than norm periods. Both mean degree and global clustering coefficients increase significantly during the dominant eruption periods, and exhibit as indications for the eruption of the HTHH. The intensity of the degree fields exhibits enhanced modality during the eruption periods. The enhanced regions spread widely over the extratropical regions for both hemispheres and exhibit zonal symmetry. The local clustering coefficient become prominent almost throughout the global scale.
5. Conclusions
The climate networks approach is an effective tool for studying interactive patterns for climate phenomena [29]. It has been applied successfully to study the impacts of large-scale extreme climate events such as El Niño, Indian Monsoon, and more [28]. It also has the potential to study the evolution of weather conditions before, during, and after the outbreak of extreme events by using evolving climate networks. In this work, we have applied this approach to study the impact of the massive eruption of the HTHH from 20 December 2021 to 15 January 2022.
Based on the temperature filed over the region between 45 S and 45 N in the lower stratosphere, insightful information about collective interaction patterns and underlying dynamical organization during the eruption period were extracted. We employed sliding time windows with 10-day to construct evolving climate networks.The sliding windows shifted successively by 1 day from 15 November 2021 to 15 February 2022, i.e., sliding day-by-day from the period before the eruption to the end of the eruption.
We found that during the eruption periods, the temperature fields in lower stratosphere were more interactive and transitive. Both degree and clustering coefficients increased significantly during the dominant eruption periods. The degree of nodes in the extratropics increased during the eruption periods, which is closely related to the impacts of the volcanic eruption on global mass circulation. The local clustering coefficients become prominent almost throughout the global scale, which indicates that under the influence of volcanic eruptions, nodes on the global scale tend to be more coherent.
Our approach developed here offers us a deeper insight into the understanding of the changes in the interactive structure of the lower stratosphere under the influence of the volcanic eruption. It has the possible potential to detect the eruption events and their direct impacts.
Author Contributions
Conceptualization, J.F. and J.M.; methodology, J.F., J.M., Y.S. and Y.Z.; software, Y.S. and Y.Z.; validation, Y.S. and Y.Z.; formal analysis, Y.S.; investigation, Y.S.; resources, J.F.; data curation, Y.S.; writing—original draft preparation, Y.S.; writing—review and editing, J.F. and J.M.; visualization, Y.S.; supervision, J.F. and J.M; project administration, J.F.; funding acquisition, J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by grants from the National Natural Science Foundation of China (Grants No. 12275020, 12135003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data/reanalysis that supports the findings of this study are publicly available online: ERA5 Reanalysis data [45], https://cds.climate.copernicus.eu/, accessed on 1 September 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Poli, P.; Shapiro, N.M. Rapid Characterization of Large Volcanic Eruptions: Measuring the Impulse of the Hunga Tonga Ha’apai Explosion From Teleseismic Waves. Geophys. Res. Lett. 2022, 49, e2022GL098123. [Google Scholar] [CrossRef]
- IMS observations of infrasound and acoustic-gravity waves produced by the January 2022 volcanic eruption of Hunga, Tonga: A global analysis. Earth Planet. Sci. Lett. 2022, 591, 117639. [CrossRef]
- Global Sulfur Dioxide Monitoring Galleries. Available online: https://so2.gsfc.nasa.gov/tropomi_2019_now.html#2022 (accessed on 25 September 2022).
- Robock, A. Volcanic eruptions and climate. Rev. Geophys. 2000, 38, 191–219. [Google Scholar] [CrossRef]
- Baldini, J.U.; Brown, R.J.; McElwaine, J.N. Was millennial scale climate change during the Last Glacial triggered by explosive volcanism? Sci. Rep. 2015, 5, 17442. [Google Scholar] [CrossRef] [PubMed]
- Miller, G.H.; Geirsdóttir, Á.; Zhong, Y.; Larsen, D.J.; Otto-Bliesner, B.L.; Holland, M.M.; Bailey, D.A.; Refsnider, K.A.; Lehman, S.J.; Southon, J.R.; et al. Abrupt onset of the Little Ice Age triggered by volcanism and sustained by sea-ice/ocean feedbacks. Geophys. Res. Lett. 2012, 39, 50168. [Google Scholar] [CrossRef]
- Büntgen, U.; Arseneault, D.; Boucher, É.; Churakova, O.V.; Gennaretti, F.; Crivellaro, A.; Hughes, M.K.; Kirdyanov, A.V.; Klippel, L.; Krusic, P.J.; et al. Prominent role of volcanism in Common Era climate variability and human history. Dendrochronologia 2020, 64, 125757. [Google Scholar] [CrossRef]
- Grattan, J.; Brayshay, M.; Sadler, J. Modelling the distal impacts of past volcanic gas emissions. Evidence of Europe-wide environmental impacts from gases emitted during the eruption of Italian and Icelandic volcanoes in 1783 [Vers la modélisation des impacts distaux des gaz d’anciennes éruptions volcaniques. Exemples européens liés à l’activité de volcans italiens et islandais en 1783]. Quaternaire 1998, 9, 25–35. [Google Scholar]
- Stothers, R.B. The great Tambora eruption in 1815 and its aftermath. Science 1984, 224, 1191–1198. [Google Scholar] [CrossRef]
- Robock, A. Snow and ice feedbacks prolong effects of nuclear winter. Nature 1984, 310, 667–670. [Google Scholar] [CrossRef]
- Mitchell, J.M., Jr. Recent secular changes of global temperature. Ann. New York Acad. Sci. 1961, 95, 235–250. [Google Scholar] [CrossRef]
- Robock, A.; Mass, C. The Mount St. Helens volcanic eruption of 18 May 1980: Large short-term surface temperature effects. Science 1982, 216, 628–630. [Google Scholar] [CrossRef] [PubMed]
- Mass, C.; Robock, A. The short-term influence of the Mount St. Helens volcanic eruption on surface temperature in the Northwest United States. Mon. Weather. Rev. 1982, 110, 614–622. [Google Scholar] [CrossRef]
- Timmreck, C. Modeling the climatic effects of large explosive volcanic eruptions. Wiley Interdiscip. Rev. Clim. Chang. 2012, 3, 545–564. [Google Scholar] [CrossRef]
- Stenchikov, G.; Robock, A.; Ramaswamy, V.; Schwarzkopf, M.D.; Hamilton, K.; Ramachandran, S. Arctic Oscillation response to the 1991 Mount Pinatubo eruption: Effects of volcanic aerosols and ozone depletion. J. Geophys. Res. Atmos. 2002, 107, ACL-28. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Li, J.; Duan, Y.; Zhu, C.; He, J. Potential Impact of Tonga Volcano Eruption on Global Mean Surface Air Temperature. J. Meteorol. Res. 2022, 36, 1–5. [Google Scholar] [CrossRef]
- Millan, L.; Santee, M.L.; Lambert, A.; Livesey, N.J.; Werner, F.; Schwartz, M.J.; Pumphrey, H.C.; Manney, G.L.; Wang, Y.; Su, H.; et al. The Hunga Tonga-Hunga Ha’apai Hydration of the Stratosphere. Geophys. Res. Lett. 2022, 49, e2022GL099381. [Google Scholar] [CrossRef]
- Vömel, H.; Evan, S.; Tully, M. Water vapor injection into the stratosphere by Hunga Tonga-Hunga Ha’apai. Science 2022, 377, 1444–1447. [Google Scholar] [CrossRef]
- Newman, M. Networks; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [CrossRef]
- Barabási, A.L. Scale-free networks: A decade and beyond. Science 2009, 325, 412–413. [Google Scholar] [CrossRef]
- Cohen, R.; Havlin, S. Complex Networks: Structure, Robustness And Function; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [CrossRef]
- Newman, M.E.J. Scientific collaboration networks. I. Network construction and fundamental results. Phys. Rev. E 2001, 64, 016131. [Google Scholar] [CrossRef] [PubMed]
- Brockmann, D.; Helbing, D. The Hidden Geometry of Complex, Network-Driven Contagion Phenomena. Science 2013, 342, 1337–1342. [Google Scholar] [CrossRef] [PubMed]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925. [Google Scholar] [CrossRef]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef]
- Fan, J.; Meng, J.; Ludescher, J.; Chen, X.; Ashkenazy, Y.; Kurths, J.; Havlin, S.; Schellnhuber, H.J. Statistical physics approaches to the complex Earth system. Phys. Rep. 2021, 896, 1–84. [Google Scholar] [CrossRef] [PubMed]
- Ludescher, J.; Martin, M.; Boers, N.; Bunde, A.; Ciemer, C.; Fan, J.; Havlin, S.; Kretschmer, M.; Kurths, J.; Runge, J.; et al. Network-based forecasting of climate phenomena. Proc. Natl. Acad. Sci. USA 2021, 118, e1922872118. [Google Scholar] [CrossRef] [PubMed]
- Tsonis, A.A.; Swanson, K.L. Topology and Predictability of El Niño and La Niña Networks. Phys. Rev. Lett. 2008, 100, 228502. [Google Scholar] [CrossRef] [PubMed]
- Yamasaki, K.; Gozolchiani, A.; Havlin, S. Climate Networks around the Globe are Significantly Affected by El Niño. Phys. Rev. Lett. 2008, 100, 228501. [Google Scholar] [CrossRef]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. Complex networks in climate dynamics. Eur. Phys. J. Spec. Top. 2009, 174, 157–179. [Google Scholar] [CrossRef]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. The backbone of the climate network. EPL Europhys. Lett. 2009, 87, 48007. [Google Scholar] [CrossRef]
- Barreiro, M.; Marti, A.C.; Masoller, C. Inferring long memory processes in the climate network via ordinal pattern analysis. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 013101. [Google Scholar] [CrossRef] [PubMed]
- Martin, E.A.; Paczuski, M.; Davidsen, J. Interpretation of link fluctuations in climate networks during El Niño periods. EPL Europhys. Lett. 2013, 102, 48003. [Google Scholar] [CrossRef]
- Fan, J.; Meng, J.; Ashkenazy, Y.; Havlin, S.; Schellnhuber, H.J. Network analysis reveals strongly localized impacts of El Niño. Proc. Natl. Acad. Sci. USA 2017, 114, 7543–7548. [Google Scholar] [CrossRef]
- Fan, J.; Meng, J.; Ludescher, J.; Li, Z.; Surovyatkina, E.; Chen, X.; Kurths, J.; Schellnhuber, H.J. Network-based approach and climate change benefits for forecasting the amount of indian monsoon rainfall. J. Clim. 2022, 35, 1009–1020. [Google Scholar]
- Ludescher, J.; Gozolchiani, A.; Bogachev, M.I.; Bunde, A.; Havlin, S.; Schellnhuber, H.J. Improved El Niño forecasting by cooperativity detection. Proc. Natl. Acad. Sci. USA 2013, 110, 11742–11745. [Google Scholar] [CrossRef] [PubMed]
- Ludescher, J.; Gozolchiani, A.; Bogachev, M.I.; Bunde, A.; Havlin, S.; Schellnhuber, H.J. Very early warning of next El Niño. Proc. Natl. Acad. Sci. USA 2014, 111, 2064–2066. [Google Scholar] [CrossRef] [PubMed]
- Malik, N.; Bookhagen, B.; Marwan, N.; Kurths, J. Analysis of spatial and temporal extreme monsoonal rainfall over South Asia using complex networks. Clim. Dyn. 2012, 39, 971–987. [Google Scholar] [CrossRef]
- Stolbova, V.; Martin, P.; Bookhagen, B.; Marwan, N.; Kurths, J. Topology and seasonal evolution of the network of extreme precipitation over the Indian subcontinent and Sri Lanka. Nonlinear Process. Geophys. 2014, 21, 901–917. [Google Scholar] [CrossRef]
- Gupta, S.; Boers, N.; Pappenberger, F.; Kurths, J. Complex network approach for detecting tropical cyclones. Clim. Dyn. 2021, 57, 3355–3364. [Google Scholar] [CrossRef]
- Cheung, K.K.; Ozturk, U. Synchronization of extreme rainfall during the Australian summer monsoon: Complex network perspectives. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 063117. [Google Scholar] [CrossRef]
- Boers, N.; Bookhagen, B.; Marwan, N.; Kurths, J.; Marengo, J. Complex networks identify spatial patterns of extreme rainfall events of the South American Monsoon System. Geophys. Res. Lett. 2013, 40, 4386–4392. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).