Evaluation of the Dynamical–Statistical Downscaling Model for Extended Range Precipitation Forecasts in China
Abstract
1. Introduction
2. Data and Methods
2.1. Datasets
2.1.1. Forecasting Data
2.1.2. Reanalysis Data
2.1.3. Study Area
2.2. Correction Methods
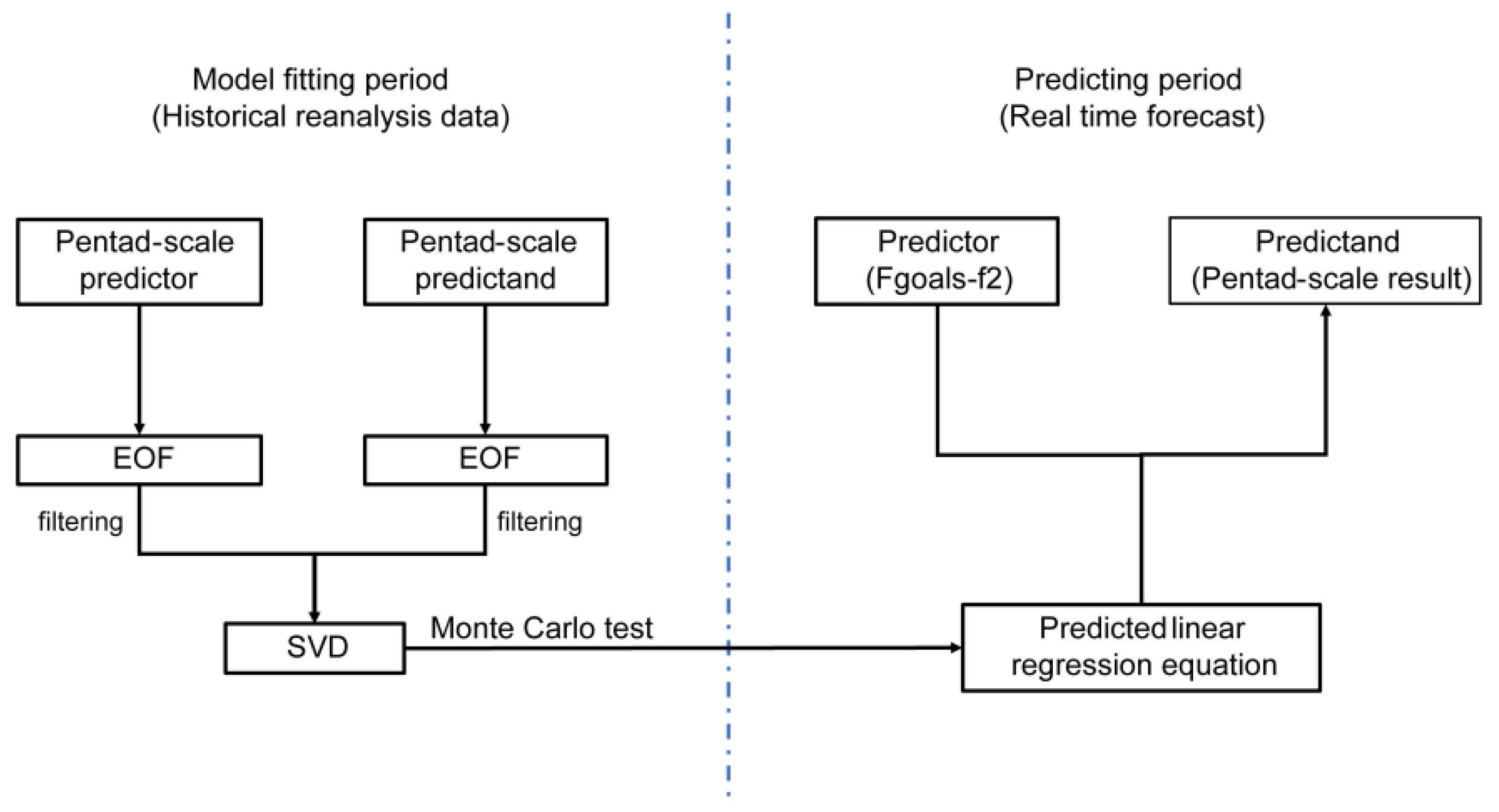
2.2.1. Dynamical–Statistical Downscaling Model
- (1)
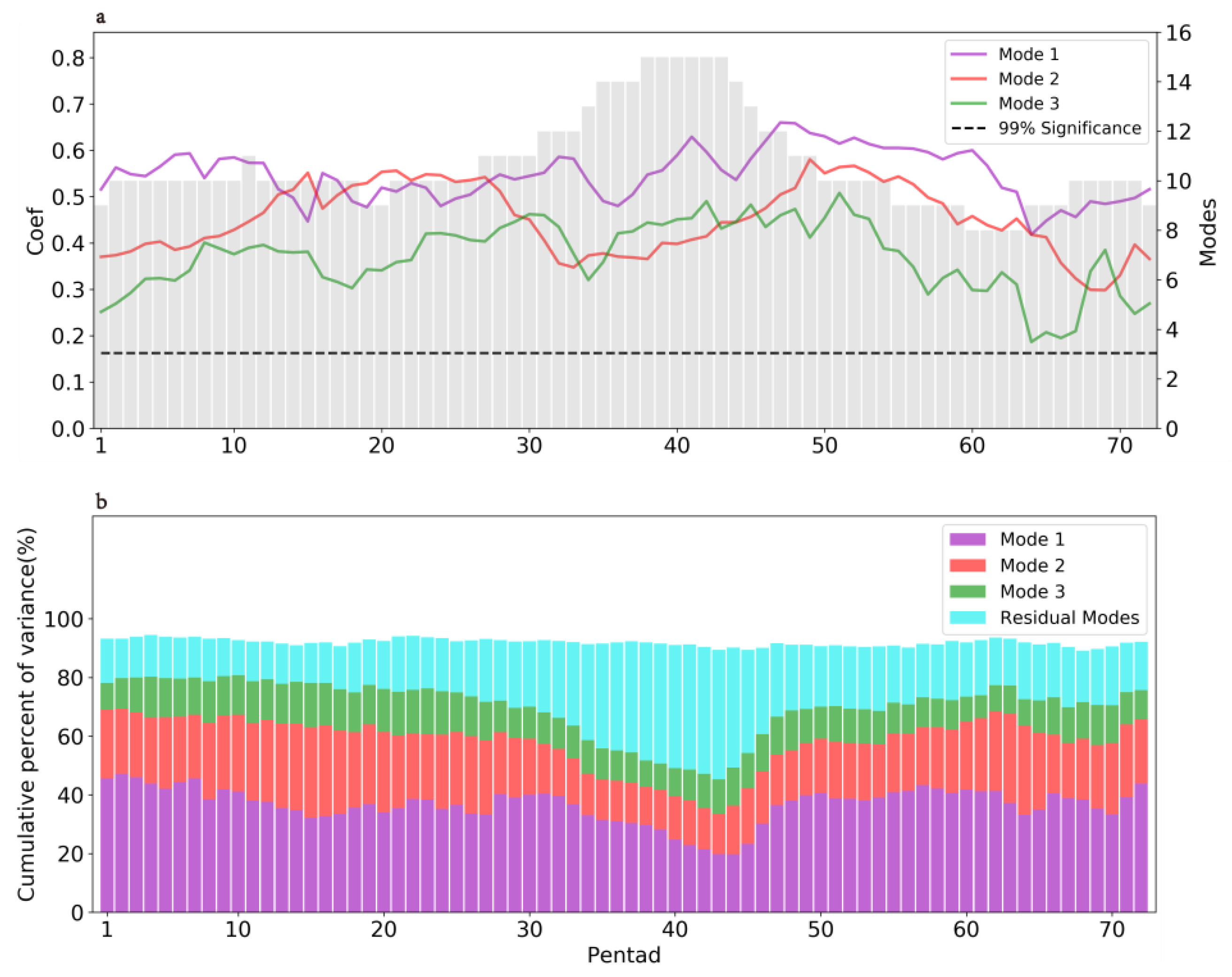
- Empirical orthogonal function (EOF) analysis was performed on the historical reanalysis data in the fitting period for each pentad (including precipitation and Z500). For each pentad, the time series of precipitation was reconstructed with its EOF principal components to filter any spatial noise. Only those time series and principal components of the first 90% of contribution variance were retained in the variable reconstruction. The Z500 field was reconstructed in the same way as the precipitation field;
- (2)
- SVD was used to obtain the coupled mode between the predictands and predictors. The coupled SVD modes, the singular values of which were above the noise level, were extracted for each pentad. It is noteworthy that all the singular values of these SVD modes passed the Monte Carlo test [25];
- (3)
- For each pentad, a linear regression equation was established via the coupled SVD time coefficients of the predictands and predictors and then a downscaling prediction model was established for each pentad. A 72 pentad DSDM was therefore established. The SVD of the model-fitting period is shown as Equations (1)–(4).
2.2.2. Ensemble Average of the Numerical Prediction Model
2.3. Evaluation Methods
2.3.1. Anomaly Correlation Coefficient
2.3.2. Temporal Correlation Coefficient
2.3.3. Mean Square Skill Score Index
2.3.4. Regional Average
2.4. Formatting of Mathematical Components
3. Evaluation of the Pentad DSDM
3.1. Evaluation of the Pentad DSDM Precipitation Reforecast
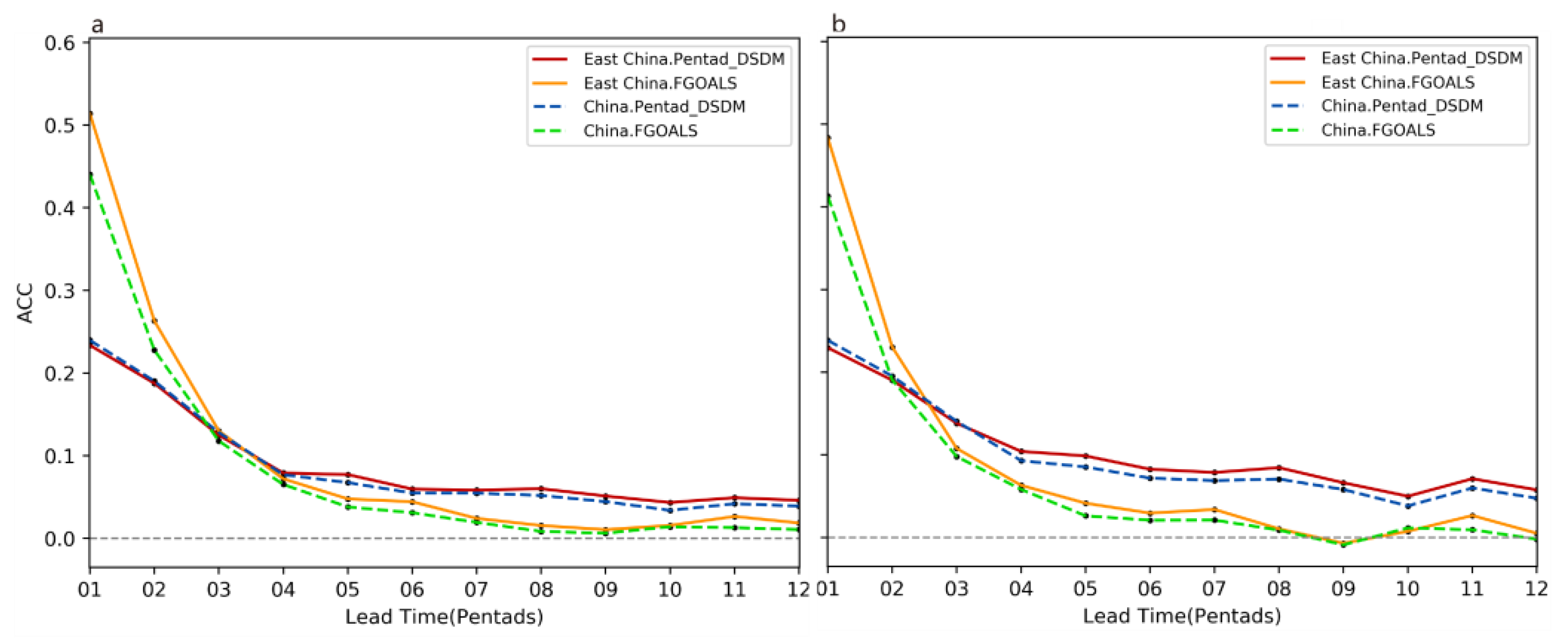
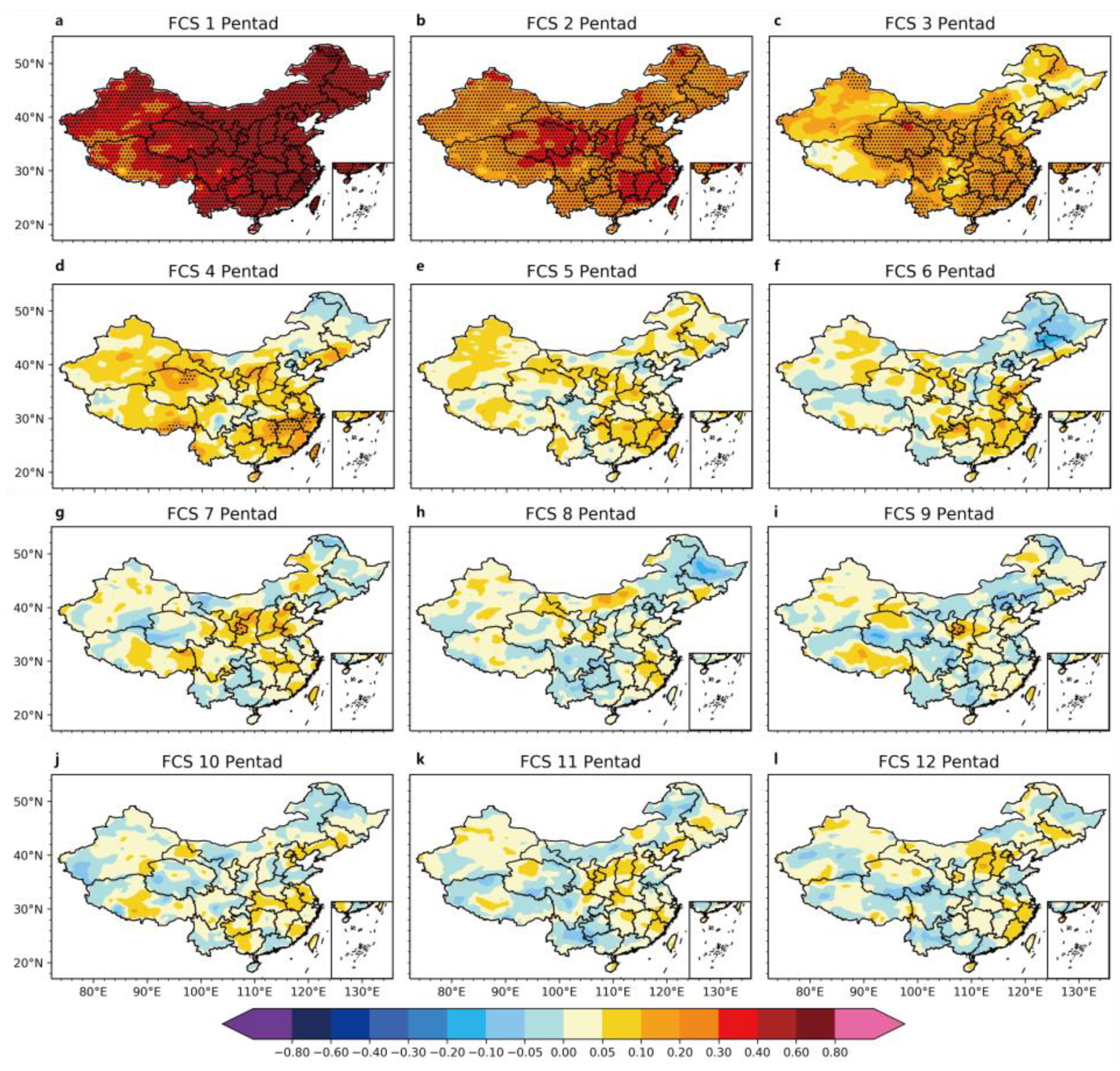
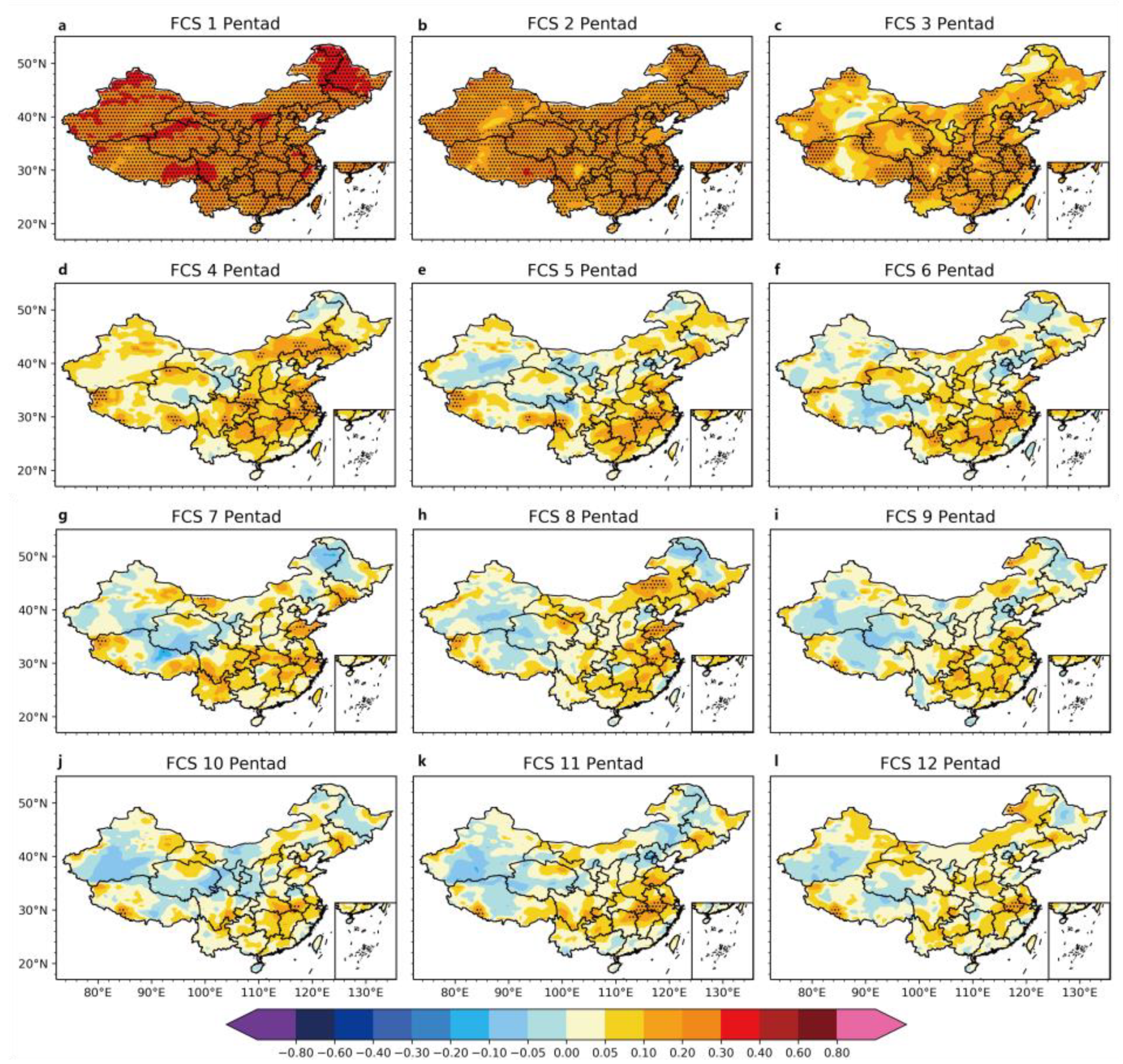
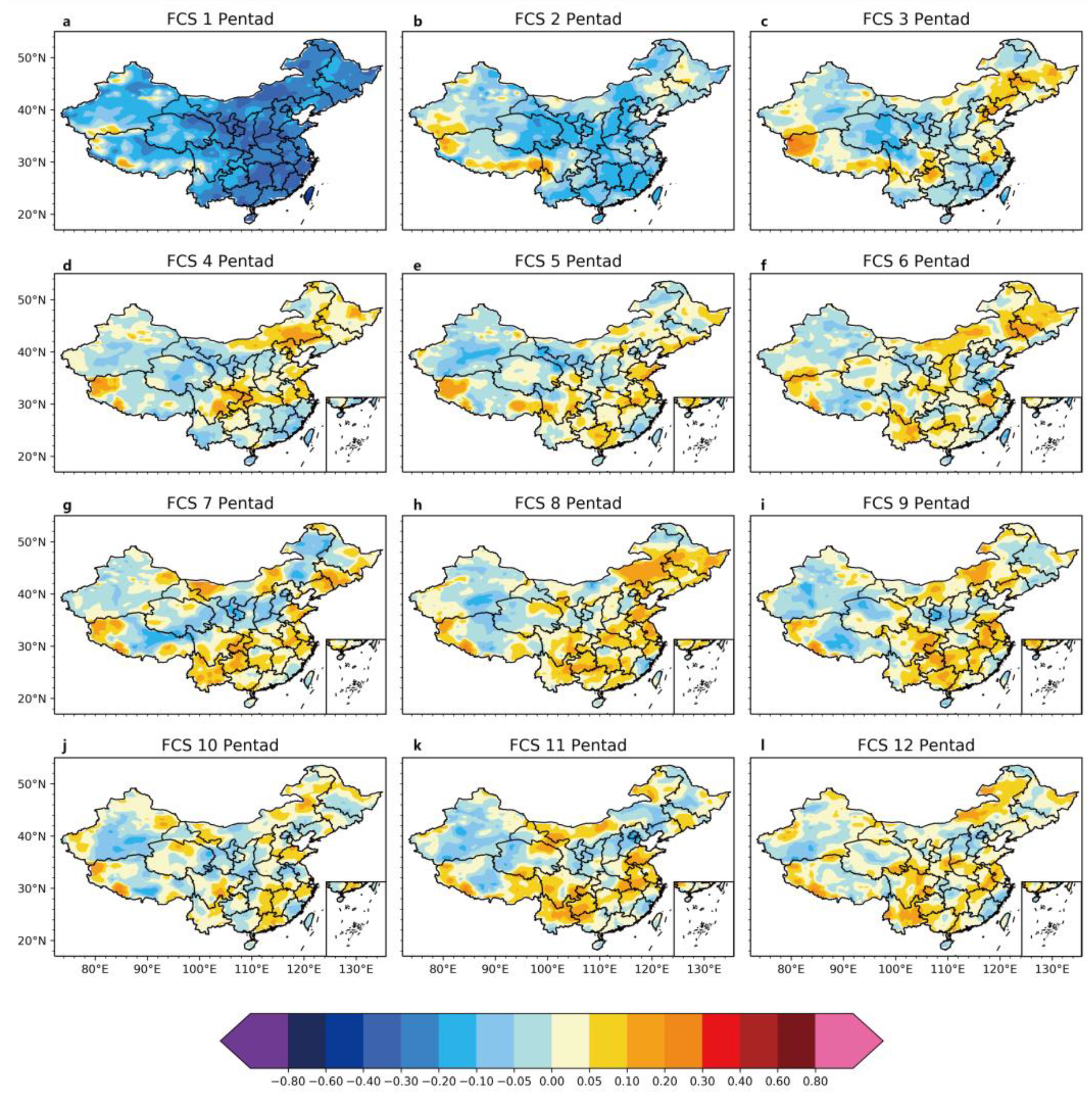
3.1.1. ACCs for Precipitation Forecast
3.1.2. TCCs for Precipitation Forecasts
3.1.3. MSSSs for Precipitation Forecasts
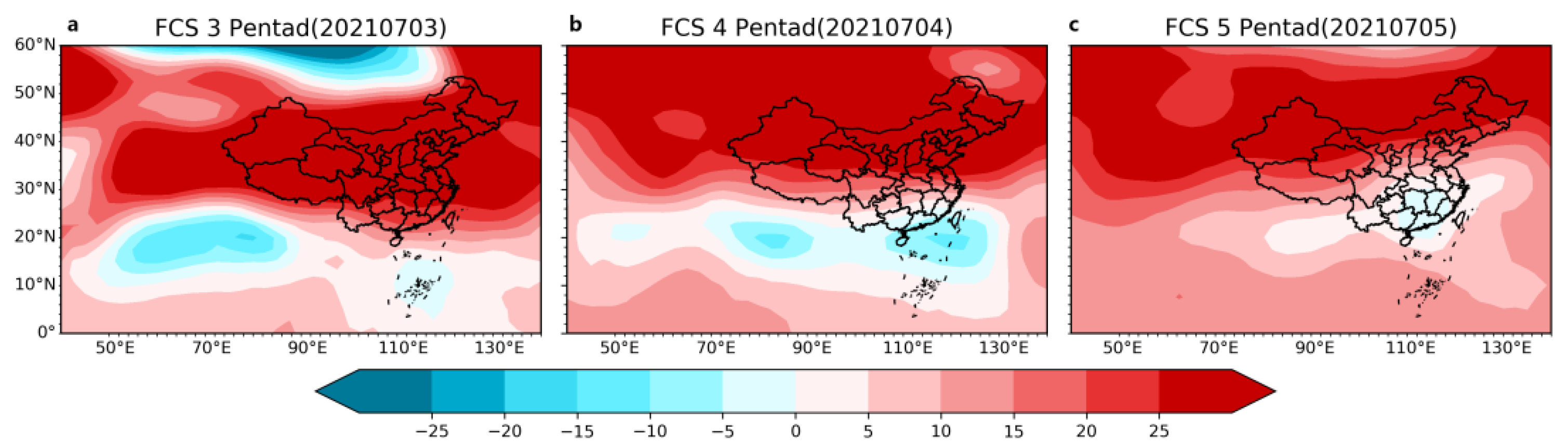
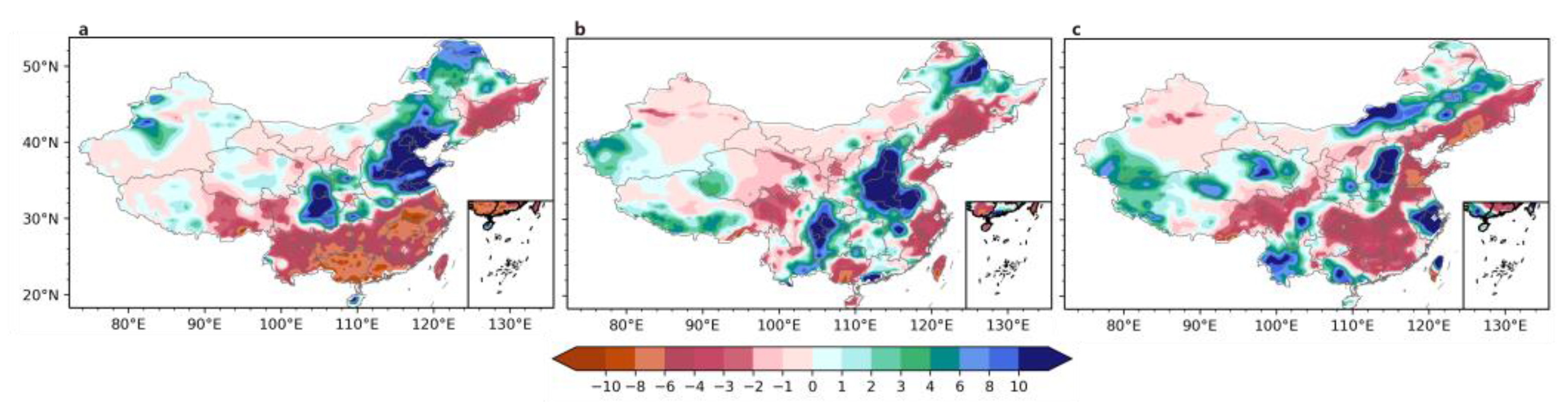
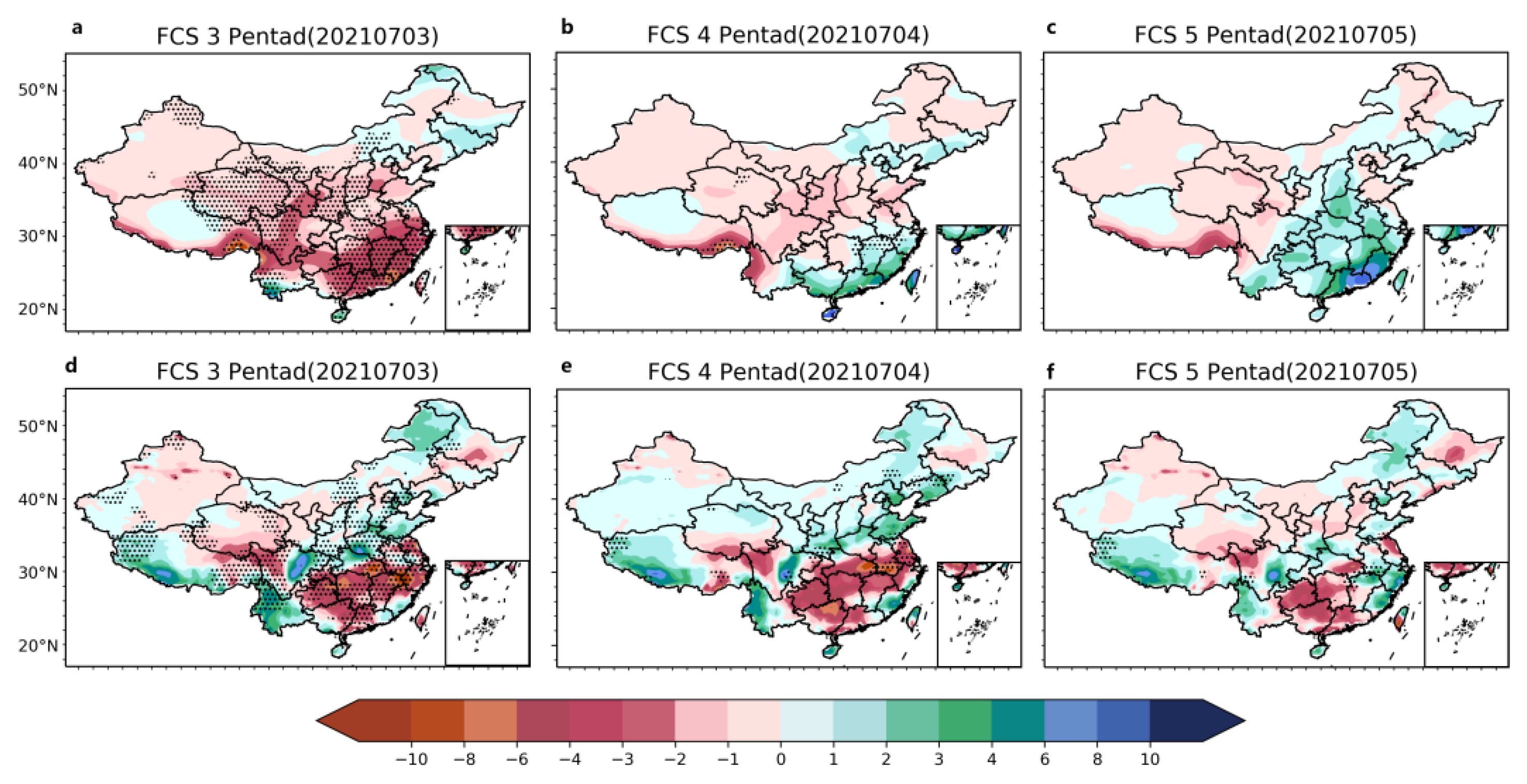
4. Reforecast Analysis of the Zhengzhou “720” Super Heavy Rainstorm Event
Comparison between Observations and Model Forecasts
5. Discussion and Conclusions
- (1)
- At lead times longer than four pentads (three pentads in summer), the pentad DSDM could effectively make up for the rapid decrease in the sub-seasonal precipitation predictability of the FGOALS-f2 model at increased lead times. With lead times greater than four pentads, the ACCs, TCCs and MSSSs of the pentad DSDM for the whole of China were higher than those of the FGOALS-f2 model;
- (2)
- In the reforecast analysis of the Zhengzhou “720” super heavy rainstorm event, the area and migration of the rain belts were predicted well by the pentad DSDM at lead times of three pentads;
- (3)
- The pentad DSDM could better predict summer precipitation in the eastern coastal areas of China at lead times of three pentads or longer by capturing the changes in the Z500 circulation of the FGOALS-f2 model;
- (4)
- The coupling signals between the Z500 anomalies and the precipitation anomalies could be retained by taking all the coupled SVD patterns that passed the Monte Carlo test to construct the pentad DSDM for each pentad. This led to better predictability in the extended range.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Lead Time (Pentad) | Pentad DSDM (ACC) | FGOALS-f2 (ACC) | Rate of Increase (%) |
|---|---|---|---|
| 1 | 0.240 | 0.440 | −45.6 |
| 2 | 0.190 | 0.228 | −16.5 |
| 3 | 0.128 | 0.118 | 8.6 |
| 4 | 0.077 | 0.065 | 18.3 |
| 5 | 0.068 | 0.038 | 77.8 |
| 6 | 0.055 | 0.031 | 76.2 |
| 7 | 0.054 | 0.019 | 181.8 |
| 8 | 0.052 | 0.008 | 520.3 |
| 9 | 0.045 | 0.006 | 633.7 |
| 10 | 0.034 | 0.014 | 142.2 |
| 11 | 0.042 | 0.013 | 227.0 |
| 12 | 0.039 | 0.011 | 269.0 |
References
- Zheng, Z.; Huang, J.; Feng, G.; Chou, J. Forecast scheme and strategy for extended-range predictable components. Sci. China Earth Sci. 2012, 56, 878–889. [Google Scholar] [CrossRef]
- Reichler, T.J.; Roads, J.O. The role of boundary and initial conditions for dynamical seasonal predictability. Nonlinear Process. Geophys. 2003, 10, 211–232. [Google Scholar] [CrossRef]
- Jie, W.; Vitart, F.; Wu, T.; Liu, X. Simulations of the Asian summer monsoon in the sub-seasonal to seasonal prediction project (S2S) database. Q. J. R. Meteorol. Soc. 2017, 143, 2282–2295. [Google Scholar] [CrossRef]
- Ma, J.; Wang, H. Design and testing of a global climate prediction system based on a coupled climate model. Sci. China Earth Sci. 2014, 57, 2417–2427. [Google Scholar] [CrossRef]
- Lin, R.; Zhu, J.; Zheng, F. The Application of the SVD Method to Reduce Coupled Model Biases in Seasonal Predictions of Rainfall. J. Geophys. Res. Atmos. 2019, 124, 11837–11849. [Google Scholar] [CrossRef]
- Liang, P.; Lin, H. Sub-seasonal prediction over East Asia during boreal summer using the ECCC monthly forecasting system. Clim. Dyn. 2017, 50, 1007–1022. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, S.; Jiang, X.; Dong, S. Sub-Seasonal Prediction of the Maritime Continent Rainfall of Wet-Dry Transitional Seasons in the NCEP Climate Forecast Version 2. Atmosphere 2016, 7, 28. [Google Scholar] [CrossRef]
- Olaniyan, E.; Adefisan, E.A.; Oni, F.; Afiesimama, E.; Balogun, A.A.; Lawal, K.A. Evaluation of the ECMWF Sub-seasonal to Seasonal Precipitation Forecasts during the Peak of West Africa Monsoon in Nigeria. Front. Environ. Sci. 2018, 6, 4. [Google Scholar] [CrossRef]
- Epstein, E.S.; Barnston, A.G. A Precipitation Climatology of 5-Day Periods. J. Clim. 1990, 3, 218–236. [Google Scholar] [CrossRef]
- Lu, Z.; Guo, Y.; Zhu, J.; Kang, N. Seasonal Forecast of Early Summer Rainfall at Stations in South China Using a Statistical Downscaling Model. Weather Forecast. 2020, 35, 1633–1643. [Google Scholar] [CrossRef]
- Hassan, W.H.; Nile, B.K. Climate change and predicting future temperature in Iraq using CanESM2 and HadCM3 modeling. Model. Earth Syst. Environ. 2020, 7, 737–748. [Google Scholar] [CrossRef]
- Hassan, W. Climate change projections of maximum temperatures for southwest Iraq using statistical downscaling. Clim. Res. 2021, 83, 187–200. [Google Scholar] [CrossRef]
- Hassan, W.H.; Hussein, H.H.; Nile, B.K. The effect of climate change on groundwater recharge in unconfined aquifers in the western desert of Iraq. Groundw. Sustain. Dev. 2022, 16, 100700. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, H.-L.; Klingaman, N.P.; Liu, J.; Zhang, P. Improving long-lead seasonal forecasts of precipitation over Southern China based on statistical downscaling using BCC_CSM1.1m. Dyn. Atmos. Ocean. 2021, 94, 101222. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, H.-L. A hybrid statistical downscaling model for prediction of winter precipitation in China. Int. J. Clim. 2014, 35, 1309–1321. [Google Scholar] [CrossRef]
- Li, C.; Zhao, T.; Shi, C.; Liu, Z. Assessment of precipitation from the CRA40 dataset and new generation reanalysis datasets in the global domain. Int. J. Clim. 2021, 41, 5243–5263. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, L.; Zhou, T.; Liu, J. The Asian Subtropical Westerly Jet Stream in CRA-40, ERA5, and CFSR Reanalysis Data: Comparative Assessment. J. Meteorol. Res. 2021, 35, 46–63. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Shi, C.X.; Zhou, Z.J.; Jiang, L.P.; Liang, X.; Zhang, T.; Liao, J.; Liu, J.W.; Wang, M.Y.; Yao, S. CMA global reanalysis (CRA-40): Status and plans. In Proceedings of the 5th International Conference on Reanalysis, Rome, Italy, 13–17 November 2017; pp. 13–17. [Google Scholar]
- Zhu, Z.; Li, T. The statistical extended-range (10–30-day) forecast of summer rainfall anomalies over the entire China. Clim. Dyn. 2016, 48, 209–224. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, K. A new statistical downscaling model for autumn precipitation in China. Int. J. Clim. 2012, 33, 1321–1336. [Google Scholar] [CrossRef]
- Nitta, T.; Hu, Z.-Z. Summer Climate Variability in China and Its Association with 500 hPa Height and Tropical Convection. J. Meteorol. Soc. Jpn. Ser. II 1996, 74, 425–445. [Google Scholar] [CrossRef]
- Tian, B.-Q.; Fan, K. Relationship between the Late Spring NAO and Summer Extreme Precipitation Frequency in the Middle and Lower Reaches of the Yangtze River. Atmos. Ocean. Sci. Lett. 2015, 5, 455–460. [Google Scholar]
- Choi, W.; Kim, K.-Y. Summertime variability of the western North Pacific subtropical high and its synoptic influences on the East Asian weather. Sci. Rep. 2019, 9, 7865. [Google Scholar] [CrossRef] [PubMed]
- De Andrade, F.M.; Coelho, C.A.S.; Cavalcanti, I.F.A. Global precipitation hindcast quality assessment of the Subseasonal to Seasonal (S2S) prediction project models. Clim. Dyn. 2018, 52, 5451–5475. [Google Scholar] [CrossRef]
- Wallace, J.M.; Smith, C.; Bretherton, C.S. Singular Value Decomposition of Wintertime Sea Surface Temperature and 500-mb Height Anomalies. J. Clim. 1992, 5, 561–576. [Google Scholar] [CrossRef]
- Overland, J.E.; Preisendorfer, R.W. A significance test for principal components applied to a cyclone climatology. Mon. Weather Rev. 1982, 110, 1–4. [Google Scholar] [CrossRef]
- Toth, Z.; Kalnay, E. Ensemble forecasting at NMC: The generation of perturbations. Bull. Am. Meteorol. Soc. 1993, 74, 2317–2330. [Google Scholar] [CrossRef]
- Hoffman, R.N.; Kalnay, E. Lagged average forecasting, an alternative to Monte Carlo forecasting. Tellus A 1983, 35, 100–118. [Google Scholar] [CrossRef]
- WMO. Standardised Verification System (SVS) for Long-Range Forecasts (LRF): New Attachment II-8 to the Manual on the GDPFS (WMO-No. 485). 2006; Volume I, 28p. [Google Scholar]
- Sahai, A.K.; Kaur, M.; Joseph, S.; Dey, A.; Phani, R.; Mandal, R.; Chattopadhyay, R. Multi-Model Multi-Physics Ensemble: A Futuristic Way to Extended Range Prediction System. Front. Clim. 2021, 3, 655919. [Google Scholar] [CrossRef]

| Lead Time (Pentad) | Pentad DSDM (TCC) | FGOALS-f2 (TCC) | Pentad DSDM (MSSS) | FGOALS-f2 (MSSS) |
|---|---|---|---|---|
| 1 | 0.239 | 0.452 | −0.226 | −0.631 |
| 2 | 0.178 | 0.239 | −0.212 | −0.554 |
| 3 | 0.105 | 0.117 | −0.122 | −0.302 |
| 4 | 0.053 | 0.052 | −0.077 | −0.192 |
| 5 | 0.042 | 0.037 | −0.050 | −0.148 |
| 6 | 0.035 | 0.018 | −0.043 | −0.136 |
| 7 | 0.029 | 0.015 | −0.045 | −0.126 |
| 8 | 0.030 | 0.005 | −0.042 | −0.126 |
| 9 | 0.023 | 0.005 | −0.043 | −0.122 |
| 10 | 0.018 | 0.007 | −0.042 | −0.119 |
| 11 | 0.021 | 0.008 | −0.041 | −0.114 |
| 12 | 0.032 | 0.009 | −0.034 | −0.113 |
| Pattern | Fourth Pentad of July 2021 |
|---|---|
| 1 | 249.9 |
| 2 | 53.9 |
| 3 | 70.6 |
| 4 | 261.9 |
| 5 | 34.8 |
| 6 | −91.1 |
| 7 | −57.6 |
| 8 | −142.8 |
| 9 | −1.6 |
| 10 | −21.0 |
| 11 | −141.1 |
| 12 | 20.12 |
| 13 | 58.6 |
| 14 | 33.8 |
| 15 | 73.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, H.; Zhao, Z.; Zheng, J.; Luo, W.; Li, H. Evaluation of the Dynamical–Statistical Downscaling Model for Extended Range Precipitation Forecasts in China. Atmosphere 2022, 13, 1663. https://doi.org/10.3390/atmos13101663
Cai H, Zhao Z, Zheng J, Luo W, Li H. Evaluation of the Dynamical–Statistical Downscaling Model for Extended Range Precipitation Forecasts in China. Atmosphere. 2022; 13(10):1663. https://doi.org/10.3390/atmos13101663
Chicago/Turabian StyleCai, Hongke, Zuosen Zhao, Jiawen Zheng, Wei Luo, and Huaiyu Li. 2022. "Evaluation of the Dynamical–Statistical Downscaling Model for Extended Range Precipitation Forecasts in China" Atmosphere 13, no. 10: 1663. https://doi.org/10.3390/atmos13101663
APA StyleCai, H., Zhao, Z., Zheng, J., Luo, W., & Li, H. (2022). Evaluation of the Dynamical–Statistical Downscaling Model for Extended Range Precipitation Forecasts in China. Atmosphere, 13(10), 1663. https://doi.org/10.3390/atmos13101663






