Abstract
Snow precipitation in mountains surrounded by semi-arid regions represents an important reservoir of fresh water during the melting season. The snow cover helps to compensate for the scarce precipitation that occurs during their long summer droughts. Knowing the phenomenology that leads to winter precipitation and snow at these areas becomes even more relevant in a context of climate change. Precipitation in Sierra de Guadarrama, a medium size mountain range in the middle of the Iberian Plateau, is the main source of fresh water for millions of inhabitants living under its area of influence, for an active industry and for agriculture and farming. In addition, scarce but heavy snow events affect logistics, transport and security in an area with abundant ground and air traffic. This work analyses the links between large scale atmospheric patterns and the complex winter precipitation and snow cover dynamics observed at local scale. Applying principal component analysis and K-means clustering on geopotential height field, a set of circulation weather types are obtained. The contribution of each circulation weather type to precipitation, snow and heavy snow events is analysed, and favouring conditions leading to snowfalls are identified. Results from this work can be useful as a framework for future modelling exercises, statistical downscaling of climate change scenarios, or even for the development of early warning systems.
1. Introduction
Snow is a fundamental element of the mountain cryosphere. Due to its high albedo and its low thermal conductivity, it plays a major role in regulating the global climate [1]. Moreover, due to the snowmelt runoff in spring, snow is a key element of the hydrological cycle, becoming the major component of the global movement of water [2]. Accumulated snow in mountains represents an important source of freshwater both in these areas and in adjacent lowlands and has a large impact on their economy since it affects tourism, communications, logistics and risks associated with its recreational use.
According to the Sixth Assessment Report (AR6) of the Intergovernmental Panel on Climate Change [3], spring snow cover has been reduced significantly across the Northern Hemisphere since the 1950s. High mountain regions have experienced significant warming since the early 20th century, resulting in a reduced snowpack on average [4]. The increase in the fraction of precipitation falling as rain versus snow seems to lead to a decline in both streamflow and groundwater storage in regions where snowmelt is the primary source of recharge [5,6]. A greater reduction of snow water equivalent (SWE) has been found at lower elevations associated, precisely, with this shift from solid to liquid precipitation. A recent synthesis of snow observations in the European Alps [7] shows a 1971–2019 seasonal (November to May) snow depth trend of −8.4% per decade, along with downward trends in the maximum snow depth and the seasonal snow cover duration. The trends are stronger and more significant during transitional seasons and at transitional (from no snow to snow) altitudes and exhibit strong regional variations, consistent with earlier reports for the Swiss and Austrian Alps [8] and the Pyrenees [9]. The amount and timing of seasonal snowmelt are not only driven by the temperature. Recent studies have shown the shortening of the snow cover duration due to dust deposition events in different mountain regions such as the Rocky Mountains [10], the European Alps [11] or the Russian Caucasus mountains [12]. Changes in the duration of snow cover in mountain areas have a significant impact on their hydrology and vegetation’s phenology.
This work aims to deepen the understanding of the synoptic circulation patterns that are related to winter precipitation, especially to snow falling and snow cover settling. Linking local snowfall observations with synoptic-scale weather patterns provided by large area models with available reanalyses for the last century and future climate scenarios will help to design correct methodologies for regional downscaling at different time horizons.
This work is structured as follows: Section 2 describes the study area. Section 3 specifies the data used and the method implemented for obtaining the circulation weather types related to winter precipitation and snow. Section 4 discusses the results obtained, with an emphasis on the big snowfalls and, finally, Section 5 shows the main conclusions and perspectives of future work.
2. Study Area
In this work, we focus our attention on winter precipitation and snowfalls in Sierra de Guadarrama (SdG hereafter), which is part of the Iberian Central System (Figure 1). This is a north-east to south-west range that divides the extensive and high plateau in the centre of the Iberian Peninsula (IP hereafter) into two parts: northern and southern sub-plateaus. Its average altitude is about 1600 m.a.s.l. and its maximum peak, called Pico de Peñalara, reaches a height of 2428 m.a.s.l.
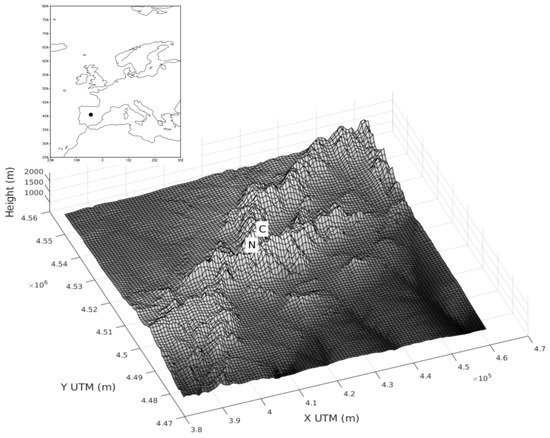
Figure 1.
Location of Sierra de Guadarrama (SdG) and elevations in a 90 × 90 km2 domain with marks on the observatories used in the study (Data source: Instituto Geografico Nacional, Madrid, Spain).
SdG, a highly environmentally protected area, became a National Park in 2013, hosts some wetlands considered to be of international importance under the Ramsar Convention and its main river basin, the Lozoya River Basin, was recently declared as a Special Area of Conservation within Natura 2000 Network. In addition, these mountains are crucial as sources of fresh water for the population, industry and agriculture of the region of Madrid (with around 6.7 million inhabitants) and other regions under its influence. Around 50% of water resources come from the river Lozoya basin [13], whose headwaters are in the study area of this work and where snowpack runoff during the melting season is key.
Despite the importance of precipitation and snowpack dynamics on these mountains, not much specific research on these issues is found in the literature. One of the first works with a time series analysis approach was done by [14]. This work, based on observations for a period of 22 years, established the main features of precipitation at this mountain range which shows features of an alpine climate immersed in a continental Mediterranean climate but with high inter-annual variability, a high contribution of snow precipitation to total precipitation, marked summer drought and a clear connection between precipitation and advection of air masses from the Atlantic. This last feature was deeply analysed by [15] using the same set of observations but with model reanalysis for the synoptic fields. This work presented a deeper explanation of the role played by the synoptic patterns and precipitation in this area. This and previous works gave a good description of the temporal variability of precipitation but lacked information about the spatial variability of the precipitation, which was expected to be high due to complex orography but was not able to capture due to the lack of enough observatories. This issue was partly solved by [16], who performed a high-resolution modelization of precipitation at SdG for a 20 years period. Here, the complexity of the spatial patterns was confirmed, differences between basins were found, and the leading role of orographic precipitation processes was determined. Regarding snow precipitation and snowpack simulation in SdG, even less research is found in the literature except for [17]. Here the authors show results for snow modelling of several mountains in the Iberian Peninsula, including SdG, with very interesting results that leave the door open for future work in the area, probably with higher resolution and better field observations.
3. Material and Methods
3.1. Observations
High mountain areas present adverse weather conditions and remoteness hampering the meteorological measurements, especially precipitation. Despite these difficulties, the Spanish Meteorological Agency (AEMET, http://www.aemet.es, accessed on 13 September 2022) has been conducting high quality observations of precipitation since 1941 at ‘Puerto de Navacerrada’ observatory, located at 1888 m.a.s.l in the heart of SdG (Figure 1). Daily precipitation is measured following World Meteorological Organisation recommendations and its historical time series are the main source of information used in this work.
In addition, the Sierra de Guadarrama National Park has been carrying out meteorological observations on a regular basis since 1998 [18]. This continued effort is nowadays known as ‘Red Meteorológica del Parque Nacional Sierra de Guadarrama’ (RMPNSG hereafter). What was first considered as a pioneer observing system of a small number of automatic weather stations for studying mountain weather and climate, has become nowadays a network that promotes and encourages collaboration among different research centres interested in mountain weather and climate research (for more information about the observation network visit https://www.parquenacionalsierraguadarrama.es, accessed on 13 September 2022). This network has several rain gauges, snow height sensors, and more recently, has been equipped with several laser disdrometers that provide valuable data about the phase and amount of precipitation. Along with these automatic measuring techniques, manual observations of total daily precipitation and snow height are also performed on a daily basis in the Cotos observatory. Information from this site has been intensively used in this study. Manual observations taken by the Park staff have been crucial for the validation of data and separation of precipitation between rain and snow. Other manual measurements (e.g., maximum and minimum temperature, relative humidity, water equivalent of snow precipitation, and snow height) have been used to validate the automatic measurements.
3.2. Model Data
This work also uses reanalysis data from ECMWF ERA5 [19] with 0.25° spatial resolution and 1 h temporal resolution. This kind of data is widely used nowadays for many purposes such as the monitoring of climate change [20,21] and the analysis of certain weather regimes [22,23,24,25].
Here, we use geopotential height (GpH hereafter) at 925 hPa data for a principal component analysis and GpH at 500 hPa, relative humidity and temperature at 850 hPa, and total column water vapour flux (TCWVF hereafter) data for calculating composite maps. Daily mean data have been employed to find a compromise between capturing intraday variability and computational cost.
3.3. Statistical Analysis of Precipitation
This work aims to identify the large-scale conditions that lead to snow precipitation at SdG using snow precipitation observations and data from models. This work uses methods similar to other analyses performed at other mountain areas such as the Alpine subregion [26], Pyrenees [27] and mountain ranges of the western USA [28] and it is a natural continuation of the methods used by [15] but with relevant improvements on calculation efficiency and statistical hypothesis contrast for the composite maps.
The analysis is conducted for the period January 2000 to April 2021. This period has been considered long enough to find the main relationships between synoptic and local scales considering the climate variability of precipitation in this area [14].
First, days at the ‘Puerto de Navacerrada’ observatory are classified as days with liquid, mixed and solid precipitation based on available SYNOP and BUFR messages issued by AEMET and other observations from RMPNSG. Then, we calculate the annual basic statistics of precipitation, and we evaluate its distribution over the year. The precipitation corresponding to mixed days is halved between rainy and snowy days.
The heaviest snowfalls are identified by choosing a threshold of 30 mm of snow water equivalent (SWE thereafter), which is very close to percentile 95 at this site. Note that in this case we only consider days with solid precipitation. To handle situations in which a heavy snow event occurs within a 24-h period that straddles midnight, we first identify all the consecutive snow days belonging to the same CWT, in which the sum of the precipitation during these days is >30 mm. Since heavy snow precipitation is related to difficulties in logistics and operation of observation networks leading to errors, an extra validation process is applied to these events using both automatic and manual observations from RMPNSG (mostly from Cotos’s station), fieldwork and other sources [29]. Particularly, snow cover measurements are used to exclude events showing large fluctuations. The reason is that a day classified as ‘snowy’ has a higher proportion of snow than rain, but if in the middle of a possible 24-h snowfall event spread over 2 days there is rain, the snow depth shows fluctuations due to melting. These situations are then classified as two separate snowfall events. If the snow depth does not show fluctuations, but a monotonic increase, the event is labelled as a possible snowfall spread over two days, and additional screening of the available hourly SYNOP reports is performed in order to make sure that the sum of the precipitation of both days is representative of the 24-h accumulation of these events.
3.4. Principal Component Analysis
Principal component analysis (PCA) is a multivariate statistical technique that explores the structure and variability of data, looking for dependency patterns between them. Its objective is to generate an orthogonal basis of vectors in the space domain that represent the main directions of variability [30]. This technique along with k-means clustering (described in the next section) is widely used to characterise synoptic circulation patterns and their relationships with local phenomena [23,31,32].
For the IP area, this methodology has also been applied for different purposes such as the study of rainfalls [22,33], snowfalls [27] and extreme temperatures [34]. In addition, this method has been successfully used to find the relationships between water vapor flux patterns over IP as predictor field, and precipitation in SdG [15].
Following this approach, this work tries to clarify the relationship between snow precipitation in SdG and the different atmospheric circulation patterns that affect the region. In this case, 925 hPa GpH is used as a predictor field.
Several spatial domains were tested and finally, a domain 30° N to 60° N in latitude and 40° W to 10° E in longitude, covering the IP and the surrounding oceanic areas, was found to be able to explain more than 96% variance with the three first eigenvalues, following the criteria established by [35]. The great advantage of using PCA is that it simplifies the original data by a reduction in the number of dimensions. This way, it is possible to analyse the evolution of the fields from the first three PC reconstructed data, increasing the computational efficiency. The lost information is minimal and is not expected to be significant, due to the high resolution of ERA5 and the large scale of the studied phenomena. In this study, we assume that 925 hPa GpH patterns with similar values of the main PCs, correspond to similar weather regimes over the IP and therefore, snow precipitation is similarly forced on SdG.
3.5. K-Means Clustering and Circulation Weather Types
Cluster analysis is a procedure that allows data to be separated into groups whose properties and even the optimum number of them are unknown. Groups are defined based on the similarities and differences between observations. There are hierarchical and non-hierarchical clustering methods. Non-hierarchical methods, e.g., the K-means algorithm, allow the reassignment of observations in groups in contrast to hierarchical methods [30].
After applying PCA analysis, we perform a two-stage clustering with the k-means algorithm using the first three PCs as input variables [36]. The centroids of the clusters are then used to build the circulation weather types (CWTs). These CWTs represent the dynamical structures that force a weather response at a regional level, which in this case, has been chosen to be the precipitation at SdG. An extended winter season, ranging from November to April, is considered for this analysis.
For selecting the optimum number of CWTs, we use an information criterion (IC) or cost function, like those applied in previous studies [15,22,37]. This criterion, formulated as Equation (1), is based on any local precipitation at SdG, for which daily precipitation data of Navacerrada observatory are used. This function calculates, for a certain number of CWTs, the difference between the number of wet days for each CWT and the expected number considering the probability of wet days for all the population and the number of days of each cluster. It compares how far each CWT is from average behaviour. Since, this difference is computed no matter the sign, drier and wetter days compute in the same direction. If for a certain number of CWTs we have a high score, this means that days are separated into groups that are drier or wetter than average. If the score is low, it means that the method is clustering using distances that are not related to the variable used in the calculation of the score function. Higher values of this score, in our case, would mean that there is a connection between large-scale synoptic configuration (distances) and local precipitation at SdG.
where k is the number of clusters, is the number of precipitation (snowy or rainy) days within the ith CWT with a precipitation amount above the threshold, is the probability of total precipitation above the threshold and the number of days within the same ith cluster. This function is evaluated from 1 to 30 CWTs.
All days are assigned to a CWT based on their minimum Euclidean distance to the cluster centroids, we do not consider ‘no regime’ days. The frequency of occurrence of each CWT is calculated for every month within the extended winter season as the ratio of the number of days of a month in each regime to the total number of days in that month. In addition, we evaluate for each CWT: (1) its frequency of occurrence (given by the ratio of the number of days in a given regime to the total number of days used in this study), (2) its contribution to total precipitation (calculated as the ratio between the sum of all the precipitation of the days in a given regime and the sum of the total precipitation taking into account all the days in this study, expressed in percentage), (3) its probability of precipitation (derived as the ratio of the number of wet days in a given regime, including liquid, mixed and solid precipitation, to the total number of days in that regime), (4) the probability that this precipitation falls as snow (calculated as the ratio between snowy days and wet days in a given regime), (5) its probability of heavy snowfall (calculated as the ratio between snowy days exceeding the 30 mm and total snowy days in a given regime), (6) its mean water precipitation rate (as total precipitation under each flux pattern divided by the number of wet days of the pattern evaluated), (7) its mean snow rate (same as before but taking into account just snow precipitation) and (8) the median of the daily mean temperature. Note that in these calculations we consider wet days as those with solid, mixed, or liquid precipitation ≥ 0.5 mm. In addition, for counting the number of snowy days we consider the days with solid precipitation ≥ 0.5 mm and we add half of the mixed days with precipitation ≥ 0.5 mm.
We also analyse for the period of study the frequency of snowy days according to their CWT and their daily intensity, grouped in three intervals: [0.5–5] mm day−¹, (5–30] mm day−¹ and >30 mm day−¹. The choice of these intervals is inspired by the three colour-coded levels of warning defined by AEMET for Sierra de Madrid (in which SdG is included) that consider the adversity of the weather conditions related to snow, both for its weirdness in terms of climatology and for its potential danger to population and its activities. The snow accumulations in 24 h established for these warnings are, respectively, >5 cm (yellow), >20 cm (orange) and >40 cm (red). The yellow warning indicates there is no weather risk to the population even though some specific activities could become hazardous. The orange warning points out there is a significant weather risk due to uncommon meteorological phenomena with a certain degree of danger for usual activities. The red warning expresses an extreme weather risk due to meteorological phenomena of exceptional intensity with a very high level of danger for people.
We tried to use the same thresholds of snow daily intensity as those defined in the AEMET warnings although it is true that in that case it is expressed in terms of cm of snow and here, we are working with SWE, and not always 1 mm is equal to 1 cm. In any case, the number of events with SWE > 40 mm day−¹ was not statistically significant, so, finally we decided to reduce the threshold to 30 mm, which is halfway between orange and red warnings.
3.6. Composite Maps
To have a more comprehensive view of the dynamical structure of each circulation CWT, composite maps of 925 hPa GpH, 500 hPa GpH anomalies, TCWVF, temperature and relative humidity at 850 hPa are performed. The three first variables are computed considering all days corresponding to each CWT. In the case of TCWVF, temperature and relative humidity five composites are performed for each CWT: (1) for all dry days, (2) for days with rain precipitation but no snow, (3) for all days with snow precipitation, (4) for days with heavy snowfalls (SWE > 30 mm), and (5) for 24 h prior to the days of heavy snowfalls.
All the composite maps are calculated over the spatial domain ‘30° N to 60° N’ in latitude and ‘40° W to 10° E’ in longitude, except for the 500 hPa GpH anomalies map that is computed over a larger domain, ‘20° N to 80° N’ and ‘60° W to 20° E’. The statistical significance of the variables represented in TCWVF, temperature and relative humidity at 850 hPa composite maps of each CWT is evaluated at each point by applying the bootstrapping technique. This method has been widely used in the analysis of climate in the last decades [38,39,40,41] and in the analysis of extraordinary weather events [42]. The bootstrap technique is a non-parametric approach that consists in the construction of data samples of the same size and the subsequent application of a statistical test. The use of this kind of method presents certain advantages over a parametric approach because in this case it is not necessary to assume a theoretical distribution for the data and there is no restriction on the statistics of the test. In this work, 100 samples of daily maps of each CWT (TCWVF, temperature and relative humidity at 850 hPa) are chosen randomly without replacement. The difference between the mean of each CWT and the mean of the whole period at that point is also calculated (this quantity will be called A). Then, the differences between the mean of each sample and the mean considering all days of that CWT are determined (this quantity will be called B). Finally, the 1st and 99th percentiles of B are compared to A and those grid points where the 1st percentile is below A and the 99th percentile is above A are statistically significant.
4. Results and Discussion
4.1. Winter Precipitation and Snow Events in Sierra de Guadarrama
The annual statistics of total precipitation at ‘Puerto de Navacerrada’ observatory from 1 October 2000 to 30 September 2020 are shown in Table 1, in terms of hydrological years. Mean total precipitation is 1315 mm year −1 where more than 37% falls as snow (488 mm year−1). The annual maximum of total precipitation during this period was reached in the hydrological year 2003–2004, while the maximum of snow took place in 2017–2018 with 725 mm year−1. On the contrary, the annual minimum of total precipitation was 948 mm year−1 in the hydrological year 2004–2005, considered to date as the driest year in Spain since records began in 1947. The year with less snow precipitation occurred in 2007–2008, with 320 mm year−1.

Table 1.
Annual basic statistics of precipitation in Navacerrada observatory in terms of hydrological years from 2000 to 2020.
Figure 2 shows the marked seasonal precipitation cycle at SdG, including the data from 1 January 2000 to 30 April 2021. The contributions of rain and snow to the total monthly precipitation of the period of study are depicted in dark and light grey, respectively. Marked summer drought can be easily identified as found by other authors [14]. In addition, November (182.8 mm month−1) and October (177.3 mm month−1) are the largest contributors to the annual total precipitation, as well as, the months with the largest amount of rain. In terms of snow, we observe that from November to April the ratio of snow is above 30%, reaching its maximum in February (74.6%) and January (57.3%).
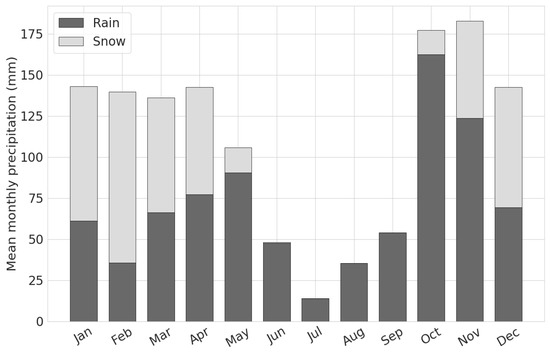
Figure 2.
Mean monthly precipitation broken down into rain and snow at Puerto de Navacerrada observatory during the period from 1 January 2000 to 30 April 2021.
It is also well-known how total annual precipitation at SdG presents a strong inter-annual variability [14]. Figure 3a shows the total accumulated rain and snow per hydrological year, defined from 1 October to 30 September. Average rain precipitation is around 800 mm per year, with some years over 1000 mm year−¹ such as 2007, 2016 and 2020. Regarding snow precipitation, the average is around 500 mm per year and the highest values were reached in 2004, 2013 and 2018. It is remarkable that the variability in the time series of rain and snow is not always coupled and there are no discernible trends during the period of study. Nevertheless, if we focus on the number of days with snowpack higher than 5 cm Figure 3b), using a Theil-Sen regression in combination with a Mann–Kendall test for the statistical significance, a downward trend of 0.5 days per year with a confidence level of 84% is found. This reduction of seasonal snow cover is quite relevant for the region, as snow acts as a natural reservoir to store water. The main hypothesis is that this trend could be related to an elevation of the zero degrees Celsius isotherm due to climate change, as pointed out by other studies for this region using different bioindicators [43,44,45,46].
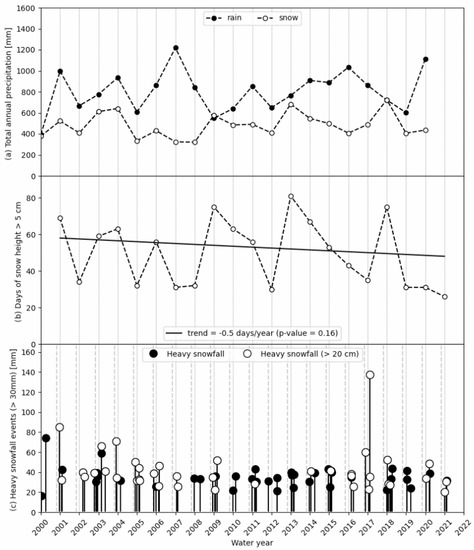
Figure 3.
Time series at Puerto de Navacerrada observatory in terms of hydrological years from 1 January 2000 to 30 April 2021 of (a) total accumulated rain and snow precipitation, (b) days with snowpack above 3 cm and (c) days of heavy snowfall, defined as those with SWE above 30 mm day−¹, and highlighting with white markers those in which an increase above 20 cm in the snowpack was simultaneously observed. The vertical dashed lines represent the beginning of the hydrological years.
Figure 3c represents the days with SWE above 30 mm day−¹ in Puerto de Navacerrada highlighting with white markers those events that also led to an increase in the snow height of more than 20 cm. No evident trend or pattern can be derived from these results.
Table 2 reports the specific information about the heaviest snowfalls, already mentioned above and plotted in Figure 3c. The three heaviest snowfalls in Puerto de Navacerrada over this period took place on 12 February 2017 (137.4 mm day−¹), on 22 December 2000 (85 mm day−¹) and on 2 April 2000 (74 mm day−¹). Available information about SWE from the Cotos observatory is also included in the second column. Finally, the last column includes the associated CWT, fully analysed in the next section, for each day between November and April.

Table 2.
Heaviest snowfalls (>30 mm day−¹) recorded in Puerto de Navacerrada and Cotos observatories from 1st January 2000 to 30th April 2021 along with their associated circulation weather type. The precipitation of the heavy snow events occurring within a 24 h period that straddles midnight is the sum of the two days.
4.2. Circulation Weather Types and Winter Precipitation
The three empirical orthogonal functions (EOF) that account for more than 96% of the variance and their corresponding principal components have been calculated (not shown) for the extended winter season from 2000 to 2021.
Figure 4 shows the value of the information criterion as defined in Equation (1) used for the selection of the optimum number of CWTs. As expected, it shows an increase in the information criterion as it grows the number of CWTs. A good compromise between a high score of the information criterion value and a small number of CWTs has been found for five, seven, and ten circulation weather types. Seven circulation weather types have been considered as a reasonable compromise and termed as: (1) Cyclonic regime (C), (2) Western regime (W), (3) NAO- regime, (4) Atlantic Ridge regime (AR), (5) NAO+ regime, (6) Scandinavian Blocking regime (SB) and (7) Anticyclonic regime (A). These results are coherent with those obtained by other authors [15,22].
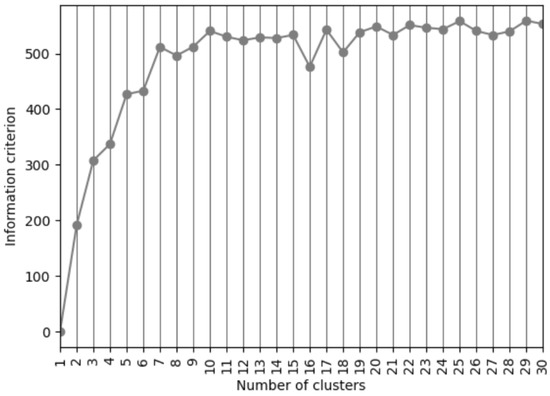
Figure 4.
Information criterion formula for CWT selection for days with precipitation above 0.5 mm.
Figure 5 represents the frequency of occurrence of each CWT for each month of the extended winter season. CWTs are shown in decreasing order of their total probability of precipitation, being cyclonic regime the one with the highest probability and anticyclonic the one with the lowest. As can be seen, the frequency of occurrence of each CWT shows a modulation throughout the months. Certain CWTs are more frequent during the central months of the winter (A, C) whereas others are more dominant at the beginning and at the end (NAO-, AR). Moreover, some CWTs are less frequent at the end (W) or at the beginning of the winter (SB), and others do not fluctuate as much in frequency (NAO+).
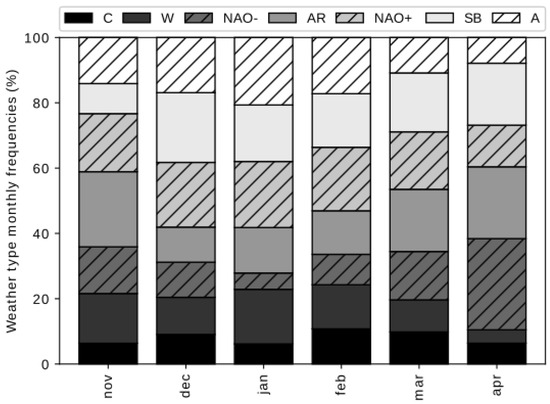
Figure 5.
Circulation weather types monthly frequencies.
Table 3 contains information about the main characteristics of each CWT. As can be seen, W, NAO- and C show the highest probability of precipitation but only W and NAO- account significantly for total winter precipitation. The high precipitation rate associated with these two CWTs seems consistent given their low frequency. At the same time, NAO- shows the highest snow precipitation rate, the lowest median air temperature and the second highest probability of heavy snowfall among all the CWT, only surpassed by C.

Table 3.
Frequency of occurrence (Freq), contribution to total precipitation (CTP), probability of precipitation higher than 0.5 mm day−¹ (PoP), probability of precipitation as snow (PoS), probability of heavy snowfall higher than 30 mm day−¹ (PoHS), mean water precipitation rate (MPR), mean snow rate (MSR) and median of air temperature (MAT) for each CWT. Relevant values are marked in bold.
Most of the information provided in Table 3 is also displayed graphically in Figure 6, helping the reader to assess the results. This figure clearly reflects how good the K-means method is separating wet from dry days. The frequency of occurrence of each CWT is represented on the x-axis while the probability of precipitation is depicted on the y-axis. Thus, the upper left corner (C) represents the least frequent CWT but with the highest probability of precipitation while the lower right corner contains the most frequent but the driest CWTs (A, SB and NAO+). The contribution of each CWT to the total precipitation is also shown by the size of each circle, being the NAO- the largest contributor. Blue and red colours are used to represent the ‘humid’ and ‘dry’ CWTs, as their PoP is above 70% and below 39%, respectively. The unfilled circles (AR, NAO- and NAO+) represent the CWTs with a probability of precipitation as snow higher than 50%. As pointed out before, a minimum of 0,5 mm day−¹ has been considered for defining a day with precipitation either snow or rain, so, the different probabilities have been calculated accordingly.
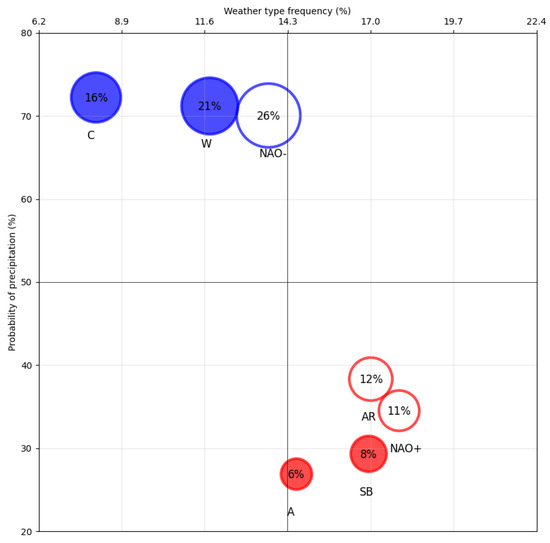
Figure 6.
Precipitation-related characteristics of each CWT. The surface of the circles and the percentage in the interior represent the contribution of each CWT to the total winter precipitation (from November to April) in the period 2000–2021. Blue (red) colour represents respectively if the CWT is considered ‘humid’ (PoP > 70%) or ‘dry’ (PoP < 39%). The probability of the precipitation being snow is represented by the interior of the circle, solid colour for probabilities < 50%, and transparent for >50%.
Snow is the major player during the extended winter season in SdG (as previously seen in Figure 2) and what controls its short-term impact on the area is its daily intensity. Figure 7 shows that during our period of study, NAO- is the most frequent CWT responsible for snowfalls (25.7%), followed by AR (19.3%). For these two CWTs, light snowfalls ([0.5–5] mm day−¹) are equally probable while for moderate ((5–30] mm day−¹) and extreme snowfalls (>30 mm day−¹), NAO- is by far the most likely CWT. In contrast, A and SB are the less common CWTs for extreme snowfalls. In relative terms, C shows the highest proportion of heavy snowfalls (11.3% of the total snowfalls under this CWT), followed by NAO- (9.3% of the total snowfalls under this CWT).
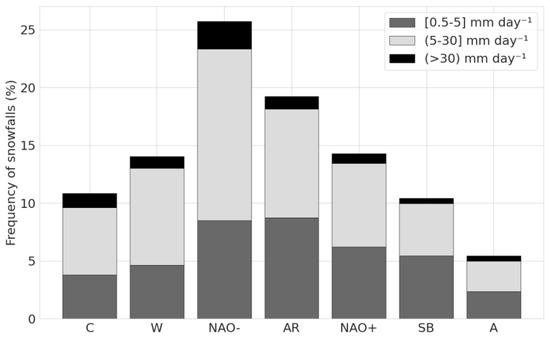
Figure 7.
Frequency of snowfalls according to its CWT and its daily intensity, grouped in three intervals: [0.5–5] mm day−¹, (5–30] mm day−¹ and >30 mm day−¹.
4.2.1. Cyclonic
Figure 8 shows the spatial structure of the CWT called cyclonic (C). Under this pattern, south-westerly fluxes are identified in the western part of the Iberian Peninsula. In addition, this CWT is characterised by an isolated centre of negative 500 hPa GpH anomalies (Figure 8b) over the North Atlantic Ocean, vertically consistent with the low values of GpH observed at 925 hPa (Figure 8a), which are signs of a high density of extratropical cyclonic systems.

Figure 8.
For the cyclonic CWT: (a) Centroid map of the GpH at 925 hPa. (b) Composite map of 796 GpH anomalies at 500 hPa. (c) Composite map of the TCWVF. From the second row onwards, left column represents the composite map of temperature at 850 hPa, central column the relative humidity at 850 hPa and right column the TCWVF for different situations: in (d–f) days with less than 0.5 mm of precipitation, in (g–i) days with >0.5 mm of rain, in (j–l) days with >0.5 mm of snow, in (m–o) heavy snow days (>30mm) and in (p–r) the previous day to the heavy snow days. In (d–r) the areas containing values statistically significant below 1st percentile (above 99th percentile) are delineated with purple (orange) coloured contour markers. Colours inside these areas represent the values of each variable, increasing from blue to red.
This pattern has also been documented by other authors [15,22] and has been associated with the passage of consecutive fronts over the IP, involving an efficient humidity transport from the North Atlantic Ocean. This extra flux of humidity can be seen in Figure 8c and makes this CWT the most probable for precipitation (72.2%, Table 3). However, this pattern does not show the highest contribution to total precipitation due to its low frequency (8.1%, Table 3). This frequency is particularly low in November, January and April (Figure 5).
More than half of the precipitation during the extended winter season from this CWT takes place as rain (54.4%) because fronts (normally coming from the SW of the IP) bring air masses not excessively cold and with significant humid content from the central part of the Atlantic Ocean. As a result, rainy days show statistically significant high values of temperature in the eastern half of the IP (Figure 8g) and high values of TCWVT and relative humidity over the entire IP (Figure 8h,i). At a local scale, this pattern might turn south direction as it interacts with the orography, leading to intense precipitation (C shows the highest value of the mean precipitation rate in Table 3).
However, in 22.7% of the C days, the fronts travel further north of the IP eluding the SdG and causing no precipitation (Figure 8d–f).
In terms of snow, this CWT does not stand out for a remarkably high probability (42.4%, Table 3) except when there is a more northern flux, due to an eastern location of the centre of low pressures, that leads to statistically significant low temperatures over the IP (Figure 8j). Under this situation, snowfalls are heavier than the other patterns (Table 3).
The heaviest snowfall events associated with this CWT seem to be predictable since significant signals of low temperature in the northwest of the IP (Figure 8p) and high relative humidity over the IP and the eastern North Atlantic (Figure 8) are observed 24 h prior to the heavy snowfall event. As shown in Table 2 the heaviest snowfall under this CWT during our period of study took place on 22 December 2000, reaching the 85 mm of snow water equivalent in Puerto de Navacerrada.
4.2.2. Western
This CWT shares many similarities with the so-called Westerly regime or West flux, obtained by [15,22]. Under this pattern there is a prevailing zonal flow that advects cold and humid air from the Atlantic Ocean. In addition, the Azores anticyclone is anomalously moved southward, and a depression is over the British Isles (Figure 9a). This configuration, also observed at higher levels (Figure 9b), generates a corridor that makes an efficient transport of humidity through the IP, reaching SdG from the West and Northwest (Figure 9c).
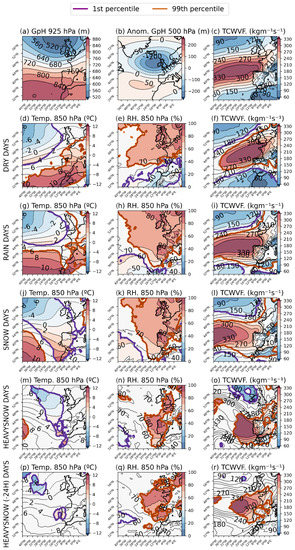
Figure 9.
Western CWT: same panels as Figure 8.
As for C regime, W is also linked to the passage of frontal systems, but it is slightly more frequent than the former CWT (11.8%, Table 3), particularly during the central winter months (Figure 5).
This CWT is one of the wettest patterns as it shows the second highest probability of precipitation (71.2%, Table 3), as well as the second major contribution to total precipitation (around 20.6%, Table 3). Most of the precipitation falls as rain (63.68%), when TCWVF is significantly high over the whole IP (Figure 9i). In contrast, for dry days (24.89% of W days) humidity is advected further to the north and TCWVF is only significantly high in the northern half of IP.
Under this CWT, snowfalls are unlikely, but occur occasionally when the corridor is curved in the central North Atlantic, bringing cooler and humid air from further north than the usual situation (Figure 9l). Around 60% of snowfalls under this CWT have a daily intensity between 5 mm and 30 mm day−¹ (Figure 6). However, heavy snowfalls (>30 mm day−¹) can exceptionally take place, as well. In these cases, we observe extraordinarily high values of TCWVF in the western part of the IP and off the Portuguese coast (Figure 9o). The heavy snowfall events, although rare, seem predictable as in the preceding 24 h it can be observed statistically significant low temperatures off the west coast of the IP (Figure 9p) and high relative humidity values over the western half of the IP and large parts of the British Islands (Figure 9q).
As shown in Table 2 the heaviest snowfall under this CWT during our period of study took place on 4 March 2009, reaching the 52 mm of snow water equivalent in Puerto de Navacerrada and 45.5 mm in Cotos.
4.2.3. NAO-
As seen in Figure 10b the most distinctive feature of this CWT is a north–south dipole on the 500 hPa geopotential height anomalies, with significant positive values over the southern part of Greenland and negative values over the Cantabrian and Celtic seas. This pattern has been documented previously by other authors [15,22] and shows a high correlation with the negative phase of the NAO (not shown).

Figure 10.
NAO- CWT: same panels as Figure 8.
Despite not being one of the most frequent CWT (13.7%, Table 3), the role of NAO- for winter precipitation at SdG is key as: (1) it is the first contributor to total precipitation, (2) it not only shows one of the highest probabilities of precipitation, but also a high probability that this precipitation falls as snow and in particular, heavy snow (3) it exhibits the second highest daily mean precipitation rate and the highest mean snow rate and (4) it presents the lowest median air temperature (Table 3).
As per months, April and January are the months when NAO- is the most and the least frequent, respectively (Figure 5). During precipitation days, NAO- shows statistically significant high values of TCWVT (Figure 10i,l,o) and relative humidity over IP (Figure 10h,k,n) while during dry days these values are statistically significantly low (Figure 10e,f), as moisture advection takes place over northern latitudes.
When the geopotential ripple at 925 hPa moves a little bit downward, there is an enhancement of cold air advection coming from the north of Europe, resulting in a southward displacement of the two-degree isotherm and therefore, bringing snow to SdG (Figure 10j,m). This further southward displacement of the isotherms over IP is precisely what distinguishes rainy (Figure 10g) and snowy days (Figure 10j,m). In contrast, relative humidity over the IP remains above 80% in both cases (Figure 10h,k,n). Lastly, heavy snowfalls seem to be associated with a deeper trough in phase at different heights, leading to a south-western flux when reaching the SdG. These extreme events appear to be predictable as statistically significant low temperatures and high relative humidity over the IP are appreciated in the preceding 24 h (Figure 10p,q). Heavy snowfalls represent close to 10% of all snowfalls under this CWT (Figure 6).
As shown in Table 2, the heaviest snowfall under this CWT represents also the heaviest one among all the CWTs during our period of study, and took place on 12 February 2017, reaching 137.4 mm of snow water equivalent in Puerto de Navacerrada and 139.4 mm in Cotos.
4.2.4. Atlantic Ridge
This CWT is characterised by an isolated centre of positive 500 hPa GpH anomalies (Figure 11b) over the North Atlantic Ocean, vertically consistent with the high values of GpH observed at 925 hPa (Figure 11a), with opposite sign than the cyclonic regime. This pattern often appears in the previous literature as one of the four recurrent patterns identified by [47] and is reminiscent of the so-called East Atlantic pattern (negative phase, [48]) viewed as a Euro-Atlantic wave train.

Figure 11.
Atlantic Ridge CWT: same panels as Figure 8.
This regime is one of the most frequent CWT (17%, Table 3), especially at the end of autumn and at the beginning of spring (Figure 5). As opposed to the CWTs previously described, AR is one of the driest CWT as its contribution to total precipitation is not very significant (12%, Table 3) and its probability of precipitation is quite low (38.3%, Table 3). During dry days (56% of AR days), temperatures are statistically significantly high over the western half of the IP (Figure 11d) and relative humidity and TCWVF values are significantly low over the whole IP (Figure 11e,f).
Despite being one of the driest CWT, AR shows curiously the highest probability of the precipitation falling in the form of snow (67.2%, Table 3). The percentage of snowfalls with daily intensities between 0.5 mm and 5 mm day−¹ is almost the same as for NAO- (Figure 6). The ridge brings hot and dry air over the North Atlantic, but the northern flow over the IP brings cold air to SdG, and significantly increases the probability of cold extremes [49]. As reported in Table 2 the heaviest snowfall under this CWT during our period of study took place on 5 December 2003, reaching 70.7 mm of snow water equivalent in Puerto de Navacerrada and 55 mm in Cotos. It is worth mentioning that the historical and recent blizzard called ‘Filomena’ that wreaked havoc across many inland areas of Spain, with exceptional amounts of snow on 8 and 9 January 2021, is also included in our Table 2. During these two days classified within the Atlantic Ridge CWT, 20.3 mm and 12.5 mm day−1 of SWE were recorded respectively in Puerto de Navacerrada, and 12.4 mm and 25.8 mm day−1 in Cotos.
4.2.5. NAO+
NAO+ regime is characterised by a dipolar structure in 500 hPa geopotential height anomalies, with opposite sign than the NAO- regime (Figure 12b). This pattern also shows an enhancement of the Azores high at 925 hPa facing the coast of Portugal and extending toward the IP (Figure 12a), which results in a blocking of the moisture advection in this area (Figure 12c). Therefore, this CWT is associated with dry weather conditions during winter, with a probability of precipitation below 35% and a contribution to the total precipitation of less than 11% (Table 3).

Figure 12.
NAO+ CWT: same panels as Figure 8.
This CWT is very similar to those obtained by [15,22], who found a statistically significant correlation with the positive phase of the NAO. Overall, NAO+ is the most frequent CWT (17.9%, Table 3) during the extended winter season. If we analyse this frequency per month, we observe that central months (DJF) show the highest values in contrast to NAO- (Figure 5).
During dry days (around 60% of days under this CWT), NAO+ shows statistically significant high temperatures (Figure 12d) and low values of TCWVT and relative humidity (Figure 12e,f) over IP. Scarce precipitation days under this CWT seem to be caused mainly by a northern intrusion of air that brings some moisture to SdG. However, these precipitation days could be also linked to transition periods from another wet CWT. Another possibility suggested by [22] is that these wet days are connected to mesoscale processes, such as cold fronts, that briefly disturb the Azores anticyclone.
Despite being one of the driest CWT, NAO+ is especially relevant in winter because it shows a probability that the precipitation falls as snow higher than 50% (Table 3). Unlike rainy days, snowy days exhibit statistically significant low temperatures at 925 hPa at SdG (Figure 12j). Relative humidity values are statistically significantly high in both cases (Figure 12h,k) while the values of TCWVF are slightly lower on snowy days and are not statistically significant at SdG (Figure 12l).
Heavy snowfalls are less common than in the previous CWTs (Table 3). During these extreme events, the northern air intrusion seems to be more pronounced as it produces a further southward displacement of the two-degree isotherm over the IP (Figure 12m). In this case the statistically significant high values of relative humidity are more restricted to the IP (Figure 12n). During the 24 h prior to the heavy snowfalls, significant signals of low temperatures and high relative humidity values are found facing the coast of Morocco and Portugal (Figure 12p,q) and low values of TCWVF toward the north-east of the British Islands. As shown in Table 2 the heaviest snowfall under this CWT during our period of study took place on 16 March 2020, reaching 48.6 mm of snow water equivalent in Puerto de Navacerrada and 42.2 mm in Cotos.
4.2.6. Scandinavian Blocking
This CWT is characterised by a high-pressure system that extends from northern Europe to the Iberian Peninsula as shown in Figure 13a. This pattern shows a strong positive anomaly of 500 hPa geopotential centred over the British Isles (Figure 13b). This is a well-known circulation weather pattern [50,51], and it plays a strong role in the climate variability of precipitation in the Iberian Peninsula [52].

Figure 13.
Scandinavian Blocking CWT: same panels as Figure 8.
This CWT is quite frequent and dry (Table 3 and Figure 7) since the advection of humid air masses is inhibited at continental level (Figure 13c,f). Precipitation in SdG is rare under this CWT (65 % of days under this CWT are dry) and it contributes only around 8% of total precipitation. These events might occur during transitions to other CWT. The probability of snowfall under the influence of this circulation weather type is below 50%, and its probability of heavy snowfall is the lowest among all the CWTs (Table 3).
As shown in Table 2, the heaviest snowfall under this CWT during our period of study took place on 26 November 2016, reaching 59.8 mm of snow water equivalent in Puerto de Navacerrada and 39.2 mm in Cotos.
4.2.7. Anticyclonic
This is a well-known circulation weather type characterised by an extended region of high pressures expanding throughout the whole Iberian Peninsula toward the south (Figure 14a) with positive anomalies at higher levels (Figure 14b) and lower values of TCWVF over the IP (Figure 14c).

Figure 14.
Anticyclonic CWT: same panels as Figure 8.
Normally, the air is drier under this CWT (Figure 14e) with higher temperatures (Figure 14d). Since zonal advection of humid air under this pattern is inhibited very efficiently, this is the driest CWT. It shows the lowest probability of precipitation (26.9%, Table 3) and the lowest contribution to total precipitation (6.2%, Table 3). This CWT is more frequent during the central months of the winter (Figure 5) and is very relevant to explain climate variability of precipitation in the Iberian Peninsula, and therefore at SdG. Although snow probability is low, it is curious that the probability of heavy snowfall is comparable to that of Western regime (Table 3). As reported in Table 2, the heaviest snowfall under this CWT during our period of study took place on 26 November 2016, reaching 40 mm of snow water equivalent in Puerto de Navacerrada and 55.3 mm in Cotos.
5. Conclusions
This work reveals some interesting features of winter precipitation and snowfalls at two sites in Sierra de Guadarrama. Over the year, more than 37% of precipitation in this area falls as snow. During the extended winter season (from November to April) the snow ratio exceeds 30%, reaching its greatest values in February (74.6%) and January (57.3%). Snow plays a crucial role as a temporary storehouse for winter precipitation at Sierra de Guadarrama and its area of influence.
As shown by other authors there is a strong interannual variability of winter precipitation, but a clear trend in total winter precipitation has not been found for the period 2000–2021. In contrast, a clear tendency of −0.5 days with snow cover above 3 cm has been observed which seem not to be attributed to lower snow precipitation. The hypothesis is that this might be due to higher ground temperatures due to climate change and elevation of the zero degrees Celsius isotherm. This hypothesis, which is coherent with other works in the area, will have to be further investigated in the future.
A clear link between winter precipitation and snow height at the sites under study has been found. Water vapor fluxes and temperature fields at large scale seem to be the main forcing phenomena for winter precipitation and snow height increases at the sites, thus results obtained here can be extended to Sierra de Guadarrama. Daily geopotential fields from ERA5 reanalysis have shown to be suitable for finding the following 7 large-scale circulation weather types: Cyclonic (C), Western (W), NAO-, Atlantic Ridge (AR), NAO+, Scandinavian Blocking (SB) and Anticyclonic (A).
It has been found that the wettest patterns at SdG, which are at the same time the least frequent, are C, W and NAO-. All together, they are responsible for more than 60% of total winter precipitation, their probabilities of precipitation are above 70% and they show the highest rates of daily total precipitation and snow.
AR, NAO+, SB and A show higher frequencies and are the driest CWTs with a low contribution to total precipitation and probability of precipitation. In fact, two of these last CWTs, AR and NAO+ along with NAO- exhibit the highest probabilities of the precipitation being snow (above 50%).
An analysis of snowfalls according to their CWT and their daily intensity (grouped in the intervals [0.5–5] mm day−¹, (5–30] mm day−¹ and >30 mm day−¹) was also performed and it was found that in absolute terms NAO- was the most common CWT for moderate and extreme snowfalls while in relative terms, C was the CWT with a higher proportion of extreme snowfalls.
Regarding heavy snowfalls, the heaviest snowfall took place on 12 February 2017 under NAO- circulation type and reached 137.4 mm of snow water equivalent in Puerto de Navacerrada and 139.4 mm in Cotos. This event led to 115 cm of snow height increment in a single day. This circulation type has a high probability of snow precipitation and shows consistent prediction capabilities with an anomalous increase of the relative humidity in a wide area over the Iberian Peninsula 24 h ahead, along with anomalous lower temperatures at 850 hPa in a very wide area.
Another outstanding circulation weather type strongly related to snow precipitation is AR. It normally leads to dry days except when the ridge is accompanied by advection of humidity entering from the SW of the Iberian Peninsula that interacts with cold air coming south along the ridge and leading to heavy snowfalls.
As shown in this work, heavy snow events at SdG follow a set of synoptic scale patterns that could be used to develop local scale warning systems. Numerical weather prediction outputs from current operative global models can be used as input data for statistical, empirical or dynamical modelling tools. Further work will be aimed towards the development of such warning tools and in the application of physical models that will help to understand the phenomena of snow precipitation and snowpack dynamics.
Finally, it is important to stress the importance of performing high-quality snow depth and density measurements on a routine basis and following high-quality standards. A combination of automatic and manual techniques has shown to be a good combination for capturing the temporal and spatial variability of the snow height. But extra measuring methods would be necessary to have a better picture of key features that lead the snowpack dynamics, like snow water content, snow density or temperature. Moreover, it would be necessary to be able to correct the intrinsic under-catching of rain gauges under windy conditions and to be able to have a precise method to determine the phase of the precipitation, for example using laser disdrometers.
Author Contributions
Material preparation, data collection, analysis and graphs were performed by C.G.-F. and Á.G.-C. L.D. contributed to the study conception, method definition, analyses, overall coordination and search for funds. All authors have read and agreed to the published version of the manuscript.
Funding
Partial funding comes from Ministerio de Ciencia e Innovación. Programa de doctorados industriales 2019, DIN2019-010482 and interMET Sistemas y Redes SME.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
We would like to thank the Agencia Estatal de Meteorología (AEMET) for providing observational data. Special thanks to Navacerrada Observatory staff for their tireless and accurate work. Thanks to the European Centre for Medium-Range Weather Forecasts (ECMWF) for providing the ERA5 Data. Thanks to staff and management of Parque Nacional Sierra de Guadarrama for providing data from Red Meteorológica del Parque Nacional Sierra de Guadarrama, for the manual snow depth observations, for their valuable support and remarks. We would like to thank the referees for their thoughtful reviews that helped to make this a better paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Barry, R.G. The role of snow and ice in the global climate system: A review. Polar Geogr. 2002, 26, 235–246. [Google Scholar] [CrossRef]
- Ballantyne, C.K. The hydrologic significance of nivation features in permafrost areas. Geogr. Ann. Ser. A Phys. Geogr. 1978, 60, 51–54. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Marty, C.; Tilg, A.M.; Jonas, T. Recent Evidence of Large-Scale Receding Snow Water Equivalents in the European Alps. J. Hydrometeorol. 2017, 18, 1021–1031. [Google Scholar] [CrossRef]
- Earman, S.; Dettinger, M. Potential impacts of climate change on groundwater resources—A global review. J. Water Clim. Change 2011, 2, 213–229. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Woods, R.A.; Hrachowitz, M.; Hrachowitz, R. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Change 2014, 4, 583–586. [Google Scholar] [CrossRef]
- Matiu, M.; Crespi, A.; Bertoldi, G.; Carmagnola, C.M.; Marty, C.; Morin, S.; Schöner, W.; Berro, D.C.; Chiogna, G.; De Gregorio, L.; et al. Observed snow depth trends in the European Alps: 1971 to 2019. Cryosphere 2021, 15, 1343–1382. [Google Scholar] [CrossRef]
- Schöner, W.; Koch, R.; Matulla, C.; Marty, C.; Tilg, A.M. Spatiotemporal patterns of snow depth within the Swiss-Austrian Alps for the past half century (1961 to 2012) and linkages to climate change. Int. J. Climatol. 2019, 39, 1589–1603. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Soubeyroux, J.M.; Gascoin, S.; Alonso-Gonzalez, E.; Durán-Gómez, N.; Lafaysse, M.; Vernay, M.; Carmagnola, C.; Morin, S. Long-term trends (1958–2017) in snow cover duration and depth in the Pyrenees. Int. J. Climatol. 2020, 40, 6122–6136. [Google Scholar] [CrossRef]
- Skiles, S.M.; Painter, T.H. Assessment of radiative forcing by light-absorbing particles in snow from in situ observations with radiative transfer modeling. J. Hydrometeorol. 2018, 19, 1397–1409. [Google Scholar] [CrossRef]
- Di Mauro, B.; Garzonio, R.; Rossini, M.; Filippa, G.; Pogliotti, P.; Galvagno, M.; Morra di Cella, U.; Migliavacca, M.; Baccolo, G.; Clemenza, M.; et al. Saharan dust events in the European Alps: Role in snowmelt and geochemical characterization. Cryosphere 2019, 13, 1147–1165. [Google Scholar] [CrossRef]
- Dumont, M.; Tuzet, F.; Gascoin, S.; Picard, G.; Kutuzov, S.; Lafaysse, M.; Cluzet, B.; Nheili, R.; Painter, T. Accelerated Snow Melt in the Russian Caucasus Mountains After the Saharan Dust Outbreak in March 2018. J. Geophys. Res. Earth Surf. 2020, 125, e2020JF005641. [Google Scholar] [CrossRef]
- Fulgencio, C.; Briviesca, E. El Canal de Isabel II. Boletín De La Soc. Española De Hidrol. Médica 2015, 30, 73–88. [Google Scholar] [CrossRef]
- Durán, L.; Sánchez, E.; Yagüe, C. Climatology of precipitation over the Iberian Central System mountain range. Int. J. Climatol. 2013, 33, 2260–2273. [Google Scholar] [CrossRef]
- Durán, L.; Rodríguez-Fonseca, B.; Yagüe, C.; Sánchez, E. Water vapour flux patterns and precipitation at Sierra de Guadarrama mountain range (Spain). Int. J. Climatol. 2015, 35, 1593–1610. [Google Scholar] [CrossRef]
- Durán, L.; Barstad, I. Multi-scale evaluation of a linear model of orographic precipitation over Sierra de Guadarrama (Iberian Central System). Int. J. Climatol. 2018, 38, 4127–4141. [Google Scholar] [CrossRef]
- Alonso-González, E.; López-Moreno, J.I.; Navarro-Serrano, F.; Sanmiguel-Vallelado, A.; Revuelto, J.; Domínguez-Castro, F.; Ceballos, A. Snow climatology for the mountains in the Iberian Peninsula using satellite imagery and simulations with dynamically downscaled reanalysis data. Int. J. Climatol. 2020, 40, 477–491. [Google Scholar] [CrossRef]
- Durán, L.; Rodríguez-Muñoz, I.; Sánchez, E. The Peñalara Mountain Meteorological Network (1999–2014): Description, Preliminary Results and Lessons Learned. Atmosphere 2017, 8, 203. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Zhang, X.; Sorteberg, A.; Zhang, J.; Gerdes, R.; Comiso, J.C. Recent radical shifts of atmospheric circulations and rapid changes in Arctic climate system. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Yuan, P.; Hunegnaw, A.; Alshawaf, F.; Awange, J.; Klos, A.; Teferle, F.N.; Kutterer, H. Feasibility of ERA5 integrated water vapor trends for climate change analysis in continental Europe: An evaluation with GPS (1994–2019) by considering statistical significance. Remote Sens. Environ. 2021, 260, 112416. [Google Scholar] [CrossRef]
- Santos, J.A.; Corte-Real, J.; Leite, S.M. Weather regimes and their connection to the winter rainfall in Portugal. Int. J. Climatol. 2005, 25, 33–50. [Google Scholar] [CrossRef]
- Farukh, M.A.; Yamada, T.J. Synoptic climatology associated with extreme snowfall events in Sapporo city of northern Japan. Atmos. Sci. Lett. 2014, 15, 259–265. [Google Scholar] [CrossRef]
- Merino, A.; Fernández, S.; Hermida, L.; López, L.; Sánchez, J.L.; García-Ortega, E.; Gascón, E. Snowfall in the northwest Iberian Peninsula: Synoptic circulation patterns and their influence on snow day trends. Sci. World J. 2014, 2014, 480275. [Google Scholar] [CrossRef] [PubMed]
- Coe, D.; Barlow, M.; Agel, L.; Colby, F.; Skinner, C.; Qian, J.H. Clustering Analysis of Autumn Weather Regimes in the Northeast United States. J. Clim. 2021, 34, 7587–7605. [Google Scholar] [CrossRef]
- Plaut, G.; Schuepbach, E.; Doctor, M. Heavy precipitation events over a few Alpine sub-regions and the links with large-scale circulation, 1971–1995. Clim. Res. 2001, 17, 285–302. [Google Scholar] [CrossRef]
- Esteban, P.; Jones, P.D.; Martín-Vide, J.; Mases, M. Atmospheric circulation patterns related to heavy snowfall days in Andorra, Pyrenees. Int. J. Climatol. 2005, 25, 319–329. [Google Scholar] [CrossRef]
- Mock, C.J.; Birkeland, K.W. Snow climatology of the western United States mountain ranges. Bull. Amer. Meteor. Soc. 2000, 81, 2367–2392. [Google Scholar] [CrossRef]
- Fernández-Cañadas, J.A. Los Aludes de Nieve en el Macizo de Peñalara. Available online: https://www.aemet.es/documentos/es/conocermas/recursos_en_linea/publicaciones_y_estudios/publicaciones/Aludes_penalara/NT_14_AEMET.pdf (accessed on 8 August 2022).
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Birkeland, K.W.; Mock, C.J.; Shinker, J.J. Avalanche extremes and atmospheric circulation patterns. Ann. Glaciol. 2001, 32, 135–140. [Google Scholar] [CrossRef]
- Solman, S.A.; Menendez, C.G. Weather regimes in the South American sector and neighbouring oceans during winter. Clim. Dyn. 2003, 21, 91–104. [Google Scholar] [CrossRef]
- Romero, R.; Ramis, C.; Guijarro, J.A.; Sumner, G. Daily rainfall affinity areas in the Mediterranean Spain. Int. J. Climatol. 1999, 19, 557–578. [Google Scholar] [CrossRef]
- Fernández-Montes, S.; Rodrigo, F.S.; Seubert, S.; Sousa, P.M. Spring and summer extreme temperatures in Iberia during last century in relation to circulation types. Atmos. Res. 2013, 127, 154–177. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F. Sampling errors in the estimation of empirical orthogonal functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A.; Algorithm, A.S. 136: A K-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar]
- Corte-Real, J.; Qian, B.; Xu, H. Regional climate change in Portugal: Precipitation variability associated with large-scale atmospheric circulation. Int. J. Climatol. 1998, 18, 619–635. [Google Scholar] [CrossRef]
- Gershunov, A.; Barnett, T.P. ENSO influence on intraseasonal extreme rainfall and temperature frequencies in the contiguous United States: Observations and model results. J. Clim. 1998, 11, 1575–1586. [Google Scholar] [CrossRef]
- Gershunov, A.; Barnett, T.P. Interdecadal modulation of ENSO teleconnections. Bull. Amer. Meteor. Soc. 1998, 79, 2715–2725. [Google Scholar] [CrossRef]
- Matthews, A.J.; Kiladis, G.N. Interactions between ENSO, transient circulation, and tropical convection over the Pacific. J. Clim. 1999, 12, 3062–3086. [Google Scholar] [CrossRef]
- Lee, S.H.; Furtado, J.C.; Charlton-Perez, A.J. Wintertime North American weather regimes and the Arctic stratospheric polar vortex. Geophys. Res. Lett. 2019, 46, 14892–14900. [Google Scholar] [CrossRef]
- Grotjahn, R.; Faure, G. Composite predictor maps of extraordinary weather events in the Sacramento, California, region. Weather Forecast. 2008, 23, 313–335. [Google Scholar] [CrossRef]
- Wilson, R.J.; Gutiérrez, D.; Gutiérrez, J.; Martínez, D.; Agudo, R.; Monserrat, V.J. Changes to the elevational limits and extent of species ranges associated with climate change. Ecol. Lett. 2005, 8, 1138–1146. [Google Scholar] [CrossRef]
- Bosch, J.; Carrascal, L.M.; Duran, L.; Walker, S.; Fisher, M.C. Climate change and outbreaks of amphibian chytridiomycosis in a montane area of Central Spain; is there a link? Proc. R. Soc. B: Biol. Sci. 2007, 274, 253–260. [Google Scholar] [CrossRef] [PubMed]
- Wilson, R.J.; Gutierrez, D.; Gutierrez, J.; Monserrat, V.J. An elevational shift in butterfly species richness and composition accompanying recent climate change. Glob. Change Biol. 2007, 13, 1873–1887. [Google Scholar] [CrossRef]
- Rubio-Romero, A.; Granados, I. Efectos del cambio climático sobre los macroinvertebrados fluviales del Alto Lozoya. In Proceedings of the XIV Congreso de la Asociación Ibérica de Limnologá, Huelva, Spain, 8–12 September 2008. [Google Scholar]
- Legras, B.; Desponts, T.; Piguet, B. Cluster analysis and weather regimes. In Proceedings of the ECMWF Seminar, The Nature and Prediction of Extratropical Weather Systems, ECMWF, Reading, UK, 7–11 September 1987. [Google Scholar]
- Barnston, A.G.; Livezey, R.E. Classifications, Seasonality, and Persistence of Low-Frequency Atmospheric Circulation Patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Cassou, C. Euro-Atlantic regimes and their teleconnections. In Proceedings of the ECMWF Seminar on Predictability in the European and Atlantic Regions, Reading, UK, 6–9 September 2010; pp. 1–14. Available online: https://www.ecmwf.int/sites/default/files/elibrary/2012/8609-euro-atlantic-regimes-and-their-teleconnections.pdf (accessed on 7 June 2022).
- Tyrlis, E.; Hoskins, B.J. Aspects of a Northern Hemisphere Atmospheric Blocking Climatology. J. Atmos. Sci. 2008, 65, 1638–1652. Available online: https://journals.ametsoc.org/view/journals/atsc/65/5/2007jas2337.1.xml (accessed on 7 June 2022). [CrossRef]
- Falkena, S.K.; de Wiljes, J.; Weisheimer, A.; Shepherd, T.G. Revisiting the identification of wintertime atmospheric circulation regimes in the Euro-Atlantic sector. Q. J. R. Meteorol. Soc. 2020, 146, 2801–2814. [Google Scholar] [CrossRef]
- Sousa, P.M.; Trigo, R.M.; Barriopedro, D.; Soares, P.M.; Ramos, A.M.; Liberato, M.L. Responses of European precipitation distributions and regimes to different blocking locations. Clim. Dyn. 2017, 48, 1141–1160. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).