Use and Scalability of OpenFOAM for Wind Fields and Pollution Dispersion with Building- and Ground-Resolving Topography
Abstract
:1. Introduction
2. Materials and Methods
2.1. Boundary Conditions
2.2. Three-Dimensional Geometry and Computational Mesh
3. Results
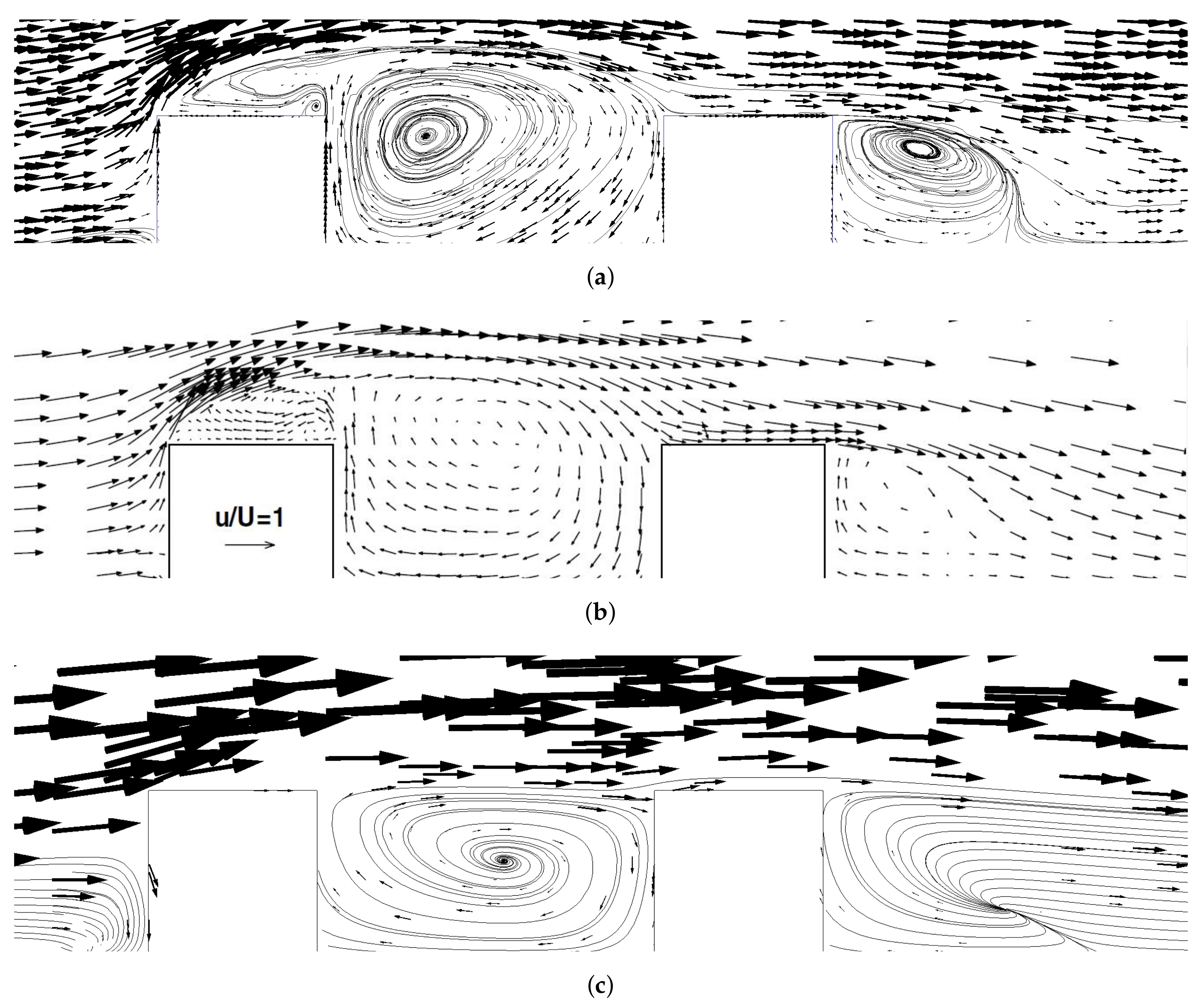
3.1. Double Bluff
3.2. Wind-Field Simulation of a Scaled-Up Double-Bluff Geometry with Atmospheric Inflow Profiles
3.3. Warsaw
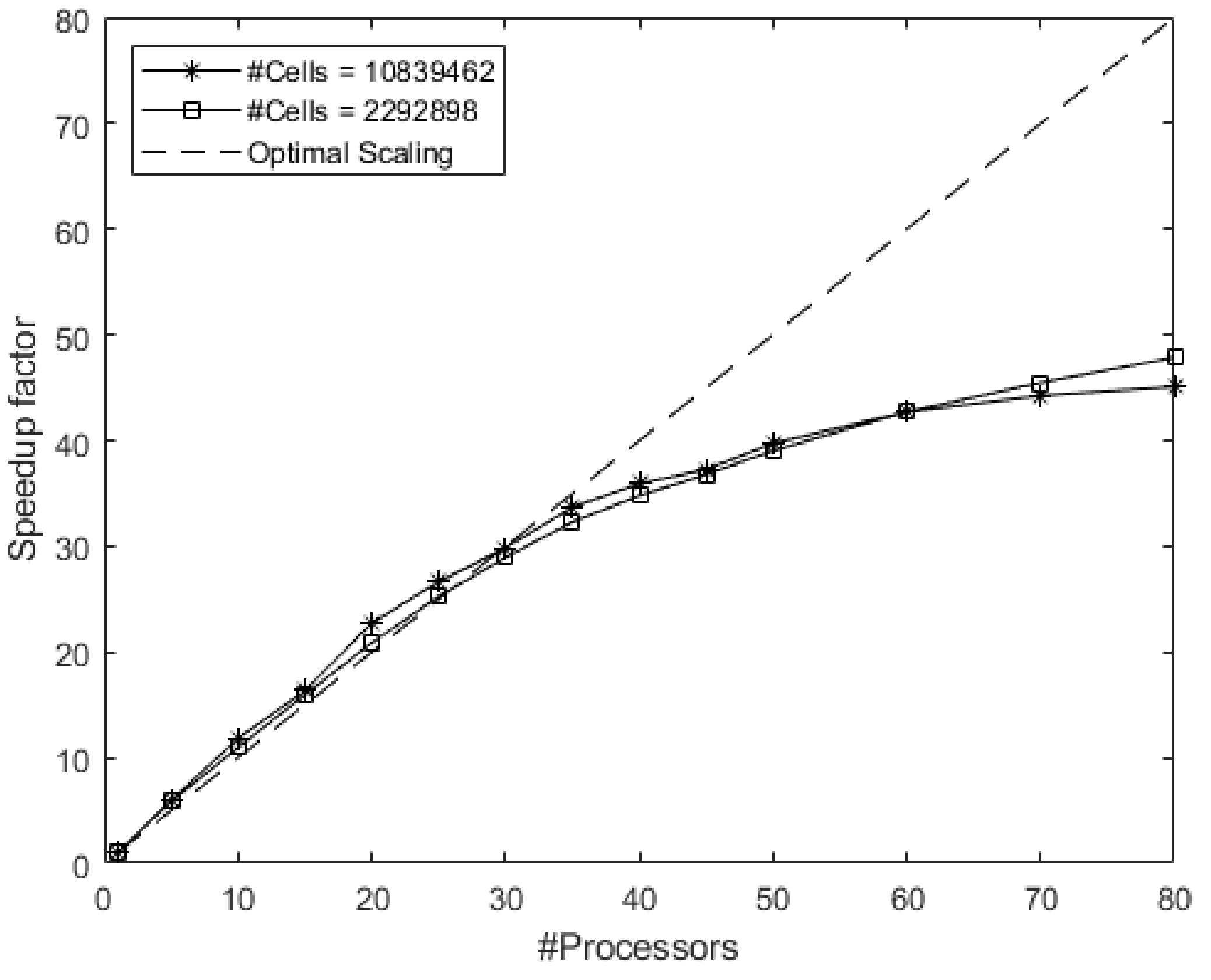
3.4. Parallel Scaling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gowardhan, A.; Pardyjak, E.; Senocak, I.; Brown, M. A CFD-based wind solver for an urban fast response transport and dispersion model. Environ. Fluid Mech. 2011, 11, 439–464. [Google Scholar] [CrossRef]
- Patnaik, G.; Moses, A.; Boris, J. Fast, Accurate Defense for Homeland Security: Bringing High-Performance Computing to First Responders. J. Aerosp. Comput. Inf. Commun. 2010, 7, 210–222. [Google Scholar] [CrossRef]
- Oldrini, O.; Armand, P.; Duchenne, C.; Perdriel, S.; Nibart, M. Accelerated Time and High-Resolution 3D Modeling of the Flow and Dispersion of Noxious Substances over a Gigantic Urban Area—The EMERGENCIES Project. Atmosphere 2021, 12, 640. [Google Scholar] [CrossRef]
- Brown, M. Urban dispersion—Challenges for fast response modeling. In Proceedings of the 5th AMS Symposium on the Urban Environment, Vancouver, BC, Canada, 23–26 August 2004. [Google Scholar]
- Röckle, R. Bestimmung der Strömungsverhältnisse im Bereich komplexer Bebauungsstrukturen. Ph.D. Thesis, Technical University Darmstadt, Darmstadt, Germany, December 1990. [Google Scholar]
- Kopka, P.; Potempski, S.; Kaszko, A.; Korycki, M. Urban Dispersion Modelling Capabilities Related to the UDINEE Intensive Operating Period 4. Bound.-Layer Meteorol. 2019, 171, 465–489. [Google Scholar] [CrossRef] [Green Version]
- Hertwig, D.; Soulhac, L.; Fuka, V.; Auerswald, T.; Carpentieri, M.; Hayden, P.; Robins, A.; Xie, Z.T.; Coceal, O. Evaluation of fast atmospheric dispersion models in a regular street network. Environ. Fluid Mech. 2018, 18, 1007–1044. [Google Scholar] [CrossRef] [Green Version]
- Soulhac, L.; Lamaison, G.; Cierco, F.X.; Salem, N.B.; Salizzoni, P.; Mejean, P.; Armand, P.; Patryl, L. SIRANERISK: Modelling dispersion of steady and unsteady pollutant releases in the urban canopy. Atmos. Environ. 2016, 140, 242–260. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.; Esch, T. Elements of industrial heat transfer predictions. In Proceedings of the 16th Brazilian Congress of Mechanical Engineering (COBEM 2001), Minas Gerais, Brazil, 26–30 November 2001; Volume 109, p. 650. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R.; Nagano, Y.; Tummers, M.J.; Hanjalic, K. Ten Years of Industrial Experience with the SST Turbulence Model. In Turbulence, Heat and Mass Transfer, 4th ed.; Internal Symposium, Turbulence, Heat and Mass Transfer; Begell House: New York, NY, USA, 2003; Volume 4, pp. 625–632. [Google Scholar]
- Yu, H.; Thé, J. Validation and optimization of SST k-ω turbulence model for pollutant dispersion within a building array. Atmos. Environ. 2016, 145, 225–238. [Google Scholar] [CrossRef]
- Trindade da Silva, F.; Reis, N.C.; Santos, J.M.; Goulart, E.V.; Engel de Alvarez, C. The impact of urban block typology on pollutant dispersion. J. Wind. Eng. Ind. Aerodyn. 2021, 210, 104524. [Google Scholar] [CrossRef]
- Martinuzzi, R.J.; Havel, B. Vortex shedding from two surface-mounted cubes in tandem. Int. J. Heat Fluid Flow 2004, 25, 364–372. [Google Scholar] [CrossRef]
- Schmitt, F.G. About Boussinesq’s turbulent viscosity hypothesis: Historical remarks and a direct evaluation of its validity. C. R. MéCanique 2007, 335, 617–627. [Google Scholar] [CrossRef] [Green Version]
- Tominaga, Y.; Stathopoulos, T. Turbulent Schmidt numbers for CFD analysis with various types of flowfield. Atmos. Environ. 2007, 41, 8091–8099. [Google Scholar] [CrossRef]
- Gualtieri, C.; Angeloudis, A.; Bombardelli, F.; Jha, S.; Stoesser, T. On the Values for the Turbulent Schmidt Number in Environmental Flows. Fluids 2017, 2, 17. [Google Scholar] [CrossRef] [Green Version]
- OpenFOAM: User Guide v2012. Available online: https://www.openfoam.com/documentation/guides/latest/doc/ (accessed on 23 July 2021).
- Doormaal, J.P.V.; Raithby, G.D. Enhancements of the simple method for predicting incompressible fluid flows. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar] [CrossRef]
- Richards, P.; Hoxey, R. Appropriate boundary conditions for computational wind engineering models using the k-ϵ turbulence model. J. Wind. Eng. Ind. Aerodyn. 1993, 46–47, 145–153. [Google Scholar] [CrossRef]
- Geoportal–Spatial Information for Everyone. Available online: https://www.gov.pl/web/archiwum-inwestycje-rozwoj/geoportal-informacja-przestrzenna-dla-kazdego (accessed on 20 November 2019).
- Geoportal Infrastruktury Informacji Przestrzennej. Główny Geodeta Kraju (eng. “Principal Surveyor of The Country“) Is the Holder of the Data. Available online: http://www.geoportal.gov.pl (accessed on 4 February 2020).
- Gröger, G.; Plümer, L. CityGML—Interoperable semantic 3D city models. ISPRS J. Photogramm. Remote Sens. 2012, 71, 12–33. [Google Scholar] [CrossRef]
- Schroeder, W.; Martin, K.; Lorensen, B. The Visualization Toolkit, 4th ed.; Kitware, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Martinuzzi, R.J.; Havel, B. Turbulent Flow Around Two Interfering Surface-Mounted Cubic Obstacles in Tandem Arrangement. J. Fluids Eng. 1999, 122, 24–31. [Google Scholar] [CrossRef]
- Cui, P.-Y.; Li, Z.; Tao, W.-Q. Numerical investigations on Re-independence for the turbulent flow and pollutant dispersion under the urban boundary layer with some experimental validations. Int. J. Heat Mass Transf. 2017, 106, 422–436. [Google Scholar] [CrossRef] [Green Version]
- Hargreaves, D.; Wright, N. On the use of the k–ε model in commercial CFD software to model the neutral atmospheric boundary layer. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 355–369. [Google Scholar] [CrossRef]
- Milliez, M.; Carissimo, B. Numerical simulations of pollutant dispersion in an idealized urban area, for different meteorological conditions. Bound.-Layer Meteorol. 2007, 122, 321–342. [Google Scholar] [CrossRef]
- Yang, Y.; Gu, M.; Chen, S.Q.; Jin, X.Y. New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering. J. Wind. Eng. Ind. Aerodyn. 2009, 97, 88–95. [Google Scholar] [CrossRef]
- Lateb, M.; Meroney, R.; Yataghene, M.; Fellouah, H.; Saleh, F.; Boufadel, M. On the use of numerical modelling for near-field pollutant dispersion in urban environments—A review. Environ. Pollut. 2016, 208, 271–283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yee, E.; Biltoft, C.A. Concentration Fluctuation Measurements in a Plume Dispersing Through a Regular Array of Obstacles. Bound.-Layer Meteorol. 2004, 111, 363–415. [Google Scholar] [CrossRef]
- Pellegrini, F.; Roman, J. Scotch: A software package for static mapping by dual recursive bipartitioning of process and architecture graphs. In High-Performance Computing and Networking; Liddell, H., Colbrook, A., Hertzberger, B., Sloot, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 493–498. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elfverson, D.; Lejon, C. Use and Scalability of OpenFOAM for Wind Fields and Pollution Dispersion with Building- and Ground-Resolving Topography. Atmosphere 2021, 12, 1124. https://doi.org/10.3390/atmos12091124
Elfverson D, Lejon C. Use and Scalability of OpenFOAM for Wind Fields and Pollution Dispersion with Building- and Ground-Resolving Topography. Atmosphere. 2021; 12(9):1124. https://doi.org/10.3390/atmos12091124
Chicago/Turabian StyleElfverson, Daniel, and Christian Lejon. 2021. "Use and Scalability of OpenFOAM for Wind Fields and Pollution Dispersion with Building- and Ground-Resolving Topography" Atmosphere 12, no. 9: 1124. https://doi.org/10.3390/atmos12091124
APA StyleElfverson, D., & Lejon, C. (2021). Use and Scalability of OpenFOAM for Wind Fields and Pollution Dispersion with Building- and Ground-Resolving Topography. Atmosphere, 12(9), 1124. https://doi.org/10.3390/atmos12091124





