Optimization of HPC Use for 3D High Resolution Urban Air Quality Assessment and Downstream Services
Abstract
:1. Introduction
1.1. General Context and Motivations
1.2. The PMSS Modeling System
- A first guess computation based on the interpolation of heterogeneous meteorological input data, a mix of surface and profile measurements, and/or possibly meso-scale model outputs;
- The modification of the first guess using analytical zones defined around isolated buildings or within groups of buildings, based the approach originally proposed by [6];
- The mass-consistency (with impermeability condition at the ground and buildings) obtained by minimizing the difference of the wind field of the second step over the volume of the domain under the mass conservation constraint. The effect of atmospheric stability on the flow around obstacles is considered through a coefficient α applied to the vertical wind component terms during the minimizing process [12].
1.3. The Different Type of High Resolution Air Quality Modeling Applications
2. Long Term Air Quality Assessment in Urban Areas
2.1. Why Is HPC Used?
2.1.1. Complex Geometry
2.1.2. Unsteady Meteorology and Unsteady Emissions
Steady versus Unsteady Approaches
Input Data Cross-Variability
2.1.3. Purifying Systems
2.1.4. Numerous Scenarios
2.1.5. Domain Extents
2.2. Annual Impact on a Coastal City with Very Complex Terrain—HPC Use Optimization with Classification
2.2.1. Presentation and Objectives
2.2.2. Model Performance without Classification
- Different neighborhoods, in order to evaluate the distribution of the concentrations, and to better consider the impact of the topography;
- Major road axes crossing the territory, and those with a canyon-type;
- The acquisition of measurements in the vicinity of atypical sources of emissions (proximity to heliports, gas stations, cruise ships quays, tunnel portals, etc.).
2.2.3. Results with SOMs Classification
2.3. Grenoble Case—Validation with High Density Sensors Network
2.3.1. Context and Model Setup
2.3.2. Results
2.4. Rome Case
2.4.1. Context and Model Setup
2.4.2. Results
3. REX from Different Forecast Systems
3.1. Paris Forecast System
3.1.1. Context and Model Setup
3.1.2. Results
3.2. Antony Forecast System
3.2.1. Context and Model Setup
3.2.2. CPU Time Performance and Optimization
4. CPU Demand Analysis and Estimation
5. Discussion
- -
- Classification with SOMs method to reduce the number of days to be considered. The study provides the quantification of the classification effect on annual average concentration and, more challengingly, on percentiles;
- -
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harrison, R.M. Urban atmospheric chemistry: A very special case for study. NPJ Clim. Atmos. Sci. 2018, 1, 20175. [Google Scholar] [CrossRef] [Green Version]
- Arya, S.P. Introduction to Micrometeorology; Academic Press: San Diego, CA, USA, 1987; p. 307. [Google Scholar]
- Oke, T.R.; Mills, G.; Christensen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017; p. 519. [Google Scholar]
- Moussafir, J.; Oldrini, O.; Tinarelli, G.; Sontowski, J.; Dougherty, C. A new operational approach to deal with dispersion around obstacles: The MSS (Micro-Swift-Spray) software suite. In Proceedings of the 9th International Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes, Garmish-Partenkirchen, Germany, 6–10 June 2004; Volume 2, pp. 114–118. [Google Scholar]
- Tinarelli, G.; Brusasca, G.; Oldrini, O.; Anfossi, D.; Trini Castelli, S.; Moussafir, J. Micro-swift-spray (MSS) A new modeling system for the simulation of dispersion at microscale, general description and validation. In Proceedings of the 27th CCMS-NATO Meeting, Banff, AB, Canada, 24–29 October 2004. [Google Scholar]
- Rockle, R. Bestimmung der Stromungsverhaltnisse im Bereich Komplexer Bebauungsstrukturen. Ph.D. Thesis, Vom Fachbereich Mechanik, der Technischen Hochschule Darmstadt, Darmstadt, Germany, 1990. [Google Scholar]
- Oldrini, O.; Olry, C.; Moussafir, J.; Armand, P.; Duchenne, C. Development of PMSS, the parallel version of Micro SWIFT SPRAY. In Proceedings of the 14th International Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes, Kos, Greece, 2–6 October 2011; pp. 443–447. [Google Scholar]
- Oldrini, O.; Armand, P.; Duchenne, C.; Olry, C.; Tinarelli, G. Description and preliminary validation of the PMSS fast response parallel atmospheric flow and dispersion solver in complex built-up areas. J. Environ. Fluid Mech. 2017, 17, 997–1014. [Google Scholar] [CrossRef]
- Trini Castelli, S.; Armand, P.; Tinarelli, G.; Duchenne, C.; Nibart, M. Validation of a Lagrangian particle dispersion model with wind tunnel and field experiments in urban environment. Atmos. Environ. 2018, 193, 273–289. [Google Scholar] [CrossRef]
- Gomez, F.; Ribstein, B.; Makké, L.; Armand, P.; Moussafir, J.; Nibart, M. Simulation of a dense gas chlorine release with a lagrangian particle dispersion model (LPDM). Atmos. Environ. 2021, 244, 117791. [Google Scholar] [CrossRef]
- Moussafir, J.; Olry, C.; Nibart, M.; Albergel, A.; Armand, P.; Duchenne, C.; Mahé, F.; Thobois, L.; Loaëc, S.; Oldrini, O. AIRCITY: A Very High Resolution Atmospheric Dispersion Modeling System for Paris. In American Society of Mechanical Engineers, Fluids Engineering Division; FEDSM: Chicago, IL, USA, 2014; Volume 1D. [Google Scholar] [CrossRef] [Green Version]
- Geai, P. Méthode d’interpolation et de reconstitution tridimensionnelle d’un champ de vent: Le code d’analyse objective SWIFT. In EDF/DER Internal Report HE34-87; EDF Group: Chatou, France, 1987. [Google Scholar]
- Hanna, S.; White, J.; Trolier, J.; Vernot, R.; Brown, M.; Gowardhan, A.; Kaplan, H.; Alexander, Y.; Moussafir, J.; Wang, Y.; et al. Comparisons of JU2003 observations with four diagnostic urban wind flow and Lagrangian particle dispersion models. Atmos. Environ. 2011, 45, 4073–4081. [Google Scholar] [CrossRef]
- Berkowicz, R.; Hertel, O.; Larsen, S.; Sørensen, N. Modelling Traffic Pollution in Streets; Ministry of Environment and Energy, National Environmental Research Institute: Roskilde, Denmark, 1997. [Google Scholar]
- Rodean, H.C. Stochastic Lagrangian Models of Turbulent Diffusion; American Meteorological Society: Boston, MA, USA, 1996; Volume 45. [Google Scholar]
- Anfossi, D.; Desiato, F.; Tinarelli, G.; Brusasca, G.; Ferrero, E.; Sacchetti, D. TRANSALP 1989 experimental campaign Part II: Simulation of a tracer experiment with Lagrangian particle models. Atmos. Environ. 1998, 32, 1157–1166. [Google Scholar] [CrossRef]
- Carvalho, J.; Anfossi, D.; Castelli, S.T.; Degrazia, G.A. Application of a model system for the study of transport and diffusion in complex terrain to the TRACT experiment. Atmos. Environ. 2002, 36, 1147–1161. [Google Scholar] [CrossRef]
- Ferrero, E.; Anfossi, D. Comparison of PDFs, closures schemes and turbulence parameterizations in Lagrangian Stochastic Models. Int. J. Environ. Pollut. 1998, 9, 384–410. [Google Scholar]
- Ferrero, E.; Anfossi, D.; Tinarelli, G. Simulations of Atmospheric Dispersion in an Urban Stable Boundary Layer. Int. J. Environ. Pollut. 2001, 16, 1–6. [Google Scholar] [CrossRef]
- Trini Castelli, S.; Anfossi, D.; Ferrero, E. Evaluation of the environmental impact of two different heating scenarios in urban area. Int. J. Environ. Pollut. 2003, 20, 207–217. [Google Scholar] [CrossRef]
- Tinarelli, G.; Anfossi, D.; Brusasca, G.; Ferrero, E.; Giostra, U.; Morselli, M.G.; Moussafir, J.; Tampieri, F.; Trombetti, F. Lagrangian particle simulation of tracer dispersion in the lee of a schematic two-dimensional hill. J. Appl. Meteorol. 1994, 33, 744–756. [Google Scholar] [CrossRef] [Green Version]
- Tinarelli, G.; Anfossi, D.; Bider, M.; Ferrero, E.; Trini Castelli, S. A new high performance version of the Lagrangian particle dispersion model SPRAY, some case studies. In Air Pollution Modelling and Its Applications XIII; Gryning, S.E., Batchvarova, E., Eds.; Kluwer Academic/Plenum Press: New York, NY, USA, 2000; pp. 499–507. [Google Scholar]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Kaplan, H.; Olry, C.; Moussafir, J.; Oldrini, O.; Mahé, F.; Albergel, A. Chemical reactions at street scale using a lagrangian particle dispersion model (LPDM). In Proceedings of the 15th International Conference on Harmonization within Atmospheric Dispersion Modeling for Regulatory Purposes, Madrid, Spain, 6–9 May 2013. [Google Scholar]
- Benson, P. CALINE4—A Dispersion Model for Predicting Air Pollutant Concentrations near Roadways. Internal Report No FHWA/CA/TL-84/15. 1989. Available online: https://trid.trb.org/view/215944 (accessed on 15 September 2021).
- Malherbe, L.; Wroblewski, A.; Letinois, L.; Rouil, L. Evaluation of numerical models used to simulaite atmospheric pollution near roadways 13. In Proceedings of the International Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes (HARMO 13), Paris, France, 1–4 June 2010; pp. 697–700. [Google Scholar]
- Hertel, O.; Berkowicz, R. Operational Street Pollution Model (OSPM). In Evaluation of the Model on Data from St. Olavs Street in Oslo, DMU Luft A-135; National Environmental Research Institute: Roskilde, Denmark, 1989. [Google Scholar]
- Soulhac, L.; Salizzoni, P.; Cierco, F.-X.; Perkins, R.J. The model SIRANE for atmospheric urban pollutant dispersion: PART I: Presentation of the model. Atmos. Environ. 2011, 45, 7379–7395. [Google Scholar] [CrossRef]
- Armand, P.; Commanay, J.; Nibart, M.; Albergel, A.; Achim, P. 3D simulations of pollutants atmospheric dispersion around the buildings of an industrial site comparison of MERCURE CFD approach with Micro-SWIFT-SPRAY semi-empirical approach. In Proceedings of the 11th International Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes (HARMO11), Cambridge, UK, 2–5 July 2007. [Google Scholar]
- Kohonen, T. Self-Organizing Maps, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Yonggang, L.; Weisberg, R.H. A Review of Self-Organizing Map Applications in Meteorology and Oceanography. In Self Organizing Maps: Applications and Novel Algorithm Design; Mwasiagi, J.I., Ed.; IntechOpen: London, UK, 2011; pp. 253–272. [Google Scholar]
- Wendum, D.; Moussafir, J. Méthodes d’interpolation spatiale utilisables pour le calcul d’écoulements atmosphériques à moyenne échelle. In EDF Internal Report EDF/DER HE/32-85.22; EDF Group: Chatou, France, 1985. [Google Scholar]
- Menut, L.; Bessagnet, B.; Khvorostyanov, D.; Beekmann, M.; Blond, N.; Colette, A.; Coll, I.; Curci, G.; Foret, G.; Hodzic, A.; et al. CHIMERE (2013): A model for regional atmospheric composition modelling. Geosci. Model Dev. 2013, 6, 981–1028. [Google Scholar] [CrossRef] [Green Version]
- Gariazzo, C.; Silibello, C.; Finardi, S.; Radice, P.; Piersanti, A.; Calori, G.; Cecinato, A.; Perrino, C.; Nussio, F.; Cagnoli, M.; et al. A gas/aerosol air pollutants study over the urban area of Rome using a comprehensive chemical transport model. Atmos. Environ. 2007, 41, 7286–7303. [Google Scholar] [CrossRef]
- Silibello, C.; Calori, G.; Brusasca, G.; Giudici, A.; Angelino, E.; Fossati, G.; Peroni, E.; Buganza, E. Modelling of PM10 Concentrations Over Milano Urban Area Using Two Aerosol Modules. Environ. Model. Softw. 2008, 23, 333–343. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Technical Note NCAR/TN-475+STR; NCAR: Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
- Barbero, D. Sviluppo e Applicazione del Metodo Kernel in Modelli Lagrangiani a Particelle a Scala Locale e a Microscala. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2019. Available online: http://hdl.handle.net/10589/146531 (accessed on 11 September 2021).
- Bessagnet, B.; Couvidat, F.; Lemaire, V. A statistical physics approach to perform fast highly-resolved air quality simulations—A new step towards the meta-modelling of chemistry transport models. Environ. Model. Softw. 2019, 116, 100–109. [Google Scholar] [CrossRef]
- Carlino, G.; Pallavidino, L.; Prandi, R.; Avidano, A.; Matteucci, G.; Ricchiuti, F.; Bajardi, P.; Bolognini, L.; Elise, P. Micro-scale modelling of urban Air quality to forecast NO2 critical level in traffic Hot-spots. In Proceedings of the Air Quality 2013, Milan, Italy, 14–18 March 2016. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer; Springer: Dordrecht, The Netherland, 1988. [Google Scholar]
- Stohl, A.; Forster, C.; Frank, A.; Seibert, P.; Wotawa, G. Technical note: The Lagrangian particle dispersion model FLEXPART version 6.2. Atmos. Chem. Phys. 2005, 5, 2461–2474. [Google Scholar] [CrossRef] [Green Version]
- Bellasio, R.; Bianconi, R. LAPMOD—Manuale D’uso; Technical report of Enviroware-Air Qual; Consult; Enviroware: Concorezzo, Italy, 2017. [Google Scholar]
- Soulhac, L.; Méjean, P.; Perkins, R.J. Modelling the transport and dispersion of pollutants in street canyons. Int. J. Environ. Pollut. 2001, 16, 404–416. [Google Scholar] [CrossRef]
- Wu, Y.; Hao, J.; Fu, L.; Wang, Z.; Tang, U. Vertical and horizontal profiles of airborne particulate matter near major roads in Macao, China. Atmos. Environ. 2002, 36, 4907–4918. [Google Scholar] [CrossRef]
- Tuckett-Jones, B.T. Reade. In City Quality at Height—Lessons for Developers & Planners; Report from WSP; Parsons Brinkerhoff: London, UK, 2017. [Google Scholar]
- Wong, P.P.Y.; Lai, P.-C.; Allen, R.; Cheng, W.; Lee, M.; Tsui, A.; Tang, R.; Thach, T.-Q.; Tian, L.; Brauer, M.; et al. Vertical monitoring of traffic-related air pollution (TRAP) in urban street canyons of Hong Kong. Sci. Total Environ. 2019, 670, 696–703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
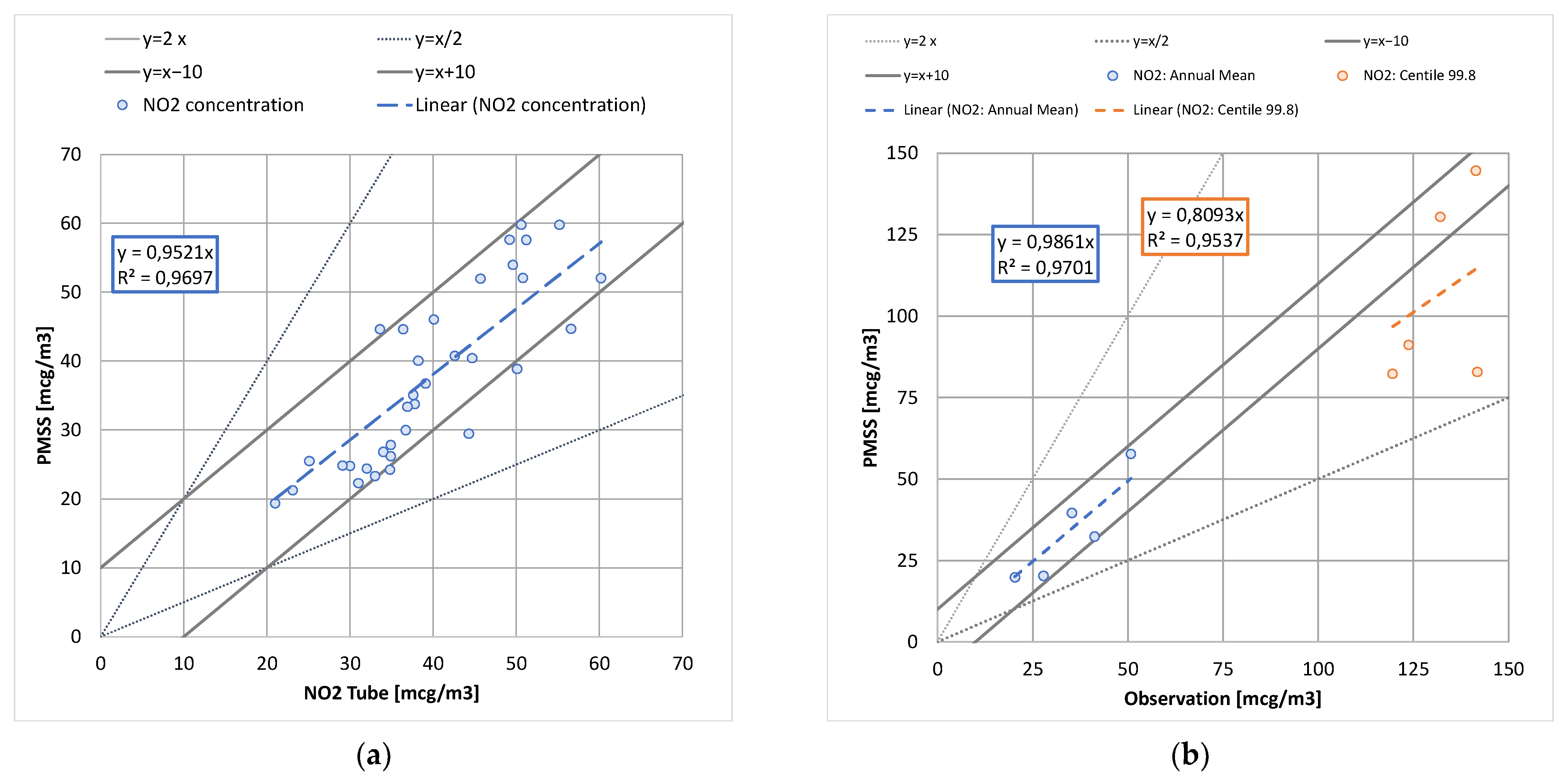
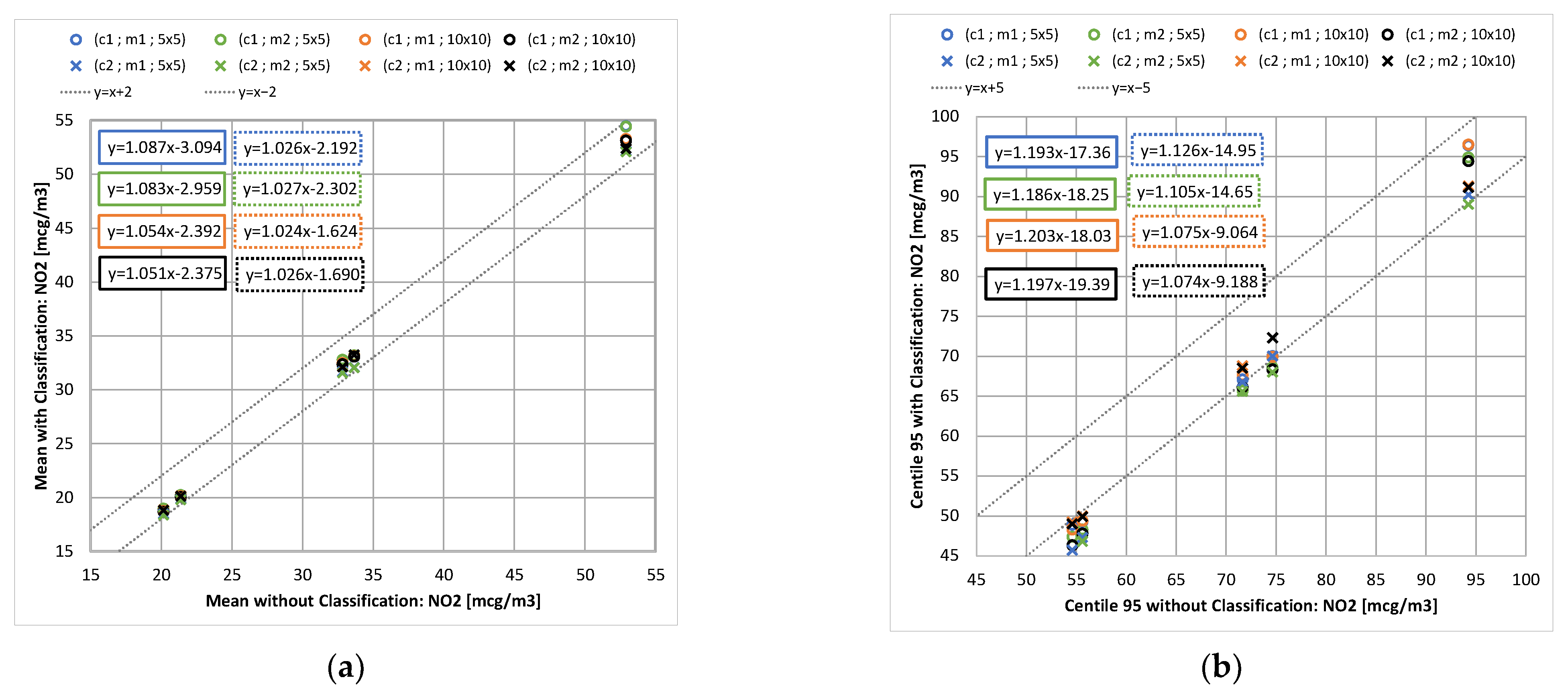
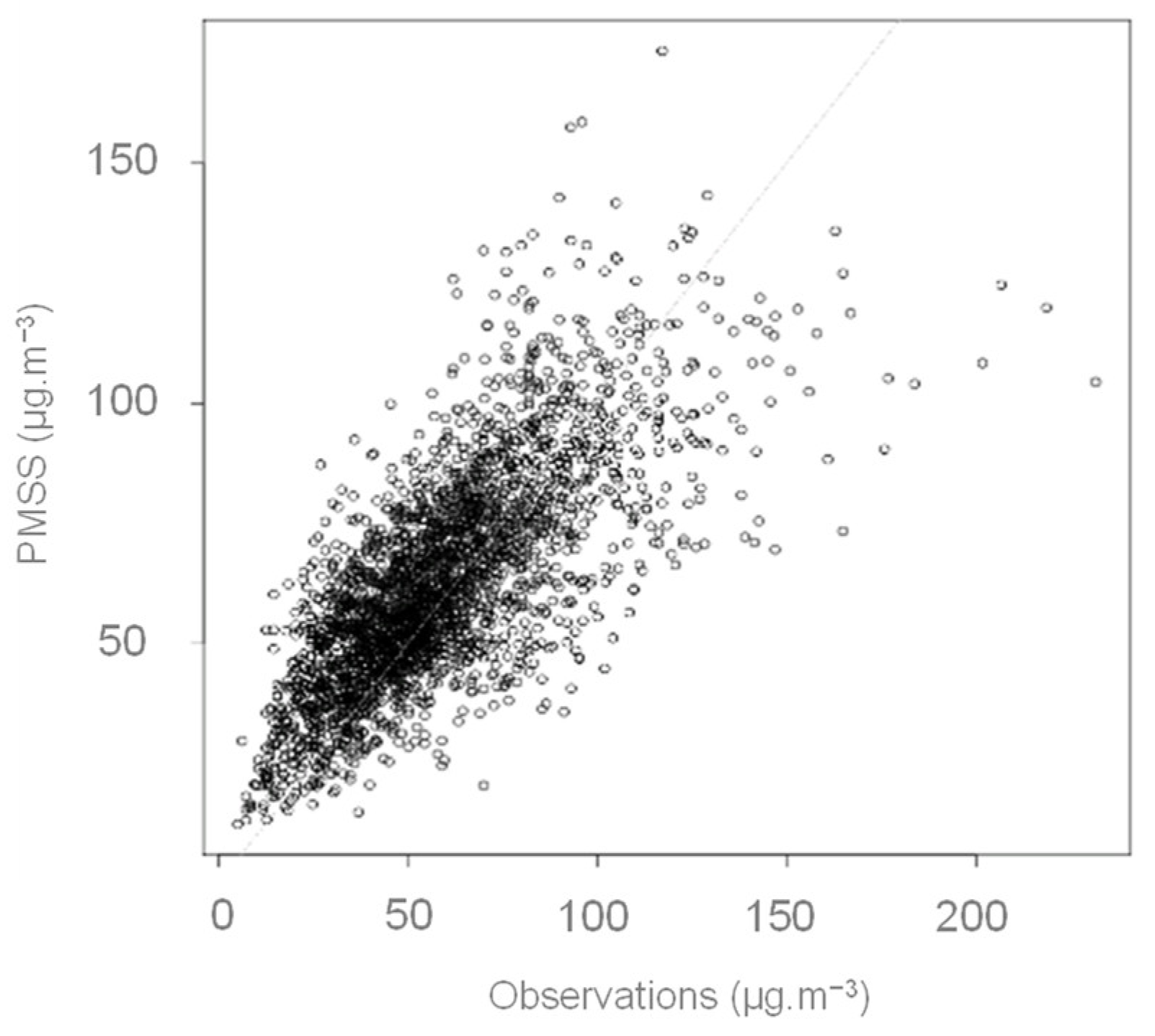

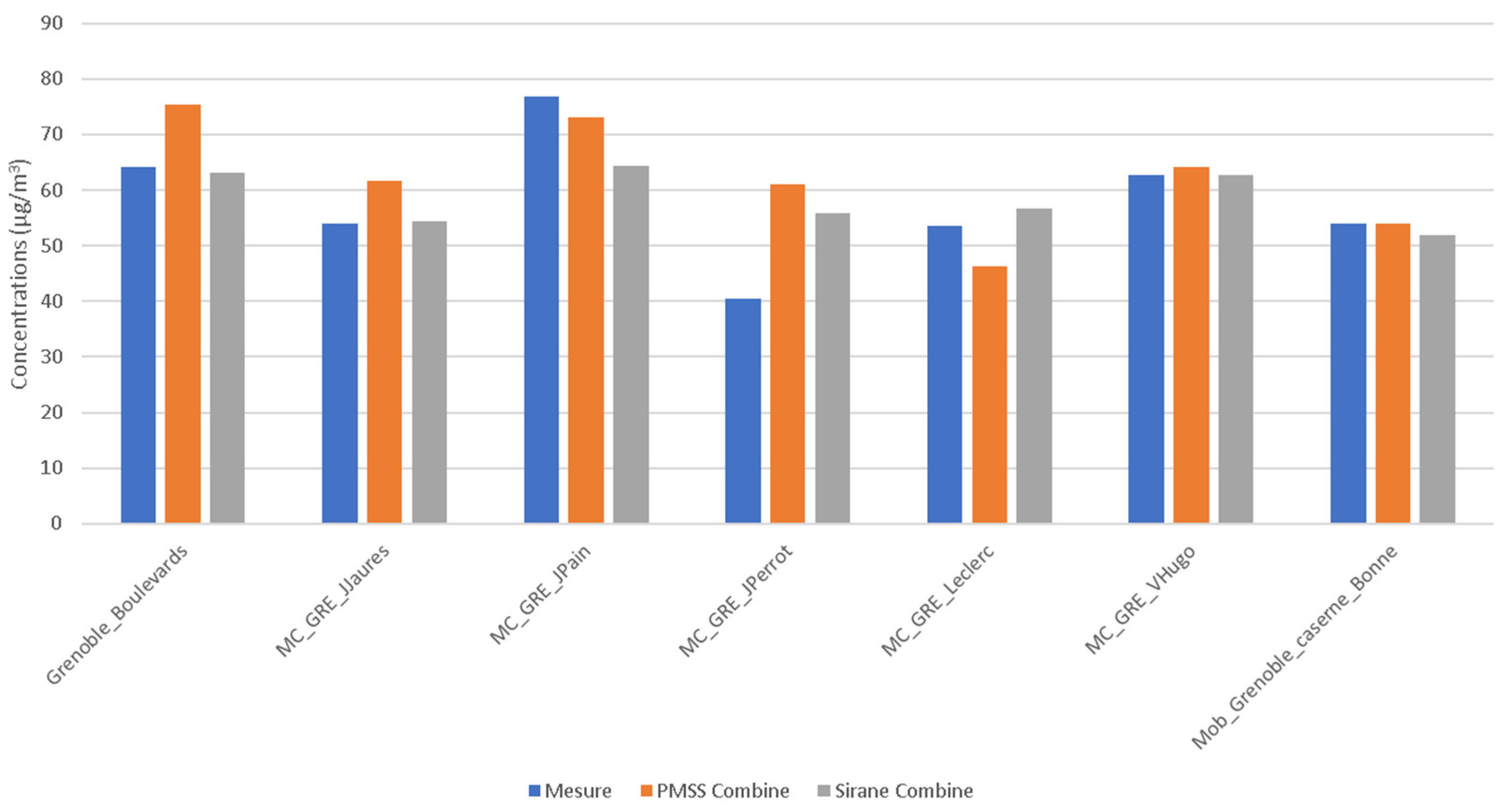


| Station | Mean Observation (µg/m3) | Mean Model (µg/m3) | Bias (µg/m3) | RMSE (µg/m3) | r |
|---|---|---|---|---|---|
| Station 1 * | 27.9 | 21.4 | −6.8 | 15.46 | 0.78 |
| Station 2 | 41.3 | 33.7 | −7.6 | 24.44 | 0.56 |
| Station 3 * | 20.4 | 20.2 | −0.4 | 5.33 | 0.95 |
| Station 4 | 50.8 | 52.9 | 2.2 | 20.89 | 0.68 |
| Station 5 | 35.3 | 32.8 | −2.3 | 20.10 | 0.57 |
| Setup | c1 | Wind speed, direction, humidity, and temperature |
| c2 | Wind speed, direction, humidity, temperature, and background concentration (PM10, PM25, NO, NO2, O3) | |
| Reconstruction | m1 | A day is equal to the day associated with its representative among the modelled days |
| m2 | A day is equal to the weighted sum of the modelled days | |
| Nc | 5 × 5 | |
| 10 × 10 |
| Station | Mean Observation (µg/m3) | Mean Model (µg/m3) | Bias (µg/m3) | RMSE (µg/m3) | r |
|---|---|---|---|---|---|
| Grenoble_Boulevards | 64.9 | 76.1 | 11.2 | 19.9 | 0.74 |
| MC_GRE_JJaures | 53.4 | 61.0 | 7.6 | 13.5 | 0.84 |
| MC_GRE_JPain | 76.5 | 72.9 | −3.6 | 24.7 | 0.73 |
| MC_GRE_JPerrot | 40.4 | 61.0 | 20.6 | 23.2 | 0.85 |
| MC_GRE_Leclerc | 52.9 | 45.6 | −7.3 | 18.1 | 0.77 |
| MC_GRE_VHugo | 62.0 | 63.6 | 1.6 | 16.2 | 0.76 |
| Mob_Grenoble_caserne_Bonne | 53.8 | 53.7 | −0.1 | 8.8 | 0.90 |
| Station | Mean Observation (µg/m3) | Mean Model (µg/m3) | Bias (µg/m3) | RMSE (µg/m3) | r |
|---|---|---|---|---|---|
| Magna Grecia | 65.2 | 61.6 | −3.6 | 18.78 | 0.56 |
| Period | 5 Months | 5 Days | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obs | Model Config 1 | Model Config 1 Upwind Background | Model Config 1 | Model Config 2 | |||||||||||||
| Mean | Mean | RMSE | Bias | r | Mean | RMSE | Bias | r | Mean | RMSE | Bias | r | Mean | RMSE | Bias | r | |
| NO2_AUT | 81.6 | 124.4 | 77.2 | 43.7 | 0.34 | 103.4 | 69.2 | 31.4 | 0.35 | 127.3 | 93.6 | 53.2 | −0.02 | 88.5 | 31.1 | 15.7 | 0.62 |
| NO2_BONAP | 48.5 | 67.7 | 22.2 | 12.1 | 0.65 | 44.8 | 19.9 | −0.2 | 0.60 | 74.8 | 28.1 | 21.3 | 0.84 | 55.5 | 14.2 | 5.0 | 0.82 |
| NO2_CELES | 58.7 | 81.7 | 26.1 | 18.6 | 0.80 | 55.8 | 19.9 | 6.6 | 0.77 | 71.5 | 24.6 | 19.3 | 0.80 | 58.9 | 14.2 | 6.5 | 0.77 |
| NO2_ELYS | 47.5 | 73.1 | 36.5 | 25.9 | 0.54 | 57.6 | 30.1 | 13.7 | 0.48 | 70.1 | 33.0 | 24.9 | 0.52 | 66.2 | 29.4 | 21.2 | 0.72 |
| NO2_HAUS | 51.6 | 66.3 | 28.1 | 15.1 | 0.66 | 51.5 | 23.0 | 2.9 | 0.63 | 82.3 | 41.4 | 32.5 | 0.51 | 63.8 | 25.8 | 14.0 | 0.58 |
| NO2_OPERA | 64.9 | 99.9 | 47.5 | 35.5 | 0.66 | 81.9 | 39.5 | 23.4 | 0.63 | 104.7 | 54.5 | 43.3 | 0.56 | 94.6 | 45.1 | 33.5 | 0.68 |
| NO2_PA04C * | 39.3 | 46.9 | 17.9 | 7.8 | 0.61 | 33.8 | 16.7 | −4.3 | 0.55 | 54.2 | 23.1 | 15.2 | 0.47 | 33.2 | 11.6 | −6.3 | 0.78 |
| NO2_PA07 * | 34.8 | 51.1 | 29.4 | 16.4 | 0.35 | 37.6 | 25.8 | 4.2 | 0.28 | 57.9 | 31.5 | 25.7 | 0.67 | 36.3 | 18.1 | 3.9 | 0.61 |
| NO2_PA12 * | 38.2 | 40.8 | 17.1 | 3.0 | 0.58 | 28.2 | 19.1 | −9.2 | 0.53 | 46.3 | 13.4 | 8.7 | 0.81 | 26.2 | 13.7 | −11.4 | 0.87 |
| NO2_PA13 * | 35.8 | 38.4 | 16.2 | 3.0 | 0.58 | 26.1 | 18.7 | −9.2 | 0.52 | 41.2 | 13.0 | 5.8 | 0.73 | 25.1 | 13.7 | −10.5 | 0.82 |
| NO2_PA18 * | 41.5 | 34.9 | 14.6 | −5.2 | 0.72 | 26.7 | 23.2 | −17.4 | 0.64 | 35.3 | 9.2 | −1.8 | 0.80 | 19.2 | 22.0 | −17.7 | 0.68 |
| PM10_AUT | 37.2 | 51.0 | 29.9 | 14.3 | 0.44 | 44.7 | 27.1 | 10.1 | 0.43 | 53.1 | 35.5 | 18.4 | 0.31 | 38.8 | 19.2 | 4.4 | 0.45 |
| PM10_ELYS | 31.0 | 36.6 | 16.1 | 5.3 | 0.55 | 31.7 | 14.7 | 0.9 | 0.54 | 35.1 | 21.9 | 8.9 | 0.43 | 32.0 | 18.3 | 5.7 | 0.47 |
| PM10_HAUS | 30.6 | 34.4 | 15.1 | 4.0 | 0.56 | 29.7 | 13.9 | −0.2 | 0.53 | 37.1 | 18.4 | 8.5 | 0.72 | 30.5 | 13.1 | 1.7 | 0.71 |
| PM10_OPERA | 29.7 | 41.0 | 19.0 | 11.7 | 0.63 | 35.7 | 16.1 | 7.5 | 0.61 | 41.8 | 24.3 | 14.2 | 0.64 | 37.0 | 20.2 | 9.4 | 0.60 |
| PM10_PA04C * | 21.3 | 28.9 | 16.3 | 7.9 | 0.48 | 24.7 | 14.5 | 3.7 | 0.42 | 28.7 | 19.2 | 10.4 | 0.69 | 21.6 | 13.2 | 2.9 | 0.67 |
| PM10_PA18 * | 21.1 | 17.9 | 8.4 | −2.5 | 0.76 | 23.5 | 11.4 | −6.7 | 0.67 | 15.9 | 6.4 | −1.5 | 0.81 | 9.2 | 12.7 | −8.3 | 0.51 |
| Paris | Coastal City | Grenoble | Antony | Rome | |||
|---|---|---|---|---|---|---|---|
| Variable | Short Name | Unit | |||||
| Domain X-axis dimension | Lx | km | 10 | 3.6 | 1.7 | 4.3 | 12 |
| Domain Y-axis dimension | Ly | km | 13 | 4.6 | 1.8 | 4.8 | 12 |
| Horizontal resolution | dx | m | 3 | 3 | 3 | 4 | 4 |
| Number of tiles | 120 | 9 | 1 | 9 | 36 | ||
| Number of line sources per unit area | nblin | km−2 | 327.7 | 1078.6 | 260.8 | 454.4 | 513.9 |
| Number of emitted particles is function of mass rate | no | no | no | yes | yes | ||
| Kernel method | no | no | no | no | yes | ||
| Emission time step | dtmin | s | 2 | 10 | 1 | 10 | 100 |
| Synchronisation time step | dtsync | s | 6 | 5 | 5 | 10 | 5 |
| Number of cores | 480 | 240 | 30 | 10 | 180 | ||
| Machine | CALMIP | CALMIP | Server 1 | Server 2 | CALMIP | ||
| CPU time for 24 h (PSPRAY only) | hour | 6.0 | 1.4 | 6.9 | 5.0 | 3.0 | |
| Number of hour·core for 24 h | hour·core | 2880 | 333 | 208 | 50 | 540 | |
| Number of hour·core per day and per km2 | CPU_cost | hour·core. km−2·day−1 | 22.2 | 20.1 | 68.0 | 2.4 | 3.8 |
| CPU_cost estimation = f(nblin/dtmin/dtsync/dx2) | CPU_cost_estim1 | hour·core·km−2·day−1 | 22.8 | 18.0 | 43.5 | 2.1 | 0.5 |
| CPU_cost estimation = f(nblin/dtmin/dtsync/) | CPU_cost_estim2 | hour·core·km−2·day−1 | 22.4 | 17.7 | 42.8 | 3.7 | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nibart, M.; Ribstein, B.; Ricolleau, L.; Tinarelli, G.; Barbero, D.; Albergel, A.; Moussafir, J. Optimization of HPC Use for 3D High Resolution Urban Air Quality Assessment and Downstream Services. Atmosphere 2021, 12, 1410. https://doi.org/10.3390/atmos12111410
Nibart M, Ribstein B, Ricolleau L, Tinarelli G, Barbero D, Albergel A, Moussafir J. Optimization of HPC Use for 3D High Resolution Urban Air Quality Assessment and Downstream Services. Atmosphere. 2021; 12(11):1410. https://doi.org/10.3390/atmos12111410
Chicago/Turabian StyleNibart, Maxime, Bruno Ribstein, Lydia Ricolleau, Gianni Tinarelli, Daniela Barbero, Armand Albergel, and Jacques Moussafir. 2021. "Optimization of HPC Use for 3D High Resolution Urban Air Quality Assessment and Downstream Services" Atmosphere 12, no. 11: 1410. https://doi.org/10.3390/atmos12111410
APA StyleNibart, M., Ribstein, B., Ricolleau, L., Tinarelli, G., Barbero, D., Albergel, A., & Moussafir, J. (2021). Optimization of HPC Use for 3D High Resolution Urban Air Quality Assessment and Downstream Services. Atmosphere, 12(11), 1410. https://doi.org/10.3390/atmos12111410






