Enhancing the Output of Climate Models: A Weather Generator for Climate Change Impact Studies
Abstract
1. Introduction
- The characteristic value, for which in one year;
- The combination value, leading, together with the characteristic value of another variable action of different nature, to a combined effect characterized by in one year;
- The frequent value, roughly exceeded from 100 to 300 times in one year;
- The quasi permanent value, exceeded for more than 50% of the design working life of the construction.
2. Methodology
2.1. Weather Generators
- Evaluation of factors of change (FCs): climate model outputs and associated climate variable statistics concerning a future time interval are compared with those obtained for the control period ;
- Implementation of a suitable weather generator (WG): random samples are generated modifying the relevant statistical properties of the parameters, which are used by the WG algorithm, according to the previously detected FCs. As discussed before, the scale of local observations is different from that of climate model outputs; therefore, the WG cannot be run directly using the statistics of climate model outputs. Adopting the FC approach, the discrepancy between RCM outputs and observations is by-passed [37];
- Assessment of climate change effects on representative values: the assessment is done directly using the generated future weather series, or deriving their influence on statistical properties of their distributions.
2.2. A Weather Generator for the Virtualization of the Outputs of Regional Climate Model
2.3. Factors of Change and Extreme Values Theory
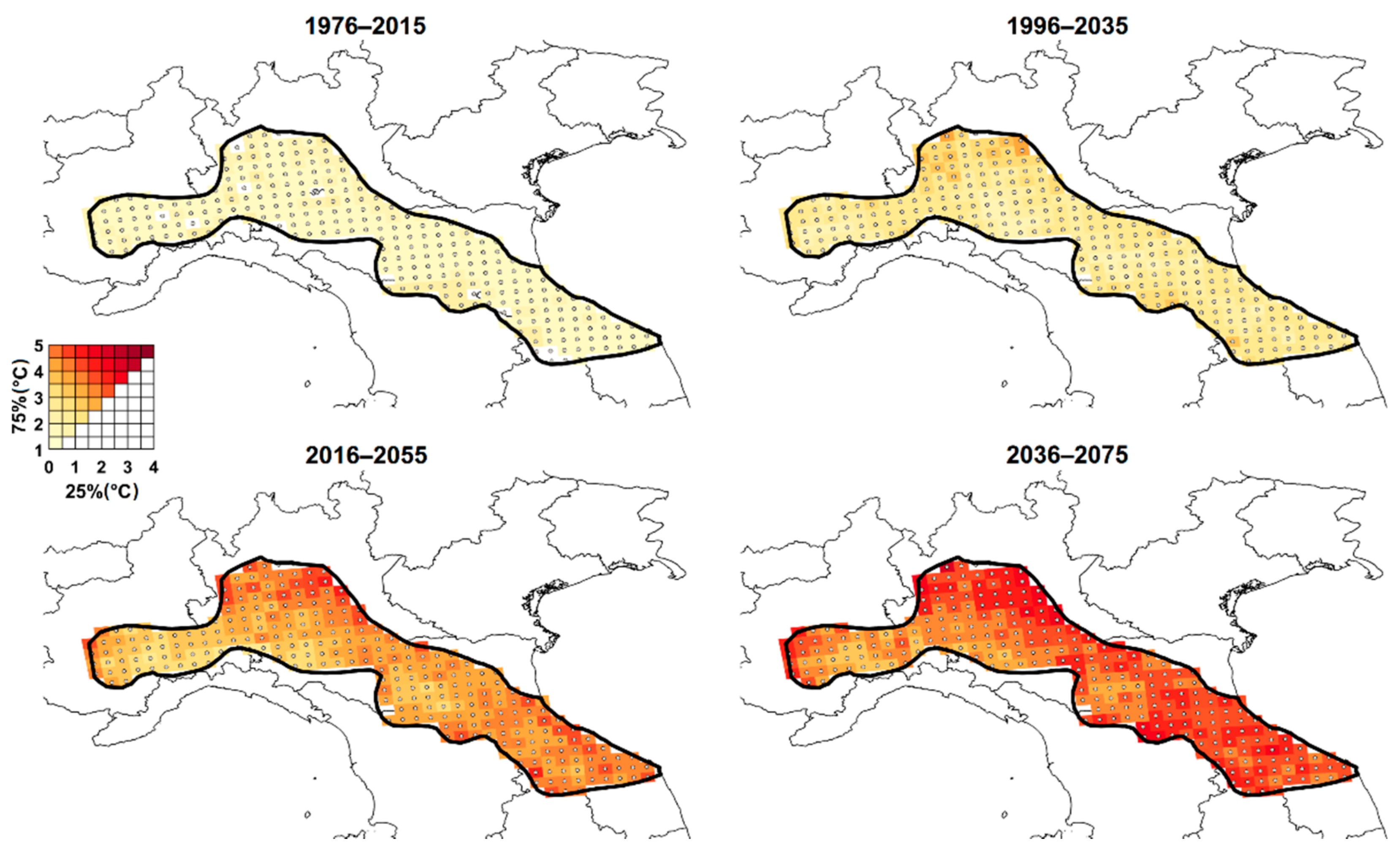
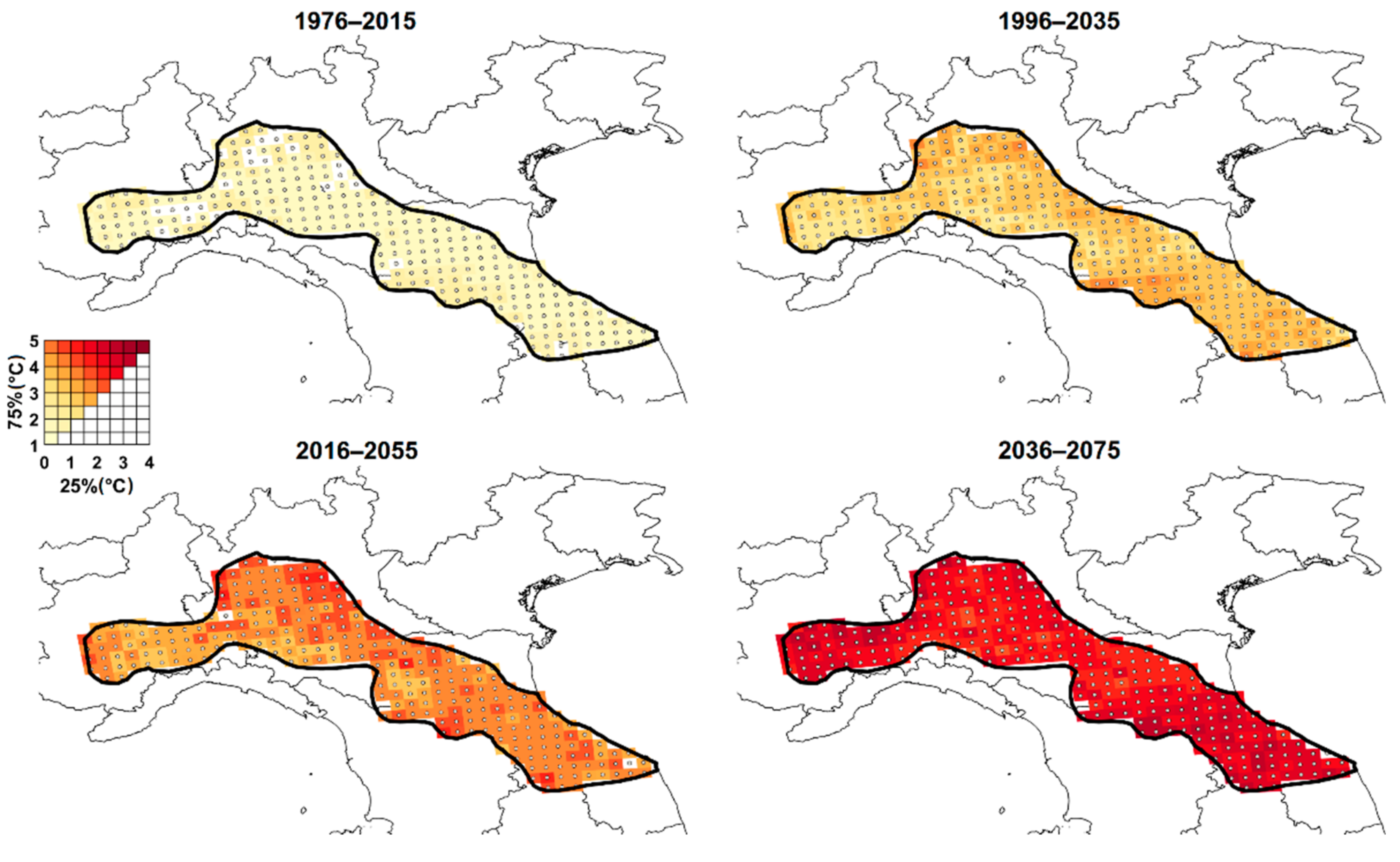
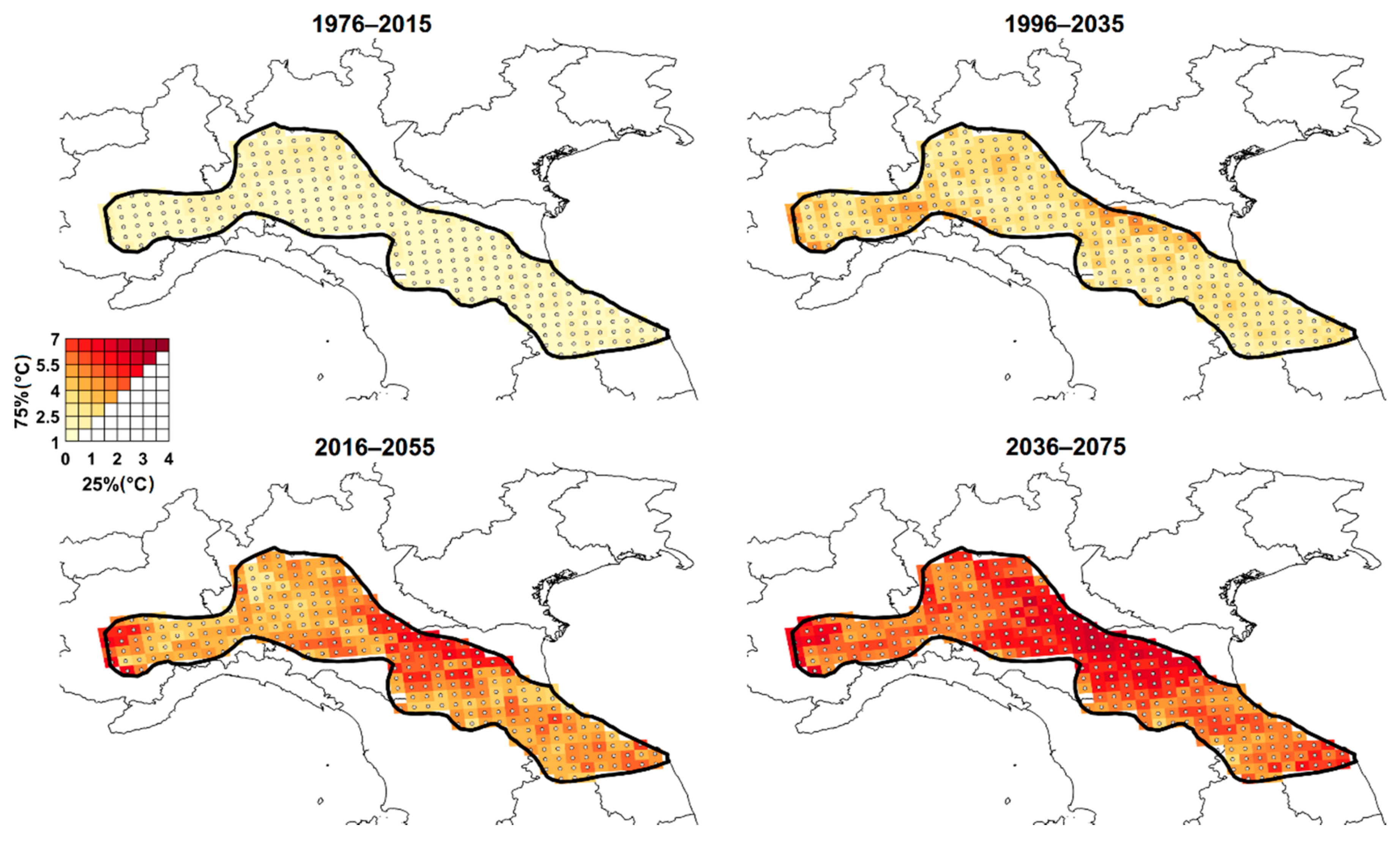
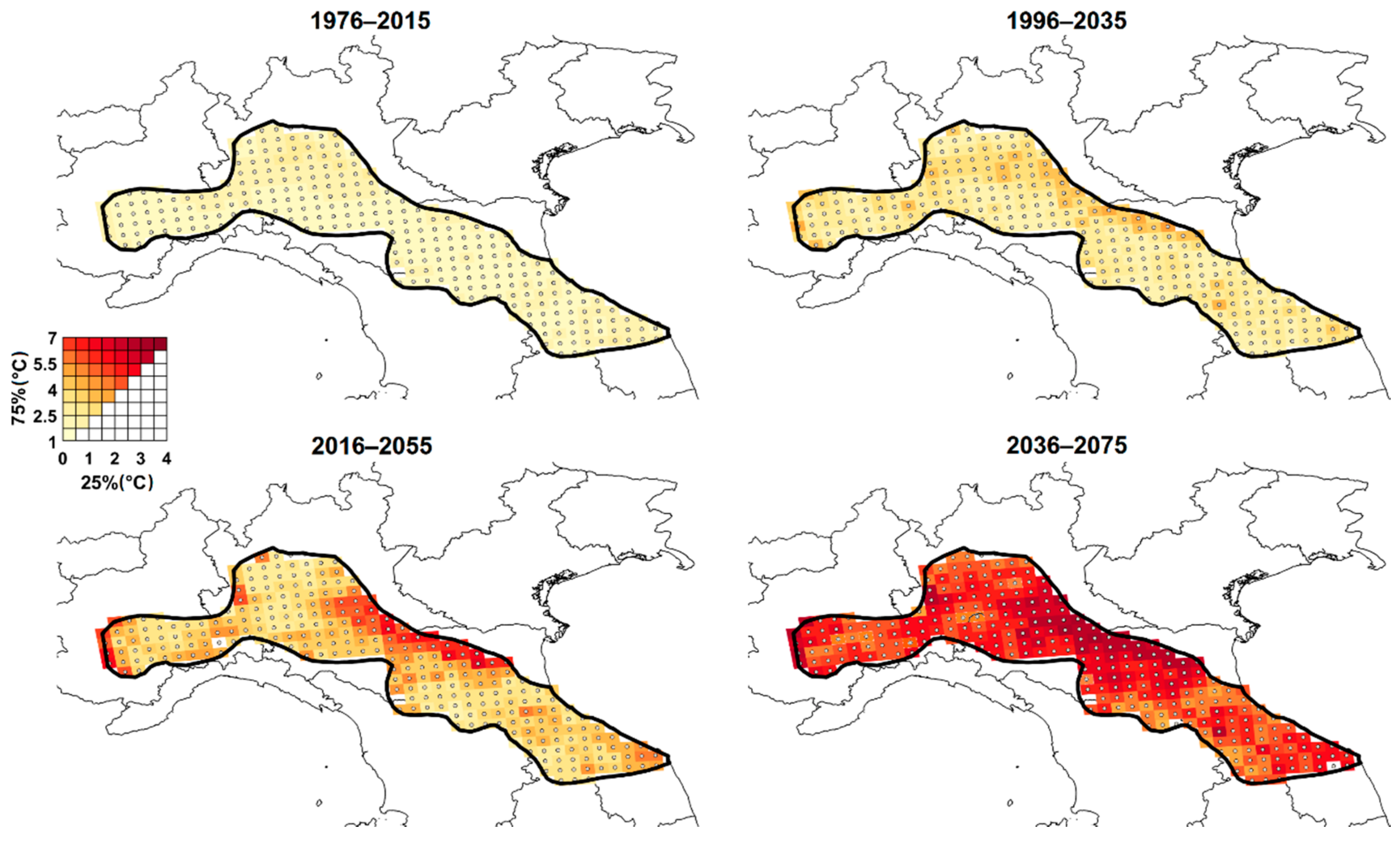
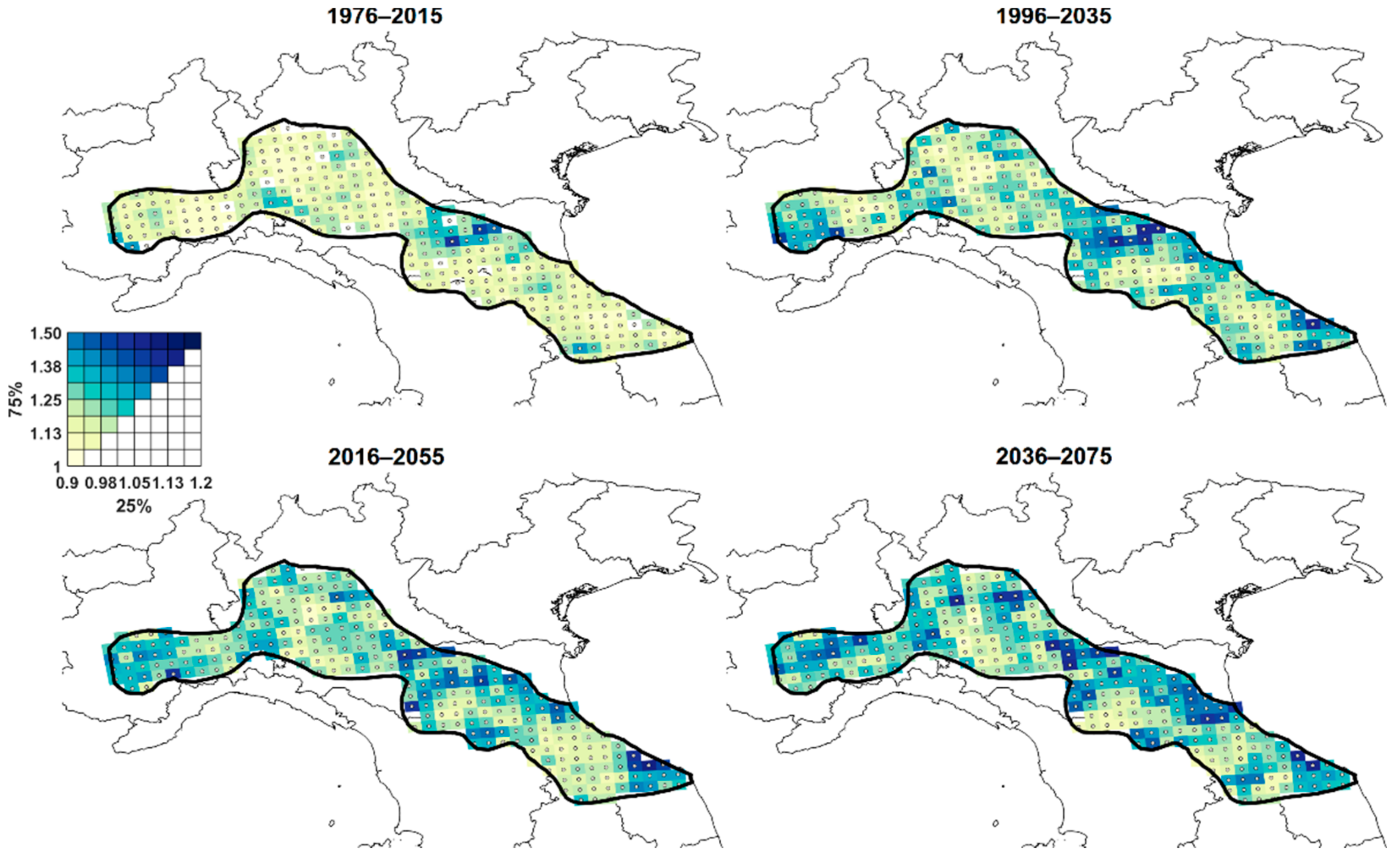
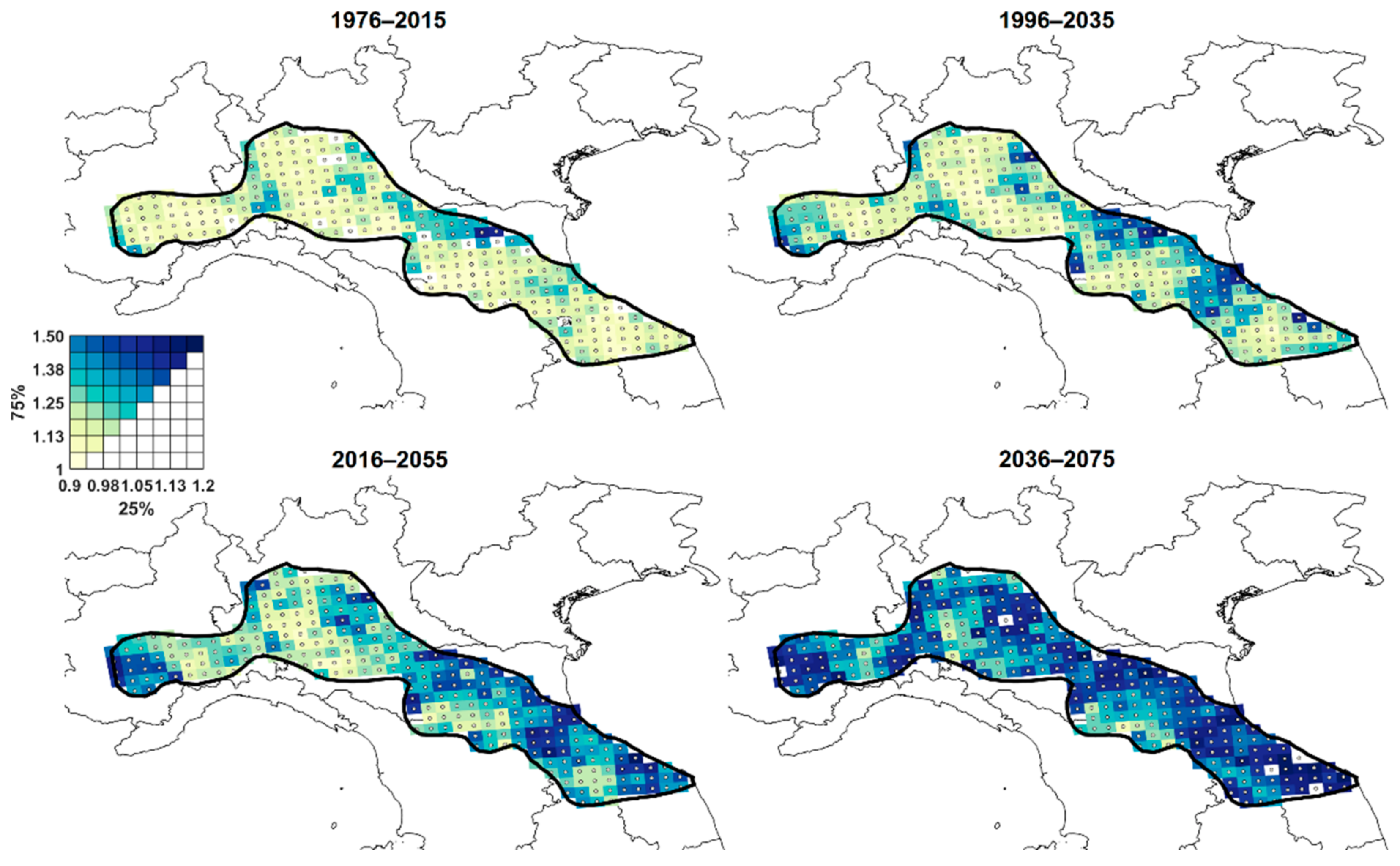
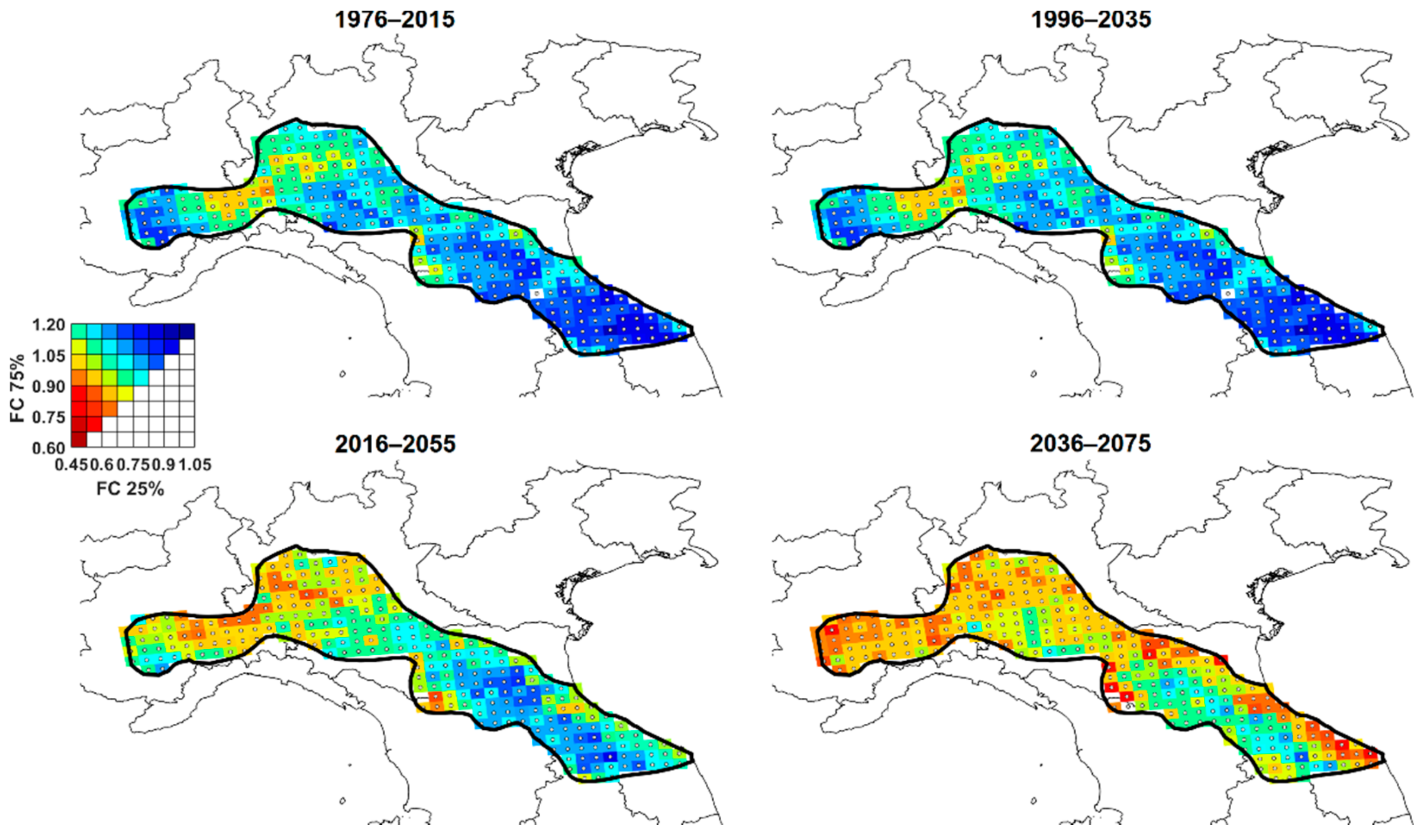
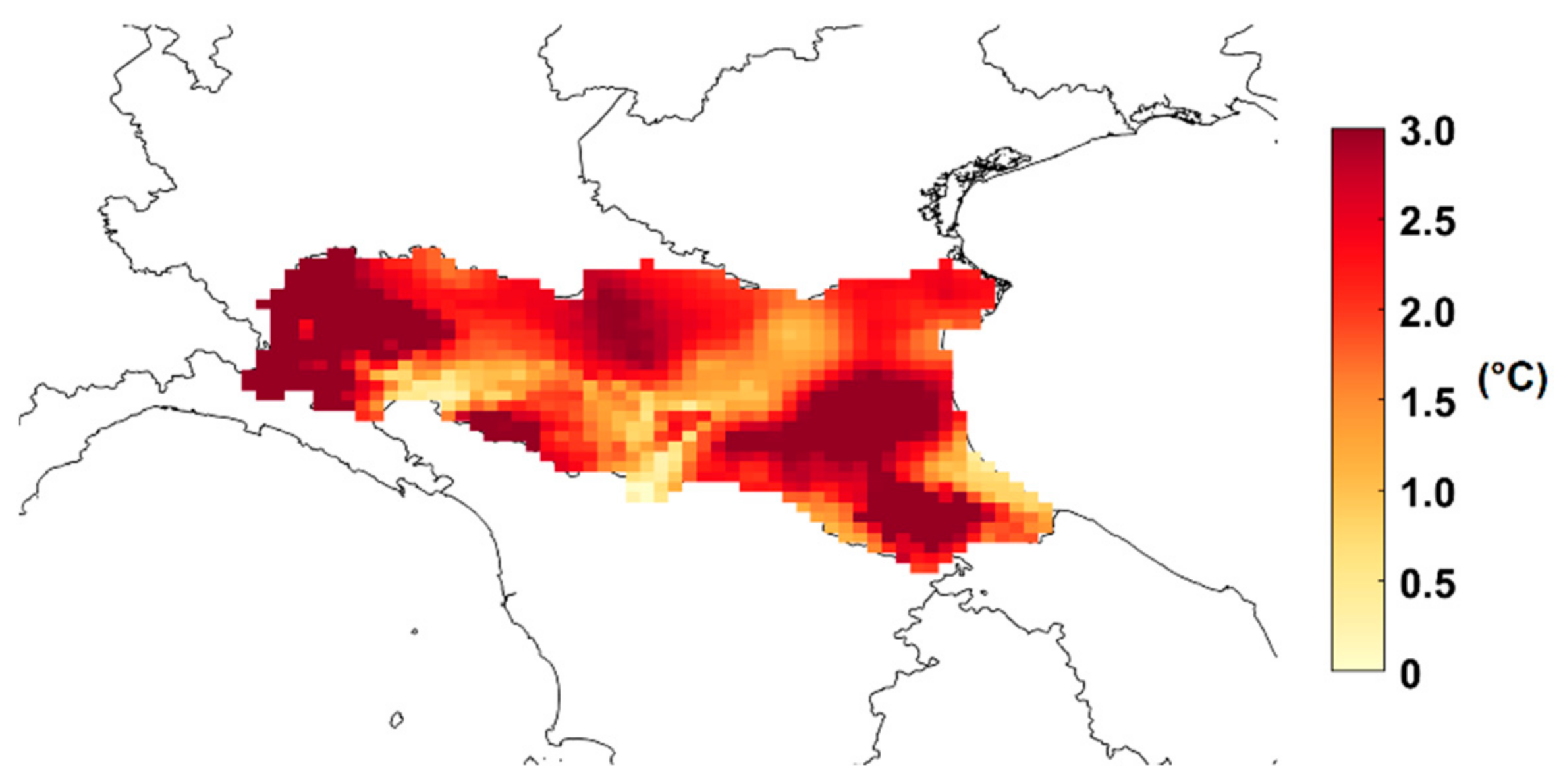
2.4. Factors of Change Maps
3. Results
3.1. Study Area and Datasets
3.2. Dataset of Daily Maximum and Minimum Temperature
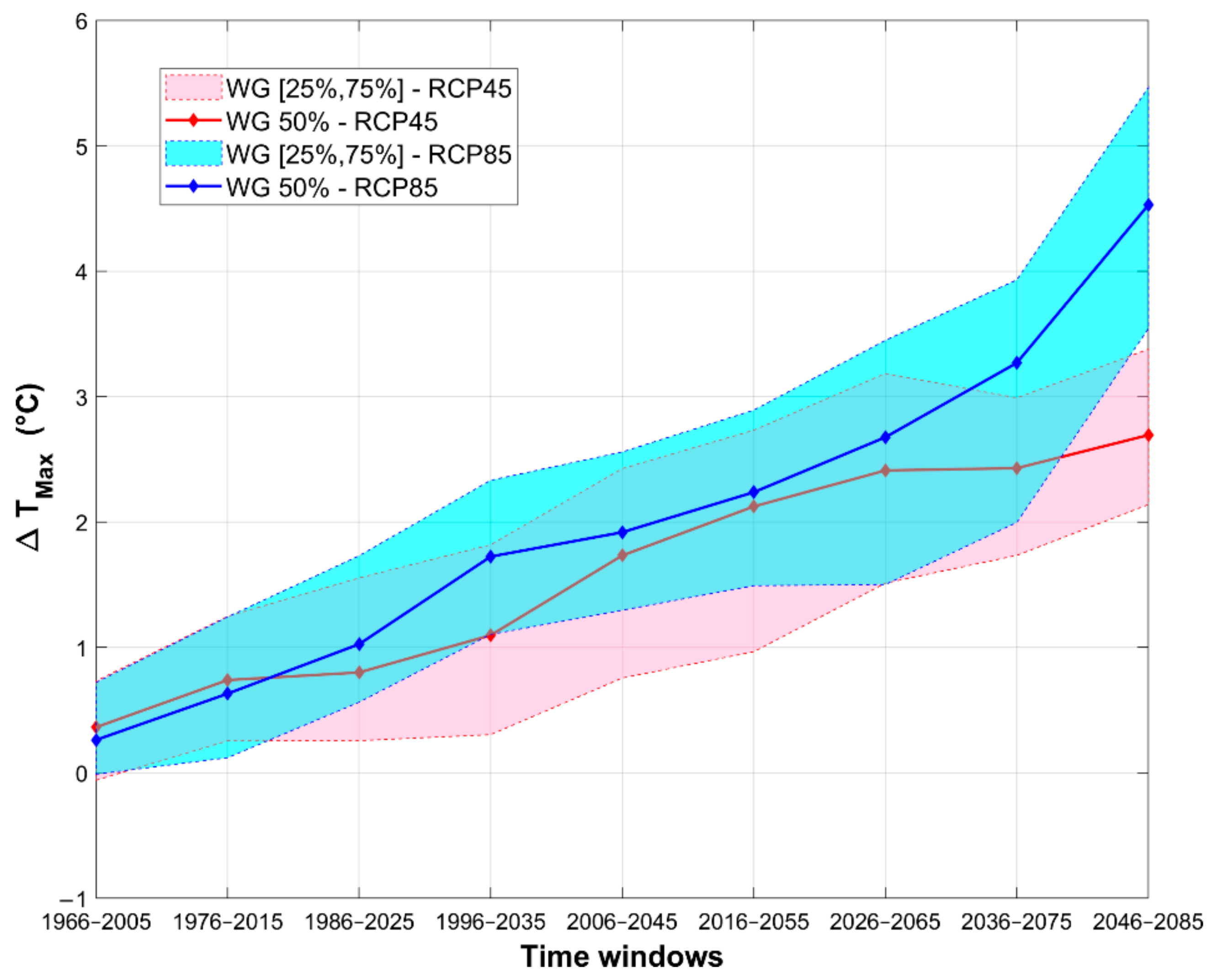
3.3. Effects of Climate Change on Extreme Temperatures
3.4. Effects of Climate Change on Extreme Precipitation
3.5. Ground Snow Loads
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bastidas-Arteaga, E.; Stewart, M. Climate Adaptation Engineering; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar]
- Madsen, H.O. Managing structural safety and reliability in adaptation to climate change. In Safety, Reliability, Risk and Life-Cycle Performance of Structures and Infrastructure; CRC Press: Boca Raton, FL, USA, 2013; pp. 81–88. [Google Scholar]
- Stewart, M.G.; Deng, X. Climate impact risks and climate adaptation engineering for built infrastructure. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2015, 1, 04014001. [Google Scholar] [CrossRef]
- Croce, P.; Formichi, P.; Landi, F. Climate change: Impacts on climatic actions and structural reliability. Appl. Sci. 2019, 9, 5416. [Google Scholar] [CrossRef]
- Forzieri, G.; Bianchi, A.; Batista e Silva, F.B.; Herrera, M.A.M.; Leblois, A.; Lavalle, C.; Aerts, J.C.J.H.; Feyen, L. Escalating impacts of climate extremes on critical infrastructures in Europe. Glob. Environ. Chang. 2018, 48, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Croce, P.; Formichi, P.; Landi, F. Structural safety and design under climate change. In 20th Congress of IABSE, New York City 2019: The Evolving Metropolis; International Association for Bridge and Structural Engineering (IABSE): Zurich, Switzerland, 2019; pp. 1130–1135. [Google Scholar]
- Croce, P.; Formichi, P.; Landi, F.; Marsili, F. Climate change: Impact on snow loads on structures. Cold Reg. Sci. Technol. 2018, 150, 35–50. [Google Scholar] [CrossRef]
- Croce, P.; Formichi, P.; Landi, F.; Mercogliano, P.; Bucchignani, E.; Dosio, A.; Dimova, S. The snow load in Europe and the climate change. Clim. Risk Manag. 2018, 20, 138–154. [Google Scholar] [CrossRef]
- Forzieri, G.; Bianchi, A.; Herrera, M.A.M.; Batista e Silva, F.; Lavalle, C.; Feyen, L. Resilience of Large Investments and Critical Infrastructures in Europe to Climate Change; EUR27906; Publications Office of the European Union: Luxembourg, 2016. [Google Scholar] [CrossRef]
- Organization for Economic Co-Operation and Development (OECD). Climate-Resilient Infrastructure; OECD ENVIRONMENT POLICY PAPER NO. 14; OECD Publishing: Paris, France, 2018. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change—Summary for Policymakers; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Pryor, S.C.; Barthelmie, R.J.; Bukovsky, M.S.; Leung, L.R.; Sakaguchi, K. Climate change impacts on wind power generation. Nat. Rev. Earth Environ. 2020, 1, 627–643. [Google Scholar] [CrossRef]
- Wagner, T.; Themeßl, M.; Schüppel, A.; Gobiet, A.; Stigler, H.; Birk, S. Impacts of climate change on stream flow and hydro power generation in the Alpine region. Environ. Earth Sci. 2017, 76, 4. [Google Scholar] [CrossRef]
- Christodoulou, A.; Christidis, P.; Bisselink, B. Forecasting the impacts of climate change on inland waterways. Transp. Res. Part D Transp. Environ. 2020, 82, 102159. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A.K.; Wada, Y.; Mann, M.E. Climate change will affect global water availability through compounding changes in seasonal precipitation and evaporation. Nat. Commun. 2020, 11, 3044. [Google Scholar] [CrossRef]
- Mbow, C.C.; Rosenzweig, L.G.; Barioni, T.G.; Benton, M.; Herrero, M.; Krishnapillai, E.; Liwenga, P.; Pradhan, M.G.; Rivera-Ferre, T.; Sapkota, F.N.; et al. Food security. In Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Stewart, M.G.; Wang, X.; Nguyen, M. Climate change impact and risks of concrete infrastructure deterioration. Eng. Struct. 2011, 33, 1326–1337. [Google Scholar] [CrossRef]
- Bastidas-Arteaga, E.; Schoefs, F.; Stewart, M.G.; Wang, X. Influence of global warming on durability of corroding RC structures: A probabilistic approach. Eng. Struct. 2013, 51, 259–266. [Google Scholar] [CrossRef]
- Bisoi, S.; Haldar, S. Impact of climate change on design of offshore wind turbine considering dynamic soil–structure interaction. J. Offshore Mech. Arct. Eng. 2017, 139, 061903. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; De Kok, J.L. Adapting to climate change: A comparison of two strategies for dike heightening design. Nat. Hazards 2008, 47, 217–228. [Google Scholar] [CrossRef][Green Version]
- Lutz, J.; Dobler, A.; Nygaard, B.E.; Mc Innes, H.; Haugen, J.E. Future projections of icing on power lines over Norway. In Proceedings of the International Workshop on Atmospheric Icing of Structures IWAIS 2019, Reykjavík, Iceland, 23–28 June 2019. [Google Scholar]
- Faggian, P.; Bonanno, R.; Pirovano, G. Research activities to cope with wet snow impacts on overhead power lines in future climate over Italy. In Proceedings of the International Workshop on Atmospheric Icing of Structures IWAIS 2019, Reykjavík, Iceland, 23–28 June 2019. [Google Scholar]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global flood risk under climate change. Nat. Clim. Chang. 2013, 3, 816–821. [Google Scholar] [CrossRef]
- European Committee for Standardization (CEN). EN 1990. Eurocode—Basis of Structural Design; CEN: Brussels, Belgium, 2002. [Google Scholar]
- European Committee for Standardization (CEN). EN 1991-1-3. Eurocode 1: Actions on Structures—Part 1–3: General Actions—Snow Loads; CEN: Brussels, Belgium, 2003. [Google Scholar]
- European Committee for Standardization (CEN). EN 1991-1-4. Eurocode 1: Actions on Structures—Part 1–4: General Actions—Wind Actions; CEN: Brussels, Belgium, 2005. [Google Scholar]
- European Committee for Standardization (CEN). EN 1991-1-5. Eurocode 1: Actions on Structures—Part 1–5: General Actions—Thermal Actions; CEN: Brussels, Belgium, 2003. [Google Scholar]
- International Organization for Standardization (ISO). ISO 2394 General Principles on Reliability for Structures; ISO: Geneva, Switzerland, 2015. [Google Scholar]
- Croce, P.; Formichi, P.; Landi, F. Evaluation of current trends of climatic actions in Europe based on observations and regional reanalysis. Remote Sens. 2021, 13, 2025. [Google Scholar] [CrossRef]
- European Commission. EU Strategy on Adaptation to Climate Change, COM (2013) 216; European Commission: Brussel, Belgium, 2013. [Google Scholar]
- European Commission. Adapting Infrastructure to Climate Change, SWD (2013) 137; European Commission: Brussel, Belgium, 2013. [Google Scholar]
- Brekke, L.D.; Barsugli, J.J. Uncertainties in projections of future changes in extremes. In Extremes in a Changing Climate; AghaKouchak, A., Easterling, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 309–346. [Google Scholar] [CrossRef]
- Wilks, D.; Wilby, R. The weather generation game: A review of stochastic weather models. Prog. Phys. Geogr. 1999, 23, 329–357. [Google Scholar] [CrossRef]
- Semenov, M.A.; Barrow, E.M. Use of a stochastic weather generator in the development of climate change scenarios. Clim. Chang. 1997, 35, 397–414. [Google Scholar] [CrossRef]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Kilsby, C.G.; Jones, P.D.; Burton, A.; Ford, A.C.; Fowler, H.J.; Harpham, C.; James, P.; Smith, A.; Wilby, R.L. A daily weather generator for use in climate change studies. Environ. Model. Softw. 2007, 22, 1705–1719. [Google Scholar] [CrossRef]
- Fatichi, S.; Ivanov, V.Y.; Caporali, E. Simulation of future climate scenarios with a weather generator. Adv. Water Resour. 2011, 34, 448–467. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R.T. The potential to narrow uncertainty in regional climate predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1107. [Google Scholar] [CrossRef]
- Buishand, T.A.; Brandsma, T. Multi-site simulation of daily precipitation and temperature in the Rhine basin by nearest-neighbor resampling. Wat. Resour. Res. 2001, 37, 2761–2776. [Google Scholar] [CrossRef]
- Buishand, T.A.; Brandsma, T. Multi-site simulation of daily precipitation and temperature conditional on the atmospheric circulation. Clim. Res. 2003, 25, 121–133. [Google Scholar] [CrossRef]
- Anandhi, A.; Frei, A.; Pierson, D.C.; Schneiderman, E.M.; Zion, M.S.; Lounsbury, D.; Matonse, A.H. Examination of change factor methodologies for climate change impact assessment. Water Resour. Res. 2011, 47, W03501. [Google Scholar] [CrossRef]
- Burgess, M.G.; Ritchie, J.; Shapland, J.; Pielke Jr, R. IPCC baseline scenarios have over-projected CO2 emissions and economic growth. Environ. Res. Lett. 2021, 16, 014016. [Google Scholar] [CrossRef]
- Ho, E.; Budescu, D.V.; Bosetti, V.; van Vuuren, D.P.; Keller, K. Not all carbon dioxide emission scenarios are equally likely: A subjective expert assessment. Clim. Chang. 2019, 155, 545–561. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Hutchinson, M.F. Methods of generation of weather sequences. In Agricultural Evironments; Bunting, A.H., Ed.; CAB International: Wallingford, UK, 1986; pp. 149–157. [Google Scholar]
- Croce, P.; Formichi, P.; Landi, F.; Marsili, F. A novel probabilistic methodology for the local assessment of future trends of climatic actions. Beton-und Stahlbetonbau 2018, 113, 110–115. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Kotlarski, S.; Keuler, K.; Christensen, O.B.; Colette, A.; Déqué, M.; Gobiet, A.; Goergen, K.; Jacob, D.; Lüthi, D.; van Meijgaard, E.; et al. Regional Climate Modelling on European Scale: A joint standard evaluation of the EURO-CORDEX ensemble. Geosci. Model Dev. 2014, 7, 1297–1333. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data, Revised Edition; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1994. [Google Scholar]
- Cooley, D.; Nychka, D.; Naveau, P. Bayesian spatial modeling of extreme precipitation return levels. J. Am. Stat. Assoc. 2007, 102, 824–840. [Google Scholar] [CrossRef]
- BjØrnstad, O.N.; Falck, W. Nonparametric spatial covariance functions: Estimation and testing. Environ. Ecol. Stat. 2001, 8, 53–70. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Gleckler, P.J.; Taylor, K.E.; Doutriaux, C. Performance metrics for climate models. J. Geophys. Res. 2008, 113, D06104. [Google Scholar] [CrossRef]
- Klein Tank, A.M.; Zwiers, F.W.; Zhang, X. Guidelines on Analysis of Extremes in a Changing Climate in Support of Informed Decisions for Adaptation; Tech. Rep. WCDMP-No. 72; World Meteorological Organization (WMO): Geneva, Switzerland, 2009. [Google Scholar]
- Cooley, D. Return periods and return levels under climate change. In Extremes in a Changing Climate; AghaKouchak, A., Easterling, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 97–114. [Google Scholar] [CrossRef]
- Croce, P.; Formichi, P.; Landi, F.; Marsili, F. Harmonized European ground snow load map: Analysis and comparison of national provisions. Cold Reg. Sci. Technol. 2019, 168, 102875. [Google Scholar] [CrossRef]
- Formichi, P.; Danciu, L.; Akkar, S.; Kale, O.; Malakatas, N.; Croce, P.; Nikolov, D.; Gocheva, A.; Luechinger, P.; Fardis, M.; et al. Eurocodes: Background and applications. Elaboration of maps for climatic and seismic actions for structural design with the Eurocodes. JRC Sci. Policy Rep. 2016. [Google Scholar] [CrossRef]
- Maraun, D. Bias correcting climate change simulations—A critical review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M. Statistical Downscaling and Bias Correction for Climate Research; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Berg, P.; Christensen, O.B.; Klehmet, K.; Lenderink, G.; Olsson, J.; Teichmann, C.; Yang, W. Precipitation extremes in a EURO-CORDEX 0.11° ensemble at hourly resolution. Nat. Hazards Earth Syst. Sci. Discuss. 2018, 362. [Google Scholar] [CrossRef]
- Gleick, P.H. Methods for evaluating the regional hydrologic impacts of global climatic changes. J. Hydrol. 1986, 88, 97–116. [Google Scholar] [CrossRef]
- Teuling, A.J.; Stöckli, R.; Seneviratne, S.I. Bivariate colour maps for visualizing climate data. Int. J. Climatol. 2011, 31, 1408–1412. [Google Scholar] [CrossRef]
- Hausfather, Z.; Peters, G. Emissions—The ‘business as usual’ story is misleading. Nature 2020, 577, 618–620. [Google Scholar] [CrossRef]
- Schwalm, C.R.; Glendon, S.; Duffy, P.B. RCP8.5 tracks cumulative CO2 emissions. Proc. Natl. Acad. Sci. USA 2020, 117, 19656–19657. [Google Scholar] [CrossRef]
- Tebaldi, C.; Knutti, R. The use of the multi-model ensemble in probabilistic climate projections. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 2053–2075. [Google Scholar] [CrossRef]
- Croce, P.; Formichi, P.; Landi, F.; Marsili, F. Evaluating the effect of climate change on thermal actions on structures. In Life-Cycle Analysis and Assessment in Civil Engineering: Towards an Integrated Vision; Caspeele, R., Taerwe, L., Frangopol, D.M., Eds.; Taylor & Francis Group: Oxfordshire, UK, 2019; pp. 1751–1758. ISBN 978-1-138-62633-1. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global increasing trends in annual maximum daily precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Chang. 2016, 6, 508–513. [Google Scholar] [CrossRef]
- Fischer, E.M.; Knutti, R. Observed heavy precipitation increase confirms theory and early models. Nat. Clim. Chang. 2016, 6, 986–991. [Google Scholar] [CrossRef]
- O’Gorman, P.A. Precipitation extremes under climate change. Curr. Clim. Chang. Rep. 2015, 1, 49–59. [Google Scholar] [CrossRef]
- O’Gorman, P.A. Contrasting responses of mean and extreme snowfall to climate change. Nature 2014, 515, 416–418. [Google Scholar] [CrossRef]
- Räisänen, J. Warmer climate: Less or more snow? Clim. Dyn. 2008, 30, 307–319. [Google Scholar] [CrossRef]
- Antolini, G.; Auteri, L.; Pavan, V.; Tomei, F.; Tomozeiu, R.; Marletto, V. A daily high-resolution gridded climatic data set for Emilia-Romagna, Italy, during 1961–2010. Int. J. Climatol. 2016, 36, 1970–1986. [Google Scholar] [CrossRef]
- Croce, P.; Formichi, P.; Landi, F. Implication of climate change on climatic actions on structures: The update of climatic load maps. In IABSE Symposium Wrocław 2020, Synergy of Culture and Civil Engineering—History and Challenges—Report; IABSE: Zurich, Switzerland, 2020; pp. 877–884. [Google Scholar]
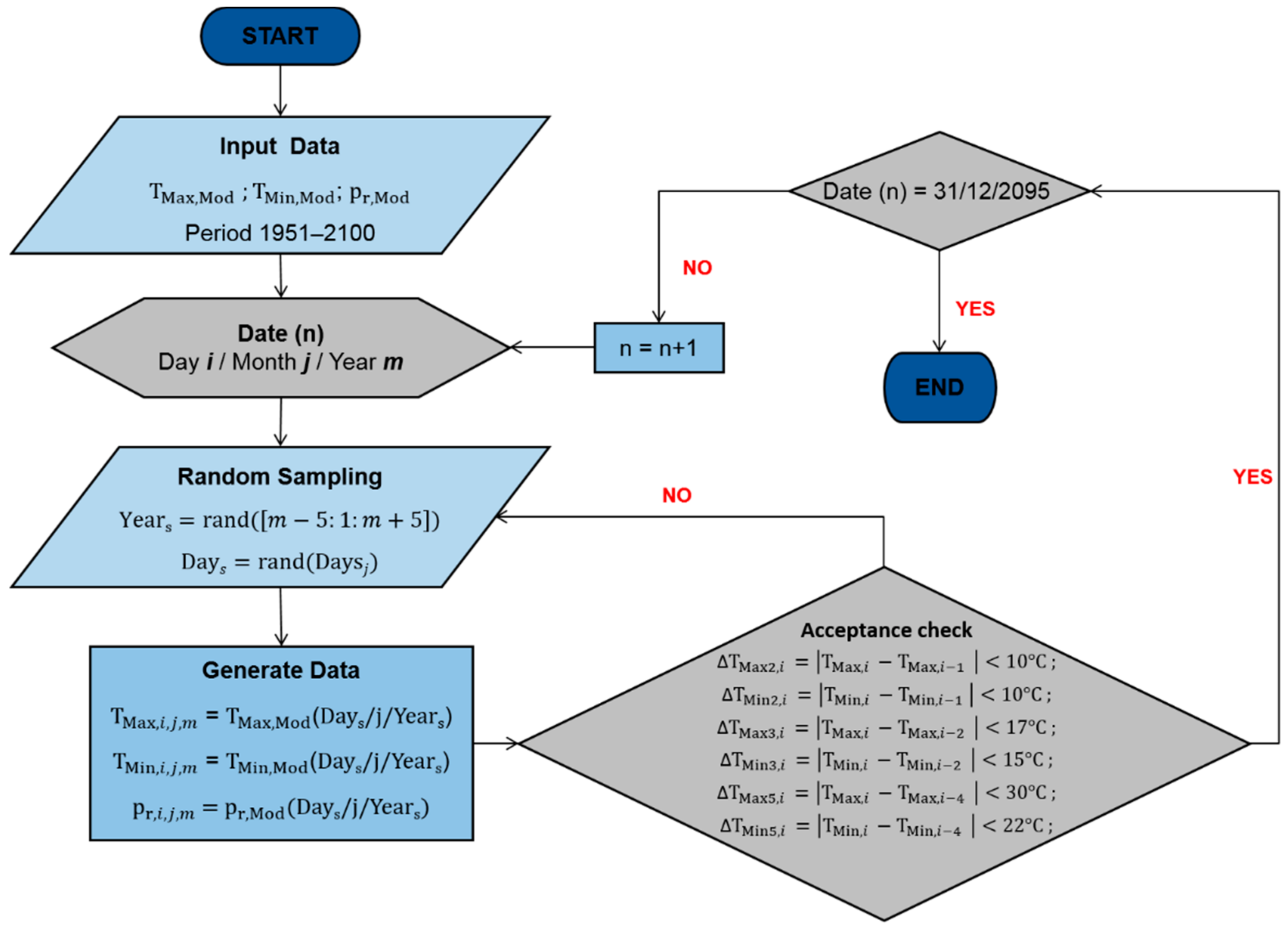
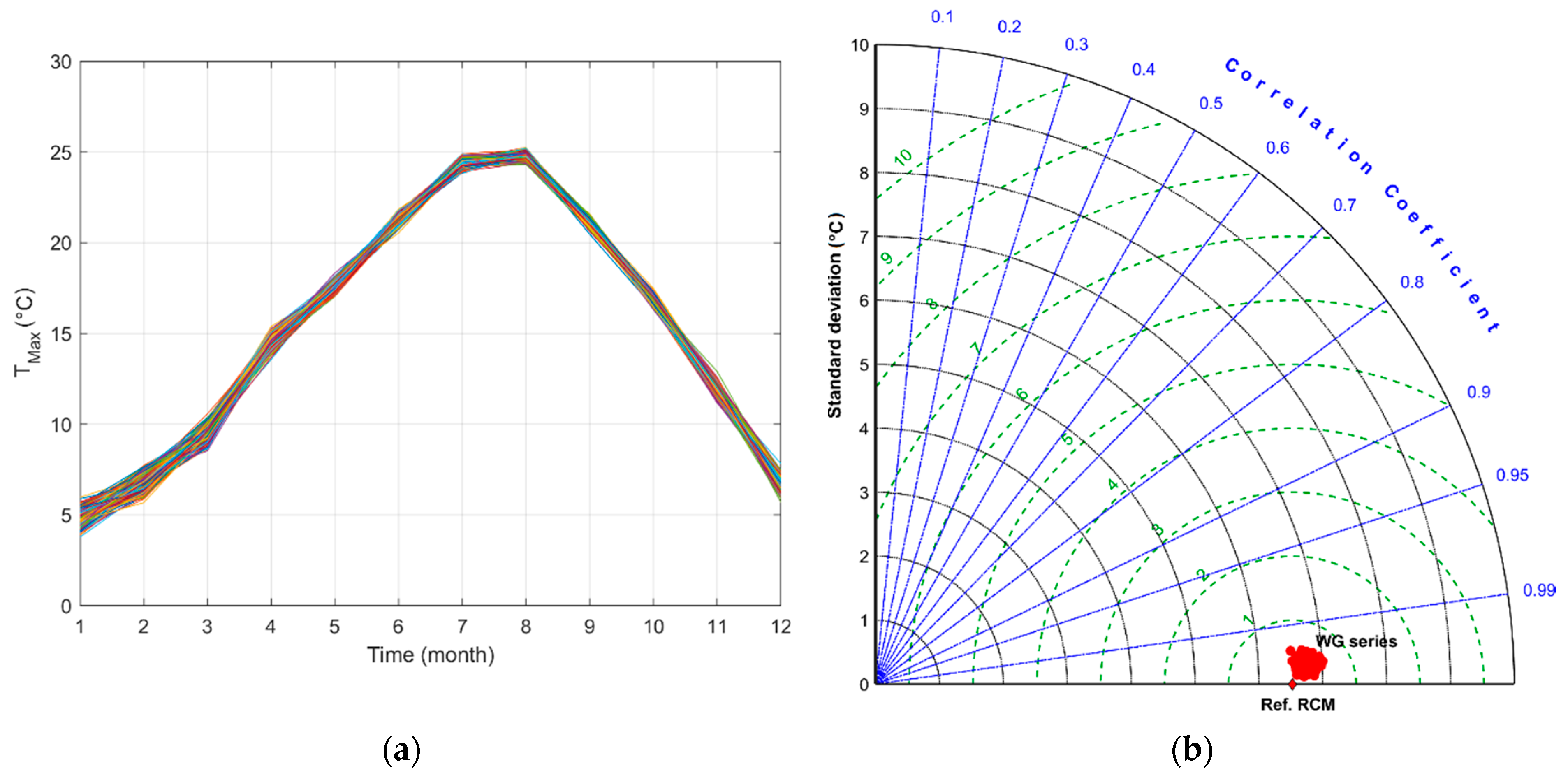
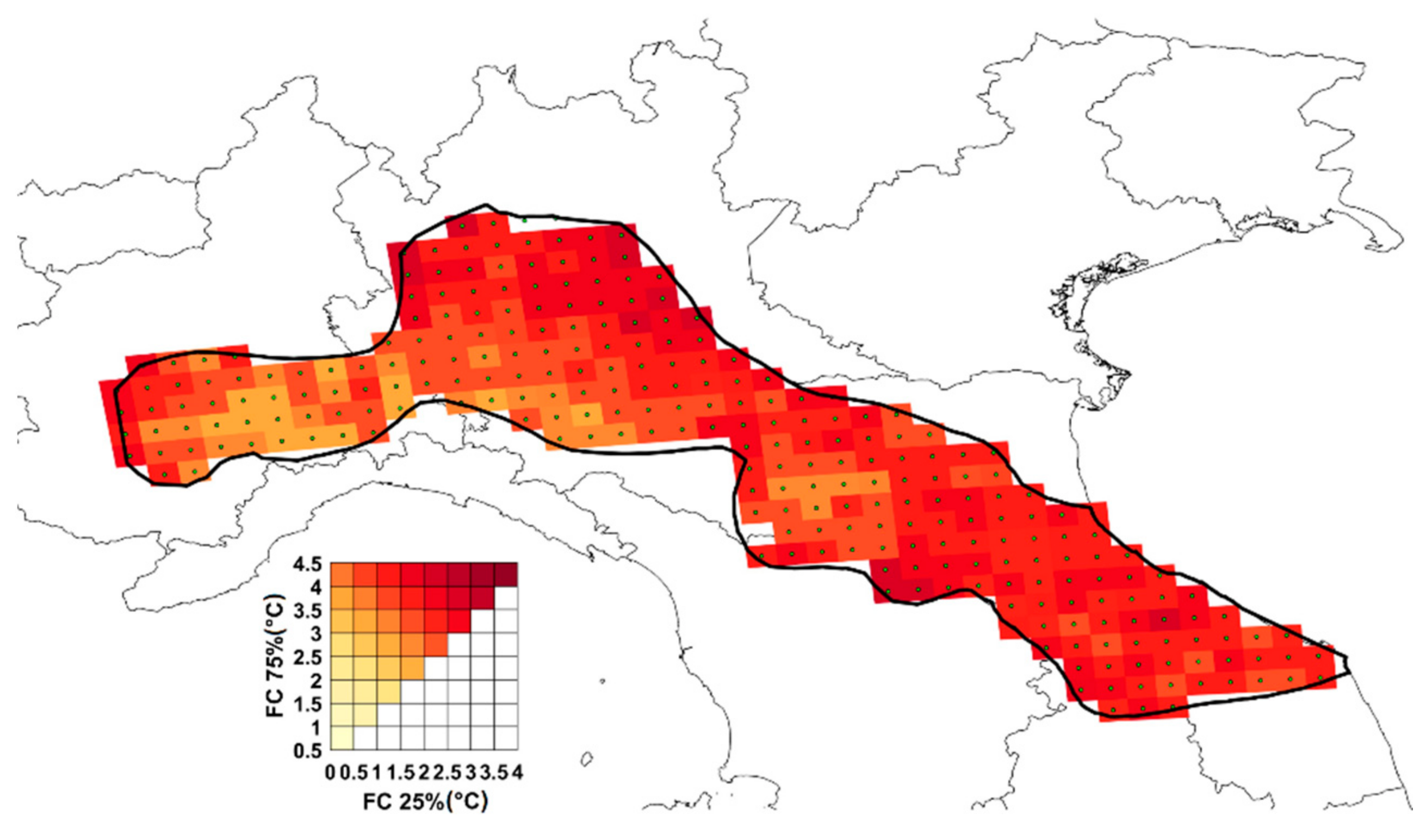



| Parameters | RCM | Weather Generated Series |
|---|---|---|
| Mean (mm/day) | 2.26 | 2.24 |
| CoV | 3.30 | 3.26 |
| (%) | 31.29 | 31.27 |
| (mm/day) | 7.18 | 7.12 |
| Institute_ID | RCM Name | Driving_GCM Name | Driving_Ensemble Member | Period |
|---|---|---|---|---|
| DMI | HIRHAM5 | EC-EARTH | r3i1p1 | 1951–2100 |
| CLMcom | CCLM4-8-17 | CNRM-CM5-LR | r1i1p1 | 1951–2100 |
| CLMcom | CCLM4-8-17 | EC-EARTH | r12i1p1 | 1951–2100 |
| KNMI | RACMO22E | EC-EARTH | r1i1p1 | 1951–2100 |
| MPI-CSC | REMO2009 | MPI-ESM-LR | r1i1p1 | 1951–2100 |
| IPSL-INERIS | WRF331F | IPSL-CM5A-MR | r1i1p1 | 1951–2100 |
| Time Window | RCP4.5 | RCP8.5 | ||||
|---|---|---|---|---|---|---|
| 25% | 50% | 75% | 25% | 50% | 75% | |
| 1966–2005 | 0.04 | 0.41 | 0.82 | 0.03 | 0.36 | 0.72 |
| 1976–2015 | 0.31 | 0.87 | 1.42 | 0.35 | 0.88 | 1.42 |
| 1986–2025 | 0.45 | 1.16 | 1.87 | 0.81 | 1.43 | 2.06 |
| 1996–2035 | 0.65 | 1.49 | 2.25 | 1.26 | 1.93 | 2.67 |
| 2006–2045 | 0.89 | 2.01 | 3.10 | 1.44 | 2.19 | 2.85 |
| 2016–2055 | 1.33 | 2.33 | 3.31 | 1.77 | 2.51 | 3.19 |
| 2026–2065 | 1.58 | 2.63 | 3.63 | 2.00 | 2.76 | 3.54 |
| 2036–2075 | 1.87 | 2.75 | 3.55 | 2.47 | 3.37 | 4.17 |
| 2046–2085 | 2.18 | 2.83 | 3.67 | 3.93 | 5.10 | 6.08 |
| Time Window | RCP4.5 | RCP8.5 | ||||
|---|---|---|---|---|---|---|
| 25% | 50% | 75% | 25% | 50% | 75% | |
| 1966–2005 | −0.30 | 0.14 | 0.73 | −0.28 | 0.15 | 0.73 |
| 1976–2015 | −0.23 | 0.56 | 1.60 | −0.16 | 0.63 | 1.66 |
| 1986–2025 | −0.12 | 0.98 | 2.48 | −0.29 | 0.84 | 2.44 |
| 1996–2035 | 0.31 | 1.57 | 3.16 | −0.08 | 1.23 | 2.92 |
| 2006–2045 | 0.65 | 2.01 | 3.89 | 0.24 | 1.63 | 3.39 |
| 2016–2055 | 1.01 | 2.59 | 4.52 | 0.83 | 2.13 | 3.67 |
| 2026–2065 | 1.48 | 3.03 | 4.87 | 1.55 | 2.75 | 4.19 |
| 2036–2075 | 1.59 | 3.18 | 5.22 | 2.29 | 3.52 | 5.23 |
| 2046–2085 | 2.40 | 3.81 | 6.02 | 2.83 | 4.42 | 8.55 |
| Time Window | RCP4.5 | RCP8.5 | ||||
|---|---|---|---|---|---|---|
| 25% | 50% | 75% | 25% | 50% | 75% | |
| 1966–2005 | 0.96 | 1.01 | 1.06 | 0.96 | 1.01 | 1.06 |
| 1976–2015 | 0.94 | 1.02 | 1.12 | 0.94 | 1.02 | 1.12 |
| 1986–2025 | 0.91 | 1.03 | 1.19 | 0.91 | 1.03 | 1.18 |
| 1996–2035 | 0.89 | 1.05 | 1.24 | 0.89 | 1.05 | 1.23 |
| 2006–2045 | 0.90 | 1.06 | 1.25 | 0.91 | 1.08 | 1.25 |
| 2016–2055 | 0.91 | 1.07 | 1.25 | 0.94 | 1.11 | 1.32 |
| 2026–2065 | 0.92 | 1.07 | 1.25 | 0.97 | 1.16 | 1.39 |
| 2036–2075 | 0.93 | 1.09 | 1.28 | 1.01 | 1.20 | 1.47 |
| 2046–2085 | 0.97 | 1.13 | 1.36 | 1.04 | 1.25 | 1.56 |
| Time Window | RCP4.5 | RCP8.5 | ||||
|---|---|---|---|---|---|---|
| 25% | 50% | 75% | 25% | 50% | 75% | |
| 1966–2005 | 0.91 | 0.98 | 1.03 | 0.91 | 0.98 | 1.03 |
| 1976–2015 | 0.85 | 0.95 | 1.04 | 0.84 | 0.94 | 1.04 |
| 1986–2025 | 0.80 | 0.92 | 1.04 | 0.78 | 0.90 | 1.02 |
| 1996–2035 | 0.76 | 0.88 | 1.01 | 0.72 | 0.84 | 0.99 |
| 2006–2045 | 0.73 | 0.85 | 0.98 | 0.69 | 0.81 | 0.95 |
| 2016–2055 | 0.69 | 0.82 | 0.95 | 0.67 | 0.78 | 0.92 |
| 2026–2065 | 0.67 | 0.79 | 0.92 | 0.65 | 0.76 | 0.88 |
| 2036–2075 | 0.64 | 0.76 | 0.89 | 0.61 | 0.72 | 0.85 |
| 2046–2085 | 0.62 | 0.73 | 0.85 | 0.56 | 0.68 | 0.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Croce, P.; Formichi, P.; Landi, F. Enhancing the Output of Climate Models: A Weather Generator for Climate Change Impact Studies. Atmosphere 2021, 12, 1074. https://doi.org/10.3390/atmos12081074
Croce P, Formichi P, Landi F. Enhancing the Output of Climate Models: A Weather Generator for Climate Change Impact Studies. Atmosphere. 2021; 12(8):1074. https://doi.org/10.3390/atmos12081074
Chicago/Turabian StyleCroce, Pietro, Paolo Formichi, and Filippo Landi. 2021. "Enhancing the Output of Climate Models: A Weather Generator for Climate Change Impact Studies" Atmosphere 12, no. 8: 1074. https://doi.org/10.3390/atmos12081074
APA StyleCroce, P., Formichi, P., & Landi, F. (2021). Enhancing the Output of Climate Models: A Weather Generator for Climate Change Impact Studies. Atmosphere, 12(8), 1074. https://doi.org/10.3390/atmos12081074








