A Novel Framework for Forecasting, Evaluation and Early-Warning for the Influence of PM10 on Public Health
Abstract
1. Introduction
2. The Developed Hybrid Framework for Forecasting, Evaluation, and Early-Warning
2.1. Part I: A Novel Forecasting Model for PM10
2.1.1. Grey Prediction Theory
2.1.2. Artificial Intelligence Optimization Arithmetic
| Algorithm 1 MRFO |
| Output: X*— X with the best fitness Parameters: T—the maximum number of iterations N—the number of population Fi—the fitness of i-th manta ray [Li, Ui] —the boundaries of the i-th variable Xi—the position of i-th manta ray t—the current iterations d—the dimension of the optimized problem. 1 /*Set the basic parameters of MRFO algorithm. */ 2 /*Initialize the manta ray Xi (i = 1, 2… N) randomly. */ 3 FOR EACH i: 1 ≤ i ≤ N DO 4 Calculate the fitness Fi for each manta ray 5 END FOR 6 /*Determine the best solution found so far X*. */ 7 WHILE (t < IterMax) DO 8 FOR EACH i: 1 ≤ i ≤ N DO 9 IF rand < 0.5 DO 10 /* Cyclone foraging strategy. */ 11 IF t/T > rand DO 12 13 14 ELSE IF t/T ≤ rand DO 15 16 17 END IF 18 ELSE IF rand > 0.5 DO 19 /* Chain foraging strategy. */ 20 21 END IF 22 END FOR 23 /* Check and modify the new positions based on [Li, Ui]. */ 24 /* Compute the fitness of each manta ray. */ 25 IF F (Xi(t + 1)) < F (Xbest) DO 26 /* Update the position of Xbest, i.e., Xbest= Xi(t + 1). */ 27 END IF 28 FOR EACH i: 1 ≤ i ≤ N DO 29 30 /* Check and modify the new positions based on [Li, Ui]. */ 31 /* Compute the fitness of each manta ray. */ 32 IF F (Xi(t+1)) < F (Xbest) DO 33 /* Update the position of Xbest, i.e., Xbest = Xi(t+1). */ 34 END IF 35 ELSE FOR 36 T = t + 1 37 END WHILE 38 RETURN the best solution found so farX* |
2.1.3. The GM (1, 1) Model Based on the Cycle Prediction Theory: C-GM (1, 1) Model
2.1.4. The Newly Developed Forecasting Model: C-MRFO-GM (1, 1) Model
2.2. Part II: The Designed Health Economic Losses Assessment Model
2.2.1. Selection of Pollution Factors, Exposure Populations and Health Effects
2.2.2. The Newly Proposed Health Economic Losses Assessment Model
3. Empirical Study
3.1. Study Area and Data Description
3.2. Results of the Developed C-MRFO-GM (1, 1) Model
3.2.1. Analysis of the Applicability of the GM (1, 1) Model
3.2.2. Forecasting Results and Analysis of the Developed Forecasting Model
3.2.3. Remark for the Performance of Different Models
3.3. Results of the Designed Health Economic Losses Evaluation Model
3.3.1. Data Sources for Health Economic Losses Assessment
3.3.2. Selection of Threshold Value of PM10’s Health Effects
3.3.3. Evaluation of the Past: 2014 to 2018
3.3.4. Evaluation of the Future: 2019 to 2021
4. Discussion of the Influence of the Threshold Value of PM10
5. Conclusions
- (1)
- Based on the results of the empirical study, the question “When will the influence of PM10 on public health end?” can be answered as follows: The influence of PM10 on public health may end in 2022 under the baseline of the national standard limited concentration values, but it will still pose a negative impact on public health and cause economic losses from 2019 to 2025 under the baseline of IT-2, IT-3 and AQG. Overall, the current situation is not very good, and Xi’an city should adopt more effective and persistent air quality control measures to control PM10 emissions.
- (2)
- Different from most previous air pollution health economic losses studies that focused on PM2.5, the present study focused on PM10, which has been neglected in previous studies and can bridge the research gap in air pollution health economic losses. The experimental results show that the changes in health effects and health economic losses caused by PM10 cannot be ignored, and people should consider emissions reduction and control of PM10.
- (3)
- This study contributes forecasting, evaluation and early-warning to the research, which are new ideas and a new research framework. Specifically, forecasting can provide future changes in PM10, while evaluation can help the public understand the basic conditions of health effects and economic losses and also predict the future conditions for the public. Most importantly, politicians can adjust their policies according to the results of the evaluation for the future. To the best of our knowledge, most previous economic losses assessment studies only focused on assessing the economic costs of past disasters while ignoring the significance of evaluating the economic losses for the past and future. As a result, the presented research framework and ideas provide a theoretical reference and academic reference for future research. In the future, the research framework and ideas based on forecasting, evaluation and early-warning can be extended and applied in other fields, such as storm surge disaster losses [38], e-commerce precision poverty alleviation benefit assessment [39], rainstorm disaster losses [40], earthquakes and flood losses [41] and impacts of haze pollution on the tourism industry [42].
- (4)
- Most previous studies focused on health economic losses caused by air pollution in different areas and at different times. On the positive side, assessing past economic losses provides support for air pollution prevention and control. However, when will the influence of air pollution on public health end? This is a significant and neglected issue, which can be considered a new research direction. As a result, this study takes PM10 as the research object and first poses the question: “When will the influence of PM10 on public health end?” The answer is provided based on forecasting, evaluation and early-warning.
- (5)
- Another interesting finding is that the traditional grey model is more applicable than other grey models for forecasting PM10 in Xi’an, China. In general, in the air quality forecasting field and other related forecasting fields, variants of the traditional grey model may perform better than the traditional grey model. For example, in Wu et al. [43], the GM (1, 1) model with fractional order accumulation performs better than the GM (1, 1) model alone. Different from previous studies, this study not only considers the fitting accuracy but also the rationality of the future development trend of things. It should be noted that the prediction of the future development trend needs to conform to the development law of things, which is obviously different from the training and testing process of the prediction model.
- (6)
- Wu and Zhao (2019) [44] employed an individual model named the fractional order accumulation GM (1, 1) model to forecast the number of lightly polluted days from 2017–2020, which proves the forecasting power of grey forecasting theory. Cycle prediction theory can capture the latest development trend and features of the studied object, while optimization can obtain the model’s optimal parameters. As a result, cycle prediction theory and optimization can improve the forecasting performance to a large extent. Considering the advantages and disadvantages of grey forecasting theory, this study further develops the findings of Wu and Zhao (2019) and introduces cycle prediction theory and optimization into air pollution’s health economic losses assessment and forecasting.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- García Nieto, P.J.; Sánchez Lasheras, F.; García-Gonzalo, E.; de Cos Juez, F.J. PM10 concentration forecasting in the metropolitan area of Oviedo (Northern Spain) using models based on SVM, MLP, VARMA and ARIMA: A case study. Sci. Total Environ. 2018, 621, 753–761. [Google Scholar] [CrossRef]
- Turner, M.C.; Krewski, D.; Pope, C.A.; Chen, Y.; Gapstur, S.M.; Thun, M.J. Long-term ambient fine particulate matter air pollution and lung cancer in a large cohort of never-smokers. Am. J. Respir. Crit. Care Med. 2011, 184, 1374–1381. [Google Scholar] [CrossRef]
- Ostro, B.D.; Eskeland, G.S.; Sanchez, J.M.; Feyzioglu, T. Air pollution and health effects: A study of medical visits among children in Santiago, Chile. Environ. Health Perspect. 1999, 107, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Saini, J.; Dutta, M.; Marques, G. Fuzzy Inference System Tree with Particle Swarm Optimization and Genetic Algorithm: A novel approach for PM10 forecasting. Expert Syst. Appl. 2021, 183, 115376. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, W.; Wang, J. Air quality early-warning system for cities in China. Atmos. Environ. 2017, 148, 239–257. [Google Scholar] [CrossRef]
- Li, R.; Jin, Y. The early-warning system based on hybrid optimization algorithm and fuzzy synthetic evaluation model. Inf. Sci. 2018, 435, 296–319. [Google Scholar] [CrossRef]
- Zhu, S.; Qiu, X.; Yin, Y.; Fang, M.; Liu, X.; Zhao, X.; Shi, Y. Two-step-hybrid model based on data preprocessing and intelligent optimization algorithms (CS and GWO) for NO2 and SO2 forecasting. Atmos. Pollut. Res. 2019, 10, 1326–1335. [Google Scholar] [CrossRef]
- Liu, H.; Xu, Y.; Chen, C. Improved pollution forecasting hybrid algorithms based on the ensemble method. Appl. Math. Model. 2019, 73, 473–486. [Google Scholar] [CrossRef]
- Hao, Y.; Tian, C. The study and application of a novel hybrid system for air quality early-warning. Appl. Soft Comput. J. 2019, 74, 729–746. [Google Scholar] [CrossRef]
- Xu, X. Forecasting air pollution PM2.5 in Beijing using weather data and multiple kernel learning. J. Forecast. 2020, 39, 117–125. [Google Scholar] [CrossRef]
- Fan, G.F.; Guo, Y.H.; Zheng, J.M.; Hong, W.C. A generalized regression model based on hybrid empirical mode decomposition and support vector regression with back-propagation neural network for mid-short-term load forecasting. J. Forecast. 2020, 39, 737–756. [Google Scholar] [CrossRef]
- Fang, Y.; Guan, B.; Wu, S.; Heravi, S. Optimal forecast combination based on ensemble empirical mode decomposition for agricultural commodity futures prices. J. Forecast. 2020, 39, 877–886. [Google Scholar] [CrossRef]
- Wang, J.; Du, P.; Lu, H.; Yang, W.; Niu, T. An improved grey model optimized by multi-objective ant lion optimization algorithm for annual electricity consumption forecasting. Appl. Soft Comput. J. 2018, 72, 321–337. [Google Scholar] [CrossRef]
- Lu, K.H.; Hong, C.M.; Han, Z.; Yu, L. New intelligent control strategy hybrid grey-RCMAC algorithm for ocean wave power generation systems. Energies 2020, 13, 241. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S. An optimized grey model for annual power load forecasting. Energy 2016, 107, 272–286. [Google Scholar] [CrossRef]
- Du, P.; Wang, J.; Yang, W.; Niu, T. A novel hybrid model for short-term wind power forecasting. Appl. Soft Comput. J. 2019, 80, 93–106. [Google Scholar] [CrossRef]
- Hao, Y.; Tian, C.; Wu, C. Modelling of carbon price in two real carbon trading markets. J. Clean. Prod. 2020. [Google Scholar] [CrossRef]
- Tian, C.; Hao, Y. Point and interval forecasting for carbon price based on an improved analysis-forecast system. Appl. Math. Model. 2020, 79, 126–144. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Niu, T.; Du, P. A hybrid forecasting system based on a dual decomposition strategy and multi-objective optimization for electricity price forecasting. Appl. Energy 2019, 235, 1205–1225. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, T.; Li, Y. Economic loss of air pollution in Xi’an City. J. Arid Land Resour. Environ. 2015, 29, 105–110. [Google Scholar] [CrossRef]
- Cai, H.D. Modern Environmental Hygiene; People’s Medical Publishing House: Beijing, China, 1995. [Google Scholar]
- Xie, N.M.; Liu, S.F.; Yang, Y.J.; Yuan, C.Q. On novel grey forecasting model based on non-homogeneous index sequence. Appl. Math. Model. 2013, 37, 5059–5068. [Google Scholar] [CrossRef]
- Pao, H.T.; Fu, H.C.; Tseng, C.L. Forecasting of CO2 emissions, energy consumption and economic growth in China using an improved grey model. Energy 2012, 40, 400–409. [Google Scholar] [CrossRef]
- Liu, S.; Dang, Y.; Fang, Z.; Xie, N. Grey System Theory and Its Application; Science Press: Beijing, China, 2010. [Google Scholar]
- Wu, L.; Zhao, H. Using FGM(1,1) model to predict the number of the lightly polluted day in Jing-Jin-Ji region of China. Atmos. Pollut. Res. 2019, 10, 552–555. [Google Scholar] [CrossRef]
- Ma, X.; Mei, X.; Wu, W.; Wu, X.; Zeng, B. A novel fractional time delayed grey model with Grey Wolf Optimizer and its applications in forecasting the natural gas and coal consumption in Chongqing China. Energy 2019, 178, 487–507. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Z. The GMC(1, n) model with optimized parameters and its application. J. Grey Syst. 2017, 29, 122–138. [Google Scholar]
- Xia, J.; Ma, X.; Wu, W.; Huang, B.; Li, W. Application of a new information priority accumulated grey model with time power to predict short-term wind turbine capacity. J. Clean. Prod. 2020, 244, 118573. [Google Scholar] [CrossRef]
- Wang, Z.X.; Li, Q. Modelling the nonlinear relationship between CO2 emissions and economic growth using a PSO algorithm-based grey Verhulst model. J. Clean. Prod. 2019, 207, 214–224. [Google Scholar] [CrossRef]
- Lewis, C.D. Industrial and Business Forecasting Method; Butter-worth-Heinemann: London, UK, 1982. [Google Scholar]
- Li, L.; Lei, Y.; Wu, S.; Huang, Z.; Luo, J.; Wang, Y.; Chen, J.; Yan, D. Evaluation of future energy consumption on PM2.5 emissions and public health economic loss in Beijing. J. Clean. Prod. 2018, 187, 1115–1128. [Google Scholar] [CrossRef]
- World Health Organization. WHO Air Quality Guidelines for Particulate Matter, Ozone, Nitrogen Dioxide and Sulfur Dioxide. Global Update 2005. Summary of Risk Assessment 2006. Available online: https://apps.who.int/iris/handle/10665/69477 (accessed on 6 August 2021).
- Li, L.; Lei, Y.; Wu, S.; Chen, J.; Yan, D. The health economic loss of fine particulate matter (PM2.5) in Beijing. J. Clean. Prod. 2017, 161, 1153–1161. [Google Scholar] [CrossRef]
- Li, H.; Liu, Z.; Liu, K.; Zhang, Z. Predictive Power of Machine Learning for Optimizing Solar Water Heater Performance: The Potential Application of High-Throughput Screening. Int. J. Photoenergy 2017, 4194251. [Google Scholar] [CrossRef]
- Li, J.S.; Chen, G.Q.; Chen, B.; Yang, Q.; Wei, W.D.; Wang, P.; Dong, K.Q.; Chen, H.P. The impact of trade on fuel-related mercury emissions in Beijing—evidence from three-scale input-output analysis. Renew. Sustain. Energy Rev. 2017, 75, 742–752. [Google Scholar] [CrossRef]
- Ielpo, P.; Paolillo, V.; de Gennaro, G.; Dambruoso, P.R. PM10 and gaseous pollutants trends from air quality monitoring networks in Bari province: Principal component analysis and absolute principal component scores on a two years and half data set. Chem. Cent. J. 2014, 8, 14. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liu, Q.; Ruan, C.; Zhong, S.; Li, J.; Yin, Z.; Lian, X. Risk assessment of storm surge disaster based on numerical models and remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 20–30. [Google Scholar] [CrossRef]
- Guan, H.; Zhao, A.; Shi, G. Research on E-Commerce Precision Poverty Alleviation; Economic Science Press: Beijing, China, 2019. [Google Scholar]
- Tan, L.; Wu, X.; Xu, Z.; Li, L. Comprehensive economic loss assessment of disaster based on CGE model and IO model—A case study on Beijing “7.21 Rainstorm.”. Int. J. Disaster Risk Reduct. 2019, 39, 101246. [Google Scholar] [CrossRef]
- Dabbeek, J.; Silva, V.; Galasso, C.; Smith, A. Probabilistic earthquake and flood loss assessment in the Middle East. Int. J. Disaster Risk Reduct. 2020, 49, 101662. [Google Scholar] [CrossRef]
- Hao, Y.; Niu, X.; Wang, J. Impacts of haze pollution on China’s tourism industry: A system of economic loss analysis. J. Environ. Manage. 2021, 295, 113051. [Google Scholar] [CrossRef]
- Wu, L.; Li, N.; Yang, Y. Prediction of air quality indicators for the Beijing-Tianjin-Hebei region. J. Clean. Prod. 2018, 196, 682–687. [Google Scholar] [CrossRef]
- Wu, W.; Ma, X.; Zeng, B.; Wang, Y.; Cai, W. Forecasting short-term renewable energy consumption of China using a novel fractional nonlinear grey Bernoulli model. Renew. Energy 2019, 140, 70–87. [Google Scholar] [CrossRef]
| Year | PM10 |
|---|---|
| 2014 | 136.08 |
| ESR | 94.40% |
| 2015 | 129.08 |
| ESR | 84.40% |
| 2016 | 146.17 |
| ESR | 108.81% |
| 2017 | 110.67 |
| ESR | 58.10% |
| 2018 | 99.17 |
| ESR | 41.67% |
| Limit | 70 |
| MAPE | ≤10% | 10–20% | 20–50% | ≥50% |
|---|---|---|---|---|
| Evaluation | Highly accurate | Good | Reasonable | Inaccurate |
| Year | PM10 | GM (1, 1) | NDGM (1, 1) | NGBM (1, 1) | Grey Verhulst | OP-NGBM | OP-FANGBM | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | APE | Value | APE | Value | APE | Value | APE | Value | APE | Value | APE | ||
| 2014 | 136.08 | 136.08 | 0 | 135.16 | 0.6761 | 136.08 | 0 | 136.08 | 0 | 136.08 | 0 | 136.08 | 0 |
| 2015 | 129.08 | 139.66 | 8.1965 | 140.96 | 9.2036 | 129.07 | 0.0077 | 112.59 | 12.775 | 129.08 | 0 | 129.08 | 0 |
| 2016 | 146.17 | 126.6 | 13.3885 | 125.13 | 14.3942 | 137.4 | 5.9999 | 141.69 | 3.0649 | 134.16 | 8.2165 | 133.95 | 8.3601 |
| 2017 | 110.67 | 114.75 | 3.6866 | 114.26 | 3.2439 | 120.77 | 9.1262 | 130.09 | 17.5477 | 120.46 | 8.8461 | 118.81 | 7.3552 |
| 2018 | 99.17 | 104.02 | 4.8906 | 106.78 | 7.6737 | 94.07 | 5.1427 | 89.11 | 10.1442 | 99.17 | 0 | 99.17 | 0 |
| 2019 | - | 94.29 | - | 101.65 | - | 67.88 | - | 49.5 | - | 77.3 | - | 78.92 | - |
| 2020 | - | 85.47 | - | 98.12 | - | 46.67 | - | 24.35 | - | 58.15 | - | 59.86 | - |
| 2021 | - | 77.48 | - | 95.7 | - | 31.13 | - | 11.26 | - | 42.73 | - | 42.77 | - |
| 2022 | - | 70.23 | - | 94.04 | - | 20.36 | - | 5.06 | - | 30.9 | - | 27.96 | - |
| 2023 | - | 63.66 | - | 92.89 | - | 13.16 | - | 2.24 | - | 22.1 | - | 15.44 | - |
| 2024 | - | 57.7 | - | 92.11 | - | 8.44 | - | 0.99 | - | 15.69 | - | 5.07 | - |
| 2025 | - | 52.31 | - | 91.57 | - | 5.38 | - | 0.43 | - | 11.08 | - | -3.35 | - |
| MAPE | 6.0324 | 7.0383 | 4.0553 | 8.7064 | 3.4125 | 3.1431 | |||||||
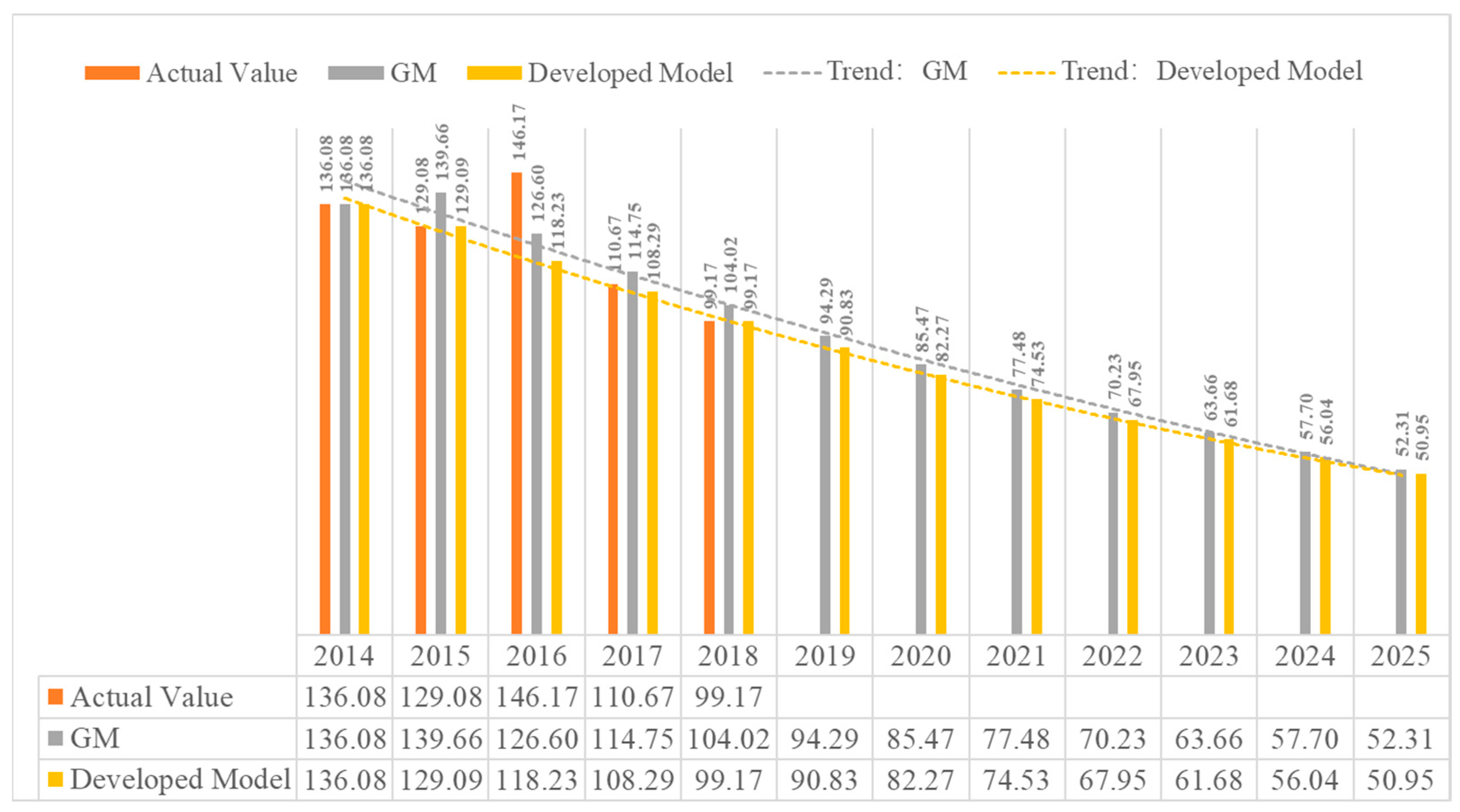
| Year | PM10 | GM | Developed Model | ||
|---|---|---|---|---|---|
| Value | APE | Value | APE | ||
| 2014 | 136.08 | 136.08 | 0 | 136.08 | 0 |
| 2015 | 129.08 | 139.66 | 8.1965 | 129.09 | 0.0077 |
| 2016 | 146.17 | 126.6 | 13.3885 | 118.23 | 19.1147 |
| 2017 | 110.67 | 114.75 | 3.6866 | 108.29 | 2.1505 |
| 2018 | 99.17 | 104.02 | 4.8906 | 99.17 | 0 |
| 2019 | 94.29 | - | 90.83 | - | |
| 2020 | 85.47 | - | 82.27 | - | |
| 2021 | 77.48 | - | 74.53 | - | |
| 2022 | 70.23 | - | 67.95 | - | |
| 2023 | 63.66 | - | 61.68 | - | |
| 2024 | 57.7 | - | 56.04 | - | |
| 2025 | 52.31 | - | 50.95 | - | |
| MAPE | 6.0324 | 4.2546 | |||
| Level | PM10 (ug/m3) |
|---|---|
| Interim target-1 (IT-1) | 70 |
| Interim target-2 (IT-2) | 50 |
| Interim target-3 (IT-3) | 30 |
| Air quality guidelines (AQG) | 20 |
| Heath Effect Ends | Changed Values (One in 1,000,000 People) |
|---|---|
| Death mortality | 6 |
| Respiratory disease outpatient rate | 12 |
| Increase of emergency cases | 235 |
| Restricted activity days | 57,500 |
| Increase of cases of lower respiratory tract infection/asthma in children | 23 |
| Increase of asthma cases | 2068 |
| Increased cases of chronic bronchitis | 61 |
| Year. | Concentration (ug/m3) | Basic Materials and Data | Per Capita Medical Expenses (Yuan) | Public Health Effects Caused by Air Pollution | Health Economic Losses (Hundred Million Yuan) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exposure Population (Ten Thousand) | Labor Force Ratio (%) | Per Capita Annual Salary (Yuan) | Per Capita Daily Wage (Yuan) | Asthma | Respiratory Tract Infection | Increased Cases of Chronic Bronchitis | Change Values of Each Heath Effect | Premature Death | Medical Expenses | Delayed Wages | Total Losses | ||||||
| Premature Death | Asthma | Respiratory Tract Infection | Increased Cases of Chronic Bronchitis | Days of Lost Work | |||||||||||||
| 2014 | 136.08 | 862.75 | 61.77 | 54,573 | 149.52 | 202.80 | 608.40 | 811.20 | 3421 | 1,178,978 | 153,928 | 34,776 | 5,062,207 | 5.7660 | 3.6096 | 7.5688 | 16.9444 |
| 2015 | 129.08 | 870.56 | 60.66 | 60,557 | 165.91 | 204.22 | 612.66 | 816.88 | 3086 | 1,063,628 | 138,868 | 31,374 | 4,484,682 | 5.6678 | 3.2792 | 7.4405 | 16.3875 |
| 2016 | 146.17 | 883.21 | 61.05 | 67,205 | 183.62 | 206.06 | 618.17 | 824.23 | 4036 | 1,391,229 | 181,640 | 41,037 | 5,903,718 | 8.2793 | 4.3278 | 10.8404 | 23.4475 |
| 2017 | 110.67 | 961.67 | 62.00 | 75,262 | 206.20 | 210.18 | 630.54 | 840.71 | 2347 | 808,818 | 105,600 | 23,858 | 3,485,630 | 5.4756 | 2.5664 | 7.1873 | 15.2293 |
| 2018 | 99.17 | 1000.37 | 62.10 | 83,821 | 229.65 | 214.17 | 642.52 | 856.69 | 1751 | 603,459 | 78,788 | 17,800 | 2,604,808 | 4.5570 | 1.9512 | 5.9819 | 12.4900 |
| Total | 14,641 | 5,046,112 | 658,824 | 148,845 | 21,541,045 | 29.7457 | 15.7341 | 39.0188 | 84.4987 | ||||||||
| Year. | Concentration (ug/m3) | Basic Materials and Data | Per capita Medical Expenses (Yuan) | Public Health Effects Caused by Air Pollution | Health Economic Losses (Hundred Million Yuan) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exposure Population (Ten Thousand) | Labor Force Ratio (%) | Per capita Annual Salary (Yuan) | Per capita Daily Wage (Yuan) | Asthma | Respiratory Tract Infection | Increased Cases of Chronic Bronchitis | Change Values of Each Heath Effect | Premature Death | Medical Expenses | Delayed Wages | Total Losses | ||||||
| Premature Death | Asthma | Respiratory Tract Infection | Increased Cases of Chronic Bronchitis | Days of Lost Work | |||||||||||||
| 2019 | 90.83 | 1064.93 | 62.64 | 93,611.70 | 256.47 | 218.35 | 655.05 | 873.39 | 1331 | 458,735 | 59,893 | 13,531 | 1,997,420 | 3.9024 | 1.5121 | 5.1228 | 10.5373 |
| 2020 | 82.27 | 1133.66 | 63.19 | 104,545.99 | 285.64 | 222.61 | 667.82 | 890.43 | 835 | 287,660 | 37,557 | 8485 | 1,263,472 | 2.7580 | 0.9667 | 3.6090 | 7.3338 |
| Total I | 10,300 | 3,549,901 | 463,478 | 104,711 | 15,255,048 | 24.9723 | 11.3242 | 32.7414 | 69.0379 | ||||||||
| 2021 | 74.53 | 1206.83 | 63.74 | 116,757.47 | 319.01 | 226.95 | 680.84 | 907.79 | 328 | 113,056 | 14,761 | 3335 | 500,911 | 1.2205 | 0.3874 | 1.5980 | 3.2058 |
| Total II | 328 | 113,056 | 14,761 | 3335 | 500,911 | 1.2205 | 0.3874 | 1.5980 | 3.2058 | ||||||||
| Total III | 2494 | 859,451 | 112,211 | 25,351 | 3,761,803 | 7.8809 | 2.8662 | 10.3298 | 21.0769 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Tang, G.; Hao, Y.; Wang, J. A Novel Framework for Forecasting, Evaluation and Early-Warning for the Influence of PM10 on Public Health. Atmosphere 2021, 12, 1020. https://doi.org/10.3390/atmos12081020
Yang W, Tang G, Hao Y, Wang J. A Novel Framework for Forecasting, Evaluation and Early-Warning for the Influence of PM10 on Public Health. Atmosphere. 2021; 12(8):1020. https://doi.org/10.3390/atmos12081020
Chicago/Turabian StyleYang, Wendong, Guolin Tang, Yan Hao, and Jianzhou Wang. 2021. "A Novel Framework for Forecasting, Evaluation and Early-Warning for the Influence of PM10 on Public Health" Atmosphere 12, no. 8: 1020. https://doi.org/10.3390/atmos12081020
APA StyleYang, W., Tang, G., Hao, Y., & Wang, J. (2021). A Novel Framework for Forecasting, Evaluation and Early-Warning for the Influence of PM10 on Public Health. Atmosphere, 12(8), 1020. https://doi.org/10.3390/atmos12081020









