Abstract
Atmospheric effects have a significant impact on the performance of airborne and space laser systems. Traditional models used to predict propagation effects rely heavily on simplified assumptions of the atmospheric properties and their interactions with laser systems. In the engineering domain, these models need to be continually improved in order to develop tools that can predict laser beam propagation with high accuracy and for a wide range of practical applications such as LIDAR (light detection and ranging), free-space optical communications, remote sensing, etc. The underlying causes of laser beam attenuation in the atmosphere are examined in this paper, with a focus on the dominant linear effects: absorption, scattering, turbulence, and non-linear thermal effects such as blooming, kinetic cooling, and bleaching. These phenomena are quantitatively analyzed, highlighting the implications of the various assumptions made in current modeling approaches. Absorption and scattering, as the dominant causes of attenuation, are generally well captured in existing models and tools, but the impacts of non-linear phenomena are typically not well described as they tend to be application specific. Atmospheric radiative transfer codes, such as MODTRAN, ARTS, etc., and the associated spectral databases, such as HITRAN, are the existing tools that implement state-of-the-art models to quantify the total propagative effects on laser systems. These tools are widely used to analyze system performance, both for design and test/evaluation purposes. However, present day atmospheric radiative transfer codes make several assumptions that reduce accuracy in favor of faster processing. In this paper, the atmospheric radiative transfer models are reviewed highlighting the associated methodologies, assumptions, and limitations. Empirical models are found to offer a robust analysis of atmospheric propagation, which is particularly well-suited for design, development, test and evaluation (DDT&E) purposes. As such, empirical, semi-empirical, and ensemble methodologies are recommended to complement and augment the existing atmospheric radiative transfer codes. There is scope to evolve the numerical codes and empirical approaches to better suit aerospace applications, where fast analysis is required over a range of slant paths, incidence angles, altitudes, and atmospheric conditions, which are not exhaustively captured in current performance assessment methods.
1. Introduction
The accuracy of predicting light propagation by empirical and simulation methods is vital in research concerning climate change [1,2], remote sensing [3] and atmospheric optics [4]. Currently, empirical models developed in the 1960s to 1970s are still widely used for laser propagation analysis [5,6] and constitute the basis of atmospheric radiative transfer codes, which are widely utilized for performance predictions. These codes are regularly improved to allow more detailed analyses, yet they do not include fully comprehensive models. The uncertainty and assumptions made in atmospheric radiative transfer codes stems from the often-omitted aspects of light propagation, including turbulence and thermodynamic impacts. The interactions of solar radiation with the constituents of the atmosphere are difficult to model and measure accurately, leading to a difficult integration in present day atmospheric radiative transfer codes for remote optical sensors [7]. The key challenge for airborne applications, and remote sensing in general, is to overcome the current limitations and make corrections accurately and quickly for atmospheric propagative effects without much information on the atmospheric conditions. For aerospace applications (typically incorporating altitude dependent atmospheric phenomena) there is a lack of understanding and/or disagreement between models, especially regarding aero-optical effects and atmospheric optical turbulence.
The effect of atmospheric properties on laser beam propagation is presented in some detail, covering the empirical methods that define the major sources of propagation. This includes absorption and scattering of molecules and aerosols, atmospheric turbulence effects and non-linear behavior caused by thermal effects such as blooming and bleaching. Laser wavelengths (both in the visible and infrared portions of the spectrum) are attenuated in the atmosphere mainly due to linear effects of absorption and scattering, and to a smaller degree, turbulence, and non-linear effects. The non-linear effects are more difficult to model and are less well understood. There are prominent models describing light propagation through turbulence, but they vary dramatically depending on height and the overlap in application is unclear.
Absorption and scattering are the dominant effects as they interact with atmospheric particles whose composition, size, and concentration are subject to large variations. The effects of aerosols are particularly important in low-altitude applications. These parameters are then related back to performance prediction based on transmittance. This work also reviews atmospheric radiative transfer models, the numerical codes, and their applicability and accuracy in assessing performance resulting from atmospheric propagation effects. Atmospheric radiative transfer models are used to estimate the atmospheric propagation by the radiative transfer equation and generalizing aspects of the atmospheric conditions. Popular models such as MODTRAN are powerful tools in determining the attenuation due to the atmosphere. These models are based on a line-by-line analysis, which allows for high accuracy, and continual updates have expanded the use of absorption and scattering models. The limitations of these models are that they largely only consider some scattering and absorption and for the most part neglect non-linear effects on propagation. This invites improvement from empirical models to add robustness these limitations. This review illustrates the gaps in the empirical modelling, and numerical codes that should be addressed for higher accuracy especially for remote sensing airborne applications.
This review outlines the classical approaches of light propagation and reviews new approaches, implementations, and atmospheric transfer codes in achieving high-fidelity predictions of laser attenuation in the atmosphere.
The development of low-weight, powerful laser sources and point systems, has led to increasing implementation in airborne and satellite platforms. The most popular of these electro-optical systems are passive visible to infrared imagining and active LIDAR for atmospheric sounding. These techniques measure the molecular and aerosol components in the atmosphere but it can be difficult to model certain aspects of the propagation effects, which in turn affects accuracy. Imaging measurements tend to be less accurate than coherent detection methods and LIDAR tends to be very accurate but over smaller ranges than imaging sensors. The different types of laser systems in aerospace applications are influenced by the need for fast and accurate results based on few known atmospheric variables. The approaches discussed tend to rely heavily on a priori knowledge, particularly in LIDAR inversion algorithm applications. The key aeronautical and space applications for laser systems and the underlying principles are summarized below.
1.1. Aerospace Laser Applications
Early aerospace applications of lasers included both range finding and various military applications, such as beam-riding and target designation (i.e., guided weapon systems) as the high irradiance and collimation of the laser beam allowed for high accuracy over long distances. More recently, 3D-scanning LIDAR systems have been widely adopted in autonomous obstacle/object detection applications largely due the high accuracy attainable and the ability of LIDAR to function across a variety of conditions [8,9]. In both manned and unmanned aerospace vehicles, the point cloud data obtained from the LIDAR supports the detection, recognition, and identification of potential obstacles to be avoided [10]. The performance and versatility of LIDAR make for a powerful aerospace sensor across a variety of applications. However, key limitations of air and space laser sensors include their susceptibility to atmospheric conditions and meteorological effects, and the relatively limited knowledge of high-altitude linear and non-linear propagation effects. Despite these limitations, the benefits of aerospace laser systems in terms of accuracy, resolution, and versatility make them ideal for a variety of civil/military multi-sensor systems and data-fusion applications. This versatility is highlighted, for instance, when considering the possible integration with passive FLIR (forward-looking infrared) sensors, which can assist manned and unmanned aerospace vehicles in safety- and mission-critical tasks such as obstacle detection, navigation and guidance, night vision, etc.
Airborne LIDAR systems are particularly useful in agricultural applications such as mapping canopy heights, profiling of crop distributions and remote sensing. Airborne remote sensing, in particular, allows for detailed analysis of vast areas, with flexibility of data capture, and high accuracy at various grazing angles across different terrains. These features are particularly important in the application to forest monitoring and food crop health-status assessment [11,12]. In geophysics applications, in combination with GNSS, highly accurate data in measuring faults and changes can be detected. An airborne remote sensing laser system, as shown in Figure 1, offers greater flexibility and accuracy in measuring vertical and horizontal profiles and is becoming more prevalent across different industries.
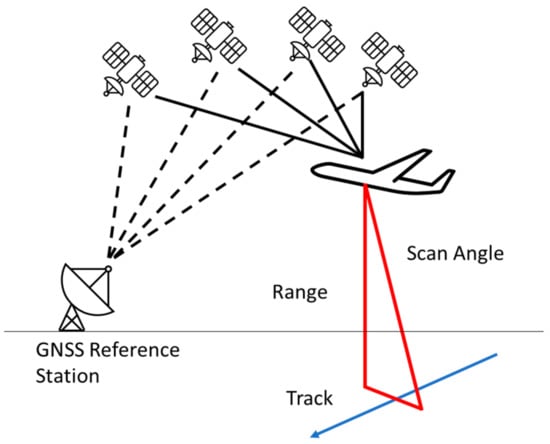
Figure 1.
Airborne laser system scanning and georeferenced. Adapted from [13].
Laser sense-and-avoid (SAA) is being developed for low-level flights, especially for helicopter and UAV applications, where radar is inadequate in obstacle warning systems (OWS). The advantage of airborne laser obstacle avoidance monitoring (LOAM) is the ability to detect terrain, wires, and buildings in low-level flight conditions [14]. The need for a high probability of detection is obvious since no obstacle must go undetected. These systems also require a minimum detection range, and to be able to perform in all weather and day and night conditions. For these systems to be effective, they need high reliability in detecting obstacles in a range of different angles with a low false alarm rate, and fast processing.
Differential absorption LIDAR is used extensively in atmospheric sounding as the technique is useful in eliminating error sources in atmospheric composition. Using ‘on’ and ‘off’ absorption wavelengths, a laser is tuned to the absorption frequency of the desired atmospheric constituent. The ‘on’ corresponding absorption wavelength is transmitted followed by a non-incident ‘off’ absorption wavelength. The difference between the received energy can then be reduced mostly as the result of absorption by the ‘on’ wavelength molecule or aerosol species. This can eliminate the uncertainty from non-linear attenuation effects such as turbulence that are difficult to model. The difference from the two pulses can then be related to the chemical concentrations in the atmosphere.
Laser Doppler radar illustrates the advantage of small particle detection for turbulence detection. Radar is generally only able to identify water droplets as the precursor to severe weather activity, where the laser system is more capable, particularly in airborne application in the detection of wind velocities. This system can measure very low velocities to very large changes for wind shear in remote sensing. Microbursts can be identified by the airborne LIDAR fitted to the nosecone, to give vital information to the control systems in critical phases of flight [15]. The narrow beam of the active laser sensor can take measurements independent of the time of day and weather conditions, which means it can be applied to difficult terrain, and densely covered areas for applications such as landslide monitoring from an airborne platform. Additionally, airborne laser systems are applied to bathymetry by utilizing green lasers and penetrating the water’s surface, the water column, and the sub region to measure different hydrological parameters [16].
As noted by [17], ultra-short laser pulses propagation is dependent on the output power. Below the critical peak power, the laser pulse intensity is rapidly reduced by beam diffraction and velocity dispersion. Above critical power, the pulse intensity increases to the point of air ionization. This intensity can be maintained for very long distances. This process is known as filamentation. High-powered long-distance propagation of ultra-short laser pulses is explored in [18] and is considered the forefront of non-linear optics. Research in femtosecond LIDAR applications has highlighted benefits that overcome the limitations of the DIAL technique, including measurement of volatile organic compounds (VOCs).
The astronomical use of LIDAR is important in correcting atmospheric distortion for telescopes. This is achieved by an artificial star image as a reference point to assist the adaptive optics. There are two types: sodium beacons, which react with the sodium in the mesosphere; and Rayleigh, which is time-gated to reduce the effect of low altitude scattering. Additionally, LIDAR is considered for Mars satellite observation missions, where the atmospheric propagation is utilized to explore the atmospheric constituents and wind velocity profiles [19].
Laser radars can be categorized by the measurement made by the laser radar, the detection technique, the type of interferometer employed in a coherent laser radar (if appropriate), the modulation technique, the demodulation technique, the type of laser or the wavelength of operation, the function performed, the type of data collected, or the data format. In addition, laser radar can be classed as monostatic or bistatic, depending on whether it uses a single aperture to transmit and to receive or separate apertures. Some of these groupings are summarized in Table 1.

Table 1.
Types of LIDAR [13].
As observed in Table 1, there are many types of laser radars, where the type is rarely sufficient to determine how well it performs. This variety in laser radar systems is indicative of their versatility, but this can also create confusion. For example, wavelength-dependent technological limitations frequently prevent simple parametric extrapolation of performance from one type of system to another. These limitations can make routine performance at a one laser wavelength well beyond the state of the art (and possibly beyond fundamental physical limitations) at another wavelength. Comparing one type of laser radar to another is inherently difficult and the extrapolation of performance must be carefully applied.
Using wavelength-specific components and technology is a major difference from passive optical systems or conventional radar systems. Laser sources limit the number of wavelengths practically available for laser radars. For passive systems or conventional radar, radio frequency (RF) through millimeter-wave (MMW) can select the wave band to optimize performance without major changes in technology. However, laser radars are limited in this regard and would need to change technologies completely (e.g., electrically pumped gas lasers versus optically pumped solid-state lasers) to effect even small changes in operating wavelength.
Laser radar operates similarly to conventional radar. Laser radar transmits a signal that is reflected by a target and then collected by the laser radar receiver. Measuring the round-trip time of the reflected light, the range to the target can be determined to a high accuracy. Radial velocity of the target is measured by either determining the Doppler shift of the reflected light or by making two (or more) range measurements and calculating the rate of change of range.
In direct detection laser radar (Figure 2), a photosensitive element generates a signal (voltage or current) directly proportional to the received optical energy, identical to the process for laser range finders and conventional passive optical receivers.
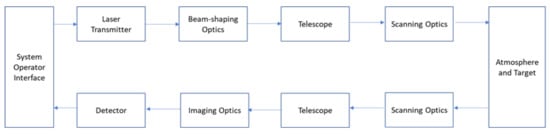
Figure 2.
Direct detection laser radar block diagram from [13].
A block diagram of a typical heterodyne (or coherent) detection laser radar is shown in Figure 3. The transmitted laser generates an optical signal; the divergence and beam diameter are then corrected by beam shaping optics to match the rest of the system, although some systems are unmodified. In monostatic operation, the aperture of the transmitter also serves as for the receiver. The transmit to receive switch allows the monostatic operation. The reflected signal from the target is collected by the scanning optics and beam expander, following which, the transmit to receive switch activates to direct the signal to the optical mixer, where it is combined by the local oscillator, the results of which are focused onto a photosensitive detector. Monostatic systems rely on the reflectance of the signal, as opposed to bistatic applications where the receiver is not collocated. In the bistatic system, there is no need for the transmit to receive switch, as the receiver has a dedicated beam expander and scanning optics, but otherwise operates on the same components of the monostatic system.
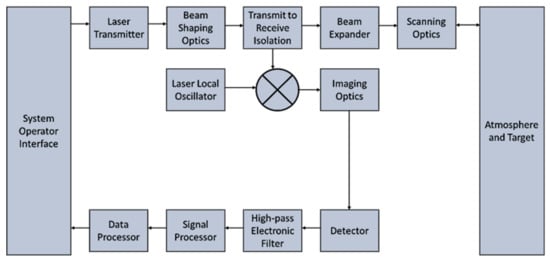
Figure 3.
Coherent detection LIDAR schematic from [13].
Additionally, conventional heterodyne receivers are distinct in needing separate laser source for the local oscillator. Homodyne receivers, on the other hand, utilize part of the laser transmission in the local oscillator for the receiver. Offset homodyne receivers use the local oscillator beam portion frequency shifted from the transmitted beam.
Although this paper focuses primarily on LIDAR systems, there are also several non-LIDAR applications of aerospace laser systems. Notably, the laser interferometer space antenna (LISA) is a space probe designed to measure gravitational waves based on laser interferometry. In this concept, three probes, one transmitter and two reflectors, allow the measurement of the relative phase shift to determine the properties of the gravitational wave [20].
Laser-based communication is a lower-powered, more-compact, higher-signal-strength alternative to radio frequency communication systems. The higher bandwidth and speed of laser communications allows more data to be sent through airborne and spaceborne platforms. Open path communication systems such as FSO utilize lasers to provide bandwidth or optical communication within the line-of-sight range. This technology has a range of applications, particularly for communications between satellites, due to the long range, high throughput and low bit error rates but is subject to atmospheric attenuation, as described in Figure 4 [21,22].

Figure 4.
Free space optical communication block diagram. Adapted from [22].
1.2. Structure of the Article
This article is structured as follows:
- Section 2 describes the effects on laser beam performance because of atmospheric attenuation. Covering the Beer–Lambert law governing transmittance, this section introduces the atmosphere composition, the dominant linear propagation effects of absorption and scattering, to then describe the non-linear effects concerning turbulence and thermodynamic propagative effects and the subsequent empirical models and theoretical backgrounds individually.
- Section 3 introduces empirical modelling to collectively combine the propagative effects in terms of laser performance. The benefits of empirical modelling in comparison to atmospheric radiative transfer codes are highlighted, and the approaches are subsequently reflected in practical radiometric measurement techniques for atmospheric extinction.
- Section 4 reviews the main atmospheric radiative transfer codes and emphasizes the underpinning methodology of the line-by-line analysis, the inherent assumptions and applications of each model and identifies trends in model development including more extensive use of absorption and scattering models.
2. Atmospheric Extinction and Transmittance
Atmosphere extinction describes laser beam attenuation as it propagates through the atmosphere, due to absorption, scattering and other phenomena. As opposed to conventional optical systems, the interactions between the atmosphere and the laser beam are unique and have significant consequences for performance. The nature of the very monochromatic laser radiation propagating within the constituents of the atmosphere results in these differences. The dominating phenomena of laser beam attenuation are molecular absorption and particle scattering. Both effects are dependent on the operating wavelength (absorption strongly so).
The Beer–Lambert law is the fundamental model to determine the overall transmittance as a function of extinction phenomena [23],
This relates the transmittance, , to the difference in irradiance at transmission, , compared to the receiver, , at distance, , away, which can be described by the attenuation coefficient, . The factors that influence this difference are related to the absorptivity and optical depth characteristics of the laser and the medium. Resolved over a single path length, the equation becomes:
where the attenuation coefficient is defined by the absorption and scattering properties of the medium:
The attenuation coefficient considers the molecular, subscript , absorption coefficient, , scattering coefficient, , and the aerosol coefficients, subscript , of absorption and scattering. The absorption and scattering coefficients are a dependent on the transmitted wavelength, the cross-section, , and concentrations, , of the individual particles being absorbed or scattered, where the subscript refers to absorption and subscript refers to scattering,
2.1. Atmospheric Properties
The dynamic nature and variability of atmospheric density, pressure, and temperature, especially in the vertical profile, as shown in Figure 5, is complex and difficult to model. The effects of the interactions within the atmosphere significantly impact laser beam performance and need to be accounted for in models attempting to simulate and determine the laser performance along a path. Attenuation along long path lengths is subject to greater interactions with aerosols and molecules, resulting in higher propagation and a decrease of laser beam performance. The distribution of aerosols and molecules along the optical path is inconsistent and variable with constant altitude. The models invariably generalize about the atmosphere, and the subsequent interactions with aerosols that attenuate performance that ultimately reduce the resolution of these atmospheric radiative transfer models.

Figure 5.
Atmosphere aerosol vertical profile. Adapted from [24,25].
The atmospheric composition of molecules is outlined in Table 2. Molecular species such ozone, water vapor, nitrous oxide, and carbon dioxide with low concentrations and high vibration and rotational states are the main contributors to molecular absorption in the visible to IR region [26]. These molecules have greater effects as they have more vibrational modes than the diatomic molecules (dominating the atmosphere constituents) that have a single vibrational mode. Absorption of the laser radiation occurs when atmospheric molecules, vibrational and rotational states coincide with the incident radiation.

Table 2.
Atmospheric molecular composition. Adapted from [27], reproduced with permission.
The atmospheric composition are nominal values of the atmosphere that do not capture the spatial and temporal variations due to a number of mixing phenomena (turbulence, convection, etc.).
For the absorption component, the wavelength range of most interest in laser beam propagation is from the visible spectrum to around 15 µm. The main atmospheric absorbers under consideration are CO2, water, and ozone, as shown in Figure 6.
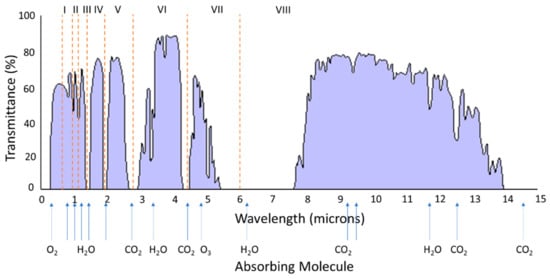
Figure 6.
Atmospheric transmittance across the spectral range at sea-level along an 1820 m path. Adapted from [28].
The areas of highest transmittance and the molecules responsible in that band are depicted in Figure 7. These transmittance peaks can be divided into atmospheric ‘windows’ with the wavelength bounds shown in Table 3. The trend in research has been away from using atmospheric windows as more sophisticated and accurate models of the absorption molecules have been developed.
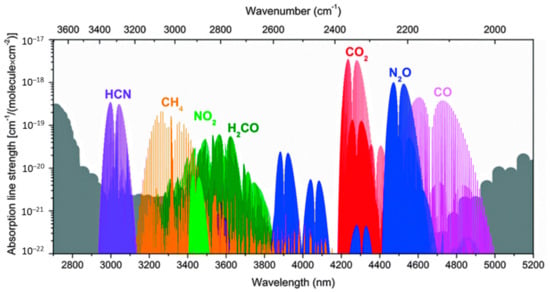
Figure 7.
Absorption line strength of selected molecules from HITRAN 2012 database [29].

Table 3.
Atmospheric windows wavelength upper and lower bounds.
2.2. Molecular Line Absorption
Molecular line absorption concerns the laser beam photons encountering molecules and aerosols in the atmosphere and transferring the laser radiation energy to the encountered atmospheric constituents. This is an incoherent process resulting from the oscillating dipoles being dampened [30]. Incoherent detection methods are generally favored in aerospace applications, due to the lower signal-to-noise ratio for lower powered lasers, and flexibility [31]. For conventional (passive) electro-optical systems, the operating bandwidth is typically large in comparison to the molecular absorption line width, resulting in the phenomena being averaged out. With laser systems (active) the effect is more significant. Typically, these systems operate over long ranges, and the laser gain medium is a naturally occurring atmosphere gas such as nitrogen or argon. This result in an inevitable coincident of the laser line with an atmospheric absorption line. Considering the transmitter or target in motion, the Doppler effect will shift the wavelength on transmission or on reflection resulting in further attenuation as the laser line coincides with a different atmospheric absorption line that have relative absorption line strength. Molecular spectroscopic databases such as the High-Resolution Transmission (HITRAN) database capture the current list of absorption lines for each particular molecule and isotope throughout the electromagnetic spectrum, allowing to visualize the relative positions and strengths, as per Figure 8. Another popular database is the Gestion et Etude des Informations Spectroscopiques Atmosphériques (GEISA). Both HITRAN and GEISA (as well as other databases) are regularly updated to capture newly characterized absorption bands for an increasing number of molecules and isotopes or to improve the spectral resolution of already known bands.
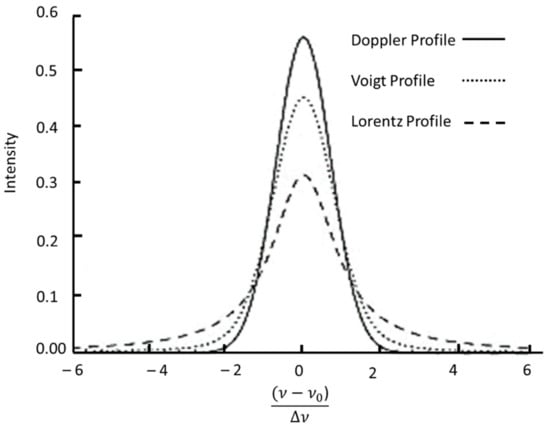
Figure 8.
Absorption line profiles, Doppler, Voigt, and Lorentz. From [32], reproduced with permission.
2.2.1. Absorption Line Profile
A zoomed-in perspective of the absorption lines in Figure 7 is shown in Figure 8, which shows the nature of the absorption lines. The lines have a natural width and are mainly affected by Doppler and pressure broadening. Doppler broadening accounts for the motion of the molecules being encountered, shifting, and broadening the absorption lines; it is most affected by molecular density and temperature. Collision broadening relates to the broadening of the absorption line because of collision energy transfer, with more pressure, more collision, and increased broadening of the absorption line. The collision broadening results in a change to the Lorentz absorption profile and the Doppler broadening effecting the Gaussian profile. These profiles are combined in the Voigt profile and are widely used in atmospheric models [33].
2.2.2. Continuum Absorption
The high-resolution transmission codes shown in Figure 8 show narrow discrete absorption lines. However, the absorption lines are continuous with narrow peaks, as shown in Figure 8. As described in Figure 9, molecular absorption lines are not discrete, and while the Voigt line profile does model the line accurately, there is an accumulative error between measured results and the Voigt profile, due to continuum absorption. The spectral lines become more spread due to broadening from collisions and Doppler shifts. The spread results in an overlap between absorption lines. Molecular absorption line clusters are influenced by strong absorption lines that can overlap with neighboring absorption lines to cause the continuum, whose contributions are difficult to distinguish. This is particularly relevant in the 8–13 µm region for water vapor [34].
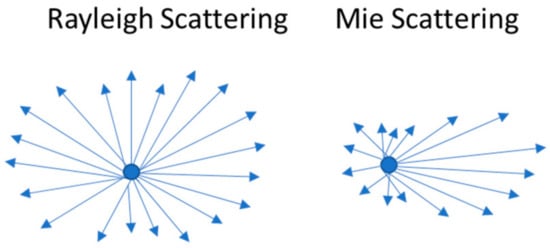
Figure 9.
Rayleigh and Mie scattering profiles.
For the “window” regions where molecular line absorption is low, the overlap from the far wings of very strong absorption lines obscures the influence of neighboring absorption lines. Where the clusters of molecular absorption are much stronger, the individual line contributions are harder to differentiate. The source and contribution of continuum absorption is not well understood. While it is a phenomenon that is accounted for and modelled semi-empirically in atmospheric radiative transfer models, due to the complexity of the continuum absorption process and an absence of experimental data, there remains uncertainty about how much continuum absorption contributes to transmission attenuation [28,32].
2.2.3. Transmittance Attenuated by Molecular Line Absorption
Isolating the molecular line absorption effect on transmittance, this is expressed as:
where defines the frequency-dependent absorption coefficient and describes the path length. This assumes that the absorption coefficient remains constant for the entirety of the path length. For cases where is not constant along the path length, a more general expression of transmittance is defined as:
In which is the absorption cross section, N is the number density of absorbing molecules and this is integrated over a propagation range of length .
2.3. Atmospheric Scattering
In atmospheric scattering, there is no energy loss; there is a directional redistribution that causes the beam intensity to reduce over long ranges. The size of the scatterer aerosol decides the kind of scattering. Air molecules due to their size (larger than electron but smaller than ) lead to Rayleigh scattering; conversely, aerosols (comparable in size to ) scatter light based on Mie theory, as described in Table 4. In Figure 9, the distribution as result of scattering is shown. Furthermore, when the scatterers are relatively large (much larger than ), such as the water droplets found in fog, clouds, rain, or snow, the scattering process is more properly described by diffraction theory.

Table 4.
Relative size of scatterer determines the type of atmospheric scattering.
2.3.1. Aerosols
The interaction of the aerosols suspended in the medium (the atmosphere), with the incident laser radiation is dependent on the size, concentration, and composition of the particles. Aerosols are assumed to be spherical, homogeneous, and defined by their refractive index and radius [28]. A key assumption is the absorption and scattering of particles that are spherical. For the spherical particle assumption, Maxwell equations can be used to determine an analytical solution. For random shapes, the T-matrix method can be used to efficiently approximate and randomize for homogeneous particles based on an extended boundary condition method [29,35].
In the vertical profile, as shown in Figure 5, the aerosol content is concentrated near the surface in the boundary layer, between the surface and around 2-km altitude and is the factor of the meteorological conditions. For example, while water vapor represents a smaller component of the overall atmosphere, it is highly concentrated around the boundary layer. Above this altitude, the aerosol concentration exponentially decreases with increased altitude; as the density decreases, the aerosol content decreases.
Dust, haze, and smoke are examples of airborne aerosols which are particles suspended in the atmosphere. The size and density of these particles range from 0.3 to 4 µm with a higher percentage of clusters in urban areas. The aerosol particle size is similar in size to solar radiation wavelengths, inducing a strong interaction in this band. There is a greater variability in aerosol scattering, presenting difficulty in accurately modelling. The atmospheric composition of aerosols is shown in Table 5 and identifies the mixture of naturally occurring and man-made particulates in the troposphere.

Table 5.
Atmospheric aerosol emission sources and estimates. Adapted from [36,37], reproduced with permission.
Atmospheric aerosols can be broadly divided into three categories: marine-based aerosols, desert aerosols and stratospheric aerosols. The marine-based aerosols make up a larger proportion due to the oceanic surface coverage. These aerosols are composed mostly of sea salt, which is dominant, and aeroplankton, micro marine biological material swept into the atmosphere [38]. Volatile organic compounds from oceanic activity can also be introduced into the atmosphere, oxidize and result in secondary marine aerosols as shown in Figure 10, which significantly impacts propagation [39]. The lack of sufficiently accurate large-scale atmospheric models in marine and coastal regions ultimately causes uncertainty and degraded expected performance of laser-based systems such as LIDAR. Recently, researchers have continued to develop new adaptive atmospheric models that are able to accurately determine the aerosol extinction coefficients, the concentration of sea salt-based aerosols, and relative meteorological conditions such as wind and humidity [40].
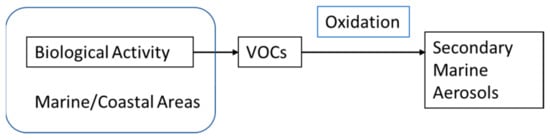
Figure 10.
Secondary marine aerosols as a result of biological activity, impacts atmospheric particle composition [39].
Dust from desert regions is the main source of land aerosols and the stratospheric aerosols are mainly sulfuric acid droplets because of volcanic activity and photochemical reactions in the lower stratosphere [25]. Using aerosol models, the optical characteristics of the particulates and the subsequent effect on propagation of the radiation can be estimated. These models can be generalized or environment specific, in terms of marine, desert, precipitation or stratospheric aerosols.
Boundary layer aerosol models include environment-specific models—marine, desert, fog, urban and rural—and rely on relative humidity and wind conditions to estimate the atmospheric propagative effects. The effect of high relative humidity results in particle size changes as water is absorbed, increasing the particle size, changing the makeup and refractive properties.
2.3.2. Rayleigh Scattering
Laser Rayleigh scattering has been extensively reviewed in the literature [41,42,43] and is a function of an induced electric dipole radiation mechanism. The resulting scattering of the small scattering cross-section is affected by the collective scattering of many molecules, the anisotropy of the molecules, and inelastic effects resulting from rotational and vibrational transitions [41]. These effects can cause depolarization and the scattering causes reflection of the molecular pressure, temperature, and energy states. Additionally, the small scale applicable for Rayleigh scattering makes it susceptible to background interference [44] and smaller particle density in comparison to molecules.
Due to the comparatively small size of the particles in the Rayleigh scattering range, these particles tend to have longer atmospheric lifetimes; i.e., once swept up or suspended in the atmosphere, the particles take more time to settle on the ground. Rayleigh scattering is a coherent process as compared to absorption, which is an incoherent process [29]. Rayleigh scattering is mostly considered linear, elastic scattering that is due to the displacement of bound electrons by the incident field. This refers to the molecule’s internal energy not being changed as a result [41]. This process is depicted in Figure 11. It is described as an incident harmonic field causes a dipole in the molecule, and the polarizability decides the displacement [28,29].
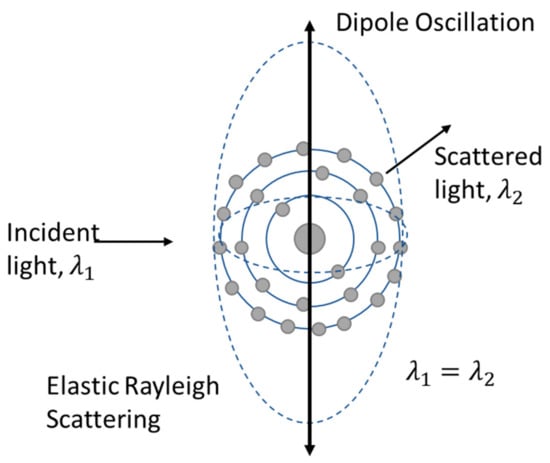
Figure 11.
Induced dipole in presence of applied harmonic field. Adapted from [45,46].
The induced dipole oscillates at the same frequency as the incident and emits electromagnetic radiation whose spatial distribution ❬S❭ is illustrated in Figure 12. This reradiated energy constitutes the scattered light.
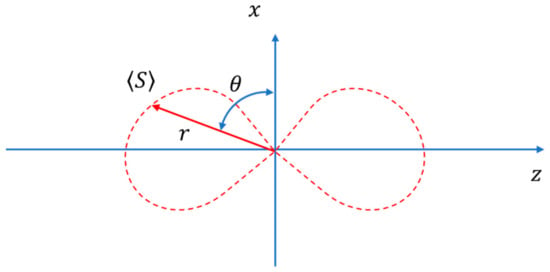
Figure 12.
Spatial distribution of radiated energy flux ❬S❭. Adapted from [28].
The scattering cross-section of a single dipole is given by [47]:
where is the natural frequency, is the electron charge, is the applied frequency, and is the damping coefficient. For the special case where the applied frequency is much lower than the natural frequency , and where the damping coefficient is small, Equation (7) becomes [47]:
To generalize this result, Equation (8) is then multiplied by the oscillator strength , to make the result more generic. The oscillator strength is defined as the effective number of electrons per molecule that oscillate at the natural frequency . The oscillator strength is limited by the quantity of electrons in the molecule. However, the inner electrons are considered too tightly bound to be included in this interaction. The incorporation of the oscillator strength into the final expression for the scattering cross section takes the form:
This is the Rayleigh scattering formula for the cross-section. For the visible and near-infrared region of the spectrum, Rayleigh scattering is often much larger than the molecular absorption. However, for wavelengths greater than 1 µm, Rayleigh scattering is replaced by Mie scattering, because of the dependence, which may be ignored.
2.3.3. Mie Scattering
The set of Rayleigh scattering equations assume that the laser beam wavelength is much longer than the radius, , of the molecule (i.e., ). This assumption means that the spatial variation of the electric field over the molecular charge distribution can be ignored. However, when considering scattering particles that are comparable in size to the laser beam wavelength, the assumptions made in the Rayleigh scattering derivation cannot be applied. Mie scattering specifically refers to the scattering because of aerosols in the atmosphere, and the subsequent propagative effects. As shown in Figure 13, the attenuation due to Mie scattering in the visible region surpasses the propagation due to Rayleigh scattering and molecular absorption, even though the aerosol particles resulting in Mie scattering are considerably smaller than molecules for Rayleigh scattering.
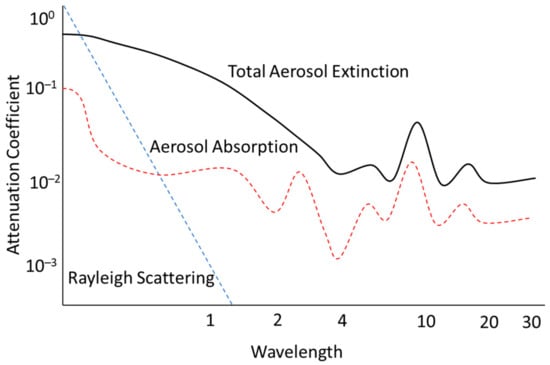
Figure 13.
Atmospheric scattering and absorption coefficients. Adapted from [28,47].
Mie scattering theory considers the shape, size, dielectric constant, and absorptivity of the particle. In Mie scattering, the properties of the scattering are identical for particles with the same product of the particle radius and propagation constant . The product along with the refractive index difference between the aerosol particle and the air determine all scattering characteristics.
The Mie attenuation coefficient is calculated based off the interaction described in Figure 14. In Figure 14, a monochromatic beam of light with a cross-sectional area and intensity is incident on an aerosol cell of volume containing an aerosol with identical spherical particles of radius a. This makes the total cross section of the particles, assuming no one particle shields another particle. Adding the effect of absorption to the scattering, the attenuation cross section per particle is increased by an attenuation factor, , the attenuation cross section, and . If no absorption occurs, the attenuation cross section is equal to the scattering cross section.
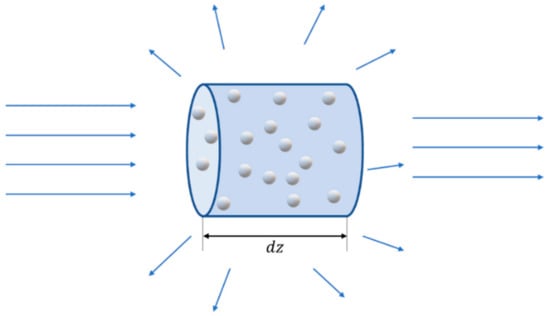
Figure 14.
Illustrative example of Mie scattering. Adapted from [28].
From this, the change in intensity of the laser beam as it propagates through, as shown in Figure 14, is determined by the attenuation coefficient for Mie scattering:
where is the density of the aerosols, and is the Mie scattering cross-section. In this process, energy is removed from the system due to scattering and absorption. This is considered in the attenuation factor, .
2.4. Nonlinear Propagation Effects
While linear propagation effects dominate the outcomes of laser performance in the atmosphere, its necessary to consider nonlinear effects such as thermal blooming, bleaching, kinetic cooling, and aerodynamic effects. Nonlinear effects mainly examine the thermal effects where the energy resulting from absorption and scattering cause localized temperature gradients, and unsteady localized atmospheric densities that ultimate create a lens effect that influences the refractive index properties. The change in refractive index changes the laser beams irradiance distribution, which again changes the refractive index, causing the nonlinear behavior.
2.4.1. Thermal Blooming
As the laser beam passes through the atmosphere, it heats the air along the beam path. Additionally, the absorption process of molecules and aerosols imparts thermal energy into the medium. The increased temperature and the absorption process create variation in the air density along the path that result in the refractive index decreasing [32]. Variation of the refractive index causes the beam to ‘bloom’ and propagate, reducing the beam’s irradiance. The irradiance profile of a laser beam propagating due to thermal blooming is observed in Figure 15. Thermal blooming is particularly relevant for high energy lasers and presents a limiting factor on the maximum power that can be transmitted [48]. For large-scale thermal blooming instabilities, it is appropriate to refer to the distortion and deflection of the whole beam path; however, recent studies have sought to explore the small-scale effects for lower-powered lasers [49].
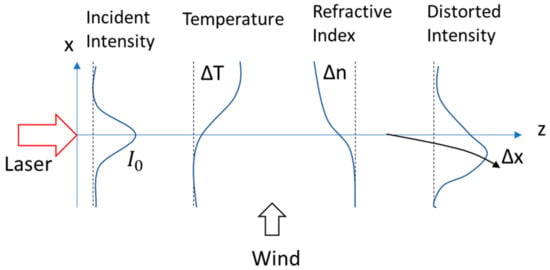
Figure 15.
Thermal blooming with a transverse wind. Adapted from [32].
Wind conditions have a significant impact on the propagation due thermal blooming. Considering high wind speeds, the air moving through the laser beam path is moved quickly through, resulting in less absorption, and thus less change to the density, and subsequently, the refractive index, and less observed propagation. For slower moving winds, the Gaussian profile of the beam shifts into a steady state profile, indicating the wind direction, where the peak irradiance is moved as a result [32].
Empirical models have been developed to show the difference between the bloomed and un-bloomed peak irradiance that consider the intensity distribution changes due to the wind. The ratio, , of the bloomed, , and unbloomed, , irradiance is given by [50]:
where:
In the above Equation (13), describes the thermal distortion parameter, which is a function of the wind velocity, the change in temperature, , density, , and specific heat, , for a collimated Gaussian beam with a radius, , power, , and range, .
2.4.2. Kinetic Cooling
As opposed to the thermal blooming effect, for certain circumstances, the laser energy briefly cools the atmosphere in the optical path. It is assumed that during the gas absorption process, the resulting energy is converted to heat instantaneously. However, there is a relaxation period, if sufficiently slow, which is particularly relevant for high-powered CO2 lasers, a temperature drop occurs [51]. As a result, the refractive index and gas density increase, focusing the laser.
2.4.3. Bleaching
Atmospheric transmittance can also be decreased by very short laser beam pulses (in the region of 1 to µs) that saturate the absorption process, a thermo-optical phenomenon known as bleaching. The absorption process being disrupted is the hydrodynamic mechanism; thermal effects result in the laser beam target expansion, causing a reduction in the absorption coefficient, , and a decrease in the density [52]. This nonlinear effect is applicable to low irradiance pulses that are strongly affected in pulse shape and energy; in contrast, high irradiance pulses are less effected, mostly around the leading edge, and the pulse energy is less attenuated [28]. The decrease in absorption coefficient is observed in Figure 16. Bleaching effects are dependent on the pulse duration, to overcome potential propagation due to bleaching, the pulse duration should satisfy , where is the time duration, is hydrodynamic time composed of , beam spot size and is the speed of sound.
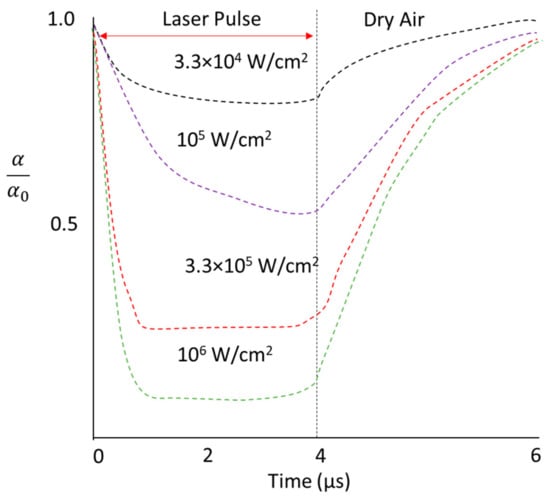
Figure 16.
Absorption coefficient saturated by short pulses [28,47].
2.4.4. Aerodynamic Effects
For airborne sensors, the propagation can be affected by the boundary layer (laminar or turbulent), and the inviscid flow as the compressible air is accelerated around the fuselage near the sensor. A window flush with the aircraft fuselage can largely negate these effects, except for high powered laser which may induce thermal propagative effects because of the window. In cases where the laser is mounted is more of a protuberance in the airflow, the boundary layer effects dictate the optical performance. Laminar boundary layers produce negligible effects, but turbulent flow behavior results in unsteady air density, resulting in refractive index flux and significant attenuation [26]. The optical wave-front variance because of aerodynamic turbulence is determined by the density flux, , the length along the optical axis, , and the length of the path through the turbulent field, as expressed in Equation (15). This is related by the Gladstone–Dale parameter, , which relates the change in refractive index to the change in atmospheric density [53],
For cases when the condition is not met, which can occur in the presence of shear layers, the effect is overestimated.
For inviscid flow, where Mach 0.3, the compressible effect of the air flow imparts a temperature increase, the density can be stable or unstable, and this distorts the optical performance. The variations in temperature and density due to increased compressible flow effects is related through well-known adiabatic processes.
2.5. Propagation through Haze, Fog and Rain
Laser beam attenuation is greatly affected by precipitation, in the atmosphere. As shown in Figure 17, the attenuation coefficients are greatly affected by fog, rain, and bulk water in the 0.6–15 µm wavelength range. Figure 17 shows the scale of attenuation because of fog compared to rain, which has a significant impact on laser performance.
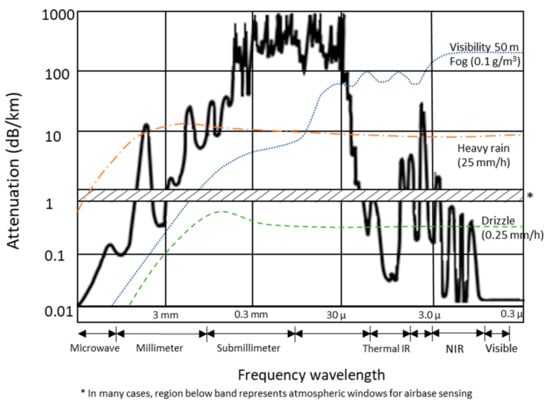
Figure 17.
Attenuation due to fog, rain, and drizzle. From [54], reproduced with permission.
The propagative effects are similarly aligned with scattering size factors associated with Mie scattering. Haze, composed of fine particles in the size region of 0.5 µm, increases in size during high humidity. Fog consists of water droplets with a radius greater than 0.5 µm. While Mie scattering attenuation depends on wavelength, for sufficiently large droplets where the radius is greater than 10 , the scattering becomes independent of wavelength. Transmittance along a 1800 m path through different rainfall rates is shown in Table 6.

Table 6.
Laser transmittance through rainfall [47].
Some computer models such as LOWTRAN give good approximations of the propagative effects of precipitation on transmittance, by using empirical methods to characterize the rain intensity, as shown in Table 7.

Table 7.
Rain intensity characterization [47].
Absorption is a factor that also needs to be considered and included into the scattering losses that the scattering coefficient, , the rainfall rate, , and the droplet radius, ,
2.6. Propagation through Atmospheric Turbulence
The distortive effect of atmospheric turbulence on laser propagation prohibits long-range FSO unless implementing adaptive optics to correct for it. To correct for the turbulence propagation, numerical modelling of different effects is implemented. Changes in temperature and convection result in atmospheric turbulence, through wind. The wind can have laminar or transition to turbulent flow. The laminar flow has uniform characteristics while turbulent flow has fluctuations of velocity and temperature, causing fluctuations of the density and refractive index [55]. The distortive effect on optical systems is substantial and necessitates accurate physical models of the propagation through turbulence. The turbulence results in unsteady, inconsistent atmospheric properties, a problem exacerbated over long path lengths. The atmosphere cannot be considered isotropic or homogeneous, as the turbulence causes the refractive index, and density to fluctuate. However, the physical models of atmospheric turbulence often assume that of homogeneous isotropic turbulence in the absence of a high-resolution model. The atmosphere can be approximated to be homogeneous and isotropic over limited time and space to a reasonable degree [56]. Non-homogeneous and anisotropic assumptions with velocity and temperature gradient profiles are challenging to implement in computer models, with the need to include multiple scales of mechanical and optical turbulence within a fine mesh [57]. Contemporary turbulence models are based on a statistical approach developed by Kolmogorov to resolve the uncertainty and random behaviors to better match the observed conditions [58]. Further improvement of this approach related the temperature changes more directly to the refractive index fluctuations as expressed by the refractive index structure coefficient . The Kolmogorov-based models can be thought of as ‘ideal’ atmospheric turbulence; however, there are cases of non-Kolmogorov statistics in atmospheric turbulence which also result in laser attenuation [59,60].
The Kolmogorov model assumes that turbulent flow is composed of large eddies which transfer their energy to smaller eddies. The larger eddies are characterized by an average outer size, which range from the lesser of 100 m or 0.2× height above ground [28,61]. From this wave number, , can be determined:
For values of , the turbulence is mainly influenced by the local terrain and wind conditions. For the smaller eddies, they are characterized by an inner scale , of range 0.1–1 cm. At this small scale, the turbulence is not capable of sustaining itself as the turbulent energy is converted to heat due to friction [58]. The wave number for this condition is:
The range between , and is called the subrange, where it is assumed by these models that the eddies are statistically homogeneous and isotropic. Additionally, the refractive index is assumed to be time-independent over very short time periods where the turbulence is ‘frozen’ and moved by the mean wind velocity into the optical path [62].
This provides the basis of contemporary approaches to optical turbulence modelling, which makes several simplifying assumptions of a complex and dynamic phenomena that is dependent on wind velocity, temperature, pressure, and humidity. This highlights the need to continue to improve these models to achieve higher accuracy in predicting laser atmospheric propagation.
2.6.1. Refractive Index Structure Coefficient
The effect of turbulence causes a change to the refractive index; these disturbances are reflected in the refractive index structure coefficient, , which is a function of a temperature structure parameter, , as expressed in Equation (19) from [47,63],
where is the pressure (mbar) and is the temperature at two points some distance, , apart. is determined by the difference in temperature between two points, related to a temperature variation power law along the path [64,65]. In Equation (20), and are the position vectors and is the magnitude. Typical value ranges for are shown in Table 8, although commonly expressed as in m−2/3 [66,67].

Table 8.
Typical refractive index structure coefficient values for turbulence adapted from [47].
Since the parameters that govern are generally themselves a function of altitude, the coefficient decreases with increased altitude. This is not always the case, as for a lot of sites, a turbulent layer at an altitude of around 12 km, there is a maximum value for [68,69]. This atmospheric fluctuations and difficulty in attempting to characterize the behavior; hence, a number of different approaches have been taken. The general expression for as a function of only height is:
In this case, particular models such Fried’s, Brookner’s, and Tatarski’s select values for , , and that best match experimental measurements, except Tatarski’s, which is theoretical. There is great disparity between all of the models, as shown in Figure 18. The model parameters are outlined in Table 7. Subsequently, the formulations based on Kolmogorov’s turbulence are collected in Table 9 and Table 10.

Table 9.
Refractive index structure coefficient model parameters.

Table 10.
Full equations for Fried’s, Brookner’s, and Tatarski’s methods.
The Hufnagel model combines two sets of parameters from Equation (21) and accounts for the average wind speed but is only valid in the altitude range of 3–24 km. Overall, Tatarski-based methods are most appropriately used for relatively low-altitude applications, while others are more suited for higher elevations. This disparity is highlighted in Figure 18. Despite the refractive index being a major factor in laser atmospheric propagation, there remain gaps in the ability to accurately model the effect of turbulence. The lack of reconciliation between the models emphasizes the discrepancy in application. For airborne sensors surveying at variable altitudes, the application of one model over another and transition between models are not well-resolved.
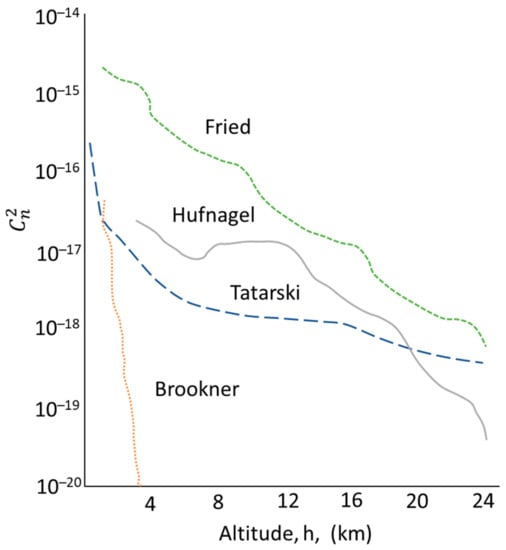

Figure 18.
Height-based refractive index structure coefficient: Fried’s, Brookner’s, Tatarski’s, and Hufnagel’s models [74].
The profile of can be accurately measured using thermosondes onboard sounding balloons, but this is largely impractical for most purposes. Table 11 shows some typical values of and how the coefficient is affected by height.

Table 11.
Refractive index structure coefficient as a function of height (typical values) adapted from [47,62].
Previous work on modeling includes Fried’s [70] estimates the coefficient using mean profiles, a methodology expanded on by Wyngaard [75] through application to the atmospheric surface layer and by Beland [76] for the stratosphere. Using a statistical approach resulted in good accuracy with observed data of the averages of the optical atmospheric turbulent effects but ultimately cannot capture the fluctuations that cause turbulent layer intensity [68]. This approach achieves high correlation with measured data; however, the causes of higher and lower correlation are unclear [77]. Factors such as the homogeneity of optical turbulence assumption and microclimate conditions that are difficult to include highlight the complexity and limitations of applying a statistical approach to the highly dynamic turbulent structure.
More recent developments to obtain are based on the work of Tatarski and the turbulence estimation theory [58]. This approach incorporates meteorological parameters with particular emphasis on the effect of the outer scale, , with altitude [78], wind shear [79], incorporating temperature gradients [80], and statistically driven profiles that are functions of altitude that aim to outperform numerical and Tatarski derived values for [81].
Dewan’s [82] model is a particularly popular Tatarski-based method because of its use of wind shear and temperature gradients in the vertical profile for applications such as ground-based telescope design and laser communication links. Dewan developed a statistical relation of the relationship modifying the Tatarski formula [79],
where relates to a linear wind shear function determined by the altitude [82],
Parameterization performed using this approach found that the linear function had inaccuracies across the lower troposphere, which resulted in the optical turbulence effects being underestimated [79].
Recent advances in the definition of optical turbulence characteristics are applied to adaptive optics to enhance image correction, particularly in telescopes where altitude variation impacts resolution. Considering the vertical profile and wind velocity profiles, these measurements change appreciably both in short and longer time intervals. The Fried’s radius of the rugged wavefront explored has the key characteristic which is estimated based on the S-DIMM+ method. The S-DIMM+ method is an example of the developing methods for estimating altitudes of atmospheric layers with strong turbulence. This relies on the cross-correlation of displacement in sub-images and vertical distribution of the refractive index fluctuations [83]. Using a Shack–Hartmann sensor, [83] demonstrated the S-DIMM+ by examining the spatial cross-correlation functions of the jitter from images taken from the large vacuum solar telescope. Scintillation detection and ranging (SCIDAR) [84] and slope detection and ranging (SLODAR) are other examples of emerging techniques being used to produce high-resolution optical turbulent characteristics for telescopic applications. Weather research and forecasting (WRF) models are increasingly being implemented in atmospheric performance prediction and are able to estimate to a high degree of accuracy at different altitudes, as highlighted in the literature [85,86] in comparison to sounding data.
2.6.2. Turbulence Effects
A laser beam encountering turbulence in the atmosphere along the optical path experiences degradation of performance as result of three phenomena: beam spreading, scintillation, and beam wander. Scintillation and spreading can be attributed to short pulse lengths and wander for long exposure times [87]. Beam spreading is a result of diffraction while scintillation is a prominent area of research involving refractive index fluctuations due to thermal effects. For scintillation, along long paths different parts of the path act as weak lenses that deflect the path for a timescale that is affected by wind [88].
Using the atmospheric turbulence characteristics described above, the laser beam performance can be assessed. As depicted in Figure 19, the laser characteristics of interest are the operating wavelength, , the focal length, including the use of a beam expander, , and the transmitting beam diameter, . The turbulent characteristics, as described before, include the refractive index structure coefficient, , and the inner, , and outer, , scales of the turbulent eddies.
Figure 19.
Laser beam performance characteristic through atmospheric turbulence [28,47].
For laser beams encountering large-scale turbulent cells along the optical path, where the scale size is greater than the beam diameter, this causes beam wander. This occurs when the turbulent cells cause a weak lens effect distorting the beam path in a random way, but the beam diameter remains the same, as shown in Figure 20. For applications where the laser beam must remain on a target for extended periods of time, this problem must be overcome for high accuracy. The work of Chiba [89] serves as the basis of beam wander formulations by considering a collimated beam, which was further expanded on through the use of the Huygens–Fresnel approach accounting for Gaussian beams and focused beam propagation [90]. The work of Tofsted used numerical methods to find that the refractive index size had the most significant impact on beam wander [91].
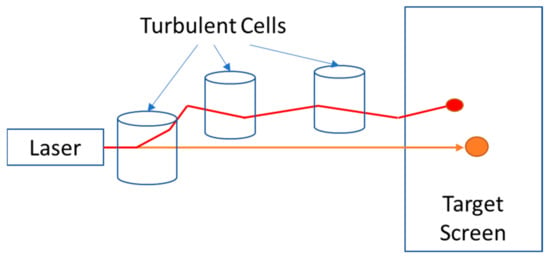
Figure 20.
Beam wander as a result of laser beam deflection by turbulent cells greater than the beam diameter. Adapted from [47].
The radial variance from the target is expressed as [89]:
where is the distance to the target, is the refractive index structure coefficient, and is the beam size at the point of transmission. Alternatively, [47] expresses the beam wander as a function of wavelength, . This demonstrates an independent relationship with wavelength.
Alternatively, when the beam encounters turbulent cells smaller than the beam diameter, scintillation occurs, wherein the laser beam’s intensity is distorted, as shown in Figure 21.
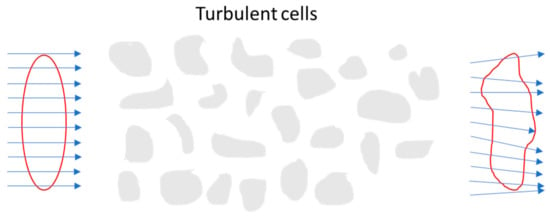
Figure 21.
Beam intensity profile is distorted by turbulent cells smaller than the beam diameter. Adapted from [47].
As a result of the scintillation, diffraction occurs, causing deflection of the laser beam intensity, which can be modelled by a log normal distribution for small fluctuations and a gamma–gamma model for medium to strong turbulence [87,92].
Turbulence will also cause the beam to spread in excess of the prediction for diffraction [87]. Diffraction of the beam diameter for a circular aperture with diameter, , is a function of the focal length, , and wavelength, [93],
In practice, the turbulent cells causing increased beam spreading has been observed experimentally [94]. Different mathematical models have been developed to predict the beam diameter due to turbulence-induced spreading [95,96,97]. These models rely on the assumptions of homogeneous turbulence and the scale of the turbulent cells, but some consider that the spread results from non-Kolmogorov turbulence [96].
2.6.3. Astronomical Refraction
For very large path lengths, the laser beam propagative path bends, dependent on the height, ; this is relevant for satellite communication links using FSO. The resulting bend arc radius, , is expressed as a function of the refractive index, ,
The beam deflection, , along the path length, , reliant on the changes in the atmospheric refractive index, is further derived based on the refractive index relationship with altitude-dependent atmospheric parameters, temperature, , and pressure, [47]:
For long optical paths, the bending is a slow phenomenon [93], and for normal atmospheric conditions, the beam will tend to bend downwards.
3. Combined and Empirical Propagation Models
For most practical applications, it is necessary to adopt a comprehensive propagation model, capturing many different linear and nonlinear effects simultaneously. In some instances, the limited knowledge of local thermodynamic conditions makes the use of empirical propagation models more opportune. This section presents theoretical and empirical formulations which allow to merge the previously introduced models in a more comprehensive manner.
Assuming a Gaussian profile, the atmospheric propagation effects can be combined into a general equation for the peak irradiance, taking into account scattering, absorption, atmospheric turbulence, jitter, thermal blooming, and diffraction effects [50]:
For Equation (34), is the path length, is the wavelength, is the transmitted power, is the effect of thermal blooming, and is the transmittance coefficient (absorption and scattering). Diffraction, , jitter, , and turbulence, , for a beam can be determined by the following relationships:
where is the beam radius for a beam, and is a beam quality factor.
where is the variance of angle jitter along a single axis, which is assumed to be equal to .
where is a refractive index structure constant.
3.1. Laser Range Equation
For lasers, the range performance can be estimated by [98]:
This shows the relationship between the received power, , with the transmitted power, , the antenna gain, , the target cross-section, , the aperture diameter, , and the atmospheric and system transmission factors, and . The antenna gain can be expressed as a function of the transmitter beamwidth, , and is applicable for only far-field applications (larger than ),
where is a function of an illumination constant, , and wavelength, :
Substituting in Equation (38), the performance of laser in the far-field can be determined by:
3.2. Signal to Noise Ratio
The receiver not only receives the transmitted beam but also receives contributions from cloud reflection, sunlight etc. These signals interfere with the interpretation of the received signal, which remains the basis for atmospheric extinction measurement. As described in Figure 22, the signal at the receiver is composed of two components, power from the source, , and the power of the signal due to optical background, .

Figure 22.
Receiver system for lasers. Adapted from [28].
The background signal is filtered out through the signal to noise ratio (SNR). The general expression for a laser system is described in Equation (42) [99],
In this instance, describes the mean square; signal current (subscript SIG), shot noise current (subscript SN), thermal noise current (subscript TH), background noise current (subscript BK), dark noise current (subscript DK), and local oscillator noise current (subscript LO). The SNR at the receiver is dependent on whether it is coherent (in phase) or incoherent (out of phase). Coherent receivers are typically immune to background noise since the receiver is only receiving in phase signals originating from the laser source.
3.3. Laser Beam Transmittance along a Slant Path
Propagation along a slant path is described in Figure 23, and expressed using the more general expression in Equation (43), and considering a slant path laser beam propagation, the transmittance because of molecular line absorption is given by:
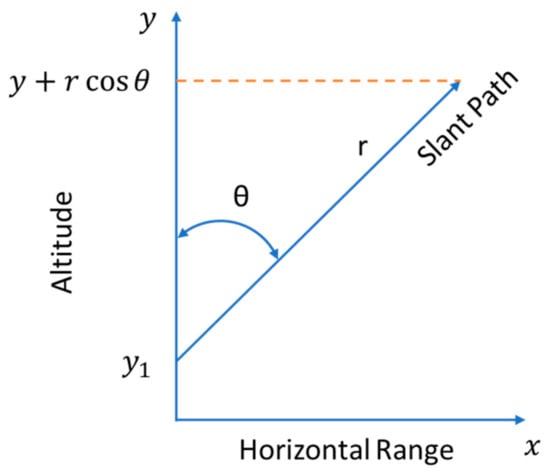
Figure 23.
Geometry of a laser beam propagation along a slant path adapted from [28].
The integrand in Equation (43), , can be expressed in terms of the altitude, , atmospheric pressure, , and the fractional concentration, , based on the ideal gas law,
Assuming for an isothermal atmosphere and air as an ideal gas, the atmospheric pressure is a function of altitude:
where and is called the scale height, which the pressure in an isothermal atmosphere of constant composition reduces by a factor of . Subsequently, is the average molecular mass and is gravity. The assumptions made in Equation (44) exclude ozone and water vapor concentrations as they are more related to altitude and relative humidity, respectively.
Assuming the absorption cross section, can be described as a Lorentz line shape consisting of line width , then:
This assumption proposes that the dominant line-broadening mechanism is caused by collisions. In Equation (46), the subscript 0 refers to a reference altitude. In the atmosphere, there occurs more collisions of the absorbing molecules with N2 and O2, resulting in the broadening pressure in Equation (46), being simplified as the total atmospheric pressure at a certain altitude. The absorption cross section is then expressed as a function of frequency and altitude,
and is the line intensity (or strength):
At laser frequency , the total molecular absorption coefficient is the sum of each molecular species present and the various allowed transitions that contribute to the total absorption coefficient:
In Equation (49), the subscript refers to the line of the molecular species with the number density .
The width of the laser is very narrow, which necessitates the need for correspondingly high-resolution spectral absorption lines. Some of the available data have quite wide ranges that are less applicable to laser beam absorption. Higher resolution spectral data is increasingly available through transmission codes (e.g., HITRAN, etc.) which is shown in Figure 8. Regarding the accuracy of these databases, the underlying assumptions ultimately determine the accuracy of the performance models.
Due to the need for high-resolution data, it is sometimes desirable to calculate the atmospheric absorption coefficient. Combining Equations (43) and (49), the atmospheric transmittance at the frequency is given by:
An exact solution for Equation (50) is not feasible and, as a result, models sometimes make broad assumptions about the atmospheric conditions to simplify the absorption coefficient. Several different models have compiled numerous known molecular absorption lines that allow for a theoretical solution of the absorption coefficient; however, these models have some limitations. Slant path modelling is highly relevant for airborne applications, with the variation of altitude over long ranges, impacting performance in ways that are not well-captured or easily determined by the above derivation.
3.4. Particle Retrieval
Using LIDAR systems, measurements of the atmospheric transmission parameters discussed above, at different wavelengths is used to retrieve the atmospheric constituents. These systems operate through processing amplitude, frequency, and polarization analysis, which is then converted to the desired atmosphere component. Inversion LIDAR algorithms are typically utilized to solve for the atmospheric data. As suggested in [28], NIR wavelengths measured use passive NIR imaging processes, from which particle concentrations can be determined by LIDAR inversion algorithms. In this case, a priori information about the transmitter including the Gaussian profile, geometry, and polarization state as well as the spectral reflectance of the target is needed for particle retrieval. Current inversion LIDAR algorithms aim to reduce the amount the prior information, especially for airborne systems, to create greater flexibility for the system and to remove the need for complimentary sensors. Inversion algorithms are difficult to evolve because the optical data (input) are inherently related to the microphysical variables through non-linear integral equations such as the Fredholm equations, shown in Equation (51), that are not able to be resolved analytically. For atmospheric retrieval, the Fredholm equation is expressed as:
where and are the optical data in terms of absorption and scattering, and is the kernel function for the atmosphere. This is inclusive of the particle size and refractive index, and is the distribution of these particles. The solution for Equation (51) is an inverse problem. The solutions are inherently characterized by uncertainty in the input data, and incompleteness of the solution space that is not accurate to real-world conditions. Solving the equation relies on prior knowledge independent of the measurements. Using a probabilistic Bayesian approach, the state vector of known prior information, with as the measurement vector (with radiances) and the concentration of a particular molecule or aerosol, as the transfer function, as the external factors and is the measurement noise, then the general remote sensing equation is:
Vector can include reflective measurement features such as BRDF and temperature as well as atmospheric properties including vertical profile data, turbulence, clouds, and water vapor, and the characteristics of the measurement equipment. The inverse problem relates to retrieving , which is an estimated value of from Equation (52). Similarly, is the estimated value of non-retrieved variables, ,
where, R is the radiative transfer function. The radiative transfer function is the cornerstone of many atmospheric simulation models and is discussed in further depth in Section 4. The prior knowledge needed by the system can be characterized by a state vector and covariance matrix , which is typically included in simulation models [100]. For most retrieval algorithms, Mie theory is predominant for the aerosols, but a trend towards more randomly distributed non-spherical particles is being developed to better represent physical conditions. The inverse problem then becomes:
Inversion techniques are continually being developed; of these, inversion with regularization is popular as it reduces the oscillations that are generally problematic for remote sensing applications [101]. This is achieved by constraining the problem, by smoothing the particle size distribution and using kernel functions to obtain the average particle radius, refractive index, and concentrations. The inversion algorithm is described in Figure 24.
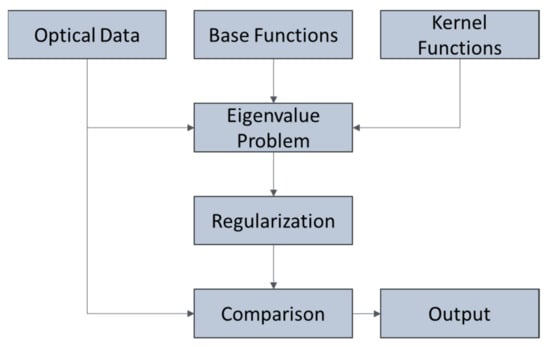
Figure 24.
Regularization approach to the inverse problem from [28].
3.5. Elder–Strong–Langer Model for Absorption
Since there is much uncertainty about the atmospheric properties, and there is limited ability to determine the exact nature of the conditions, it becomes necessary to examine empirical models for atmospheric modelling. The case for atmospheric radiative transfer codes is undermined by a lack of comprehensive coverage and representation of the realistic atmospheric conditions and subsequent propagative effects. Empirical modelling is better able to support the uncertainty propagation and statistical analysis, which is an integral aspect of the propagative effects. These effects, as previously demonstrated, are underpinned by statistical analysis, and fitting-based models that are subjective to field measurement instruments and techniques (highlighted below). The advantage of the empirical models is that they are more explainable, and can be used to design and size instrumentation, and parametric/sensitivity studies can be performed to better understand the comparative attenuation effects. The comprehensive and flexible nature of empirical models contrasts with radiative transfer codes and their limited view on the atmospheric conditions. One such empirical model, the Elder–Strong–Langer (ESL) approach was proposed as an appropriate methodology to estimate the absorption coefficient that has seen widespread use in the defense sector. Elder and Strong developed an approximate value for the coefficient [5]. This was later modified by Langer, who incorporated humidity. The advantage of this approach is that it relates the transmission window to the relative humidity, which is easy to measure. The ESL model assumes that fluctuations in the transmission are directly related to the humidity, as the water content changes the absorption and increases the size of the particles and droplets in the atmosphere, which influences the scattering component. This assumption considers the other atmospheric constituents as uniform in each atmospheric window, with the greatest variation being the water content. The ESL model considers the water content in the beam path to be measured as the precipitable water in millimeters, , condensed, which can be determined by:
where is the density (humidity component), is the path length, and is the total precipitable water.
The relationship between the density of the water vapor and the relative humidity () (and temperature can be determined based on Middleton’s contribution to ESL, which is useful in implementation in computer models [6],
Langer developed two empirical formulas, based on Elder and Strong’s work to calculate the absorption transmittance, , applicable to each transmission window and precipitable water content [28],
For each of the , transmission windows, the constants, , , , and are compiled in Table 12.

Table 12.
Constant values used in Equations (58) and (59) adapted from [28].
This approach is valid for horizontal path lengths near sea level, for wavelengths within the transmission windows. The total transmittance must also consider the propagative effects of scattering, .
3.6. Elder–Strong–Langer Model for Scattering
It is difficult to quantify an analytical relationship of the scattering effect on transmittance that is accurate over a wide range of conditions, as demonstrated by [25]. An empirical approach is typical used to determine the scattering coefficient:
where , and are constants based on the concentration and size of the aerosol distribution. The second term in the equation, , is associated with Rayleigh scattering, and its effects become negligible for wavelengths greater than 0.3 µm. is a typical value that has been used to produce good results for particle-sized aerosol applications [47].
To relate the constants, , and to atmospheric properties, the subjective property of visibility is used, as demonstrated by [102]. This exploits the relative contrast, , between the apparent radiance of the source, , and in the background, , at some distance, , away,
For a wavelength value of µm (where the absorption factor becomes insignificant), the distance ratio between them is the visual range,
where is the visual range, as opposed the standard observer visibility, , which is defined as the distance at which the naked eye can identify objects. Observer visibility is very subjective, based on the observer, but visibility itself is a function of the scattering properties of the aerosols suspended in the atmosphere. In some cases, can be used to estimate the meteorological range, [6],
Furthermore, the assumption that the radiance at the source is significantly greater than for the background can be made, and that the background radiance is constant. This results in and for , which, based on Equation (62), makes the follow derivation:
From this derivation, the contribution to scattering transmittance in the middle of the atmospheric transmission window is determined as:
3.7. Combined ESLM Model
The principal equations for transmittance propagation through the atmosphere across a number of conditions are summarized below in Table 13 [28]. This provides a comprehensive determination of the horizontal laser propagation under a variety of conditions at sea level. This combined ESLM model provides a more accurate representation of the atmospheric transmittance in comparison to the simulation models, which have significant limitations and make assumptions that lessen the accuracy of the model.

Table 13.
Transmittance equations for collocated transmitter and receiver [28].
3.8. Radiometric Measurements of Atmosphere Extinction
Radiometric techniques are used to measure the optical intensity distribution. Typically, absorption and scattering as the dominant features of attenuation are combined in this measurement process but can be separated. Techniques as illustrated in the literature [103] determine the scattering-based attenuation as a result of the detection of the diverging radiation from the direct transmission. Photodetectors are the prevalent method for capturing the radiation power. Photodetectors vary based on the primary effect measure. Thermal detectors measure the increase in temperature as a result of absorbed radiation, while quantum detectors consider photoemissive, photovoltaic, and photoconductive effects. These photodetectors are arranged to emphasize the spectral responsivity, the difference between the input and the output. The physical photodetectors input radiant power or spectral photon flux, which is then converted into a voltage or current signal. It is important to note that the photodetectors introduce uncertainty propagation, where the responsivity of the system is subject to bias effects, temperature effects, nonlinearity, fatigue, polarization effects, magnetic effect, and nonuniformity [104].
The empirical models and theoretical background of the propagative effects, as discussed above, are affected by the measurement techniques and instruments used. These techniques, instrumentation, and calibration all contribute to an uncertainty propagation. These measurements are fundamental to the development of the fitting-based models regarding turbulence and linear/non-linear effects. In radiometry, to measure the optical flux and energy, a comparison is made between the power received directly at a physical detector to the known transmission and reflectance properties of the laser and target. To achieve high-accuracy measurements in determining the transmittance attenuation of the laser beam, a few methods are suggested following the work of Sabatini [28]. These methodologies rely on knowing the reflective and geometric characteristics of the target, and then measuring the intensity and spatial distribution of the laser energy. The surface characteristics of the target are measured by infrared cameras and detectors through radiance. The first extinction measurement technique (EMT) uses DEA detectors to determine the laser energy directly at a known location and target. A NIR non-calibrated camera is used to capture and process the intensity profile, from which extinction can be calculated. This methodology is highlighted in Figure 25, wherein, from a focused image, direct energy measurements are determined, forming an intensity matrix that leads to an extinction profile.
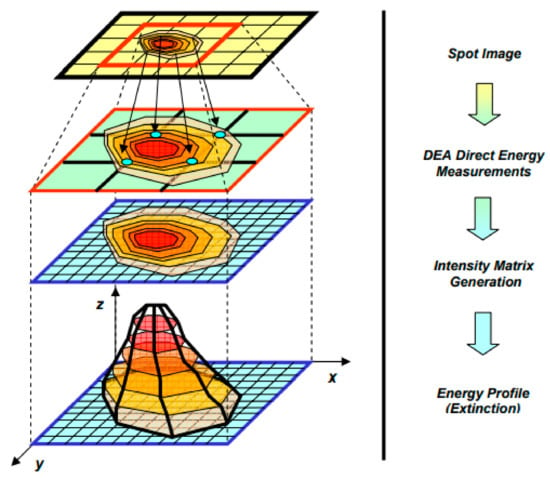
Figure 25.
Extinction measurement using laser spot energy to determine the intensity as a result of extinction [13].
The first techniques used a non-calibrated NIR camera; using a calibrated NIR camera allows for a more direct conversion between pixel intensity and atmospheric extinction. Previous work by Sabatini introduces the ESLM empirical model to differentiate between the propagative effects of scattering and absorption using this methodology. The third methodology, as outlined in Figure 26, involves a laser pulsed at an initial target with known surface characteristics (i.e., spectral reflectance, BDRF) at a known distance away. Secondly, the laser is aimed at a second target, further away, with the same surface characteristics but at a different laser power output.
Figure 26.
Laser transmission measurement technique [28].
From this, the extinction coefficient can be obtained by the difference in the two measurements. Where is the voltage, is the power, and is the distances for the measurements,
Measurements using pulsed laser energy from airborne platforms directly to the target can be used to calibrate instruments. In this example, the reflective characteristics are also known, and then using NIR cameras, the image is processed through software that includes target reflectance data and geometric inputs to calculate the radiance. Using this methodology, two energy measurement techniques were developed [28] for calibrated and non-calibrated cameras.
Finally, a bistatic approach is also proposed. A bistatic LIDAR system uses a transmitter and receiver that are not collocated. This is beneficial for less weight on airborne systems, and the light undergoes less propagation. Using a differential absorption LIDAR scheme, a laser is pulsed at an ‘on’ absorption wavelength, intended to coincide with the molecular absorption of a particular molecule, and then pulsed at an ‘off’ absorption wavelength that does not coincide with a particular molecular absorption band. Using the difference between the two measurements, some of the propagative effects can be ignored, and the difference between the two laser pulses is an indication of molecular absorption alone. Equation (77) shows the relationship between the ‘on’ and ‘off’ absorption received power, and using this difference, the molecular absorption of carbon dioxide can be equated based on the laser energy,
3.9. Application of Machine Learning in Laser Propagation
Machine learning (ML) has emerged in the area of LIDAR beam propagation in the atmosphere. Similar to other applications, ML is introduced to improve the performance of a laser beam, and at the same time obtain a better understanding about the atmosphere in terms of particles, gases, and aerosols. For example, Zeng et al. [105] introduced a method that combines joint retrieval method and Gaussian process machine learning (GPML) in order to retrieve the extinction coefficient of horizontal aerosol. This work shows that the Fernald method is not efficient for far range operation; hence, it offers low SNR. Therefore, this study particularly considers ensemble Kalman filter for noise reduction during the data assimilation from LIDAR and substantiates its efficiency through applying their designed LIDAR that has a large range of propagation of 3.3 km. In addition, Farhani et al. [106] proposed both the supervised (i.e., gradient boosting tree, support vector machine (SVM), random forest, and decision tree) and unsupervised (t-distributed stochastic neighbor embedding method (t-SNE) and density-based spatial clustering) ML algorithms to identify the noise and anomalies (e.g., smoke) and measure the particle extinction profiles from the collected data by Rayleigh–Raman LIDAR. In this work, supervised ML approaches, particularly random forest and gradient booting tree, show their efficacy in rigorously separating high background counts from low laser power and distorted shape with high background counts. Moreover, t-SNE can successfully depict clusters of clouds, high backgrounds, and anomalies such as the smoke of a wildfire on the night atmosphere. Interestingly, t-SNE defines bad profiles as small groups; hence, it distinguishes high background counts as a smaller group that is finally labelled as noise; this is how t-SNE helps to increase SNR. Yorks et al. [107] also worked in improving SNR of backscatter LIDARs in daytime and discriminating cloud and aerosol. In order to proceed with that, this study considers an ML approach, convolutional neural network (CNN), as it is a time-efficient and widely used approach. This work adopts four denoising techniques—principal component analysis, wavelet denoising, Butterworth filtering and Gaussian filtering—and finds that wavelet denoising surpasses others in improving the SNR of the LIDAR data. Hence, it is considered as the default denoise technique of SNR for the LIDAR that is further compared with CNN. Surprisingly, CNN shows an improvement of 75% of the default denoising technique; meanwhile, shows its strength in detecting aerosol and timeous cloud parts while the default operational algorithm shows poor performance in detecting the aerosol and even cannot detect the cloud at the microscopic level that the system with CNN is able to. In addition, the existing operational algorithm augmented with the CNN technique enhances its performance by 40% more in detecting atmospheric features at a horizontal resolution of 5 km during the daytime, while the earlier system requires a resolution of 60 km to achieve the same. However, detecting wrong layers of atmospheric particles, particularly during nighttime, is an undeniable fact of the CNN-augmented approach; hence, Yorks et al. strongly suggest considering a larger dataset to train the model, which may help to overcome the shortcoming.
Another approach of improving the performance of laser beam in atmospheric propagation is considering sensor fusion where a laser beam is fused with other sensor data with the help of an ML algorithm. Jiang et al. [108] propose a data fusion approach where the satellite sensing data (i.e., RADAR) is fused with LIDAR data to monitor and predict the spatial and temporal ozone concentration that is performed by an RNN–CNN approach. This study compares the performance of a recurrent neural network (RNN), CNN and RNN–CNN separately for fusing data from RADAR and LIDAR and able to substantiate the efficacy of RNN–CNN over individual RNN and CNN, where their performances are evaluated by evaluation indicators such as RMSE, MAE, and IOA. Here, LIDAR data is considered as the standard to verify the prediction of the models.
In order to improve the laser propagation in atmospheric turbulence, Sanchez [109] proposed an artificial neural network (ANN) algorithm with the structure constant of the refractive index that fundamentally depends on temperature structure constant . This study derives the temperature structure constant using the temperature profile [73] at different velocities and designs the prediction model using ANN to explain laser beam propagation. Hence, this study shows that using an ANN approach in the presence of atmospheric turbulence makes the laser propagation estimation easier and more time-efficient.
Table 14 offers an overview of applied ML algorithms in atmospheric laser beam propagation and their contributions.

Table 14.
Overview of the contributions of ML algorithms to atmospheric beam propagation.
4. Atmospheric Radiative Transfer Models
Atmospheric radiative transfer models, codes, and simulators have been developed and continually improved for the use of determining the atmospheric propagation conditions and ultimately the performance of the optical transmission in a set of comprehensive conditions. Atmospheric propagation necessarily involves many parameters requiring complex numerical calculations. The accuracy and underlining assumption of these calculations predict and determine the degree of accuracy of the transmittance through the atmosphere based on a predetermined path, the atmospheric conditions, the wavelength, and a combination of predicted and measured meteorological variables. The transmission models or computer codes generate the transmittance, or a transmittance spectrum based on these inputs.
Considered as the most accurate measure for deriving atmospheric absorptions are the ‘line-by-line’ and ‘layer-by-layer’ methodologies that sum the absorption coefficients of all lines in the spectrum for an absorbing gas and including the continuum absorption as seen in Figure 27. This method is prohibitive in computation time to achieve high resolution results across larger spectral distances. To achieve higher-resolution results faster, a number of approaches have been taken.
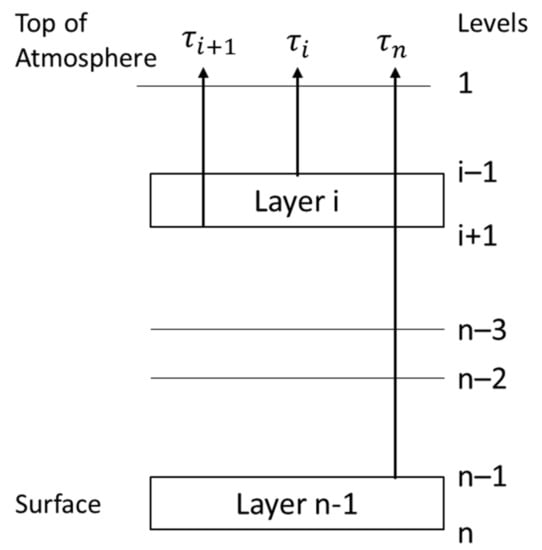
Figure 27.
Line-by-line approach of atmospheric models for radiative transfer, considering atmospheric layers from the top of the atmosphere. Adapted from [110].
The radiative transmission models use the radiative transfer equation as described below using the differential of the specific intensity, [111],
The parameters included in the above Equation (78) include the absorption coefficient, , and the Plank function, , along path, . This expression is valid for monochromatic applications, as is the case for the lasers. The process to solve Equation (78), as outlined in [111], is to 1) determine the absorption coefficients, 2) integrate the radiative transfer function and then 3) determine the Jacobians. The line-by-line method is determined based on the line strength and shape profile of the absorbing molecular species along the spectra. The absorptive properties and species are determined from spectroscopic databases such as HITRAN, JPL, or GEISA (see ref. Section 2). From this path, propagation can be calculated and incorporated into solving the radiative transfer equation.
To achieve higher-resolution results faster, several approaches have been taken. Physical line-by-line models such as the atmospheric radiative transfer simulator (ARTS) integrate the radiative transfer equation (RTE) across a set of wavelengths as opposed to band transmission models such as RTTOV, which applies the RTE across channel average transmissions. Both approaches optical depth and absorption is dependent on atmospheric conditions: pressure, temperature, and gas concentrations. Particulates and clouds induce scattering, a complex modelling problem to account for. The underlying assumptions made in each model influence differ and result in solutions that are difficult to validate and are computationally expensive to estimate the optical performance.
For many applications, atmospheric data can be largely unknown, or unrepresented in the training data. Physical models such as ARTS are better in this respect, as the model is less reliant on the viewing angle and the parameterization of models such as RTTOV lead to large errors where the precalculated coefficients are not representative of the atmospheric conditions [112]. To speed up the ‘line-by-line’ method, some tools use parameterization, but in the process, these models lose information relating to the absorbing gases [113]. The Automated Atmospheric Absorption Atlas (4A/OP) approach avoids this by calculating the monochromatic optical depths, so a large database of the ‘layer-by-layer’ method, an absorption look-up table, is stored by 4A, which allows for quick cross-referencing still using the ‘line-by-line’ method [114]. These tables can then be interpolated to extract the solution based on the atmospheric pressure, temperature, wavelength, and humidity stored values. The parameterization process of the atmospheric radiative transfer codes is outlined in Figure 28.
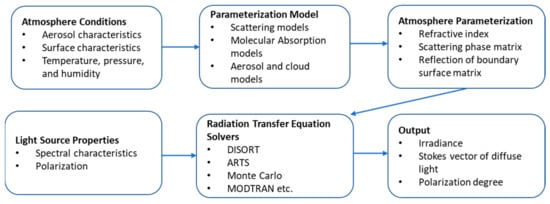
Figure 28.
Simulation process of the radiative transfer model. Adapted from [115], reproduced with permission.
Current atmospheric radiative transfer models can be distinguished by the primary methodology, i.e., line-by-line or band transmission, the wavelength spectrum under observation and whether the model considers scattering and polarization effects. In practical applications, fast atmospheric transfer models are needed that are less dependent on atmospheric conditions, where there may be limited knowledge. The current models have limited applications and make broad assumptions that lower accuracy for speed and simplicity.
4.1. 4A/OP
Developed by CNES, LMD/CNRS, and NOVELTIS, the Automated Atmospheric Absorption Atlas (4A/OP) radiative transmission software is a fast line-by-line method optimized to perform simulations in IR band across different climates and elevation angles [116]. 4A/OP accounts for a wide range of atmospheric conditions, including: the absorbing gas mixing ratios, temperature scattering, polarization, and zenith angle based on the monochromatic transmittances of individual layers of a stratified atmosphere across a number of atmospheric conditions that allows for wide application and flexibility [113,117]. Initially developed in 1981, 4A was applied to satellite observations including radiometric measurements, infrared images, and interferometric measurements. At the time of implementation, the method offered faster computation times, higher flexibility, and sufficient accuracy while accounting for atmospheric inhomogeneities and instrumental functions, as compared to the line-by-line methodology [113]. The 4A dataset can then be used to predict the atmospheric transmittance for any condition assuming that the pressure and stratification are matched in the 4A dataset. To derive the transmittance, the tool multiplies the individual monochromatic layer transmittances between the surface and the sensor and a correcting factor applied for the mixing ration and zenith angle [117]. To speed up the ‘line-by-line’ method, some tools use parameterization, but in the process lose information relating to the absorbing gases [113]. The 4A approach avoids this by calculating the monochromatic optical depths, so a large database of the ‘layer-by-layer’ method is stored by 4A, which allows for quick cross-referencing, still using the ‘line-by-line’ method [114].
4.2. ARTS
The atmospheric radiative transfer simulator (ARTS) is a popular physics-based model that uses a line-by-line absorption methodology to calculate the transfer in the thermal IR to microwave spectral regions. The model incorporates scattering and polarization, with support for a range of meteorological conditions. The model considers a wide variety of precipitation and aerosol sizes for the scattering modelling. ARTS additionally accounts for continuum absorption for water vapor, oxygen, nitrogen, and carbon dioxide. The ARTS model uses an analytical approach in calculating the derivatives of the molecular concentrations and a semi-empirical approach for other parameters as a way to speed up processing [118]. In the model, Stokes equations provide the basis for the polarization determination, the model can represent the atmosphere in 1D, 2D, or 3D view, taking into account the curvature of the Earth geoid, and the scattering components are solved using tow algorithms, one based on Monte Carlo, and the other on a discrete ordinate iterative method [119]. This allows the randomization of assumed spherically shaped particles in the atmosphere model.
4.3. LIDORT/VLIDORT
Vector linearized discrete ordinate radiative transfer (LIDORT) is based on the DISORT algorithm, with a focus on multiple scattering models for better calculations of the radiance, the Jacobians (partially derived radiance) in conditions that considered more atmospheric and surface properties [120]. Jacobians are an important measure, often used to compare different methods and determine the accuracy of the model.
4.4. 6S/6SV1
6S (Second Simulation of a Satellite Signal in the Solar Spectrum, Vector, version 1) aims to solve the radiative transfer equations for airborne sensors operating in the visible to NIR, focusing on the solar radiation reflection from a target to the sensor [121]. Recently, 6S has been used to interpret satellite imagery to help characterize surface parameters taking into account atmospheric and vegetation effects [122] and correct Landsat imagery [123]. 6S takes into account downward-looking observations allowing for target elevation (through bidirectional reflectance distribution function), the surface conditions, and a variety of absorbing molecules. It relies on successive order of scattering algorithm to approximate the Rayleigh and aerosol attenuation effects, but when this is decoupled, the accuracy of the model reduces significantly around strong absorption bands [124].
4.5. MODTRAN
MODTRAN codes are extensively used for light propagation predictions; it features the line-by-line process coupled with scattering codes with customizable aerosols that allow for high-resolution radiative transfer calculations [125]. Recent modifications of the MODTRAN codes now includes a line-by-line algorithm for high-resolution RT calculations as well as coupling to optical scattering codes for easy implementation of custom aerosols and clouds. The radiative transfer equation is solved through the use of discreet ordinates (DISORT) and combined with a statistical based simulation of the absorption and scattering effects [126]. MODTRAN is one of the more popular and well-validated methods for atmospheric correction, as it is more general purpose, has a spectral resolution of 1 cm−1 and coupled with absorption and scattering codes [7,125]. The analysis presented in previous work [7] highlights some of the limitations in the area of remote sensing where it is difficult to calculate the top of radiances and the code is computationally expensive due to the aerosol scattering and absorption modelling. For such cases, faster but less accurate models such as 6S are often substituted [124]. The application of MODTRAN is evident in the works in atmospheric correction [127], sensor simulation, calibration, and simulating realistic scenarios.
Aerosol models have been incorporated into MODTRAN and used to determine the propagation characteristics resulting from sea spray [128]. In considering aerosol content in marine and coastal areas, there is uncertainty in interpreting the aerosol atmospheric extinction coefficients due to unreliable models. Continued development of aerosol models is dependent on air mass, wind speed, relative humidity, and altitude to accurately determine the aerosol optical characteristics [40]. MODTRAN is utilized as a comparative tool to analyze the effectiveness of new aerosol models, as presented with the sea salt aerosols, while also taking into account anomalies in experimental data.
4.6. LBLRTM
The line by line radiative transfer model (LBLRTM) is based on FASCODE and is used to retrieve atmospheric components from satellites focusing on the troposphere [129]. LBLRTM is considered high-resolution and has a heavy focus of incorporating continuum models of molecules, Rayleigh scattering, in cooperation with the HITRAN line database [1]. The performance of this model is validated for temperature and particle retrieval [130] and with a focus on water vapor [131].
4.7. COART
Coupled ocean atmospheric transfer (COART) is an extension of the DISORT algorithm (CDISORT), taking into account the refractive index changes along coastal/marine areas at the sea–air crossing point and the effect of surface roughness of the ocean on radiance [132,133]. In the COART analysis, the ocean is considered as atmospheric layers (with different optical properties) to resolve the vertical profile of water content in the atmosphere. Absorption and scattering are similarly determined. This highlights the effect of marine-based aerosols, the variability in such dynamic environments require careful consideration of the appropriate radiative transfer simulations.
4.8. DISORT
The DISORT (discrete-ordinate radiative transfer) algorithm is considered a benchmarking standard for comparison of other radiative transfer solvers. DISORT is applicable to solve for unpolarized monochromatic radiation and used in radiative transfer codes like MODTRAN. Recent improvements to the algorithm have expanded on the BRDF calculations that result in greater accuracy and speed [134].
4.9. MOSART
MOSART (moderate spectral atmospheric radiance and transmittance) developed by the US DoD, is used in the UV-to-MMW range. It is used in determining atmospheric transmission along the path, for background radiance, and target identification. MOSART uses the HITRAN database but is becoming outdated.
4.10. RTTOV
Radiative transfer for TOVs (RTTOV) is a fast model used in satellite applications, with its strength being simulation of the top-of-atmosphere radiances in the visible-to-microwave region, as well as being able to perform physical retrievals assuming a linear relationship in the atmospheric properties [135].
4.11. Summary
Radiative transfer codes are continually being updated to incorporate a wider view of the atmosphere and the propagation effects therein. These codes are supported by databases such as HITRAN and GEISA, which themselves are regularly expanded to include more of the atmospheric constituents and higher accuracy absorptivity. The observed trend in the radiative transfer codes is increasing specificity in application, i.e., differentiating between marine/coastal areas with subsequently higher sea salt aerosols in COART, as well as increasing incorporation of absorption and scattering modelling. There is a burgeoning interest in the application of sophisticated aerosol models, but the application of further propagation effects is impaired by slow processing of the line-by-line technique. MODTRAN remains the benchmark of radiative transfer code performance, but faster codes, not higher accuracy, represents more of a key driver in the development of radiative transfer codes.
5. Conclusions
This article reviewed the various factors affecting laser beam propagation in the atmosphere and its impacts on aerospace LIDAR system performance. While absorption and scattering are well-covered as the dominant attenuation causes in most models, there are several outstanding gaps in both linear and non-linear propagation. For linear propagation effects, further considerations into continuum absorption, the assumptions of absorption line profiles and uncertainty regarding aerosol content and distribution are some of the areas highlighted towards the development of more representative propagation models. Existing radiative transfer codes are gradually incorporating more detailed absorption and scattering phenomena but are hampered by slow processing and aerosol particle distribution models that do not fully capture atmospheric characteristics in a sufficiently broad array of operating conditions. Lack of progress on non-linear propagation modelling is observed, with thermodynamic effects not being well-represented in present-day atmospheric transfer codes, as the effects are considered minimal in comparison to their linear counterparts and are an impediment to faster processing. However, for high-power laser systems, thermal blooming and other non-linear effects can have a significant impact on atmospheric laser beam propagation. The ability to model the relative changes in refraction index structure coefficient because of macro- and micro-physical atmospheric effects would contribute to higher accuracy in estimating laser beam propagation performance. As discussed, atmospheric turbulence modelling on laser beam propagation is imbued with uncertainty. The fundamental concepts of Kolmogorov-based statistical analysis of the turbulence have led to continual development and improvement of empirical models, notably Hufnagel and Tatarski’s as the basis, but the discrepancies existing between the models highlight the need for further research, particularly in the vertical dimension. In aerospace applications, there is a clear need for practical propagation models, which can be utilized for mission planning/execution and post-mission data analysis. As such, empirical modelling based on field atmospheric propagation measurements are juxtaposed to analytical/theoretical radiative transfer models in this review. It is concluded that empirical models have several advantages, in that they provide robust and comprehensive accounts of the key atmosphere propagation factors but without relying on extensive meteorological modelling. This is crucial for aerospace applications where limited knowledge of atmospheric parameters is often an important consideration and there is a need for both low-cost and high-accuracy implementations. Thus, an ensemble method is often appropriate in this context. Using multiple models based on accumulated data samples and determining the associated statistical distributions introduces greater flexibility into the modelling and offers several benefits in both design/development and flight test environments. Based on the critical review performed, it is observed that published research in this field has not progressed as desired, despite a clear need for high accuracy, and fast and reliable models. The expansion and update of radiative transfer codes has added more flexibility and has striven for greater accuracy, but the existing models, in general, do not address non-linear phenomena. The current codes typically focus on scattering and absorption models and rely on multiple databases for different application (e.g., COARTS for marine areas and RTTOV for satellite imagery). So, in many aerospace applications, using appropriate empirical models would allow more accurate analyses that better capture the nature of complex linear/non-linear interaction of laser beams with the atmosphere. There is clearly scope for current empirical and semi-empirical models to be further evolved. While they are often more robust than many of the existing analytical methods, more of the propagation phenomena should be included in the analysis, especially for nonlinear effects (turbulence, thermal blooming, etc.) and their variation as a function of altitude and platform dynamics. However, as of today, empirical and semi-empirical models are better suited for preliminary sizing and analysis, for advanced parametric studies that inform design and performance prediction in comparison to the atmospheric radiative transfer codes. This approach supports uncertainty propagation and statistical analysis that are more readily explainable/interpretable than radiative transfer codes, particularly when they are fitting-based. The transfer codes themselves are not natively supportive of parametric studies/sensitivity analysis and, in many practical applications, the codes need to be executed several times to produce useful data. Extensions of the ESLM (an example of a semi-empirical approach) would be able to capture realistic conditions beyond precipitation and visibility, including turbulence and wavelength-selective absorption processes depending on the atmospheric conditions. The poor reconciliation between atmospheric turbulence models emphasizes the need for these models to be further developed especially for airborne applications, where a significant disparity of results is observed as a function of altitude.
Author Contributions
Conceptualization, R.S., A.G. and T.F.; methodology, R.S. and T.F.; writing—original draft preparation, T.F., M.I. and R.S.; writing—review and editing, A.G. and R.S.; supervision, R.S. and A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This project was sponsored by the Food Agility Cooperative Research Centre (CRC) under Project No. FA042. The Food Agility CRC is funded by the Australian Government CRC Program, which supports medium to long-term industry-led research collaborations to improve the competitiveness, productivity and sustainability of Australian industries.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Clough, S.; Shephard, M.; Mlawer, E.; Delamere, J.; Iacono, M.; Cady-Pereira, K.; Boukabara, S.; Brown, P. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Tanré, D.; Bréon, F.; Deuzé, J.; Dubovik, O.; Ducos, F.; François, P.; Goloub, P.; Herman, M.; Lifermann, A.; Waquet, F. Remote sensing of aerosols by using polarized, directional and spectral measurements within the A-Train: The PARASOL mission. Atmos. Meas. Tech. 2011, 4, 1383–1395. [Google Scholar] [CrossRef]
- Hess, M.; Koepke, P.; Schult, I. Optical properties of aerosols and clouds: The software package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Elder, T.; Strong, J. The infrared transmission of atmospheric windows. J. Frankl. Inst. 1953, 255, 189–208. [Google Scholar] [CrossRef]
- Middleton, W.E.K. Vision through the atmosphere. In Geophysik II/Geophysics II; Springer: Berlin/Heidelberg, Germany, 1957; pp. 254–287. [Google Scholar]
- Guanter, L.; Richter, R.; Kaufmann, H. On the application of the MODTRAN4 atmospheric radiative transfer code to optical remote sensing. Int. J. Remote Sens. 2009, 30, 1407–1424. [Google Scholar] [CrossRef]
- Douillard, B.; Underwood, J.; Kuntz, N.; Vlaskine, V.; Quadros, A.; Morton, P.; Frenkel, A. On the segmentation of 3D LIDAR point clouds. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2798–2805. [Google Scholar]
- Dewan, A.; Caselitz, T.; Tipaldi, G.D.; Burgard, W. Motion-based detection and tracking in 3d lidar scans. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4508–4513. [Google Scholar]
- Gao, H.; Cheng, B.; Wang, J.; Li, K.; Zhao, J.; Li, D. Object classification using CNN-based fusion of vision and LIDAR in autonomous vehicle environment. IEEE Trans. Ind. Inform. 2018, 14, 4224–4231. [Google Scholar] [CrossRef]
- Van Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. For. Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Fahey, T.; Pham, H.; Gardi, A.; Sabatini, R.; Stefanelli, D.; Goodwin, I.; Lamb, D.W. Active and Passive Electro-Optical Sensors for Health Assessment in Food Crops. Sensors 2021, 21, 171. [Google Scholar] [CrossRef]
- Sabatini, R.; Richardson, M.A.; Gardi, A.; Ramasamy, S. Airborne laser sensors and integrated systems. Prog. Aerosp. Sci. 2015, 79, 15–63. [Google Scholar] [CrossRef]
- Sabatini, R.; Gardi, A.; Ramasamy, S. A laser obstacle warning and avoidance system for unmanned aircraft sense-and-avoid. In Proceedings of the Applied Mechanics and Materials, Benevento, Italy, 29–30 May 2014; pp. 355–360. [Google Scholar]
- Thobois, L.; Cariou, J.P.; Gultepe, I. Review of lidar-based applications for aviation weather. Pure Appl. Geophys. 2019, 176, 1959–1976. [Google Scholar] [CrossRef]
- Schwarz, R.; Mandlburger, G.; Pfennigbauer, M.; Pfeifer, N. Design and evaluation of a full-wave surface and bottom-detection algorithm for LiDAR bathymetry of very shallow waters. ISPRS J. Photogramm. Remote Sens. 2019, 150, 1–10. [Google Scholar] [CrossRef]
- Prade, B.; Houard, A.; Larour, J.; Pellet, M.; Mysyrowicz, A. Transfer of microwave energy along a filament plasma column in air. Appl. Phys. B 2017, 123, 40. [Google Scholar] [CrossRef]
- Bergé, L.; Skupin, S.; Nuter, R.; Kasparian, J.; Wolf, J.-P. Ultrashort filaments of light in weakly ionized, optically transparent media. Rep. Prog. Phys. 2007, 70, 1633. [Google Scholar] [CrossRef]
- Cremons, D.R.; Abshire, J.; Allan, G.; Sun, X.; Riris, H.; Smith, M.; Guzewich, S.; Yu, A.; Hovis, F. Development of a Mars lidar (MARLI) for measuring wind and aerosol profiles from orbit. In Proceedings of the Lidar Technologies, Techniques, and Measurements for Atmospheric Remote Sensing XIV, Berlin, Germany, 11–12 September 2018; p. 1079106. [Google Scholar]
- Danzmann, K.; Team, L.S. LISA—an ESA cornerstone mission for the detection and observation of gravitational waves. Adv. Space Res. 2003, 32, 1233–1242. [Google Scholar] [CrossRef]
- Killinger, D. Free space optics for laser communication through the air. Opt. Photonics News 2002, 13, 36–42. [Google Scholar] [CrossRef]
- Alkholidi, A.G.; Altowij, K.S. Free space optical communications—theory and practices. Contemp. Issues Wirel. Commun. 2014, 159–212. [Google Scholar]
- Sulaiman, S.A.; Ismail, A.K.A.A.; Azman, M.N.F.N. Scattering Effects in Laser Attenuation System for Measurement of Droplet Number Density. Energy Procedia 2014, 50, 79–86. [Google Scholar] [CrossRef]
- Willers, C.J. Electro-Optical System Analysis and Design: A Radiometry Perspective; SPIE Press: Bellingham, WA, USA, 2013. [Google Scholar]
- Shettle, E.P. Models of Aerosols, Clouds, and Precipitation for Atmospheric Propagation Studies; AGARD: Neuilly sur Seine, France, 1990. [Google Scholar]
- Smith, F.G.; Accetta, J.S.; Shumaker, D.L. The Infrared Electro-Optical Systems Handbook. Atmospheric Propagation of Radiation; Infrared Information and Analysis Center: Ann Arbor, MI, USA, 1993; Volume 2. [Google Scholar]
- Liou, K.-N. An Introduction to Atmospheric Radiation, 2nd ed.; Elsevier: Los Angeles, CA, USA, 2002; ISBN 9780124514515. [Google Scholar]
- Sabatini, R.; Richardson, M.; Jia, H.; Zammit-Mangion, D. Airborne Laser Systems for Atmospheric Sounding in the Near Infrared. Proc SPIE 2012, 33. [Google Scholar] [CrossRef]
- Van Zandt, N.R.; Cusumano, S.J.; Bartell, R.J.; Basu, S.; McCrae, J.E., Jr.; Fiorino, S.T. Comparison of coherent and incoherent laser beam combination for tactical engagements. Opt. Eng. 2012, 51, 104301. [Google Scholar]
- Vainio, M.; Halonen, L. Mid-infrared optical parametric oscillators and frequency combs for molecular spectroscopy. Phys. Chem. Chem. Phys. 2016, 18, 4266–4294. [Google Scholar] [CrossRef]
- Moosmüller, H.; Chakrabarty, R.; Arnott, W. Aerosol light absorption and its measurement: A review. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 844–878. [Google Scholar] [CrossRef]
- Fussman, C.R. High Energy Laser Propagation in Various Atmospheric Conditions Utilizing a New Accelerated Scaling Code; Naval Postgraduate School: Monterey, CA, USA, 2014. [Google Scholar]
- He, J.; Zhang, Q. Principle of temperature, velocity and pressure of upper atmospheric wind measurement for the Voigt profile. Opt. Int. J. Light Electron Opt. 2013, 124, 3345–3347. [Google Scholar] [CrossRef]
- Thomas, M.E.; Duncan, D.D. Atmospheric transmission. Atmos. Propag. Radiat. 1993, 2, 1–156. [Google Scholar]
- Mishchenko, M.I.; Travis, L.D.; Mackowski, D.W. T-matrix computations of light scattering by nonspherical particles: A review. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 535–575. [Google Scholar] [CrossRef]
- Hinds, W.C. Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles, 2nd ed.; John Wiley Sons: Hoboken, NJ, USA, 1999; ISBN 978-04-7119-410-1. [Google Scholar]
- Ricklin, J.C.; Hammel, S.M.; Eaton, F.D.; Lachinova, S.L. Atmospheric channel effects on free-space laser communication. J. Opt. Fiber Commun. Rep. 2006, 3, 111–158. [Google Scholar] [CrossRef]
- Lewis, E.R.; Lewis, R.; Karlstrom, K.E.; Lewis, E.R.; Schwartz, S.E. Sea Salt Aerosol Production: Mechanisms, Methods, Measurements, and Models; American Geophysical Union: Washington, DC, USA, 2004; Volume 152. [Google Scholar]
- Mayer, K.J.; Wang, X.; Santander, M.V.; Mitts, B.A.; Sauer, J.S.; Sultana, C.M.; Cappa, C.D.; Prather, K.A. Secondary Marine Aerosol Plays a Dominant Role over Primary Sea Spray Aerosol in Cloud Formation. ACS Cent. Sci. 2020, 6, 2259–2266. [Google Scholar] [CrossRef]
- Kaloshin, G.A. Modeling the Aerosol Extinction in Marine and Coastal Areas. IEEE Geosci. Remote Sens. Lett. 2020, 18, 376–380. [Google Scholar] [CrossRef]
- Miles, R.B.; Lempert, W.R.; Forkey, J.N. Laser Rayleigh scattering. Meas. Sci. Technol. 2001, 12, R33. [Google Scholar] [CrossRef]
- Witschas, B. Light scattering on molecules in the atmosphere. In Atmospheric Physics; Schumann, U., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 69–83. [Google Scholar]
- Young, A.T.; Kattawar, G.W. Rayleigh-scattering line profiles. Appl. Opt. 1983, 22, 3668–3670. [Google Scholar] [CrossRef]
- Shimizu, H.; Lee, S.; She, C.-Y. High spectral resolution lidar system with atomic blocking filters for measuring atmospheric parameters. Appl. Opt. 1983, 22, 1373–1381. [Google Scholar] [CrossRef] [PubMed]
- Bushberg, J.T.; Boone, J.M. The Essential Physics of Medical Imaging, 3rd ed.; Lippincott Williams Wilkins: Philadelphia, PA, USA, 2011; ISBN 978-0-7817-8057-5. [Google Scholar]
- Buzug, T.; Mihailidis, D. Computed Tomography from Photon Statistics to Modern Cone-Beam CT. Med Phys. 2009, 36, 3858. [Google Scholar] [CrossRef]
- Weichel, H. Laser Beam Propagation in the Atmosphere; SPIE Press: Bellingham, WA, USA, 1990; ISBN 0-8194-0487-X. [Google Scholar]
- Gebhardt, F.G. Twenty-five years of thermal blooming: An overview. In Proceedings of the Propagation of High-Energy Laser Beams Through the Earth’s Atmosphere, Los Angeles, CA, USA, 14 January 1990; pp. 2–25. [Google Scholar]
- Karr, T. Thermal blooming compensation instabilities. JOSA A 1989, 6, 1038–1048. [Google Scholar] [CrossRef]
- Gebhardt, F.G. High Power Laser Propagation. Appl. Opt. 1976, 15, 1479–1493. [Google Scholar] [CrossRef] [PubMed]
- Gebhardt, F.G.; Smith, D.C. Kinetic cooling of a gas by absorption of CO2 laser radiation. Appl. Phys. Lett. 1972, 20, 129–132. [Google Scholar] [CrossRef]
- Kucherov, A. Bleaching channel in a fluid layer under laser pulse propagation. Tech. Phys. 2004, 49, 876–883. [Google Scholar] [CrossRef]
- Stathopoulos, F.; Constantinou, P.; Panagopoulos, A.D. Impact of various flow-fields on laser beam propagation. In Proceedings of the 2009 International Workshop on Satellite and Space Communications, Siena, Italy, 9–11 September 2009; pp. 157–161. [Google Scholar]
- Fingas, M.; Brown, C.E. Chapter 5—Oil Spill Remote Sensing. In Oil Spill Science and Technology, 2nd ed.; Fingas, M., Ed.; Gulf Professional Publishing: Boston, MA, USA, 2017; pp. 305–385. [Google Scholar]
- Siegenthaler, J.P.; Jumper, E.; Gordeyev, S. Atmospheric Propagation Vs. Aero-Optics. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar]
- Smith, F.G.; Brown, C.E. Atmospheric propagation of radiation. In The Infrared and Electro-Optical Systems Handbook-IR/EO Systems Handbook; Rogatto, W.D., Ed.; SPIE Press: Washington, DC, USA, 2017; Volume 3, pp. 305–385. [Google Scholar]
- Mahalov, A.; Moustaoui, M. Characterization of atmospheric optical turbulence for laser propagation. Laser Photonics Rev. 2010, 4, 144–159. [Google Scholar] [CrossRef]
- Schmidt, J. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB; SPIE Press: Bellingham, Washington, USA, 2010.
- Stribling, B.E.; Welsh, B.M.; Roggemann, M.C. Optical propagation in non-Kolmogorov atmospheric turbulence. In Proceedings of the Atmospheric Propagation and Remote Sensing IV, Orlando, FL, USA, 17–21 April 1995; pp. 181–196. [Google Scholar]
- Li, J.; Wang, W.; Duan, M.; Wei, J. Influence of non-Kolmogorov atmospheric turbulence on the beam quality of vortex beams. Opt. Express 2016, 24, 20413–20423. [Google Scholar] [CrossRef]
- Shaik, K. Atmospheric propagation effects relevant to optical communications. TDA Prog. Rep. 1988, 42, 180–200. [Google Scholar]
- Cherubini, T.; Businger, S. Another look at the refractive index structure function. J. Appl. Meteorol. Climatol. 2013, 52, 498–506. [Google Scholar] [CrossRef]
- Shao, S.; Qin, F.; Xu, M.; Liu, Q.; Han, Y.; Xu, Z. Temporal and spatial variation of refractive index structure coefficient over South China sea. Results Eng. 2021, 9, 100191. [Google Scholar] [CrossRef]
- Libich, J.; Perez, J.; Zvanovec, S.; Ghassemlooy, Z.; Nebuloni, R.; Capsoni, C. Combined effect of turbulence and aerosol on free-space optical links. Appl. Opt. 2017, 56, 336–341. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005; ISBN 9781510643703. [Google Scholar]
- Gladkikh, V.; Mamyshev, V.; Odintsov, S. Experimental estimates of the structure parameter of the refractive index for optical waves in the surface air layer. Atmos. Ocean. Opt. 2015, 28, 426–435. [Google Scholar] [CrossRef]
- Botygina, N.; Kovadlo, P.; Kopylov, E.; Lukin, V.; Tuev, M.; Shikhovtsev, A.Y. Estimation of the astronomical seeing at the large solar vacuum telescope site from optical and meteorological measurements. Atmos. Ocean. Opt. 2014, 27, 142–146. [Google Scholar] [CrossRef]
- Wu, S.; Yang, Q.; Xu, J.; Luo, T.; Qing, C.; Su, C.; Huang, C.; Wu, X.; Li, X. A reliable model for estimating the turbulence intensity and integrated astroclimatic parameters from sounding data. Mon. Not. R. Astron. Soc. 2021, 503, 5692–5703. [Google Scholar] [CrossRef]
- Shikhovtsev, A.; Kovadlo, P.; Lukin, V.; Nosov, V.; Kiselev, A.; Kolobov, D.; Kopylov, E.; Shikhovtsev, M.; Avdeev, F. Statistics of the Optical Turbulence from the Micrometeorological Measurements at the Baykal Astrophysical Observatory Site. Atmosphere 2019, 10, 661. [Google Scholar] [CrossRef]
- Fried, D.L. Statistics of a Geometric Representation of Wavefront Distortion. J. Opt. Soc. Am. 1965, 55, 1427–1435. [Google Scholar] [CrossRef]
- Brookner, E. Improved model for the structure constant variations with altitude. Appl. Opt. 1971, 10, 1960–1962. [Google Scholar] [CrossRef] [PubMed]
- Fried, D. Propagation of a spherical wave in a turbulent medium. JOSA 1967, 57, 175–180. [Google Scholar] [CrossRef]
- Lawrence, R.S.; Ochs, G.; Clifford, S. Measurements of atmospheric turbulence relevant to optical propagation. JOSA 1970, 60, 826–830. [Google Scholar] [CrossRef]
- Lei, F.; Tiziani, H.J. Atmospheric influence on image quality of airborne photographs. Opt. Eng. 1993, 32, 2271–2280. [Google Scholar] [CrossRef]
- Wyngaard, J.C.; Izumi, Y.; Collins, S.A. Behavior of the Refractive-Index-Structure Parameter near the Ground. J. Opt. Soc. Am. 1971, 61, 1646–1650. [Google Scholar] [CrossRef]
- Beland, R.R.; Brown, J.H. A deterministic temperature model for stratospheric optical turbulence. Phys. Scr. 1988, 37, 419. [Google Scholar] [CrossRef]
- Tunick, A. Statistical analysis of optical turbulence intensity over a 2.33 km propagation path. Opt. Express 2007, 15, 3619–3628. [Google Scholar] [CrossRef] [PubMed]
- Coulman, C.E.; Vernin, J.; Coqueugniot, Y.; Caccia, J.L. Outer scale of turbulence appropriate to modeling refractive-indexstructure profiles. Appl. Opt. 1988, 27, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Jackson, A. Modified-Dewan Optical Turbulence Parameterizations; Air Force Research Lab Hanscom Afb Ma Space Vehicles Directorate: Albuquerque, NM, USA, 2004. [Google Scholar]
- Ruggiero, F.H.; DeBenedictis, D.A. Forecasting optical turbulence from mesoscale numerical weather prediction models. In Proceedings of the DoD High Performance Modernization Program Users Group Conference, Austin, TX, USA, 11–14 June 2002; pp. 10–14. [Google Scholar]
- Trinquet, H.; Vernin, J. A model to forecast seeing and estimate C2N profiles from meteorological data. Publ. Astron. Soc. Pac. 2006, 118, 756. [Google Scholar] [CrossRef]
- Dewan, E.M.; Good, R.E.; Beland, R.; Brown, J. A Model for C2n (Optical Turbulence) Profiles Using Radiosonde Data; Directorate of Geophysics; Air Force Materiel Command: Greene County, OH, USA, 1993. [Google Scholar]
- Kovadlo, P.G.; Shikhovtsev, A.Y.; Kopylov, E.A.; Kiselev, A.V.; Russkikh, I.V. Study of the Optical Atmospheric Distortions using Wavefront Sensor Data. Russ. Phys. J. 2021, 63, 1952–1958. [Google Scholar] [CrossRef]
- Osborn, J.; Wilson, R.; Sarazin, M.; Butterley, T.; Chacón, A.; Derie, F.; Farley, O.; Haubois, X.; Laidlaw, D.; LeLouarn, M. Optical turbulence profiling with Stereo-SCIDAR for VLT and ELT. Mon. Not. R. Astron. Soc. 2018, 478, 825–834. [Google Scholar] [CrossRef]
- Rafalimanana, A.; Giordano, C.; Ziad, A.; Aristidi, E. Prediction of atmospheric turbulence by means of WRF model for optical communications. In Proceedings of the International Conference on Space Optics—ICSO 2020, Online, 30 March–2 April 2021; p. 118524G. [Google Scholar]
- Ullwer, C.; Sprung, D.; Sucher, E.; Kociok, T.; Grossmann, P.; van Eijk, A.M.; Stein, K. Global simulations of Cn2 using the Weather Research and Forecast Model WRF and comparison to experimental results. In Proceedings of the Laser Communication and Propagation through the Atmosphere and Oceans VIII, San Diego, CA, USA, 11–15 August 2019; p. 111330I. [Google Scholar]
- Mahdieh, M.H.; Pournoury, M. Atmospheric turbulence and numerical evaluation of bit error rate (BER) in free-space communication. Opt. Laser Technol. 2010, 42, 55–60. [Google Scholar] [CrossRef]
- Kim, I.I.; Hakakha, H.; Adhikari, P.; Korevaar, E.J.; Majumdar, A.K. Scintillation reduction using multiple transmitters. In Proceedings of the Free-Space Laser Communication Technologies IX, San Jose, CA, USA, 8–14 February 1997; pp. 102–113. [Google Scholar]
- Chiba, T. Spot dancing of the laser beam propagated through the turbulent atmosphere. Appl. Opt. 1971, 10, 2456–2461. [Google Scholar] [CrossRef]
- Yuksel, H.; Milner, S.; Davis, C. Aperture averaging for optimizing receiver design and system performance on free-space optical communication links. J. Opt. Netw. 2005, 4, 462–475. [Google Scholar] [CrossRef]
- Tofsted, D.H. Outer-scale effects on beam-wander and angle-of-arrival variances. Appl. Opt. 1992, 31, 5865–5870. [Google Scholar] [CrossRef]
- Katsilieris, T.D.; Latsas, G.P.; Nistazakis, H.E.; Tombras, G.S. An accurate computational tool for performance estimation of FSO communication links over weak to strong atmospheric turbulent channels. Computation 2017, 5, 18. [Google Scholar] [CrossRef]
- Buck, A. Effects of the atmosphere on laser beam propagation. Appl. Opt. 1967, 6, 703–708. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Cai, Y. Propagation of Partially Coherent Beam in Turbulent Atmosphere: A Review (Invited Review). Prog. Electromagn. Res. Pier 2015, 150, 123–143. [Google Scholar] [CrossRef]
- Young, C.Y.; Gilchrest, Y.V.; Macon, B. Turbulence induced beam spreading of higher order mode optical waves. Opt. Eng. 2002, 41, 1097–1103. [Google Scholar]
- Wu, G.; Guo, H.; Yu, S.; Luo, B. Spreading and direction of Gaussian–Schell model beam through a non-Kolmogorov turbulence. Opt. Lett. 2010, 35, 715–717. [Google Scholar] [CrossRef]
- Lukin, V.P.; Konyaev, P.A.; Sennikov, V.A. Beam spreading of vortex beams propagating in turbulent atmosphere. Appl. Opt. 2012, 51, C84–C87. [Google Scholar] [CrossRef]
- Jelalian, A.V. Laser radar systems. In Proceedings of the EASCON’80; Electronics and Aerospace Systems Conference, Arlington, VA, USA, 29 September–1 October 1980; pp. 546–554. [Google Scholar]
- Sabatini, R.; Richardson, M. Airborne Laser Systems Testing and Analysis; The Research and Technology Organisation: Neuilly, France, 2010. [Google Scholar]
- Veselovskii, I.; Dubovik, O.; Kolgotin, A.; Lapyonok, T.; Di Girolamo, P.; Summa, D.; Whiteman, D.N.; Mishchenko, M.; Tanré, D. Application of randomly oriented spheroids for retrieval of dust particle parameters from multiwavelength lidar measurements. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Müller, D.; Wandinger, U.; Ansmann, A. Microphysical particle parameters from extinction and backscatter lidar data by inversion with regularization: Simulation. Appl. Opt. 1999, 38, 2358–2368. [Google Scholar] [CrossRef] [PubMed]
- Salman, S.A.; Khaleel, J.M. Calculation of the attenuation of infrared laser beam propagation in the atmosphere. J. Res. Diyala Humanit. 2009. Available online: https://www.iasj.net/iasj/download/117c3e95a0d724ca. (accessed on 17 July 2021).
- Bukshtab, M. Applied Photometry, Radiometry, and Measurements of Optical Losses; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Pravilov, A.M. Radiometry in Modern Scientific Experiments; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zeng, X.; Guo, W.; Yang, K.; Xia, M. Noise reduction and retrieval by modified lidar inversion method combines joint retrieval method and machine learning. Appl. Phys. B 2018, 124, 1–9. [Google Scholar] [CrossRef]
- Farhani, G.; Sica, R.J.; Daley, M.J. Classification of lidar measurements using supervised and unsupervised machine learning methods. Atmos. Meas. Tech. 2021, 14, 391–402. [Google Scholar] [CrossRef]
- Yorks, J.E.; Selmer, P.A.; Kupchock, A.; Nowottnick, E.P.; Christian, K.E.; Rusinek, D.; Dacic, N.; McGill, M.J. Aerosol and Cloud Detection Using Machine Learning Algorithms and Space-Based Lidar Data. Atmosphere 2021, 12, 606. [Google Scholar] [CrossRef]
- Jiang, Y.; Qiao, R.; Zhu, Y.; Wang, G. Data fusion of atmospheric ozone remote sensing Lidar according to deep learning. J. Supercomput. 2021, 77, 1–16. [Google Scholar] [CrossRef]
- Sanchez, L.F.R. Machine Learning Analysis to Characterize Phase Variations in Laser Propagation Through Deep Turbulence. Ph.D Thesis, The University of Texas at El Paso, El Paso, TX, USA, January 2020. [Google Scholar]
- Yuan, Y.; Huang, X.; Shuai, Y.; Mao, Q.-J. Study on the Influence of Aerosol Radiation Balance in One-Dimensional Atmospheric Medium Using P n -Approximation Method. Math. Probl. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Buehler, S.A.; Eriksson, P.; Kuhn, T.; von Engeln, A.; Verdes, C. ARTS, the atmospheric radiative transfer simulator. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 65–93. [Google Scholar] [CrossRef]
- Buehler, S.A.; Eriksson, P.; Lemke, O. Absorption lookup tables in the radiative transfer model ARTS. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1559–1567. [Google Scholar] [CrossRef]
- Scott, N.; Chedin, A. A fast line-by-line method for atmospheric absorption computations: The Automatized Atmospheric Absorption Atlas. J. Appl. Meteorol. 1981, 20, 802–812. [Google Scholar] [CrossRef]
- Scott, N. A direct method of computation of the transmission function of an inhomogeneous gaseous medium—I: Description of the method. J. Quant. Spectrosc. Radiat. Transf. 1974, 14, 691–704. [Google Scholar] [CrossRef]
- Hu, S.; Gao, T.-C.; Li, H.; Liu, L.; Liu, X.-C.; Zhang, T.; Cheng, T.-J.; Li, W.-T.; Dai, Z.-H.; Su, X. Effect of atmospheric refraction on radiative transfer in visible and near-infrared band: Model development, validation, and applications. J. Geophys. Res. Atmos. 2016, 121, 2349–2368. [Google Scholar] [CrossRef]
- Artaud, G.; Benammar, B.; Jouglet, D.; Canuet, L.; Lacan, J. Impact of molecular absorption on the design of free space optical communications. In Proceedings of the International Conference on Space Optics—ICSO 2018, Chania, Greece, 9–12 October 2019; p. 111801F. [Google Scholar]
- Ottlé, C.; Vidal-Madjar, D. Estimation of land surface temperature with NOAA9 data. Remote Sens. Environ. 1992, 40, 27–41. [Google Scholar] [CrossRef]
- Schreier, F.; Gimeno García, S.; Hedelt, P.; Hess, M.; Mendrok, J.; Vasquez, M.; Xu, J. GARLIC—A general purpose atmospheric radiative transfer line-by-line infrared-microwave code: Implementation and evaluation. J. Quant. Spectrosc. Radiat. Transf. 2014, 137, 29–50. [Google Scholar] [CrossRef]
- Eriksson, P.; Buehler, S.; Davis, C.; Emde, C.; Lemke, O. ARTS, the atmospheric radiative transfer simulator, version 2. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1551–1558. [Google Scholar] [CrossRef]
- Spurr, R.; Christi, M. The LIDORT and VLIDORT linearized scalar and vector discrete ordinate radiative transfer models: Updates in the last 10 years. In Springer Series in Light Scattering; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–62. [Google Scholar]
- Vermote, E.; Tanré, D.; Deuzé, J.; Herman, M.; Morcrette, J.; Kotchenova, S. Second simulation of a satellite signal in the solar spectrum-vector (6SV). 6s User Guide Version 2006, 3, 1–55. [Google Scholar]
- Gómez-Dans, J.L.; Lewis, P.E.; Disney, M. Efficient emulation of radiative transfer codes using Gaussian processes and application to land surface parameter inferences. Remote Sens. 2016, 8, 119. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, L.; Liu, L.; Peng, D.; Jiao, Q.; Zhang, H. A Landsat-5 atmospheric correction based on MODIS atmosphere products and 6S model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 1609–1615. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.-J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; Van Den Bosch, J. MODTRAN® 6: A major upgrade of the MODTRAN® radiative transfer code. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; pp. 1–4. [Google Scholar]
- Vicent, J.; Verrelst, J.; Sabater, N.; Alonso, L.; Rivera-Caicedo, J.P.; Martino, L.; Muñoz-Marí, J.; Moreno, J. Comparative analysis of atmospheric radiative transfer models using the Atmospheric Look-up table Generator (ALG) toolbox (version 2.0). Geosci. Model Dev. 2020, 13, 1945–1957. [Google Scholar] [CrossRef]
- Miesch, C.; Poutier, L.; Achard, V.; Briottet, X.; Lenot, X.; Boucher, Y. Direct and inverse radiative transfer solutions for visible and near-infrared hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1552–1562. [Google Scholar] [CrossRef]
- Gathman, S.G.; van Eijk, A.M.; Cohen, L.H. Characterizing large aerosols in the lowest level of the marine atmosphere. In Proceedings of the Propagation and Imaging through the Atmosphere II, San Diego, CA, USA, 19–24 July 1998; pp. 41–52. [Google Scholar]
- Beer, R.; Glavich, T.A.; Rider, D.M. Tropospheric emission spectrometer for the Earth Observing System’s Aura satellite. Appl. Opt. 2001, 40, 2356–2367. [Google Scholar] [CrossRef] [PubMed]
- Shephard, M.; Clough, S.; Payne, V.; Smith, W.; Kireev, S.; Cady-Pereira, K. Performance of the line-by-line radiative transfer model (LBLRTM) for temperature and species retrievals: IASI case studies from JAIVEx. Atmos. Chem. Phys. 2009, 9, 7397–7417. [Google Scholar] [CrossRef]
- Alvarado, M.; Payne, V.; Mlawer, E.; Uymin, G.; Shephard, M.; Cady-Pereira, K.; Delamere, J.; Moncet, J.-L. Performance of the Line-By-Line Radiative Transfer Model (LBLRTM) for temperature, water vapor, and trace gas retrievals: Recent updates evaluated with IASI case studies. Atmos. Chem. Phys. 2013, 13, 6687–6711. [Google Scholar] [CrossRef]
- Jin, Z.; Stamnes, K. Radiative transfer in nonuniformly refracting layered media: Atmosphere–ocean system. Appl. Opt. 1994, 33, 431–442. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Charlock, T.P.; Rutledge, K.; Stamnes, K.; Wang, Y. Analytical solution of radiative transfer in the coupled atmosphere-ocean system with a rough surface. Appl. Opt. 2006, 45, 7443–7455. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Stamnes, S.; Jin, Z.; Laszlo, I.; Tsay, S.C.; Wiscombe, W.J.; Stamnes, K. Improved discrete ordinate solutions in the presence of an anisotropically reflecting lower boundary: Upgrades of the DISORT computational tool. J. Quant. Spectrosc. Radiat. Transf. 2015, 157, 119–134. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).