A Bayesian Hierarchical Spatial Copula Model: An Application to Extreme Temperatures in Extremadura (Spain)
Abstract
:1. Introduction
2. Statistical Model
2.1. Data Level
2.2. Process Level
2.3. Prior Distribution
3. Estimation
3.1. Posterior Distribution
3.2. Assessment of the Models’ Goodness-Of-Fit
- (a)
- is the parameter vector of interest in the model (GEV parameters in a BHM model, and GEV and Gaussian copula parameters in a BHGCM model).
- (b)
- measures the model’s goodness-of-fit, where the deviance , i.e., times the logarithm of the likelihood of the random variably Y under study. In a BHGCM model, the likelihood is defined by Equation (A5), and in a BHM model, by the GEV pdf.
- (c)
- is a parameter that controls the complexity of the model (effective number of parameters), where is the deviance of the posterior mean of the parameter of interest.
3.3. Inference
| Algorithm 1 Ungauged Site |
Do for :
|
| Algorithm 2 Observations |
Do for :
|
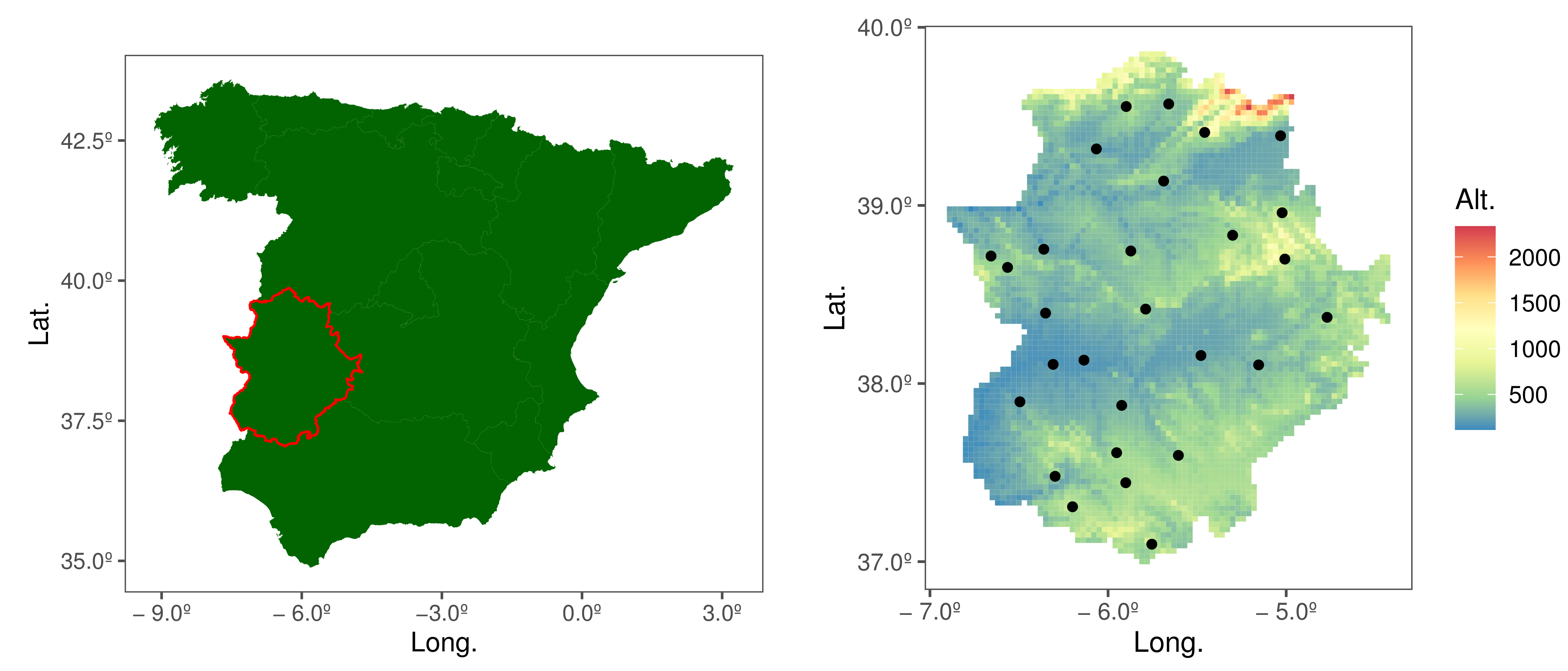
4. Data
5. Results
5.1. Evaluation of the Models
5.2. Parameter Estimates
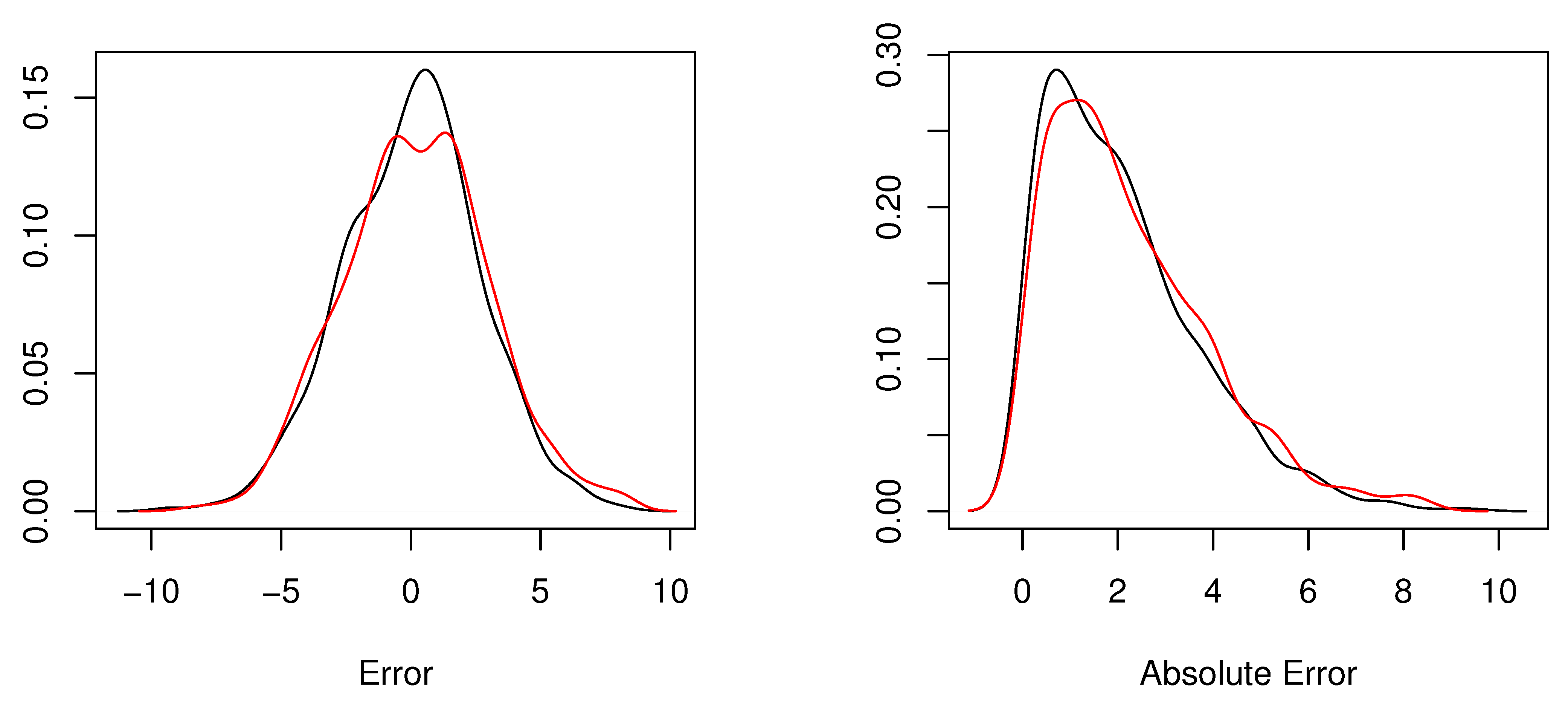
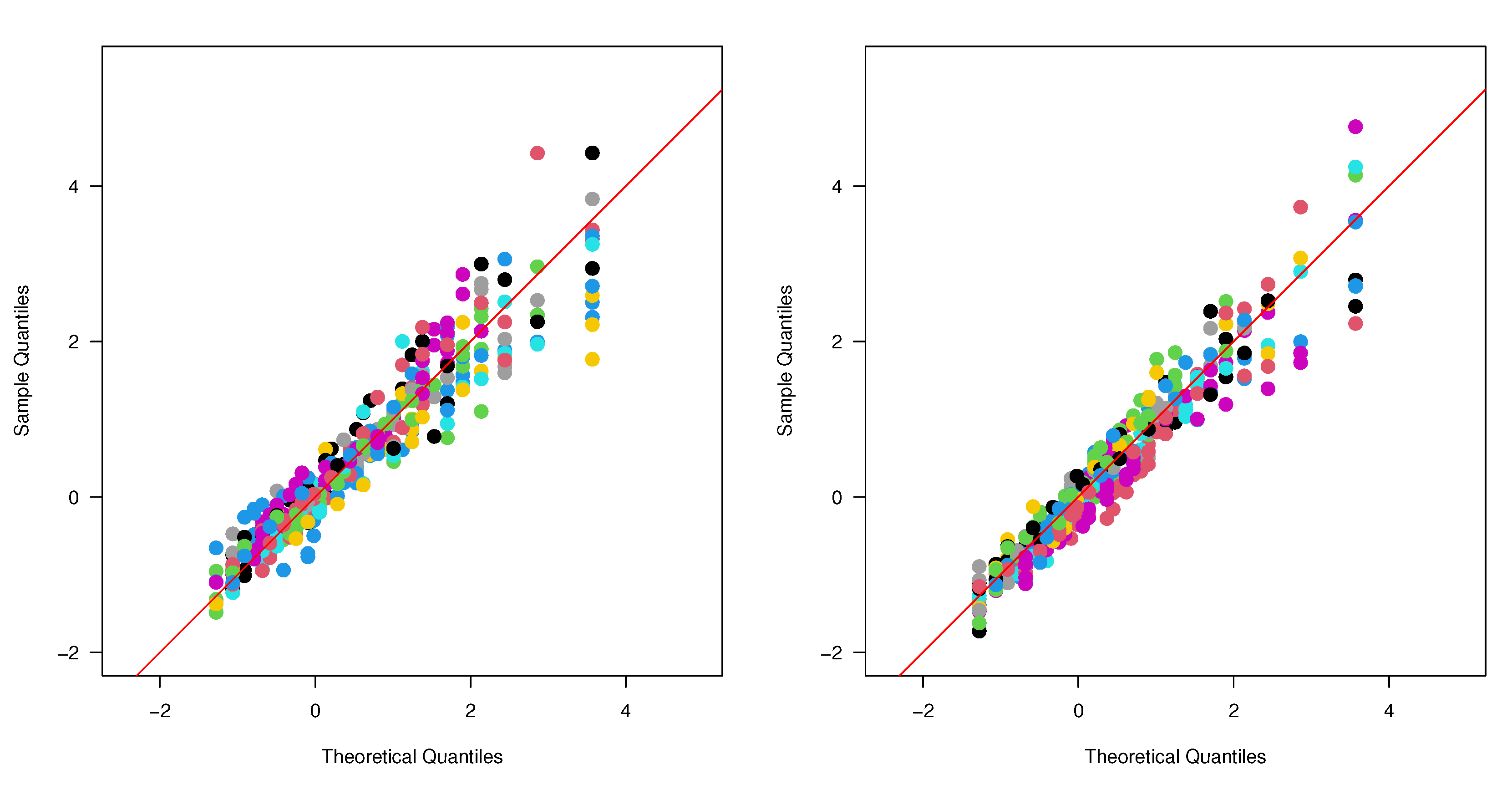
5.3. Validation of the Models
5.4. Inference
6. Conclusions
- Bayesian hierarchical models, BHM, proposed by García et al. [18] present the problem of assuming spatial independence between observations at different sites. The present work has addressed this problem by introducing a copula.
- A Gaussian copula is assumed as a joint distribution with at-site GEV marginal distributions. In this way, the spatial dependence of observations from different sites is represented by a correlation matrix. In addition, spatial regression models of the GEV parameters are proposed.
- Two BHGCM models are proposed: BHGCM-200 takes a spatial regression model for while the parameters and are constant; BHGCM-210 takes spatial models for and , while the parameter is constant.
- The BHGCM-210 model has a better DIC goodness-of-fit value than the BHGCM-200 model and the noncopula BHM-210 model.
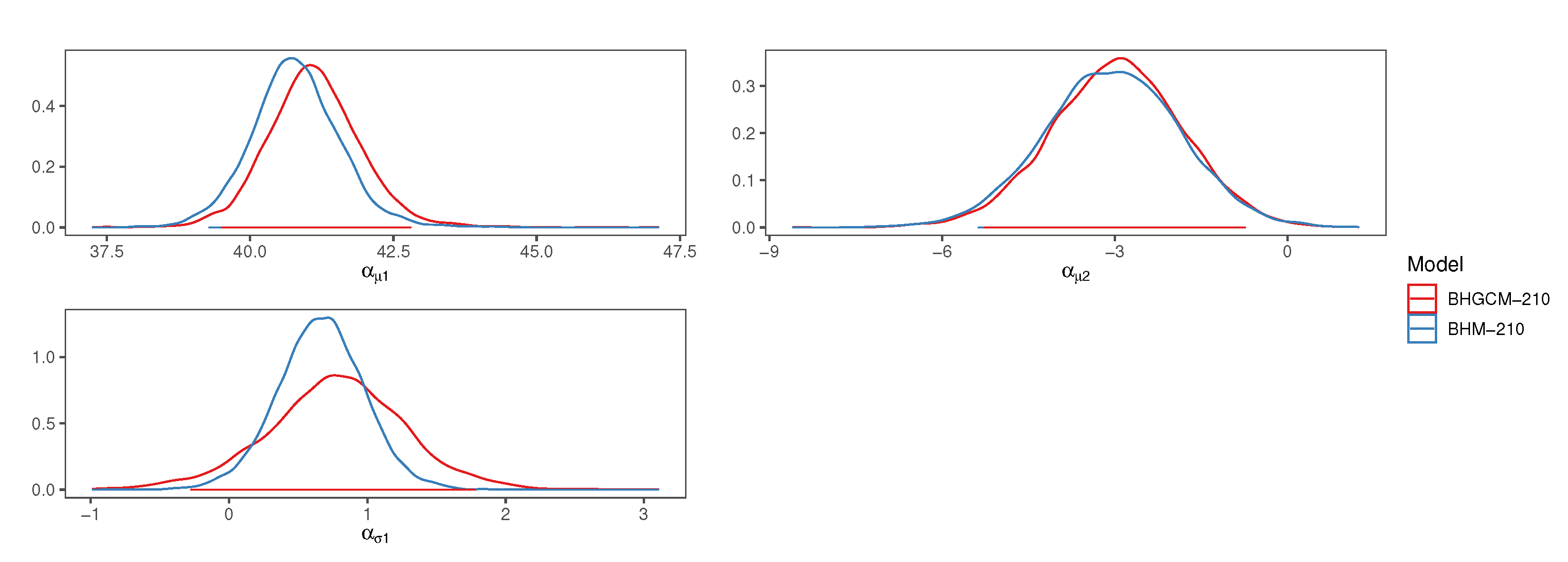
- For the GEV distribution’s location parameter, the BHGCM-210 and BHM-210 models give qualitatively similar estimates of the regression parameter posterior distributions.
- For the GEV distribution’s scale parameter, the BHGCM-210 model gives a distribution with greater variance than that given by the BHM-210 model.
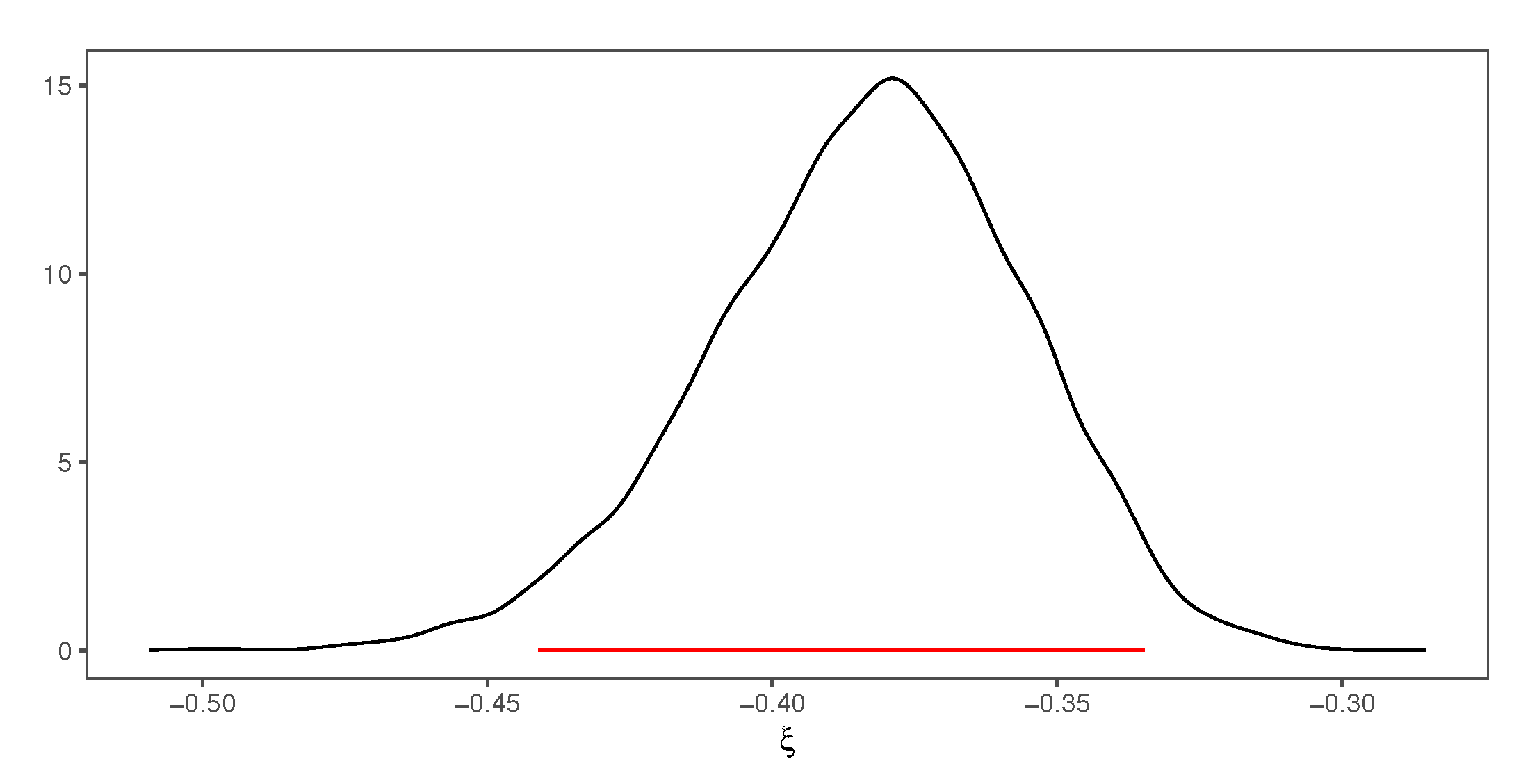
- In the BHGCM-210 model, the GEV shape parameter takes negative values, and its posterior distribution is symmetrical and highly concentrated around −0.38. Therefore, the extreme temperature distribution is not expected to increase too much.
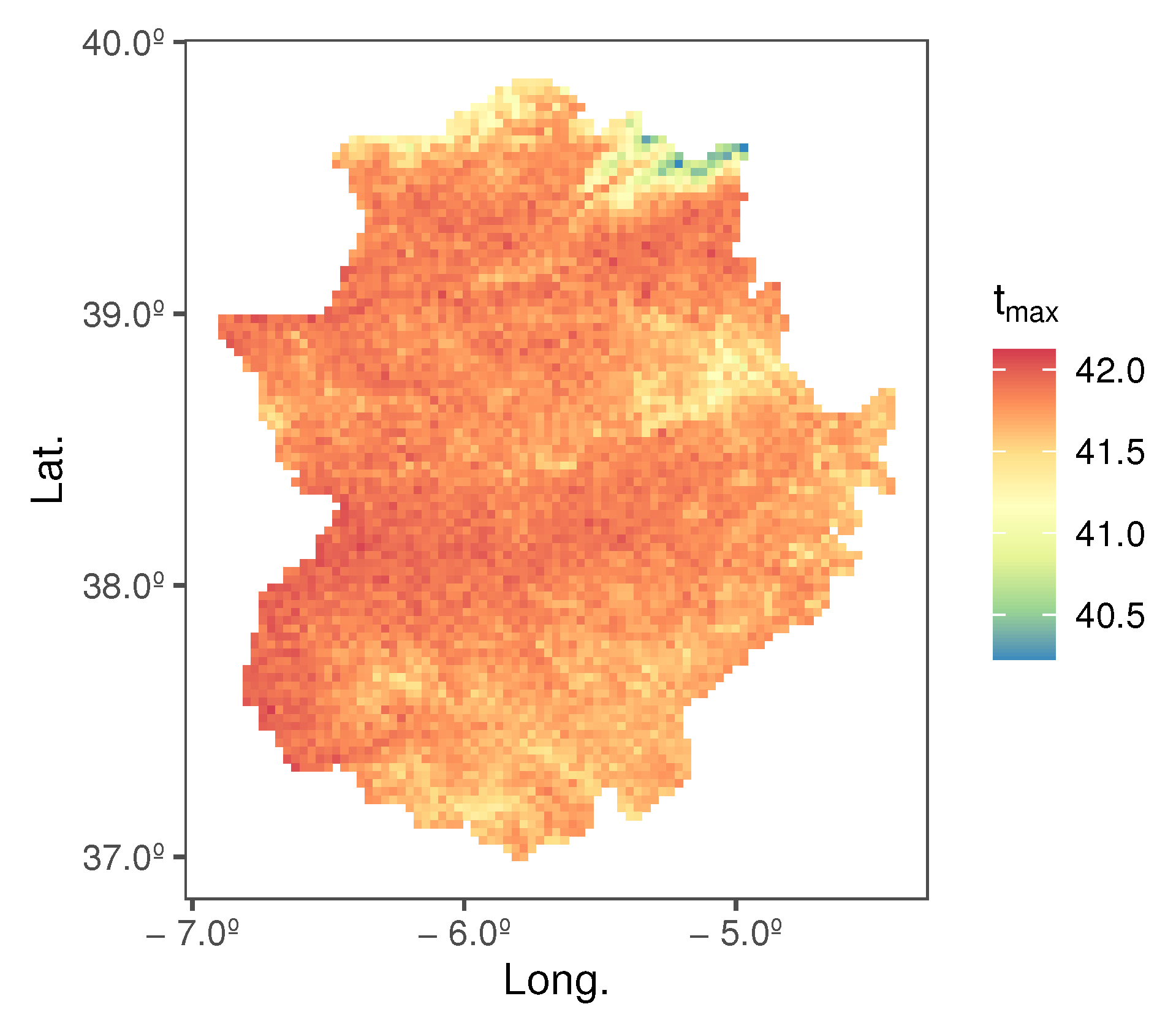
- The BHGCM-210 model gives a spatial posterior distribution for the location parameter that is strongly dependent on altitude, unlike the scale parameter. The location parameter’s mean values in the region lie between 39.29 °C and 41.12 °C.
- In the BHGCM-210 model, the scale parameter’s spatial posterior distribution is very concentrated, taking very similar values throughout the region.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Gaussian Copula
Appendix B. Estimation
References
- García, J.; Gallego, M.C.; Serrano, A.; Vaquero, J. Trends in Block-Seasonal Extreme Rainfall over the Iberian Peninsula in the Second Half of the Twentieth Century. J. Clim. 2007, 20, 113–130. [Google Scholar] [CrossRef]
- Re, M.; Barros, V.R. Extreme rainfalls in SE South America. Clim. Chang. 2009, 96, 119–136. [Google Scholar] [CrossRef]
- Acero, F.J.; García, J.A.; Gallego, M.C. Peaks-over-Threshold Study of Trends in Extreme Rainfall over the Iberian Peninsula. J. Clim. 2011, 24, 1089–1105. [Google Scholar] [CrossRef]
- Acero, F.J.; Parey, S.; Hoang, T.T.H.; Dacunha-Castelle, D.; García, J.A.; Gallego, M.C. Non-stationary future return levels for exteme rainfall over Extremadura (SW Iberian Peninsula). Hydrol. Sci. J. 2017, 62, 1394–1411. [Google Scholar] [CrossRef] [Green Version]
- Wi, S.; Valdés, J.B.; Steinschneider, S.; Kim, T.W. Non-stationary frequency analysis of extreme precipitation in South Korea using peaks-over-threshold and annual maxima. Stoch. Environ. Res. Risk Assess. 2016, 30, 583–606. [Google Scholar] [CrossRef]
- Nogaj, M.; Yiou, P.; Parey, S.; Malek, F.; Naveau, P. Amplitude and frequency of temperature extremes over the North Atlantic region. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Coelho, C.A.S.; Ferro, C.A.T.; Stephenson, D.B.; Steinskog, D.J. Methods for Exploring Spatial and Temporal Variability of Extreme Events in Climate Data. J. Clim. 2008, 21, 2072–2092. [Google Scholar] [CrossRef] [Green Version]
- Acero, F.J.; Fernández-Fernández, M.I.; Carrasco, V.M.S.; Parey, S.; Hoang, T.T.H.; Dacunha-Castelle, D.; García, J.A. Changes in heat wave characteristics over Extremadura (SW Spain). Theor. Appl. Climatol. 2018, 133, 605–617. [Google Scholar] [CrossRef] [Green Version]
- Ramos, A.A. Extreme value theory and the solar cycle. Astron. Astrophys. 2007, 472, 293–298. [Google Scholar] [CrossRef] [Green Version]
- Acero, F.J.; Carrasco, V.M.S.; Gallego, M.C.; García, J.A.; Vaquero, J.M. Extreme Value Theory Applied to the Millennial Sunspot Number Series. Astrophys. J. 2018, 853, 80. [Google Scholar] [CrossRef] [Green Version]
- Longin, F.M. From value at risk to stress testing: The extreme value approach. J. Bank. Financ. 2000, 24, 1097–1130. [Google Scholar] [CrossRef]
- Castillo, E.; Hadi, A.S.; Balakrishnan, N.; Sarabia, J.M. Extreme Value and Related Models with Applications in Engineering and Science; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Casson, E.; Coles, S. Spatial regression models for extremes. Extremes 1999, 1, 449–468. [Google Scholar] [CrossRef]
- Cooley, D.; Nychka, D.; Naveau, P. Bayesian spatial modeling of extreme precipitation return levels. J. Am. Stat. Assoc. 2007, 102, 824–840. [Google Scholar] [CrossRef]
- Portero, J.; Acero, F.J.; García, J.A. Analysis of Extreme Temperature Events over the Iberian Peninsula during the 21st Century Using Dynamic Climate Projections Chosen Using Max-Stable Processes. Atmosphere 2020, 11, 506. [Google Scholar] [CrossRef]
- Davison, A.C.; Padoan, S.A.; Ribatet, M. Statistical modeling of spatial extremes of spatial extremes. Stat. Sci. 2012, 27, 161–186. [Google Scholar] [CrossRef] [Green Version]
- Acero, F.J.; García, J.A.; Gallego, M.C.; Parey, S.; Dacunha-Castelle, D. Trends in summer extreme temperatures over the Iberian Peninsula using nonurban station data. J. Geophys. Res. Atmos. 2014, 119, 39–53. [Google Scholar] [CrossRef]
- García, A.; Martín, J.; Naranjo, L.; Acero, F.J. A Bayesian hierarchical spatio-temporal model for extreme rainfall in Extremadura (Spain). Hydrol. Sci. J. 2018, 63, 878–894. [Google Scholar] [CrossRef]
- Renard, B.; Lang, M. Use of a Gaussian copula for multivariate extreme value analysis: Some case studies in hydrology. Adv. Water Resour. 2007, 30, 897–912. [Google Scholar] [CrossRef] [Green Version]
- Renard, B. A Bayesian hierarchical approach to regional frequency analysis. Water Resour. Res. 2011, 47, 11513. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.R.; Li, Y.P.; Ma, Y.; Jia, Q.M.; Su, Y.Y. Development of a Bayesian-copula-based frequency analysis method for hydrological risk assessment—The Naryn River in Central Asia. J. Hydrol. 2020, 580, 124349. [Google Scholar] [CrossRef]
- Beck, N.; Genest, C.; Jalbert, J.; Mailhot, M. Predicting extreme surges from sparse data using a copula-based hierarchical Bayesian spatial model. Environmetrics 2020, 31, e2616. [Google Scholar] [CrossRef] [Green Version]
- Salvadori, G.; De Michele, C.; Kottegoda, N.T.M.; Rosso, R. Extremes in Nature: An Approach Using Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 56. [Google Scholar]
- Sklar, A. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Genest, C.; Favre, A.C.; Béliveau, J.; Jacques, C. Metaelliptical copulas and their use in frequency analysis of multivariate hydrological data. Water Resour Res. 2007, 43, W09401. [Google Scholar] [CrossRef] [Green Version]
- Favre, A.C.; El Adlouni, S.; Perreault, L.; Thiémonge, N.; Bobée, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Wikle, C.K.; Berliner, M.L.; Cressie, N. Hierarchical Bayesian space-time models. Environ. Ecol. Stat. 1998, 5, 117–154. [Google Scholar] [CrossRef]
- Sun, X.; Thyer, M.; Renard, B.; Lang, M. A general regional frequency analysis framework for quantifying local-scale climate effects: A case study of ENSO effects on Southeast Queensland rainfall. J. Hydrol. 2014, 512, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Dyrrdal, A.V.; Lenkoski, A.; Thorarinsdottir, T.L.; Stordal, F. Bayesian hierarchical modeling of extreme hourly precipitation in Norway. Environmetrics 2015, 26, 89–186. [Google Scholar] [CrossRef] [Green Version]
- Ragulina, G.; Reitan, T. Generalized extreme value shape parameter and its nature for extreme precipitation using long time series and Bayesian approach. Hydrol. Sci. J. 2017, 62, 863–879. [Google Scholar] [CrossRef]
- Barlow, A.M.; Rohrbeck, C.; Sharkey, P.; Shooter, R.; Simpson, E.S. A Bayesian spatio-temporal model for precipitation extremes-STOR team contribution to the EVA2017 challenge. Extremes 2018, 21, 431–439. [Google Scholar] [CrossRef] [Green Version]
- Craigmile, P.F.; Guttorp, P. Can a regional climate model reproduce observed extreme temperatures? Statistica 2013, 73, 103–122. [Google Scholar]
- Daraio, J.A.; Amponsah, A.O.; Sears, K.W. Bayesian Hierarchical Regression to Assess Variation of Stream Temperature with Atmospheric Temperature in a Small Watershed. Hydrology 2017, 4, 44. [Google Scholar] [CrossRef] [Green Version]
- Gnedenko, B. Sur la distribution limite du terme maximum d’une serie aleatorie. Ann. Math. 1943, 44, 423–453. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1928; Volume 24, pp. 180–190. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208. [Google Scholar]
- Gilks, W.R.; Richardson, S.; Spiegelhalter, D.J. Introducing Markov Chain Monte Carlo. In Markov Chain Monte Carlo in Practice; Chapman & Hall: New York, NY, USA, 1996. [Google Scholar]
- Cowles, M.K.; Carlin, B.P. Markov chain Monte Carlo convergence diagnostics: A comparative review. J. Am. Stat. Assoc. 1996, 91, 883–904. [Google Scholar] [CrossRef]
- Martyn, P.; Nicky, B.; Kate, C.; Karen, V. CODA: Convergence diagnosis and output analysis for MCMC. R News 2006, 6, 7–11. [Google Scholar]
- Wickham, H. ggplot2. Elegant Graphics for Data Analysis; Version, 2 (1); Springer-Verlag: New York, NY, USA, 2016. [Google Scholar]
- Centro Nacional de Información Geográfica. Modelo Digital del Terreno 2015 CC-BY 4.0. Available online: http://www.scne.es/ (accessed on 9 July 2021).
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; van der Linde, A. The deviance information criterion: 12 years on. J. R. Stat. Soc. 2014, 76, 485–493. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.; Stern, H.; Rubin, D. Bayesian Data Analysis, 2nd ed.; Texts in Statistical Science; Chapman and Hall: New York, NY, USA, 1995; 696p. [Google Scholar]


| Model | DIC | |||
|---|---|---|---|---|
| BHGCM-200 | 3697.57 | 3668.49 | 29.08 | 3726.64 |
| BHGCM-210 | 3589.41 | 3536.57 | 52.83 | 3642.24 |
| Model | DIC | |||
|---|---|---|---|---|
| BHM-210 | 4046.96 | 3997.51 | 49.46 | 4096.42 |
| BHGCM-210 | 3589.41 | 3536.57 | 52.83 | 3642.24 |
| Model | Location Sill | Location Range | Scale Sill | Scale Range |
|---|---|---|---|---|
| BHM-210 | 0.52 (0.18, 2.08) | 395.07 (132.90, 885.62) | 0.25 (0.11, 0.62) | 554.84 (235.55, 1110.02) |
| BHGCM-210 | 0.53 (0.18, 2.15) | 389.82 (125.59, 872.49) | 0.27 (0.12, 0.71) | 562.47 (233.41, 1133.02) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García, J.A.; Pizarro, M.M.; Acero, F.J.; Parra, M.I. A Bayesian Hierarchical Spatial Copula Model: An Application to Extreme Temperatures in Extremadura (Spain). Atmosphere 2021, 12, 897. https://doi.org/10.3390/atmos12070897
García JA, Pizarro MM, Acero FJ, Parra MI. A Bayesian Hierarchical Spatial Copula Model: An Application to Extreme Temperatures in Extremadura (Spain). Atmosphere. 2021; 12(7):897. https://doi.org/10.3390/atmos12070897
Chicago/Turabian StyleGarcía, J. Agustín, Mario M. Pizarro, F. Javier Acero, and M. Isabel Parra. 2021. "A Bayesian Hierarchical Spatial Copula Model: An Application to Extreme Temperatures in Extremadura (Spain)" Atmosphere 12, no. 7: 897. https://doi.org/10.3390/atmos12070897
APA StyleGarcía, J. A., Pizarro, M. M., Acero, F. J., & Parra, M. I. (2021). A Bayesian Hierarchical Spatial Copula Model: An Application to Extreme Temperatures in Extremadura (Spain). Atmosphere, 12(7), 897. https://doi.org/10.3390/atmos12070897







