Abstract
Atmospheric aerosol and ultraviolet index (UVI) measurements performed in Racibórz (50.08° N, 18.19° E) were analyzed for the period June–September 2019. Results of the following observations were taken into account: columnar characteristics of the aerosols (aerosol thickness, Angstrom exponent, single scattering albedo, asymmetry factor) obtained from standard CIMEL sun-photometer observations and parameters of aerosol layers (ALs) in the free troposphere (the number of layers and altitudes of the base and top) derived from continuous monitoring by a CHM-15k ceilometer. Three categories of ALs were defined: residues from the daily evolution of the planetary boundary layer (PBL) aerosols, from the PBL-adjacent layer, and from the elevated layer above the PBL. Total column ozone measurements taken by the Ozone-Monitoring Instrument on board NASA’s Aura satellite completed the list of variables used to model UVI variability under clear-sky conditions. The aim was to present a hybrid model (radiative transfer model combined with a regression model) for determining ALs’ impact on the observed UVI series. First, a radiative transfer model, the Tropospheric Ultraviolet–Visible (TUV) model, which uses typical columnar characteristics to describe UV attenuation in the atmosphere, was applied to calculate hypothetical surface UVI values under clear-sky conditions. These modeled values were used to normalize the measured UVI data obtained during cloudless conditions. Next, a regression of the normalized UVI values was made using the AL characteristics. Random forest (RF) regression was chosen to search for an AL signal in the measured data. This explained about 55% of the variance in the normalized UVI series under clear-sky conditions. Finally, the UVI values were calculated as the product of the RF regression and the relevant UVIs by the columnar TUV model. The root mean square error and mean absolute error of the hybrid model were 1.86% and 1.25%, respectively, about 1 percentage point lower than corresponding values derived from the columnar TUV model. The 5th–95th percentile ranges of the observation/model differences were [−2.5%, 2.8%] and [−3.0%, 5.3%] for the hybrid model and columnar TUV model, respectively. Therefore, the impact of ALs on measured surface UV radiation could be demonstrated using the proposed AL characteristics. The statistical analysis of the UVI differences between the models allowed us to identify specific AL configuration responsible for these differences.
1. Introduction
The importance of atmospheric aerosols on surface ultraviolet (UV) radiation has been recognized [1,2,3,4]. Aerosol parameters should be of special interest when searching for UV variability, especially in the summer season, when the total columnar ozone variability is usually small but the aerosol optical thickness can vary considerably even within a day [1]. Recent studies have reported specific properties of aerosols in the UV range of the solar spectrum which should be taken into account in UV irradiance modeling [4,5,6]. However, measurements of aerosols’ properties in the UV range are sparse (and in some cases highly uncertain), especially in the UV-B range [7,8]. Therefore, measured values in the visible range or fixed climatological values are often used instead.
To inform the public of the intensity of UV radiation that might cause various harmful effects, the so-called UV index (UVI), i.e., the erythemal irradiance (in Wm−2) multiplied by 40 m2W−1, was proposed. This scaling, which provides a dimensionless characteristic of the UV radiation, describes UV intensity as varying from 0 to above 20 (over high altitudes in the tropics [9]), helping people to better understand the risk of overexposure to UV radiation [10]. Scenarios of outdoor behavior have been released to encourage avoidance of exposure to strong UV radiation [11]. For example, if the UVI is above 3, people should start to protect themselves against UV radiation, and if the UVI exceeds 8, it is recommended to stay at home over the midday hours. However, recent findings have shown that protection should start even if UVI > 1 for some persons with light skin [12].
Aerosols’ effects on UV radiation are typically estimated via a radiative transfer model (RTM) using aerosol optical depth (AOD) [1,13,14,15,16] and other aerosol characteristics like Ångström exponent (AE) [17] and single scattering albedo (SSA) [18]. It is also assumed that the concentration of aerosol particles decreases with altitude, but distinct aerosol layers can sometimes be found above the planetary boundary layer (PBL) [19,20,21,22,23]. The modeled radiative effect of the aerosols in the aerosol layers (ALs) above the PBL may vary depending on the type of the aerosols (e.g., industrial, rural, biomass burning), altitude of the layers, and wavelength range [24,25]. These effects are especially pronounced for dust aerosols, which exhibit stronger absorption in the UV range. One of the most widely used RTM is the Tropospheric Ultraviolet–Visible (TUV) model, which has been proven to be a credible tool for reproducing the amount of UV radiation that reaches the surface [26,27,28].
Because the vertical distribution of aerosol properties is usually unknown to UVI modelers, they assume a standard vertical profile, such as that proposed by Elterman derived for continental regions [29], or that proposed by Shettle and Fenn [30]. The Elterman and Shettle aerosol profiles have been used in several studies, e.g., [31,32] and [33,34], respectively. Modelers then use columnar aerosol characteristics, which are much easier to obtain from ground-based observations taken with sun-photometers. The Eltermann profile states that 45% of total AOD is due to aerosols within the first kilometer, and 65% within the 2 km deep layer. Studies performed in different regions show that the average ratio between the AOD of the free troposphere and its total columnar value is around 25% for Wuhan [35], and over 40% for Taipei [36] and Warsaw [37].
In this study, we investigated how the distribution of ALs above the PBL affects the UVI variability. Continuous measurements of backscattered laser light data taken at Racibórz (50.08° N, 18.19° E) by the CHM-15k ‘Nimbus’ ceilometer were archived for the period 2017–2019. The presence of multi-layered aerosol structures in the free troposphere can sometimes be identified. These cases were further analyzed to determine the AL types in the free troposphere and their basic characteristics (number of layers and altitudes of the base and top of each layer).
Comparing the UVI differences calculated by two models, one containing only the columnar characteristics of aerosols (standard TUV model) and the other (a proposed hybrid model also including information on the characteristics of ALs), we investigated the aerosol layering signal hidden in the UVI values measured with a standard broad-band UV meter.
2. Materials and Methods
Concurrent measurements of backscatter profiles, columnar aerosol optical parameters, and solar UV radiation were carried out in the Raciborz observatory (50.08° N, 18.19° E), operated by the Institute of Geophysics (IG), Polish Academy of Sciences (PAS), between January 2017 and December 2019. Raciborz is a town in southern Poland, close to the Czech Republic border, located in a depression between the Sudetes and the Carpathian Mountains (also known as the Moravian Gate). This area is affected by local urban and industrial pollution from the densely populated area of Silesia in southwest Poland and the northeast Czech Republic (the Ostrava industrial zone). Moreover, aerosols originating from remote locations may play an important role in the modification of UV radiation [21,38].
2.1. Measurements
The observatory at Racibórz is equipped with a CHM-15k ‘Nimbus’ ceilometer (aerosol backscatter profiles), a triple sun-sky-lunar CIMEL photometer (columnar optical characteristics of aerosols), and a Kipp & Zonen UVS-E-T biometer measuring the intensity of the erythemal solar radiation.
Continuous measurements of the UV index (UVI) with a 1 min resolution have been taken at the site by the Kipp & Zonen UVS-E-T biometer (KZB) since June 2019, and the results are archived using three significant digits. It is worth mentioning that only rounded integers are used to inform the public about UV intensity. The biometer typically measures the total daily erythemal irradiance with standard uncertainty of ~5% as provided by the producer (https://www.kippzonen.com/Product/428/SUV-E-UVE-Radiometer, accessed on 21 June 2021). The KZB was calibrated (May 2018) with the Brewer spectroradiometer (Mark II No. 64) operating at the IG PAS Central Geophysical Laboratory, Belsk (51.84° N, 20.79° E), before monitoring began in Raciborz. The Brewer spectrometers, besides their primary goal of making observations of the atmospheric ozone, are also used for AOD and UV spectral measurements [39].
Ceilometers are designed primarily for measurement of cloud base height. However, newer LIDAR (light detection and ranging)-based designs can be used to obtain some information on aerosols’ vertical structures [40]. Technical details of the CHM-15k ‘Nimbus’ ceilometer and the benefits of using LIDAR soundings of atmospheric aerosols are shown in [41,42]. Unfortunately, precise retrieval of aerosol optical parameters from ceilometer profiles is a difficult task, due to the necessity of assuming parameters associated with the type of the observed aerosols as well as the insufficient signal-to-noise ratio at higher altitudes. Therefore, we focused here on only basic information on the aerosol layering, including the geometrical parameters of each layer and its type, derived from the position of the layer base relative to the top of the PBL (Figure 1).
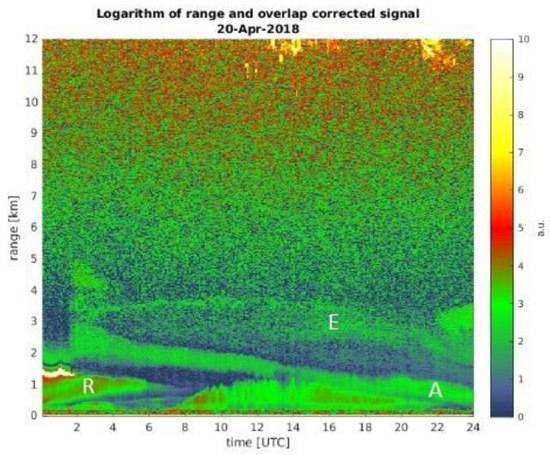
Figure 1.
Examples of the attenuated backscattered signal received by the CHM-15k Nimbus ceilometer on 29 August 2017 in Racibórz. The colored scale on the right shows the intensity of the backscattered LIDAR light. The letters R, A, and E denote the residual layer, the layer adjacent to the PBL top, and the elevated layer above the PBL.
Classification of ALs above the PBL has been proposed based on the location of the ALs’ boundaries in relation to the PBL top, i.e., the residual layer appearing in the decay phase of the daytime PBL, the layer existing on the top of the PBL (this AL is hereinafter referred to as the adjacent layer), and a separate elevated layer above the top of the PBL. Various AL types may exist at the same time. For example, Figure 1 illustrates the presence of an elevated AL at the level of ~3 km, which persisted for 24 h. Moreover, an adjacent AL was identified after 4 pm, and a residual AL between 0–6 a.m. on 20 April 2018. In further calculations, each AL is characterized by the following parameters: the altitude of its base and top, and the flag denoting the abovementioned AL’s type.
The ceilometer observations were combined with concurrent measurements of the columnar properties of aerosols taken by the CIMEL sun-photometer, which is a part of the Aerosol Robotic Network (AERONET). The instrument provides the various microphysical parameters of aerosols [41,43,44,45]. In this study, we used AOD at 340 nm, AE for the 340–440 nm range, single scattering albedo (SSA), and total asymmetry factor (AF) at 440 nm derived from the AERONET aerosol inversion algorithm ver. 3 [46]. The quality level of the aerosol data at the start of the analysis was 1.5 (cloud screened), i.e., the highest possible at the start of this analysis. The technical details of the CIMEL observations and the algorithms used are on the web page of the AERONET global network (https://aeronet.gsfc.nasa.gov/, accessed on 21 June 2021). The results obtained from this network allow for a global view of aerosol distribution [44].
2.2. Hybrid UVI Model
The following multistep approach to reveal the impact of ALs on surface UVI is proposed. The TUV model, using typical columnar characteristics describing UV attenuation in the atmosphere (AOD, SSA, and AE from the CIMEL sun-photometer measurements), was applied to calculate synthetic UVI values at the ground level under clear-sky conditions. Moreover, a surface albedo of 0.05 in the UV range was assumed as representative for the UV measurement site (grass in the summer period). Moreover, the Elterman profile for the vertical distribution of aerosols and the US Standard Atmosphere at 45° N for the ozone vertical profile were used in the UV calculations. TUV uses atmospheric constituent profiles (for the UV range these are O3, SO2, and NO2) based on standard profiles proposed by the Air Force Geophysics Laboratory (AFGL) [47]. Moreover, the absorption cross-sections (dependent on temperature) for these gases were taken into account. Rayleigh scattering by air molecules was parameterized using an empirical formula by Nicolet [48]. The TUV radiative transfer model calculates spectral radiative parameters in 120–750 nm range with a 0.01 nm resolution, allowing various biologically effective irradiations including UVI (erythemal irradiation) to be obtained [26,27,28]. Here, the TUV radiative transfer model was used with the columnar properties of aerosols determined by the CIMEL instrument and the total columnar amount of ozone as input parameters. The total ozone was obtained from the Ozone-Monitoring Instrument (OMI) [49] onboard NASA’s Aura satellite, which is a part of the Earth Observing System (EOS). Here, total ozone over Racibórz was interpolated from the gridded data product: OMI/Aura Ozone Differential Absorption Spectroscopy (DOAS) Total Column L3 1 day 0.25° × 0.25° Version 3 (https://disc.gsfc.nasa.gov/datasets/OMDOAO3e_003/summary, accessed on 21 June 2021).
Next, synthetic UVI values were used to normalize the measured UVI data obtained under cloudless conditions. A regression of these normalized UVI values on the AL characteristics was built. The following aerosol layer characteristics were considered: the total number of layers, the number of adjacent layers and residual layers, the mean values of AL base and top height, and the total geometrical thickness of all ALs. The random forest (RF) regression was selected to find a relationship between the variability of the normalized UVI from KZB measurements and the abovementioned AL characteristics. Here, RF regression was applied to the normalized 15 min mean UVI values measured under clear-sky conditions, which were calculated by averaging the results of the 1 min KZB observations after the normalization for every quarter of an hour from sunset to sunrise. The RF model combines many decision trees into a single regression model. It uses an artificial intelligence technique to search for the complex (nonlinear) impact of model input on its output [50,51].
Finally, the UVI values by the hybrid model were calculated as the product of the RF regression output (normalized UVI values affected by aerosol layering) and the relevant synthetic UVI values (determined by the columnar TUV modeled). These data were compared with the UVI values measured by the KZB in Raciborz.
3. Results
Aerosol profiles were measured for 931 days between 1 January 2017 and 30 September 2019 at Racibórz station. This equates to 92.8% temporal coverage of all days within this period. Some gaps in measurements were related to instrument technical issues and service-associated downtime. A layered structure in the backscattered light was found on 57.5% of measurement days. The presence of possibly existing ALs could not be detected for the rest of the days due to noise caused by the scattering of LIDAR light by clouds. Days with neither clouds nor ALs were not found. A manual procedure was used to reveal ALs in the free troposphere. Areas with a stronger backscattered signal should exist for several hours without abrupt changes in the intensity of the backscattered signal and have sharp boundaries in order to be classified as ALs. It is worth mentioning that a more objective method for AL searching is needed. To some extent, AL statistics show the individual observer’s ability to analyze vertical profiles of backscattered LIDAR light rather than the actual state of the atmosphere.
Monthly mean values of frequency for the days with observed aerosol layers are depicted in Figure 2. The corresponding contribution of each aerosol layer class to the total number of identified layers is also presented. These contributions for the residual, adjacent (on the PBL top), and the elevated free troposphere ALs add up to 100%. The adjacent class also comprises cases when the layer contained residual aerosols from the decaying daily PBL. The highest frequency was found in August, when ALs were found in ~80% of days with the backscattered profiles. The lowest frequency was in November, when aerosol layers were only identified on ~15–20% of the days, which was mostly due to persistent and heavy cloudiness in this month. The contribution of the elevated ALs in the free troposphere and the adjacent layers was almost constant throughout the year and varied between approximately 40% and 50%. The contribution of the residual aerosols is about 10% and the highest value was in September.
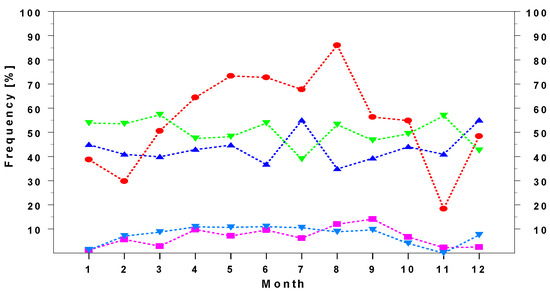
Figure 2.
Monthly frequencies of days with aerosol layers (red circles), and the following categories of the aerosol layer: adjacent (blue upward triangles), residual (magenta squares), adjacent & residual (blue downward triangles), and elevated in the free troposphere (green downward triangles).
The mean AL thickness was lower during winter (around 0.5–0.7 km) and higher in the summer (around 1.25 km). The maximum thickness often reached ~3 km, with extreme cases above 4 km. The total number of layers per day, between one and four, did not show seasonal variability.
The 15 min averages of the UVIs are shown in Figure 3a for measurements taken under cloudless conditions in the period June–September 2019. The presence of direct sun observations by the CIMEL photometer (data with quality level 1.5, i.e., cloud screened and quality controlled, were used) and the smoothed UVI pattern (clouds cause strong oscillations in UV signal recorded by the biometer) supported clear-sky conditions. The average UVI values measured over a quarter of an hour, for which at least three CIMEL direct sun measurements were taken, were considered for further statistical analysis. In total, 291 observation/model pairs are available for the model–observation UVI comparison. High UVI values up to 8 were found around noon in June, but low values of ~0.5–1.0 were found every early morning because of low solar elevation.
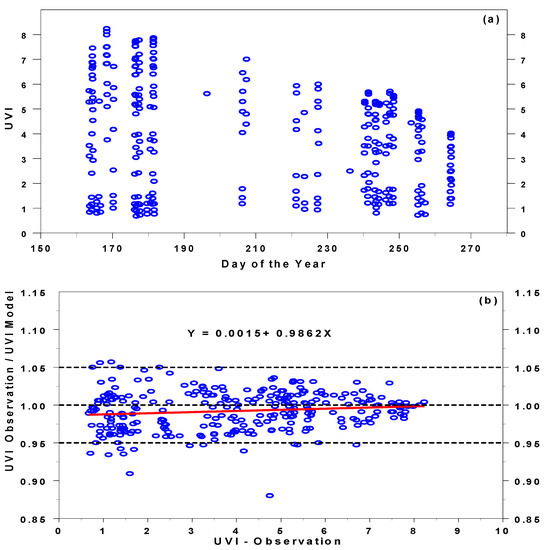
Figure 3.
The measurements of UVI for cloudless periods in Racibórz (June–September 2019): (a) UVI as a function of the calendar day in 2019, (b) the normalized UVI (by the corresponding estimate by the columnar TUV model) versus the measured UVI.
A good agreement between the observed UVI and columnar TUV model values was found (Figure 3b). The measured UVI values after normalization with the relevant columnar TUV model were within the ±5% range for almost 95% of the cases. The mean and median were equal to 0.99, and the corresponding standard deviation was ~0.03. The range (minimum to maximum) was between 0.88 and 1.06. The linear regression (red line) of the normalized UVI on the UVI value showed that the agreement was better for large UVIs. Further, we investigated whether RF regression, including the considered parameters of the aerosols layering above PBL, improved the model–observation agreement for clear-sky conditions.
The RF regression explained ~52% of the variance of the normalized UVIs and provided a ranking of the explaining variables. This was computed for the i-th variable as the percentage rise of the sum-of-squared errors when the i-th variable was removed from the set of the explaining variables [50,51]. Table 1 shows the ranking, with the most important variable being no. 3 and the least important variable being no. 5.

Table 1.
Ranking of the explaining AL variables in the RF regression of the normalized 15 min clear-sky UVI means for the period of June–September 2019.
The performance of the two examined UVI models was compared using the differences between the observed and modeled UVIs as the percentage of the observed values, i.e., the so-called fractional deviation between the model and observation values. Figure 4a,b shows the performance of the columnar TUV and hybrid model (including all possible AL characteristics shown in Table 1), respectively.
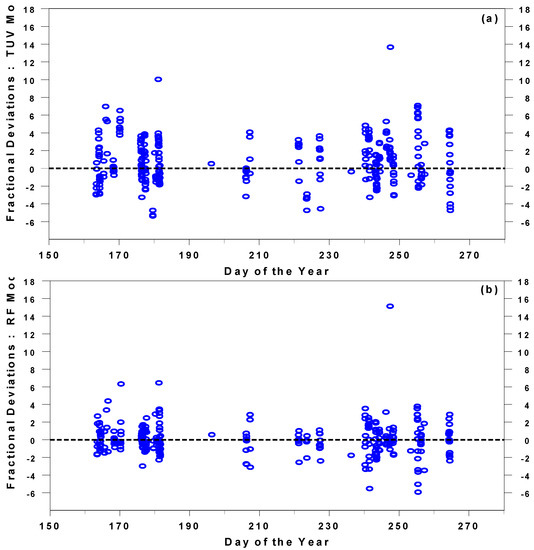
Figure 4.
(a) Fractional deviations between modeled (by columnar TUV) and measured (by Raciborz’s biometer) UV indices; (b) fractional deviations between modeled (by the hybrid model) and measured UV indices.
Statistical characteristics of the model’s performance and the differences between the UVIs determined by the columnar TUV and hybrid models are shown in Table 2. UVIs determined by the hybrid model were closer to the measured ones, as the mean of the differences and median were ~0 and the standard deviation (SD), mean absolute error (MAE), the 5th–95th percentile range, and root mean square error (RMSE) were ~1 percentage point lower than the respective values determined by the columnar TUV model. The statistical characteristics of UVI differences between the models (fourth column in Table 2) suggested a significant difference between the outputs of the models. The two-sample Kolmogorov–Smirnov test of the difference between the two samples confirmed that the difference was statistically significant at a confidence level better than 99%.

Table 2.
Statistical characteristics of the differences between the UVIs from observations (UVIOB), columnar TUV model (UVICL), and hybrid model (UVIHY).
Figure 5 show the histograms of the fractional deviations corresponding to the examined UVI pairs shown in Table 2 (i.e., Figure 5a–c corresponds with the second, third, and fourth columns of Table 2). The Kolmogorov–Smirnov test showed that none of the distribution shown in Figure 5 was a normal one. From the comparison of Figure 5a,b, a narrower distribution and more frequent cases in the range [−1%, 1%] was noticed for the output of the hybrid model, which confirmed a better agreement of the this model with the measured UVIs.
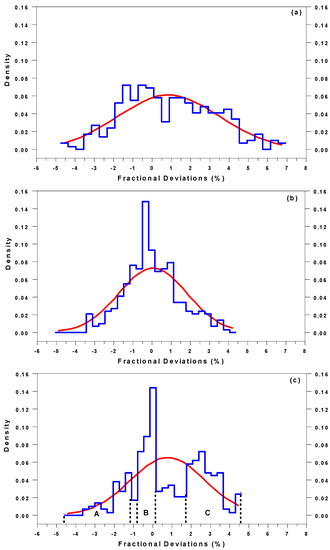
Figure 5.
Histograms of the normalized differences between UVI values from the biometer measurements, UVIOB; simulations by the columnar TUV model, UVICL; and the hybrid model UVIHY: (a) (UVICL−UVIOB)/UVIOB × 100%; (b) (UVIHY−UVIOB)/UVIOB × 100% and (c) (UVICL−UVIHY)/UVICL × 100%. The red curve shows the normal distribution based on the mean value and standard deviation. The following ranges for Classes A, B, and C, which were based on (UVICL−UVIHY)/UVICL × 100% values, were selected: (−5.2, −1.17), (−0.75, 0.00), and (1.7, 5.1), respectively.
The distribution of the normalized difference between UVIs determined by the columnar TUV and hybrid models allowed the selection of three classes of the differences i.e., significantly higher UVI values returned by the hybrid model compared to those returned by the columnar TUV model (Class A in Figure 5c), almost equal (Class B), and significantly lower (Class C). Table 3 shows the AL characteristics for these classes. For Class C, more ALs were found (approximately two layers existed in each 15 min interval of UVI measurements). Usually, a single AL appeared during the interval for Classes A and B. The adjacent layers were less frequent in Class A and B compared to Class C. There was a similar frequency of the residual layers in Classes B and C, but a very low frequency (0.04) appeared in Class A. The AOD at 340 nm and AE (for the 340–440 nm range) were almost equal in all analyzed classes at ~0.32, and 1.1, respectively.

Table 3.
Mean values of the AL characteristics for the three AL classes shown in Figure 5c. In addition, aerosol optical depth (AOD) at 340 nm and the Angstrom exponent (AE) for the 340–440 nm range (from the concurrent measurements by the CIMEL sun-photometer) are included for these classes.
In the case of Class C, it seems that at least one of the ALs identified in the 15 min interval of UVI measurements probably had a high concentration of absorbing aerosols, since Class C included cases with lower UVI estimates returned by the hybrid model compared to the columnar TUV model. Class A comprised ALs with larger UVIs returned by the hybrid model compared to the TUV estimates. An elevated and ~2 km thick layer in the free troposphere was typical for Class A (a low frequency of the adjacent and residual ALs was observed in this case). Columnar values of AOD and AE did not help to categorize ALs based on the differences between the models.
4. Discussion
The TUV model, supplied with satellite-based ozone concentrations and aerosol columnar properties measured by the CIMEL sun-photometer, proved to be a credible tool for modeling surface UV indices during cloud-free conditions. It explained most of the time-averaged 15 min UV indices’ variances (see Figure 3b) regardless of the use of several assumptions concerning the spectral dependence of the aerosols’ characteristics, constant ground albedo, vertical profiles of ozone, and AOD. The AERONET retrieval does not provide aerosol characteristics in the UV-B range (290–315 nm), which are more appropriate for UVI modeling. Finally, our selection of input to the TUV model provided rather small bias (~1%) and standard deviation of the model/observation differences (2.5%). This corresponded to ~5% uncertainty (for a coverage factor of 2) of UV radiation by RTM, taking into account reasonable variability of the input parameters [52,53]. There is, however, still room for improvement in the surface UV modeling, as the normalized UVIs (normalized by the corresponding results of the TUV model) were found to be dependent on aerosol layering in the atmosphere, as was supported by the RF regression approach. The complex nature of interactions between aerosols and radiation (e.g., multiple scattering of solar light between the aerosols layers) requires a more advanced approach. The random forest regression, supplied with basic aerosol layer properties (but without the aerosols’ concentration in the layers), significantly improved fit to the observed UVI. It explained more than 50% of the observed variance of the normalized UVI values. This was possible despite the subjective nature of the manual procedure applied to disclose AL characteristics. This procedure apparently provided valuable information, indicating that a signal from aerosol layering is hidden in the observed UVI values.
Statistical analysis of the differences between the hybrid model (comprising the radiative transfer model and the RF regression) and the radiation transfer model using columnar aerosols characteristics allowed three AL categories to be distinguished. The most significant differences between these classes were in the number of layers above the PBL and the frequencies of residual and adjacent layer per 15 min interval of UVI measurements. For the category of the UVI values returned smaller by the hybrid model compared to the columnar TUV model (refer to Class C in Figure 5c), one layer was close to the PBL top. It might have been the residual or adjacent layer, but the adjacent layer was about 2 times more probable. The second AL resided in the free troposphere. For the category of UVI values returned larger by the hybrid model than by the columnar TUV model (see Class A in Figure 5c), one layer was typically observed per 15 min interval. The probability of the appearance of an adjacent layer was small (~0.2), and there was practically no chance of a residual layer appearing. This means that this category probably included one elevated AL in the free troposphere.
The aforementioned statistical approach used only the basic characteristics of aerosol layers, being mainly geometrical properties and the AL type. Other optical and microphysical aerosol parameters of the layers, like size distribution, and complex refractive indices, were not included in present analysis. It seems that the inclusion of these parameters into the analytical scheme might further improve the modeling. This will require the use of a more advanced experimental setup, e.g., Raman LIDAR collocated with a sunphotometer, and a special numerical approach to retrieve profiles of asymmetry parameters and SSA. The most promising tool is a generalized retrieval of aerosol and surface properties (GRASP) [42,54].
To conclude this work, we can state that the surface UVI measured in cloudless conditions by standard biometer (Kipp & Zonen UVS-E-T) operating in Racibórz was well modeled by the TUV model based only on the columnar aerosol and ozone properties. Measurements of the aerosol vertical structure by the means of CHM-15k ‘Nimbus’ ceilometer provided valuable information on aerosol layering that could be incorporated into advanced statistical modeling of AL impact on surface UV radiation. RF regression emerged as a prospective statistical tool to study such effects.
Author Contributions
A.F. performed a manual analysis of aerosol layers over Racibórz based on ceilometer observations; A.P. formulated the concept of the work and drew conclusions based on the obtained results; A.S. contributed to the analysis of the results and formulation of conclusions, as well as preparation of the figures; J.K. performed statistical analysis and compared the results with the TUV model deliverables. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Science Centre (Poland) under grant No.2017/25/B/ST1001650. This work was supported by a subsidy from the Polish Ministry of Eduction and Science for the Institute of Geophysics, Polish Academy of Sciences.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The sun-photometer data is available through the AERONET website https://aeronet.gsfc.nasa.gov/cgi-bin/data_display_aod_v3?site=Raciborz&nachal=2&level=2&place_code=10 (accessed on 21 June 2021). Metadata information for the remaining optical measurements is available on the IG PAS Data Portal https://dataportal.igf.edu.pl/organization/atmospheric-physics (accessed on 21 June 2021). For raw data please contact the data steward: data_steward@igf.edu.pl.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Krzyścin, J.W.; Puchalski, S. Aerosol impact on the surface UV radiation from the ground-based measurements taken at Belsk, Poland, 1980–1996. J. Geophys. Res. Atmos. 1998, 103, 16175–16181. [Google Scholar] [CrossRef]
- Jarosławski, J.P.; Krzyścin, J.W. Importance of aerosol variations for surface UV-B level: Analysis of ground-based data taken at Belsk, Poland, 1992–2004. J. Geophys. Res. Atmos. 2005, 110, D16. [Google Scholar] [CrossRef]
- Krzyścin, J.W.; Jarosławski, J. Factors affecting solar UV radiation changes: A study of the new Robertson-Berger meter (UV-biometer model 501A) and Brewer data records taken at Belsk, Poland, 1993–1994. J. Atmos. Sol. Terr. Phys. 1997, 59, 1133–1142. [Google Scholar] [CrossRef]
- Kim, J.; Cho, H.K.; Mok, J.; Yoo, H.D.; Cho, N. Effects of ozone and aerosol on surface UV radiation variability. J. Photochem. Photobiol. B Biol. 2013, 119, 46–51. [Google Scholar] [CrossRef] [PubMed]
- Mok, J.; Krotkov, N.A.; Torres, O.; Jethva, H.; Li, Z.; Kim, J.; Koo, J.; Go, S.; Irie, H.; Labow, G.; et al. Comparisons of spectral aerosol single scattering albedo in Seoul, South Korea. Atmos. Meas. Tech. 2018, 11, 2295–2311. [Google Scholar] [CrossRef]
- Fountoulakis, I.; Natsis, A.; Siomos, N.; Drosoglou, T.; Bais, A.F. Deriving aerosol absorption properties from solar ultraviolet radiation spectral measurements at Thessaloniki, Greece. Remote Sens. 2019, 11, 2019. [Google Scholar] [CrossRef]
- Kazadzis, S.; Raptis, P.; Kouremeti, N.; Amiridis, V.; Arola, A.; Gerasopoulos, E.; Schuster, G.L. Aerosol absorption retrieval at ultraviolet wavelengths in a complex environment. Atmos. Meas. Tech. 2016, 9, 5997–6011. [Google Scholar] [CrossRef]
- Raptis, I.P.; Kazadzis, S.; Eleftheratos, K.; Amiridis, V.; Fountoulakis, I. Single scattering albedo’s spectral dependence effect on UV irradiance. Atmosphere 2018, 9, 364. [Google Scholar] [CrossRef]
- Cabrol, N.A.; Feister, U.; Häder, D.P.; Piazena, H.; Grin, E.A.; Klein, A. Record solar UV irradiance in the tropical Andes. Front. Environ. Sci. 2014, 2. [Google Scholar] [CrossRef]
- Vanicek, K.; Frei, T.; Litynska, Z.; Schmalwieser, A. UV-Index for the Public. Brussels. 2000. Available online: http://www.temis.nl/uvradiation/info/Vanicek_et_al_COST-713_2000.pdf (accessed on 21 June 2021).
- WHO; WMO; UNEP; ICNIRP. Global Solar UV Index: A Practical Guide; A Joint Recommendation of the World Health Organiz; World Health Organization: Geneva, Switzerland, 2002. [Google Scholar]
- Lehmann, M.; Pfahlberg, A.B.; Sandmann, H.; Uter, W.; Gefeller, O. Public health messages associated with low uv index values need reconsideration. Int. J. Environ Res. Public Health 2019, 16, 2067. [Google Scholar] [CrossRef]
- Kim, W.; Kim, J.; Park, S.S.; Cho, H.K. UV sensitivity to changes in ozone, aerosols, and clouds in Seoul, South Korea. J. Appl. Meteorol. Climatol. 2017, 53, 310–322. [Google Scholar] [CrossRef]
- Krzyścin, J.W.; Jarosławski, J.; Sobolewski, P. On an improvement of UV index forcast: UV index diagnosis and forecast for Belsk, Poland, in Spring/Summer 1999. J. Atmos. Sol. Terr. Phys. 2001, 63, 1593–1600. [Google Scholar] [CrossRef]
- Lamy, K.; Portafaix, T.; Josse, B.; Brogniez, C.; Godin-Beekmann, S.; Bencherif, H.; Revell, L.; Akiyoshi, H.; Bekki, S.; Hegglin, M.I.; et al. Clear-sky ultraviolet radiation modelling using output from the Chemistry Climate Model Initiative. Atmos. Chem. Phys. 2019, 198, 10087–10110. [Google Scholar] [CrossRef]
- Kylling, A.; Bais, A.F.; Blumthaler, M.; Schreder, J.; Zerefos, C.S.; Kosmidis, E. Effect of aerosols on solar UV irradiances during the Photochemical Activity and Solar Ultraviolet Radiation campaign. J. Geophys. Res. Atmos. 1998, 103, 26051–26060. [Google Scholar] [CrossRef]
- Jarosławski, J.; Krzyścin, J.W.; Puchalski, S.; Sobolewski, P. On the optical thickness in the UV range: Analysis of the ground-based data taken at Belsk, Poland. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Bais, A.F.; Kazantzidis, A.; Kazadzis, S.; Balis, D.S.; Zerefos, C.S.; Meleti, C. Deriving an effective aerosol single scattering albedo from spectral surface UV irradiance measurements. Atmos. Environ. 2005, 39, 1093–1102. [Google Scholar] [CrossRef]
- Baars, H.; Ansmann, A.; Ohneiser, K.; Haarig, M.; Engelmann, R.; Althausen, D.; Hanssen, I.; Gausa, M.; Pietruczuk, A.; Szkop, A.; et al. The unprecedented 2017–2018 stratospheric smoke event: Decay phase and aerosol properties observed with the EARLINET. Atmos. Chem. Phys. 2019, 19, 15183–15198. [Google Scholar] [CrossRef]
- Markowicz, K.M.; Chilinski, M.T.; Lisok, J.; Zawadzka, O.; Stachlewska, I.S.; Janicka, L.; Rozwadowska, A.; Makuch, P.; Pakszys, P.; Zielinski, T.; et al. Study of aerosol optical properties during long-range transport of biomass burning from Canada to Central Europe in July 2013. J. Aerosol Sci. 2016, 101, 156–173. [Google Scholar] [CrossRef]
- Szkop, A.; Pietruczuk, A. Analysis of aerosol transport over southern Poland in August 2015 based on a synergy of remote sensing and backward trajectory techniques. J. Appl. Remote Sens. 2017, 11, 016039. [Google Scholar] [CrossRef]
- Amiridis, V.; Balis, D.S.; Kazadzis, S.; Bais, A.; Giannakaki, E.; Papayannis, A.; Zerefos, C. Four-year aerosol observations with a Raman lidar at Thessaloniki, Greece, in the framework of European Aerosol Research Lidar Network (EARLINET). J. Geophys. Res. Atmos. 2005, 110, 1–12. [Google Scholar] [CrossRef]
- Barragan, R.; Sicard, M.; Totems, J.; Léon, J.F.; Dulac, F.; Mallet, M.; Pelon, J.; Alados-Arboledas, L.; Amodeo, A.; Augustin, P.; et al. Spatio-temporal monitoring by ground-based and air- and space-borne lidars of a moderate Saharan dust event affecting southern Europe in June 2013 in the framework of the ADRIMED/ChArMEx campaign. Air Qual. Atmos. Health 2017, 10, 261–285. [Google Scholar] [CrossRef]
- Mishra, A.K.; Koren, I.; Rudich, Y. Effect of aerosol vertical distribution on aerosol-radiation interaction: A theoretical prospect. Heliyon 2015, 1, 36. [Google Scholar] [CrossRef] [PubMed]
- Siomos, N.; Fountoulakis, I.; Natsis, A.; Drosoglou, T.; Bais, A. Automated aerosol classification from spectral UV measurements using machine learning clustering. Remote Sens. 2020, 12, 965. [Google Scholar] [CrossRef]
- Madronich, S.; Flocke, S. The Role of Solar Radiation in Atmospheric Chemistry; Springer: Berlin/Heidelberg, Germany, 1999; pp. 1–26. [Google Scholar]
- Madronich, S.; Flocke, S. Theoretical Estimation of Biologically Effective UV Radiation at the Earth’s Surface. In Solar Ultraviolet Radiation; Springer: Berlin/Heidelberg, Germany, 1997; pp. 23–48. [Google Scholar]
- Madronich, S.; McKenzie, R.L.; Björn, L.O.; Caldwell, M.M. Changes in biologically active ultraviolet radiation reaching the Earth’s surface. J. Photochem. Photobiol. B Biol. 1998, 46, 5–19. [Google Scholar] [CrossRef]
- Elterman, L. UV, Visible and IR Attenuation for Alititudes to 50 km. Available online: https://apps.dtic.mil/sti/pdfs/AD0671933.pdf (accessed on 21 June 2021).
- Shettle, E.P.; Fenn, R.W. Models for the Aerosols of the Lower Atmosphere and the Effects of Humidity Variations on Their Optical Properties; Springer: Cambridge, MA, USA, 1979. [Google Scholar]
- Barbaro, E.; de Arellano, J.V.G.; Ouwersloot, H.G.; Schröter, J.S.; Donovan, D.P.; Krol, M.C. Aerosols in the convective boundary layer: Shortwave radiation effects on the coupled land-atmosphere system. J. Geophys. Res. 2014, 119, 5845–5863. [Google Scholar] [CrossRef]
- Michalsky, J.J.; Kiedron, P.W. Comparison of UV-RSS spectral measurements and TUV model runs for clear skies for the May 2003 ARM aerosol intensive observation period. Atmos. Chem. Phys. 2008, 8, 1813–1821. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations—Description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Dudhia, J.; Gueymard, C.A. A simple parameterization of the short-wave aerosol optical properties for surface direct and diffuse irradiances assessment in a numerical weather model. Geosci. Model Dev. 2014, 7, 1159–1174. [Google Scholar] [CrossRef]
- Shao, J.; Yi, F.; Yin, Z. Aerosol layers in the free troposphere and their seasonal variations as observed in Wuhan, China. Atmos. Environ. 2020, 224, 117323. [Google Scholar] [CrossRef]
- Chen, W.N.; Chen, Y.W.; Chou, C.C.K.; Chang, S.Y.; Lin, P.H.; Chen, J.P. Columnar optical properties of tropospheric aerosol by combined lidar and sunphotometer measurements at Taipei, Taiwan. Atmos. Environ. 2009, 43, 2700–2708. [Google Scholar] [CrossRef]
- Wang, D.; Szczepanik, D.; Stachlewska, I.S. Interrelations between surface, boundary layer, and columnar aerosol properties derived in summer and early autumn over a continental urban site in Warsaw, Poland. Atmos. Chem. Phys. 2019, 19, 13097–13128. [Google Scholar] [CrossRef]
- Szkop, A.; Pietruczuk, A. Synergy of satellite-based aerosol optical thickness analysis and trajectory statistics for determination of aerosol source regions. Int. J. Remote Sens. 2019, 40, 8450–8464. [Google Scholar] [CrossRef]
- Kerr, J.B. The brewer spectrophotometer. In UV Radiation in Global Climate Change: Measurements, Modeling and Effects on Ecosystems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 160–191. [Google Scholar]
- Markowicz, K.M.; Flatau, P.J.; Kardas, A.E.; Remiszewska, J.; Telmaszczyk, K.; Woeste, L. Ceilometer retrieval of the boundary layer vertical aerosol extinction structure. J. Atmos. Ocean. Technol. 2008, 25, 928–944. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Dubovik, O.; Herman, M.; Holdak, A.; Lapyonok, T.; Tanré, D.; Deuzé, J.L.; Ducos, F.; Sinyuk, A.; Lopatin, A. Statistically optimized inversion algorithm for enhanced retrieval of aerosol properties from spectral multi-angle polarimetric satellite observations. Atmos. Meas. Tech. 2011, 4, 975–1018. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A flexible inversion algorithm for retrieval of aerosol optical properties from Sun and sky radiance measurements. J. Geophys. Res. Atmos. 2000, 105, 20673–20696. [Google Scholar] [CrossRef]
- Eck, T.F.; Holben, B.N.; Slutsker, I.; Setzer, A. Measurements of irradiance attenuation and estimation of aerosol single scattering albedo for biomass burning aerosols in Amazonia. J. Geophys. Res. Atmos. 1998, 103, 31865–31878. [Google Scholar] [CrossRef]
- NO’Neill, T.; Eck, T.F.; Smirnov, A.; Holben, B.N.; Thulasiraman, S. Spectral discrimination of coarse and fine mode optical depth. J. Geophys. Res. Atmos. 2003, 108, 4559. [Google Scholar] [CrossRef]
- Giles, D.M.; Sinyuk, A.; Sorokin, M.G.; Schafer, J.S.; Smirnov, A.; Slutsker, I.; Eck, T.F.; Holben, B.N.; Lewis, J.R.; Campbell, J.R.; et al. Advancements in the Aerosol Robotic Network (AERONET) Version 3 database—Automated near-real-time quality control algorithm with improved cloud screening for Sun photometer aerosol optical depth (AOD) measurements. Atmos. Meas. Tech. 2019, 12, 169–209. [Google Scholar] [CrossRef]
- Anderson, G.P.; Chetwynd, J.H.; Clough, S.A.; She1tle, E.P.; Kneizys, F.X. AFGL Atmospheric Constituent Profiles (0–120 km); Air Force Geophys. Lab., Hanscom Air Force Base: Bedford, MA, USA, 1986; Available online: https://apps.dtic.mil/sti/citations/ADA175173 (accessed on 16 June 2021).
- Nicolet, M. On the molecular scattering in the terrestrial atmosphere: An empirical formula for its calculation in the homosphere. Planet. Space Sci. 1984, 32, 1467–1468. [Google Scholar] [CrossRef]
- Levelt, P.F.; Joiner, J.; Tamminen, J.; Veefkind, J.P.; Bhartia, P.K.; Zweers, D.C.S.; Duncan, B.N.; Streets, D.G.; Eskes, H.; van der A, R.; et al. The Ozone Monitoring Instrument: Overview of 14 years in space. Atmos. Chem. Phys. 2018, 18, 5699–5745. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random Forests. In Ensemble Machine Learning; Springer: Boston, MA, USA, 2012; pp. 157–175. [Google Scholar]
- Belluardo, G.; Barchi, G.; Baumgartner, D.; Rennhofer, M.; Weihs, P.; Moser, D. Uncertainty analysis of a radiative transfer model using Monte Carlo method within 280–2500 nm region. Sol. Energy 2016, 132, 558–569. [Google Scholar] [CrossRef]
- Koepke, P.; Bais, A.; Balis, D.; Buchwitz, M.; de Backer, H.; de Cabo, X.; Eckert, P.; Eriksen, P.; Gillotay, D.; Heikkilä, A.; et al. Comparison of Models Used for UV Index Calculations. Photochem. Photobiol. 1998, 67, 657–662. [Google Scholar] [CrossRef]
- Lopatin, A.; Dubovik, O.; Chaikovsky, A.; Goloub, P.; Lapyonok, T.; Tanré, D.; Litvinov, P. Enhancement of aerosol characterization using synergy of lidar and sun-photometer coincident observations: The GARRLiC algorithm. Atmos. Meas. Tech. 2013, 6, 2065–2088. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).