The Optimization of Aircraft Acceleration Response and EDR Estimation Based on Linear Turbulence Field Approximation
Abstract
:1. Introduction
2. Methodology
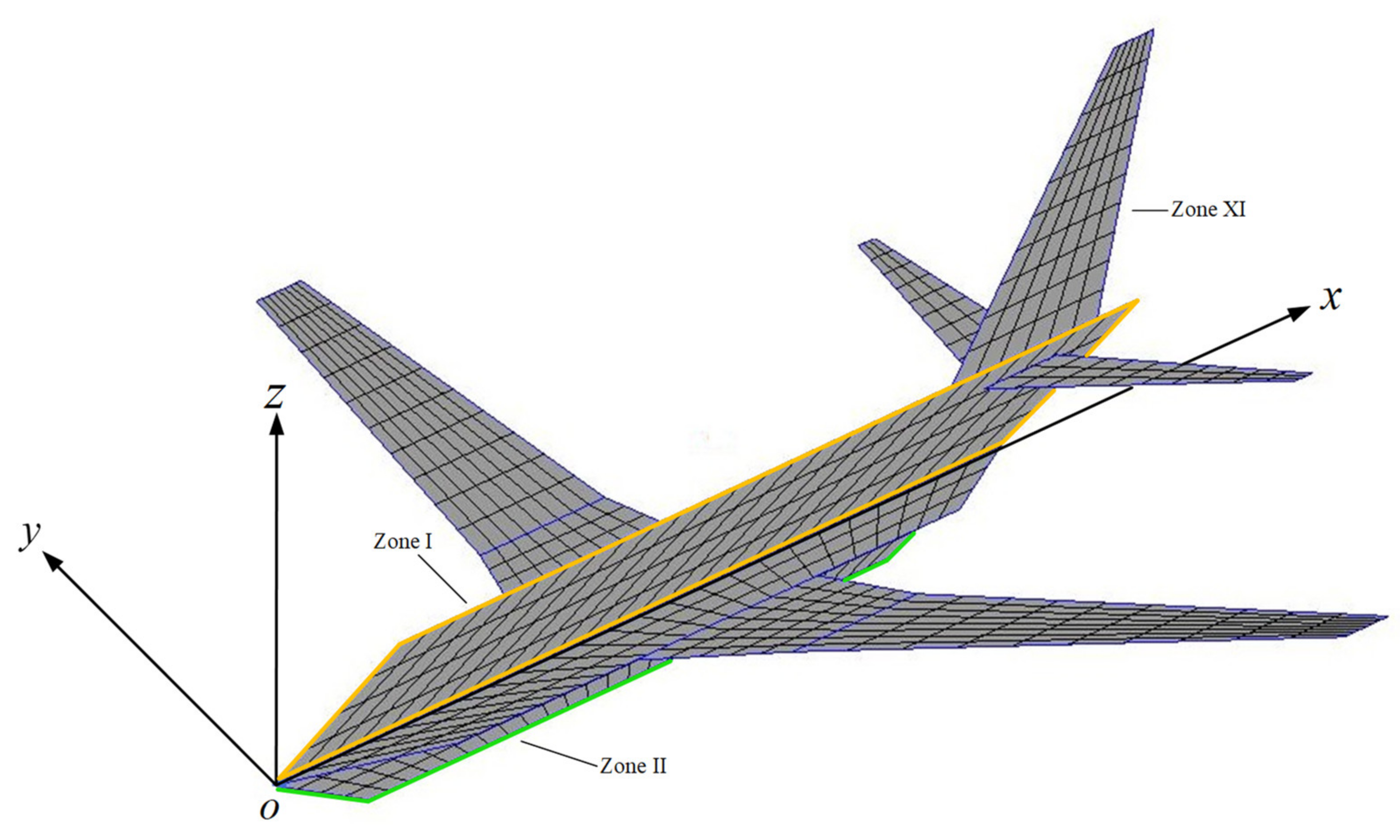
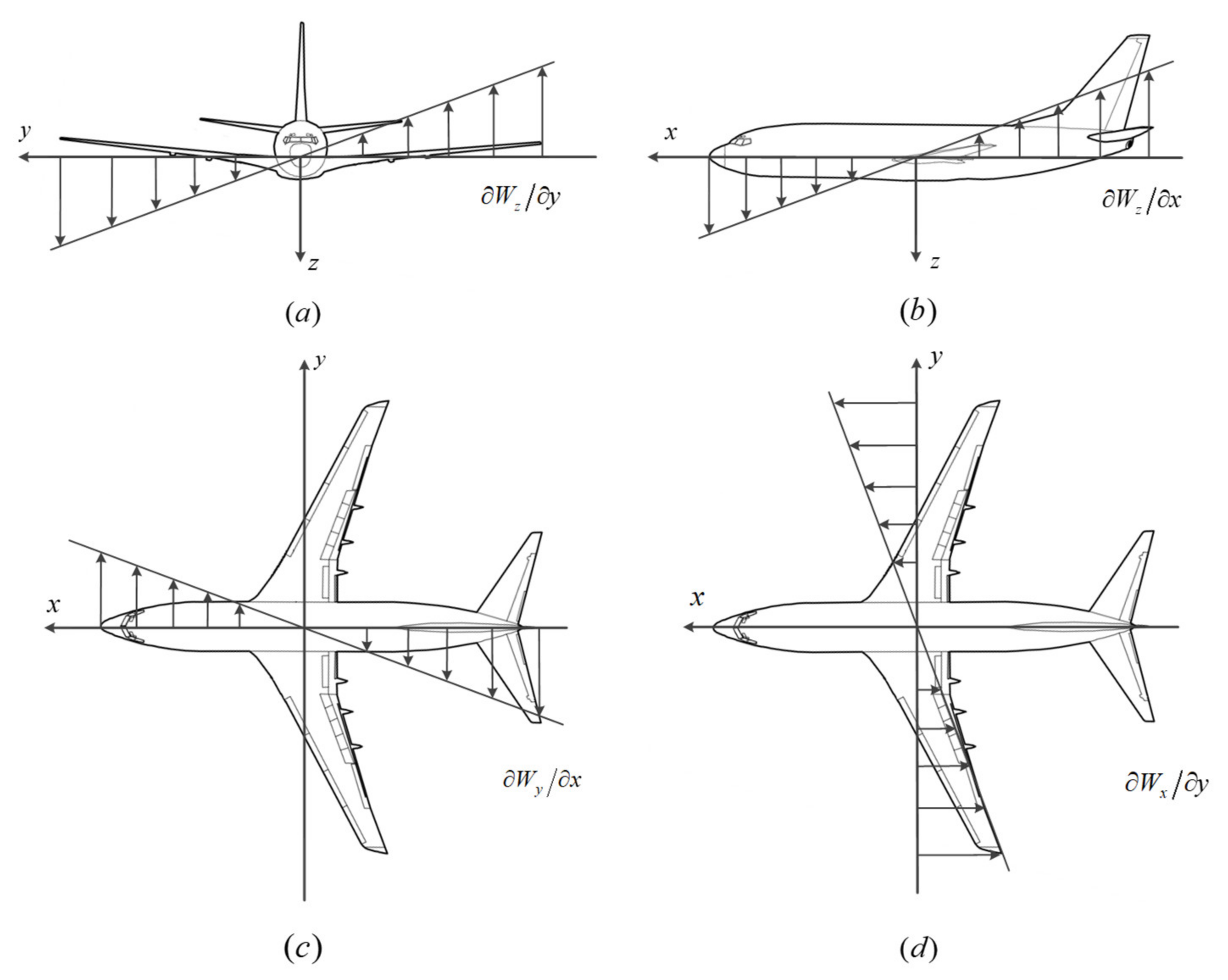
2.1. Deriving Wind Components from Flight Data
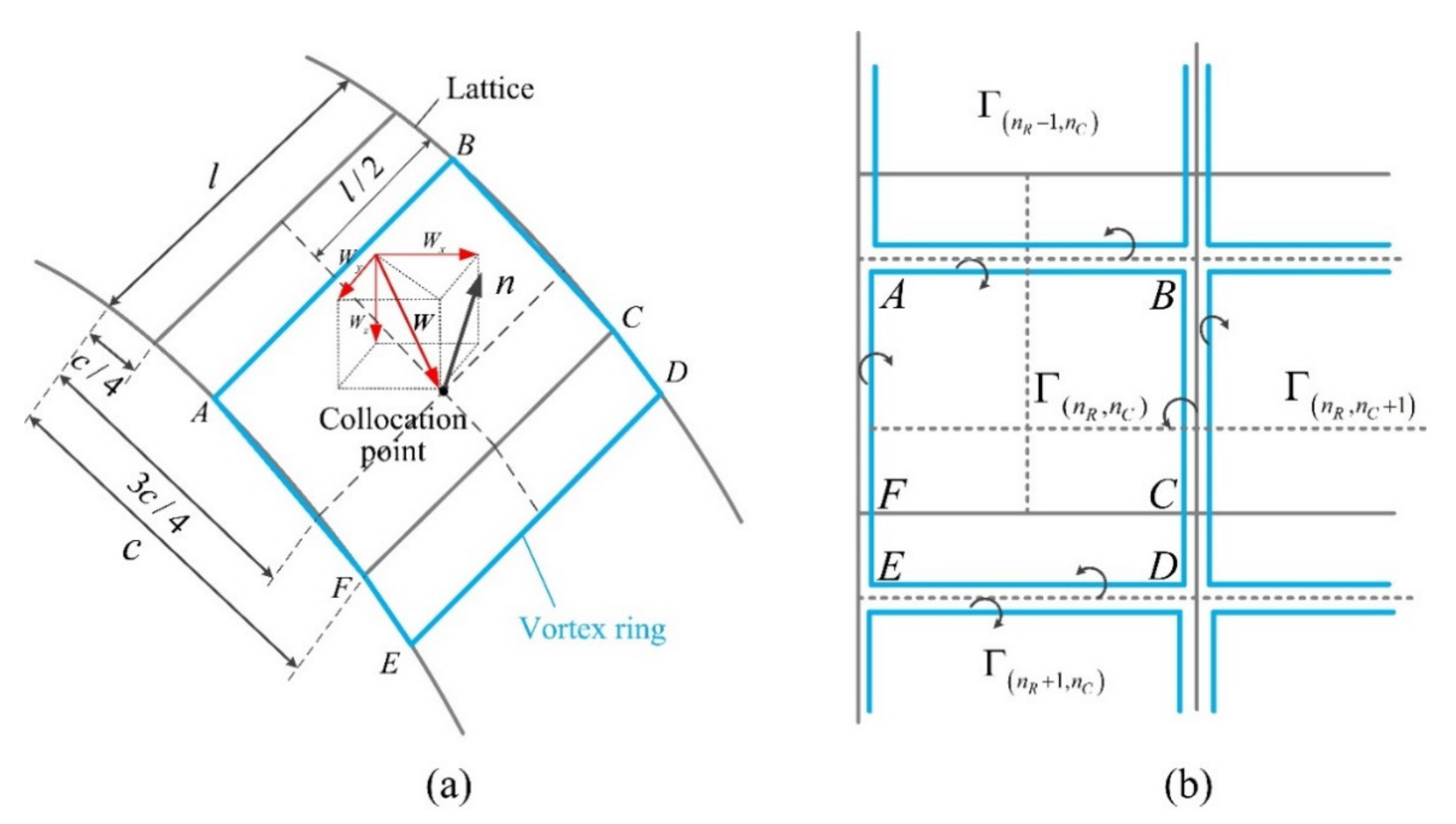
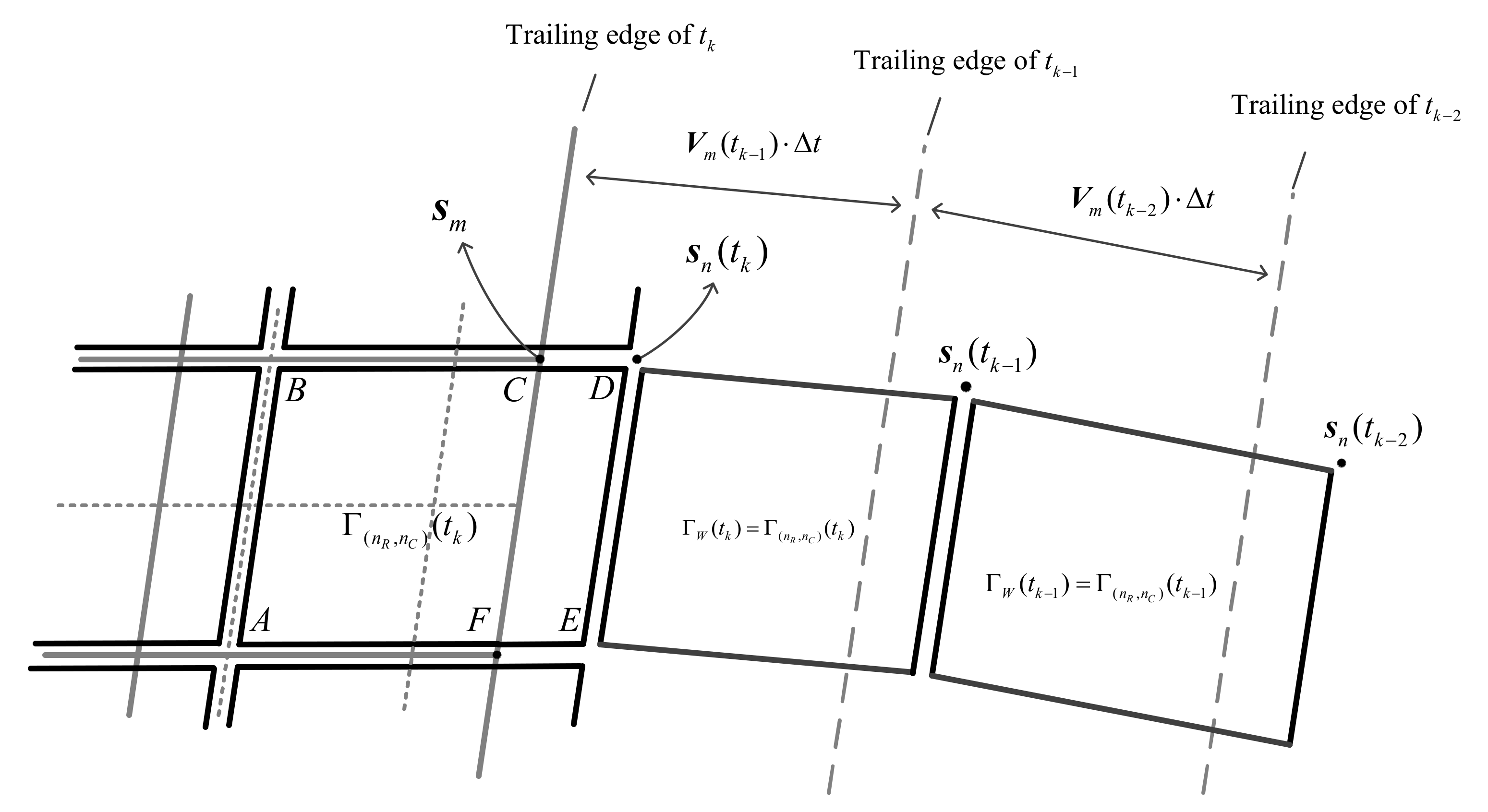
2.2. Building the Influence Coefficient Matrix
2.3. Aircraft Acceleration Response in Turbulence
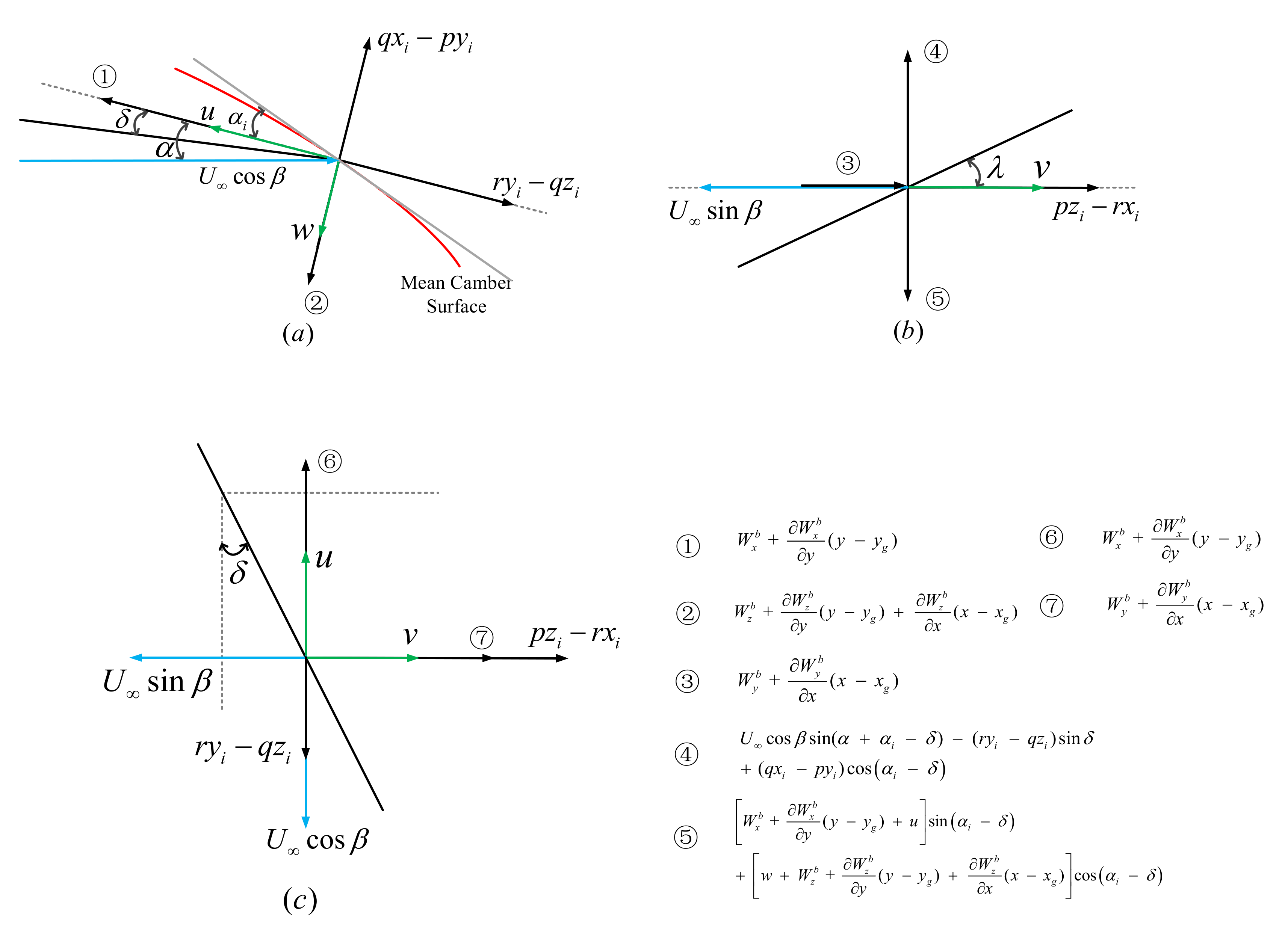
2.3.1. Local Velocity Induced by Aircraft Unsteady Motion
2.3.2. Computing Unsteady Aerodynamic Force
2.3.3. Aerodynamics Response with Air Compressibility Correction
3. Results and Discussion
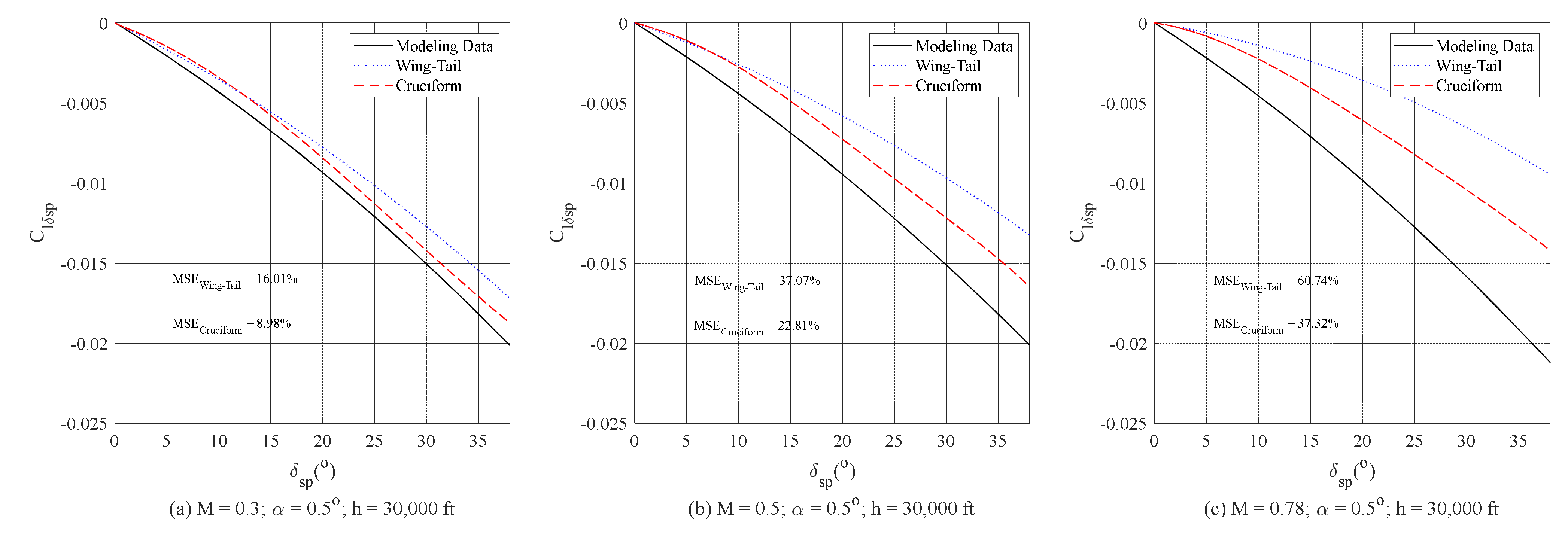
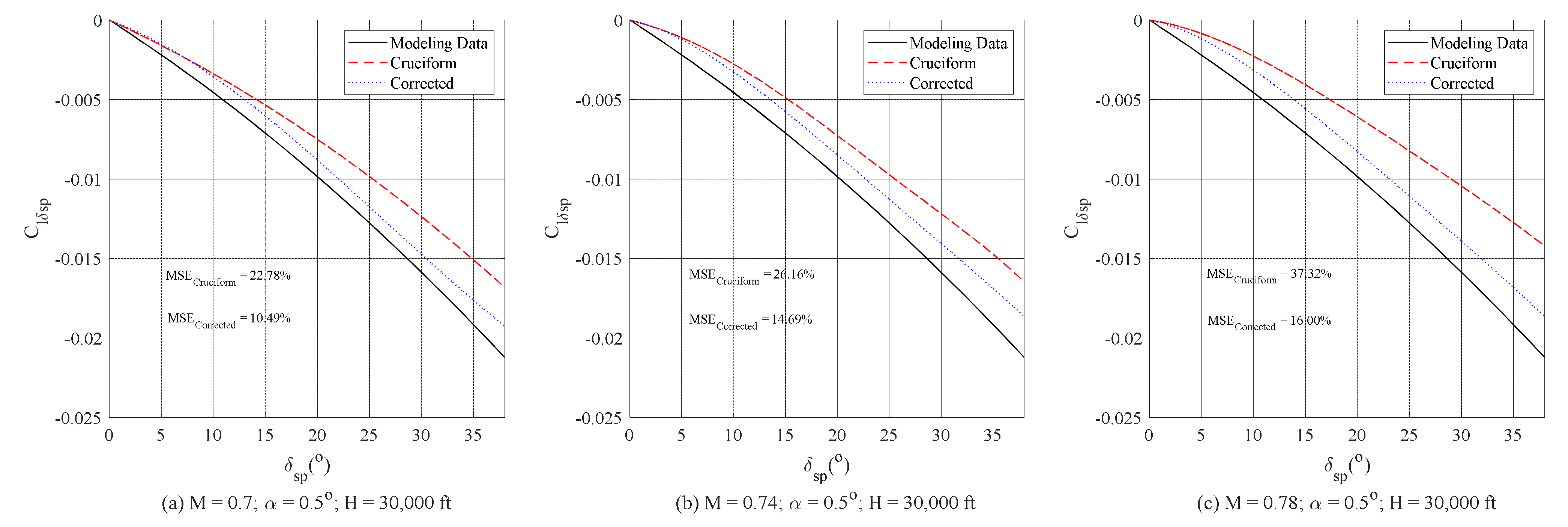
3.1. Aerodynamic Performance Verification by UVLM
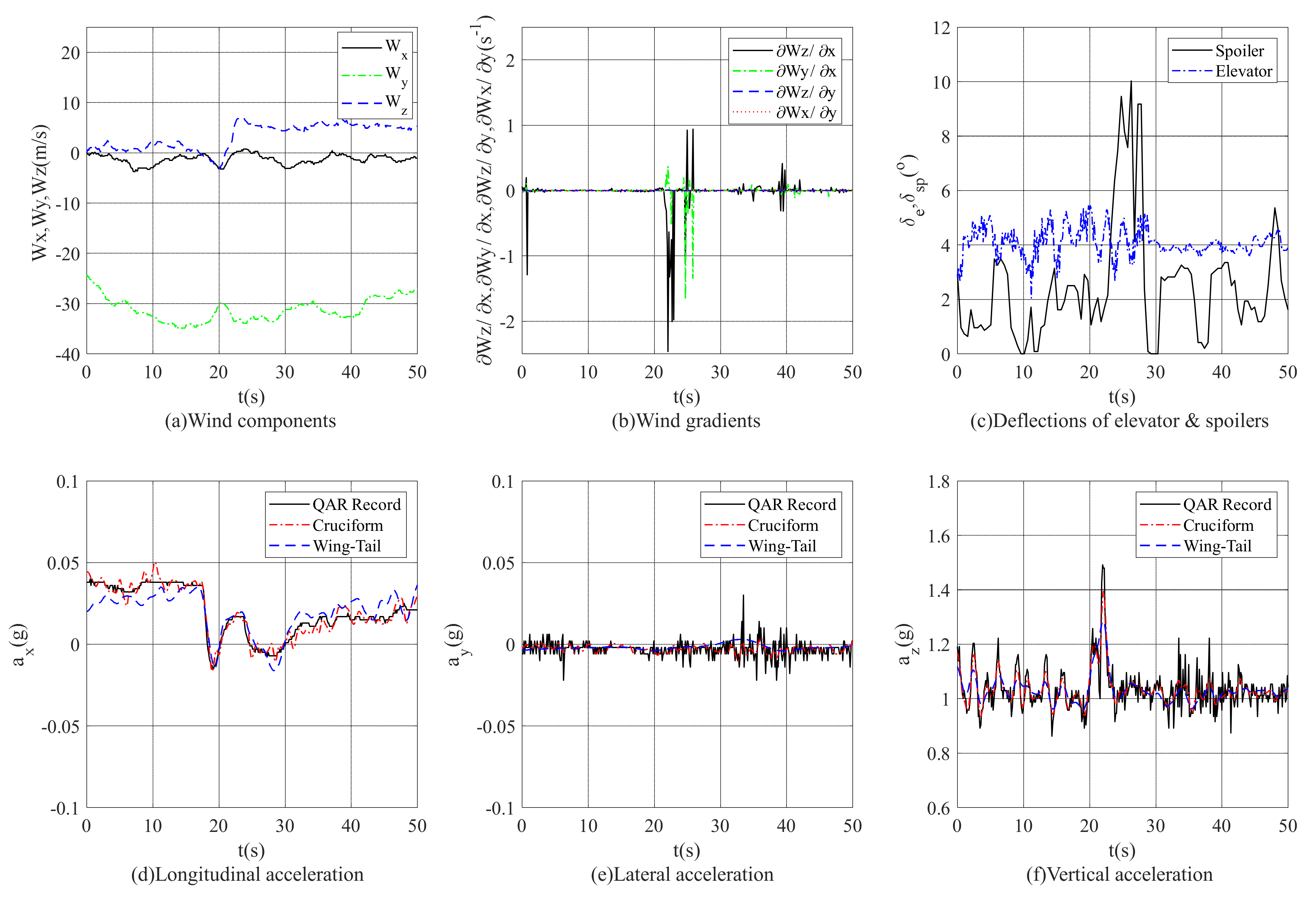
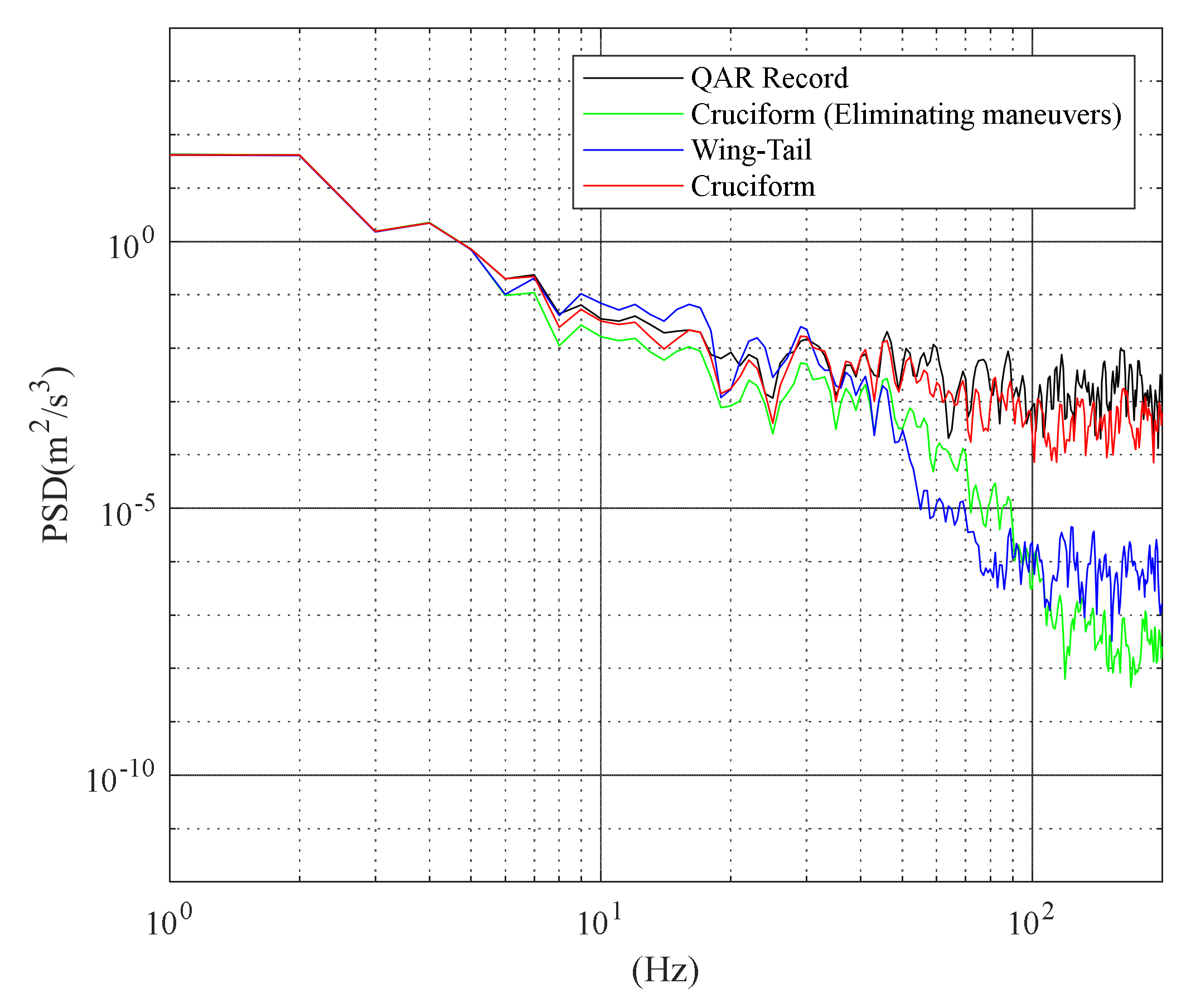
3.2. Vertical Acceleration Response
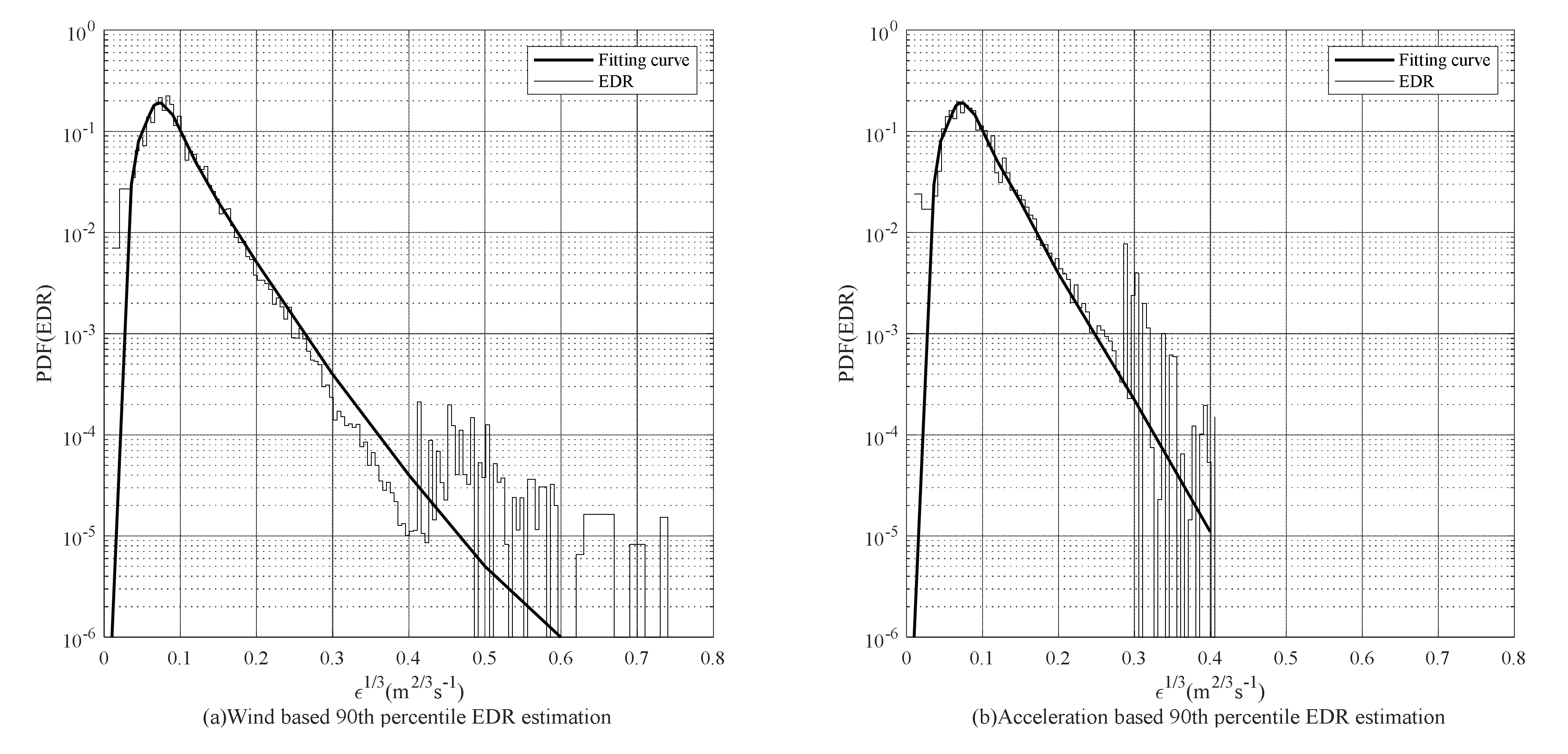
3.3. Application on EDR Estimation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Sharman, R.; Lane, T. Aviation Turbulence; Springer: Cham, Switzerland, 2016; Volume 10, pp. 978–983. [Google Scholar]
- Gao, Z.X.; Fu, J. Research on Robust LPV modeling and control of aircraft flying through wind disturbance. Chin. J. Aeronaut. 2019, 32, 1588–1602. [Google Scholar] [CrossRef]
- Barleben, A.; Haussler, S.; Müller, R.; Jerg, M. A Novel Approach for Satellite-Based Turbulence Nowcasting for Aviation. Remote Sens. 2020, 12, 2255. [Google Scholar] [CrossRef]
- Kim, J.H.; Park, J.R.; Kim, S.H.; Kim, J.; Lee, E.; Baek, S.; Lee, G. A Detection of Convectively Induced Turbulence Using In Situ Aircraft and Radar Spectral Width Data. Remote Sens. 2021, 13, 726. [Google Scholar] [CrossRef]
- Guo, J.; He, J.X.; Hu, C.J.; Wu, J.Y. Analysis of Wind Induced Vibration of Stayed Cable of Sea-crossing Bridge Based on Monitoring Data. EASEC16: Proceedings of the 16th East Asian-Pacific Conference on Structural Engineering and Construction, Brisbane, Australia, 6–9 December 2019; Springer: Singapore, 2021; pp. 187–198. [Google Scholar]
- Gao, Z.; Wang, H.; Qi, K.; Xiang, Z.; Wang, D. Acceleration-Based in Situ Eddy Dissipation Rate Estimation with Flight Data. Atmosphere 2020, 11, 1247. [Google Scholar] [CrossRef]
- Kim, S.H.; Chun, H.Y.; Kim, J.H.; Sharman, R.D.; Strahan, M. Retrieval of eddy dissipation rate from derived equivalent vertical gust included in Aircraft Meteorological Data Relay (AMDAR). Atmos. Meas. Tech. 2020, 13, 1373–1385. [Google Scholar] [CrossRef] [Green Version]
- Etkin, B. Turbulent wind and its effect on flight. J. Aircr. 1981, 18, 327–345. [Google Scholar] [CrossRef]
- Podglajen, A.; Bui, T.P.; Dean-Day, J.M.; Pfister, L.; Jensen, E.I.; Alexander, M.J.; Hertzog, A.; Kärcher, B.; Plougonwen, R.; Randell, W.J. Small-Scale Wind Fluctuations in the Tropical Tropopause Layer from Aircraft Measurements: Occurrence, Nature, and Impact on Vertical Mixing. J. Atmos. Sci. 2017, 74, 3847–3869. [Google Scholar] [CrossRef]
- Kimberlin, R.D.; Sims, J.P. Gust Alleviation for General Aviation Aircraft; SAE Technical Paper; SAE International: Warrendae, PA, USA, 1996. [Google Scholar]
- Wright Patterson Air Force Base. Flying Qualities of Piloted Airplanes; MIL-F-8785C; U.S. Air Force: Dayton, OH, USA, 1980. [Google Scholar]
- Joseph, G.; Golubev, V.V.; Gudmundsson, S. Towards Development of a Dynamic-Soaring, Morphing-Wing UAV. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, Reston, VA, USA, 15–19 June 2020. [Google Scholar]
- Cornman, L.B.; Morse, C.S.; Cunning, G. Real-time estimation of atmospheric turbulence severity from in-situ aircraft measurements. J. Aircr. 1995, 32, 171–177. [Google Scholar] [CrossRef]
- Huang, R.; Sun, H.; Wu, C.; Wang, C.; Lu, B. Estimating eddy dissipation rate with QAR flight big data. Appl. Sci. 2019, 9, 5192. [Google Scholar] [CrossRef] [Green Version]
- Billy, K.B.; Brett, A.N. Aircraft Acceleration prediction due to atmospheric disturbances with flight data validation. J. Aircr. 2006, 43, 72–81. [Google Scholar]
- Williams, P.D. Increased light, moderate, and severe clear-air turbulence in response to climate change. Adv. Atmos. Sci. 2017, 34, 576–586. [Google Scholar] [CrossRef] [Green Version]
- Nasir, S.; Javaid, M.T.; Shahid, M.U.; Raza, A.; Siddiqui, W.; Salamat, S. Applicability of Vortex Lattice Method and its Comparison with High Fidelity Tools. Pak. J. Eng. Technol. 2021, 4, 207–211. [Google Scholar]
- Jones, B.R.; Crossley, W.A.; Lyrintzis, A.S. Aerodynamic and aeroacoustic optimization of rotorcraft airfoils via a parallel genetic algorithm. J. Aircr. 2000, 37, 1088–1096. [Google Scholar] [CrossRef]
- Hosangadi, P.; Gopalarathnam, A. Low-Order Method for Prediction of Separation and Stall on Unswept Wings. J. Aircr. 2020, 58, 420–435. [Google Scholar] [CrossRef]
- Oliviu, S.G.; Koreanschi, A.; Botez, R.M.; Mamou, M.; Mebarki, Y. Analysis of the aerodynamic performance of a morphing wing-tip demonstrator using a novel nonlinear vortex lattice method. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Vicroy, D.D.; Bowles, R.L. Effect of spatial wind gradients on airplane aerodynamics. J. Aircr. 1989, 26, 523–530. [Google Scholar] [CrossRef]
- Süelzgen, Z.; Wüstenhagen, M. Operational modal analysis for simulated flight flutter test of an unconventional aircraft. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Savannah, GA, USA, 10–13 June 2019. [Google Scholar]
- Meddaikar, Y.M.; Dillinger, J.; Klimmek, T.; Krueger, W.; Wuestenhagen, M.; Kier, T.M.; Hermanutz, A.; Hornung, M.; Rozov, V.; Breitsamter, C.; et al. Aircraft aeroservoelastic modelling of the FLEXOP unmanned flying demonstrator. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Meng, Y.; Wan, Z.; Xie, C.; An, C. Time-domain nonlinear aeroelastic analysis and wind tunnel test of a flexible wing using strain-based beam formulation. Chin. J. Aeronaut. 2021, 34, 380–396. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, H.H.T. Aerodynamics modeling and analysis of close formation flight. J. Aircr. 2017, 54, 2192–2204. [Google Scholar] [CrossRef]
- Parenteau, M.; Sermeus, K.; Laurendeau, E. VLM coupled with 2.5 d RANS sectional data for high-lift design. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Dreier, M.E. Introduction to Helicopter and Tiltrotor Flight Simulation; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007. [Google Scholar]
- Gao, Z.; Wang, D.; Xiang, Z. A Method for Estimating Aircraft Vertical Acceleration and Eddy Dissipation Rate in Turbulent Flight. Appl. Sci. 2020, 10, 6798. [Google Scholar] [CrossRef]
- Boeing Company. Aerodynamic Data and Flight Control System Description for the 737-600/-700/-800/-900 Training Simulator; D611A001-vol1, rev H.; Boeing Company: Chicago, IL, USA, 2003. [Google Scholar]
- Boeing Company. Aerodynamic Data and Flight Control System Description for the 737-600/-700/-800/-900 Training Simulator; D611A001-vol3, rev H.; Boeing Company: Chicago, IL, USA, 2003. [Google Scholar]
- Stoica, P.; Moses, R. Spectral Analysis of Signals; Pearson Education: Cranbury, NJ, USA, 2005. [Google Scholar]



| Horizontal Plane of the Fuselage | ||||
|---|---|---|---|---|
| 1400 | 1600 | 1600 | 320 | 360 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Gao, Z.; Gu, H.; Guan, X. The Optimization of Aircraft Acceleration Response and EDR Estimation Based on Linear Turbulence Field Approximation. Atmosphere 2021, 12, 799. https://doi.org/10.3390/atmos12060799
Wang D, Gao Z, Gu H, Guan X. The Optimization of Aircraft Acceleration Response and EDR Estimation Based on Linear Turbulence Field Approximation. Atmosphere. 2021; 12(6):799. https://doi.org/10.3390/atmos12060799
Chicago/Turabian StyleWang, Debao, Zhenxing Gao, Hongbin Gu, and Xinyu Guan. 2021. "The Optimization of Aircraft Acceleration Response and EDR Estimation Based on Linear Turbulence Field Approximation" Atmosphere 12, no. 6: 799. https://doi.org/10.3390/atmos12060799
APA StyleWang, D., Gao, Z., Gu, H., & Guan, X. (2021). The Optimization of Aircraft Acceleration Response and EDR Estimation Based on Linear Turbulence Field Approximation. Atmosphere, 12(6), 799. https://doi.org/10.3390/atmos12060799






