Abstract
The Model Output Statistics (MOS) model is a dynamic statistical weather forecast model based on multiple linear regression technology. It is greatly affected by the selection of parameters and predictors, especially when the weather changes drastically, or extreme weather occurs. We improved the traditional MOS model with the machine learning method to enhance the capabilities of self-learning and generalization. Simultaneously, multi-source meteorological data were used as the input to the model to improve the data quality. In the experiment, we selected the four areas of Nanjing, Beijing, Chengdu, and Guangzhou for verification, with the numerical weather prediction (NWP) products and observation data from automatic weather stations (AWSs) used to predict the temperature and wind speed in the next 24 h. From the experiment, it can be seen that the accuracy of the prediction values and speed of the method were improved by the ML-MOS. Finally, we compared the ML-MOS model with neural networks and support vector machine (SVM), the results show that the prediction result of the ML-MOS model is better than that of the above two models.
1. Introduction
With the development of atmospheric detection technology, such as automatic weather stations (AWSs), radar, satellite remote sensing, and GPS, human understanding of the mechanism of weather change and the numerical weather prediction (NWP) model has continuously improved. Simultaneously, the development of new technologies has made full use of conventional and unconventional observations. The machine learning methods using big data have more extensive application prospect in regional weather interpretation and forecasting.
There are mainly two traditional weather interpretation and forecasting methods: physical statistical methods and NWP methods [1]. Physical statistical methods are standard in the field of meteorology [2]. In the 1980s, meteorological interpretation and forecasting based on atmospheric and oceanic dynamic equations began to develop, among which model output statistics (MOS) was a typical example [3]. Cleveland and Bjerknes proposed the NWP method at the beginning of the 20th century. The weather forecast was initially regarded as an initial value problem in mathematical physics by establishing a set of linear partial differential equations describing the fundamental laws of the movement of the Earth’s atmosphere and substituting the initial values under certain conditions. Researchers can solve the equations and obtain the numerical solutions of relevant meteorological elements in the future. However, due to the complex calculation of the original equations and the disturbance of initial values, regional forecasting accuracy needs to be improved [4].
To improve the availability of regional weather interpretation and forecasting, improvements can be made in two aspects One is to enhance the quality of the input data. Traditional regional meteorological interpretation and forecasting input data sources are relatively singular, relying primarily on observation data from discrete sites. The data are in a singular form and contain limited meteorological elements. The extensive use of multiple observational data (such as satellites, radar, marine buoys) to obtain high-precision, multi-element, multi-source meteorological fusion data is an effective solution to improve the quality of input data. Multi-source meteorological data fusion includes precipitation fusion, land surface data fusion, sea surface data fusion, and three-dimensional cloud fusion [5]. The other method is the algorithm model. With artificial intelligence technology development, statistical machine learning methods have been gradually developed and used to predict short-term weather forecasts ranging from a few hours to two weeks [6,7,8]. This method can also be used for coarse-grained long-term climate forecasts where target variables accumulate over months or years [9,10]. Dedicated machine learning solutions are widely used in early warning and forecast of extreme weather [11]. Jessica Hwang et al. [12] have developed a forecasting system based on machine learning and a subseasonal Rodeo dataset suitable for training and benchmark sub-seasonal forecasting, improving the forecast of temperature and precipitation. Burke et al. [13] used the random forest to correct the hail output in NWP. The forecast results obtained have higher accuracy and avoid the complicated physical correction process. However, the data source used is single and has not been fully verified. In order to improve the correction efficiency, Scher et al. [14] used deep learning methods such as a Convolutional neural network (CNN) to replace random forest, but due to the lack of training samples available, it is not easy to further improve the forecasting effect.
Combined with previous work [3,4,5,6,7], we propose a regional automatic interpretation forecast system supported by multi-source data to predict the temperature (maximum and minimum temperature) and maximum wind speed of the region in the next 24 h and combined machine learning methods to improve the performance of traditional interpretation forecast models.
The main contributions of this article include:
- (1)
- A multi-source meteorological data processing method based on accurate and meticulous interpolation of grid data and data regionalization is proposed.
- (2)
- Two types of automatic regional interpretation and forecasting models under holonomic and non-holonomic subsets are designed.
The rest of this paper is structured as follows. The Section 2 summarizes the Model Output Statistics (MOS) and Machine Learning Model Output Statistics ML-MOS model principles. In the Section 3, we present the implementation of the ML-MOS model, including the multi-source meteorological data processing method and two types of automatic regional interpretation and forecasting models. The Section 4 outlines the experimental data source and experimental analysis; Finally, the Section 5 gives the conclusion and future work.
2. Preliminary Knowledge
2.1. MOS Model Principle
The MOS model is a dynamic statistical weather forecasting model proposed by the American meteorologist Klein in the last century [15]. The MOS model uses historical data and actual meteorological parameters of forecast objects as forecasting factors to establish statistical equations [3]. It is based on multiple linear regression and establishes the quantitative statistical relationship between the predictand and multiple predictors:
In Equations (1) and (2), is the forecasting object, is the regression coefficient, is the forecasting factor, and is the error matrix.
The MOS model uses stepwise regression (SWR) for modeling. Firstly, calculate each forecasting factor variance contribution is calculated. The forecasting factor with the most significant variance contribution and reaching a certain significance level were introduced from all forecasting factors that had not yet entered the equation to establish the regression equation. Simultaneously, each forecasting factor variance contribution in the original equation is calculated after introducing the new forecasting factors and the non-significant forecasting factors are eliminated to establish a new regression equation. New forecasting factors with significant variance contributions are gradually introduced through the above process. Forecasting factors with poor significance are gradually eliminated to ensure that only the forecasting factors with significant variance for the dependent variable are always retained in the equation. This process ends when no significant variance contributing forecasting factor can be introduced.
The MOS model workflow is shown in Figure 1.
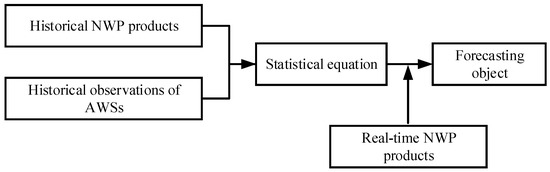
Figure 1.
MOS model workflow.
The MOS model has many advantages. It is a relatively mature interpretation model and has also achieved a range of applications [16,17,18]. However, the selection of parameters and the selection of forecasting factors in the regression equation affect the quality of the forecasting object. Therefore, significant upfront work is required to identify the forecasting factors. For nowcasting, the real-time data acquisition of fixed predictors is often incomplete, which affects the model processing effect. When the weather changes drastically, and extreme weather occurs, the MOS model is no longer applicable. For weather phenomena that reflect the multi-scale comprehensive effect, the MOS model has a poor forecasting effect and cannot reach the availability level.
2.2. ML-MOS Model
The MOS based on machine learning (ML-MOS) model is a MOS model based on multi-source data support combined with the machine learning method proposed to improve the traditional MOS model. The input data of the ML-MOS model adopts the accurate and meticulous grid data obtained from the fusion of multi-source meteorological data, such as NWP products, radar, satellites, and AWS, to ensure the model of data input quality. We used random forest to replace the traditional SWR method of the MOS model to improve the self-learning and generalization capabilities of the MOS model. Random forest [19] is a highly flexible machine learning algorithm. It uses the classifier combination to randomly select n groups of samples from the original samples and carry out decision tree modeling for each sample group. Then, the results of each decision tree are considered comprehensively to vote, and the principle of majority rule obtains the final result predicted by the model.
The specific operation process is as follows:
STEP1: Use the classifier combination to randomly select n groups of samples from the sample data.
STEP2: Build a decision tree for n groups of samples, select some attributes randomly and classify each node according to these attributes.
STEP3: Repeat STEP1 and STEP2 to construct T decision trees, and each decision tree will grow freely without pruning, thus forming a forest.
STEP4: The voting mechanism is adopted to output the results.
In the following, we explain the multi-source data processing method in the ML-MOS model and the model realization method under different constraints in detail.
3. ML-MOS Model Design and Implementation
This section mainly describes the specific implementation of the ML-MOS model. Firstly, we propose a multi-source meteorological data processing method to ensure the efficient utilization and organization of multi-source meteorological data. Secondly, the process of improving the self-learning and generalization capabilities of the traditional MOS model based on the random forest algorithm is described. We propose an ML-MOS model to adapt to the automatic interpretation and forecasting of different regions. Finally, we outline the framework of the ML-MOS model.
3.1. Multi-Source Meteorological Data Processing Method
The commonly used data in the meteorological field, such as NWP products, AWS observation data, meteorological radar data, and meteorological satellite data, are not unified in macroscopic data storage. The above data can be divided into grid data and discrete data in a spatial distribution manner. The general data format of grid data represented by NWP products is “grib” or “grib2”, and the grid design is carried out according to longitude and latitude. Take the high-resolution product of the ECMWF atmospheric model as an example, the grid resolution of the atmospheric surface is 0.125° × 0.125°; the barometric grid resolution is 0.25° × 0.25°. The discrete data represented by the observation data of AWSs are usually the longitude and latitude of a single site, and the observation data of the site are stored independently. Therefore, when using the above data as the ML-MOS model data, the necessary format conversion and quality control of multi-source meteorological data are required. The proposed multi-source meteorological data processing method is divided into the following two parts.
3.1.1. Accurate and Meticulous Interpolation of Grid Data
Due to the differences in the resolution of different grid data and different elements of the same grid data, to make full use of the grid data and meet the efficient utilization of multi-source meteorological data, we used distance-weighted interpolation to achieve accurate and meticulous interpolation from low-resolution to high-resolution grid data.
Definition 1.
The known grid point is the initial grid point of the grid point data, that is, the original grid point without interpolation processing.
Definition 2.
The unassigned grid point is the high-resolution grid points of the original grid point data after interpolation processing. There is a corresponding relationship with the known grid point.
The specific realization of distance-weighted interpolation can be described as Equation (3):
where is the value of the known grid point, and is the distance-weighted of .
Since the low-resolution grid may contain multiple high-resolution grid points, the use of the distance-weighted interpolation method can effectively avoid the problem of the same value of adjacent grid points to be assigned so that the interpolated grid point data (high-resolution) has higher availability.
As shown in Figure 2, suppose the resolution of the known grid point dataset is , and the resolution of the unassigned grid point dataset is , where . Let be the i-th unassigned grid point in , and the latitude and longitude of are expressed as in tuple. , , , are known grid points in , and the horizontal grid enclosed by , , , is the smallest horizontal grid enclosed by . , , , is the grid point value in , and its longitude and latitude are represented as , , , . The distance , , , between and , , , can be calculated by Euclidean distance as follows:
where is the i-th unassigned grid point, and is the j-th known grid point.
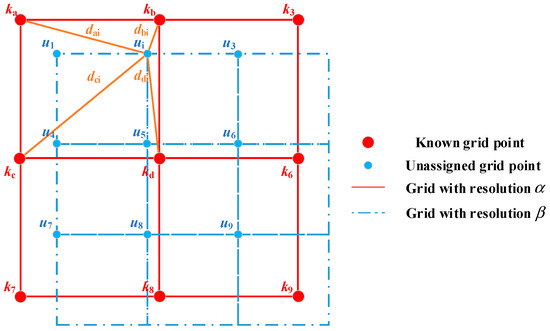
Figure 2.
Schematic diagram of accurate and meticulous interpolation of grid data.
Then the distance-weighted of corresponding to , , , is:
where .
From Equation (3):
3.1.2. Accurate and Meticulous Interpolation of Grid Data
To avoid poor regional representation caused by single grid points and single station representing various forecast regions, we obtained the grid point data by calculating the mean value of the grid point data in the forecast area. The discrete data are obtained by averaging the output observation values of the AWS contained in the forecast area. The mean value obtained above is defined as the representative value of the forecast area at the current moment.
Take Figure 3 as an example, where the gray area is the forecast area. Let f, g, j, and k in Figure 3a be the grid points included in the forecast area. Take the ground pressure in the ground layer element in the NWP product as an example. Suppose the representative value of the pressure in the forecast area at the current moment is , and the pressure of each grid point is , where , . Then:
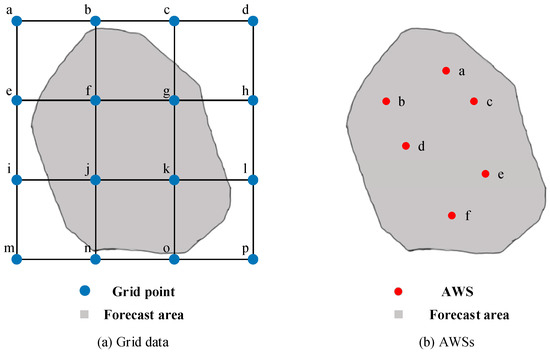
Figure 3.
Schematic diagram of the forecast area including (a) grid points and (b) AWSs.
Let a~f in Figure 3b be the AWSs included in the forecast area. Take the 2 m temperature in the observation elements of the AWS as an example, suppose the 2 m temperature representative value of the forecast area at the current moment is , and the 2 m temperature of each AWS is , where , . Then, there is:
3.2. Two Types of Automatic Regional Interpretation and Forecasting Models
As mentioned above, the traditional MOS model cannot receive real-time meteorological data, especially NWP products, and short-term weather forecasts have particular difficulties because of the current station communication conditions. The factors and equations selected in the dynamic statistical forecasting equations established by the traditional MOS model are all fixed [3]. However, these factors may be vacant due to incomplete data available on the forecast day, so these traditional methods cannot meet real-time forecasting needs. We selected factors through the traditional MOS model to generate factor subsets. According to the completeness of the factor subset, the automatic regional interpretation and forecasting are divided under the condition of holonomic and non-holonomic factor subset.
3.2.1. Regional Forecast under the Condition of Holonomic Factor Subset
Under the condition of holonomic factor subsets, the regional forecast needs to solve reliable datasets with multi-source meteorological data. The quality of the dataset directly determines the availability of machine learning models. In the production of the dataset, we comprehensively considered the time and space levels. The time level was used to determine the time range of the factor subset, and the space level was used to determine the area range of the factor subset. In time levels, for the forecast at a certain moment, for the forecast data (such as numerical weather forecast), two forecast times before and after the time effect were selected as factor fields. Real-time observation data (such as AWSs, weather radar, meteorological satellites) were chosen for the forecast aging before this time as the factor field. The forecast time limit is 24 h. In space levels, according to the geographic location of the forecast area, combined with the distribution of AWS in the forecast area, the area range of the forecast area corresponding to the forecast factor field is determined. The area range changes within the entire data area as the location of the forecast station changes.
Take the prediction of the highest ground temperature of 2 m (), the lowest temperature of 2 m (), and the highest wind speed of 10 m () in the next 24 h in a region as an example. As shown in Figure 4, each forecast area corresponds to a set of datasets. For example, forecast area I corresponds to dataset A, and forecast area II corresponds to dataset B. All datasets are divided by moment corresponding to n groups of data, and each group of data is composed of input elements and labels. Take the data at (UT: 00:00:00) as an example. The data of 48 h before and after the forecast product and 24 h before the real-time observation and detection data at are obtained. The data are extracted according to the factor subset elements to form the input dataset at the moment . Then, , and of the next 24 h at the moment are used as labels. Random forest is used to train the dataset and establish statistical mode. This model is denoted as model I, which outputs the predicted value of , , and for a certain area in the next 24 h.
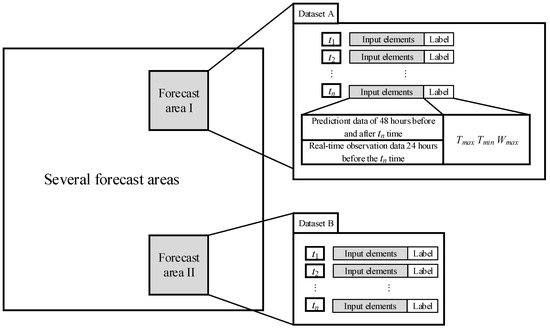
Figure 4.
Schematic diagram of dataset composition.
3.2.2. Regional Forecast under the Condition of Non-Holonomic Factor Subset
There are frequently missing observational data in actual automatic interpretation and forecasting of areas (such as remote areas) and NWP products that have not been received and processed in time. At this time, the factor subset obtained through the traditional MOS model is missing relative to the complete factor subset, and the factor subset is incomplete. For the regional forecast under the non-holonomic factor subset, a similar forecast method fills in the missing data. The implementation steps are as follows:
STEP1: Calculate the similarity between the data obtained at the current moment and the data at the historical moment to obtain the groups of data similar to the moment in the historical moment data, and the corresponding similarity is denoted as .
The similarity calculation formula is the calculation method in [20]:
represents the similarity, the smaller the value, the higher the similarity. is the hyperparameter, adjusted according to the acquired dataset. is the number of factors in . is the time window, and .
STEP2: Set the similarity threshold , when , remove the group data, where , and finally obtain the available groups data.
STEP3: Input the above groups of data into the model I, and output groups of data, denoted as , where .
STEP4: Calculate the mean value of the groups of data, and obtain the output , and in the next 24 h in this area at the moment .
3.3. Two Types of Automatic Regional Interpretation and Forecasting Models
In summary, the ML-MOS model includes multi-source weather data processing methods and two types of automatic regional interpretation and forecasting models. The multi-source meteorological data processing method ensures the reliability of the input data quality of the ML-MOS model through refined interpolation of grid data and data regionalization.
For different forecast areas, regional forecasts under the holonomic factor subset conditions and regional forecasts under the non-holonomic factor subset based on similar forecasts are designed. The ML-MOS model uses random forest as the core algorithm to generate statistical models, establishes the relationship between input elements and output elements in the dataset, and realizes automatic interpretation and forecasting of designated areas. The ML-MOS model framework is shown in Figure 5.
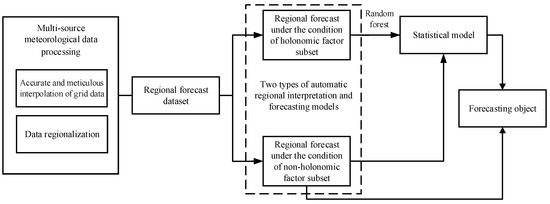
Figure 5.
ML-MOS model framework.
4. Experiment and Analysis
4.1. Data Source and Preprocessing
We used the European Centre for Medium-Range Weather Forecasts (ECMWF) and GRAPES_GFS as two types of NWP products, with date from January 2019 to October 2020 (UT, the same below) with a total of 670 days, and hourly observation data of Chinese AWSs were the interpretation objects of the ML-MOS model.
The relevant meteorological background and the traditional MOS model were combined, considering the correlation between the two types of NWP products, the output elements of AWSs (such as dew-point temperature, wind direction, cloud cover), and the elements to be forecasted. The factor subset of the highest temperature , lowest temperature , and maximum wind speed in a certain area in the next 24 h were determined. The elements shown in Tab 1. were used as the factor subset of the ML-MOS model.
In Table 1, the input time interval of atmospheric surface elements is 3 h. The input time interval of barometric elements is 3 h, including five levels of 600, 700, 800, 850, and 925 hPa. The input time interval of observation elements is 1 h; the label is the extreme value of the corresponding element output by the automatic station on the next day. The time interval is 24 h. Every eight groups of atmospheric surface elements, barometric elements, and 24 groups of observation elements correspond to the label set.

Table 1.
ML-MOS model input elements.
Data preprocessing is one of the essential processes in machine learning. To address the problems of missing data and varying dimensions in the input data, the input data were preprocessed utilizing median interpolation and data normalization using the time series of the input data. The details are as follows:
- (1)
- Default data processing of the AWSs. In the AWS observation data, due to abnormal problems such as equipment and data transmission links, the data at some moments were missing. We used the time series of the input data, based on the data correlation of the previous and next moments, and used the median padding to fill in the default data.
- (2)
- Normalized input elements: Since the dimensions of each element are not consistent, such as pressure measured in hPa, east–west wind (U) measured in m/s, and 2 m temperature measured in °C, inputting unnormalized data directly into the ML-MOS model will adversely affect the generalization ability of the model. We normalized each element separately to solve the problem of incomparability caused by dimensionless disunity among the elements.
4.2. ML-MOS Model Training and Evaluation
In the training process of the ML-MOS model, the input data must be divided into a training set and a test set. We selected 80% of the input dataset as the training set and 20% as the test set. The optimal selection of the three hyperparameters of the number of random forest estimators (N_ estimators), the maximum number of features (Max_ feature), and the maximum depth of the tree (Max_ depth) in the ML-MOS model was achieved through grid search, and the model training was completed. An Intel(R) Xeon(R) W-2104 CPU @3.20Hz, 16GB RAM computer was used for model training in this work.
For the trained model, the root means square error (RMSE) and mean absolute error (MAE) were used as the evaluation indicators of the ML-MOS model. The calculation of RMSE and MAE is shown in Equations (10) and (11):
where is the total output of a type of element (, s or ), is the -th predicted value, and is the -th observed value. The larger the RMSE and MAE, the better the performance of the ML-MOS model, that is, the smaller the error between , , and the actual observation value.
The ML-MOS model data processing and training process is summarized in Figure 6.
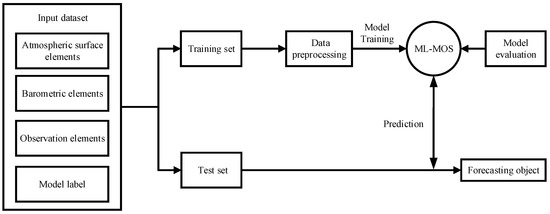
Figure 6.
ML-MOS model data processing and training flowchart.
4.3. Experimental Results and Analysis
4.3.1. Parameter Selection
During the experiment, the number of features output by the random forest was analyzed by the traditional MOS model, and Max_ feature could be determined. Max_ depth usually ranges from 10 to 100, and Max_ depth = 50 was used in this experiment. During the experiment, the dataset was randomly divided 200 times by adjusting N_ estimators, and the RMSE of the test set was observed to change with M_ estimators, as shown in Figure 7. It can be concluded from Figure 7 that when the value is 300, the RMSE value begins to decrease slowly. When the value of N_ estimators is 800, the error remains basically unchanged.
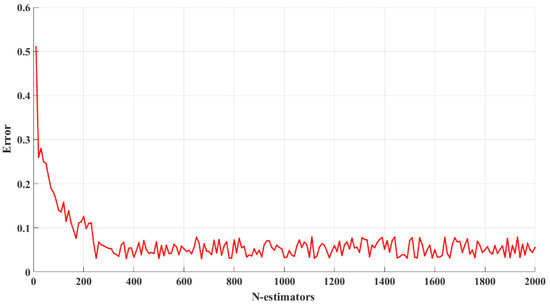
Figure 7.
The influence of the estimator on the performance of the model.
In summary, we used an N_ estimators value of 1000 to ensure that the model had better performance.
4.3.2. Results and Analysis
Aiming at the automatic interpretation and forecasting of different regions, we selected Nanjing, Beijing, Chengdu, and Guangzhou (regional scope delineated by administrative regions) for experimentation. The experiment first verifies the feasibility of the regional forecast method under the condition of the holonomic factor subset in the ML-MOS model. By randomly extracting 20 days of data (without missing values) from the data from June 2020 to August 2020, the 20-day data were input into the above model to obtain , and for the 20 days in Nanjing, Beijing, Chengdu, and Guangzhou. Taking the Nanjing area as an example, the results are shown in Figure 8.
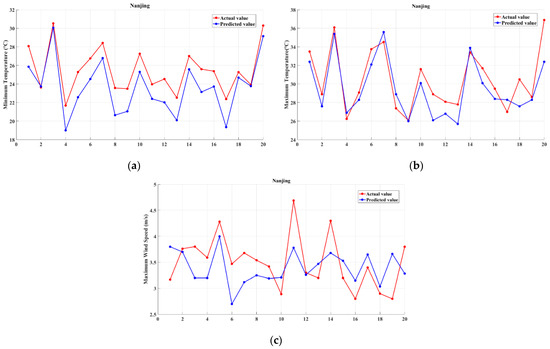
Figure 8.
Comparison of actual and predicted values of Nanjing area (a) Tmax, (b) Tmin and (c) Wmax.
The predicted value of , and in Nanjing, Beijing, Chengdu, and Guangzhou obtained by the ML-MOS model basically coincides with the changing trend of the actual value. The RMSE and MAE values of , and are shown in Table 2.

Table 2.
The RMSE and MAE values corresponding to Nanjing, Beijing, Chengdu, and Guangzhou (holonomic factor subset).
It can be seen in Table 2 that the RMSE and MAE in Nanjing, Beijing, Chengdu, and Guangzhou are basically maintained at a relatively low level.
We compared ML-MOS with MOS, Neural networks and an SVM.
- (1)
- Neural networks
We used a six-layer neural network, containing three input layers, one output layer, three hidden layers, and three FC layers. The number of neurons in each of the three hidden layers was the same. In the training process, the number of neurons was set to 16, 32, 64, 128, and 256, respectively, and the ReLU loss function was used. The training results show that the convergence state can be reached after about 12,000 iterations, and the network parameters and convergence effect can reach the optimal state when the number of neurons is set to 128. Eight, six, and six inputs were used for the three input layers, corresponding to Atmospheric surface elements, Barometric elements and Observation elements. The number of neurons in the fully connected layer is 384, 24 and 8 respectively. The output layer includes three outputs, i.e., , , . The network structure is shown in the Figure 9.
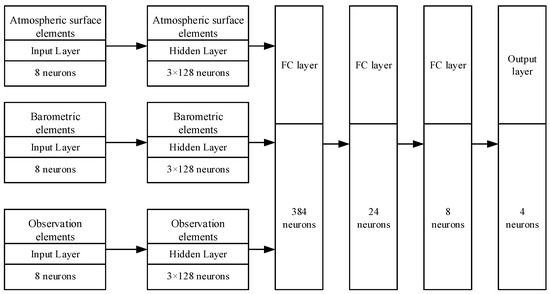
Figure 9.
Schematic diagram of neural network structure.
- (2)
- SVM
The decision function adopted for the SVM was:
where is the number of support vector machines. is the Lagrange coefficient of the -th support vector. is the class identifier of the -th support vector. is the kernel function.
For the kernel function, we chose the RBF kernel function, i.e.,
where and represent samples and vectors respectively; γ is a hyperparameter; and is the norm of .
From Equations (12) and (13), we can obtain:
In the regional forecast comparison experiment under the holonomic factor subset, the ML-MOS model has the best effect. The specific experimental results are shown in Figure 9.
From Figure 10, it can be concluded that the performance of the prediction results obtained by the MOS, neural network and SVM for different elements is different. The RMSE and MAE values of , and obtained by the MOS, neural networks, SVM, and ML-MOS model are shown in Table 3.
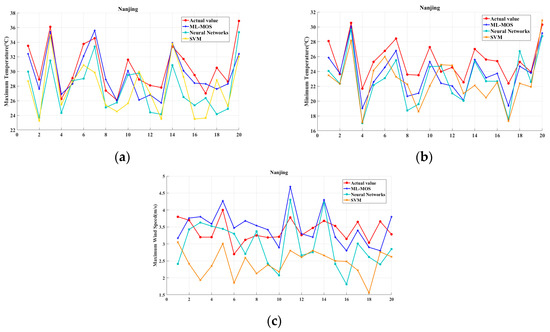
Figure 10.
Comparison of the prediction results of (a) Tmax, (b) Tmin and (c) Wmax with different models.

Table 3.
RMSE and MAE values corresponding to the neural networks, SVM, and ML-MOS model.
It can be seen from the above Table 3 that although the MOS, neural network and SVM can solve the nonlinear regression problem, the RMSE and MAE values obtained by the ML-MOS model show better performance.
To verify the regional forecast under the condition of the non-holonomic factor subset, it was assumed that the selected 20-day data of Nanjing, Beijing, Chengdu, and Guangzhou failed to obtain the NWP product data in time. The RMSE and MAE values of , and obtained through the ML-MOS model proposed in this paper are shown in Table 4. The RMSE and MAE values remained at a low level.

Table 4.
The RMSE and MAE values corresponding to Nanjing, Beijing, Chengdu, and Guangzhou (non-holonomic factor subset).
5. Conclusions
Based on the automatic regional interpretation and forecasting system supported by multi-source data, we propose a multi-source meteorological data processing method based on an accurate and meticulous interpolation of grid data and data regionalization. According to the factor subset type obtained in the forecast area, we design two models with automatic interpretation and forecasting under different factor subsets. Through NWP products and AWS observation data, we selected four areas for verification in the experiment. The RMSE and MAE values of , , and obtained by the ML-MOS model are significantly lower than those of the neural networks and SVM. In future work, the ML-MOS model will be combined with weather radar and other data to improve the precipitation prediction and enrich the model data source, further improving the model prediction accuracy and obtaining more forecasting objects.
Author Contributions
Conceptualization, C.Y. and K.X.; methodology, C.Y.; software, C.D.; validation, C.Y., K.X. and J.F.; formal analysis, C.Y.; investigation, K.X.; resources, J.F.; data curation, K.X.; writing—original draft preparation, C.Y.; writing—review and editing, C.Y.; visualization, C.Y.; supervision, J.F.; project administration, J.F.; funding acquisition, C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The National Natural Science Foundation of China under contract No. 61371119; Blue project of Jiangsu Province.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The pollution data used in this study were supplied by the China Meteorological Administration (CMA) of China under license and so cannot be made freely available. Requests for access to these data should be made to the CMA. (http://data.cma.cn, accessed on 20 June 2021).
Acknowledgments
This project was funded by National Natural Science Foundation of China under the grant 61371119 and the Blue Project of Jiangsu Province. Inspired by the discussion with Yang Pinglv, the code of the proposed algorithm has been better optimized.
Conflicts of Interest
The authors declare that they have no conflict of interest to report regarding the present study.
References
- Jian, S.; Zhuo, C.; Li, H.; Simeng, Q.; Xin, W.; Limin, Y.; Wei, X. Application of Artificial Intelligence Technology to Numerical Weather Prediction. J. Appl. Meteorol. Sci. 2021, 32, 1–11. [Google Scholar]
- Gedzelman, S. Calculating the Weather: Meteorology in the 20th Century. (book reviews). J. R. Soc. Med. 1992, 85, 271–273. [Google Scholar]
- Huan-zhu, L.; Shen-rong, Z.; Zhi-shan, L.; Cui-guang, Z.; Yuan-qin, Y.; Yu-hua, L. Objective Element Forecasts at NMC—A MOS System. J. Appl. Meteorol. Sci. 2004, 2, 181–191. [Google Scholar]
- Dai, K.; Zhu, J.Y.; Bi, B.G. The Review of Statistical Post-process Technologies for Quantitative Precipitation Forecast of Ensemble Prediction System. Acta Meteorol. Sin. 2018, 76, 493–510. [Google Scholar]
- Chunxiang, S.; Yang, P.; Junxia, G.; Bin, X.; Shuai, H.; Zhi, Z.; Lei, Z.; Shuai, S.; Zhiwei, J. A Review of Multi-source Meteorological Data Fusion Products. Acta Meteorol. Sin. 2019, 77, 774–783. [Google Scholar]
- Ghaderi, A.; Sanandaji, B.; Ghaderi, F. Deep Forecast: Deep Learning-based Spatio-Temporal Forecasting. arXiv 2017, arXiv:1707.08110. [Google Scholar]
- Hernández, E.; Sanchez-Anguix, V.; Julian, V.; Palanca, J.; Duque, N. Rainfall Prediction: A Deep Learning Approach. In Proceedings of the International Conference on Hybrid Artificial Intelligence Systems, Seville, Spain, 18–20 April 2016. [Google Scholar]
- Shi, X.J.; Chen, Z.R.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Proc. NIPS 2015. [Google Scholar] [CrossRef] [Green Version]
- Totz, S.; Tziperman, E.; Coumou, D.; Pfeiffer, K.; Cohen, J. Winter Precipitation Forecast in the European and Mediterranean Regions Using Cluster Analysis. Geophys. Res. Lett. 2017, 44, 12418–12426. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J.; Coumou, D.; Hwang, J.; Mackey, L.; Orenstein, P.; Totz, S.; Tziperman, E. S2S reboot: An argument for Greater Inclusion of Machine Learning in Subseasonal to Seasonal Forecasts. WIREs Clim. Chang. 2019, 10, e00567. [Google Scholar] [CrossRef] [Green Version]
- Racah, E.; Beckham, C.; Maharaj, T.; Kahou, S.E.; Prabhat; Pal, C. ExtremeWeather: A Large-scale Climate Dataset for Semi-supervised Detection, Localization, and Understanding of Extreme Weather Events. arXiv 2017, arXiv:1612.02095. [Google Scholar]
- Lin, H. Subseasonal Forecast Skill over the Northern Polar Region in Boreal Winter. J. Clim. 2020, 33, 1935–1951. [Google Scholar] [CrossRef]
- Amanda, B.; Nathan, S.; Gagne, D.J., II; McCorkle, S.; McGovern, A. Calibration of Machine Learning–Based Probabilistic Hail Predictions for Operational Forecasting. Weather Forecast. 2020, 35, 149–168. [Google Scholar]
- Scher, S.; Messori, G. Predicting weather forecast uncertainty with machine learning. Q. J. R. Meteorol. Soc. 2018, 144, 2830–2841. [Google Scholar] [CrossRef]
- Klein, W.H.; Lewis, F. Computer forecasts of maximum and minimum temperatures. J. Appl. Meteor. 1970, 9, 350–359. [Google Scholar] [CrossRef] [Green Version]
- Congwu, H.; Baozhang, C.; Chaoqun, M.; Tijian, W. WRF-CMAQ-MOS Studies Based on Extremely Randomized Trees. Acta Meteorol. Sin. 2018, 76, 779–789. [Google Scholar]
- Di, C.; Yu-ying, C.; Jin-ren, M.; Jing-xin, N.; Qiang, L. Influence of MOS Methods of Different Time Scale on Temperature Forecast in Ningxia. Arid Land Geogr. 2019, 42, 94–102. [Google Scholar]
- Xiao, Q.Y.; Hu, F.; Fang, S.J. Model Output Statistics and Wind Power Numerical Prediction. Resour. Sci. 2017, 39, 116–124. [Google Scholar]
- Fang, K.N.; Wu, J.B.; Zhu, J.P. A Review of Technologies on Random Forests. Stat. Inf. Forum 2011, 3, 32–38. [Google Scholar]
- Delle Monache, L.; Eckel, F.A.; Rife, D.L.; Nagarajan, B.; Searight, K. Probabilistic Weather Prediction with an Analog Ensemble. Mon. Weather Rev. 2013, 141, 3498–3516. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).