Presence of Longitudinal Roll Structures during Synoptic Forced Conditions in Complex Terrain
Abstract
1. Introduction
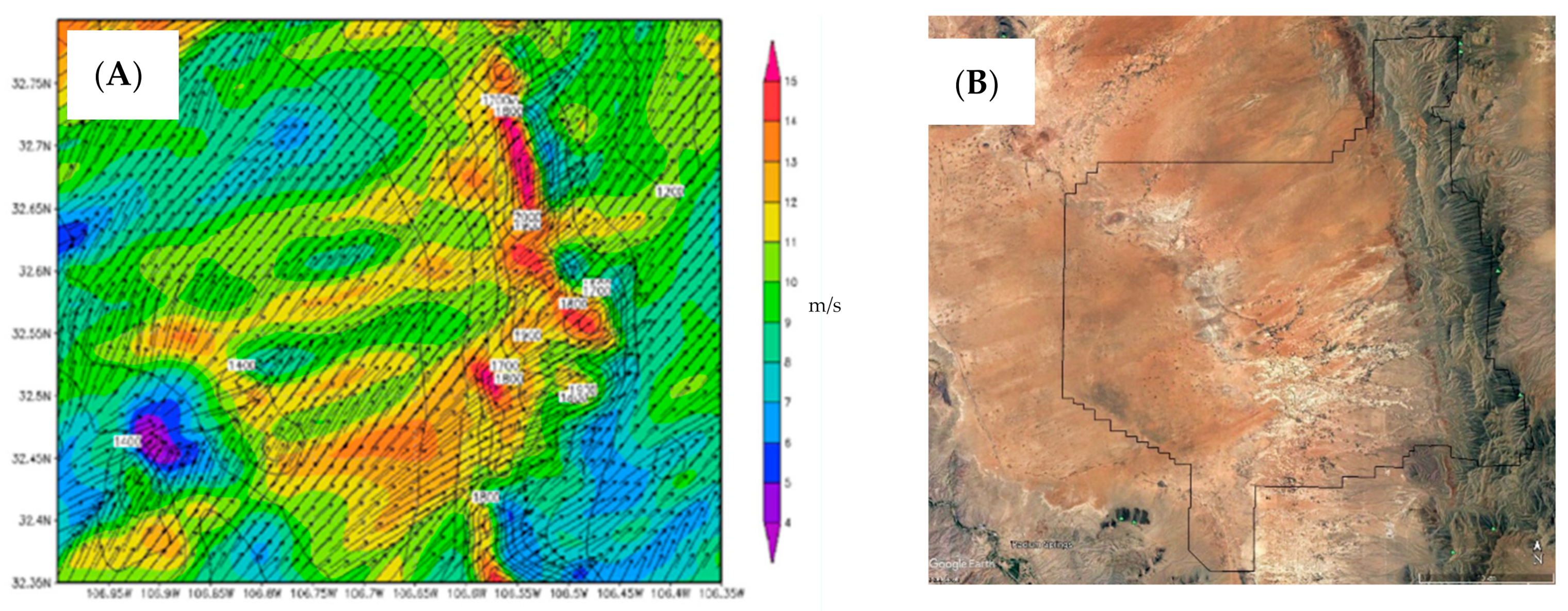
2. Methods
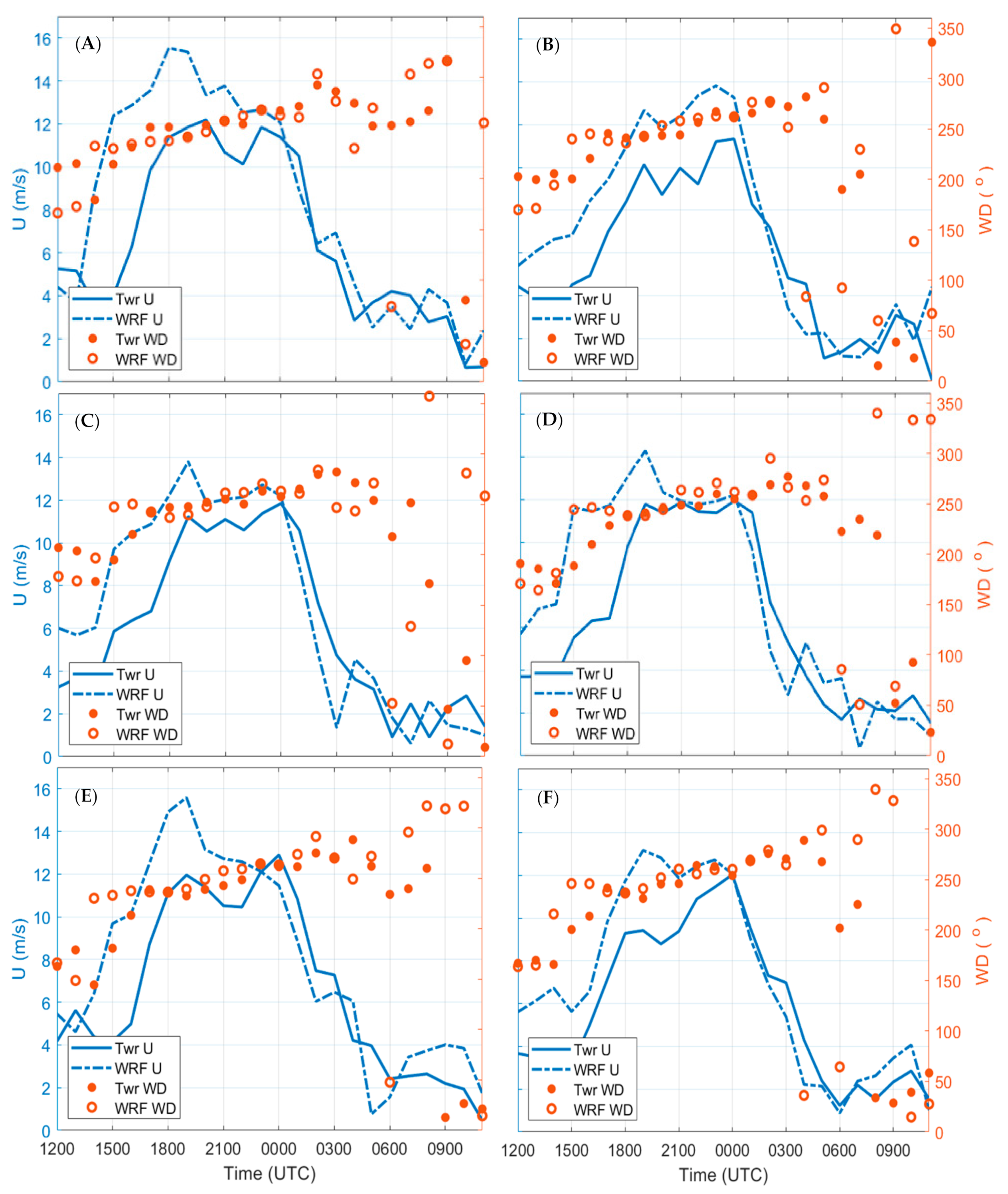
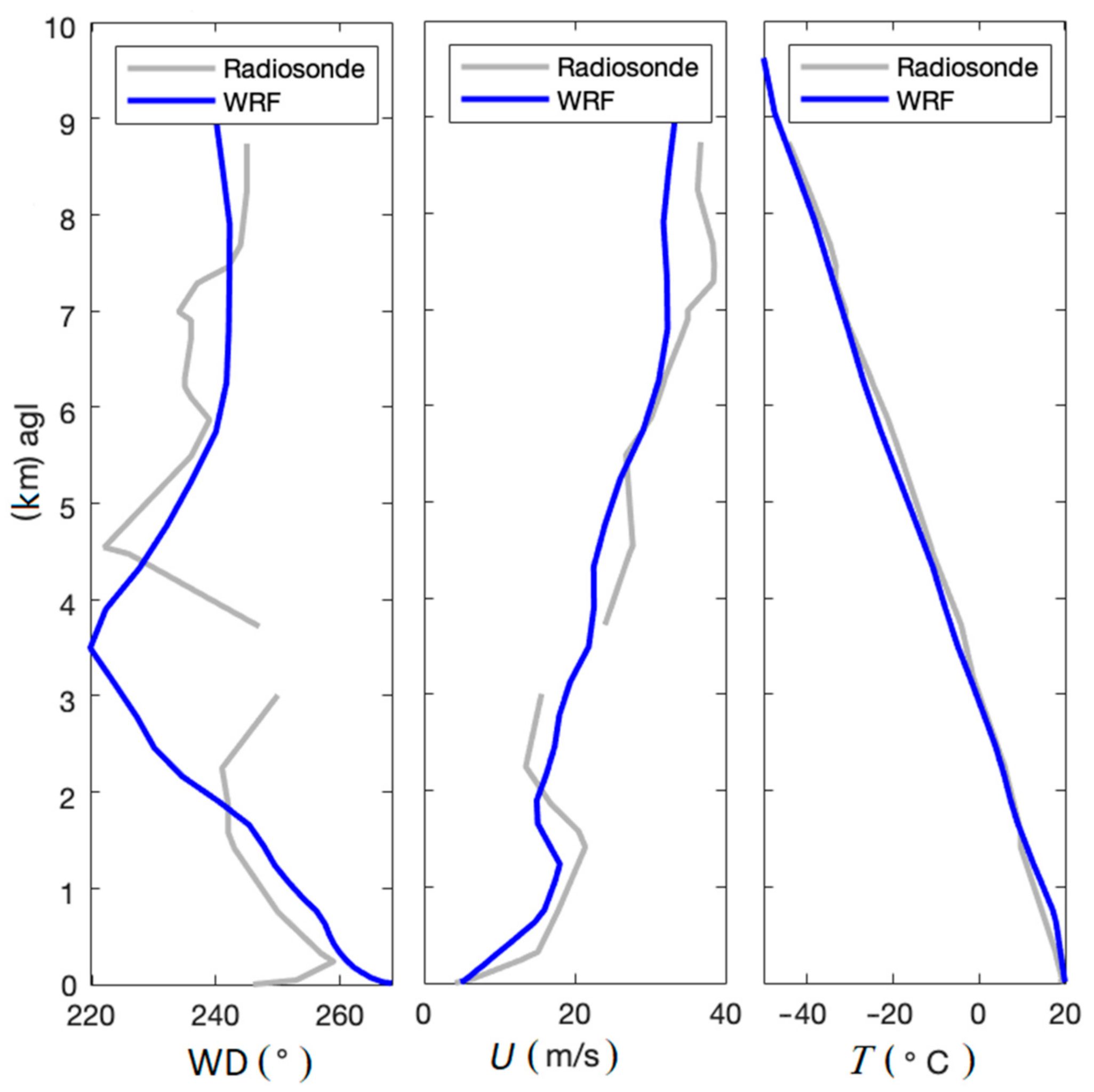
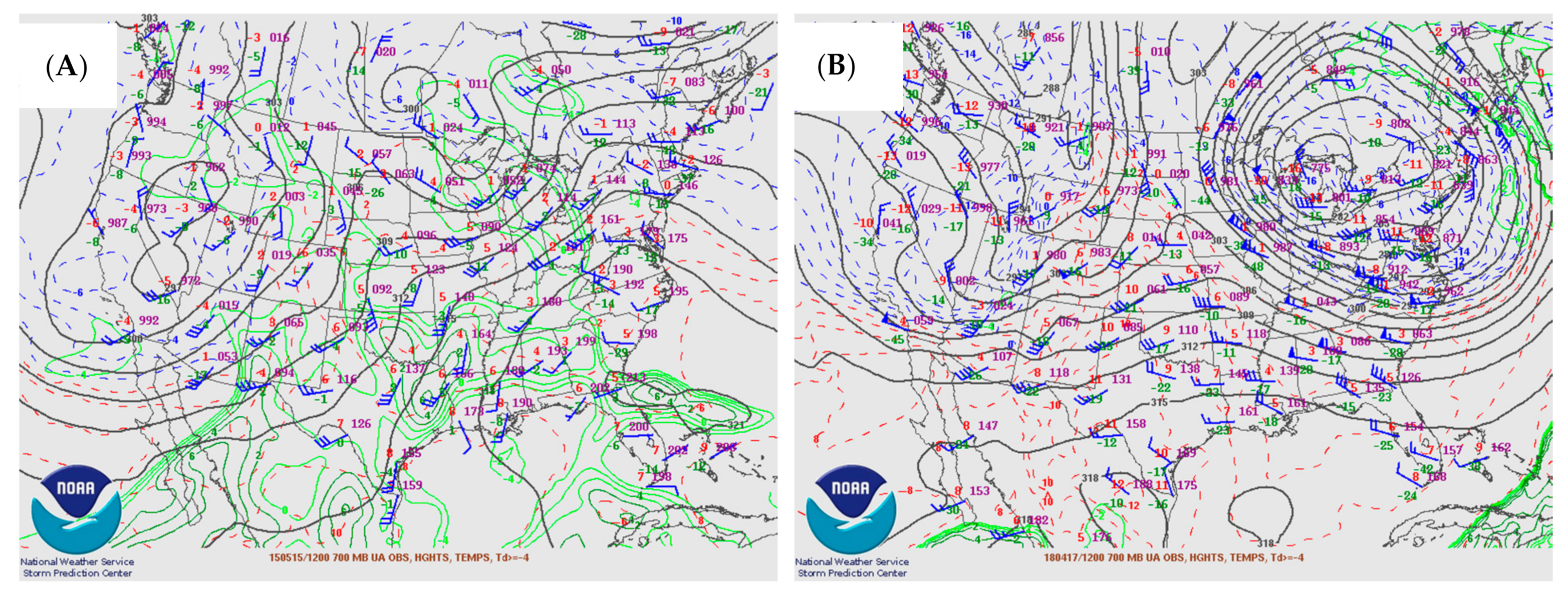
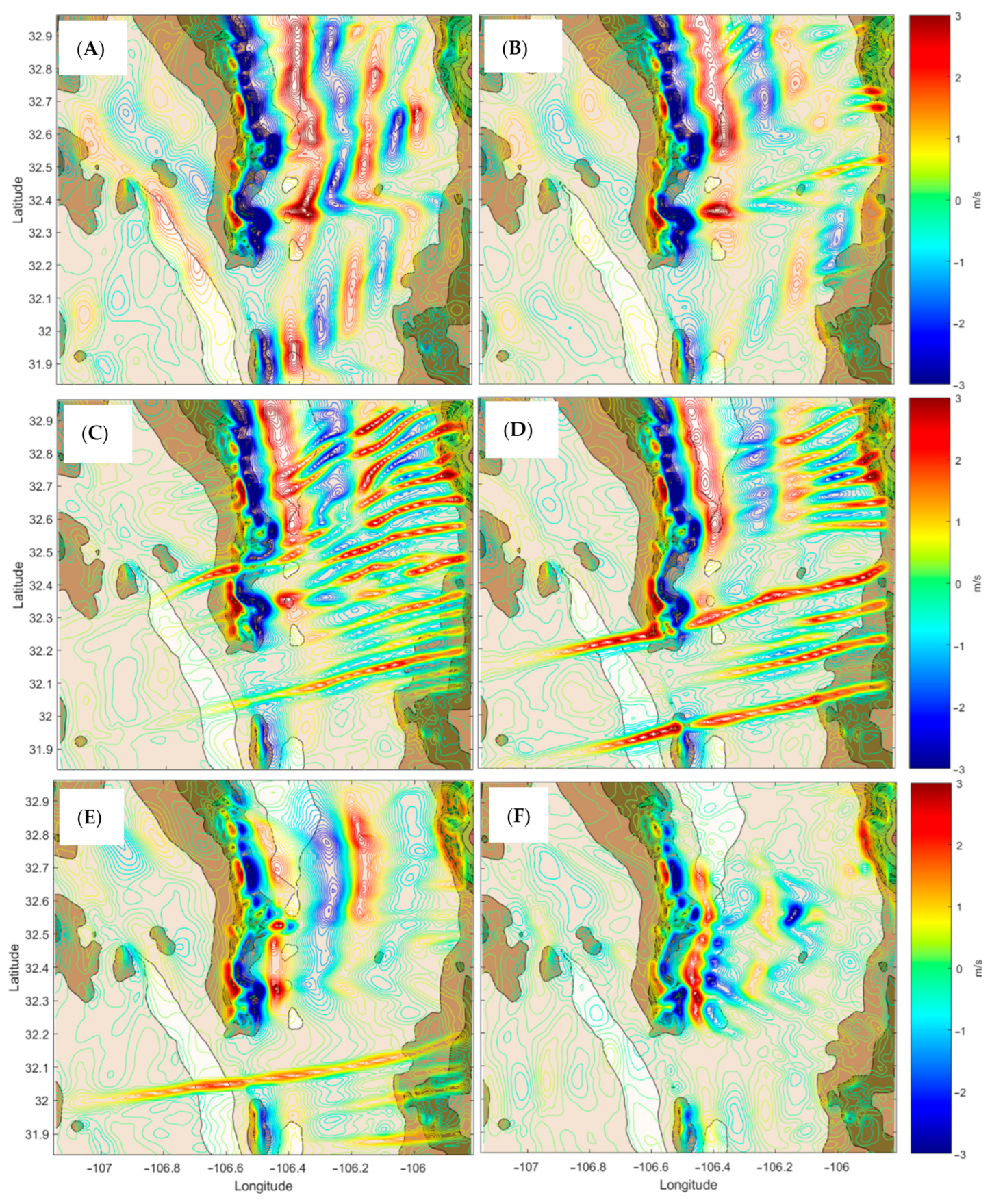
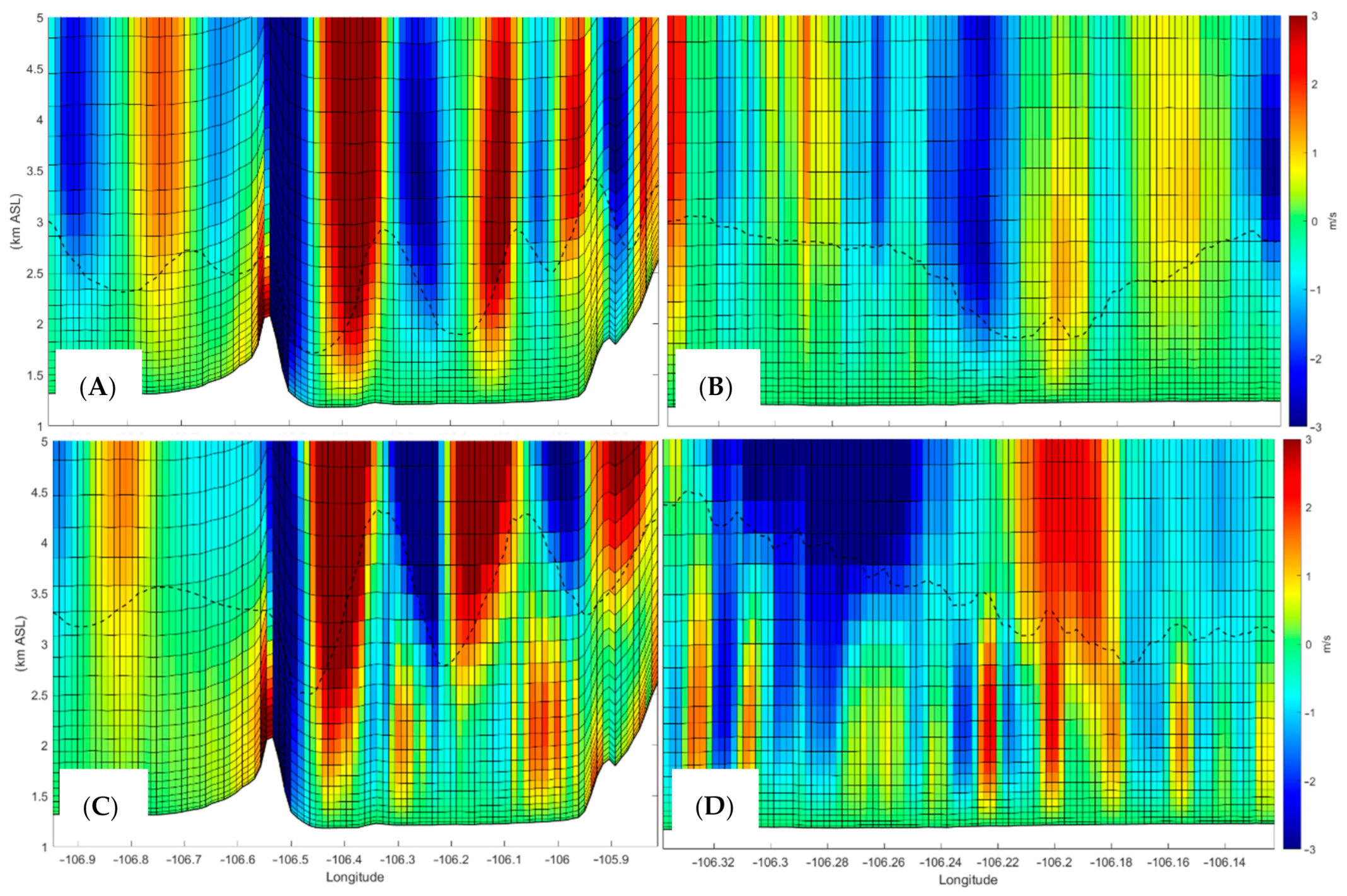
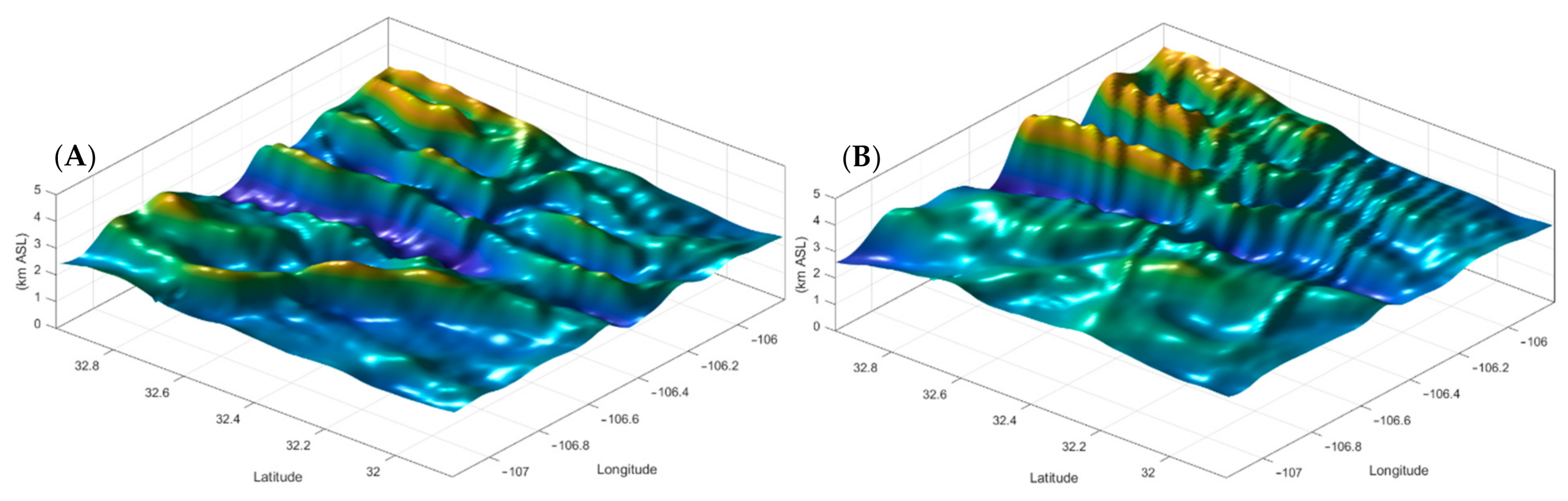
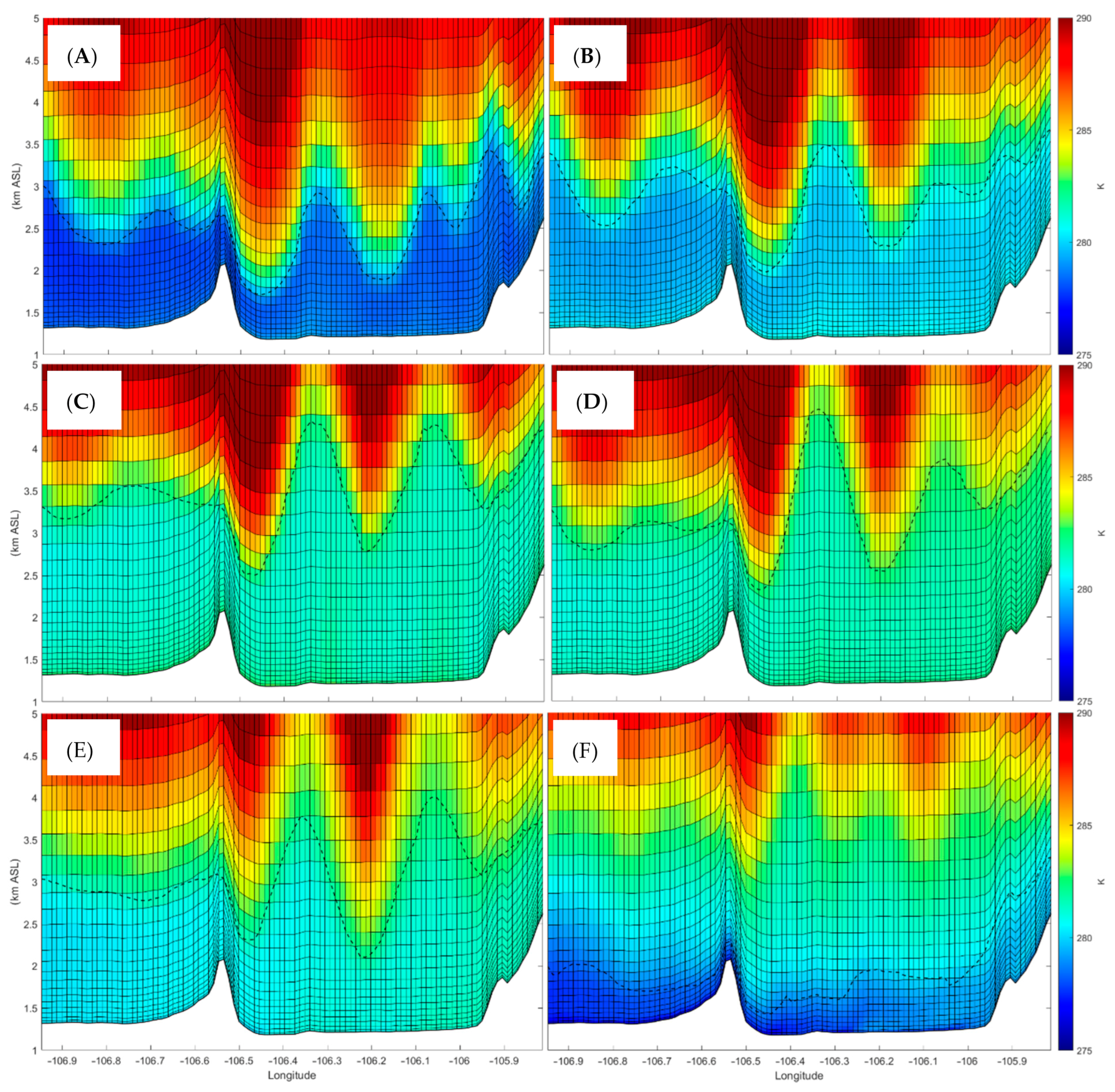
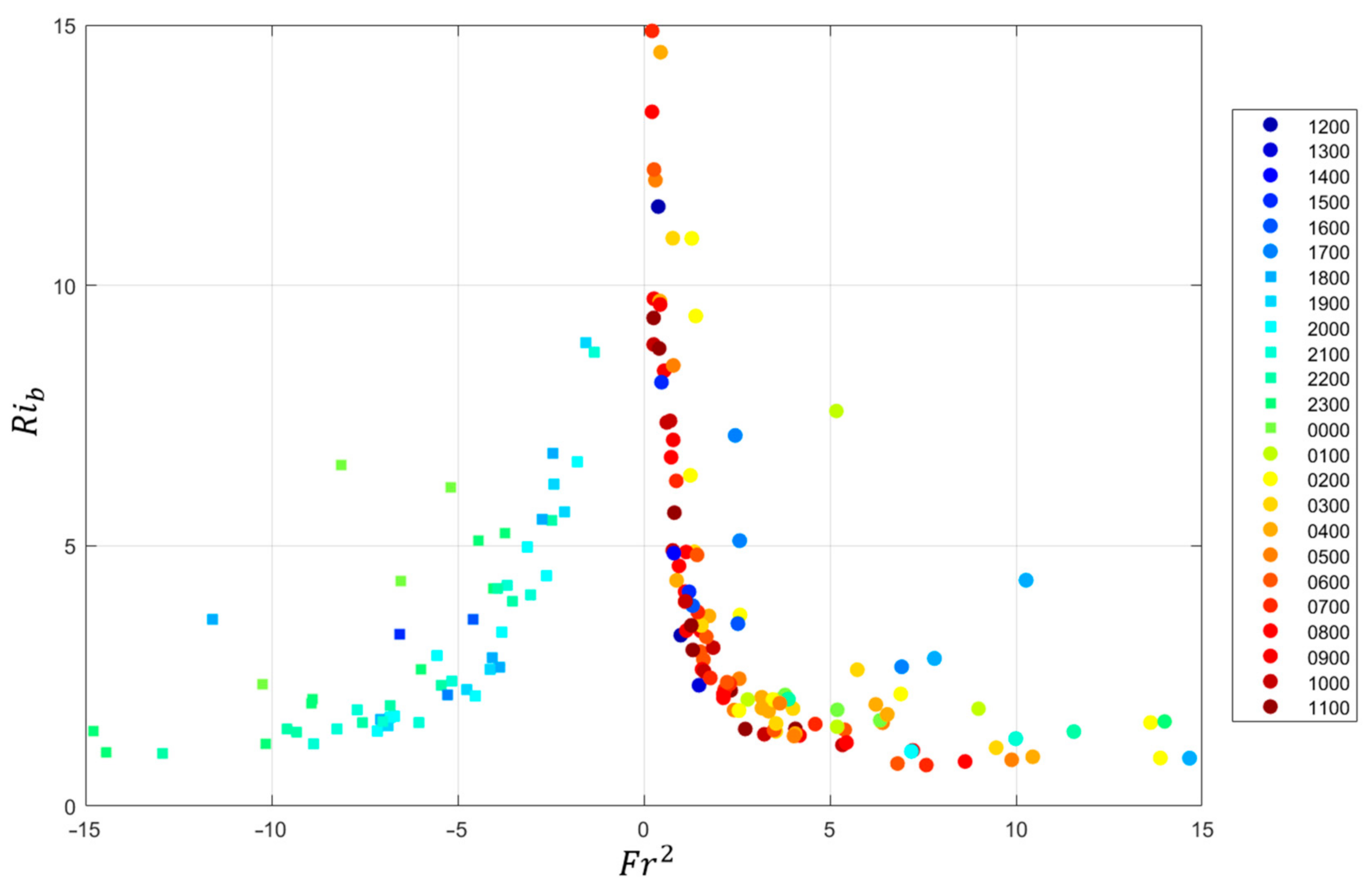
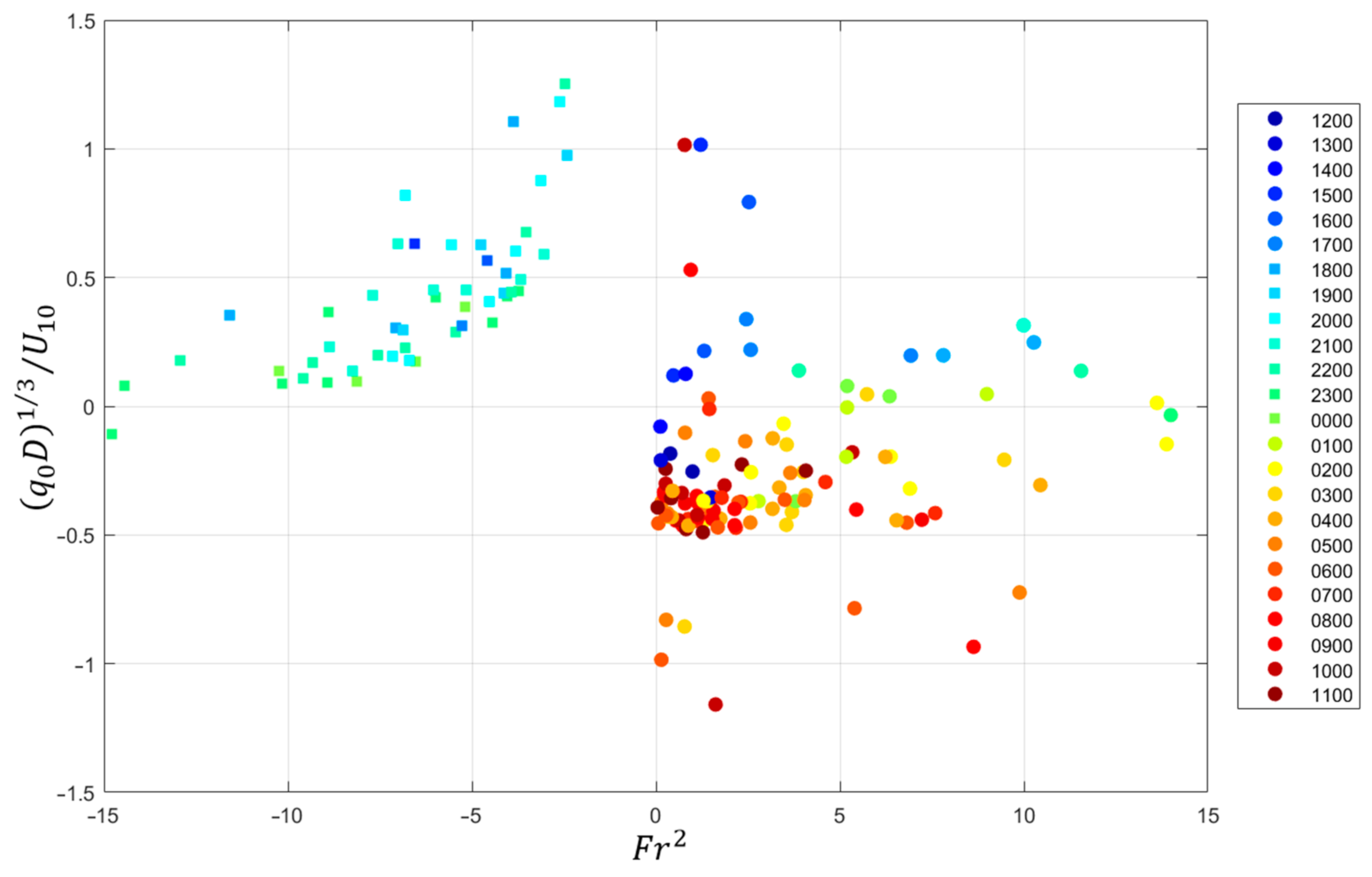
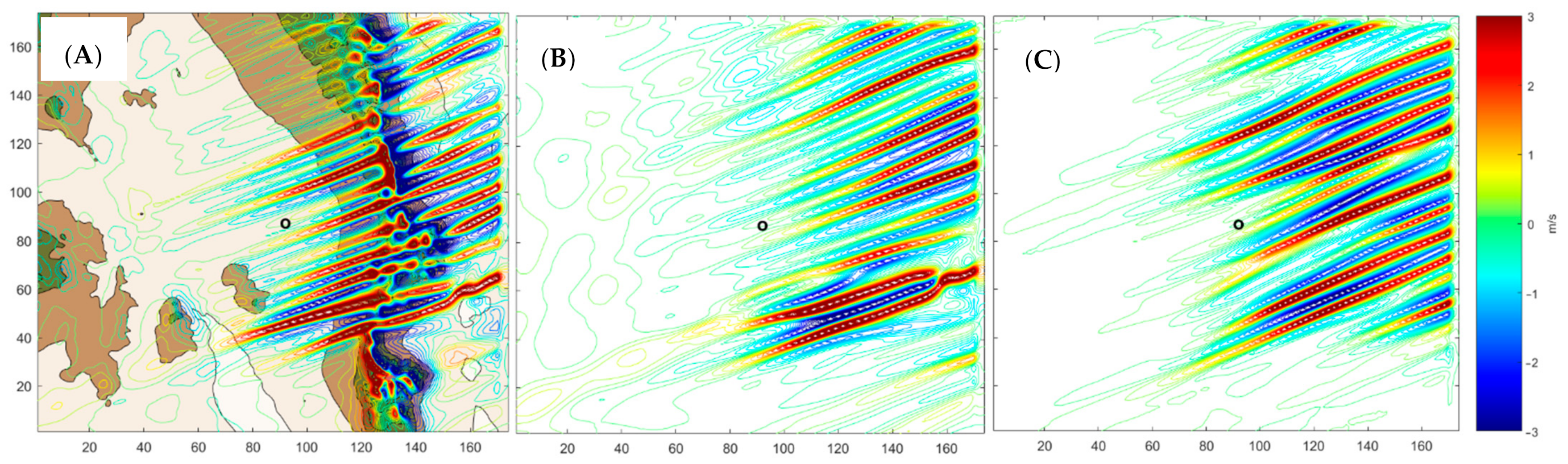
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whiteman, C.D. Mountain Meteorology: Fundamentals and Applications; Oxford University Press: New York, NY, USA, 2000; p. 355. [Google Scholar]
- Dimitrova, R.; Silver, Z.; Zsedrovits, T.; Hocut, C.M.; Leo, L.S.; Sabatino, S.D.; Fernando, H.J.S. Assessment of Planetary Boundary-Layer Schemes in the Weather Research and Forecasting Mesoscale Model Using MATERHORN Field Data. Bound. Layer Meteorol. 2016, 159, 589–609. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Pardyjak, E.R.; Sabatino, S.D.; Chow, F.K.; De Wekker, S.F.J.; Hoch, S.W.; Zsedrovits, T. The MATERHORN: Unraveling the Intricacies of Mountain Weather. Bull. Am. Meteorol. Soc. 2015, 96, 1945–1967. [Google Scholar] [CrossRef]
- Hocut, C.M.; Liberzon, D.; Fernando, H.J.S. Separation of upslope flow over a uniform slope. J. Fluid Mech. 2015, 775, 266–287. [Google Scholar] [CrossRef]
- Angevine, W.M.; Olson, J.; Kenyon, J.; Gustafson, W.I.; Endo, S., Jr.; Suselj, K.; Turner, D.D. Shallow Cumulus in WRF Parameterizations Evaluated against LASSO Large-Eddy Simulations. Mon. Weather Rev. 2018, 146, 4303–4322. [Google Scholar] [CrossRef]
- Doyle, J.D.; Gaberšek, S.; Jiang, Q.; Bernardet, L.; Brown, J.M.; Dörnbrack, A.; Filaus, E.; Grubišić, V.; Kirshbaum, D.J.; Knoth, O.; et al. An Intercomparison of T-REX Mountain-Wave Simulations and Implications for Mesoscale Predictability. Mon. Weather Rev. 2011, 139, 2811–2831. [Google Scholar] [CrossRef]
- Wilson, T.H.; Fovell, R.G. Modeling the evolution and life cycle of radiative cold pools and fog. Weather Forecast. 2018, 33, 203–220. [Google Scholar] [CrossRef]
- Rao, P.A.; Fuelberg, H.E. An Investigation of Convection behind the Cape Canaveral Sea-Breeze Front. Mon. Weather Rev. 2000, 128, 3437–3458. [Google Scholar] [CrossRef]
- Rife, D.L.; Warner, T.T.; Chen, F.; Astling, E.G. Mechanisms for diurnal boundary layer circulations in the Great Basin Desert. Mon. Weather Rev. 2002, 130, 921–938. [Google Scholar] [CrossRef][Green Version]
- Arthur, R.S.; Lundquist, K.A.; Mirocha, J.D.; Chow, F.K. Topographic effects on radiation in the WRF Model with the immersed boundary method: Implementation, validation, and application to complex terrain. Mon. Weather Rev. 2018, 146, 3277–3292. [Google Scholar] [CrossRef]
- Frame, J.W.; Petters, J.L.; Markowski, P.M.; Harrington, J.Y. An application of the tilted independent pixel approximation to cumulonimbus environments. Atmos. Res. 2009, 91, 127–136. [Google Scholar] [CrossRef]
- Brown, R.A. On the inflection point instability of a stratified Ekman boundary layer. J. Atmos. Sci. 1972, 29, 851–859. [Google Scholar] [CrossRef]
- Sachsperger, J.; Serafin, S.; Grubišić, V. Lee waves on the boundary-layer inversion and their dependence on free-atmospheric stability. Front. Earth Sci. 2015, 3, 70. [Google Scholar] [CrossRef]
- Lemone, M.A. The structure and dynamics of horizontal roll vortices in the planetary boundary layer. J. Atmos. Sci. 1973, 30, 1077–1091. [Google Scholar] [CrossRef]
- Weckwerth, T.M.; Wilson, J.W.; Wakimoto, R.M.; Crook, N.A. Horizontal Convective Rolls: Determining the Environmental Conditions Supporting their Existence and Characteristics. Mon. Weather Rev. 1997, 125, 505–526. [Google Scholar] [CrossRef]
- Banghoff, J.R.; Sorber, J.D.; Stensrud, D.J.; Young, G.S.; Kumjian, M.R. A 10-Year Warm-Season Climatology of Horizontal Convective Rolls and Cellular Convection in Central Oklahoma. Mon. Weather Rev. 2020, 148, 21–42. [Google Scholar] [CrossRef]
- Clark, T.L.; Hauf, T.; Kuettner, J.P. Convectively forced internal gravity waves: Results from two-dimensional numerical experiments. Q. J. R. Meteorol. Soc. 1986, 112, 899–925. [Google Scholar] [CrossRef]
- Salesky, S.T.; Chamecki, M.; Bou-Zeid, E. On the nature of the transition between roll and cellular organization in the convective boundary layer. Bound. Layer Meteorol. 2017, 163, 41–68. [Google Scholar] [CrossRef]
- Babić, N.; De Wekker, S.F.J. Characteristics of roll and cellular convection in a deep and wide semiarid valley: A large-eddy simulation study. Atmos. Res. 2019, 223, 74–87. [Google Scholar] [CrossRef]
- Davis, C.; Warner, T.; Astling, E.; Bowers, J. Development and application of an operational, relocatable, mesogamma-scale weather analysis and forecasting system. Tellus 1999, 51, 710–727. [Google Scholar] [CrossRef]
- Mass, C.F.; Ovens, D.; Westrick, K.; Colle, B.A. Does increasing horizontal resolution produce more skillful forecasts? BAMS 2002, 83, 407–430. [Google Scholar] [CrossRef]
- Svensson, N.; Sahlée, E.; Bergström, H.; Nilsson, E.; Badger, M.; Rutgersson, A. A case study of offshore advection of boundary layer rolls over a stably stratified sea surface. Adv. Meteorol. 2017, 4, 1–15. [Google Scholar] [CrossRef]
- Emmit, G.D.; Foster, R.; Wekker, S.D. Investigation of the Representation of OLEs and Terrain Effects Within the Coastal Zone in the EDMF Parameterization Scheme: An Airborne Doppler Wind Lidar Perspective. In Proceedings of the Annual Report to Defense Contract Management Agency, Charlottesville, VA, USA, 6 July 2012. [Google Scholar]
- Wyngaard, J.C. Toward numerical modeling in the “terra incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Bryan, G. Recommendations for WRF simulations with horizontal grid spacing between 100 m and 1 km. In Proceedings of the 15th WRF Users’ Workshop, Boulder, CO, USA, 25 June 2014. [Google Scholar]
- Knievel, J.C.; Bryan, G.H.; Hacker, J.P. Explicit numerical diffusion in the WRF model. Mon. Weather Rev. 2007, 135, 3808–3824. [Google Scholar] [CrossRef]
- Skamarock, W.C. Evaluating Mesoscale NWP Models Using Kinetic Energy Spectra. Mon. Weather Rev. 2004, 132, 3019–3032. [Google Scholar] [CrossRef]
- Ching, J.; Rotunno, R.; LeMone, M.A.; Martilli, A.; Kosović, B.; Jiménez, P.; Dudhia, J. Convectively induced secondary circulations in fine-grid mesoscale numerical weather prediction models. Mon. Weather Rev. 2014, 42, 3284–3302. [Google Scholar] [CrossRef]
- Zhou, B.; Simon, J.S.; Chow, F.K. The convective boundary layer in the terra incognita. J. Atmos. Sci. 2014, 71, 2545–2563. [Google Scholar] [CrossRef]
- Kealing, J. Probing the ‘grey zone’ of NWP–is higher resolution always better? Q. J. R. Meteorol. Soc. 2019, 74, 246–249. [Google Scholar]
- Honnert, R.; Efstathiou, G.A.; Beare, R.J.; Ito, J.; Lock, A.; Neggers, R.; Plant, R.S.; Shin, H.H.; Tomassini, L.; Zhou, B. The atmospheric boundary layer and the “gray zone” of turbulence: A critical review. J. Geophys. Res. 2020, 125, e2019JD030317. [Google Scholar] [CrossRef]
- Efstathiou, G.A.; Beare, R.J. Quantifying and improving sub-grid diffusion in the boundary-layer grey zone. Q. J. R. Meteorol. Soc. 2015, 141, 3006–3017. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.-Y. Representation of the subgrid-scale turbulent transport in convective boundary layers at gray-zone resolutions. Mon. Weather Rev. 2015, 143, 250–270. [Google Scholar] [CrossRef]
- Doubrawa, P.; Muñoz-Esparza, D. Simulating Real Atmospheric Boundary Layers at Gray-Zone Resolutions: How Do Currently Available Turbulence Parameterizations Perform? Atmosphere 2020, 11, 345. [Google Scholar] [CrossRef]
- Angevine, W.; Olson, J.; Gristey, J.; Glenn, I.; Feingold, G.; Turner, D. Scale Awareness, Resolved Circulations, and Practical Limits in the MYNN–EDMF Boundary Layer and Shallow Cumulus Scheme. Mon. Weather Rev. 2020, 148, 1–34. [Google Scholar] [CrossRef]
- Freitas, S.R.; Grell, G.A.; Molod, A.; Thompson, M.A.; Putman, W.M.; Santos, E.; Silva, C.M.; Souza, E.P. Assessing the Grell-Freitas Convection Parameterization in the NASA GEOS Modeling System. J. Adv. Model. Earth Syst. 2018, 10, 1266–1289. [Google Scholar] [CrossRef]
- Passner, J.E. Advanced Research Version of the Weather Research and Forecasting (WRF-ARW) Model Runs at Jornada Experimental Range. Army Research Laboratory, White Sands Missile Range. In Proceedings of the 12th Conference on Aviation Range and Aerospace Meteorology, White Sands Missile Range, NM, USA, 23 September 2019. [Google Scholar]
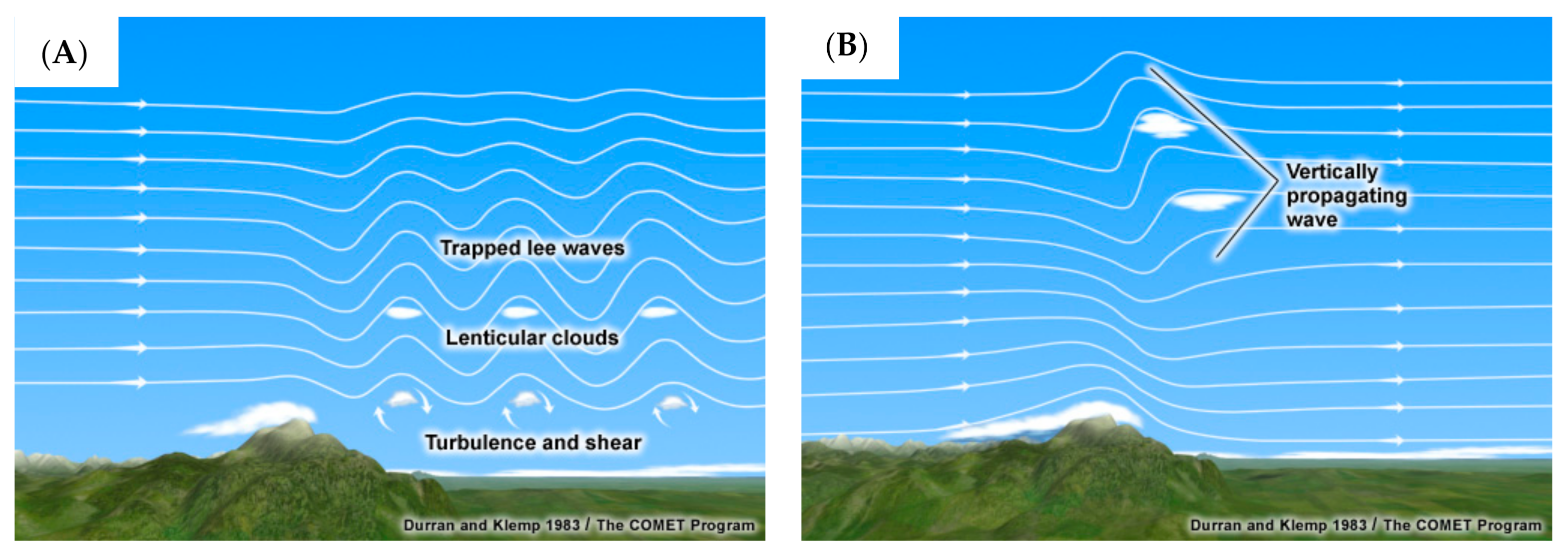
- EUMetrain. Physical Background of Lee Waves. Available online: http://www.eumetrain.org/data/4/452/navmenu.php?tab=4&page=1.0.0 (accessed on 13 February 2021).
- Young, G.S.; Kristovich, D.A.R.; Hjelmfelt, M.R.; Foster, R.C. Supplement to rolls, streets, waves, and more. BAMS 2002, 83, 997–1002. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A description of the advanced research WRF version 3. In National Center for Atmospheric Research; NCAR Technical Note: Boulder, CO, USA, 2008; p. 475. Available online: http://www2.mmm.ucar.edu/wrf/users/docs/arw_v3.pdf (accessed on 27 January 2021).
- Deng, A.; Stauffer, D.; Gaudet, B.; Dudhia, J.; Hacker, J.; Bruyere, C.; Wu, W.; Vandenberghe, F.; Liu, Y.; Bourgeois, A. Update on WRF-ARW end-to-end multi-scale FDDA system. In Proceedings of the 10th Annual WRF Users’ Workshop, NCAR, Boulder, CO, USA, 23–26 June 2009; Available online: http://www.mmm.ucar.edu/wrf/users/workshops/WS2009/abstracts/1-09.pdf (accessed on 11 March 2021).
- Leo, L.S.; Thompson, M.; Sabatino, S.D.; Fernando, H.J.S. Stratified Flow Past a Hill: Dividing Streamline Concept Revisited. Bound. Layer Meteorol. 2016, 159, 611–634. [Google Scholar] [CrossRef]
- Kundu, P.K.; Choen, I.M.; Dowling, D.R. Fluid Mechanics, 5th ed.; Elsevier: Oxford, UK, 2012; pp. 294–295. [Google Scholar]
- Hocut, C.M. Multi-Scale Flow and Turbulence in Complex Terrain Under Weak Synoptic Conditions. Ph.D. Dissertation, University of Notre Dame, South Bend, IN, USA, 2013. [Google Scholar]
- Glossary of Meteorology: Bulk Richardson Number. Available online: https://glossary.ametsoc.org/wiki/Bulk_richardson_number (accessed on 19 May 2021).
- Colomer, J.; Boubnov, B.M.; Fernando, H.J.S. Turbulent convection from isolated sources. Dyn. Atmos. Ocean. 1999, 30, 125–148. [Google Scholar] [CrossRef]



| Parameterizations | Reference |
|---|---|
| Mellor-Yamada Nakanishi Niino (MYNN) level 2.5 planetary boundary layer scheme | Nakanishi and Niino, 2009 |
| Mellor-Yamada Nakanishi Niino surface layer scheme | Nakanishi and Niino, 2009 |
| RRTMG longwave and shortwave radiation schemes | Iacono et al., 2008 |
| Thompson aerosol-aware microphysics scheme | Thompson and Eidhammer, 2014 |
| Grell-Freitas Scale and aerosol-aware deep ensemble cumulus scheme (with shallow cumulus treatment) | Grell and Freitas, 2014 |
| Noah Land Surface Model | Tewari et al., 2004 |
| 6th-order numerical diffusion filter | Knievel, Bryan and Hacker, 2005 |
| MSA Tower | WD (°) | U (m/s) |
|---|---|---|
| 11 | 2.37 | 0.86 |
| 13 | 4.90 | 0.25 |
| 18 | 3.35 | 0.54 |
| 20 | 3.69 | 1.35 |
| 23 | 4.26 | 0.78 |
| 33 | 3.90 | 1.05 |
| Case | WD (°) | U (m/s) |
|---|---|---|
| 25 April 2015 | 260 | 10 |
| 15 May 2015 | 230 | 21 |
| 12 April 2018 | 255 | 21 |
| 17 April 2018 | 250 | 23 |
| 20 May 2018 | 230 | 25 |
| 15 May 2018 | 250 | 9 |
| 20 May 2019 | 240 | 16 |
| 15 December 2019 | 260 | 25 |
| 10 January 2020 | 290 | 7 |
| 22 January 2020 | 305 | 11 |
| 27 January 2020 | 290 | 11 |
| 18 March 2020 | 230 | 17 |
| 19 March 2020 | 250 | 19 |
| 27 March 2020 | 230 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Payne, C.M.; Passner, J.E.; Dumais, R.E.; Abdelkefi, A.; Hocut, C.M. Presence of Longitudinal Roll Structures during Synoptic Forced Conditions in Complex Terrain. Atmosphere 2021, 12, 737. https://doi.org/10.3390/atmos12060737
Payne CM, Passner JE, Dumais RE, Abdelkefi A, Hocut CM. Presence of Longitudinal Roll Structures during Synoptic Forced Conditions in Complex Terrain. Atmosphere. 2021; 12(6):737. https://doi.org/10.3390/atmos12060737
Chicago/Turabian StylePayne, Cory M., Jeffrey E. Passner, Robert E. Dumais, Abdessattar Abdelkefi, and Christopher M. Hocut. 2021. "Presence of Longitudinal Roll Structures during Synoptic Forced Conditions in Complex Terrain" Atmosphere 12, no. 6: 737. https://doi.org/10.3390/atmos12060737
APA StylePayne, C. M., Passner, J. E., Dumais, R. E., Abdelkefi, A., & Hocut, C. M. (2021). Presence of Longitudinal Roll Structures during Synoptic Forced Conditions in Complex Terrain. Atmosphere, 12(6), 737. https://doi.org/10.3390/atmos12060737







