Evaluating the NDVI–Rainfall Relationship in Bisha Watershed, Saudi Arabia Using Non-Stationary Modeling Technique
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Normalized Difference Vegetation Index (NDVI)
2.3. Climate Hazard InfraRed Precipitation with Stations (CHIRPS)
2.4. Methods of Modeling
2.4.1. Ordinary Least Squares (OLS) Model
2.4.2. Geographically Weighted Regression Model (GWR)
2.4.3. Model Performance Evaluation
2.4.4. Measuring Spatial Autocorrelations
2.4.5. Scale Dependency of Non-stationarity
3. Results
3.1. Rainfall Data Analysis
3.2. Scale-Dependency Bandwidth
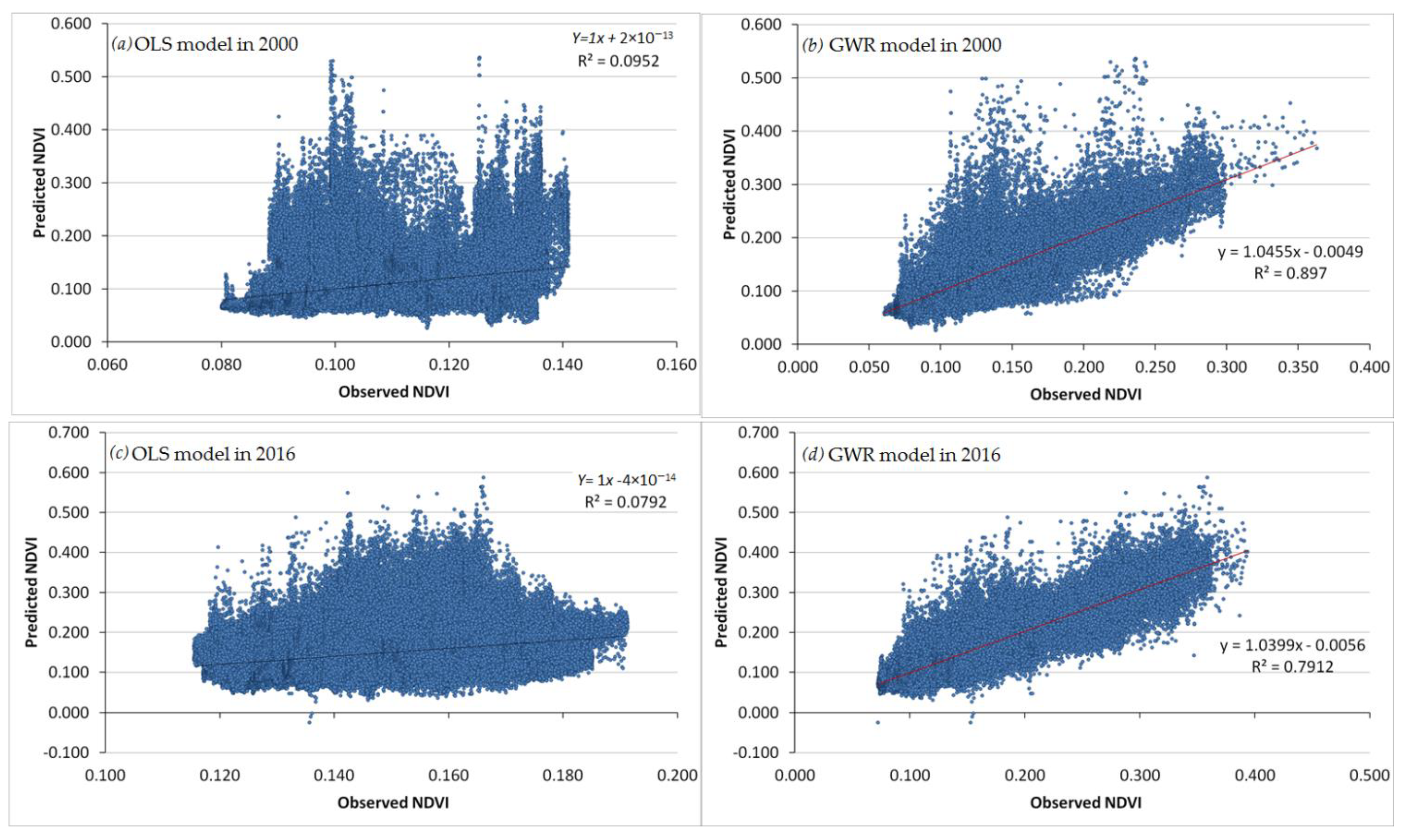
3.3. The GWR and OLS Model Assessment
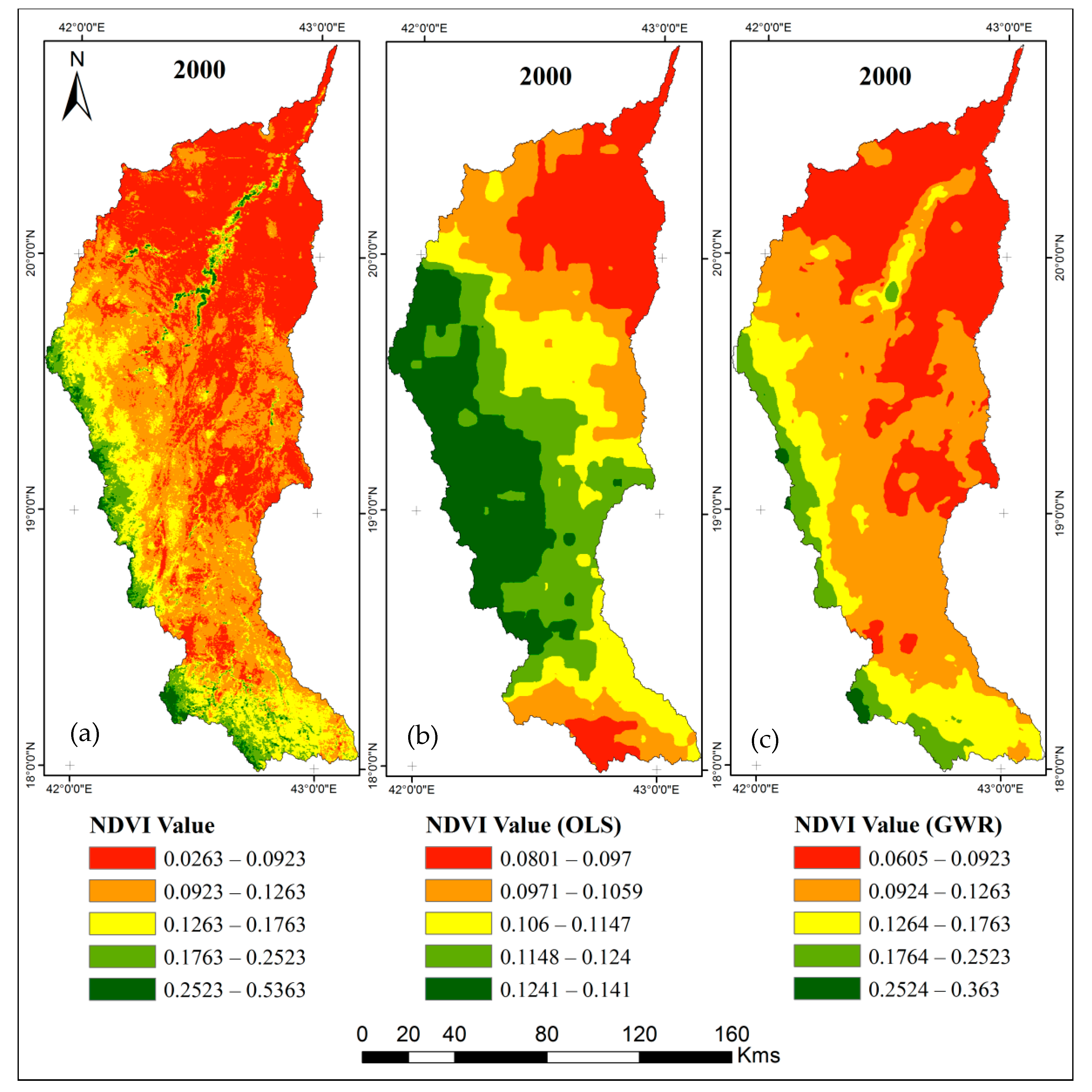
3.4. The NDVI–Rainfall Relationship’s Spatial Pattern
3.5. Predicted Trends of Spatial Heterogeneity
4. Discussion
Limitation of the Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nanzad, L.; Zhang, J.; Tuvdendorj, B.; Nabil, M.; Zhang, S.; Bai, Y. NDVI anomaly for drought monitoring and its correlation with climate factors over Mongolia from 2000 to 2016. J. Arid Environ. 2019, 164, 69–77. [Google Scholar] [CrossRef]
- Lu, J.; Carbone, G.J.; Gao, P. Mapping the agricultural drought based on the long-term AVHRR NDVI and North American Regional Reanalysis (NARR) in the United States, 1981–2013. Appl. Geogr. 2019, 104, 10–20. [Google Scholar] [CrossRef]
- Quarmby, N.A.; Milnes, M.; Hindle, T.L.; Silleos, N. The use of multi-temporal NDVI measurements from AVHRR data for crop yield estimation and prediction. Int. J. Remote Sens. 1993, 14, 199–210. [Google Scholar] [CrossRef]
- Huang, J.; Wang, H.; Dai, Q.; Han, D. Analysis of NDVI data for crop identification and yield estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4374–4384. [Google Scholar] [CrossRef]
- Heumann, B.W.; Seaquist, J.W.; Eklundh, L.; Jönsson, P. AVHRR derived phenological change in the Sahel and Soudan, Africa, 1982–2005. Remote Sens. Environ. 2007, 108, 385–392. [Google Scholar] [CrossRef]
- Pereira Coltri, P.; Zullo, J.; Ribeiro Do Valle Goncalves, R.; Romani, L.A.S.; Pinto, H.S. Coffee crop’s biomass and carbon stock estimation with usage of high resolution satellites images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1786–1795. [Google Scholar] [CrossRef]
- Liu, B.; Chen, J.; Chen, J.; Zhang, W. Land Cover Change Detection Using Multiple Shape Parameters of Spectral and NDVI Curves. Remote Sens. 2018, 10, 1251. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Worthy, L.D. Land-cover change detection using multi-temporal MODIS NDVI data. Remote Sens. Environ. 2006, 105, 142–154. [Google Scholar] [CrossRef]
- Tadesse, T.; Brown, J.F.; Hayes, M.J. A New Approach for Predicting Drought-Related Vegetation Stress: Integrating Satellite, Climate, and Biophysical Data over the U.S. Central Plains. ISPRS J. Photogramm. Remote Sens. 2005, 59, 244–253. [Google Scholar] [CrossRef]
- Song, X.; Saito, G.; Kodama, M.; Sawada, H. Early detection system of drought in East Asia using NDVI from NOAA/AVHRR data. Int. J. Remote Sens. 2004, 25, 3105–3111. [Google Scholar] [CrossRef][Green Version]
- Kogan, F.N. Global Drought Watch from Space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar] [CrossRef]
- Kawabata, A.; Ichii, K.; Yamaguchi, Y. Global monitoring of interannual changes in vegetation activities using NDVI and its relationships to temperature and precipitation. Int. J. Remote Sens. 2001, 22, 1377–1382. [Google Scholar] [CrossRef]
- Potter, C.S.; Brooks, V. Global analysis of empirical relations between annual climate and seasonality of NDVI. Int. J. Remote Sens. 1998, 19, 2921–2948. [Google Scholar] [CrossRef]
- Nezlin, N.P.; Kostianoy, A.G.; Li, B.L. Inter-annual variability and interaction of remote-sensed vegetation index and atmospheric precipitation in the Aral Sea region. J. Arid Environ. 2005, 62, 677–700. [Google Scholar] [CrossRef]
- Evans, J.; Geerken, R. Discrimination between climate and human-induced dryland degradation. J. Arid Environ. 2004, 57, 535–554. [Google Scholar] [CrossRef]
- Li, J.; Lewis, J.; Rowland, J.; Tappan, G.; Tieszen, L. Evaluation of land performance in Senegal using multi-temporal NDVI and rainfall series. J. Arid Environ. 2004, 59, 463–480. [Google Scholar] [CrossRef]
- Budde, M.; Tappan, G.; Rowland, J.; Lewis, J.; Tieszen, L. Assessing land cover performance in Senegal, West Africa using 1-km integrated NDVI and local variance analysis. J. Arid Environ. 2004, 59, 481–498. [Google Scholar] [CrossRef]
- Weiss, E.; Marsh, S.E.; Pfirman, E.S. Application of NOAA-AVHRR NDVI time-series data to assess changes in Saudi Arabia’s rangelands. Int. J. Remote Sens. 2001, 22, 1005–1027. [Google Scholar] [CrossRef]
- Xiao, J.; Moody, A. Trends in vegetation activity and their climatic correlates: China 1982 to 1998. Int. J. Remote Sens. 2004, 25, 5669–5689. [Google Scholar] [CrossRef]
- Tucker, C.J.; Slayback, D.A.; Pinzon, J.E.; Los, S.O.; Myneni, R.B.; Taylor, M.G. Higher northern latitude normalized difference vegetation index and growing season trends from 1982 to 1999. Int. J. Biometeorol. 2001, 45, 184–190. [Google Scholar] [CrossRef]
- Amini, A.; Abdeh Kolahchi, A.; Al-Ansari, N.; Karami Moghadam, M.; Mohammad, T. Application of TRMM Precipitation Data to Evaluate Drought and Its Effects on Water Resources Instability. Appl. Sci. 2019, 9, 5377. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef]
- Paredes Trejo, F.J.; Barbosa, H.A.; Peñaloza-Murillo, M.A.; Alejandra Moreno, M.; Farías, A. Intercomparison of improved satellite rainfall estimation with CHIRPS gridded product and rain gauge data over Venezuela. Atmosfera 2016, 29, 323–342. [Google Scholar] [CrossRef]
- Toté, C.; Patricio, D.; Boogaard, H.; van der Wijngaart, R.; Tarnavsky, E.; Funk, C. Evaluation of Satellite Rainfall Estimates for Drought and Flood Monitoring in Mozambique. Remote Sens. 2015, 7, 1758–1776. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Dinku, T.; Ruiz, F.; Connor, S.J.; Ceccato, P. Validation and intercomparison of satellite rainfall estimates over Colombia. J. Appl. Meteorol. Climatol. 2010, 49, 1004–1014. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Some, B.; McCollum, J.; Nelkin, E.; Klotter, D.; Berte, Y.; Diallo, B.M.; Gaye, I.; Kpabeba, G.; Ndiaye, O.; et al. Validation of TRMM and other rainfall estimates with a high-density gauge dataset for West Africa. Part II: Validation of TRMM rainfall products. J. Appl. Meteorol. 2003, 42, 1355–1368. [Google Scholar] [CrossRef]
- Laurent, H.; Jobard, I.; Toma, A. Validation of satellite and ground-based estimates of precipitation over the Sahel. Atmos. Res. 1998, 47–48, 651–670. [Google Scholar] [CrossRef]
- Franchito, S.H.; Rao, V.B.; Vasques, A.C.; Santo, C.M.E.; Conforte, J.C. Validation of TRMM precipitation radar monthly rainfall estimates over Brazil. J. Geophys. Res. 2009, 114, D02105. [Google Scholar] [CrossRef]
- Mallick, J.; Singh, R.K.; Khan, R.A.; Singh, C.K.; Kahla, N.B.; Warrag, E.I.; Islam, S.; Rahman, A. Examining the rainfall–topography relationship using non-stationary modelling technique in semi-arid Aseer region, Saudi Arabia. Arab. J. Geosci. 2018, 11, 1–16. [Google Scholar] [CrossRef]
- Bai, L.; Shi, C.; Li, L.; Yang, Y.; Wu, J. Accuracy of CHIRPS satellite-rainfall products over mainland China. Remote Sens. 2018, 10, 362. [Google Scholar] [CrossRef]
- Wang, J.; Price, K.P.; Rich, P.M. Spatial patterns of NDVI in response to precipitation and temperature in the central Great Plains. Int. J. Remote Sens. 2001, 22, 3827–3844. [Google Scholar] [CrossRef]
- Farrar, T.J.; Nicholson, S.E.; Lare, A.R. The influence of soil type on the relationships between NDVI, rainfall, and soil moisture in semiarid Botswana. II. NDVI response to soil oisture. Remote Sens. Environ. 1994, 50, 121–133. [Google Scholar] [CrossRef]
- Richard, Y.; Poccard, I. A statistical study of NDVI sensitivity to seasonal and interannual rainfall variations in Southern Africa. Int. J. Remote Sens. 1998, 19, 2907–2920. [Google Scholar] [CrossRef]
- Ji, L.; Peters, A.J. A spatial regression procedure for evaluating the relationship between AVHRR-NDVI and climate in the northern Great Plains. Int. J. Remote Sens. 2004, 25, 297–311. [Google Scholar] [CrossRef]
- Yang, L.; Wylie, B.K.; Tieszen, L.L.; Reed, B.C. An analysis of relationships among climate forcing and time-integrated NDVI of grasslands over the U.S. northern and central Great Plains. Remote Sens. Environ. 1998, 65, 25–37. [Google Scholar] [CrossRef]
- Georganos, S.; Abdi, A.M.; Tenenbaum, D.E.; Kalogirou, S. Examining the NDVI-rainfall relationship in the semi-arid Sahel using geographically weighted regression. J. Arid Environ. 2017, 146, 64–74. [Google Scholar] [CrossRef]
- Wang, T.; Kou, X.; Xiong, Y.; Mou, P.; Wu, J.; Ge, J. Temporal and spatial patterns of NDVI and their relationship to precipitation in the loess plateau of China. Int. J. Remote Sens. 2010, 31, 1943–1958. [Google Scholar] [CrossRef]
- Udelhoven, T.; Stellmes, M.; del Barrio, G.; Hill, J. Assessment of rainfall and NDVI anomalies in Spain (1989-1999) using distributed lag models. Int. J. Remote Sens. 2009, 30, 1961–1976. [Google Scholar] [CrossRef]
- Fabricante, I.; Oesterheld, M.; Paruelo, J.M. Annual and seasonal variation of NDVI explained by current and previous precipitation across Northern Patagonia. J. Arid Environ. 2009, 73, 745–753. [Google Scholar] [CrossRef]
- Huber, S.; Fensholt, R.; Rasmussen, K. Water availability as the driver of vegetation dynamics in the African Sahel from 1982 to 2007. Glob. Planet. Chang. 2011, 76, 186–195. [Google Scholar] [CrossRef]
- Martiny, N.; Camberlin, P.; Richard, Y.; Philippon, N. Compared regimes of NDVI and rainfall in semi-arid regions of Africa. Int. J. Remote Sens. 2006, 27, 5201–5223. [Google Scholar] [CrossRef]
- Kang, L.; Di, L.; Deng, M.; Shao, Y.; Yu, G.; Shrestha, R. Use of geographically weighted regression model for exploring spatial patterns and local factors behind NDVI-precipitation correlation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4530–4538. [Google Scholar] [CrossRef]
- McMillen, D.P. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. Am. J. Agric. Econ. 2004, 86, 554–556. [Google Scholar] [CrossRef]
- Stewart Fotheringham, A.; Charlton, M.; Brunsdon, C. The geography of parameter space: An investigation of spatial non-stationarity. Int. J. Geogr. Inf. Syst. 1996, 10, 605–627. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 2010, 28, 281–298. [Google Scholar] [CrossRef]
- Cahill, M.; Mulligan, G. Using Geographically Weighted Regression to Explore Local Crime Patterns. Soc. Sci. Comput. Rev. 2007, 25, 174–193. [Google Scholar] [CrossRef]
- Hu, M.; Li, Z.; Wang, J.; Jia, L.; Liao, Y.; Lai, S.; Guo, Y.; Zhao, D.; Yang, W. Determinants of the Incidence of Hand, Foot and Mouth Disease in China Using Geographically Weighted Regression Models. PLoS ONE 2012, 7, e38978. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Gao, J.; Wang, Y.; Liu, J.; Li, S. Exploring spatially variable relationships between NDVI and climatic factors in a transition zone using geographically weighted regression. Theor. Appl. Climatol. 2015, 120, 507–519. [Google Scholar] [CrossRef]
- Gaughan, A.E.; Waylen, P.R. Spatial and temporal precipitation variability in the Okavango-Kwando-Zambezi catchment, southern Africa. J. Arid Environ. 2012, 82, 19–30. [Google Scholar] [CrossRef]
- Wang, Q.; Ni, J.; Tenhunen, J. Application of a geographically-weighted regression analysis to estimate net primary production of Chinese forest ecosystems. Glob. Ecol. Biogeogr. 2005, 14, 379–393. [Google Scholar] [CrossRef]
- Foody, G.M. Spatial nonstationarity and scale-dependency in the relationship between species richness and environmental determinants for the sub-Saharan endemic avifauna. Glob. Ecol. Biogeogr. 2004, 13, 315–320. [Google Scholar] [CrossRef]
- Foody, G.M. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI-rainfall relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Peter Vincent Saudi Arabia: An Environmental Overview—1st Edition. Available online: https://www.routledge.com/Saudi-Arabia-An-Environmental-Overview/Vincent/p/book/9780367387815 (accessed on 16 March 2021).
- Al-Ahmadi, K.; Al-Ahmadi, S. Rainfall-altitude relationship in Saudi Arabia. Adv. Meteorol. 2013, 2013. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Wu, Y.L.; Li, Z.C.; Wang, Y.F.; Luan, Q.; Tian, G.Z. Responses of Vegetation Index (NDVI) in Typical Ecological Areas of Shanxi Province to Climate Change. Available online: http://www.cje.net.cn/EN/abstract/abstract15343.shtml (accessed on 16 March 2021).
- Gong, Z.; Zhao, S.; Gu, J. Correlation analysis between vegetation coverage and climate drought conditions in North China during 2001–2013. J. Geogr. Sci. 2017, 27, 143–160. [Google Scholar] [CrossRef]
- Mallick, J.; Talukdar, S.; Alsubih, M.; Salam, R.; Ahmed, M.; Kahla, N.B.; Shamimuzzaman, M. Analysing the trend of rainfall in Asir region of Saudi Arabia using the family of Mann-Kendall tests, innovative trend analysis, and detrended fluctuation analysis. Theor. Appl. Climatol. 2021, 143, 823–841. [Google Scholar] [CrossRef]
- Wheater, H.S.; Laurentis, P.; Hamilton, G.S. Design Rainfall Characteristics for South-West Saudi Arabia. Proc. Inst. Civ. Eng. 1989, 87, 517–538. [Google Scholar] [CrossRef]
- Baillie, J.E.M.; Groombridge, B. IUCN Red List of Threatened Species. Available online: https://www.iucnredlist.org/resources/baillie1996 (accessed on 16 March 2021).
- Davis, S.D.; Heywood, V. Centres of Plant Diversity: A Guide and Strategy for Their Conservation, v.1. Europe, Africa, South West Asia and the Middle East | IUCN. Available online: https://www.iucn.org/content/centres-plant-diversity-a-guide-and-strategy-their-conservation-v1-europe-africa-south-west-asia-and-middle-east (accessed on 16 March 2021).
- Hosni, H.A.; Hegazy, A.K. Contribution to the flora of Asir, Saudi Arabia. Candollea 1996, 51, 169–202. [Google Scholar]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Zhu, A.-X. Resampling, Raster. In International Encyclopedia of Geography: People, The Earth, Environment and Technology; John Wiley & Sons, Ltd.: Oxford, UK, 2017; pp. 1–5. [Google Scholar]
- Behnke, R.; Vavrus, S.; Allstadt, A.; Albright, T.; Thogmartin, W.E.; Radeloff, V.C. Evaluation of downscaled, gridded climate data for the conterminous United States. Ecol. Appl. 2016, 26, 1338–1351. [Google Scholar] [CrossRef] [PubMed]
- Kalogirou, S. The Statistical Analysis and Modelling of Internal Migration Flows within England and Wales by Stamatis Kalogirou. Ph.D. Thesis, Newcastle University, Newcastle upon Tyne, UK, 2003. [Google Scholar]
- Fotheringham, A.S.B. Geographically Weighted Regression; The Analysis of Spatially Varying Relationships | HimalDoc. Available online: https://lib.icimod.org/record/32858 (accessed on 16 March 2021).
- Caruso, C.; Quarta, F. Interpolation methods comparison. Comput. Math. Appl. 1998, 35, 109–126. [Google Scholar] [CrossRef]
- Dai, X.; Guo, Z.; Zhang, L.; Li, D. Spatio-temporal exploratory analysis of urban surface temperature field in Shanghai, China. Stoch. Environ. Res. Risk Assess. 2010, 24, 247–257. [Google Scholar] [CrossRef]
- Xu, S.; Wu, C.; Wang, L.; Gonsamo, A.; Shen, Y.; Niu, Z. A new satellite-based monthly precipitation downscaling algorithm with non-stationary relationship between precipitation and land surface characteristics. Remote Sens. Environ. 2015, 162, 119–140. [Google Scholar] [CrossRef]
- Anselin, L. Lagrange Multiplier Test Diagnostics for Spatial Dependence and Spatial Heterogeneity. Geogr. Anal. 2010, 20, 1–17. [Google Scholar] [CrossRef]
- Osborne, P.E.; Suárez-Seoane, S. Should data be partitioned spatially before building large-scale distribution models? Ecol. Modell. 2002, 157, 249–259. [Google Scholar] [CrossRef]
- Propastin, P.; Kappas, M.; Erasmi, S. Application of Geographically Weighted Regression to Investigate the Impact of Scale on Prediction Uncertainty by Modelling Relationship between Vegetation and Climate. Int. J. Spat. Data Infrastruct. Res. 2008, 3, 73–94. [Google Scholar]
- Jetz, W.; Rahbek, C.; Lichstein, J.W. Local and global approaches to spatial data analysis in ecology. Glob. Ecol. Biogeogr. 2005, 14, 97–98. [Google Scholar] [CrossRef]
- Propastin, P.A.; Kappas, M. Reducing uncertainty in modeling the NDVI-precipitation relationship: A comparative study using global and local regression techniques. GIScience Remote Sens. 2008, 45, 47–67. [Google Scholar] [CrossRef]
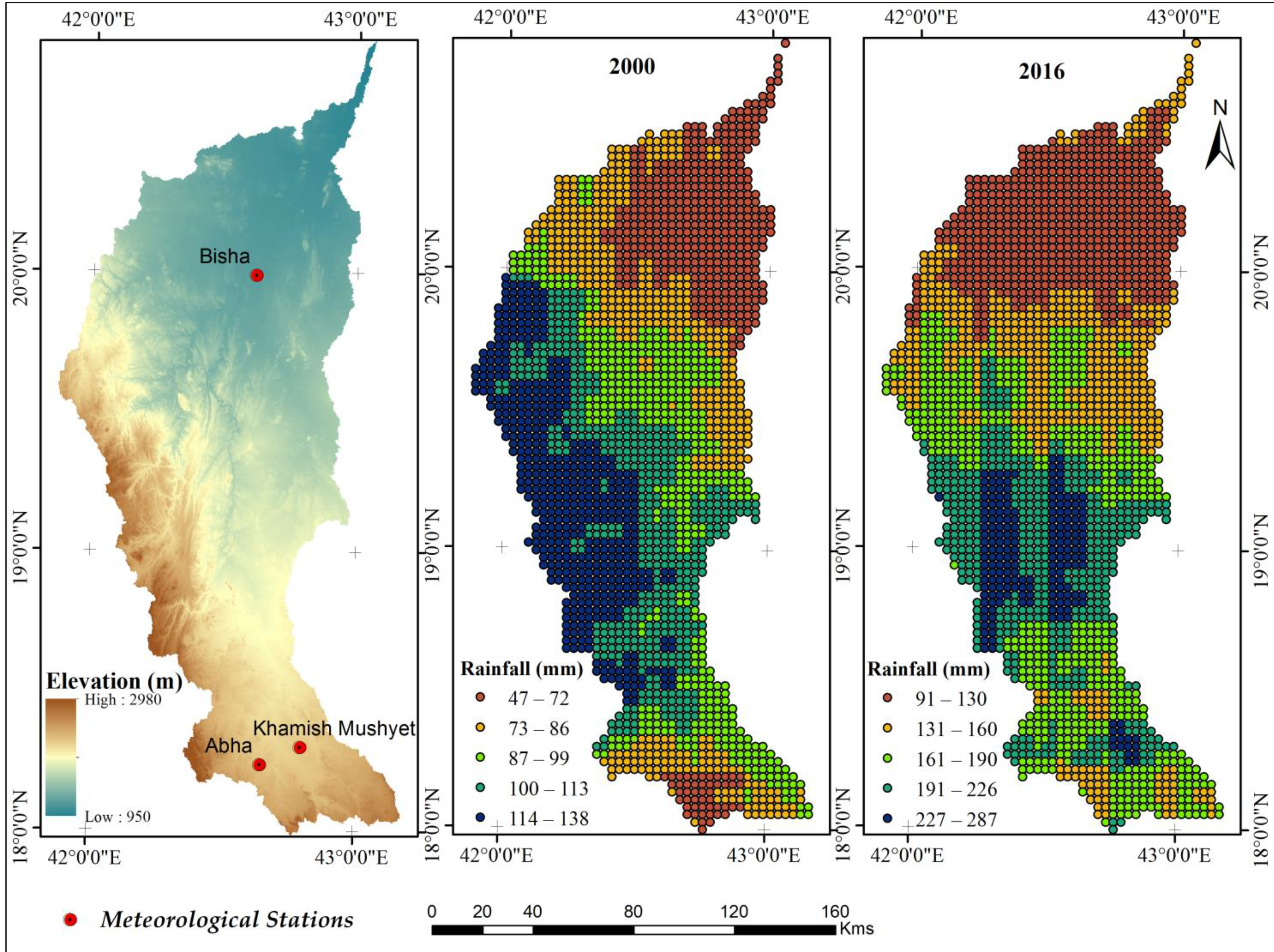







| Year | Minimum | Maximum | Mean | Median | SD | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| 2000 | 10.9 | 148.2 | 73.4 | 69.3 | 24.9 | 0.44 | −0.65 |
| 2016 | 23.2 | 370.8 | 147.7 | 143.0 | 42.7 | 0.57 | 0.48 |
| Year | Models | RMSE | MAE | R2 |
|---|---|---|---|---|
| 2000 | Global OLS Model | 0.04120 | 0.1654 | 0.095 |
| Local GWR Model | 0.02119 | 0.09100 | 0.897 | |
| 2016 | Global OLS Model | 0.05253 | 0.1978 | 0.079 |
| Local GWR Model | 0.02508 | 0.01712 | 0.791 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallick, J.; AlMesfer, M.K.; Singh, V.P.; Falqi, I.I.; Singh, C.K.; Alsubih, M.; Kahla, N.B. Evaluating the NDVI–Rainfall Relationship in Bisha Watershed, Saudi Arabia Using Non-Stationary Modeling Technique. Atmosphere 2021, 12, 593. https://doi.org/10.3390/atmos12050593
Mallick J, AlMesfer MK, Singh VP, Falqi II, Singh CK, Alsubih M, Kahla NB. Evaluating the NDVI–Rainfall Relationship in Bisha Watershed, Saudi Arabia Using Non-Stationary Modeling Technique. Atmosphere. 2021; 12(5):593. https://doi.org/10.3390/atmos12050593
Chicago/Turabian StyleMallick, Javed, Mohammed K. AlMesfer, Vijay P. Singh, Ibrahim I. Falqi, Chander Kumar Singh, Majed Alsubih, and Nabil Ben Kahla. 2021. "Evaluating the NDVI–Rainfall Relationship in Bisha Watershed, Saudi Arabia Using Non-Stationary Modeling Technique" Atmosphere 12, no. 5: 593. https://doi.org/10.3390/atmos12050593
APA StyleMallick, J., AlMesfer, M. K., Singh, V. P., Falqi, I. I., Singh, C. K., Alsubih, M., & Kahla, N. B. (2021). Evaluating the NDVI–Rainfall Relationship in Bisha Watershed, Saudi Arabia Using Non-Stationary Modeling Technique. Atmosphere, 12(5), 593. https://doi.org/10.3390/atmos12050593







