Method for Measuring the Second-Order Moment of Atmospheric Turbulence
Abstract
1. Introduction
- Zero-order, m = 0, for evaluating the seeing r0;
- Five-thirds-order, m = 5/3, for evaluating the isoplanatic angle θ0;
- Second-order, m = 2, for evaluating overall tilt errors [1].
2. Theoretical Basis
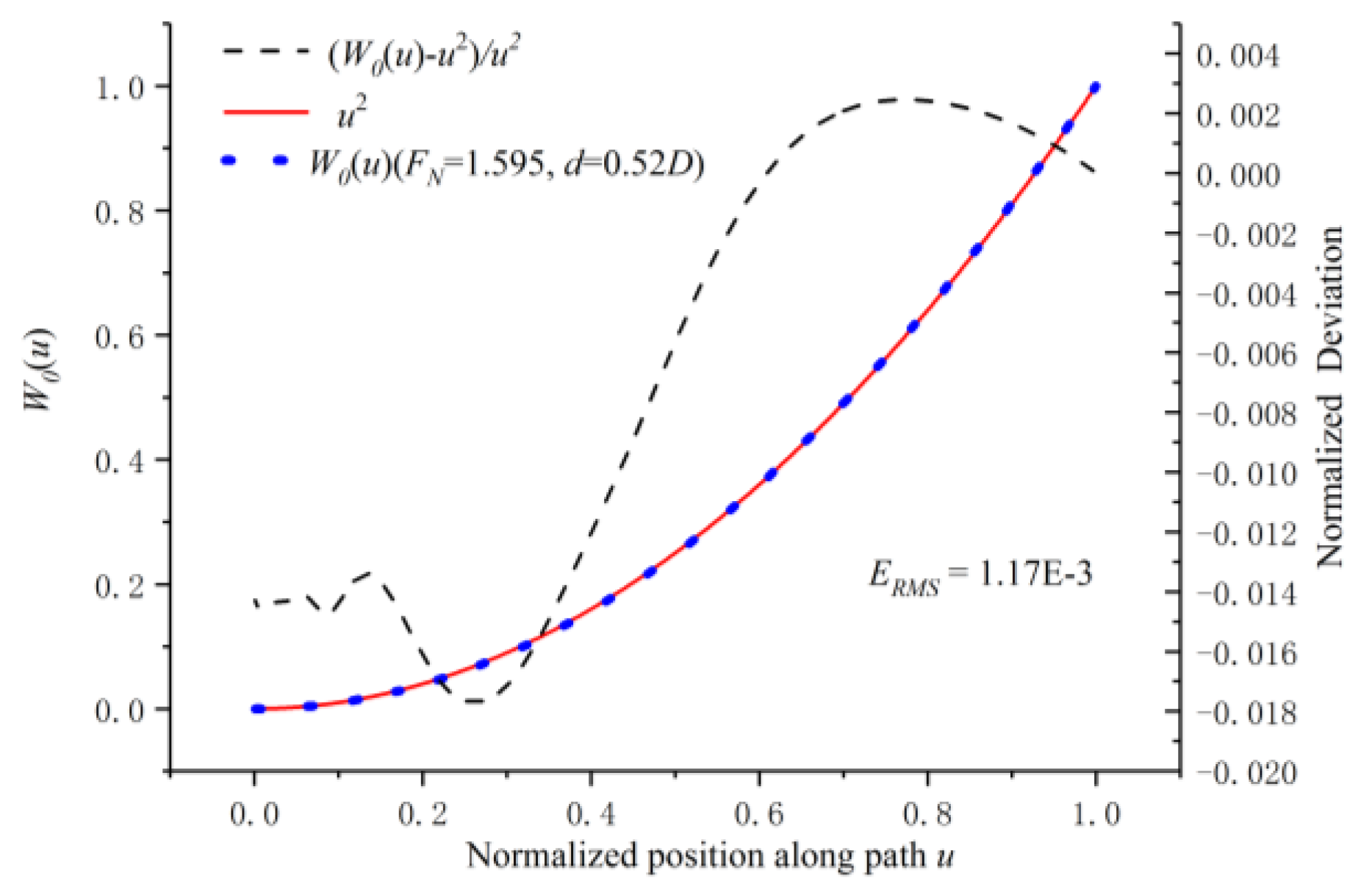
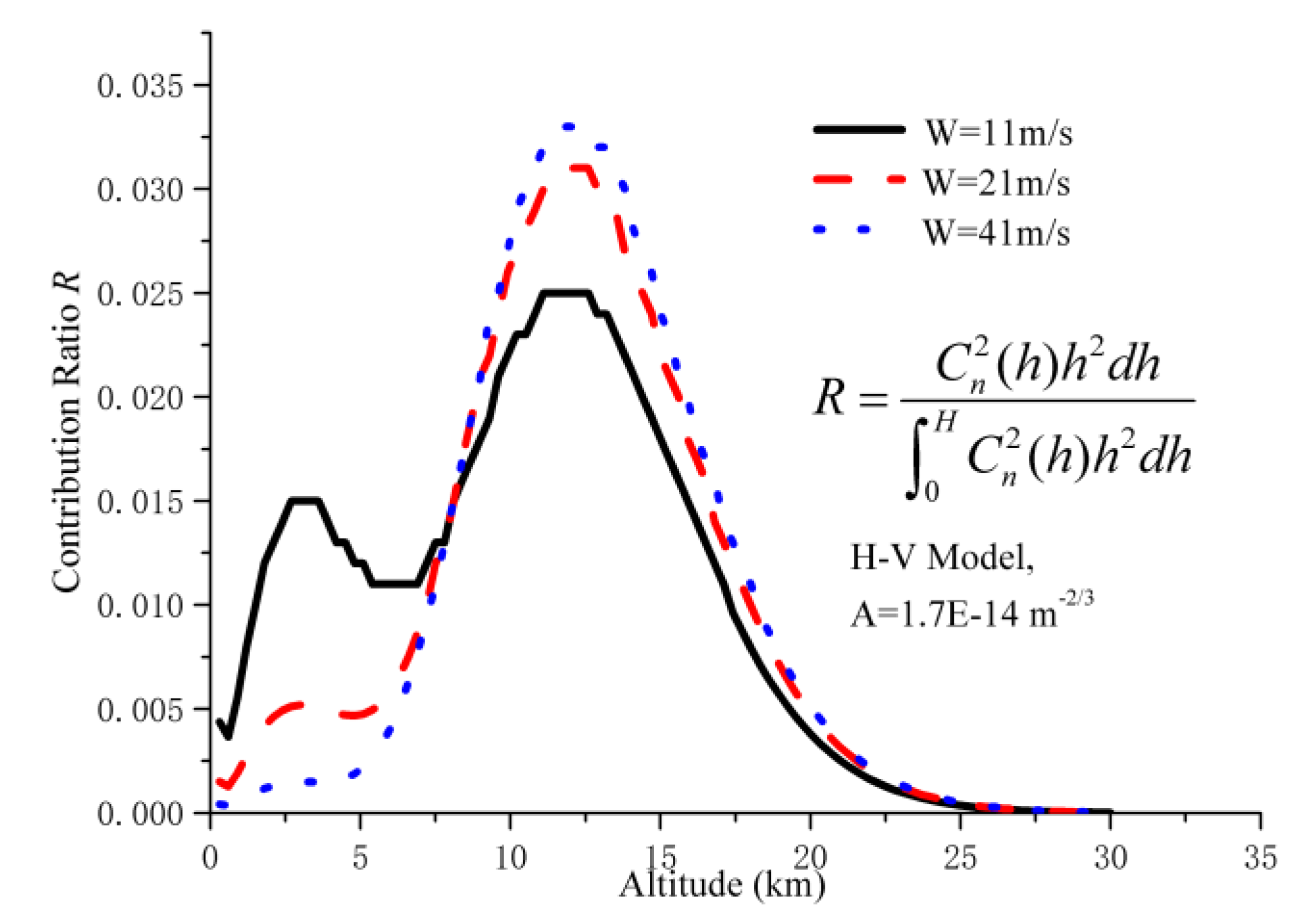
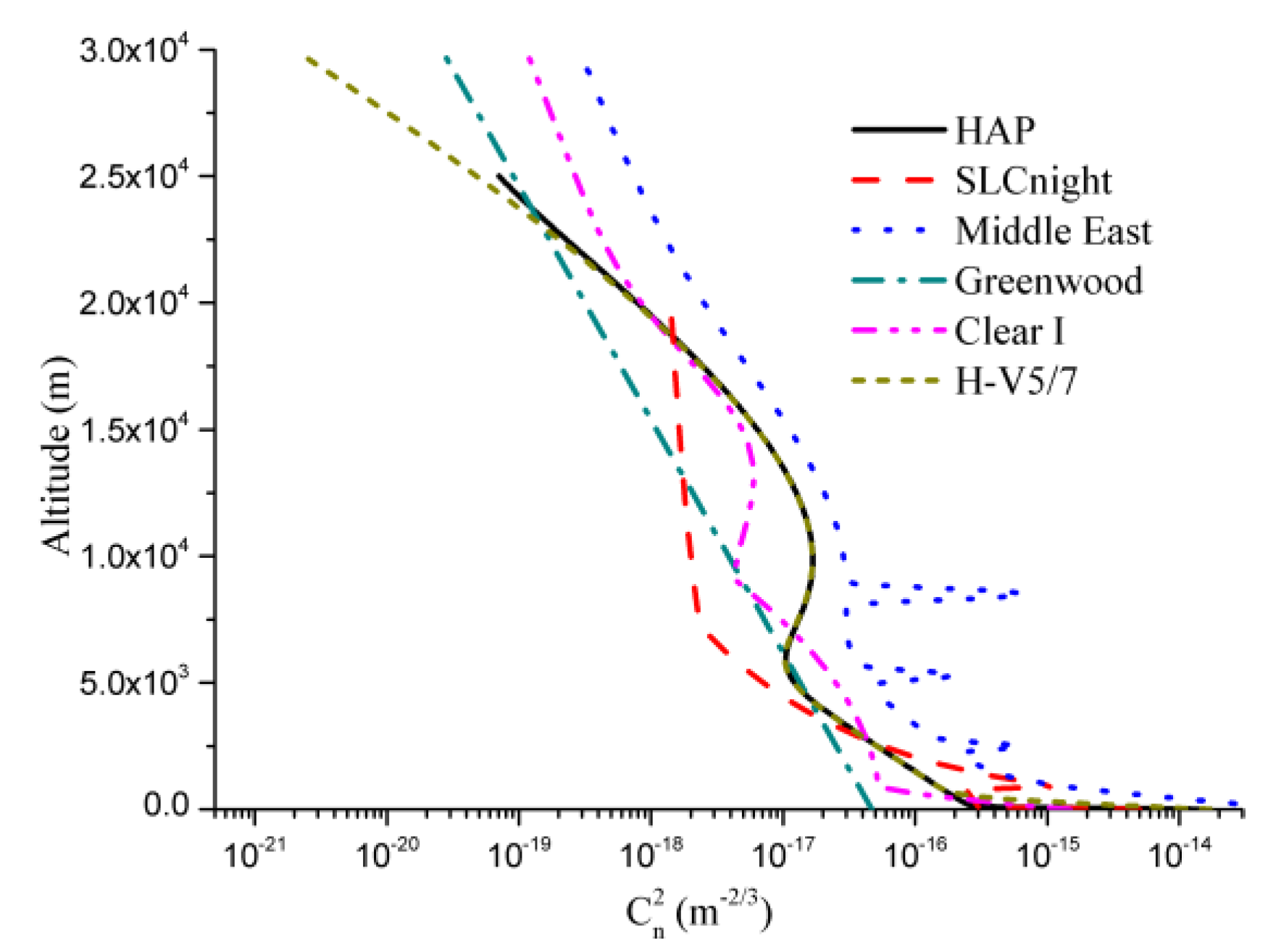
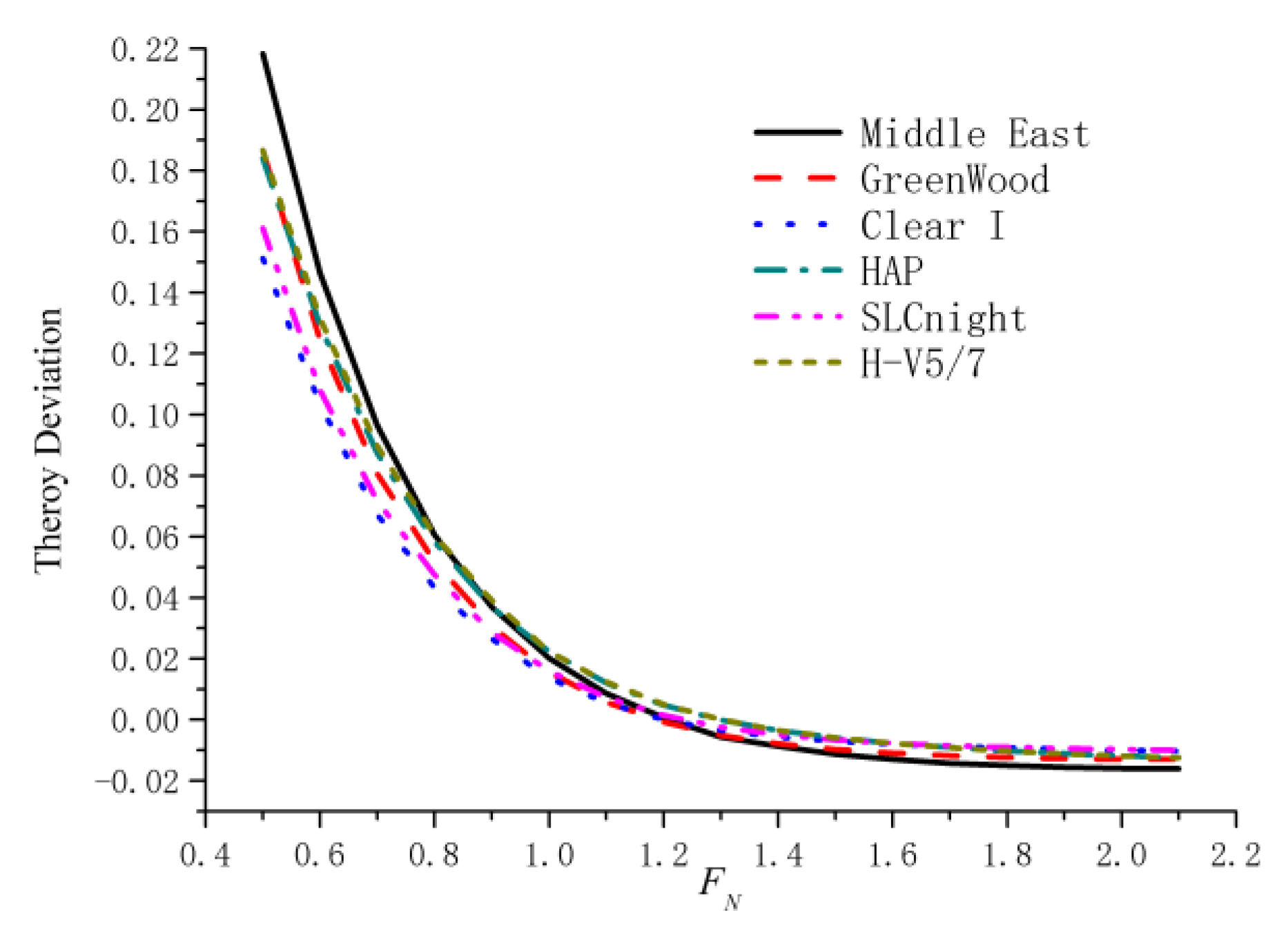
3. Numerical Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hardy, J.W. Adaptive Optics for Astronomical Telescopes; Oxford University Press: New York, NY, USA, 1998; pp. 98–268. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE Press: Bellingham, WA, USA, 2005; pp. 14–32. [Google Scholar]
- Sasiela, R.J. Electromagnetic Wave Propagation in Turbulence: Evaluation and Application of Mellin Transforms; SPIE Press: Bellingham, WA, USA, 2007; pp. 69–88. [Google Scholar]
- Roggemann, M.C.; Welsh, B.M.; Hunt, B.R. Imaging through Turbulence; CRC Press: London, UK; New York, NY, USA, 2018. [Google Scholar]
- Tyson, R.K. Principles of Adaptive Optics, 4th ed.; CRC Press: London, UK; New York, NY, USA, 2016; pp. 37–54. [Google Scholar]
- Olivier, S.S.; Max, C.E.; Gavel, D.T.; Brase, J.M. Tip-Tilt Compensation: Resolution Limits for Ground-based Telescopes Using Laser Guide Star Adaptive Optics. Astrophys. J. 1993, 407, 428–439. [Google Scholar] [CrossRef]
- Kaiser, N.; Tonry, J.L.; Luppino, G.A. A new strategy for deep wide-field high-resolution optical imaging. Publ. Astron. Soc. Pac. 2000, 112, 768–800. [Google Scholar] [CrossRef][Green Version]
- Sarazin, M.; Roddier, F. The ESO differential image motion monitor. Astron. Astrophys. 1990, 227, 294–300. [Google Scholar]
- Aristidi, E.; Agabi, A.; Fossat, E.; Azouit, M.; Martin, F.; Sadibekova, T.; Travouillon, T.; Vernin, J.; Ziad, A. Site testing in summer at Dome C., Antarctica. Astron. Astrophys. 2005, 444, 651–659. [Google Scholar] [CrossRef]
- Skidmore, W.; Els, S.; Travouillon, T.; Riddle, R.; Schöck, M.; Bustos, E.; Seguel, J.; Walker, D. Thirty Meter Telescope site testing V: Seeing and isoplanatic angle. Publ. Astron. Soc. Pac. 2009, 121, 1151–1166. [Google Scholar] [CrossRef]
- Kornilov, V.; Tokovinin, A.; Shatsky, N.; Voziakova, O.; Potanin, S.; Safonov, B. Combined MASS–DIMM instruments for atmospheric turbulence studies. Mon. Not. R. Astron. Soc. 2007, 382, 1268–1278. [Google Scholar] [CrossRef]
- Wilson, R.; Bate, J.; Guerra, J.C.; Hubin, N.; Sarazin, M.; Saunter, C. Development of a portable SLODAR turbulence profiler. Advancements in Adaptive Optics. In Proceedings of the SPIE Astronomical Telescopes and Instrumentation, Glasgow, UK, 25 October 2004. [Google Scholar] [CrossRef]
- Townson, M.J. Correlation Wavefront Sensing and Turbulence Profiling for Solar Adaptive Optics. Ph.D. Thesis, The University of Durham, Durham, UK, March 2016. [Google Scholar]
- Shikhovtsev, A.Y.; Kiselev, A.V.; Kovadlo, P.G.; Kolobov, D.Y.; Lukin, V.P.; Tomin, V.E. Method for Estimating the Altitudes of Atmospheric Layers with Strong Turbulence. Atmos. Ocean Opt. 2020, 33, 295–301. [Google Scholar] [CrossRef]
- Blary, F.; Ziad, A.; Borgnino, J.; Fanteï-Caujolle, Y.; Aristidi, E.; Lanteri, H. Monitoring atmospheric turbulence profiles with high vertical resolution using PML/PBL instrument. Ground-based and Airborne Telescopes V. In Proceedings of the SPIE Astronomical Telescopes and Instrumentation, Montréal, QC, Canada, 22 July 2014. [Google Scholar] [CrossRef]
- Kovadlo, P.G.; Shikhovtsev, A.Y.; Kopylov, E.A.; Kiselev, A.V.; Russkikh, I.V. Study of the Optical Atmospheric Distortions using Wavefront Sensor Data. Russ. Phys. J. 2021, 63, 1952–1958. [Google Scholar] [CrossRef]
- Tokovinin, A.A. Polychromatic scintillation. J. Opt. Soc. Am. A 2003, 20, 686–689. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.K.; Shen, H.; Jing, X.; Hou, Z.H. Study on the measurement of isoplanatic angle using stellar scintillation. Acta Optica Sinica 2014, 34, 0301001-1. [Google Scholar]
- Loos, G.C.; Hogge, C.B. Turbulence of the upper atmosphere and isoplanatism. Appl. Opt. 1979, 18, 2654–2661. [Google Scholar] [CrossRef] [PubMed]
- Smith, F.G. Atmospheric Propagation of Radiation; Infrared and Electro-Optical Systems Handbook; SPIE: Bellingham, WA, USA, 1993; p. 157. [Google Scholar]
- Andrews, L.C.; Phillips, R.L.; Wayne, D.; Leclerc, T.; Sauer, P.; Crabbs, R.; Kiriazes, J. Near-ground vertical profile of refractive-index fluctuations. Atmospheric Propagation VI. In Proceeding of the SPIE Defense Security and Sensing, Orlando, FL, USA, 30 April 2009. [Google Scholar] [CrossRef]
- Zilberman, A.; Kopeika, N.S. Middle East model of vertical turbulence profile. Atmospheric Propagation II. In Proceedings of the SPIE Defense and Security, Orlando, FL, USA, 25 May 2005. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, H.; Yu, L.; Jing, X.; Tan, F. Method for Measuring the Second-Order Moment of Atmospheric Turbulence. Atmosphere 2021, 12, 564. https://doi.org/10.3390/atmos12050564
Shen H, Yu L, Jing X, Tan F. Method for Measuring the Second-Order Moment of Atmospheric Turbulence. Atmosphere. 2021; 12(5):564. https://doi.org/10.3390/atmos12050564
Chicago/Turabian StyleShen, Hong, Longkun Yu, Xu Jing, and Fengfu Tan. 2021. "Method for Measuring the Second-Order Moment of Atmospheric Turbulence" Atmosphere 12, no. 5: 564. https://doi.org/10.3390/atmos12050564
APA StyleShen, H., Yu, L., Jing, X., & Tan, F. (2021). Method for Measuring the Second-Order Moment of Atmospheric Turbulence. Atmosphere, 12(5), 564. https://doi.org/10.3390/atmos12050564




