Variations in Wave Energy and Amplitudes along the Ray Paths of Barotropic Rossby Waves in Horizontally Non-Uniform Basic Flows
Abstract
1. Introduction
2. Wave Energy Equation in the Non-Uniform Basic Flow
3. Results
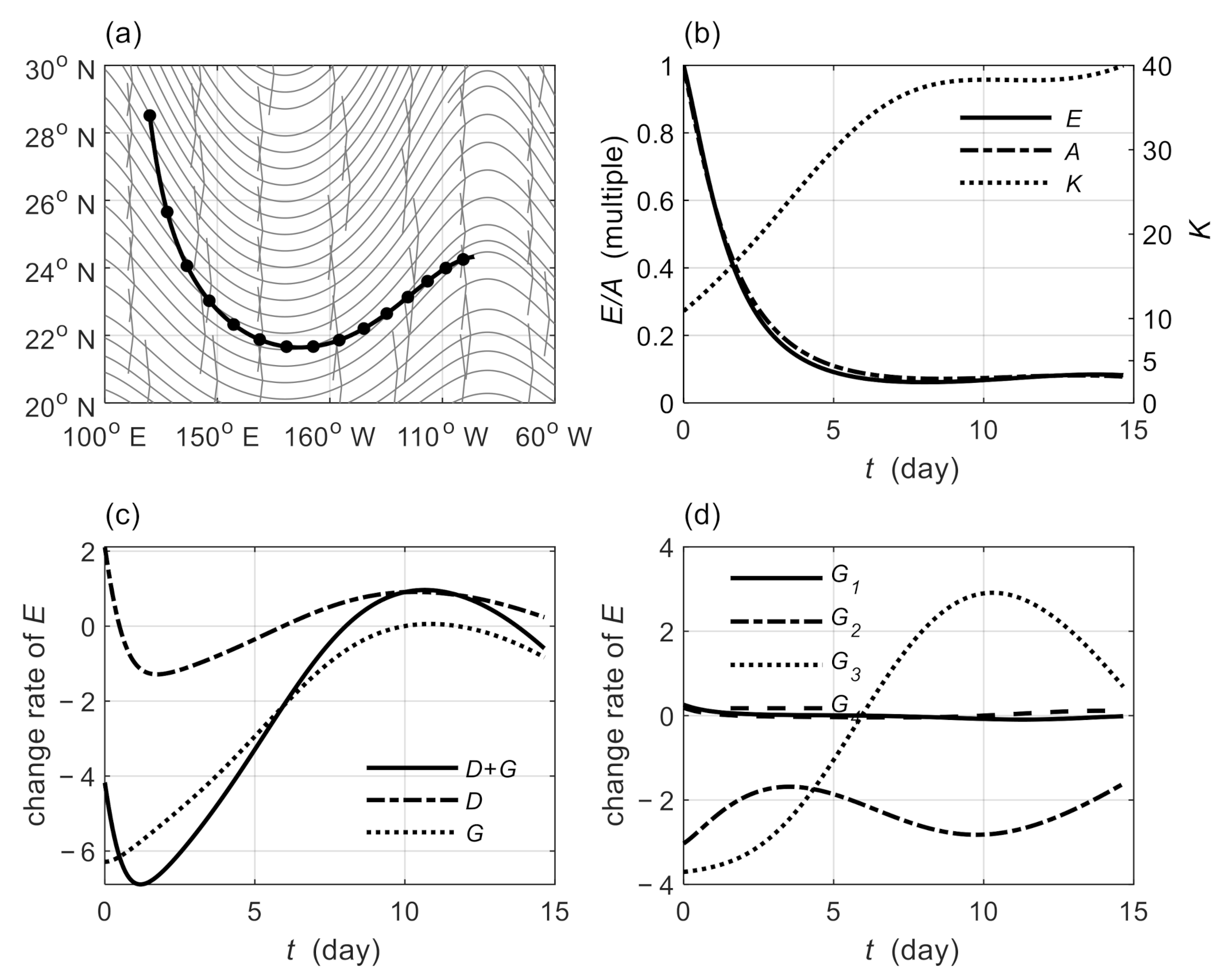
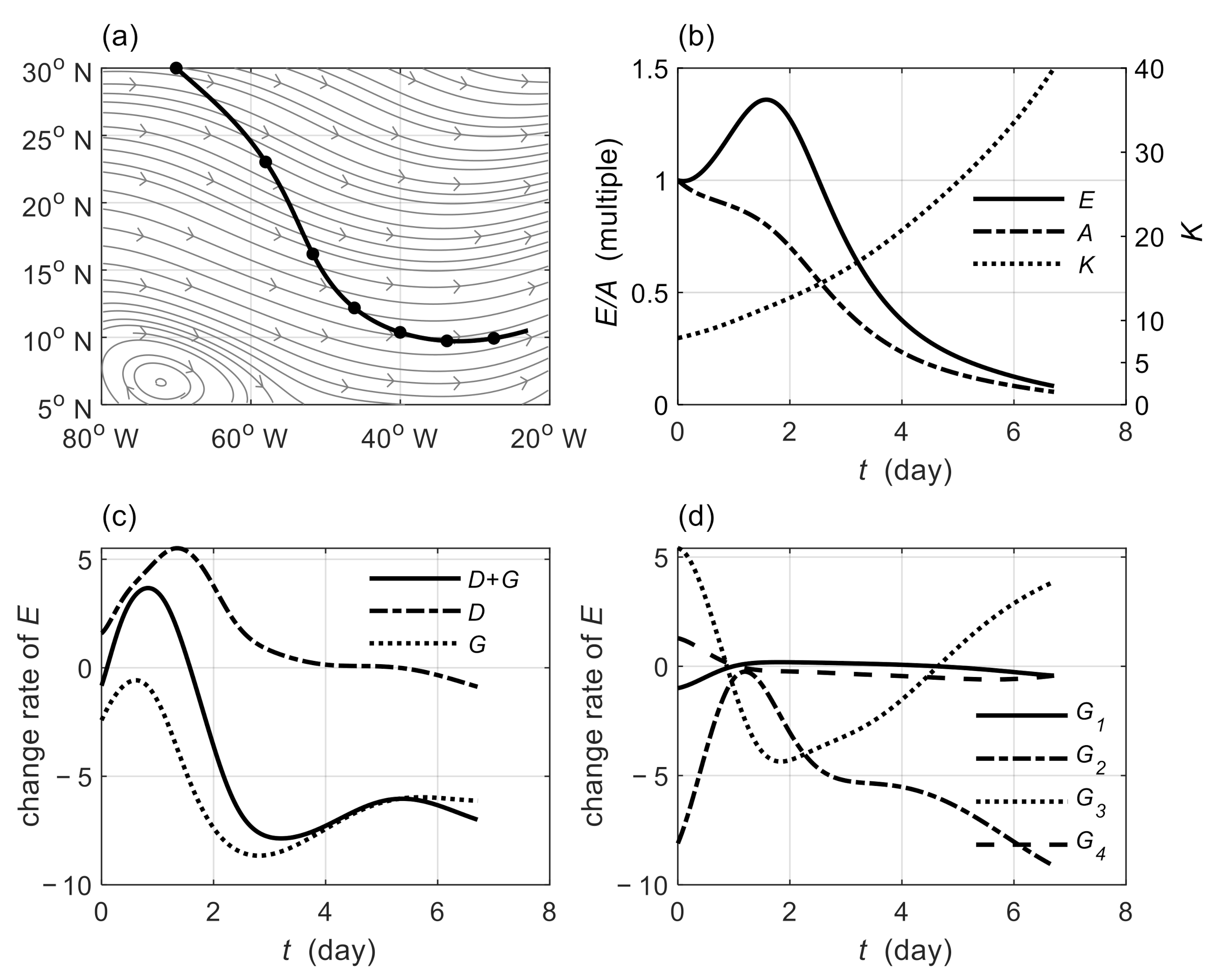
3.1. Analytical Horizontally Non-Uniform Basic Flow
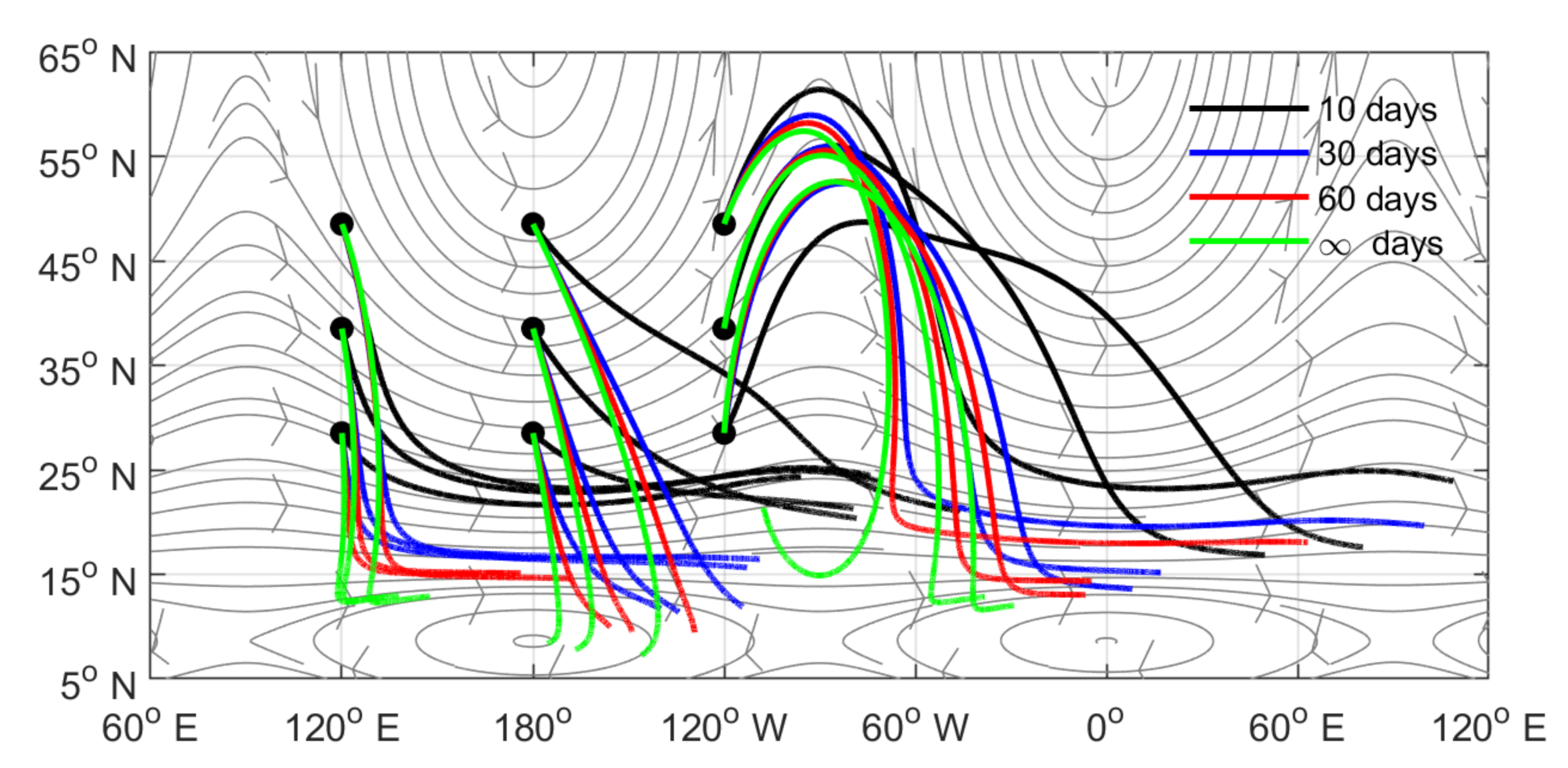
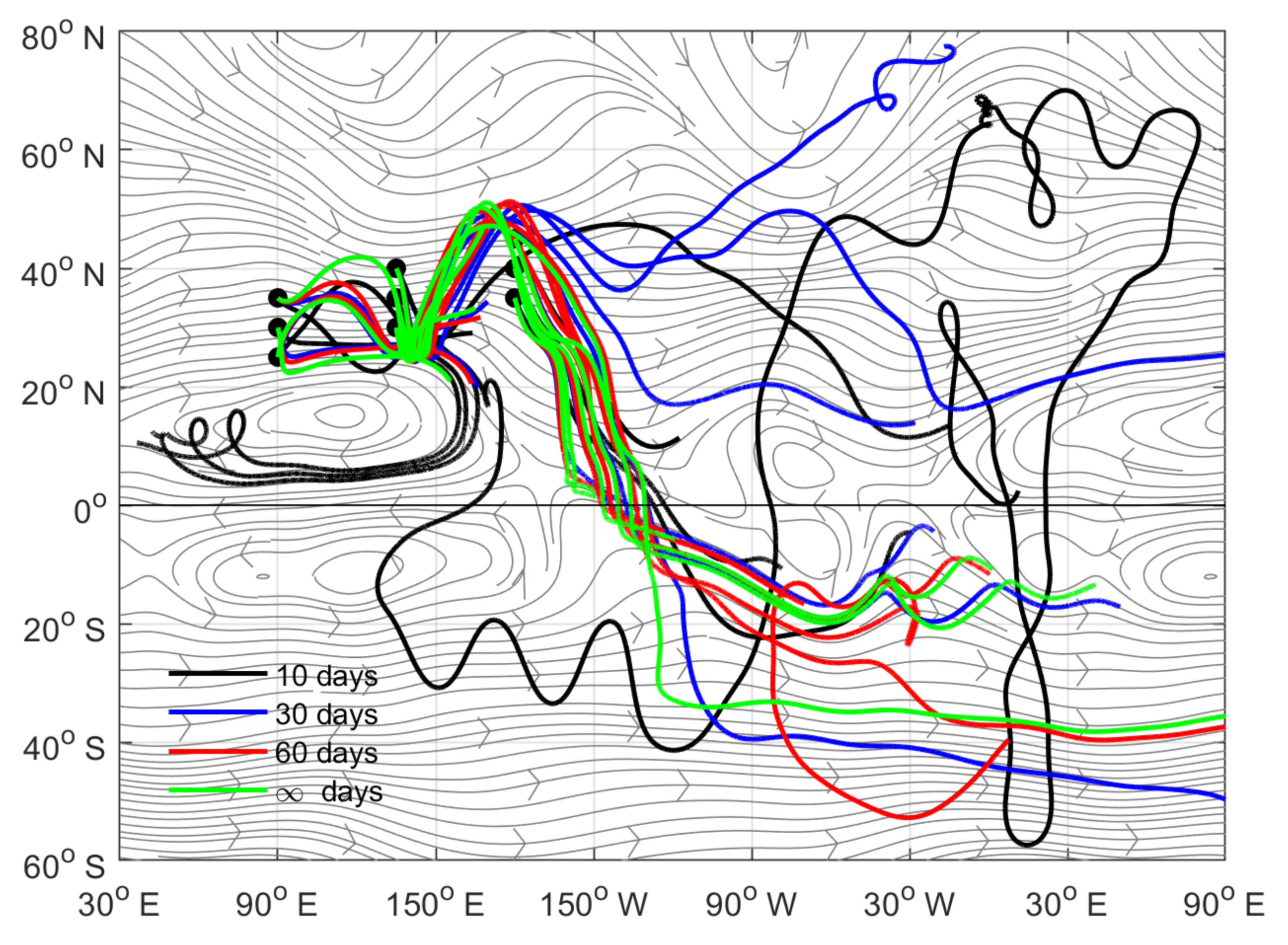
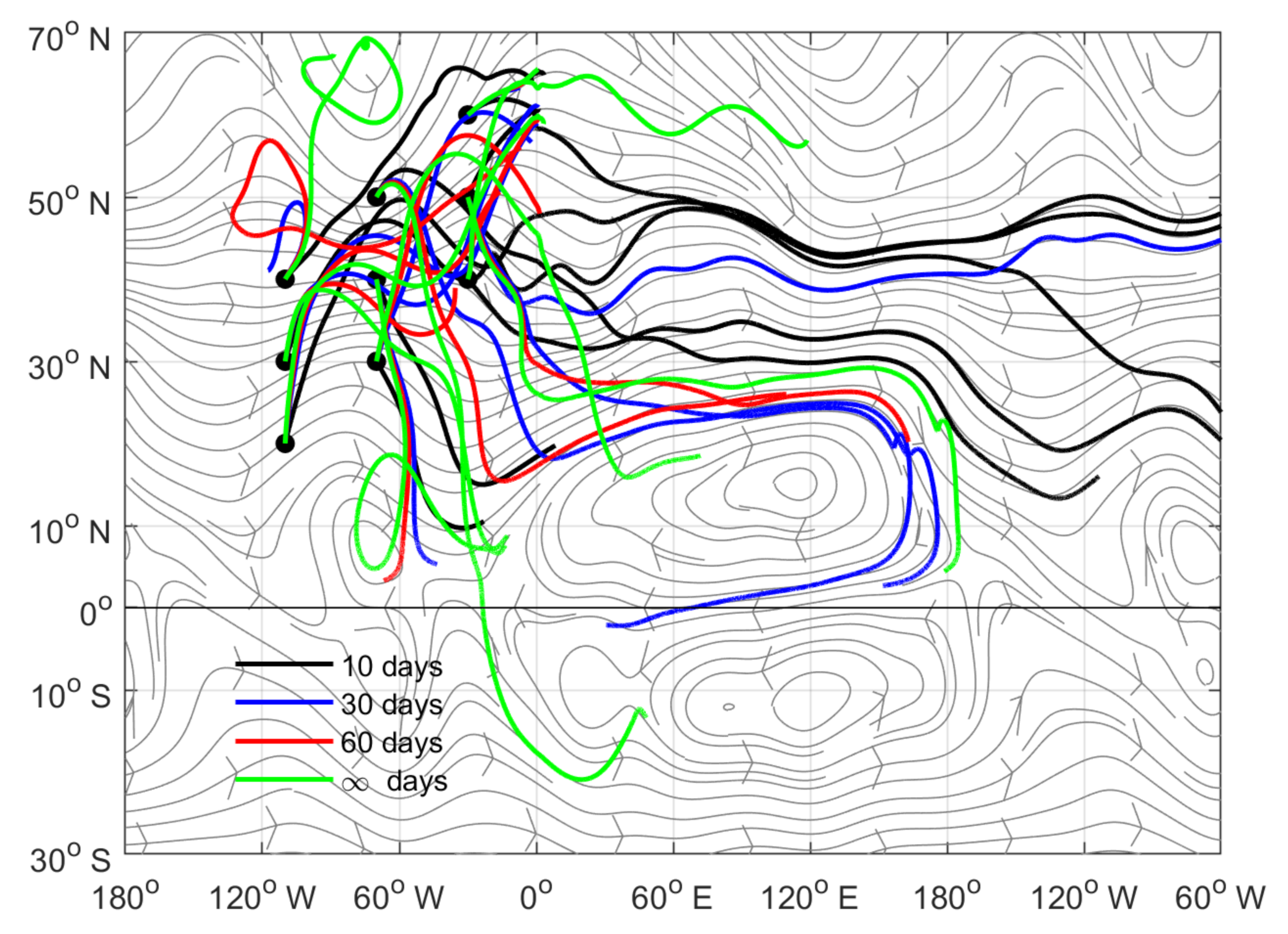
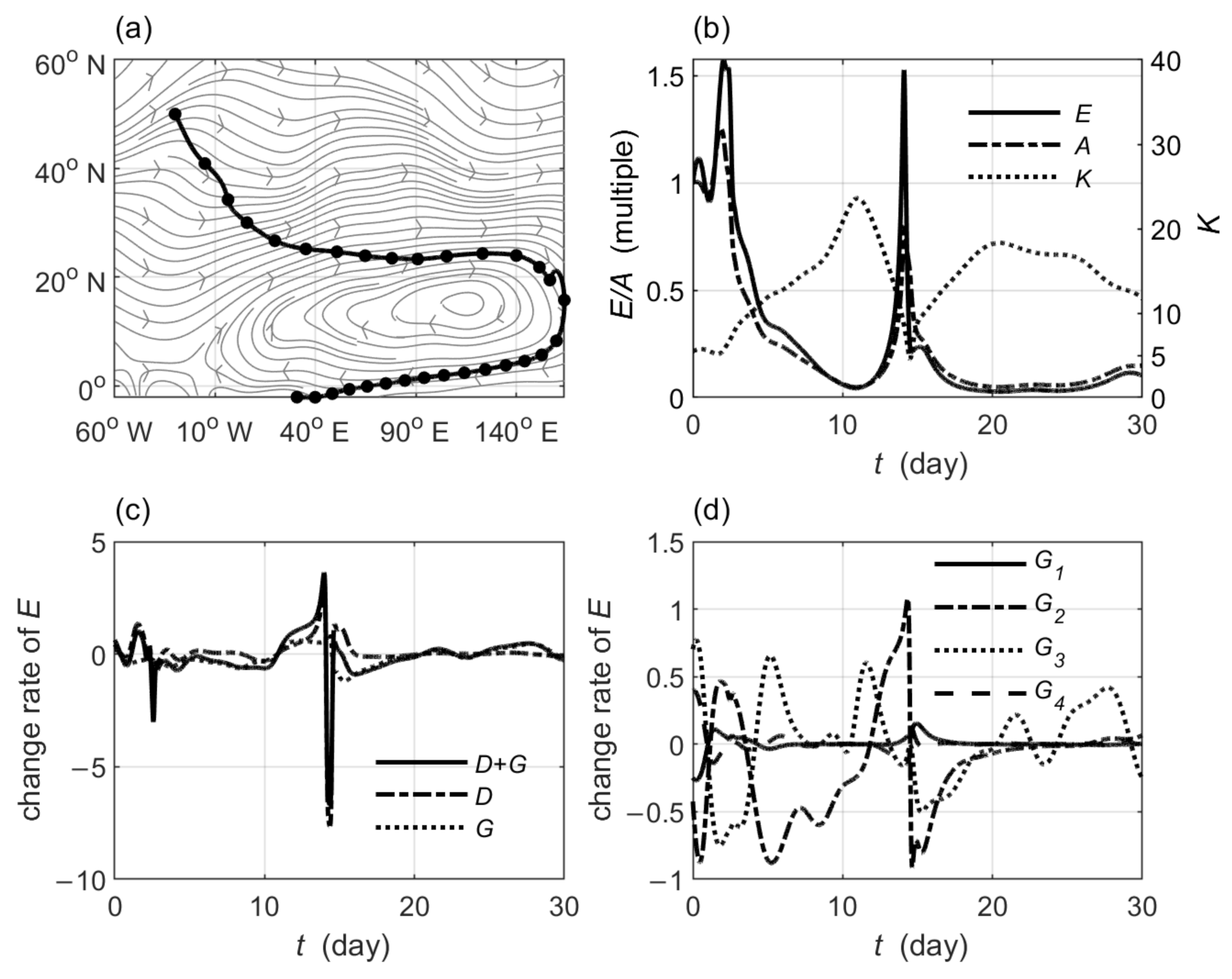
3.2. Observed Horizontally Non-Uniform Basic Flow
4. Conclusions
5. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Chelton, D.B.; Schlax, M.G. Global observations of oceanic rossby waves. Science 1996, 272, 234–238. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Albekioni, M.; Ballester, J.L.; Bekki, Y.; Biancofiore, L.; Birch, A.C.; Dikpati, M.; Gizon, L.; Gurgenashvili, E.; Heifetz, E.; et al. Rossby waves in astrophysics. Space Sci. Rev. 2021, 217, 1–93. [Google Scholar] [CrossRef]
- Yeh, T. On energy dispersion in the amtosphere. J. Meteorol. 1949, 6, 1–16. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. Planetary waves on a rotating sphere. R. Soc. Lond. Ser. A Math. Phys. Sci. 1964, 279, 446–473. [Google Scholar]
- Hoskins, B.J.; Karoly, D.J. The steady linear response of a spherical atmosphere to thermal and orographic forcing. J. Atmos. Sci. 1981, 38, 1179. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Ambrizzi, T. Rossby wave propagation on a realistic longitudinally varying flow. J. Atmos. Sci. 1993, 50, 1661–1671. [Google Scholar] [CrossRef]
- Li, L.; Nathan, T.R. The global atmospheric response to low-frequency tropical forcing: Zonally averaged basic states. J. Atmos. Sci. 1994, 51, 3412–3426. [Google Scholar] [CrossRef]
- Yang, G.; Hoskins, B.J. Propagation of rossby waves of nonzero frequency. J. Atmos. Sci. 1996, 53, 2365–2378. [Google Scholar] [CrossRef]
- Li, Y.; Chao, J.; Kang, Y. Variations in wave energy and amplitudes along the energy dispersion paths of nonstationary barotropic rossby waves. Adv. Atmos. Sci. 2021, 38, 49–64. [Google Scholar] [CrossRef]
- Ratnam, J.V.; Behera, S.K.; Yamagata, T. Role of cross-equatorial waves in maintaining long periods of low convective activity over Southern Africa. J. Atmos. Sci. 2015, 72, 682–692. [Google Scholar] [CrossRef]
- Liu, T.; Li, J.; Li, Y.; Zhao, S.; Zheng, F.; Zheng, J.; Yao, Z. Influence of the may southern annular mode on the South China Sea summer monsoon. Clim. Dyn. 2017, 51, 4095–4107. [Google Scholar] [CrossRef]
- Zhao, S.; Li, J.; Li, Y.; Jin, F.-F.; Zheng, J. Interhemispheric influence of Indo-Pacific convection oscillation on Southern Hemisphere rainfall through southward propagation of Rossby waves. Clim. Dyn. 2019, 52, 3203–3221. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Wagner, C.P.; Cartwright, T.J.; Oosterhof, D. Wave trains excited by cross-equatorial passage of the monsoon annual cycle. Mon. Weather Rev. 1997, 125, 2709–2715. [Google Scholar] [CrossRef]
- Lin, H. Global extratropical response to diabatic heating variability of the Asian summer monsoon. J. Atmos. Sci. 2009, 66, 2697–2713. [Google Scholar] [CrossRef]
- Li, Y.J.; Li, J.P. Propagation of planetary waves in the horizontal non-uniform basic flow. Chin. J. Geophys. 2012, 55, 361–371. (In Chinese) [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Jin, F.F.; Zhao, S. Interhemispheric propagation of stationary rossby waves in a horizontally nonuniform background flow. J. Atmos. Sci. 2015, 72, 3233–3256. [Google Scholar] [CrossRef]
- Karoly, D.J. Rossby wave propagation in a barotropic atmosphere. Dyn. Atmos. Ocean. 1983, 7, 111–125. [Google Scholar] [CrossRef]
- Li, L.; Nathan, T.R. Effects of low-frequency tropical forcing on intraseasonal tropical–extratropical interactions. J. Atmos. Sci. 1997, 54, 332–346. [Google Scholar] [CrossRef]
- Li, Y.; Feng, J.; Li, J.; Hu, A. Equatorial windows and barriers for stationary rossby wave propagation. J. Clim. 2019, 32, 6117–6135. [Google Scholar] [CrossRef]
- Lu, P.S.; Zeng, Q.C. On the evolution process of disturbances in the barotropic atmosphere. Chin. J. Atmos. Sci. 1981, 5, 1–8. (In Chinese) [Google Scholar]
- Bretherton, F.P.; Garrett, C.J.R. Wavetrains in inhomogeneous moving media. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 302, 529–554. [Google Scholar] [CrossRef]
- Whitham, G.B. A note on group velocity. J. Fluid Mech. 1960, 9, 347–352. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Chao, J.P. Conservation of wave action and development of spiral rossby waves. Sci. China Ser. B Earth Sci. 1983, 661–672. (In Chinese) [Google Scholar] [CrossRef]
- Young, W.R.; Rhines, P.B. Rossby wave action, enstrophy and energy in forced mean flows. Geophys. Astrophys. Fluid Dyn. 1980, 15, 39–52. [Google Scholar] [CrossRef]
- Plumb, R.A. Three-dimensional propagation of transient quasi-geostrophic eddies and its relationship with the eddy forcing of the time-mean flow. J. Atmos. Sci. 1986, 43, 1657–1678. [Google Scholar] [CrossRef]
- Lighthill, J. Waves in Fluids; Cambridge University Press: Cambridge, UK, 1978; pp. 317–325. [Google Scholar]
- Karoly, D.J.; Hoskins, B.J. Three dimensional propagation of planetary waves. J. Meteorol. Soc. Jpn. Ser. II 1982, 60, 109–123. [Google Scholar] [CrossRef]
- Schneider, E.K.; Watterson, I.G. Stationary rossby wave propagation through easterly layers. J. Atmos. Sci. 1984, 41, 2069–2083. [Google Scholar] [CrossRef][Green Version]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Besedina, Y.N.; Popel, S.I. Synoptic-scale cyclonic vortices and possible transport of fine particles from the troposphere into the stratosphere. Dokl. Earth Sci. 2008, 423, 1475–1478. [Google Scholar] [CrossRef]
- Hathaway, D.H.; Upton, L.A. Hydrodynamic properties of the sun’s giant cellular flows. arXiv 2020, arXiv:2006.06084. [Google Scholar]
- Dikpati, M.; Gilman, P.A.; Chatterjee, S.; McIntosh, S.W.; Zaqarashvili, T.V. Physics of magnetohydrodynamic rossby waves in the sun. Astrophys. J. 2020, 896, 141. [Google Scholar] [CrossRef]
- Dikpati, M.; McIntosh, S.W. Space weather challenge and forecasting implications of rossby waves. Space Weather 2020, 18. [Google Scholar] [CrossRef]
- Dikpati, M.; McIntosh, S.W.; Bothun, G.; Cally, P.S.; Ghosh, S.S.; Gilman, P.A.; Umurhan, O.M. Role of interaction between magnetic rossby waves and tachocline differential rotation in producing solar seasons. Astrophys. J. 2018, 853, 144. [Google Scholar] [CrossRef]
- Dikpati, M.; Cally, P.S.; McIntosh, S.W.; Heifetz, E. The origin of the “seasons” in space weather. Sci. Rep. 2017, 7, 1–7. [Google Scholar] [CrossRef]
- Dikpati, M.; Belucz, B.; Gilman, P.A.; McIntosh, S.W. Phase speed of magnetized rossby waves that cause solar seasons. Astrophys. J. 2018, 862, 159. [Google Scholar] [CrossRef]
- Dikpati, M. Nonlinear evolution of global hydrodynamic shallow-water instability in the solar tachocline. Astrophys. J. 2012, 745, 128. [Google Scholar] [CrossRef]
- Tissot, G.; Lajús, F.C., Jr.; Cavalieri, A.V.; Jordan, P. Wave packets and Orr mechanism in turbulent jets. Phys. Rev. Fluids 2017, 2. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Chao, J.; Kang, Y. Variations in Wave Energy and Amplitudes along the Ray Paths of Barotropic Rossby Waves in Horizontally Non-Uniform Basic Flows. Atmosphere 2021, 12, 458. https://doi.org/10.3390/atmos12040458
Li Y, Chao J, Kang Y. Variations in Wave Energy and Amplitudes along the Ray Paths of Barotropic Rossby Waves in Horizontally Non-Uniform Basic Flows. Atmosphere. 2021; 12(4):458. https://doi.org/10.3390/atmos12040458
Chicago/Turabian StyleLi, Yaokun, Jiping Chao, and Yanyan Kang. 2021. "Variations in Wave Energy and Amplitudes along the Ray Paths of Barotropic Rossby Waves in Horizontally Non-Uniform Basic Flows" Atmosphere 12, no. 4: 458. https://doi.org/10.3390/atmos12040458
APA StyleLi, Y., Chao, J., & Kang, Y. (2021). Variations in Wave Energy and Amplitudes along the Ray Paths of Barotropic Rossby Waves in Horizontally Non-Uniform Basic Flows. Atmosphere, 12(4), 458. https://doi.org/10.3390/atmos12040458





